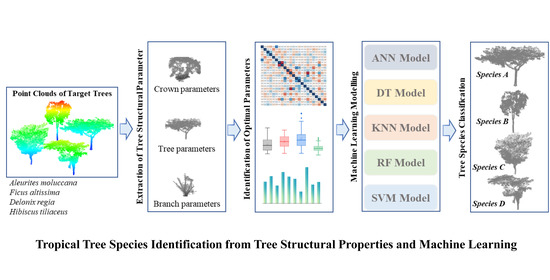
Tropical Species Classification with Structural Traits Using Handheld Laser Scanning Data
Abstract
1. Introduction
2. Research Site and Data and Methods
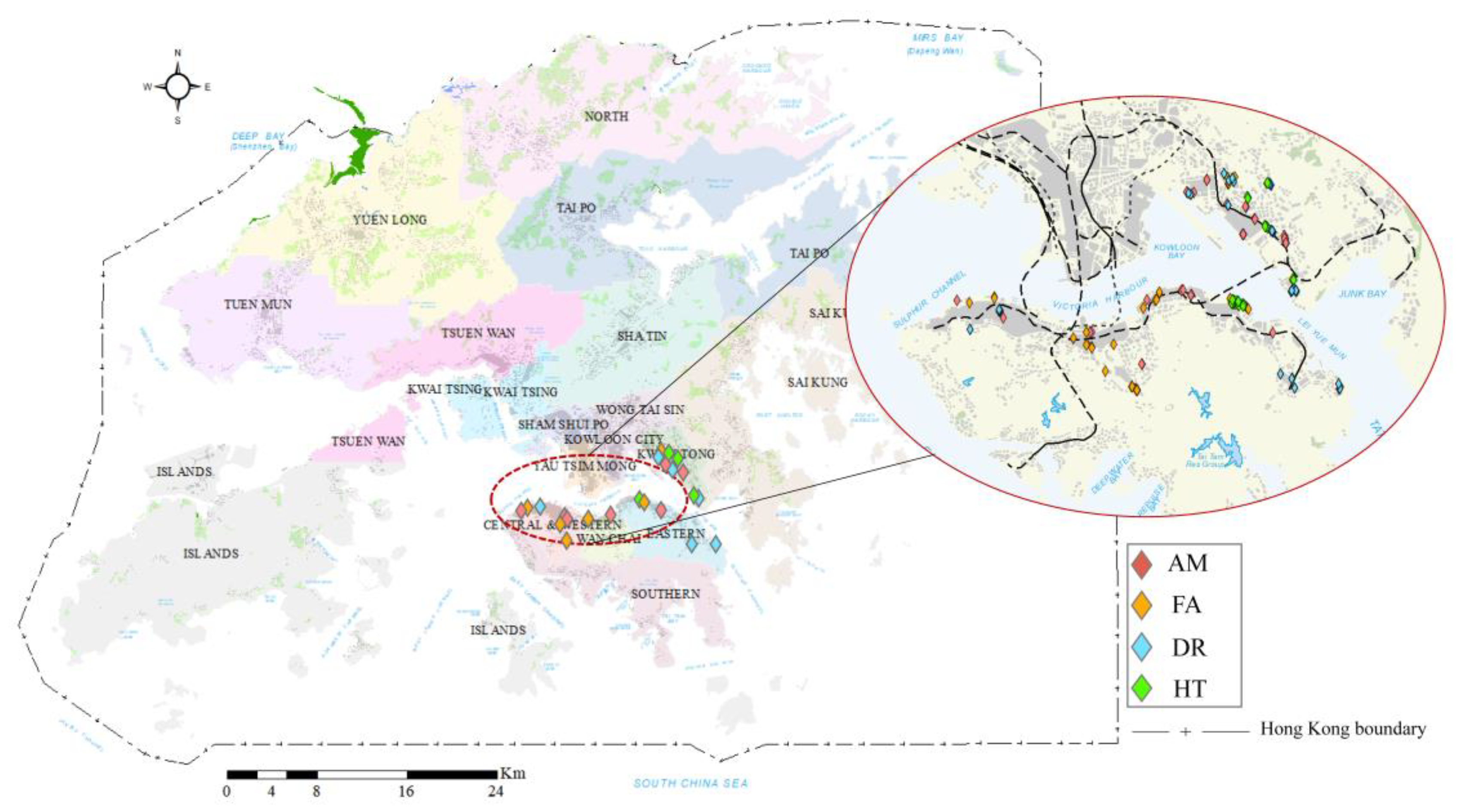
2.1. Research Area and Tree Species
2.2. Data Collection and Preprocessing
3. Research Methodology
3.1. Separation of Tree Components
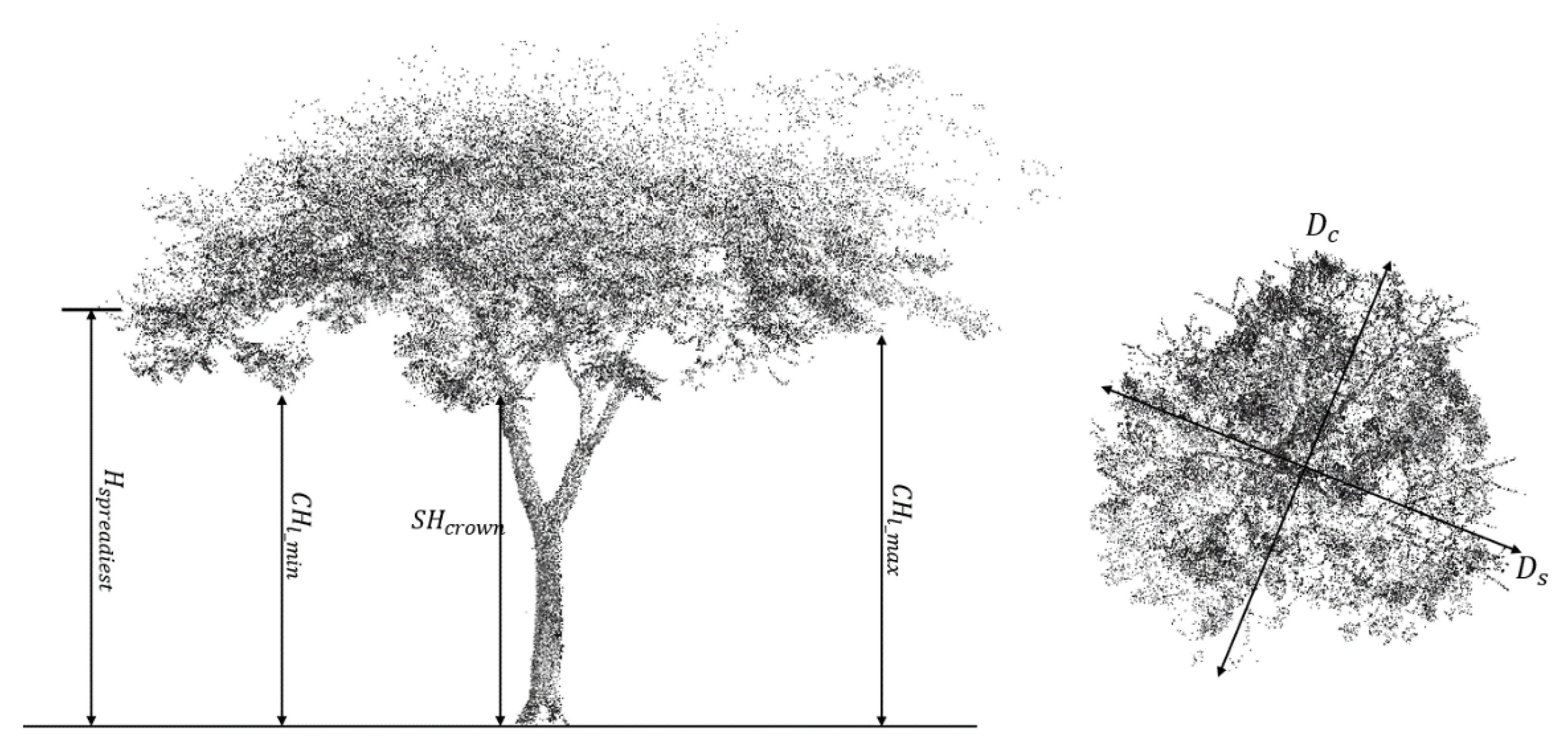
3.2. Derivation of Structural Parameters
3.3. Species Classification Approach
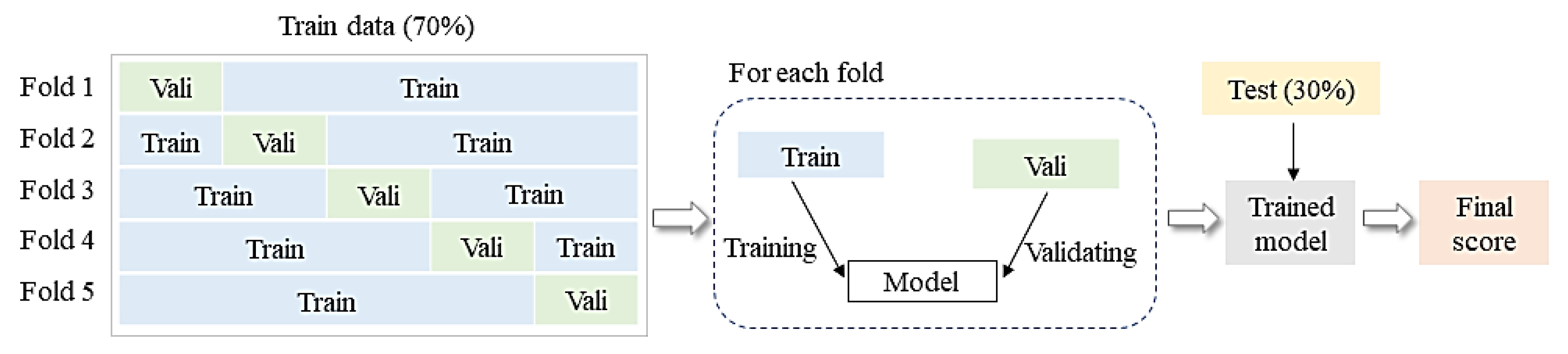
3.4. Assessment of Classification Results and Structural Parameters Importance
4. Results
4.1. Derived Structural Parameters
4.2. Correlations Analysis Results
4.3. Species Classification Results
4.3.1. Ability of Single Parameters for Species Classification
4.3.2. Ability of Parameter Sets in Species Classification
4.4. Optimal Parameter Sets
5. Discussion
5.1. Influences and Limitations
5.2. Applicability Analysis
5.3. Potential Improvements
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chai, Y.; Zhu, N.; Han, H. Dust removal effect of urban tree species in Harbin. Ying Yong Sheng Tai Xue Bao J. Appl. Ecol. 2002, 13, 1121–1126. [Google Scholar]
- Rahman, M.A.; Armson, D.; Ennos, A.R. A comparison of the growth and cooling effectiveness of five commonly planted urban tree species. Urban. Ecosyst. 2015, 18, 371–389. [Google Scholar] [CrossRef]
- Wong, M.S.; Nichol, J.; Kwok, K.H. The urban heat island in Hong Kong: Causative factors and scenario analysis. In Proceedings of the 2009 Joint Urban Remote Sensing Event, Shanghai, China, 20–22 May 2009. [Google Scholar]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban tree species mapping using hyperspectral and lidar data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- Pu, R.; Landry, S. A comparative analysis of high spatial resolution IKONOS and WorldView-2 imagery for mapping urban tree species. Remote Sens. Environ. 2012, 124, 516–533. [Google Scholar] [CrossRef]
- Collis, R. Lidar. Appl. Optics. 1970, 9, 1782–1788. [Google Scholar] [CrossRef] [PubMed]
- Dong, P.; Chen, Q. LiDAR Remote Sensing and Applications; CRC Press: Boca Raton, FL, USA, 2017; pp. 60–108. [Google Scholar]
- Dubayah, R.O.; Drake, J.B. Lidar remote sensing for forestry. J. Forest. 2000, 98, 44–46. [Google Scholar]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog Phys. Geog. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, J.; Tao, S.; Xue, B.; Li, L.; Xu, G.; Li, W.; Wu, G.; Li, Y.; Chen, L.; et al. Perspectives and prospects of LiDAR in forest ecosystem monitoring and modeling. Chin. Sci. Bull. 2014, 59, 459–478. [Google Scholar]
- Silva, C.; Hudak, A.; Rowell, E.; Seielstad, C.; Klauberg, C.; Bright, B.; Loudermilk, E.L.; O’Brien, J.J. Comparison of terrestrial and airborne LiDAR derived crown metrics for describing forest structure at Eglin Air Force Base, Florida, USA. In Proceedings of the 2017 ESA Annual Meeting, Portland, OR, USA, 6–11 August 2017. [Google Scholar]
- Tao, S.; Labrière, N.; Calders, K.; Fischer, F.J.; Rau, E.P.; Plaisance, L.; Chave, J. Mapping tropical forest trees across large areas with lightweight cost-effective terrestrial laser scanning. Ann. Forest Sci. 2021, 78, 103. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest inventory with terrestrial LiDAR: A comparison of static and hand-held mobile laser scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Lin, Y.; Herold, M. Tree species classification based on explicit tree structure feature parameters derived from static terrestrial laser scanning data. Agric. For. Meteorol. 2016, 216, 105–114. [Google Scholar] [CrossRef]
- Ryding, J.; Williams, E.; Smith, M.J.; Eichhorn, M.P. Assessing handheld mobile laser scanners for forest surveys. Remote Sens. 2015, 7, 1095–1111. [Google Scholar] [CrossRef]
- Stal, C.; Verbeurgt, J.; Sloover, L.D.; Wulf, A.D. Assessment of handheld mobile terrestrial laser scanning for estimating tree parameters. J. For. Res. 2020, 32, 1503–1513. [Google Scholar] [CrossRef]
- Vatandaşlar, C.; Zeybek, M. Application of handheld laser scanning technology for forest inventory purposes in the NE Turkey. Turk. J. Agri. For. 2020, 44, 229–242. [Google Scholar] [CrossRef]
- Lindquist, E.J.; D’Annunzio, R.; Gerrand, A.; MacDicken, K.; Achard, F.; Beuchle, R.; Brink, A.; Eva, H.D.; Mayaux, P.; San-Miguel-Ayanz, J.; et al. Global Forest Land-Use Change 1990–2005; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2012; p. 169. [Google Scholar]
- Åkerblom, M.; Raumonen, P.; Mäkipää, R.; Kaasalainen, M. Automatic tree species recognition with quantitative structure models. Remote Sens. Environ. 2017, 191, 1–12. [Google Scholar] [CrossRef]
- Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
- Gov, H.K. The Natural Environment, Plants & Animals in Hong Kong. Nature Conservation. November 2021. Available online: https://www.gov.hk/en/residents/environment/conservation/naturalenvplantsanimals.htm (accessed on 22 January 2022).
- Jim, C. Roadside trees in urban Hong Kong: Part II species coomposition. Arboric J. 1996, 20, 279–298. [Google Scholar] [CrossRef]
- Jim, C. Tree–habitat relationships in urban Hong Kong. Environ. Conserv. 1992, 19, 209–218. [Google Scholar] [CrossRef]
- Kuuluvainen, T. Tree architectures adapted to efficient light utilization: Is there a basis for latitudinal gradients? Oikos 1992, 65, 275–284. [Google Scholar] [CrossRef]
- Lindh, M.; Falster, D.S.; Zhang, L.; Dieckmann, U.; Brännström, Å. Latitudinal effects on crown shape evolution. Ecol. Evol. 2018, 8, 8149–8158. [Google Scholar] [CrossRef]
- Barrie, F.R.; Buck, W.R.; Demoulin, V.; Greuter, W.; Hawksworth, D.L.; Herendeen, P.S.; Knapp, S.; Marhold, K.; Prado, J.; Prudhomme, V.R.W.F.; et al. International Code of Nomenclature for Algae, Fungi and Plants (Melbourne Code); Koeltz Scientific Books: Königstein, Germany, 2012. [Google Scholar]
- Howes, F.N. Nuts, Their Production and Everyday Uses; Faber and Faber: London, UK, 1948. [Google Scholar]
- Cooper, W.; Cooper, W.T. Fruits of the Australian Tropical Rainforest; Nokomis Editions: Buxton, Australia, 2004. [Google Scholar]
- Nadel, H.; Frank, J.H.; Knight, J.R. Escapees and accomplices: The naturalization of exotic Ficus and their associated faunas in Florida. Fla Entomol. 1992, 75, 29–38. [Google Scholar] [CrossRef]
- Dressler, S.; Schmidt, M.; Zizka, G. Introducing African Plants—A photo guide—An interactive photo database and rapid identification tool for continental Africa. Taxon 2014, 63, 1159–1164. [Google Scholar] [CrossRef]
- Little, E.L. Common Forest Trees of Hawaii: Native and Introduced; US Department of Agriculture: North Bend, WA, USA, 1989.
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm Eng. Rem. S. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Nurunnabi, A.; Sadahiro, Y.; Lindenbergh, R.; Belton, D. Robust cylinder fitting in laser scanning point cloud data. Measurement 2019, 138, 632–651. [Google Scholar] [CrossRef]
- Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and wood classification framework for terrestrial LiDAR point clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Sapiro, G. Three-dimensional point cloud recognition via distributions of geometric distances. Graph. Models 2009, 71, 22–31. [Google Scholar] [CrossRef]
- Raumonen, P.; Casella, E.; Calders, K.; Murphy, S.; Åkerblom, M.; Kaasalainen, M. Massive-scale tree modelling from TLS data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 189–196. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Halloy, S. A morphological classification of plants, with special reference to the New Zealand alpine flora. J. Veg Sci. 1990, 1, 291–304. [Google Scholar] [CrossRef]
- Dansereau, P.; Arros, J. Essais d’application de la dimension structurale en phytosociologie. I. Quel ques exemples Europeens. Vegetatio 1959, 9, 48–99. [Google Scholar] [CrossRef]
- Orshan, G.; Roux, A.L.; Montenegro, G. Distribution of monocharacter growth form types in mediterranean plant communities of Chile, South Africa and Israel. Bull. De La Société Bot. De France. Actual. Botaniques. 1984, 131, 427–439. [Google Scholar] [CrossRef][Green Version]
- Terryn, L.; Calders, K.; Disney, M.; Origo, N.; Malhi, Y.; Newnham, G.; Raumonen, P.; Åkerblom, M.; Verbeeck, H. Tree species classification using structural features derived from terrestrial laser scanning. ISPRS J. Photogramm. 2020, 168, 170–181. [Google Scholar] [CrossRef]
- Wei, T.; Lin, Y.; Yan, L.; Zhang, L. Tree species classification based on stem-related feature parameters derived from static terrestrial laser scanning data. Int. J. Remote Sens. 2016, 37, 4420–4440. [Google Scholar] [CrossRef]
- Colaço, A.F.; Trevisan, R.G.; Molin, J.P.; Rosell-Polo, J.R. A method to obtain orange crop geometry information using a mobile terrestrial laser scanner and 3D modeling. Remote Sens. 2017, 9, 763. [Google Scholar] [CrossRef]
- Di Gennaro, S.F.; Matese, A. Evaluation of novel precision viticulture tool for canopy biomass estimation and missing plant detection based on 2.5 D and 3D approaches using RGB images acquired by UAV platform. Plant. Methods 2020, 16, 91. [Google Scholar] [CrossRef]
- Brandtberg, T. Classifying individual tree species under leaf-off and leaf-on conditions using airborne lidar. ISPRS J. Photogramm. Remote Sens. 2007, 61, 325–340. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin, Germany, 2009; pp. 1–4. [Google Scholar]
- Naidoo, L.; Cho, M.A.; Mathieu, R.; Asner, G. Classification of savanna tree species, in the Greater Kruger National Park region, by integrating hyperspectral and LiDAR data in a Random Forest data mining environment. ISPRS J. Photogramm. 2012, 69, 167–179. [Google Scholar] [CrossRef]
- Xi, Z.; Hopkinson, C.; Rood, S.; Peddle, D. See the forest and the trees: Effective machine and deep learning algorithms for wood filtering and tree species classification from terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2020, 168, 1–16. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, L.; Suganthan, P.N. Ensemble classification and regression-recent developments, applications and future directions. IEEE Comput. Intell. Mag. 2016, 11, 41–53. [Google Scholar] [CrossRef]
- Agatonovic-Kustrin, S.; Beresford, R. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. 2000, 22, 717–727. [Google Scholar] [CrossRef]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Ho, T.K. A data complexity analysis of comparative advantages of decision forest constructors. Pattern Anal. Appl. 2002, 5, 102–112. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. Rev. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Chang, Y.W.; Hsieh, C.J.; Chang, K.W.; Ringgaard, M.; Lin, C.J. Training and testing low-degree polynomial data mappings via linear SVM. J. Mach. Learn. Res. 2010, 11, 1471–1490. [Google Scholar]
- Howley, T.; Madden, M.G. The genetic kernel support vector machine: Description and evaluation. Artif. Intell. Rev. 2005, 24, 379–395. [Google Scholar] [CrossRef]
- Othmani, A.; Piboule, A.; Dalmau, O.; Lomenie, N.; Mokrani, S.; Voon, L.F.C.L.Y. Tree species classification based on 3D bark texture analysis. In Pacific-Rim Symposium on Image and Video Technology; Springer: Berlin, Germany, 2013; pp. 279–289. [Google Scholar]
- Calders, K.; Disney, M.; Nightingale, J.; Origo, N.; Barker, A.; Raumonen, P.; Lewis, P.; Burt, A.; Brennan, J.; Fox, N. Traceability of essential climate variables through forest stand reconstruction with terrestrial laser scanning. In Proceedings of the SilviLaser 2015, La Grande Motte, France, 28–30 September 2015. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Zhang, J.; Rivard, B.; Sánchez-Azofeifa, A.; Castro-Esau, K. Intra-and inter-class spectral variability of tropical tree species at La Selva, Costa Rica: Implications for species identification using HYDICE imagery. Remote Sens. Environ. 2006, 105, 129–141. [Google Scholar] [CrossRef]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef]
- Shi, Y.; Skidmore, A.K.; Wang, T.; Holzwarth, S.; Heiden, U.; Pinnel, N.; Zhu, X.; Heurich, M. Tree species classification using plant functional traits from LiDAR and hyperspectral data. Int. J. Appl. Earth Obs. 2018, 73, 207–219. [Google Scholar] [CrossRef]
- MacFarlane, D.W.; Kane, B. Neighbour effects on tree architecture: Functional trade-offs balancing crown competitiveness with wind resistance. Funct. Ecol. 2017, 31, 1624–1636. [Google Scholar] [CrossRef]
- Aiba, M.; Nakashizuka, T. Architectural differences associated with adult stature and wood density in 30 temperate tree species. Funct. Ecol. 2009, 23, 265–273. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random Forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Kohyama, T.; Suzuki, E.; Partomihardjo, T.; Yamada, T.; Kubo, T. Tree species differentiation in growth, recruitment and allometry in relation to maximum height in a Bornean mixed dipterocarp forest. J. Ecol. 2003, 91, 797–806. [Google Scholar] [CrossRef]
- Poorter, L.; Bongers, L.; Bongers, F. Architecture of 54 moist-forest tree species: Traits, trade-offs, and functional groups. Ecology 2006, 87, 1289–1301. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, X. Object-based tree species classification using airborne hyperspectral images and LiDAR data. Forests 2020, 11, 32. [Google Scholar] [CrossRef]

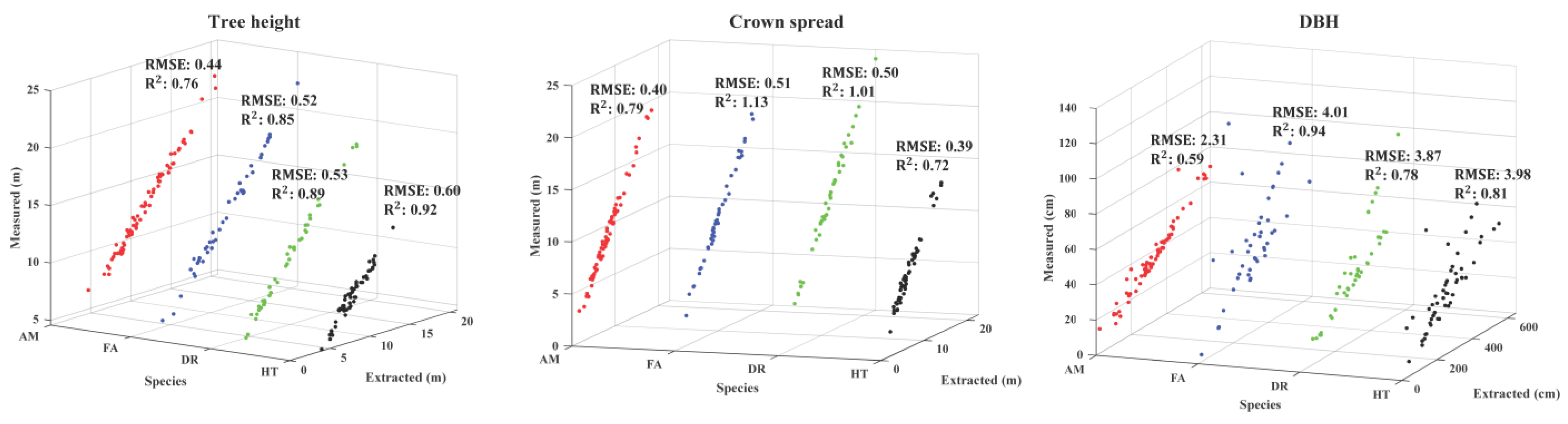



| Species | Number | Structure Information | |||
|---|---|---|---|---|---|
| Mean | Max | Min | |||
| AM | 63 | TH (m) | 13.27 | 21.27 | 7.458 |
| CS (m) | 9.02 | 15.35 | 4.68 | ||
| DBH (cm) | 35.29 | 58.92 | 21.38 | ||
| FA | 53 | TH (m) | 12.96 | 19.53 | 5.31 |
| CS (m) | 10.79 | 18.72 | 4.74 | ||
| DBH (cm) | 31.16 | 65.80 | 26.01 | ||
| DR | 52 | TH (m) | 10.76 | 18.33 | 5.84 |
| CS (m) | 11.47 | 21.75 | 4.65 | ||
| DBH (cm) | 23.86 | 30.44 | 13.61 | ||
| HT | 57 | TH (m) | 9.55 | 13.12 | 4.74 |
| CS (m) | 7.37 | 13.71 | 3.48 | ||
| DBH (cm) | 28.46 | 46.50 | 22.31 | ||
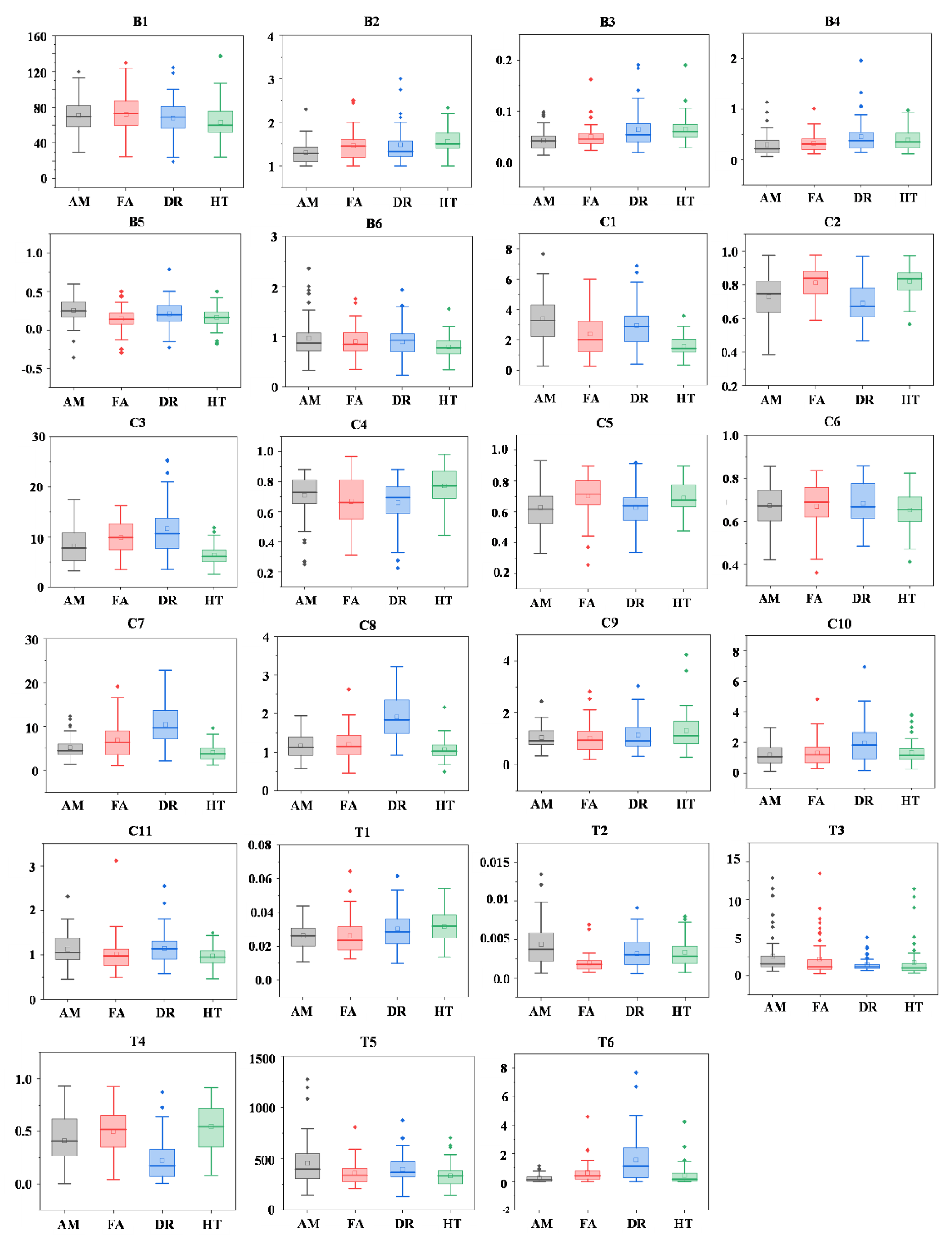
| Type | No. | Definition | Formula |
|---|---|---|---|
| Branch | B1 | Stem branch angle | |
| B2 | Stem branch cluster size | ||
| B3 | Stem branch radius | ||
| B4 | Stem branch length | ||
| B5 | Stem branch distance | ||
| B6 | Average of ratio between angles of first branches and second branches | ||
| Entire tree | T1 | Ratio between DBH and tree height | |
| T2 | Ratio between DBH and tree volume | ||
| T3 | Ratio between DBH and minimum stem radius | ||
| T4 | Volume below 55% of the tree | ||
| T5 | Cylinder length/tree volume | ||
| T6 | Relative volume ratio | ||
| Crown | C1 | Crown lowest heights/tree height | |
| C2 | Height difference between the start and end heights of a crown | ||
| C3 | Ratio between crown diameter and vertical height | ||
| C4 | Ratio between minimum and maximum height of the crown bottom | ||
| C5 | Ratio between crown vertical length and tree height | ||
| C6 | Ratio between heights of the widest crown and the tree | ||
| C7 | Ratio between crown cover area and tree height | ||
| C8 | Ratio between crown horizontal and vertical areas | ||
| C9 | Ratio between the maximum diameters of crown horizontal projection | ||
| C10 | Ratio between the maximum diameters of crown vertical projection | ||
| C11 | Ratio between heights of the crown and its widest part |
| Type | Par | |||||
|---|---|---|---|---|---|---|
| Branch | B1 | 28.57 | 42.31 | 41.67 | 35.71 | 37.88 |
| B2 | 7.14 | 30.43 | 41.94 | 66.67 | 36.36 | |
| B3 | 18.18 | 50.00 | 15.79 | 8.33 | 27.27 | |
| B4 | 23.08 | 26.67 | 40.00 | 16.67 | 27.27 | |
| B5 | 40.00 | 28.57 | 30.00 | 26.67 | 30.30 | |
| B6 | 33.33 | 22.73 | 17.65 | 13.33 | 21.21 | |
| Average | 25.05 | 25.05 | 31.17 | 27.89 | 30.04 | |
| Crown | C1 | 26.67 | 9.09 | 47.37 | 20.00 | 25.76 |
| C3 | 42.86 | 47.06 | 43.75 | 47.37 | 45.45 | |
| C4 | 20.00 | 20.00 | 23.81 | 50.00 | 25.76 | |
| C5 | 33.33 | 35.29 | 27.27 | 26.67 | 30.30 | |
| C6 | 7.14 | 25.00 | 26.09 | 26.67 | 22.73 | |
| C7 | 35.71 | 33.33 | 31.25 | 28.57 | 31.82 | |
| C8 | 11.76 | 30.00 | 57.89 | 45.00 | 37.88 | |
| C9 | 22.22 | 27.27 | 5.56 | 23.53 | 19.70 | |
| C10 | 33.33 | 47.06 | 32.00 | 20.00 | 33.33 | |
| C11 | 34.21 | 33.33 | 40.31 | 29.57 | 36.18 | |
| Average | 26.72 | 30.74 | 33.53 | 31.74 | 30.89 | |
| Entire tree | T1 | 50.00 | 10.53 | 22.22 | 35.29 | 27.27 |
| T2 | 25.00 | 57.14 | 13.33 | 11.11 | 28.79 | |
| T3 | 20.00 | 38.46 | 32.00 | 27.78 | 30.30 | |
| T4 | 22.22 | 16.67 | 45.00 | 21.05 | 27.27 | |
| T5 | 33.33 | 35.00 | 27.78 | 12.50 | 27.27 | |
| T6 | 43.75 | 26.67 | 40.00 | 35.00 | 36.36 | |
| Average | 32.38 | 30.75 | 30.05 | 23.78 | 29.54 |
| Branch | Crown | Entire Tree | |
|---|---|---|---|
| √ | 57.86 | ||
| √ | 61.27 | ||
| √ | 60.34 | ||
| √ | √ | 73.14 | |
| √ | √ | 79.59 | |
| √ | √ | 80.64 | |
| √ | √ | √ | 84.09 |
| Classification Results | ANN | DT | KNN | RF | SVMpoly | SVMrbf | SVMsig |
|---|---|---|---|---|---|---|---|
| 78.57 | 58.82 | 80.00 | 90.00 | 92.86 | 100.00 | 100.00 | |
| 66.67 | 68.42 | 63.16 | 66.67 | 72.22 | 61.90 | 63.64 | |
| 90.48 | 70.00 | 88.89 | 78.95 | 89.48 | 78.89 | 85.00 | |
| 62.50 | 80.00 | 57.89 | 68.75 | 73.33 | 61.90 | 70.59 | |
| 75.10 | 69.47 | 72.94 | 75.63 | 84.09 | 77.75 | 79.08 |
| Prediction | ||||||
|---|---|---|---|---|---|---|
| AM | FA | DR | HT | Total | ||
| Reference | AM | 58.82 | 80.00 | 90.00 | 92.86 | 100.00 |
| FA | 68.42 | 63.16 | 66.67 | 72.22 | 61.90 | |
| DR | 70.00 | 88.89 | 78.95 | 89.48 | 78.89 | |
| HT | 80.00 | 57.89 | 68.75 | 73.33 | 61.90 | |
| Total | 69.47 | 72.94 | 75.63 | 84.09 | 77.75 | |
| Optimal Parameter Sets | |||||
|---|---|---|---|---|---|
| B3, B5, B6, C4, C5, C6, T3, T4, T5, T6 | 92.86 | 72.22 | 89.48 | 73.33 | 84.09 |
| B3, B6, T1, T2, T3, T4, C7, C8 | 90.48 | 70.67 | 88.89 | 72.73 | 83.96 |
| B6, C1, C3, C4, C5, C6, C8, T1, T2, T3, T4 | 90.48 | 66.67 | 88.89 | 70.59 | 83.83 |
| B2, B4, B6, C4, C7, T1, T2, T3 | 90.00 | 66.67 | 85.00 | 70.59 | 83.70 |
| B2, B3, B5, C3, C5, C7, C10, T1, T2, T3, T4, T5, T6 | 90.00 | 68.42 | 85.00 | 68.75 | 83.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Wong, M.S.; Abbas, S. Tropical Species Classification with Structural Traits Using Handheld Laser Scanning Data. Remote Sens. 2022, 14, 1948. https://doi.org/10.3390/rs14081948
Wang M, Wong MS, Abbas S. Tropical Species Classification with Structural Traits Using Handheld Laser Scanning Data. Remote Sensing. 2022; 14(8):1948. https://doi.org/10.3390/rs14081948
Chicago/Turabian StyleWang, Meilian, Man Sing Wong, and Sawaid Abbas. 2022. "Tropical Species Classification with Structural Traits Using Handheld Laser Scanning Data" Remote Sensing 14, no. 8: 1948. https://doi.org/10.3390/rs14081948
APA StyleWang, M., Wong, M. S., & Abbas, S. (2022). Tropical Species Classification with Structural Traits Using Handheld Laser Scanning Data. Remote Sensing, 14(8), 1948. https://doi.org/10.3390/rs14081948