The Global Patterns of Interannual and Intraseasonal Mass Variations in the Oceans from GRACE and GRACE Follow-On Records
Abstract
1. Introduction
2. Data
2.1. GRACE (-FO) Data
2.2. Co-Related Datasets: Wind Stress Curl, Sea Level Anomaly, and Climate Indices
3. Spatiotemporal Pattern Definition
4. Results
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the Global Mass Change Data Record: GRACE Follow-On Instrument and Science Data Performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Chambers, D.P. Evaluation of new GRACE time-variable gravity data over the ocean. Geophys. Res. Lett. 2006, 33, L17603. [Google Scholar] [CrossRef]
- Chambers, D.P.; Wahr, J.; Nerem, R.S. Preliminary observations of global ocean mass variations with GRACE. Geophys. Res. Lett. 2004, 31, L13310. [Google Scholar] [CrossRef]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Poropat, L.; Thomas, M.; Dahle, C.; Esselborn, S.; König, R.; Flechtner, F. A new high-resolution model of non-tidal atmosphere and ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL06. Geophys. J. Int. 2017, 211, 263–269. [Google Scholar] [CrossRef]
- Han, S.; Jekeli, C.; Shum, C.K. Time-variable aliasing effects of ocean tides, atmosphere, and continental water mass on monthly mean GRACE gravity field. J. Geophys. Res. Solid Earth 2004, 109, B04403. [Google Scholar] [CrossRef]
- Quinn, K.J.; Ponte, R.M. Estimating high frequency ocean bottom pressure variability. Geophys. Res. Lett. 2011, 38, L08611. [Google Scholar] [CrossRef]
- Piecuch, C.G.; Landerer, F.W.; Ponte, R.M. Tide gauge records reveal improved processing of gravity recovery and climate experiment time-variable mass solutions over the coastal ocean. Geophys. J. Int. 2018, 214, 1401–1412. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Chambers, D.P.; Willis, J.K. Analysis of large-scale ocean bottom pressure variability in the North Pacific. J. Geophys. Res. Ocean. 2008, 113, C11003. [Google Scholar] [CrossRef]
- Fukumori, I.; Wang, O.; Fenty, I.; Forget, G.; Heimbach, P.; Ponte, R.M. Synopsis of the ECCO Central Production Global Ocean and Sea-Ice State Estimate, Version 4 Release 4; ECCO Consortium: Washington, DC, USA, 2021.
- Köhl, A.; Siegismund, F.; Stammer, D. Impact of assimilating bottom pressure anomalies from GRACE on ocean circulation estimates. J. Geophys. Res. Ocean. 2012, 117, C04032. [Google Scholar] [CrossRef]
- Cazenave, A.; Palanisamy, H.; Ablain, M. Contemporary sea level changes from satellite altimetry: What have we learned? What are the new challenges? Adv. Space Res. 2018, 62, 1639–1653. [Google Scholar] [CrossRef]
- Cheng, X.; Ou, N.; Chen, J.; Huang, R.X. On the seasonal variations of ocean bottom pressure in the world oceans. Geosci. Lett. 2021, 8, 29. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. Assessing Global Water Storage Variability from GRACE: Trends, Seasonal Cycle, Subseasonal Anomalies and Extremes. Surv. Geophys. 2016, 37, 357–395. [Google Scholar] [CrossRef]
- Johnson, G.C.; Chambers, D.P. Ocean bottom pressure seasonal cycles and decadal trends from GRACE Release-05: Ocean circulation implications. J. Geophys. Res. Ocean. 2013, 118, 4228–4240. [Google Scholar] [CrossRef]
- Kanzow, T.; Flechtner, F.; Chave, A.; Schmidt, R.; Schwintzer, P.; Send, U. Seasonal variation of ocean bottom pressure derived from Gravity Recovery and Climate Experiment (GRACE): Local validation and global patterns. J. Geophys. Res. Ocean. 2005, 110, C09001. [Google Scholar] [CrossRef]
- Ponte, R.M.; Quinn, K.J.; Wunsch, C.; Heimbach, P. A comparison of model and GRACE estimates of the large-scale seasonal cycle in ocean bottom pressure. Geophys. Res. Lett. 2007, 34, L09603. [Google Scholar] [CrossRef]
- Piecuch, C.G.; Quinn, K.J.; Ponte, R.M. Satellite-derived interannual ocean bottom pressure variability and its relation to sea level. Geophys. Res. Lett. 2013, 40, 3106–3110. [Google Scholar] [CrossRef]
- Quinn, K.J.; Ponte, R.M. High frequency barotropic ocean variability observed by GRACE and satellite altimetry. Geophys. Res. Lett. 2012, 39, L07603. [Google Scholar] [CrossRef]
- Ponte, R.M. Understanding the relation between wind-and pressure-driven sea level variability. J. Geophys. Res. Ocean. 1994, 99, 8033–8039. [Google Scholar] [CrossRef]
- Gill, A.E.; Niller, P.P. The theory of the seasonal variability in the ocean. Deep. Sea Res. Oceanogr. Abstr. 1973, 20, 141–177. [Google Scholar] [CrossRef]
- Willebrand, J.; Philander, S.G.H.; Pacanowski, R.C. The Oceanic Response to Large-Scale Atmospheric Disturbances. J. Phys. Oceanogr. 1980, 10, 411–429. [Google Scholar] [CrossRef][Green Version]
- Afroosa, M.; Rohith, B.; Paul, A.; Durand, F.; Bourdallé-Badie, R.; Sreedevi, P.V.; de Viron, O.; Ballu, V.; Shenoi, S.S.C. Madden-Julian oscillation winds excite an intraseasonal see-saw of ocean mass that affects Earth’s polar motion. Commun. Earth Environ. 2021, 2, 139. [Google Scholar] [CrossRef]
- Rohith, B.; Paul, A.; Durand, F.; Testut, L.; Prerna, S.; Afroosa, M.; Ramakrishna, S.S.V.S.; Shenoi, S.S.C. Basin-wide sea level coherency in the tropical Indian Ocean driven by Madden–Julian Oscillation. Nat. Commun. 2019, 10, 1257. [Google Scholar] [CrossRef] [PubMed]
- Stammer, D.; Cazenave, A.; Ponte, R.M.; Tamisiea, M.E. Causes for Contemporary Regional Sea Level Changes. Annu. Rev. Mar. Sci. 2013, 5, 21–46. [Google Scholar] [CrossRef]
- Bingham, R.J.; Hughes, C.W. The relationship between sea-level and bottom pressure variability in an eddy permitting ocean model. Geophys. Res. Lett. 2008, 35, L03602. [Google Scholar] [CrossRef]
- Vinogradova, N.T.; Ponte, R.M.; Stammer, D. Relation between sea level and bottom pressure and the vertical dependence of oceanic variability. Geophys. Res. Lett. 2007, 34, L03608. [Google Scholar] [CrossRef]
- Fu, L.-L.; Davidson, R.A. A note on the barotropic response of sea level to time-dependent wind forcing. J. Geophys. Res. 1995, 100, 24955. [Google Scholar] [CrossRef]
- Piecuch, C.G.; Fukumori, I.; Ponte, R.M.; Wang, O. Vertical Structure of Ocean Pressure Variations with Application to Satellite-Gravimetric Observations. J. Atmos. Ocean. Technol. 2015, 32, 603–613. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Piecuch, C.G.; Reager, J.T.; Chandanpurkar, H.; Frederikse, T.; Nerem, R.S.; Fasullo, J.T.; Cheon, S. Origin of interannual variability in global mean sea level. Proc. Natl. Acad. Sci. USA 2020, 117, 13983–13990. [Google Scholar] [CrossRef] [PubMed]
- Han, W.; Meehl, G.A.; Stammer, D.; Hu, A.; Hamlington, B.; Kenigson, J.; Palanisamy, H.; Thompson, P. Spatial Patterns of Sea Level Variability Associated with Natural Internal Climate Modes. In Integrative Study of the Mean Sea Level and Its Components; Cazenave, A., Champollion, N., Paul, F., Benveniste, J., Eds.; Space Sciences Series of ISSI; Springer International Publishing: Cham, Switzerland, 2017; pp. 221–254. ISBN 978-3-319-56490-6. [Google Scholar]
- Chambers, D.P. ENSO-correlated fluctuations in ocean bottom pressure and wind-stress curl in the North Pacific. Ocean. Sci. 2011, 7, 685–692. [Google Scholar] [CrossRef]
- Volkov, D.L.; Lee, S.; Landerer, F.W.; Lumpkin, R. Decade-long deep-ocean warming detected in the subtropical South Pacific. Geophys. Res. Lett. 2017, 44, 927–936. [Google Scholar] [CrossRef] [PubMed]
- Von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Liau, J.; Chao, B.F. Variation of Antarctic circumpolar current and its intensification in relation to the southern annular mode detected in the time-variable gravity signals by GRACE satellite. Earth Planets Space 2017, 69, 93. [Google Scholar] [CrossRef]
- Piecuch, C.G.; Fukumori, I.; Ponte, R.M. Intraseasonal Sea Level Variability in the Persian Gulf. J. Phys. Oceanogr. 2021, 51, 1687–1704. [Google Scholar] [CrossRef]
- Wang, Z.; Hamilton, J.; Su, J. Variations in freshwater pathways from the Arctic Ocean into the North Atlantic Ocean. Prog. Oceanogr. 2017, 155, 54–73. [Google Scholar] [CrossRef]
- Marcos, M.; Calafat, F.M.; Llovel, W.; Gomis, D.; Meyssignac, B. Regional distribution of steric and mass contributions to sea level changes. Glob. Planet. Change 2011, 76, 206–218. [Google Scholar] [CrossRef]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Vejmelka, M.; Pokorná, L.; Hlinka, J.; Hartman, D.; Jajcay, N.; Paluš, M. Non-random correlation structures and dimensionality reduction in multivariate climate data. Clim Dyn 2015, 44, 2663–2682. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Seo, K. S2 tide aliasing in GRACE time-variable gravity solutions. J. Geod. 2009, 83, 679–687. [Google Scholar] [CrossRef]
- De Linage, C.; Rivera, L.; Hinderer, J.; Boy, J.-P.; Rogister, Y.; Lambotte, S.; Biancale, R. Separation of coseismic and postseismic gravity changes for the 2004 Sumatra-Andaman earthquake from 4.6 yr of GRACE observations and modelling of the coseismic change by normal-modes summation. Geophys. J. Int. 2009, 176, 695–714. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Monthly Averaged Data on Single Levels from 1979 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS): Brussels, Belgium, 2019. [Google Scholar]
- Taburet, G.; Sanchez-Roman, A.; Ballarotta, M.; Pujol, M.; Legeais, J.; Fournier, F.; Faugere, Y.; Dibarboure, G. DUACS DT2018: 25 years of reprocessed sea level altimetry products. Ocean. Sci. 2019, 15, 1207–1224. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Surrogate time series. Phys. D Nonlinear Phenom. 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Statist. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Durbin, J.; Koopman, S.J. Time Series Analysis by State Space Methods, 2nd ed.; Oxford Statistical Science Series; Oxford University Press: Oxford, UK, 2012; ISBN 978-0-19-964117-8. [Google Scholar]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and Statistical Modeling with Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 92–96. [Google Scholar]
- Tozer, B.; Sandwell, D.T.; Smith, W.H.F.; Olson, C.; Beale, J.R.; Wessel, P. Global Bathymetry and Topography at 15 Arc Sec: SRTM15+. Earth Space Sci. 2019, 6, 1847–1864. [Google Scholar] [CrossRef]
- Gramazio, C.C.; Laidlaw, D.H.; Schloss, K.B. Colorgorical: Creating discriminable and preferable color palettes for information visualization. IEEE Trans. Visual. Comput. Graph. 2017, 23, 521–530. [Google Scholar] [CrossRef]
- Fukumori, I.; Wang, O.; Llovel, W.; Fenty, I.; Forget, G. A near-uniform fluctuation of ocean bottom pressure and sea level across the deep ocean basins of the Arctic Ocean and the Nordic Seas. Prog. Oceanogr. 2015, 134, 152–172. [Google Scholar] [CrossRef]
- Peralta-Ferriz, C.; Morison, J.H.; Wallace, J.M.; Bonin, J.A.; Zhang, J. Arctic Ocean Circulation Patterns Revealed by GRACE. J. Clim. 2014, 27, 1445–1468. [Google Scholar] [CrossRef]
- Volkov, D.L.; Landerer, F.W. Nonseasonal fluctuations of the Arctic Ocean mass observed by the GRACE satellites. J. Geophys. Res. Ocean. 2013, 118, 6451–6460. [Google Scholar] [CrossRef]
- Fukumori, I.; Menemenlis, D.; Lee, T. A Near-Uniform Basin-Wide Sea Level Fluctuation of the Mediterranean Sea. J. Phys. Oceanogr. 2007, 37, 338–358. [Google Scholar] [CrossRef]
- Piecuch, C.G.; Ponte, R.M. A wind-driven nonseasonal barotropic fluctuation of the Canadian inland seas. Ocean. Sci. 2015, 11, 175–185. [Google Scholar] [CrossRef]
- Tsimplis, M.N.; Calafat, F.M.; Marcos, M.; Jordà, G.; Gomis, D.; Fenoglio-Marc, L.; Struglia, M.V.; Josey, S.A.; Chambers, D.P. The effect of the NAO on sea level and on mass changes in the Mediterranean Sea. J. Geophys. Res. Ocean. 2013, 118, 944–952. [Google Scholar] [CrossRef]
- Volkov, D.L.; Baringer, M.; Smeed, D.; Johns, W.; Landerer, F.W. Teleconnection between the Atlantic Meridional Overturning Circulation and Sea Level in the Mediterranean Sea. J. Clim. 2019, 32, 935–955. [Google Scholar] [CrossRef]
- Landerer, F.W.; Wiese, D.N.; Bentel, K.; Boening, C.; Watkins, M.M. North Atlantic meridional overturning circulation variations from GRACE ocean bottom pressure anomalies. Geophys. Res. Lett. 2015, 42, 8114–8121. [Google Scholar] [CrossRef]
- Piecuch, C.G.; Ponte, R.M. Nonseasonal mass fluctuations in the midlatitude North Atlantic Ocean. Geophys. Res. Lett. 2014, 41, 4261–4269. [Google Scholar] [CrossRef]
- Peralta-Ferriz, C.; Woodgate, R.A. The Dominant Role of the East Siberian Sea in Driving the Oceanic Flow Through the Bering Strait—Conclusions From GRACE Ocean Mass Satellite Data and In Situ Mooring Observations Between 2002 and 2016. Geophys. Res. Lett. 2017, 44, 11–472. [Google Scholar] [CrossRef]
- Bingham, R.J.; Hughes, C.W. Observing seasonal bottom pressure variability in the North Pacific with GRACE. Geophys. Res. Lett. 2006, 33, L08607. [Google Scholar] [CrossRef]
- Song, Y.T.; Qu, T. Multiple Satellite Missions Confirming the Theory of Seasonal Oceanic Variability in the Northern North Pacific. Mar. Geod. 2011, 34, 477–490. [Google Scholar] [CrossRef]
- Song, Y.T.; Zlotnicki, V. Subpolar ocean bottom pressure oscillation and its links to the tropical ENSO. Int. J. Remote Sens. 2008, 29, 6091–6107. [Google Scholar] [CrossRef]
- Moon, J.; Song, Y.T. Sea level and heat content changes in the western North Pacific. J. Geophys. Res. Ocean. 2013, 118, 2014–2022. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S. Interannual-to-Decadal Variability in the Bifurcation of the North Equatorial Current off the Philippines. J. Phys. Oceanogr. 2010, 40, 2525–2538. [Google Scholar] [CrossRef]
- Timmermann, A.; McGregor, S.; Jin, F. Wind Effects on Past and Future Regional Sea Level Trends in the Southern Indo-Pacific. J. Clim. 2010, 23, 4429–4437. [Google Scholar] [CrossRef]
- Cheng, X.; Li, L.; Du, Y.; Wang, J.; Huang, R. Mass-induced sea level change in the northwestern North Pacific and its contribution to total sea level change. Geophys. Res. Lett. 2013, 40, 3975–3980. [Google Scholar] [CrossRef]
- Llovel, W.; Terray, L. Observed southern upper-ocean warming over 2005–2014 and associated mechanisms. Environ. Res. Lett. 2016, 11, 124023. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J.; Sutton, P.; Zilberman, N. Multidecadal Change of the South Pacific Gyre Circulation. J. Phys. Oceanogr. 2016, 46, 1871–1883. [Google Scholar] [CrossRef]
- Mazloff, M.R.; Boening, C. Rapid variability of Antarctic Bottom Water transport into the Pacific Ocean inferred from GRACE. Geophys. Res. Lett. 2016, 43, 3822–3829. [Google Scholar] [CrossRef]
- Piecuch, C.G.; Ponte, R.M. Annual Cycle in Southern Tropical Indian Ocean Bottom Pressure. J. Phys. Oceanogr. 2014, 44, 1605–1613. [Google Scholar] [CrossRef]
- Manche, S.S.; Nayak, R.K.; Mohanty, P.C.; Shesasai, M.V.R.; Dadhwal, V.K. Assessment of mass-induced sea level variability in the Tropical Indian Ocean based on GRACE and altimeter observations. J. Geod. 2021, 95, 19. [Google Scholar] [CrossRef]
- Drouin, K.L.; Lozier, M.S.; Johns, W.E. Variability and Trends of the South Atlantic Subtropical Gyre. J. Geophys. Res. Ocean. 2021, 126, e2020JC016405. [Google Scholar] [CrossRef]
- Ruiz-Etcheverry, L.A.; Saraceno, M. Sea Level Trend and Fronts in the South Atlantic Ocean. Geosciences 2020, 10, 218. [Google Scholar] [CrossRef]
- Ponte, R.M.; Quinn, K.J. Bottom pressure changes around Antarctica and wind-driven meridional flows. Geophys. Res. Lett. 2009, 36, L13604. [Google Scholar] [CrossRef]
- Feng, G.; Jin, S.; Reales, J.M.S. Antarctic circumpolar current from satellite gravimetric models ITG-GRACE2010, GOCE-TIM3 and satellite altimetry. J. Geodyn. 2013, 72, 72–80. [Google Scholar] [CrossRef]
- Ponte, R.M.; Piecuch, C.G. Interannual Bottom Pressure Signals in the Australian–Antarctic and Bellingshausen Basins. J. Phys. Oceanogr. 2014, 44, 1456–1465. [Google Scholar] [CrossRef]
- Kuhlmann, J.; Dobslaw, H.; Petrick, C.; Thomas, M. Ocean bottom pressure signals around Southern Africa from in situ measurements, satellite data, and modeling. J. Geophys. Res. Ocean. 2013, 118, 4889–4898. [Google Scholar] [CrossRef][Green Version]
- Piecuch, C.G. Dynamics of satellite-derived interannual ocean bottom pressure variability in the western tropical North Pacific. J. Geophys. Res. Ocean. 2013, 118, 5117–5128. [Google Scholar] [CrossRef]
- Piecuch, C.G. Bottom-pressure signature of annual baroclinic Rossby waves in the northeast tropical Pacific Ocean. J. Geophys. Res. Ocean. 2015, 120, 2449–2459. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
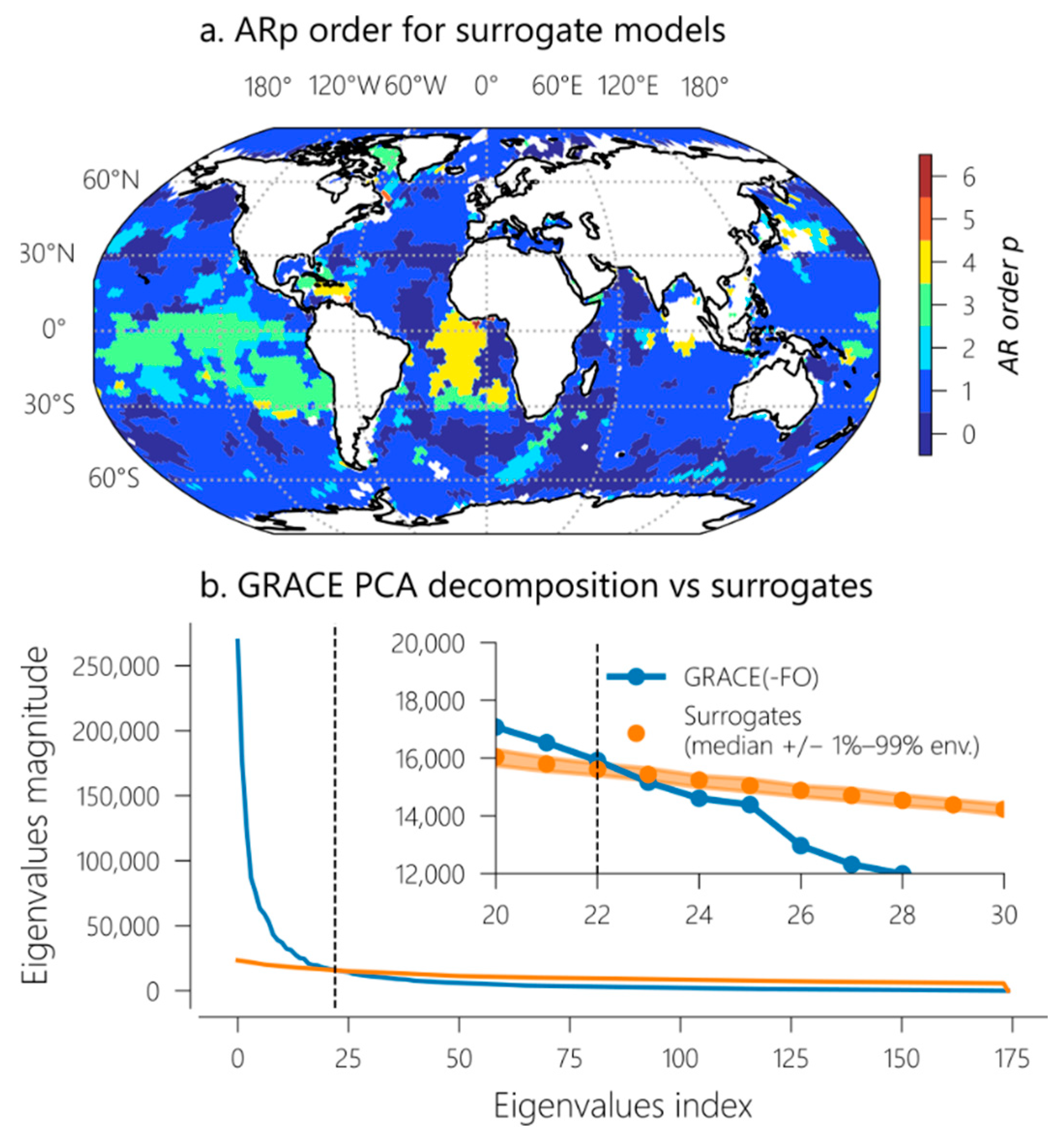
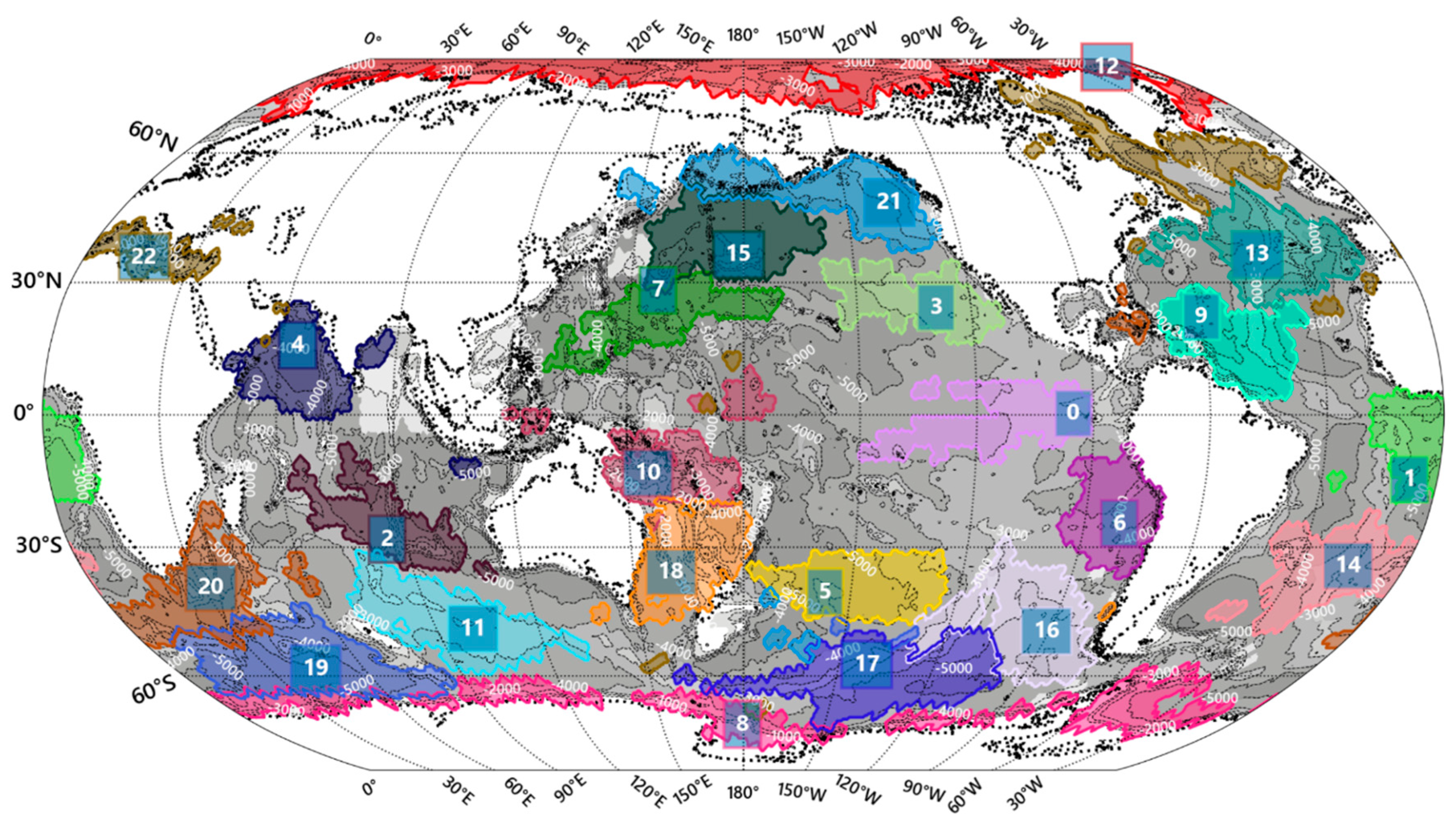
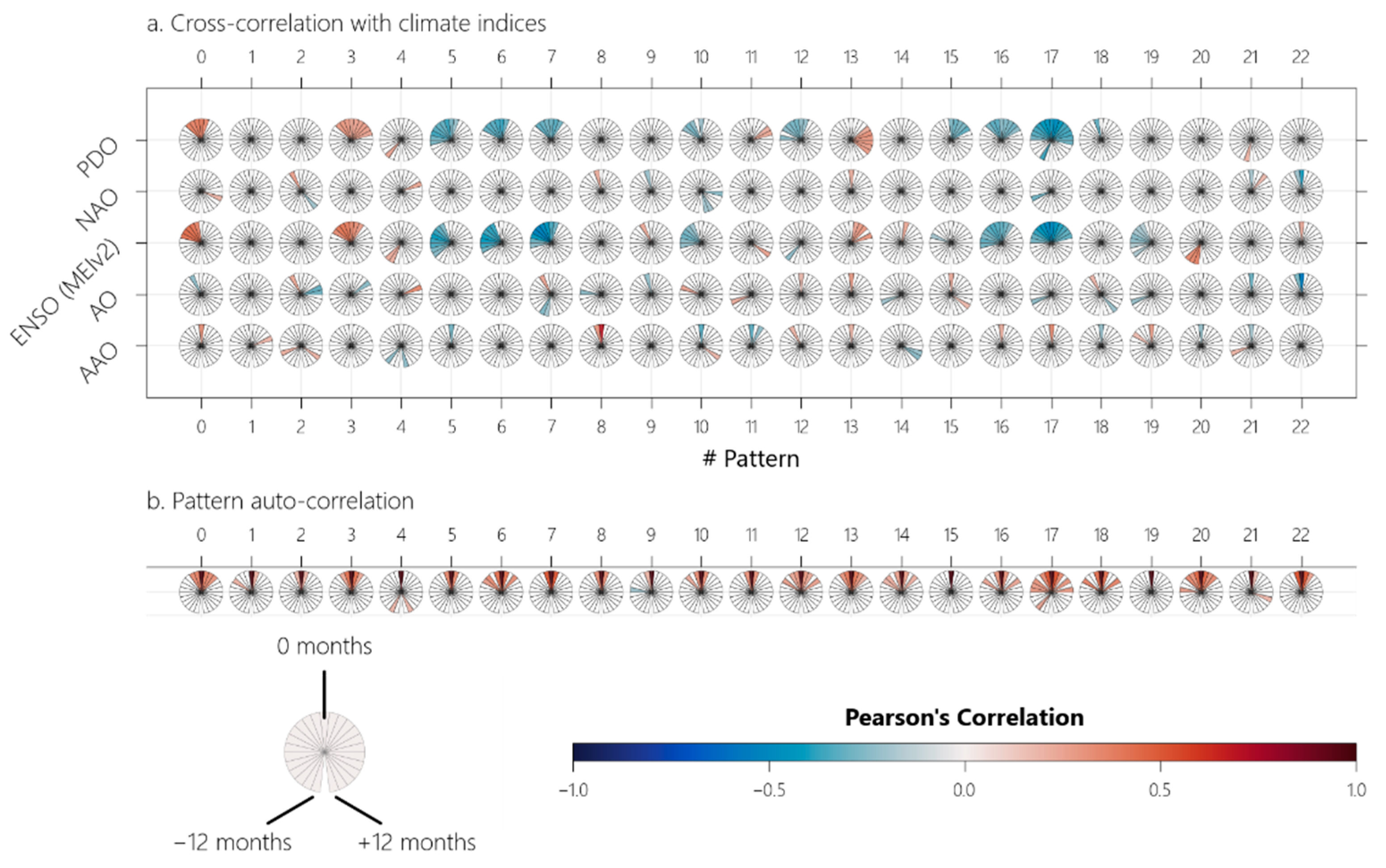
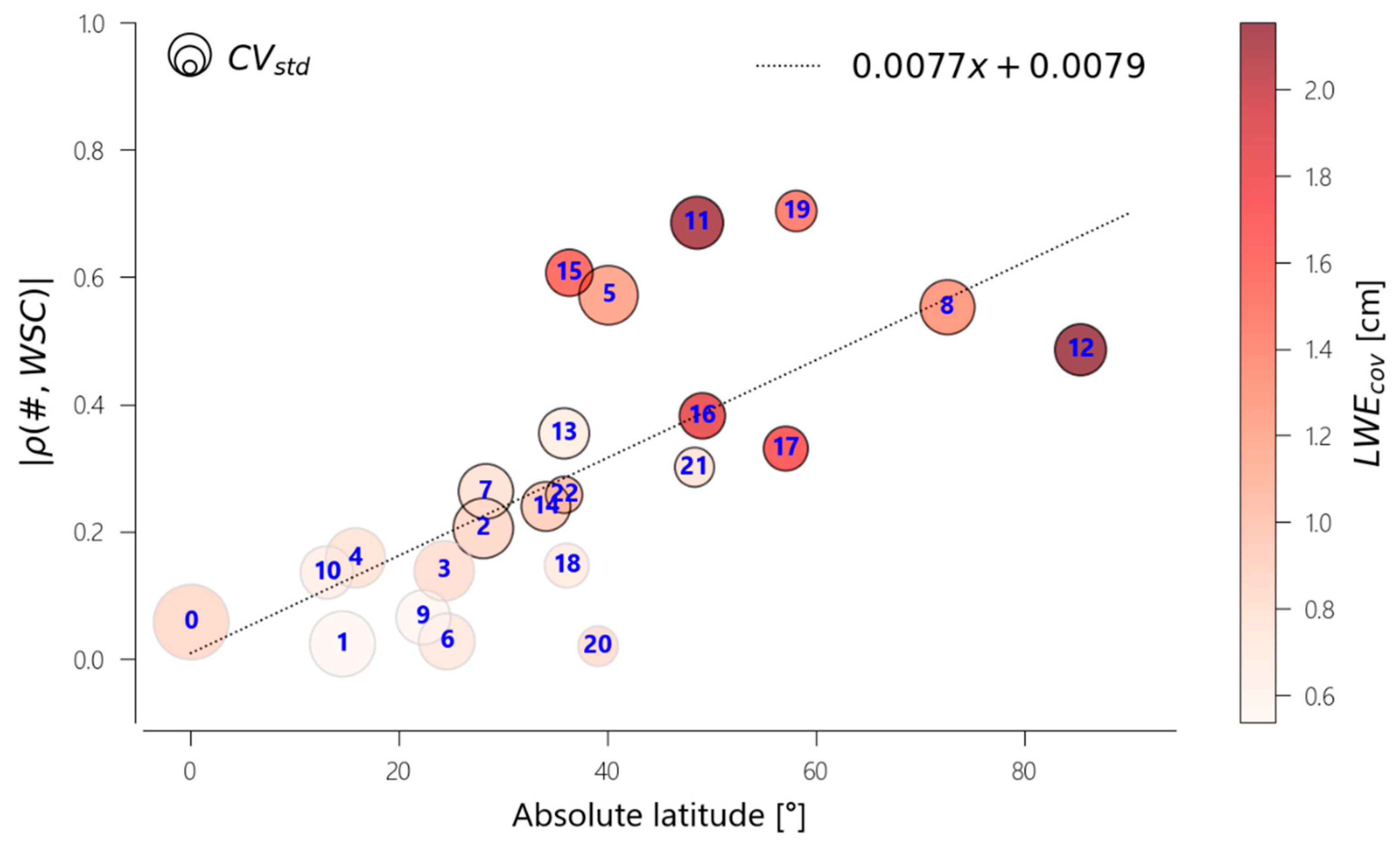
| # | Lat. °N | cm | % | [0,1] | [0,1] |
|---|---|---|---|---|---|
| 0 | −0.13 | 0.85 | 6.42 | 0.39 | 0.06 |
| 1 | −14.63 | 0.54 | 4.84 | 0.23 | 0.02 |
| 2 | −28.13 | 0.86 | 4.07 | 0.40 | 0.20 |
| 3 | 24.38 | 0.81 | 4.07 | 0.37 | 0.14 |
| 4 | 15.88 | 0.77 | 4.01 | 0.16 | 0.16 |
| 5 | −40.13 | 1.21 | 3.95 | 0.15 | 0.57 |
| 6 | −24.63 | 0.73 | 3.57 | 0.36 | 0.03 |
| 7 | 28.38 | 0.79 | 3.40 | 0.12 | 0.26 |
| 8 | −72.63 | 1.30 | 3.37 | 0.34 * | 0.55 |
| 9 | 22.38 | 0.55 | 3.36 | 0.23 | 0.07 |
| 10 | −13.13 | 0.64 | 3.15 | 0.00 | 0.14 |
| 11 | −48.63 | 2.11 | 3.11 | 0.67 | 0.69 |
| 12 | 85.38 | 2.15 | 3.01 | 0.58 * | 0.49 |
| 13 | 35.88 | 0.68 | 2.88 | 0.24 | 0.35 |
| 14 | −34.13 | 0.92 | 2.74 | 0.19 | 0.24 |
| 15 | 36.38 | 1.58 | 2.49 | 0.40 | 0.61 |
| 16 | −49.13 | 1.85 | 2.37 | 0.73 | 0.38 |
| 17 | −57.13 | 1.71 | 2.24 | 0.71 | 0.33 |
| 18 | −36.13 | 0.69 | 2.22 | 0.06 | 0.15 |
| 19 | −58.13 | 1.45 | 1.89 | 0.64 | 0.70 |
| 20 | −39.13 | 0.81 | 1.81 | 0.09 | 0.02 |
| 21 | 48.38 | 0.76 | 1.76 | 0.11 | 0.30 |
| 22 | 35.88 | 1.00 | 1.53 | 0.42 | 0.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delforge, D.; de Viron, O.; Durand, F.; Dehant, V. The Global Patterns of Interannual and Intraseasonal Mass Variations in the Oceans from GRACE and GRACE Follow-On Records. Remote Sens. 2022, 14, 1861. https://doi.org/10.3390/rs14081861
Delforge D, de Viron O, Durand F, Dehant V. The Global Patterns of Interannual and Intraseasonal Mass Variations in the Oceans from GRACE and GRACE Follow-On Records. Remote Sensing. 2022; 14(8):1861. https://doi.org/10.3390/rs14081861
Chicago/Turabian StyleDelforge, Damien, Olivier de Viron, Fabien Durand, and Véronique Dehant. 2022. "The Global Patterns of Interannual and Intraseasonal Mass Variations in the Oceans from GRACE and GRACE Follow-On Records" Remote Sensing 14, no. 8: 1861. https://doi.org/10.3390/rs14081861
APA StyleDelforge, D., de Viron, O., Durand, F., & Dehant, V. (2022). The Global Patterns of Interannual and Intraseasonal Mass Variations in the Oceans from GRACE and GRACE Follow-On Records. Remote Sensing, 14(8), 1861. https://doi.org/10.3390/rs14081861







