SOLS: An Open-Source Spaceborne Oceanic Lidar Simulator

Abstract

In recent years, oceanic lidar has seen a wide range of oceanic applications, such as optical profiling and detecting bathymetry. Furthermore, spaceborne lidars, CALIOP and ICESat-2, designed for atmospheric and ice science applications, have been used for ocean backscattering retrievals, but, until now, there has been no spaceborne lidar specifically designed for ocean detection. There is a demand for an effective lidar simulator to study the detection potential capability of spaceborne oceanic lidar. In this study, an open-source spaceborne oceanic lidar simulator named SOLS was developed, which is available freely. Moreover, the maximum detectable depth and corresponding optimal wavelength for spaceborne lidar were analyzed at a global scale by using SOLS. The factors controlling detection limits of a spaceborne ocean profiling lidar in different cases were discussed. Then, the maximum detectable depths with different relative measurement errors and the influence of solar background radiance were estimated. Subsequently, the effects of laser and detector parameters on maximum detectable depths were studied. The relationship between the lidar detectable depth and the ocean mixed layer depth was also discussed. Preliminary results show that the maximum detectable depth could reach deeper than 120 m in the oligotrophic sea at low latitudes. We found that 490 nm is the optimal wavelength for most of the open seawater. For coastal water, 532 nm is a more suitable choice considering both the technical maturity and geophysical parameters. If possible, a lidar equipped with 440 nm could achieve the greatest depth in oligotrophic seawater in subtropical gyres north and south of the equator. The upper mixed layer vertical structure in most of the global open ocean is within the lidar maximum detectable depth. These results show that SOLS can help the design of future spaceborne oceanic lidar systems a lot.

1. Introduction

In the past decades, passive ocean color remote sensing has shown extraordinary global data acquisition capabilities [1]. Using these data, we have expanded our understanding of ocean plankton ecosystems, particulate organic carbon in the ocean [2], and ocean productivity [3] under climate change, into a global view. In brief, the passive ocean color data led to a major revolution in oceanography [4]. However, this measurement cannot provide the vertical structure within the water column [4], it only provides limited information about the inner water below sea surface [5] where a physical–biogeochemical process often occurs and the upper layer of aquatic ecosystems exists [6,7]. Moreover, it is limited to daylight [8].

Researchers are drawn to oceanic light detection and ranging (lidar) because of its depth-resolving ability and its capability of working at night, which could address the limitations mentioned above. In practice, shipborne and airborne lidar have been widely used in optical profiling [9,10,11], detecting plankton layers [12,13,14], and bathymetry surveys [15,16] in recent years. Furthermore, spaceborne lidar, CALIOP/CALIPSO and ATLAS/ ICESat-2 instruments designed for atmospheric and ice science applications, have shown remarkable application potential in ocean optical profiling [17,18,19] where lidar data are used for the particulate backscattering coefficient (bbp) and the particulate organic carbon (POC) inversion [20]. At present, a spaceborne lidar “Guanlan” designed for oceanic detection in China is under development [21]. Although lidar systems lack the swath width of passive remote sensing, spaceborne oceanic lidar will be an effective complement to passive ocean color remote sensing [8].

However, until now, there has been no spaceborne oceanic lidar. It is necessary and significant to study the detection potential capability of spaceborne lidar. Studies on appropriate spaceborne oceanic lidar system parameters, including laser energy, laser wavelength, receiver aperture size, field of view, and so on, are rare. Among them, the analysis of the maximum detectable depth and corresponding optimal wavelength is vital for oceanic detection capability and lidar design. The optimal wavelength with great penetration ability can improve the detectable depth [22]. In previous shipborne and airborne lidar, the wavelength of 532 nm was widely used [14,23,24,25] due to its availability for an efficient, compact, rugged laser [5]. However, it is just a compromise because 532 nm is suitable for coastal water, while it does not work so well in clear open ocean waters that constitute most of the global oceans. It has been shown that a shorter wavelength will be better for open-ocean applications [5,22,26]. However, the estimate of the detection potential capability of spaceborne lidar demands a spaceborne lidar simulator. Therefore, there is a major need to develop a spaceborne lidar simulator. The simulator could provide a reference for the design of future spaceborne oceanic lidar systems and contribute to the processing of lidar echo signals by analyzing optimal wavelengths and corresponding maximum detectable depth for oceanic lidar.

Thus far, several researchers have discussed the laser optimal wavelength, but the impact of background light [26], which may overestimate the penetration depths in open ocean water, has been neglected. Other researchers did not take into account the responsivity of the detector and detector noise [27]. Moreover, the dynamic range of the lidar receiver, one of the most critical parameters [5], has not been considered. Importantly, their codes are closed-source, which limits their application.

In this paper, an open-source spaceborne oceanic lidar simulator named SOLS was developed, which is freely available to the public (https://github.com/soedchen/, accessed on 20 February 2022). The framework of SOLS is shown in Figure A1. SOLS takes general consideration of the lidar system and environmental parameters. Compared with other models, SOLS can deal with stratified water and be used for both full waveform simulation with analog detection and photon-counting lidar simulation.

The structure of this article is as follows. First, a bio-optical model was built to describe the optical properties of water; then, the optimal wavelength for detecting the characteristics of the water was analyzed based on a spaceborne lidar model, the background light, and detector noise models (Section 2). After its establishment, the lidar’s maximum detectable depth and corresponding optimal wavelength were estimated (Section 3). Influences of other parameters, including laser energy, detector field of view, and filter bandwidth, are discussed in Section 4. Subsequently, the relationship between lidar maximum detectable depth and ocean mixed layer depth is discussed.

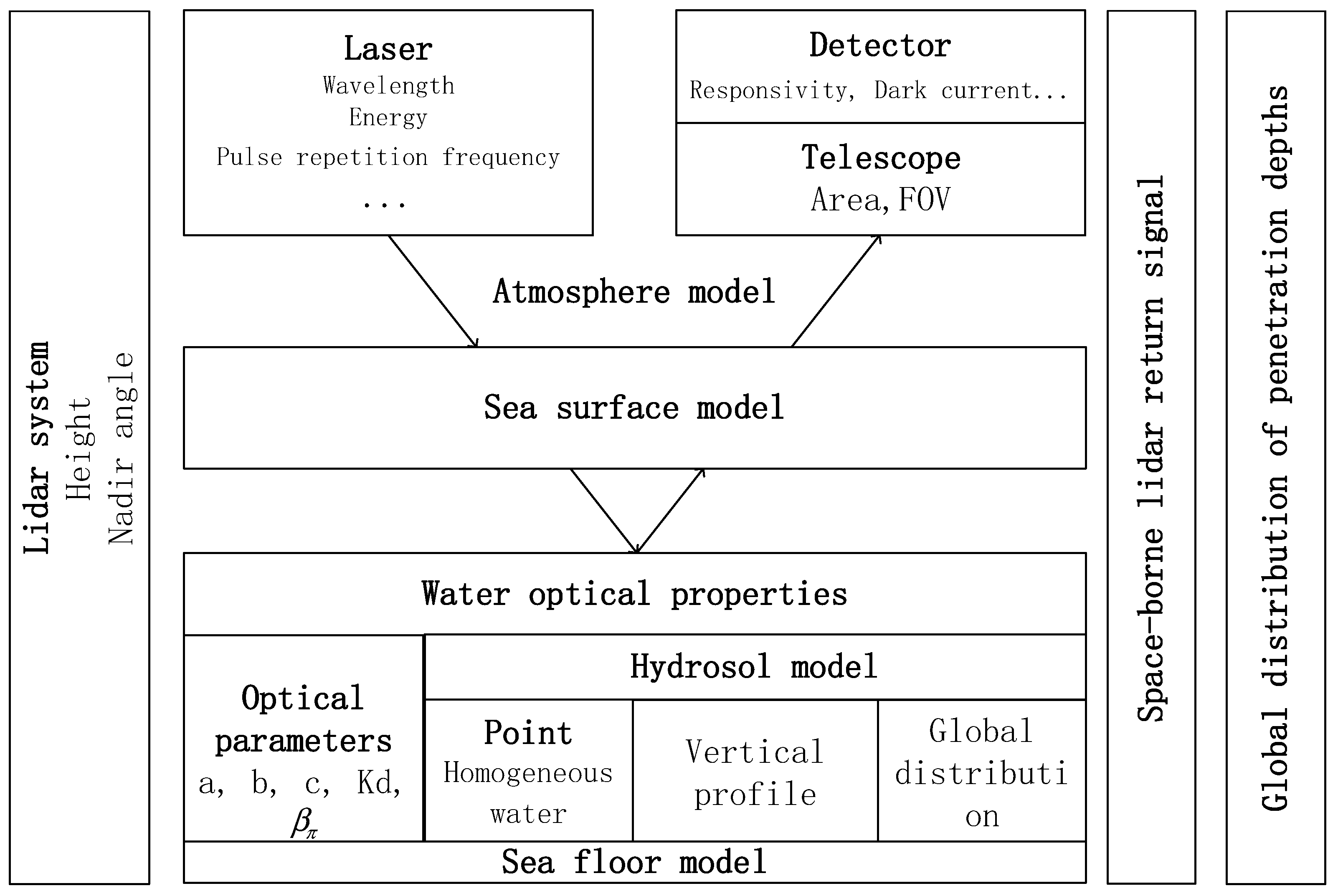
2. Materials and Methods

As shown in Figure 1, in a spaceborne oceanic lidar system, a laser emits a short pulse toward the atmosphere and ocean; then a telescope is pointed in the same direction as the laser beam and collects the backscattered light from particles and molecules. The system uses a time-of-flight ranging technique to convert time-profile as a function of depth. The receiver not only collects the lidar return signal, but also the solar background radiance scattered by the atmosphere and sea surface. Moreover, the inner noise of the detector exerts a subtle influence on the return signals. A detailed model including these impacts is given here.

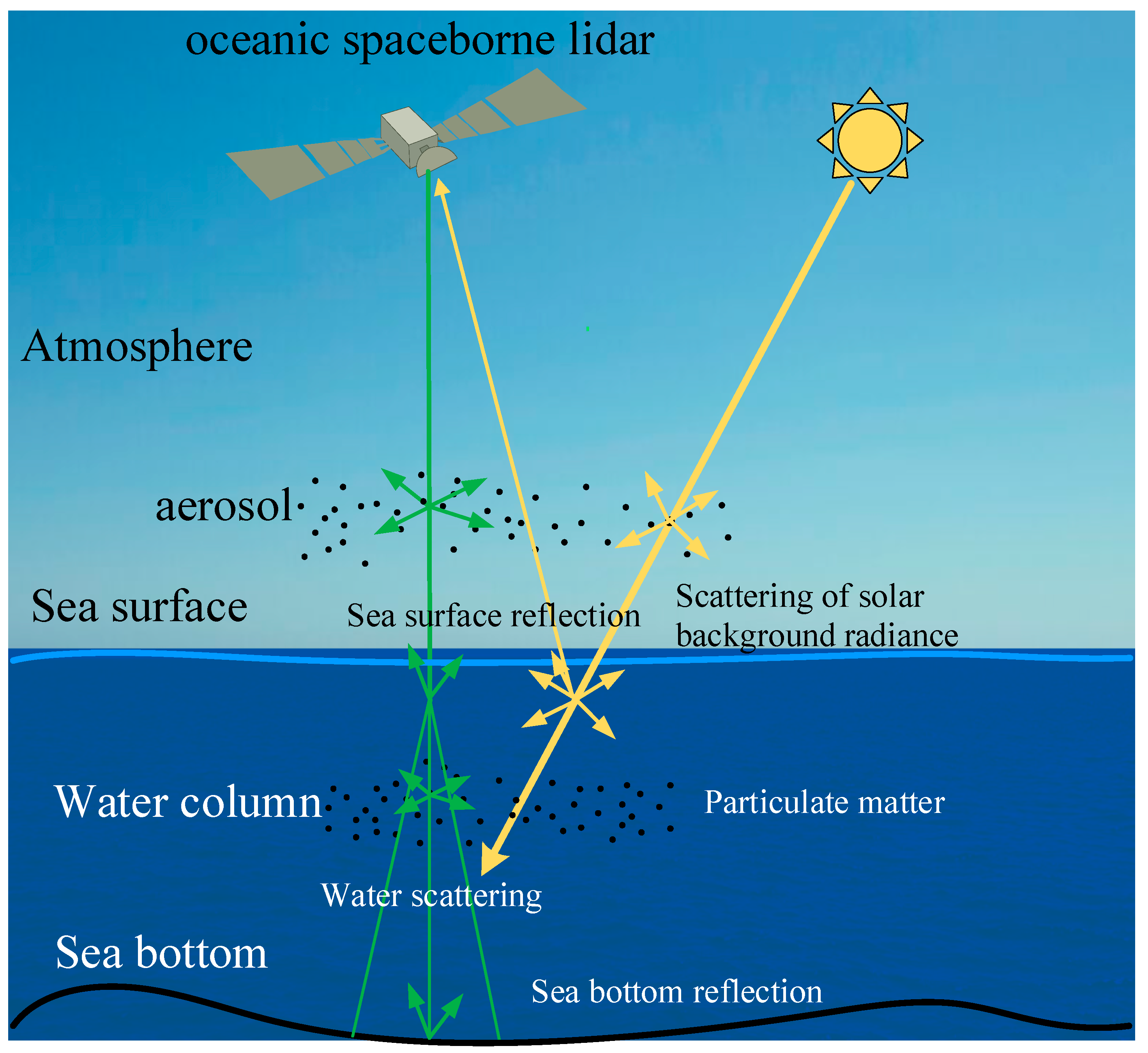
2.1. Lidar Return Signal Model

Based on the propagation process and theory, the depth-dependent lidar return signal $N_s\left(\lambda ,z\right)$ is described as follows [5]:

$$N_s\left(\lambda ,z\right)=\frac{E_{0}AO{T}_O{T}_a^2{T}_s^{2}v\eta \Delta t{\cos }^2\left(\theta \right)}{2n{\left(nH+z\right)}^{2}h\upsilon }\cdot {\beta }_{\pi }\left(\lambda ,z\right)\cdot \exp \left(-\frac{2{{\displaystyle \int }}_0^z{K}_{lidar}\left(\lambda ,z^{\prime }\right)d{z}^{\prime }}{\cos {\theta }_w}\right)$$

(1)

where $E_0$ is laser pulse energy, $A$ is receiver aperture area, $O$ is the overlap factor equal to 1 for spaceborne oceanic lidar, $T_O$ is the transmission of receiver optics, $T_a$ is the one-way transmission through the atmosphere, $T_s$ is the surface transmission, $v$ is the speed of light in vacuum, $\eta$ is the quantum efficiency of the detector, $n$ is the water index of refraction, $H$ is the lidar altitude, $\upsilon$ is the frequency of the laser, $h$ is the Planck constant which is $6.626\times {10}^{-34}\mathrm{J}·\mathrm{s}$, ${\beta }_{\pi }\left(\mathsf{\lambda },\mathrm{z}\right)$ is the angular volume scattering coefficient at the scattering angle of $\mathsf{\pi }$, $\Delta t$ is the pulse width, $\theta$ is the zenith angle of laser in the atmosphere, and ${\theta }_w$ is the zenith angle of laser in the ocean. $K_{lidar}\left(\lambda ,z^{\prime }\right)$ is the effective lidar attenuation coefficient that is expressed as follows [5]:

$$K_{lidar}=K_d+\left(c-K_d\right)\exp \left(-0.85cD\right)$$

(2)

where $K_d$ is the diffuse attenuation coefficient, $c$ is the beam attenuation coefficient, and $D$ is the lidar spot diameter on the water surface.

Consider the emitted laser pulse as a Gaussian distribution [28], as follows:

$$w\left(t_x\right)=\frac{2}{\Delta t}\sqrt{\frac{\ln 2}{\pi }}\exp \left(-4\ln 2\frac{{\left(t-t_x\right)}^2}{\Delta t}\right)$$

(3)

where $t_x$ is the two-way time delay of the laser pulse from the sea surface $t_{ss}$, water column $t_{wc}$ or seafloor $t_{sf}$ to the detector.

The echo photon density function of the photon-counting lidar system can be expressed as follows:

$$N_T\left(t\right)=N_{ss}\ast w\left(t_{ss}\right)+N_{wc}\ast w\left(t_{wc}\right)+N_{sf}\ast w\left(t_{sf}\right)+N_{bg}+N_d$$

(4)

where $N_{ss}$, $N_{wc}$, and $N_{sf}$ are the returned photons from the sea surface, water column, and seafloor, respectively. $N_{bg}$ is the background light noise rate, and $N_d$ is the dark counting rate of the detector.

The returned signal from the sea surface is given by:

$$N_{ss}=\frac{E_{0}AO{T}_O{T}_a^2\eta {\gamma }_s{\cos }^2\left(\theta \right)}{H^{2}h\upsilon }$$

(5)

$$t_{ss}=\frac{2H}{v\cos \left(\theta \right)}$$

(6)

where ${\gamma }_s$ is the sea surface lidar backscatter.

The returned signal from the water column is given by Equation (1) and $t_{wc}$ is expressed as follows:

$$t_{wc}=t_{ss}+\frac{2z}{ \raisebox{1ex}{$v$}\!\left/ \!\raisebox{-1ex}{$n$}\right.\cos {\theta }_w}$$

(7)

The returned signal from the seafloor is given by:

$$N_{sf}=\frac{E_{0}AO{T}_O{T}_a^2{T}_s^2\eta {\cos }^2\left(\theta \right)R_b}{\pi {\left(nH+\mathrm{Z}\right)}^{2}h\upsilon }\exp \left(-\frac{2{{\displaystyle \int }}_0^Z{K}_{lidar}\left(\lambda ,z^{\prime }\right)d{z}^{\prime }}{\cos {\theta }_w}\right)$$

(8)

$$t_{sf}=t_{ss}+\frac{2Z}{\raisebox{1ex}{$v$}\!\left/ \!\raisebox{-1ex}{$n$}\right.\cos {\theta }_w}$$

(9)

where $Z$ is the bathymetry and $R_b$ is the bottom reflectance.

The background light noise rate is calculated as follows:

$$N_{bg}=\frac{L_{B}A{\mathsf{\Omega }}_{\mathrm{FOV}}\Delta \lambda T_o}{h\upsilon }$$

(10)

where ${\mathsf{\Omega }}_{\mathrm{FOV}}$ is the receiver solid angle that is equal to $\mathsf{\pi }{\left(\frac{\mathrm{FOV}}{2}\right)}^2$, FOV is the field angle of view of the receiver, $\Delta \lambda$ is the filter bandwidth, and $L_B$ is the spectral radiance of background sunlight that can be expressed as follows [29]:

$$L_B\left(\lambda \right)=\frac{\omega F\left(\lambda \right)\cos \left(\theta \right)}{\pi }$$

(11)

where $\omega$ is the ocean albedo that equals 0.1 [29] and $F\left(\lambda \right)$ is the solar spectral irradiance given in [30].

Subsequently, the average number of photons for each time bin can be calculated as follows [31]:

$$\overline{N}\left(n\right)={{\displaystyle \int }}_{\left(n-1\right)\Delta }^{n\Delta }{N}_T\left(t\right)dt$$

(12)

where $\Delta$ is each event timing precision.

Considering the receiver’s dead time, the detection probability for each bin in the multi-trigger model is given by [31]

$$P\left(n+1\right)=\{\begin{array}{c}\left(\frac{\exp \left(-\overline{N}\left(n\right)\right)}{1-\exp \left(-\overline{N}\left(n\right)\right)}P\left(n\right)+P\left(n-\left(d-1\right)\right)\right)\left(1-\exp \left(-\overline{N}\left(n+1\right)\right)\right), \left(n\ge d\right)\\ \frac{\exp \left(-\overline{N}\left(n\right)\right)\left(1-\exp \left(-\overline{N}\left(n+1\right)\right)\right)}{1-\exp \left(-\overline{N}\left(n\right)\right)}P\left(n\right), (n<d)\end{array}$$

(13)

where $d=ceil\left(t_d/\Delta \right)$ means the dead time would occupy the number of bins, and $t_d$ is the receiver’s dead time.

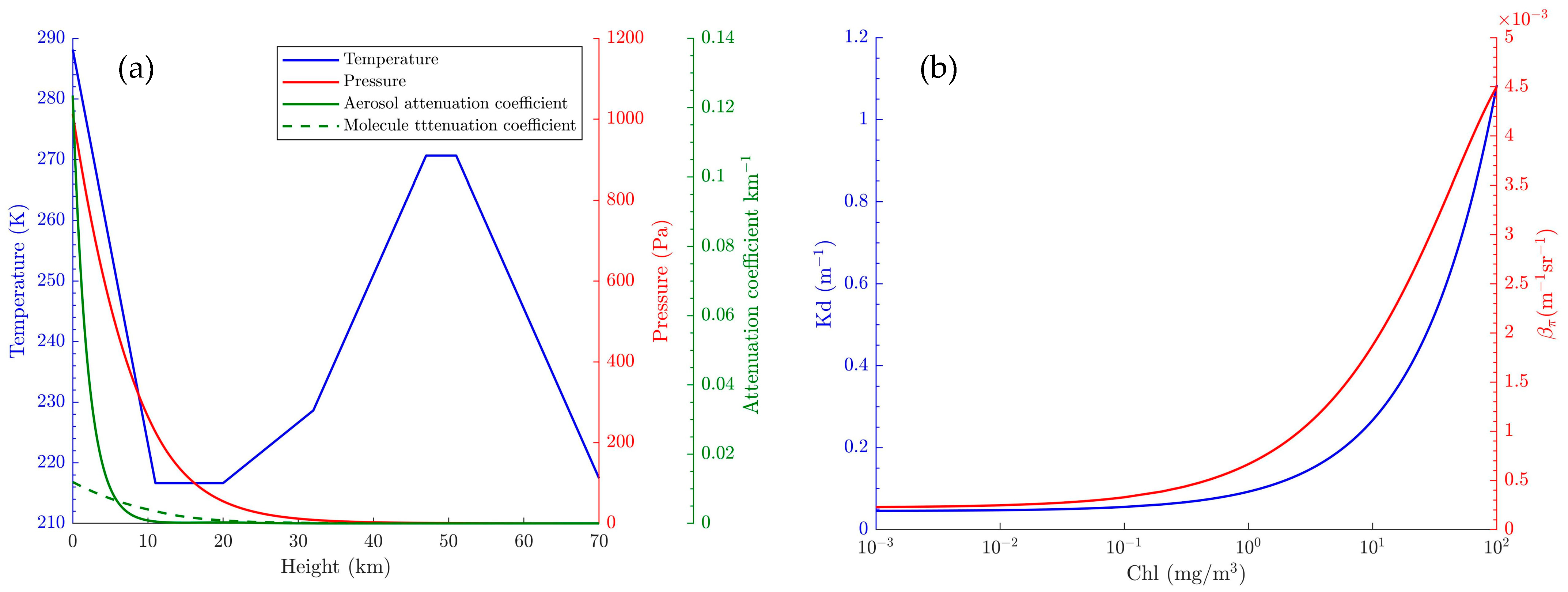
2.2. Atmosphere Model

The molecular scattering is taken into account to calculate the atmosphere transmission for various wavelengths. According to the atmospheric attenuation model [32], the molecular attenuation coefficient is expressed as follows:

$${\alpha }_m\left(h_a\right)={\sigma }_m\cdot N_m\left(h_a\right)\cdot {10}^5$$

(14)

where ${\alpha }_m$ is the molecular attenuation coefficient (${\mathrm{km}}^{-1}$), ${\sigma }_m$ is the molecular scattering cross-section (${\mathrm{cm}}^2$) expressed in the atmospheric attenuation model, $N_m$ is the molecular number density (${\mathrm{cm}}^{-3}$) obtained from the U.S. Standard Atmosphere, 1976 [33], and $h_a$ is the altitude (km).

The aerosol attenuation coefficient is calculated based on [34] as follows:

$${\alpha }_a\left(h_a\right)=\left[2.47\times {10}^{-3}\exp \left(-\frac{h_a}{2}\right)+5.13\times {10}^{-6}\exp \left(-\frac{{\left(h_a-20\right)}^2}{36}\right)\left(\frac{532}{\lambda }\right)\right]\times 50$$

(15)

After the calculation of the molecular attenuation coefficient and aerosol attenuation coefficient, the transmittance through the atmosphere can be derived as follows:

$$T_a=\exp (-{{\displaystyle \int }}_0^H\left({\alpha }_m\left(h_a\right)+{\alpha }_a\left(h_a\right)\right)d{h}_a)$$

(16)

The temperature and pressure profiles used in our model and aerosol and molecular attenuation coefficient at 532 nm are shown in Figure 2a. It is shown that aerosols make a great contribution to light attenuation near the surface, while molecular scattering becomes more dominant, gradually, with the increase of height.

2.3. Hydrosol Model

$K_d\left(\lambda \right)$ is the sum of the attenuation due to pure water $K_w\left(\lambda \right)$ and attenuation due to biological components $K_{bio}\left(\lambda \right)$:

$$K_d\left(\lambda \right)=K_w\left(\lambda \right)+K_{bio}\left(\lambda \right)$$

(17)

$K_w\left(\lambda \right)$ is given directly in [35]. $K_{bio}\left(\lambda \right)$ is calculated as a function of chlorophyll concentration $Chl$ as follows:

$$K_{bio}\left(\lambda \right)=\chi \left(\lambda \right)\cdot Ch{l}^{e\left(\lambda \right)}$$

(18)

where $\chi \left(\lambda \right)$ and $e\left(\lambda \right)$ are scaling factors retrieved from [35].

Accounting for both molecular scattering and particle scattering, ${\beta }_{\pi }\left(\lambda \right)$ can be computed as follows:

$${\beta }_{\pi }\left(\lambda \right)={\tilde{\beta }}_{\pi ,w}{b}_w\left(\lambda \right)+{\tilde{\beta }}_{\pi ,p}\left(chl\right)b_p\left(chl,\lambda \right)$$

(19)

where ${\tilde{\beta }}_w\left(\psi \right)$ and $b_w\left(\lambda \right)$ are the scattering phase function and scattering coefficient of optically pure seawater, respectively. According to [36], we have:

$${\tilde{\beta }}_w\left(\psi \right)=\frac{3}{4\pi \left(3+p\right)}\left(1+p{\cos }^2\psi \right),p=0.84$$

(20)

$$b_w\left(\lambda \right)=b_{w550}{\left(\frac{\lambda }{550}\right)}^{-4.3},b_{w550}=1.7\times {10}^{-3}{\mathrm{m}}^{-1}$$

(21)

${\tilde{\beta }}_{\pi ,p}\left(chl\right)$ is the particulate phase function that can be obtained by extrapolating from the results of [37]:

$${\tilde{\beta }}_{\pi ,p}=0.151\frac{b_{bp}}{b_p}$$

(22)

where $b_{bp}$ and $b_p$ are the backscattering coefficient and scattering coefficient of the particulate. Their ratio can be approximated by [36]:

$$\frac{b_{bp}}{b_p}=0.002+0.01\left[0.5-0.25{\log }_{10}\left(chl\right)\right]$$

(23)

$b_p\left(\lambda \right)$ is calculated as a function of the chlorophyll concentration $Chl$ [35]:

$$b_p\left(\lambda \right)=b_{p,550}\left(chl\right)\ast {\left(\frac{\lambda }{550}\right)}^{v_e}$$

(24)

$$b_{p550}\left(Chl\right)=0.416{\left(Chl\right)}^{0.766}$$

(25)

where $v_e$ is the varying exponent given in [35].

The $K_d$ and ${\beta }_{\pi }$ calculated with the wavelength of 532 nm are shown in Figure 2b.

For coastal waters, the total absorption coefficient includes seawater, particles, and colored dissolved organic matter (CDOM), as follows:

$$a\left(\lambda \right)=a_w\left(\lambda \right)+a_p\left(\lambda \right)+a_g\left(\lambda \right)$$

(26)

where $a_w\left(\lambda \right)$ is the absorption coefficient of pure water that has been measured in [38]. $a_p\left(\lambda \right)$ is the absorption coefficient of the particles and is mainly contributed by chlorophyll-a. It can be estimated by [39]:

$$a_p\left(\lambda \right)=A\left(\lambda \right){\left(Chl\right)}^{E\left(\lambda \right)}$$

(27)

where $A\left(\lambda \right)$ is the specific absorption coefficient and $E\left(\lambda \right)$ is the index absorption coefficient. The used data come from the Ocean Optics Web Book [40]. $a_g\left(\lambda \right)$ is the absorption coefficient of CDOM, which can be estimated as follows [41]:

$$a_g\left(\lambda \right)=a_g\left({\lambda }_0\right)\times \exp \left(-S\left(\lambda -{\lambda }_0\right)\right)$$

(28)

where $S$ is the spectral absorption slope, and $a_g\left({\lambda }_0\right)$ is the absorption coefficient of CDOM at the reference wavelength ${\lambda }_0$.

2.4. Sea Surface and Seafloor Modeling

The wind-driven rough sea surface can be approximated by the Cox and Munk sea surface slope probability distribution function [42,43]:

$$p\left({\mu }_n,{\phi }_n\right)=\frac{1}{\pi {\sigma }^2{\mu }_n^3}\exp \left(-\frac{1-{\mu }_n^2}{{\sigma }^2{\mu }_n^2}\right)$$

(29)

where ${\mu }_n=\cos \left({\theta }_n\right)$, ${\theta }_n$, and ${\phi }_n$ are the polar and azimuth angles of the wave facet normal vector $\overrightarrow{n}$, respectively. ${\sigma }^2$ is the wave slope variance that is the function of the sea surface wind $W$:

$${\sigma }^2=0.003+0.00512W$$

(30)

The transmission of wave facets $T_w\left({\mu }_0,{\phi }_0,\mu ,\phi \right)$ can be expressed as follows:

$$T_w\left({\mu }_0,{\phi }_0,\mu ,\phi \right)=S\left(\mu ,{\mu }^{\prime }\right)\frac{\pi p\left({\mu }_n,{\phi }_n\right)}{4\left|\mu \right|\left|{\mu }^{\prime }\right|{\mu }_n}{T}_F\frac{n^2\cos {\theta }_t^a\cos {\theta }_i^a}{{\left(n\cos {\theta }_t^a-\cos {\theta }_i^a\right)}^2}$$

(31)

where $S\left(\mu ,{\mu }^{\prime }\right)$ is the shadowing function, $T_F$ is the Fresnel transmittance, ${\theta }_i^a$ and ${\theta }_t^a$ are the incidence angle and refraction angle relative to the wave facet normal vector.

Then, the sea surface transmittance can be calculated as follows:

$$T_s\left({\mu }_0\right)=\frac{1}{\pi }{{\displaystyle \int }}_0^1\mu d\mu {{\displaystyle \int }}_0^{2\pi }d\phi T_w\left({\mu }_0,{\phi }_0,\mu ,\phi \right)$$

(32)

The sea surface lidar backscatter ${\gamma }_s$ (in the unit of ${\mathrm{sr}}^{-1}$) is written as follows [44]:

$${\gamma }_s=\frac{R_F}{4\pi {\sigma }^2{\cos }^4\theta }\exp \left(-\frac{{\tan }^2\theta }{2{\sigma }^2}\right)$$

(33)

where $R_F$ is the Fresnel reflectance.

The Lambertian reflectance model is used to calculate the returned signal from the seafloor.

2.5. Background Light and Detector Noise Model

To compute the signal-to-noise (SNR) ratio, we take into account the shot noise of the receiver. For the analog detection mode of a receiver, the standard deviation of the detector signal for a single lase shot can be expressed as follows [45]:

$$\delta N\left(z\right)=\sqrt{F_m\left[N_s\left(z\right)+N_b\right]+\frac{I_d^2\Delta t}{M^2{e}^2}}$$

(34)

where $e$ is the elementary charge, $F_m$ is the detector excess noise factor, $I_d$ is the noise current of the detector, $M$ is the multiplication factor, and $N_b$ is background signal power due to solar radiance that is given as follows:

$$N_b=N_{bg}\Delta t$$

(35)

For a photon-counting mode detector, the standard deviation of the detected photoelectron number is given as follows [45]:

$$\delta N\left(z\right)=\sqrt{N_s\left(z\right)+N_b+N_d\Delta t}$$

(36)

where $N_d$ is the dark count rate of the detector.

Then, the signal to noise ratio of the return signal can be expressed as follows [45]:

$$\mathrm{SNR}=\frac{\sqrt{m}{N}_s}{\delta N\left(z\right)}$$

(37)

where m is the number of laser shots integrated.

Meanwhile, signal noise causes uncertainty in the detector signal, then the signal uncertainty leads to the uncertainty (error) in the signal measured by lidar. The relative error of the measurement is given by [46]:

$$\frac{\delta N\left(z\right)}{\sqrt{m}{N}_s}=\frac{1}{\mathrm{SNR}}$$

(38)

Thus, higher SNR leads to smaller measurement errors.

3. Results

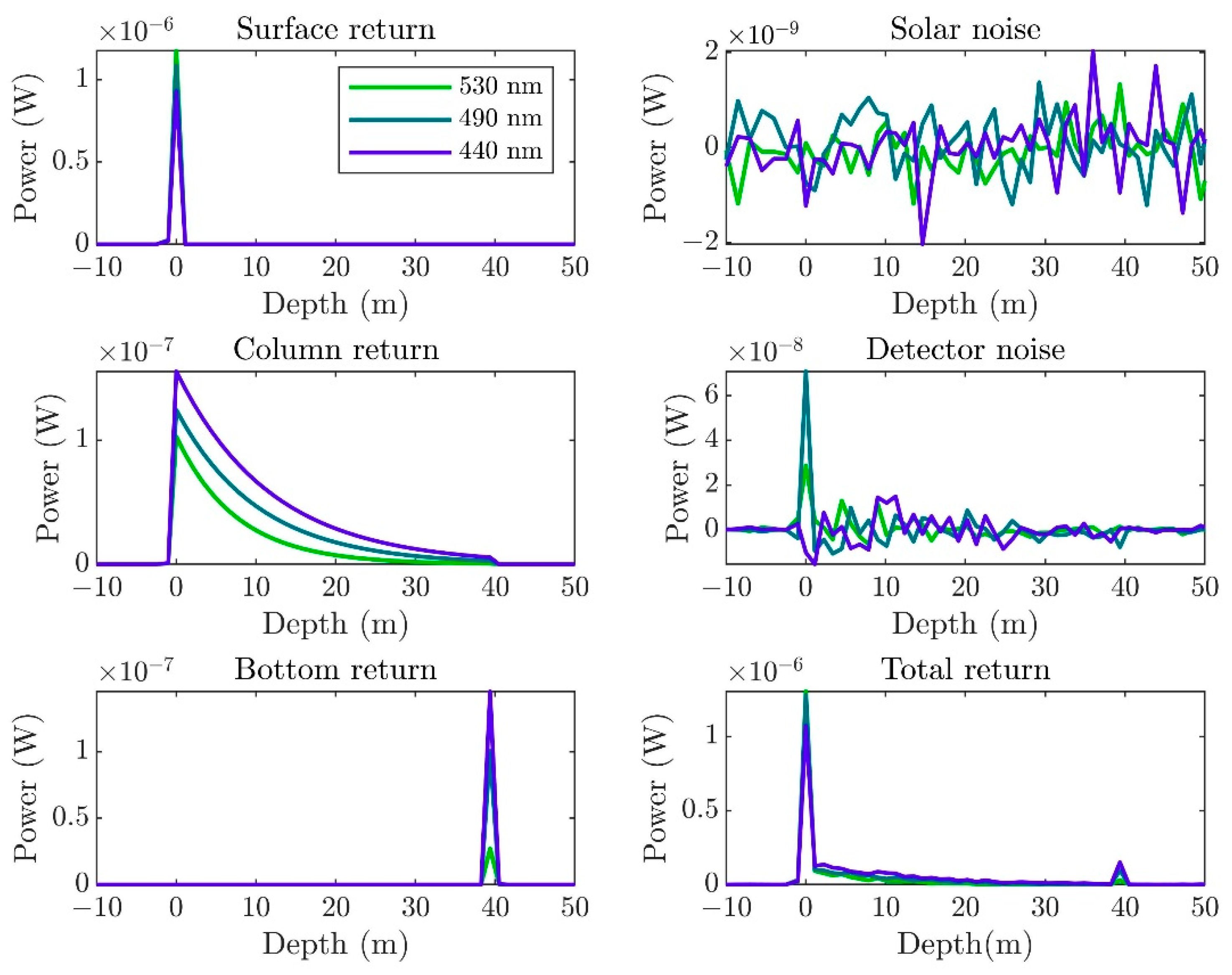
3.1. Simulation for Spaceborne Lidar with Analog Detection

The spaceborne lidar-simulated waveforms are calculated based on the lidar system parameters given in

Table 1. Parameters of spaceborne oceanic lidar system.

Parameter	Value	Parameter	Value
$\mathrm{Wavelength}\lambda$	532 nm	Refractive index n	1.33
Lidar altitude H	400 km	Dark current Id	$1.31\times {10}^{-13}{\mathrm{A}\mathrm{Hz}}^{-1/2}$
Pulse energy E0	1.3 J	Transmittance of the receiver optics TO	0.9
$\mathrm{Pulse}\mathrm{width}\Delta t$	7.2 ns	Transmittance through the sea surface Ts	0.95
PMT excess noise factor F	1.3	Aperture of the telescope D	1.5 m
Multiplication factor	100	Pulse repetition frequency	10 Hz
FOV of the receiver FOV	0.15 mrad	$\mathrm{Bandwidth}\mathrm{of}\mathrm{the}\mathrm{filter}\Delta \lambda$	0.1 nm

using SOLS. These parameters for spaceborne oceanic lidar system are partly derived from existing studies [45,47], and the detector parameters are consistent with previous studies [45].

Figure 3 shows the simulated waveforms of each part (sea surface return, sea column return, sea bottom return, solar background noise, detector shot noise, and total return signal, respectively) in clear water with a chlorophyll concentration of 0.1 mg/m³ and wavelengths of 530 nm, 490 nm, and 440 nm with a 40-m sea bottom depth. For CDOM, $a_g\left({\lambda }_0\right)=0.01 {\mathrm{m}}^{-1}$,${\lambda }_0=440 \mathrm{nm}, S=0.014 {\mathrm{nm}}^{-1}$. The temperature and pressure profiles are fixed. They come from U.S. Standard Atmosphere 1976, which used the sea surface level of the latitude $45°{32}^{\prime }{33}^{″}$ as a reference. Moreover, the temperature ${\mathrm{T}}_0=288.15 \mathrm{K}$, density ${\mathsf{\rho }}_0=1.225\mathrm{kg}/{\mathrm{m}}^3,$ pressure at the sea level ${\mathrm{P}}_0=\mathrm{101,325}\mathrm{kg}/{\mathrm{m}}^2$, and mean molecular mass of air ${\mathrm{M}}_0=28.9644\mathrm{g}/\mathrm{mol}$. For convenience, each wavelength is represented by its corresponding color. The lidar returns a large signal at the surface, and the signal falls off sharply with the increasing of depth. Finally, the bottom reflects a signal that can be distinguished from noise in very clear water. Total received photons show an apparent peak at the bottom as well, which indicates the potential for determining the bathymetry of spaceborne lidar sensors.

Figure 4 shows the SNR and the maximum detectable depths versus several different relative measurement errors. In the case of a water condition with a chlorophyll concentration of 0.1 $\mathrm{mg}/{\mathrm{m}}^3$, the wavelengths of 440 and 490 nm have close detectable depths, and they could penetrate 20 m more than 530 nm when the SNR is 4, as shown in Figure 4a, which indicates that the wavelength is vital for the lidar system. If we broaden the threshold, the differences between the three wavelengths will increase. When the relative measurement is 100%, their difference reaches 40 m.

Figure 5 shows the results with different types of water. In clean water where chlorophyll concentration is 0.03 mg/m³, the lidar can penetrate more than 100 m and the corresponding optimum wavelength is 440 nm. Moreover, the detectable depth varies greatly between different wavelengths. As shown in Figure 5, the wavelength of 440 nm could reach 50 m more than 530 nm for clean water. However, in areas with higher chlorophyll concentrations, such as coastal water, and the chlorophyll concentration is about 0.3 mg/m³, the detectable depths are much smaller, and the corresponding optimum wavelength turns into 490 nm. As the chlorophyll concentration continues to increase, the corresponding optimum wavelength moves into green bands, and the wavelength of 530 nm has the maximum depth in this condition. This result shows an apparent fact that different types of water correspond to different optimum wavelengths, and the results between wavelengths have large differences. Figure 5b shows the echo signals and their corresponding solar background. Compared with Figure 5a, the depth where the echo signal equals the solar background is a little deeper than the maximum detectable depth indicated by the SNR in Figure 5a. This is largely because the SNR takes into account not only the solar background but also the detector noise. The results show that a proper wavelength can greatly improve the detection capability of the lidar system.

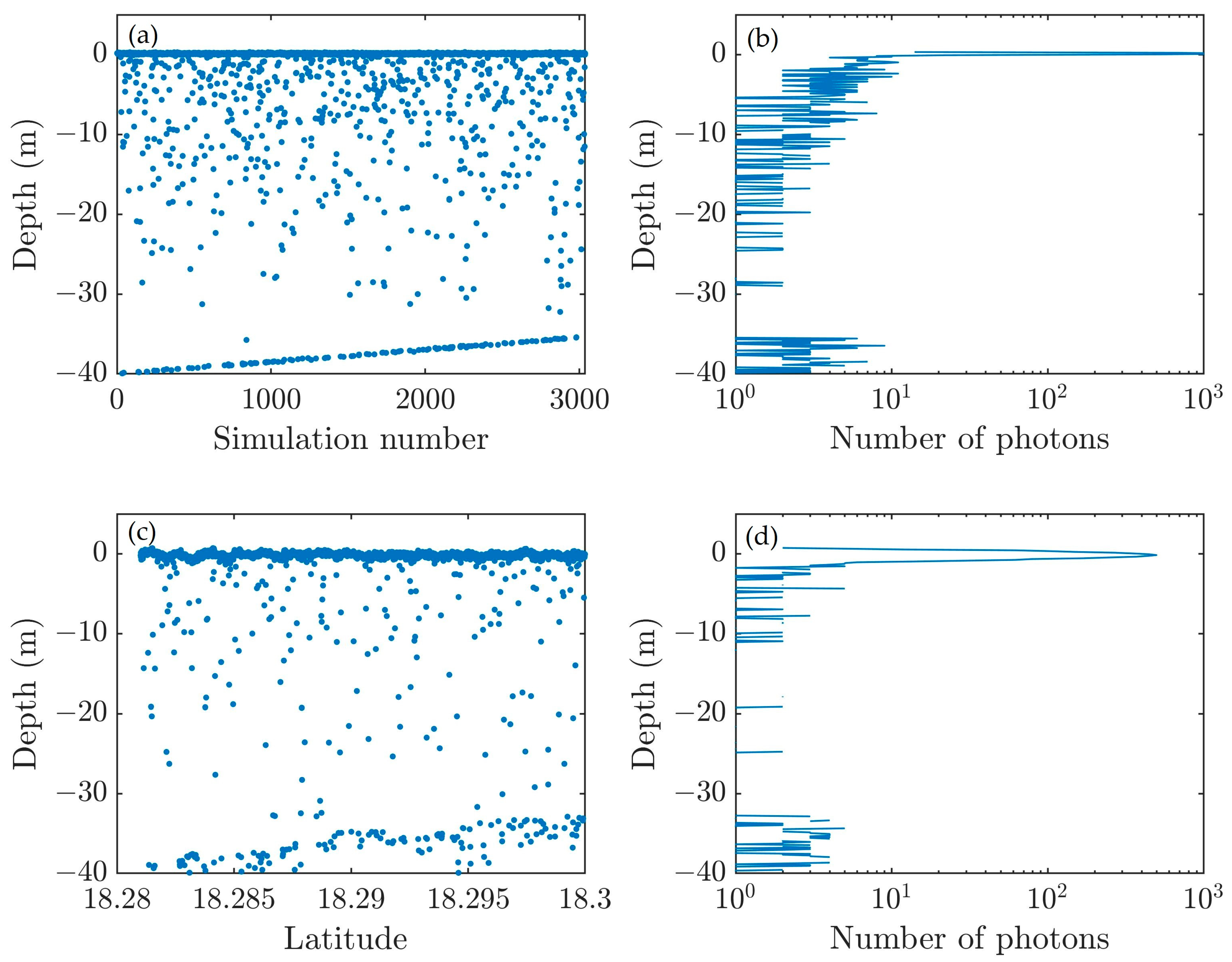
3.2. Simulation for Spaceborne Photon Counting Lidar with ICESat-2 Parameters

Then we compared the simulated results with ICESat-2 parameters [48,49].

Table 2. Parameters of ICESat-2 [48,49].

Parameter	Value	Parameter	Value
$\mathrm{Wavelength}\lambda$	532.27 nm	$\mathrm{Receiver}\mathrm{counting}\mathrm{efficiency}\eta$	0.15
Lidar altitude H	500 km	$\mathrm{Dark}\mathrm{count}\mathrm{rate}{N}_d$	$1000\mathrm{Hz}$
Pulse energy E0	93.5 μJ	Transmittance of the receiver optics TO	0.41
$\mathrm{Pulse}\mathrm{width}\Delta t$	1.25 ns	$\mathrm{Bandwidth}\mathrm{of}\mathrm{the}\mathrm{filter}\Delta \lambda$	38 pm
Receiver effective area A	0.41 m	Pulse repetition frequency	10 kHz
Receiver dead time	3.2 ns	$\mathrm{Event}\mathrm{timing}\mathrm{precision}\Delta$	200 ps
FOV of the receiver FOV	$83.5\mathsf{\mu }\mathrm{rad}$	Laser beam divergence	$24\mathsf{\mu }\mathrm{rad}$

and the measured result in ATL03 dataset ATL03_20181122060325_08340107_004_01 located at St. Thomas Island. The dataset from 18.281°N to 18.3°N, where the seafloor is relatively flat, was extracted for verification. The region spans 2125.3 m and the number of corresponding laser shots is 3037, considering the pulse repetition frequency of ICESat-2. As shown in Figure 6, the detected photon events have similar distributions and the number of integrated photons at the sea surface and the seafloor are close. The results have verified the effectiveness of SOLS.

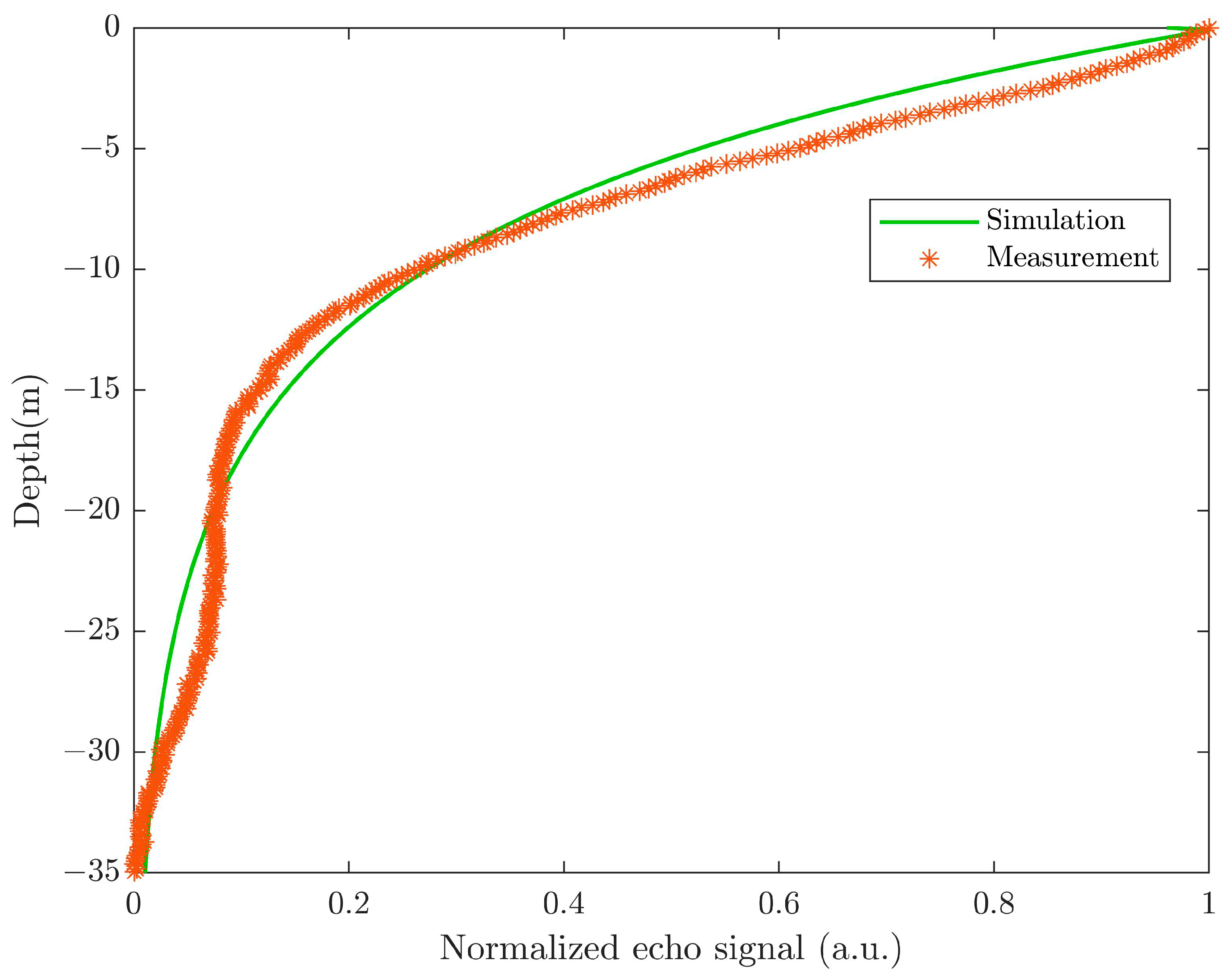
3.3. Simulation for Airborne Lidar with HawkEye System Parameters

SOLS can be used for simulation of airborne lidar as well. The results were simulated by using SOLS with HawkEye system parameters, as shown in

Table 3. Parameters of Hawkeye system parameters [47].

Parameter	Value	Parameter	Value
$\mathrm{Wavelength}\lambda$	532 nm	Refractive index n	1.33
Lidar altitude H	200 m	Dark current Id	$10\times {10}^{-8}\mathrm{A}$
Pulse energy E0	3 mJ	Transmittance of the receiver optics TO	0.9
$\mathrm{Pulse}\mathrm{width}\Delta t$	7 ns	Transmittance through the sea surface Ts	0.95
PMT excess noise factor F	3	Receiver area A	$0.025{\mathrm{m}}^2$
Detector bandwidth B	142 MHz	$\mathrm{Detector}\mathrm{responsivity}{R}_{\lambda }$	0.3 A/W
FOV of the receiver FOV	30 mrad	$\mathrm{Bandwidth}\mathrm{of}\mathrm{the}\mathrm{filter}\Delta \lambda$	1 nm

. The wavelengths of 440 and 490 nm were simulated as well. Figure 7 shows the simulated waveforms of each part in clear water with a chlorophyll concentration of 0.1 mg/m³. Similar to previous results, there is a peak at the surface, which then decays rapidly until a small peak occurs again at the bottom. Because of the lower laser energy of HawkEye, the return signal from the seafloor is much less, but it is distinguished from noise and the water column signal in logarithmic coordinates, as shown in Figure 7. The results demonstrate the ability of SOLS to simulate airborne lidar systems.

To validate its simulation ability for airborne lidar system, we compared the simulation results with in situ measurements using the system parameters of Mapper 5000 developed by the Shanghai Institute of Optics and Fine Mechanics (SIOM). Its wavelength is 532 nm and the detector telescope’s diameter is 200 mm. The detailed system configurations are in [9,12]. The in situ measurement was carried out at the station of 109.8164°E, 18.3144°N off Wuzhizhou Island on 30 September 2017. The comparison result is shown in Figure 8. The coefficient of determination (R²) is 0.98, the mean absolute difference (MAD) is 0.03, and the root mean square error (RMSE) is 0.029. The simulation result is in good agreement with the measurement, which demonstrates the validation of SOLS to simulate airborne lidar systems in real oceanic conditions.

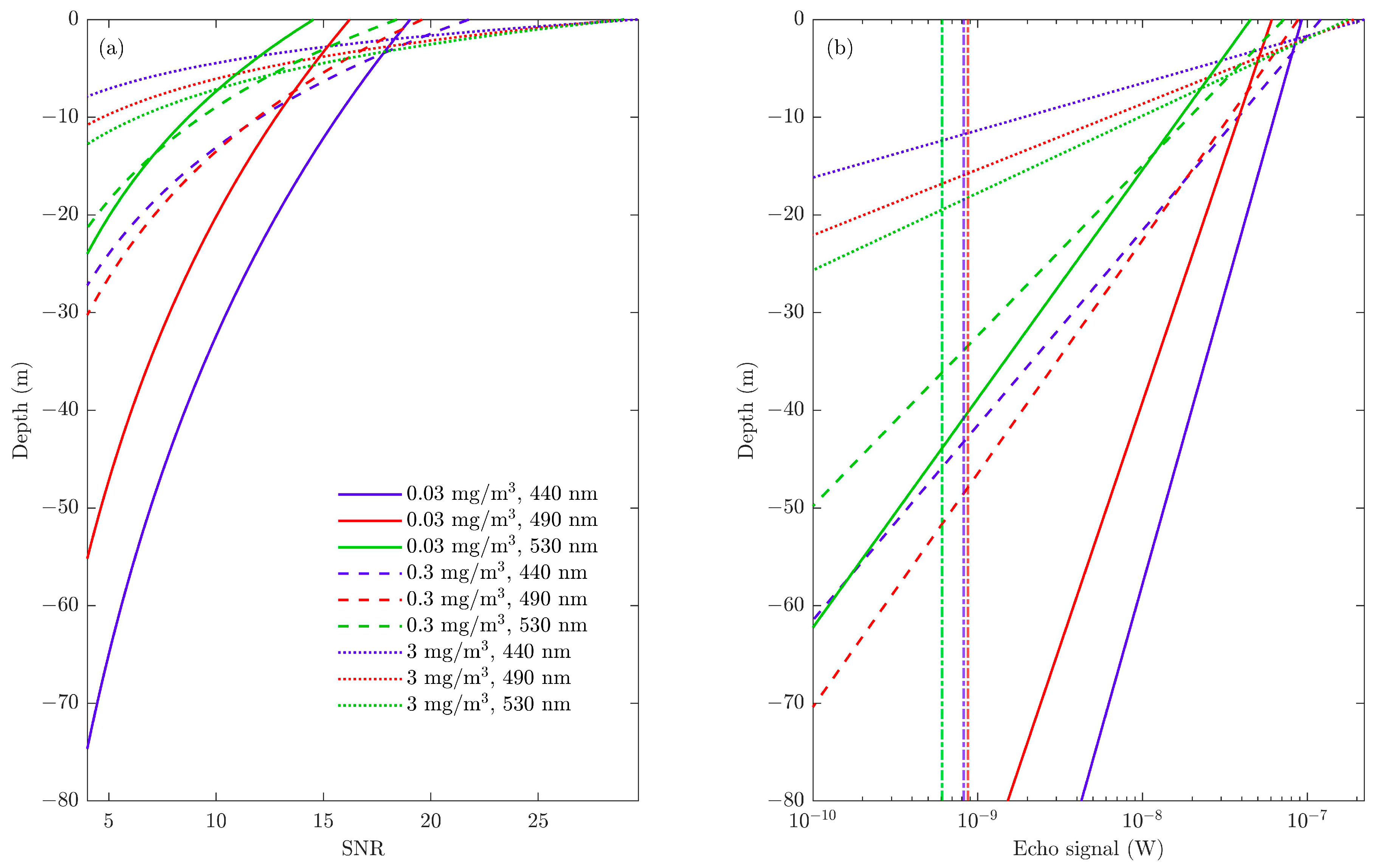
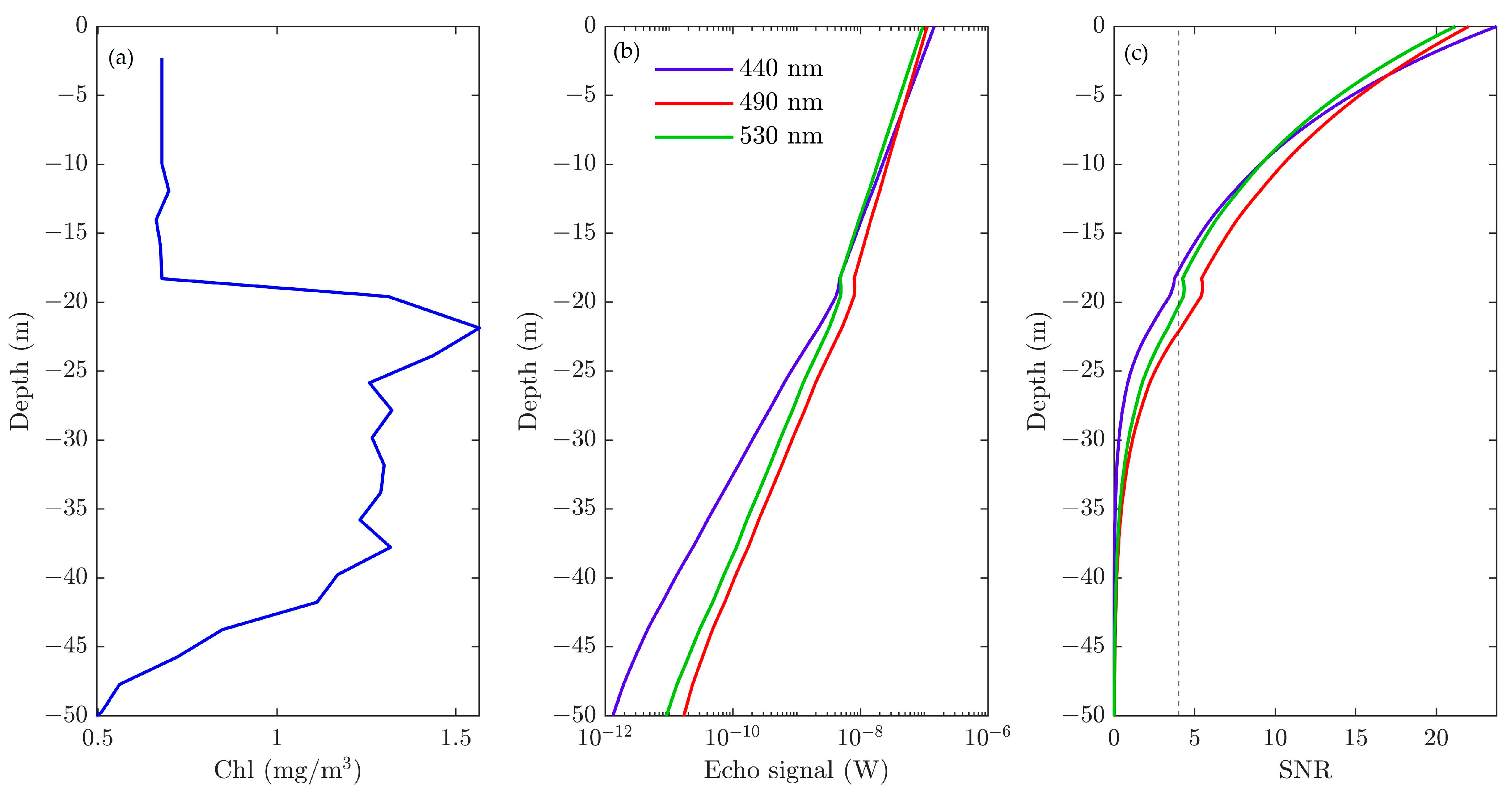
3.4. Simulation for Stratified Water with Bio-Argo Input Data

The biogeochemical Argo dataset named BD1902303_046 is used here to simulate stratified water. First, the corresponding optical parameters were calculated based on the hydrosol model in Section 2.3. Then the integral of $K_{lidar}\left(\lambda ,z\right)$ was used for stratified water. In particular, the MATLAB function cumtrapz was used to integrate a set of discrete data. Figure 9 shows the chlorophyll concentration profile measured by biogeochemical Argo and simulated return power based on the same lidar parameters shown in Table 1. There is an apparent chlorophyll maximum layer shown in the profile, and a corresponding bulge occurs in the echo signal that can be used to detect the chlorophyll maximum layer. The SNR in Figure 9c shows that the change caused by chlorophyll concentration can be distinguished from the noise for wavelengths of 490 and 530 nm, while the SNR of 440 nm is below 4 at depth of 20 m. Considering the high chlorophyll concentration, 532 nm has the best penetration and the maximum depth is much shallower. The results show that SOLS can deal with stratified water.

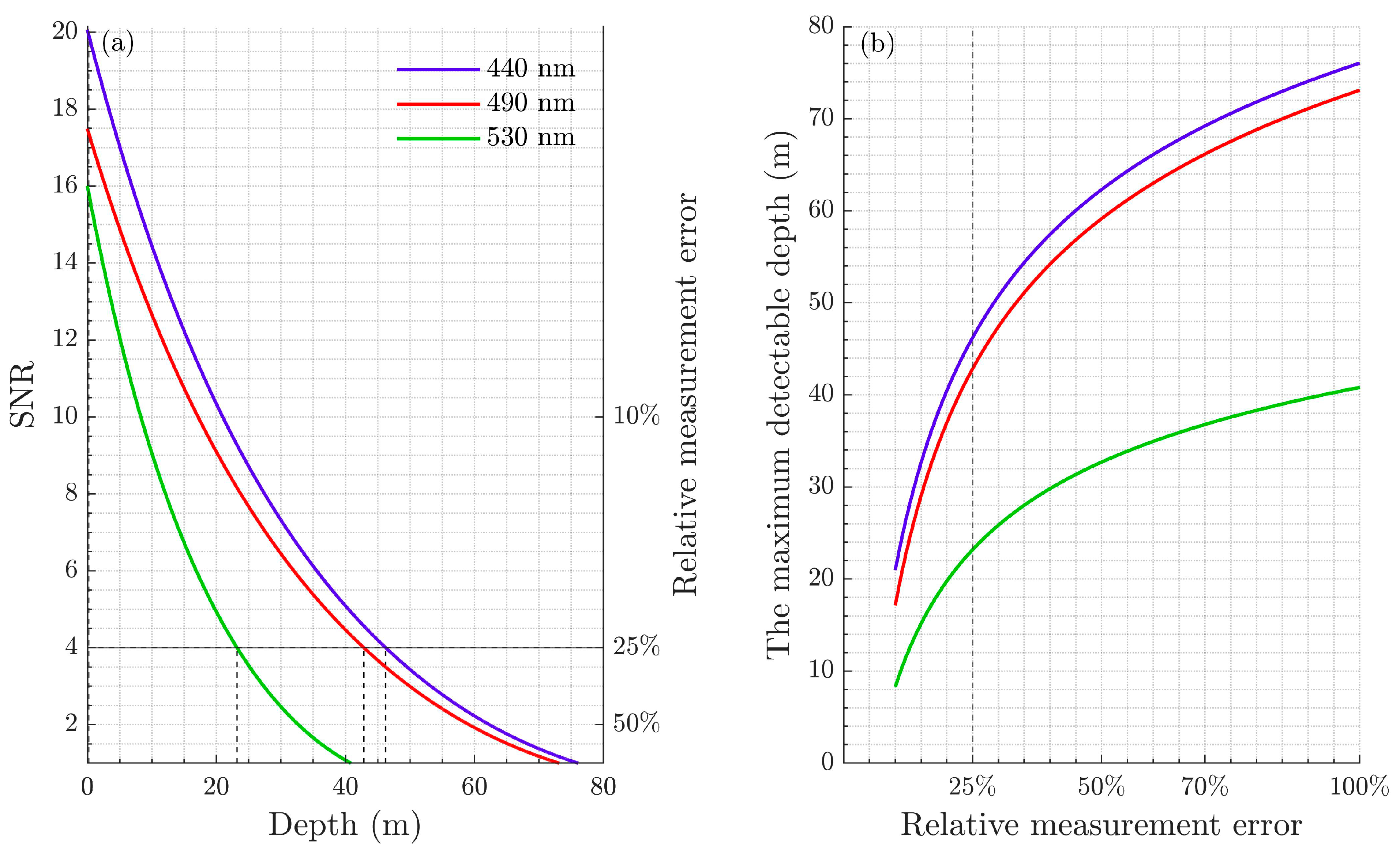
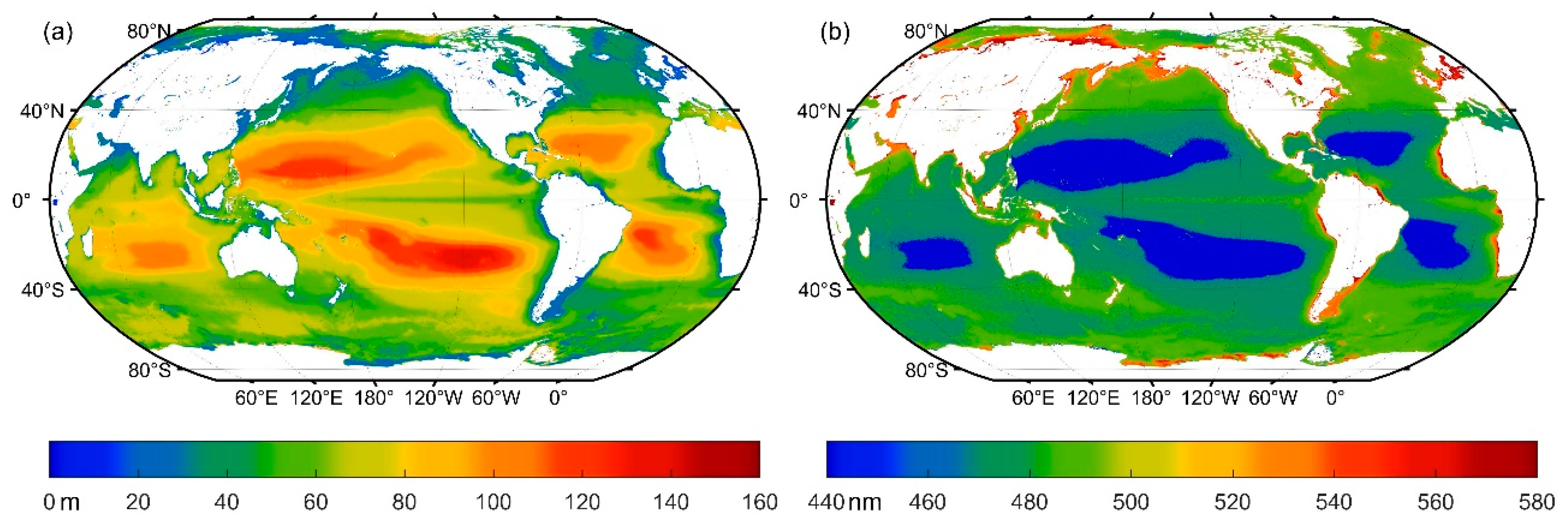
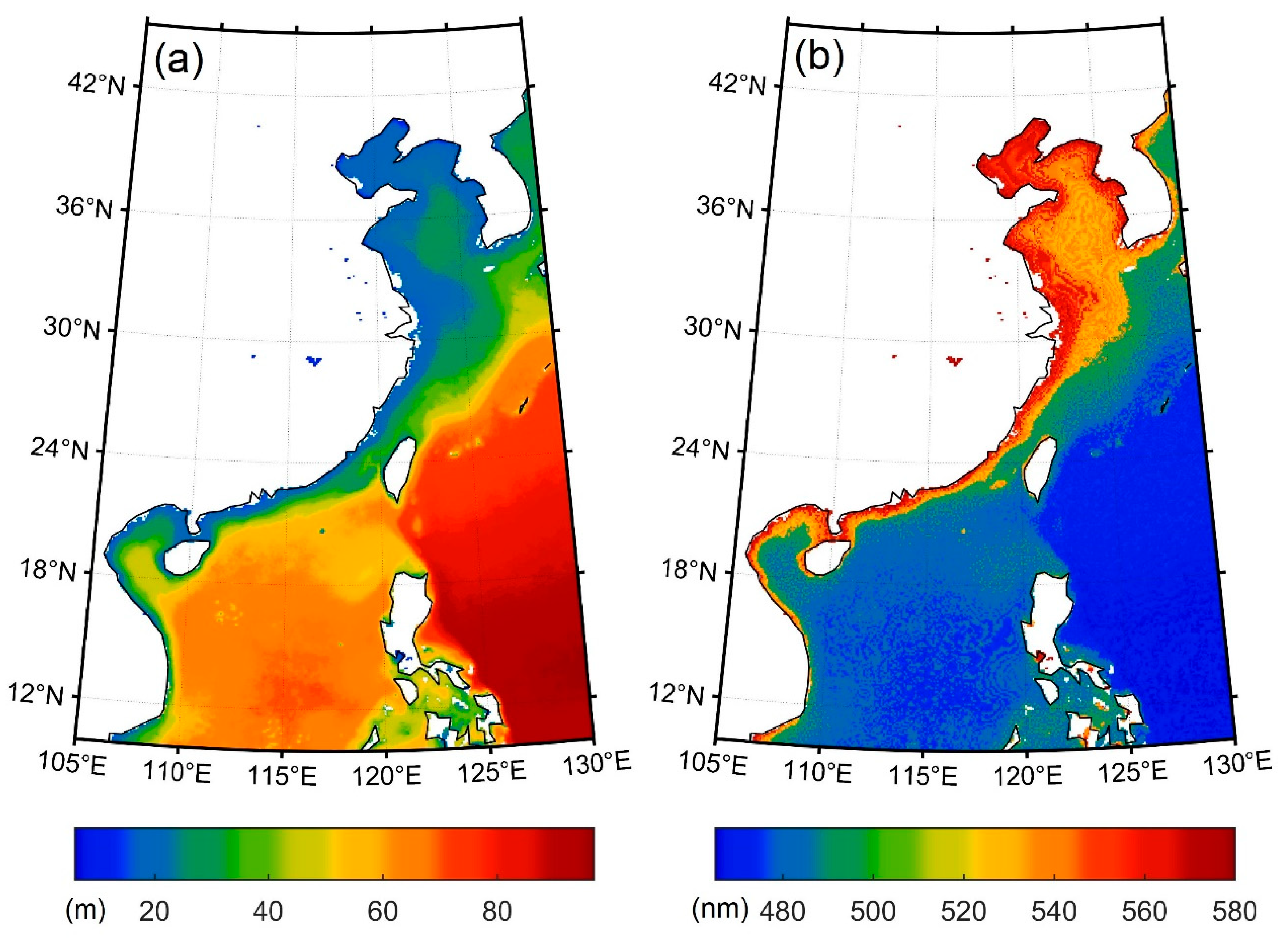
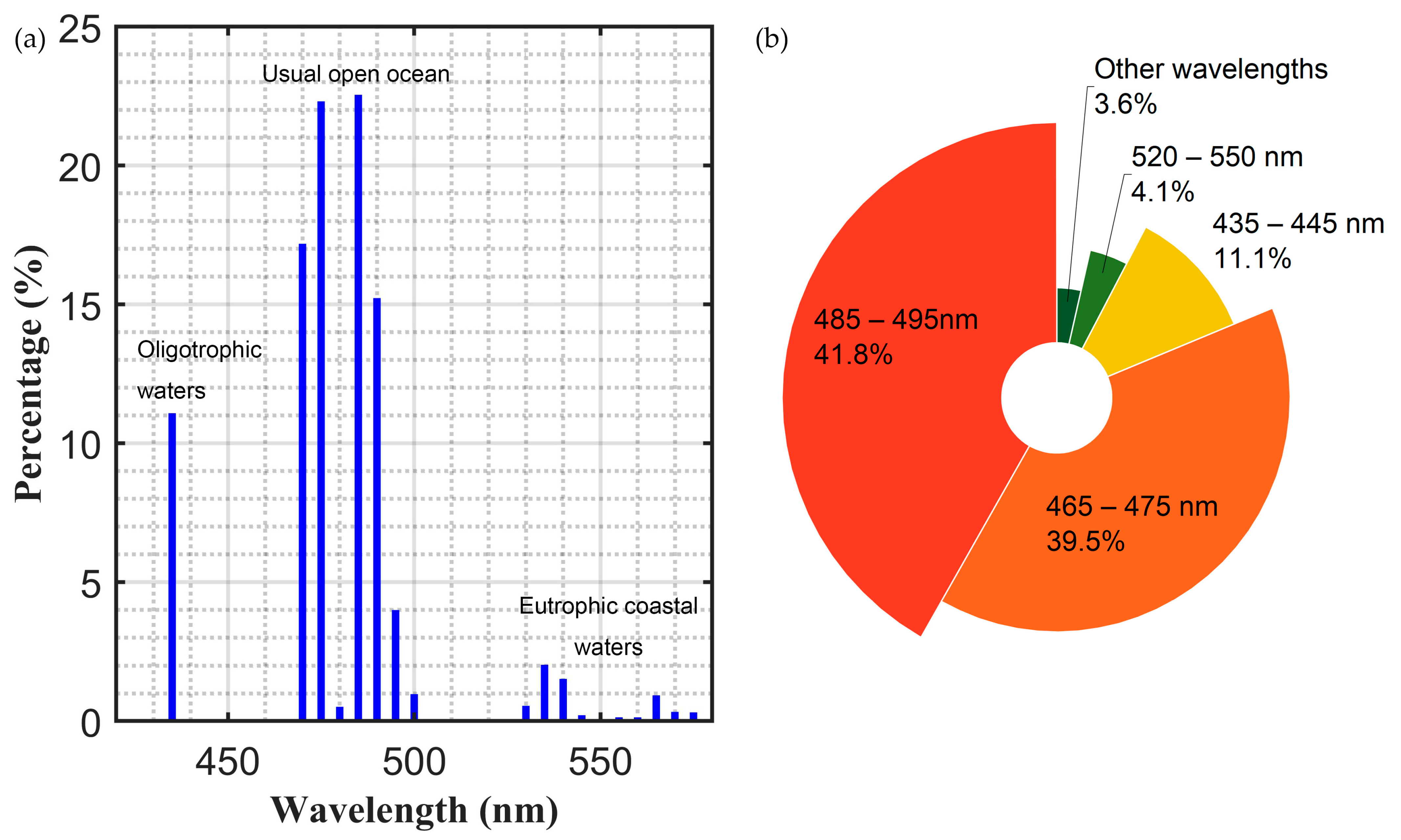
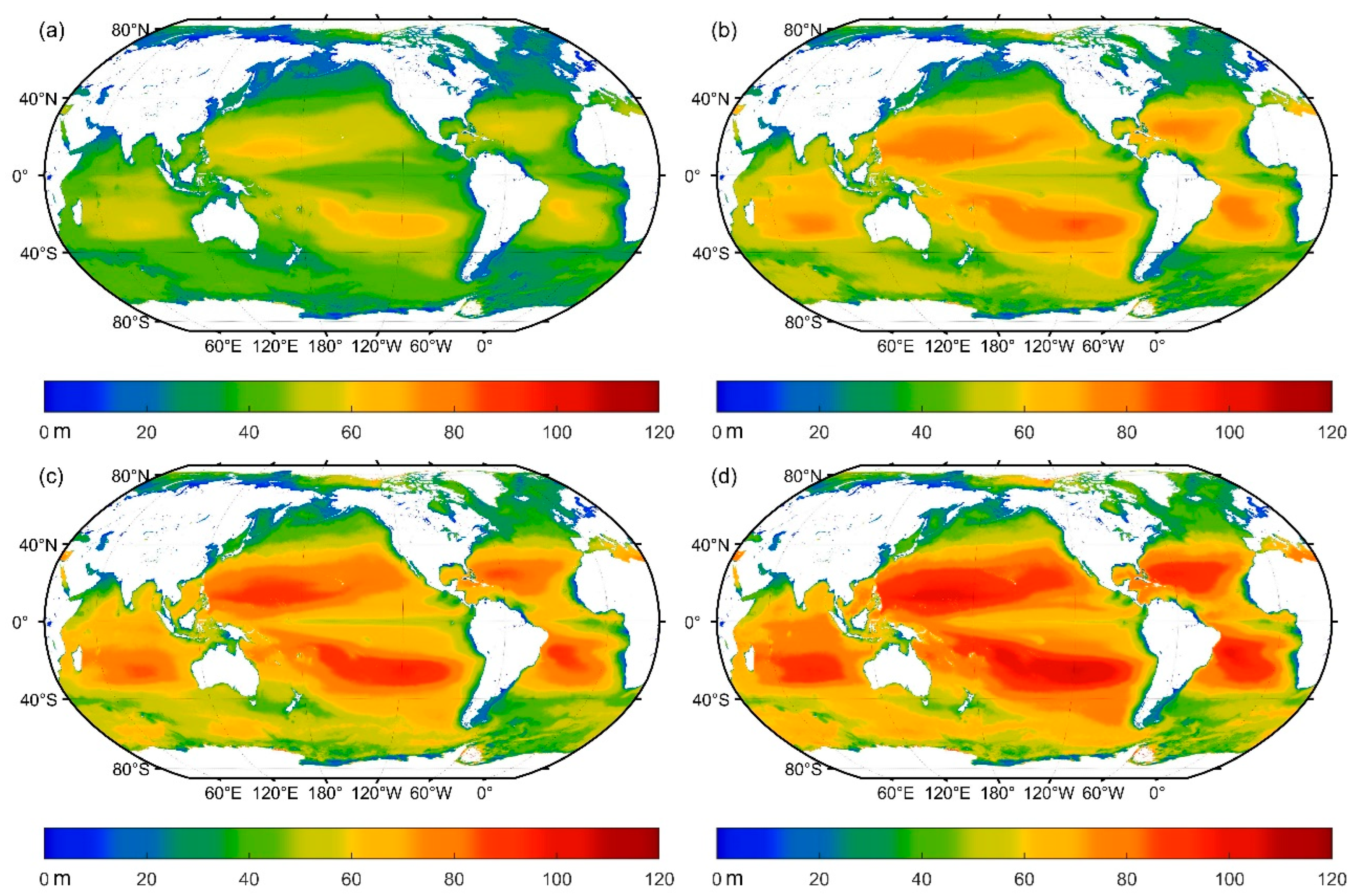
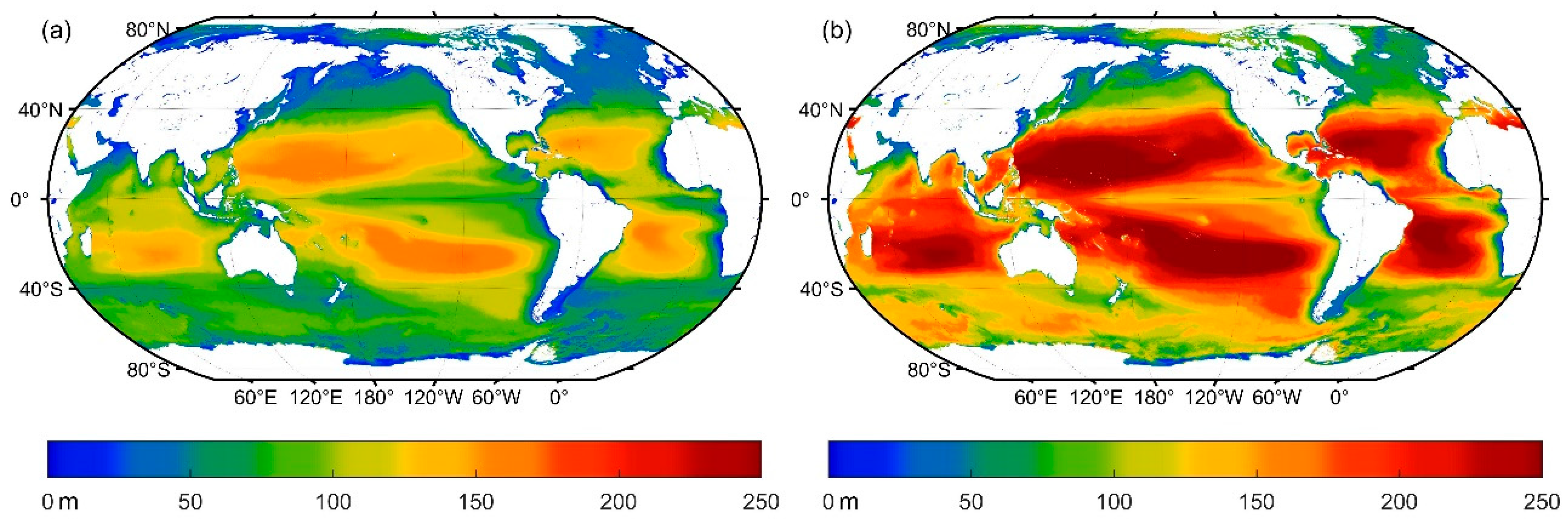
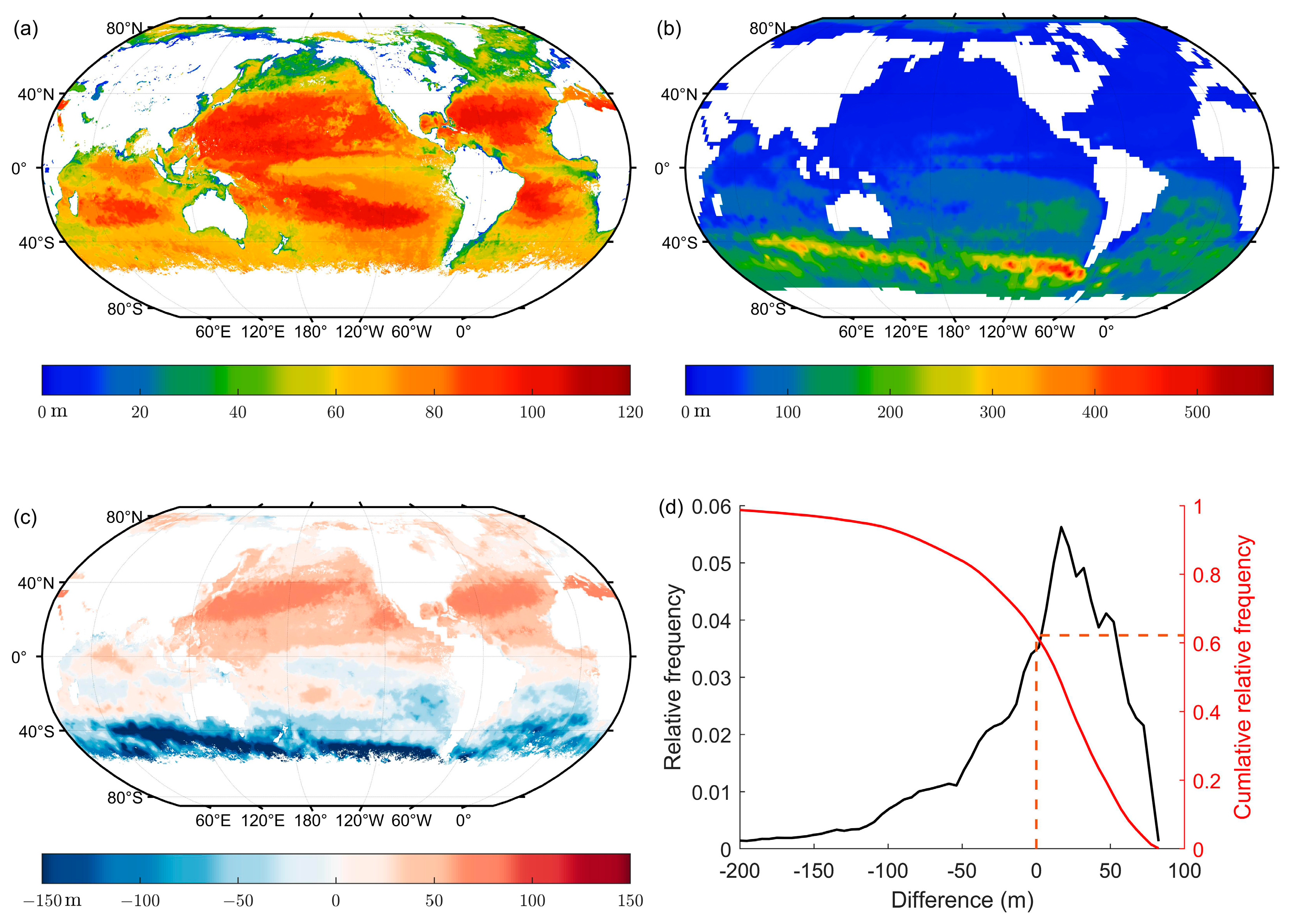
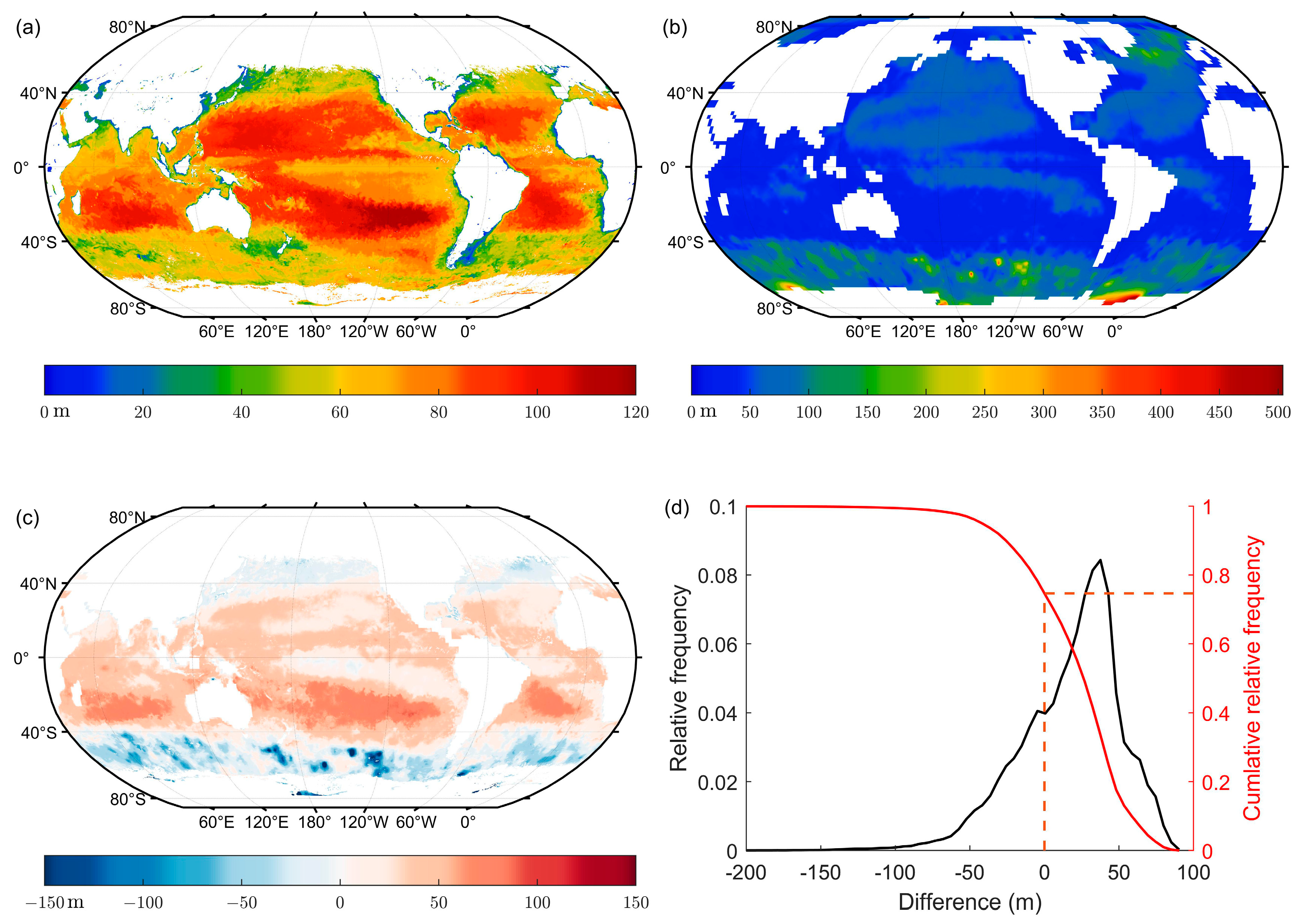
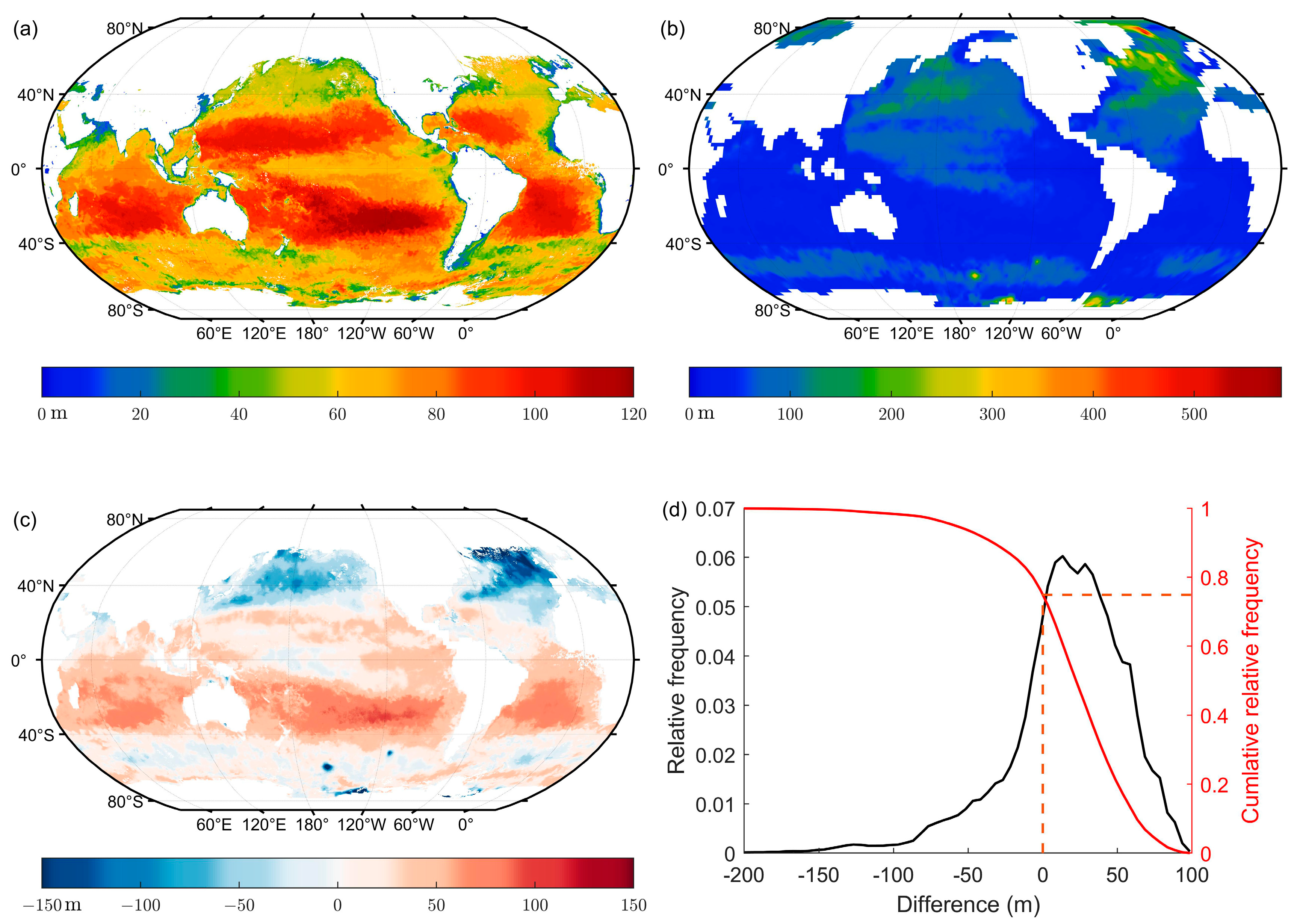
3.5. Maximum Detectable Depth and Corresponding Optimal Wavelength Analysis

The maximum detectable depth and corresponding optimal wavelength for spaceborne oceanic lidar at a global scale were studied. The input data of the average chlorophyll concentration in the global oceans were from a level-three standard mapped image of a composite chlorophyll product from 2002 to present, named A20021852021031.L3m_CU_CHL_chlor_a_9km.nc (https://oceancolor.gsfc.nasa.gov/products/ accessed on 1 March 2021). The horizontal resolution of the data used was 9 × 9 km. Other used parameters have been mentioned above.

The lidar maximum detectable depths under different bands from 400 to 700 nm were calculated based on our model described in Section 2. By comparing the maximum depths of these 300 bands, the global distribution of lidar maximum detectable depths at night and corresponding optimal wavelengths were obtained with the relative measurement error of 100%. As shown in Figure 10, the maximum depths could reach about 160 m in an oligotrophic sea at low latitudes on both sides of the equator (red colors in Figure 10a), and the corresponding optimal wavelengths near 440 nm (blue colors in Figure 10b). The maximum depths in high latitude and equator areas could reach 60 m (green color), and the corresponding optimal wavelengths near 490 nm (light green color in Figure 10b). The maximum depths in coastal waters are shallow, namely, under 20 m (blue color in Figure 10a) and the corresponding optimal wavelengths are about 535 and 565 nm (red color in Figure 10b). This indicates that a combination of multiple optimal wavelengths can be employed by future spaceborne lidar in order to improve the maximum detectable capability.

Figure 11 shows the lidar maximum detectable depths and corresponding optimal laser wavelengths in China coastal areas. The CDOM input files are a level-three standard mapped image of composite Absorption, due to gelbstof and detritus at a 443 nm product from 2002 to present, named A20021852021031.L3m_CU_IOP_adg_443_giop_9km.nc, and absorption due to the gelbstof and detritus slope parameter product named A20021852021031.L3m_CU_IOP_adg_s_giop_9km.nc (https://oceancolor.gsfc.nasa.gov/products/ accessed on 1 March 2021). Compared with Figure 10, the maximum detectable depths are much smaller due to the absorption of CDOM, but the optimal wavelengths are still above 520 nm in coastal areas. Therefore, 532 nm is a good choice for coastal zone environmental monitoring.

Figure 12 shows the statistical distribution of the optimal wavelengths. The wavelengths between 435 and 445 nm are suitable for the cleanest water detection in the oligotrophic sea on both sides of the equator, which accounts for about 11.1%. The wavelengths between 520 and 550 nm are suitable for the sea area nearest the coastline, which may have the maximum primary productivity. However, their area percentage is the smallest. The commonly used wavelength of 532 nm is in the wavelength between this range that is suitable for coastal water detection. The wavelengths between 485 and 495 nm account for the largest areas of the global oceans (41.8%), which are suitable for open ocean waters. The wavelengths between 465 and 475 nm have close proportions, which indicate that these close wavelengths have similar detectable capabilities. Considering the results, if only one band is equipped, the wavelength of 490 nm is the best choice. Taking the availability of an efficient, compact, rugged laser into consideration, the wavelength is an eclectically secondary option for a dual-wavelength lidar. If possible, 440 nm is a better choice than 532 nm due to its maximum penetration depth in clear water. With a wavelength of 440 nm, the lidar can even reach more than 150 m in the oligotrophic sea waters as shown in Figure 10a.

Figure 13 shows the maximum detectable depths with different relative measurement errors when the wavelength is 490 nm, while the corresponding numbers of optical depths are shown in Figure 14. The input data of the average Kd490 in the global oceans are from a level-three standard mapped image of the composite Kd490 product from 2002 to present, named A20021852021031.L3m_CU_KD490_Kd_490_9km.nc (https://oceancolor.gsfc.nasa.gov/products/, accessed on 1 March 2021). The average detectable depths increase about 40 m when the relative measurement errors change to 100% from 30%. With the relative measurement error of 30%, the maximum detectable is about 70 m, shown in Figure 13a, and equals about one or two optical depths, shown in Figure 14a. When the relative measurement error is 100%, the lidar penetrates much deeper and the number of optical depths is about three to four in most areas, which is consistent with the previous study [50]. However, in the oligotrophic sea, at low latitudes on both sides of the equator, the number of optical depths is still below three. This is mainly because the Kd490 in these areas is quite small. The penetration depth computed using three or four optical depths may be overestimated in these areas.

3.6. Difference of Penetration Depths during Day and at Night

To determine the impacts of solar background radiance on penetration depths, the maximum depths with different receiver parameters and their differences with the results at night were calculated, as shown in Figure 15. The results show that with a small FOV and bandwidth of the filter, the solar background radiance has little influence as shown in Figure 15a,b, while their differences are below 1 m in general, as shown in Figure 15b. When the FOV and bandwidth are not small enough to suppress the solar background radiance, the penetration depths during the daytime will decrease by almost 50 m as shown in Figure 15c,d, which indicates that the influence of solar background radiance cannot be neglected. The results show that the suitable parameters can effectively reduce the influence of solar background radiance.

4. Discussion

There are several similar studies that have simulated the penetration depths of oceanic lidar systems [26,27]. One of them only took the solar background light into account, and the solar background was a fixed value, which was 1.4 ${\mathrm{Wm}}^{-2}{\mathrm{nm}}^{-1}{\mathrm{sr}}^{-1}$, in [27]. This value is abnormally high and was only 0.06 ${\mathrm{Wm}}^{-2}{\mathrm{nm}}^{-1}{\mathrm{sr}}^{-1}$ in this research when the wavelength was 532 nm. In other studies, this value was usually between 0.01 and 0.1 ${\mathrm{W}\mathrm{m}}^{-2}{\mathrm{nm}}^{-1}{\mathrm{sr}}^{-1}$ [5,25,47]. Moreover, in our study, the solar background radiance varied with different wavelengths, which is more realistic. Another study only used diffuse attenuation coefficient Kd to estimate the maximum detectable depths [26], which may overestimate the penetration depths in open ocean water. Compared with other results, we conducted thorough and detailed research and considered as many factors. SOLS has several features: (1) it can be applied to a full waveform simulation with analog detection and photon-counting lidar simulation; (2) it can deal with stratified water, which allows SOLS to use profile data, such as biogeochemical Argo profiling floats as the input; (3) it considers the background light impact and lidar detector internal noise, which could provide a more realistic simulation result; (4) it can simulate both day and night results; (5) it can be used for simulation of airborne lidar.

In the above section, the lidar maximum detectable depths with different relative measurement errors were calculated, but they were all based on constant lidar system parameters. In this section, we will discuss other factors that influence lidar detection capability, including laser energy, field of view of the receiver, and filter bandwidth. Then, the results with previous studies will be compared. The difference between lidar maximum detectable depth and ocean mixed layer depth (MLD) will be discussed as well.

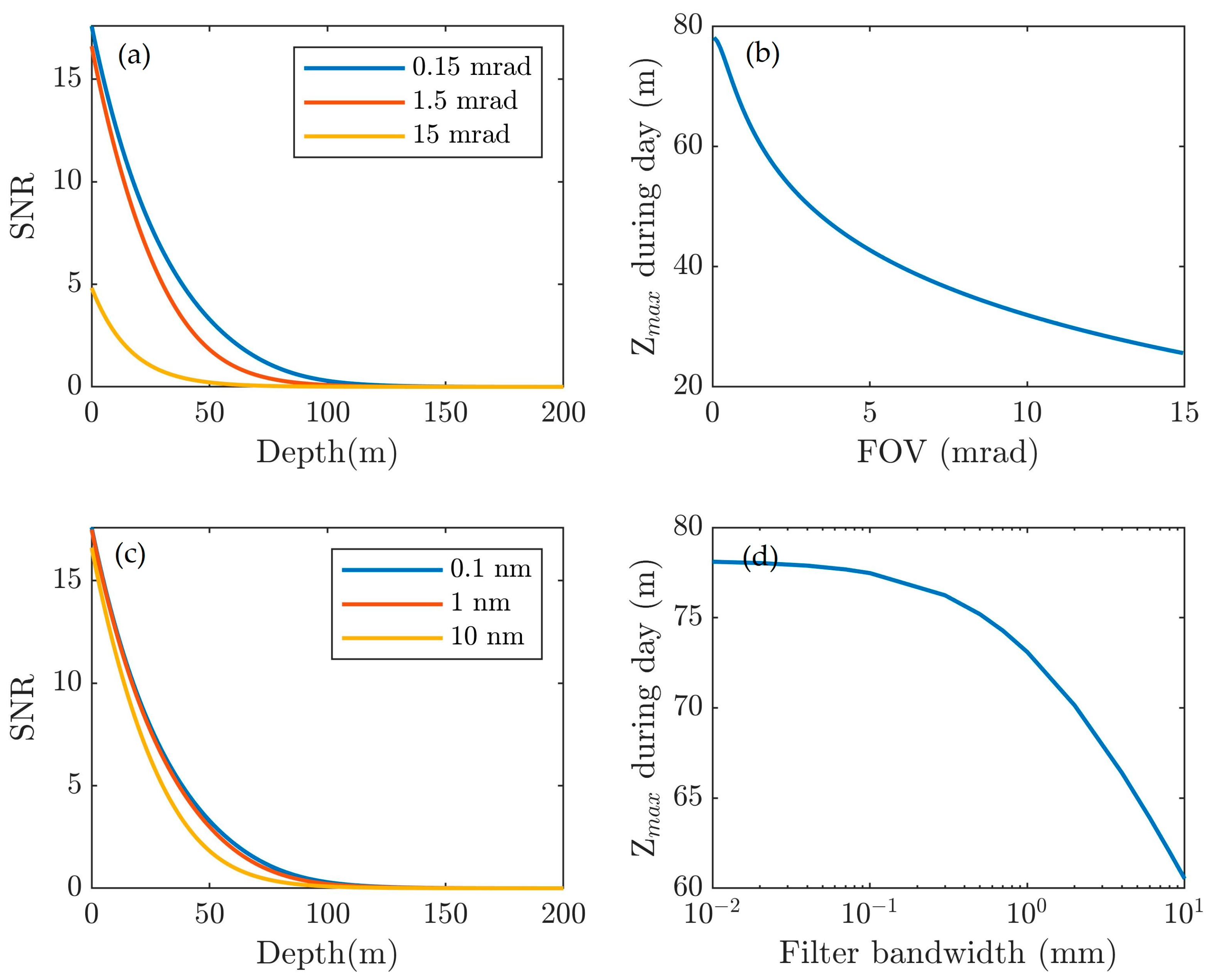
4.1. Lidar System Parameters’ Effects

4.1.1. Influence of Laser Energy and Lidar Geometry

Return signals with different laser powers at 490 nm at a chlorophyll concentration of 0.1 mg/m³ were simulated, as shown in Figure 16. The maximum depth of detection was proportional to the logarithm of the laser energy, as shown in Figure 16b. As a result, the higher the laser energy is, the deeper the lidar could detect. However, the energy cannot increase without limitation, and it is inefficient at enhancing detection depth only by improving laser energy, especially given the expense of a high-energy laser. The maximum detectable depth will be very shallow with much lower laser energy power. Therefore, relatively high energy (1 J or so) is appropriate here. Figure 16b shows that the penetration depths during day and at night have similar results.

As shown in Figure 3, the surface return is strong due to the backscattering of the sea surface. As a result, the dynamic range that is needed to penetrate to a given depth must be higher. A less strong surface return will reduce the demand of the dynamic range. An appropriate incident angle will reduce the surface return effectively. As shown in Figure 17, which is drawn according to [44], the sea surface backscatter coefficient is reduced by two orders of magnitude when the incidence angle is greater than 15 degrees. Then the surface return will be reduced accordingly. Therefore, the incidence angle of 15 degrees is a good choice.

4.1.2. Influence of Receiver Parameters

We analyzed the SNR during daytime for spaceborne lidar with various FOV and filter bandwidths. FOV from 0.15 to 15 mrad for a specific 0.1-nm filter bandwidth and a filter bandwidth from 0.01 to 10 nm for a specific FOV of 0.15 were tested, respectively. The results are shown in Figure 18. It appears that decreasing FOV and the filter bandwidth improves the SNR during the daytime because small FOV and filter bandwidth suppress the background light. With the least access of background light, the result indicates that the detectable depth reaches its maximum value with a 0.15-mrad FOV and a 0.1-nm filter bandwidth. Therefore, an oceanography lidar will perform better if FOV and the filter bandwidth are as small as possible. However, the result shows that FOV and the filter bandwidth have different importance in improving SNR in the daytime. To reach the same detectable depth, FOV needs fewer changes. In other words, decreasing FOV is more efficient than narrowing the filter bandwidth, as shown in Figure 18b,d.

Moreover, the dynamic range of the digitizers is one of the most critical parameters in the lidar system [5], which is necessary for great depth penetration. A ${10}^5$ dynamic range demands a high-speed digitizer with 16.6 bits. Here, we analyzed the penetration the lidar could achieve with a ${10}^5$ dynamic range, as shown in Figure 19. In general, surface return demands a ${10}^2$ dynamic range due to strong backscattering of the sea surface [44], so there is only a ${10}^3$ dynamic range left for the water body shown in Figure 19a. Figure 19b shows the penetration depths with a ${10}^7$ dynamic range used for water column detection. Compared with the results in Figure 13d, a great penetration depth demands a wild dynamic range for the receiver.

4.2. Eye Safety

Ocular safety needs to be considered because of the intense pulses of visible light [5]. According to the American National Standard for Safe Use of Lasers [51], the single-pulse exposure limit of a nanosecond pulse laser is $5\times {10}^{-7}\mathrm{J}/{\mathrm{cm}}^2$. Figure 20 shows the laser exposure at the sea surface versus different laser energy and the divergence angle. The exposure is usually below the limit. Only the energy exceeds 5 J; there is some risk, but it is difficult to achieve such high energy. According to the standard, the visible wavelengths have the same exposure limit, so it has little influence on the optimal laser wavelength.

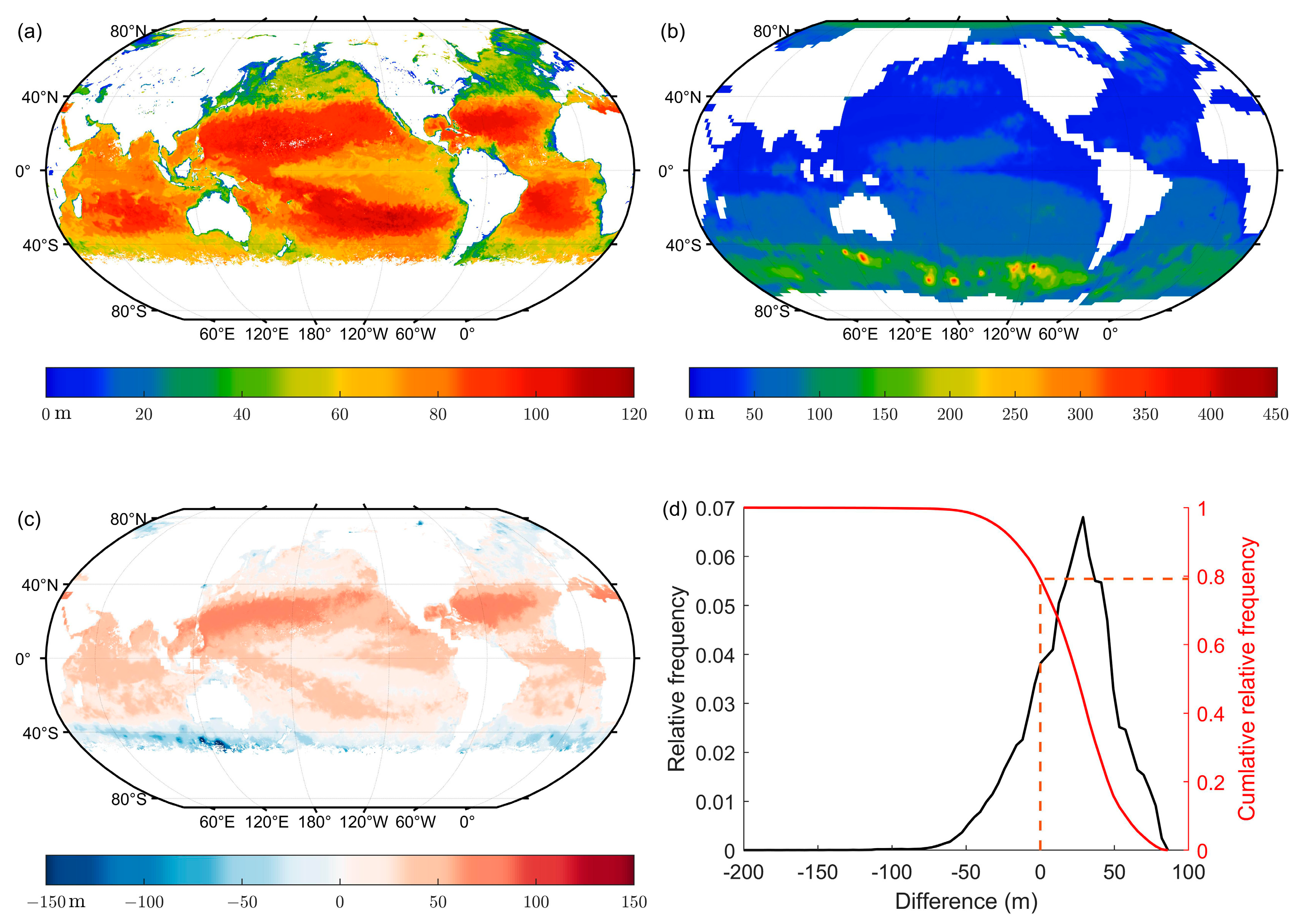
4.3. Temporal and Spatial Variation of the Comparison between Lidar Maximum Detectable Depth and MLD

Since the upper-ocean MLD plays an important role in oceanic physical–biogeochemical processes and ocean–atmosphere interactions [52,53], it is significant to discuss the relationship between lidar maximum detectable depth and upper-ocean MLD. Figure 21, Figure 22, Figure 23 and Figure 24 represent the lidar maximum detectable depth at 490-nm laser wavelength at daytime and its difference with the MLD in different seasons—spring, summer, autumn, and winter, respectively. The chlorophyll concentrations used here are monthly merged products from GlobData (http://hermes.acri.fr/, accessed on 1 March 2021); MLD data are downloaded from http://www.ifremer.fr/cerweb/deboyer/mld/Surface_Mixed_Layer_Depth.php (accessed on 1 March 2021) based on [53]. Compared with upper-ocean MLD, the results in Figure 21c, Figure 22c, Figure 23c and Figure 24c show that red color areas where lidar maximum detectable depth minus upper-ocean MLD greater than zero take up most of the global ocean, which indicates that 490-nm lidar can penetrate the upper mixed layer in most of the global oceans in different seasons. Some temporal and spatial distribution characteristics of the differences between lidar maximum detectable depth and upper-ocean MLD exist. In the spring (the northern hemisphere), the 490-nm lidar is not able to penetrate the MLD in some southern mid-to-high altitudes denoted in blue in Figure 21c. It is mainly because MLD in these areas is deeper in this season as shown in Figure 21b. In the summer (the northern hemisphere), the areas denoted in blue in Figure 22, where the lidar is not able to penetrate the MLD, appear much larger in southern mid-to-high altitudes than those in the spring in Figure 21c. This is because the MLD in these areas is deeper in the summer (the southern hemisphere) as shown in Figure 22b. When MLD in northern high altitudes becomes much deeper in the winter (the northern hemisphere), as shown in Figure 24b, the lidar cannot reach below the MLD as shown in Figure 24c. The relative frequency of the differences between lidar maximum detectable depth and MLD are shown in Figure 21d, Figure 22d, Figure 23d and Figure 24d. In the spring, autumn, and winter, the relative frequency of areas where lidar maximum detectable depth minus upper-ocean MLD is greater than zero is about 70% (Figure 21d, Figure 23d and Figure 24d), and it is still about 60%, even in the summer (Figure 22d). The lidar penetration capability for upper-ocean MLD is higher in the spring and autumn, but lower in the summer and winter. It indicates that spaceborne lidar has the potential to penetrate the upper mixed layer in most of the global oceans in different seasons.

As for the maximum detectable depth, the lidar can always reach above 100 m in the oligotrophic sea at both sides of the equator, as denoted by the red colors in Figure 21a, Figure 22a, Figure 23a and Figure 24a, although the maximum detectable depth decreases by about 10 m in the summer, as shown in Figure 22a. The maximum depth in coastal areas and high latitudes have more complex and varying patterns. The results show that the maximum depth continuously becomes shallower in coastal areas and mid-to-high latitudes, which are denoted in green in Figure 21a, Figure 22a, Figure 23a and Figure 24a. This phenomenon may be caused by chlorophyll concentration seasonal variability.

Overall, the results show that the lidar system can penetrate the upper mixed layer in most of the global oceans in different seasons (about 70% in spring, autumn, and winter, and about 60% in the summer, as mentioned above). It is only in high-latitude areas with strong vertical mixing where the upper mixed layer cannot be penetrated, especially in the summer (Figure 22). The maximum detectable depths in oligotrophic seas on both sides of the equator are stable and even reach 120 m. On the contrary, coastal and high-altitude areas have varying maximum detectable depths, which may be caused by chlorophyll concentration seasonal variability. It indicates that future spaceborne oceanic lidar will be an effective detection tool for understanding vertical structure information of the upper-ocean mixed layer.

5. Conclusions

We conducted thorough and detailed research and considered as many factors as possible, such as laser parameters, receiver parameters, solar background radiance, and detector noise, to obtain a more reliable and practical simulation result. An open-source spaceborne oceanic lidar simulator called SOLS was developed. The results show its ability to simulate full-waveform echo signals and photon-counting lidar with stratified water. Furthermore, SOLS was applied for the simulation of airborne lidar as well. Then potential capability of spaceborne lidar for global ocean optical profiling was studied with SOLS. Preliminary results showed that the maximum detectable depth could reach deeper than 120 m in the oligotrophic sea at low latitudes based on SNR during the daytime. However, the background solar light contributes greatly to the variance distortion of return signals. So, it is vital and meaningful to suppress the background solar light. Moreover, we find 490 nm to be the optimal wavelength for most of the open seawater, and 532 nm for coastal water, after considering the area proportion of the maximum detectable depth under different laser wavelengths. Compared with the upper-ocean MLD, the lidar can penetrate it and detect the profile below it in most of the global oceans (about 70% in the spring, autumn, and winter, and about 60% in the summer, as mentioned above). In view of these new results, we make the following recommendations:

(a)

Considering the development and technology of lasers, several wavelength ranges are listed for application: wavelengths between 465 and 495 nm are suitable for most of the global oceans; wavelengths between 530 and 540 nm can be used for coastal water detection, which has high primary productivity in marine ecosystems; and wavelengths between 425 and 435 nm have shown potential detection depth of deeper than 150 m in the oligotrophic sea on both sides of the equator. A combination of multiple wavelengths can be employed by future spaceborne lidar to improve its maximum detectable capability.

(b)

Considering the strong sea surface backscattering, it is better to tilt the laser beam at an angle to avoid direct reflection from the sea surface.

(c)

With small enough FOVs and a filter bandwidth, the solar background radiance can be efficiently suppressed.

(d)

Polarization information is an important and complicated feature for LIDAR. In practice, it is difficult to simulate the complex, non-spherical particles found in the ocean. Therefore, the polarization feature was neglected in this paper, but this will be dealt with in the future.