A New Method for Long-Term River Discharge Estimation of Small- and Medium-Scale Rivers by Using Multisource Remote Sensing and RSHS: Application and Validation
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.3. Methods
2.3.1. Discharge Calculation: Remote Sensing Hydrological Station
2.3.2. Image Downscaling: Linear Regression Algorithm
2.3.3. Water Identification Assessment: Water Continuity Index & River Length Ratio
2.3.4. Runoff Accuracy Assessment: Error Index
3. Results
3.1. Result of Linear Regression Downscaling Method
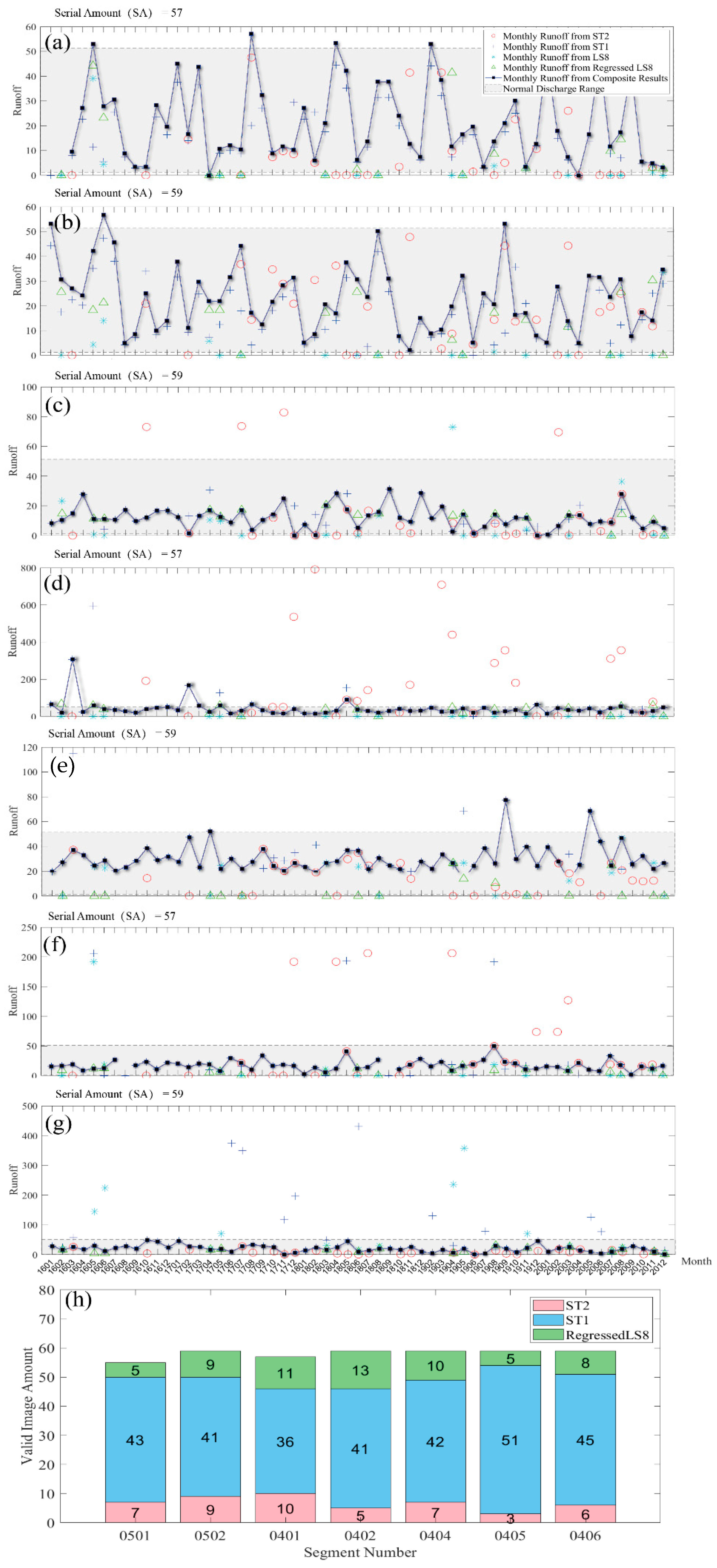
3.2. Effect of Extension to Runoff Series from Multisource Data
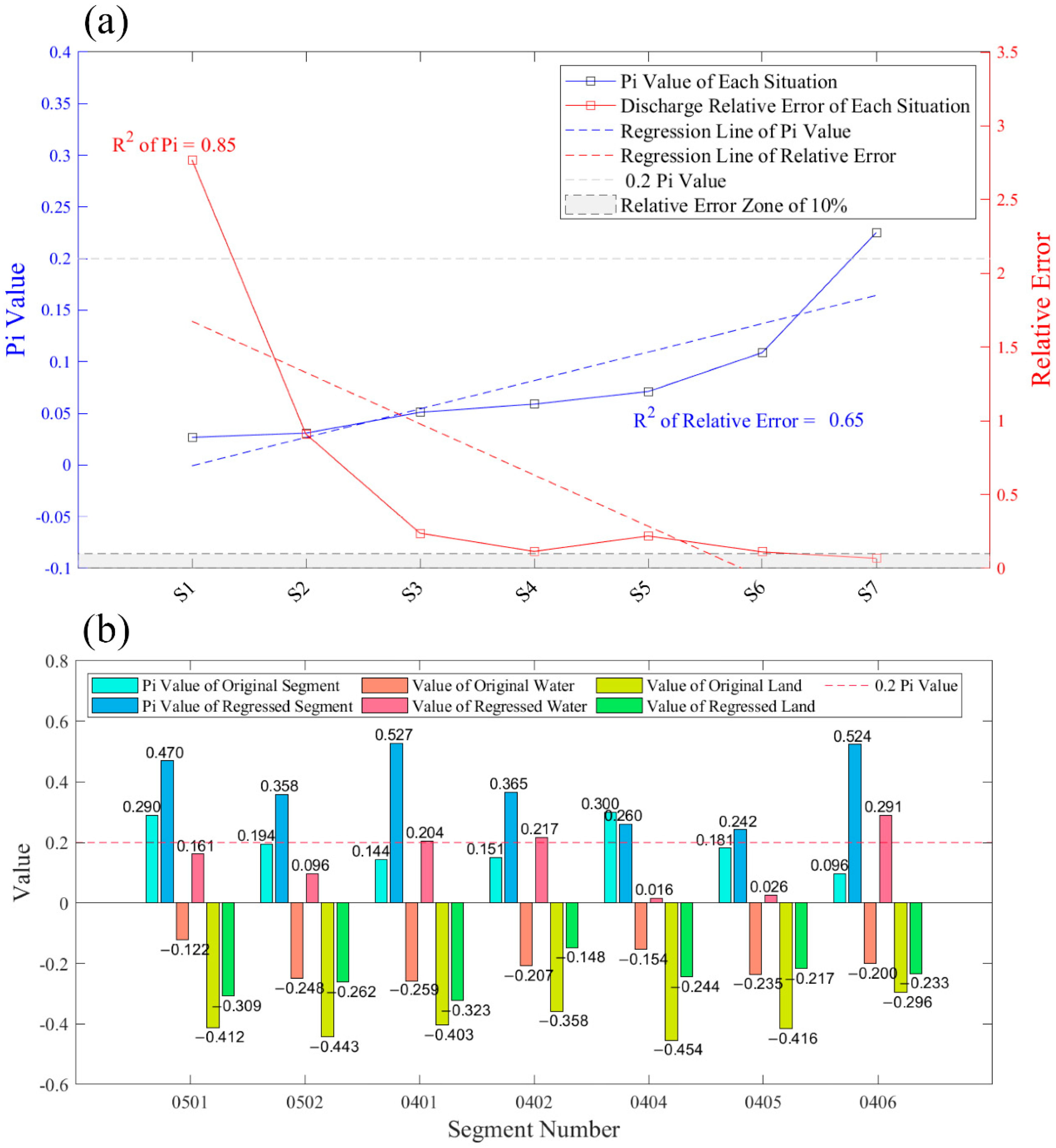
3.3. Accuracy Comparison between Runoff Results from Original and Regressed Images
4. Discussion
4.1. What Affects the Accuracy of This Method?
4.2. What Are the Main Influences on the Long-Term Discharge Generation of Small- and Medium-Scale Rivers?
4.3. What Are the Differences between Discharges in Flood and Nonflood Seasons?
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Ashmore, P.; Sauks, E. Prediction of discharge from water surface width in a braided river with implications for at-a-station hydraulic geometry. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Bao, W.; Zhang, X.; Yu, Z.; Qu, S. Real-Time Equivalent Conversion Correction on River Stage Forecasting with Manning’s Formula. J. Hydrol. Eng. 2011, 16, 1–9. [Google Scholar] [CrossRef][Green Version]
- Birkett, C.M.; Mertes, L.A.K.; Dunne, T.; Costa, M.H.; Jasinski, M.J. Surface water dynamics in the Amazon Basin: Application of satellite radar altimetry. J. Geophys. Res. Atmos. 2002, 107, LBA 26-1–LBA 26-21. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Dingman, S.L.; Vorosmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the potential for measuring river discharge from space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Moller, D.; Smith, L.C.; Dingman, S.L. Estimating discharge in rivers using remotely sensed hydraulic information. J. Hydrol. 2005, 309, 191–209. [Google Scholar] [CrossRef]
- Chang, X.Y. Studies on Guizhou Less Sunny More Rainy Days. Master’s Thesis, Guizhou Normal University, Guiyang, China, 2014. [Google Scholar]
- Chastain, R.; Housman, I.; Goldstein, J.; Finco, M.; Tenneson, K. Empirical cross sensor comparison of Sentinel-2A and 2B MSI, Landsat-8 OLI, and Landsat-7 ETM+ top of atmosphere spectral characteristics over the conterminous United States. Remote Sens. Environ. 2018, 221, 274–285. [Google Scholar] [CrossRef]
- Chen, J.; Yu, J.; Bai, X.; Zeng, Y.; Wang, J. Fragility of karst ecosystem and environment: Long-term evidence from lake sediments. Agric. Ecosyst. Environ. 2020, 294, 106862. [Google Scholar] [CrossRef]
- Chokmani, K.; Ouarda, T.B.M.J. Physiographical space-based kriging for regional flood frequency estimation at ungauged sites. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Dinar, S. The Geographical Dimensions of Hydro-politics: International Freshwater in the Middle East, North Africa, and Central Asia. Eurasian Geogr. Econ. 2012, 53, 115–142. [Google Scholar] [CrossRef]
- Duan, P.; Wang, M.; Lei, Y.; Li, J. Research on Estimating Water Storage of Small Lake Based on Unmanned Aerial Vehicle 3D Model. Water Resour. 2021, 48, 690–700. [Google Scholar] [CrossRef]
- Durand, M.; Rodriguez, E.; Alsdorf, D.E.; Trigg, M. Estimating River Depth From Remote Sensing Swath Interferometry Measurements of River Height, Slope, and Width. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 3, 20–31. [Google Scholar] [CrossRef]
- Flener, C.; Vaaja, M.; Jaakkola, A.; Krooks, A.; Kaartinen, H.; Kukko, A.; Kasvi, E.; Hyyppä, H.; Hyyppä, J.; Alho, P. Seamless Mapping of River Channels at High Resolution Using Mobile LiDAR and UAV-Photography. Remote Sens. 2013, 5, 6382–6407. [Google Scholar] [CrossRef]
- Huang, C.; Thomas, N.; Goward, S.N.; Masek, J.G.; Zhu, Z.; Townshend, J.R.G.; Vogelmann, J. Automated masking of cloud and cloud shadow for forest change analysis using Landsat images. Int. J. Remote Sens. 2010, 31, 5449–5464. [Google Scholar] [CrossRef]
- Immerzeel, W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Irish, R.R.; Barker, J.L.; Goward, S.N.; Arvidson, T. Characterization of the Landsat-7 ETM+ Automated Cloud-Cover Assessment (ACCA) Algorithm. Photogramm. Eng. Remote Sens. 2006, 72, 1179–1188. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, M.; Hu, H.; Xu, J. Evaluating the Performance of Sentinel-1A and Sentinel-2 in Small Waterbody Mapping over Urban and Mountainous Regions. Water 2021, 13, 945. [Google Scholar] [CrossRef]
- Borah, D.K.; Bera, M. Watershed-scale hydrologic and nonpoint-source pollution models: Review of applications. Am. Soc. Agric. Eng. 2004, 47, 789–803. [Google Scholar] [CrossRef]
- Kebede, M.G.; Wang, L.; Yang, K.; Chen, D.; Li, X.; Zeng, T.; Hu, Z. Discharge Estimates for Ungauged Rivers Flowing over Complex High-Mountainous Regions based Solely on Remote Sensing-Derived Datasets. Remote Sens. 2020, 12, 1064. [Google Scholar] [CrossRef]
- Kim, Y.; Park, N.-W. Comparison of regression models for spatial downscaling of coarse scale satellite-based precipitation products. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4634–4637. [Google Scholar] [CrossRef]
- Lin, C.-H.; Tsai, P.-H.; Lai, K.-H.; Chen, J.-Y. Cloud Removal from Multitemporal Satellite Images Using Information Cloning. IEEE Trans. Geosci. Remote Sens. 2012, 51, 232–241. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Zhang, Z. A conceptual data model coupling with physically-based distributed hydrological models based on catchment discretization schemas. J. Hydrol. 2015, 530, 206–215. [Google Scholar] [CrossRef]
- Lou, H.; Wang, P.; Yang, S.; Hao, F.; Ren, X.; Wang, Y.; Shi, L.; Wang, J.; Gong, T. Combining and Comparing an Unmanned Aerial Vehicle and Multiple Remote Sensing Satellites to Calculate Long-Term River Discharge in an Ungauged Water Source Region on the Tibetan Plateau. Remote Sens. 2020, 12, 2155. [Google Scholar] [CrossRef]
- Lumbroso, D.; Gaume, E. Reducing the uncertainty in indirect estimates of extreme flash flood discharges. J. Hydrol. 2012, 414–415, 16–30. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef]
- Morel, M.; Booker, D.J.; Gob, F.; Lamouroux, N. Consistent Theoretical and Empirical Predictions of at-a-Station Hydraulic Geometry Exponents in Stream Reaches. Water Resour. Res. 2020, 56, e2020WR027242. [Google Scholar] [CrossRef]
- Passalacqua, P.; Trung, T.D.; Foufoula-Georgiou, E.; Sapiro, G.; Dietrich, W.E. A geometric framework for channel network extraction from lidar: Nonlinear diffusion and geodesic paths. J. Geophys. Res. Earth Surf. 2010, 115, F01002. [Google Scholar] [CrossRef]
- Platnick, S.; King, M.D.; Ackerman, S.A.; Menzel, W.P.; Baum, B.A.; Riédi, J.C.; Frey, R.A. The MODIS cloud products: Algorithms and examples from terra. IEEE Trans. Geosci. Remote Sens. 2003, 41, 459–473. [Google Scholar] [CrossRef]
- Rusnák, M.; Sládek, J.; Kidová, A.; Lehotský, M. Template for high-resolution river landscape mapping using UAV technology. Measurement 2018, 115, 139–151. [Google Scholar] [CrossRef]
- Spiliotopoulos, M.; Adaktylou, N.; Loukas, A.; Michalopoulou, H.; Mylopoulos, N.; Toulios, L. A spatial downscaling pro-cedure of MODIS derived actual evapotranspiration using Landsat images at central Greece. In Proceedings of the First International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2013), Paphos, Cyprus, 5 August 2013. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; McIntyre, P.B.; Gessner, M.O.; Dudgeon, D.; Prusevich, A.; Green, P.; Glidden, S.; Bunn, S.E.; Sullivan, C.A.; Liermann, C.R.; et al. Global threats to human water security and river biodiversity. Nature 2010, 467, 555–561. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, J.; Li, J.; Meng, Y.; Pokhrel, Y.; Zhang, H. Basin-scale high-resolution extraction of drainage networks using 10-m Sentinel-2 imagery. Remote Sens. Environ. 2021, 255, 112281. [Google Scholar] [CrossRef]
- Wu, G.; Liu, Y. Downscaling Surface Water Inundation from Coarse Data to Fine-Scale Resolution: Methodology and Accuracy Assessment. Remote Sens. 2015, 7, 15989–16003. [Google Scholar] [CrossRef]
- Xu, K.; Zhang, J.; Watanabe, M.; Sun, C. Estimating river discharge from very high-resolution satellite data: A case study in the Yangtze River, China. Hydrol. Process. 2004, 18, 1927–1939. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Sosa, J.; Bates, P.D.; Allen, G.H.; Pavelsky, T.M. MERIT Hydro: A High-Resolution Global Hydrography Map Based on Latest Topography Dataset. Water Resour. Res. 2019, 55, 5053–5073. [Google Scholar] [CrossRef]
- Yang, S.; Bai, J.; Zhao, C.; Lou, H.; Zhang, C.; Guan, Y.; Zhang, Y.; Wang, Z.; Yu, X. The assessment of the changes of biomass and riparian buffer width in the terminal reservoir under the impact of the South-to-North Water Diversion Project in China. Ecol. Indic. 2018, 85, 932–943. [Google Scholar] [CrossRef]
- Yang, S.; Guan, Y.; Zhao, C.; Zhang, C.; Bai, J.; Chen, K. Determining the influence of catchment area on intensity of gully erosion using high-resolution aerial imagery: A 40-year case study from the Loess Plateau, northern China. Geoderma 2019, 347, 90–102. [Google Scholar] [CrossRef]
- Yang, S.; Li, C.; Lou, H.; Wang, P.; Wang, J.; Ren, X. Performance of an Unmanned Aerial Vehicle (UAV) in Calculating the Flood Peak Discharge of Ephemeral Rivers Combined with the Incipient Motion of Moving Stones in Arid Ungauged Regions. Remote Sens. 2020, 12, 1610. [Google Scholar] [CrossRef]
- Yang, S.; Wang, J.; Wang, P.; Gong, T.; Liu, H. Low Altitude Unmanned Aerial Vehicles (UAVs) and Satellite Remote Sensing Are Used to Calculated River Discharge Attenuation Coefficients of Ungauged Catchments in Arid Desert. Water 2019, 11, 2633. [Google Scholar] [CrossRef]
- Yang, S.; Wang, P.; Lou, H.; Wang, J.; Zhao, C.; Gong, T. Estimating River Discharges in Ungauged Catchments Using the Slope–Area Method and Unmanned Aerial Vehicle. Water 2019, 11, 2361. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, X. A new statistical precipitation downscaling method with Bayesian model averaging: A case study in China. Clim. Dyn. 2015, 45, 2541–2555. [Google Scholar] [CrossRef]
- Zhou, N.; Li, X.; Shen, Z.; Wu, T.; Luo, J. Geo-Parcel-Based Change Detection Using Optical and SAR Images in Cloudy and Rainy Areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1326–1332. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]


| Data Type | Data Name | Source | Timespan (Time Resolution) | Spatial Resolution | Purpose |
|---|---|---|---|---|---|
| Remote sensing data | UAV remote sensing | DJI Mavic Air 2 | 2020/11/4~2020/11/5 (/) | 5 cm | Construct digital river model |
| Landsat-8 surface reflectance (LS8) | GEE | 2016~2020 (15 days) | 30 m | Identify water body | |
| Sentinel-1 C-band synthetic aperture radar (ST1) | GEE | 2016~2020 (10 days) | 10 m | ||
| Sentinel-2 surface reflectance (ST2) | GEE | 2016~2020 (10 days) | 10 m | ||
| Measured data | Measured velocity of flow and water depth of river section | Rotating Element Current Meter and Deeper Smart Sonar | 2020/11/4~2020/11/5 (/) | / | Establish RSHS |
| Statistical data | Daily measured discharge | Hydrologic Yearbook | 2016 (day) | / | Obtain in-situ discharge data |
| Parameter | Symbol | Source |
|---|---|---|
| River width | - | NDWI calculated from satellite images |
| Area of water passage | A | River width and depth measured in situ with the mathematical relationship based on the shape of river channel |
| Discharge | Q | Manning formula |
| Conversion factor | k | Refer to [28,34,44] |
| Roughness | n | In situ measurement |
| Water-cycle length | P | River width and depth measured in situ with the mathematical relationship based on the shape of river channel |
| Hydraulic gradient | S | UAV images |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, H.; Zhang, Y.; Yang, S.; Wang, X.; Pan, Z.; Luo, Y. A New Method for Long-Term River Discharge Estimation of Small- and Medium-Scale Rivers by Using Multisource Remote Sensing and RSHS: Application and Validation. Remote Sens. 2022, 14, 1798. https://doi.org/10.3390/rs14081798
Lou H, Zhang Y, Yang S, Wang X, Pan Z, Luo Y. A New Method for Long-Term River Discharge Estimation of Small- and Medium-Scale Rivers by Using Multisource Remote Sensing and RSHS: Application and Validation. Remote Sensing. 2022; 14(8):1798. https://doi.org/10.3390/rs14081798
Chicago/Turabian StyleLou, Hezhen, Yujia Zhang, Shengtian Yang, Xuelei Wang, Zihao Pan, and Ya Luo. 2022. "A New Method for Long-Term River Discharge Estimation of Small- and Medium-Scale Rivers by Using Multisource Remote Sensing and RSHS: Application and Validation" Remote Sensing 14, no. 8: 1798. https://doi.org/10.3390/rs14081798
APA StyleLou, H., Zhang, Y., Yang, S., Wang, X., Pan, Z., & Luo, Y. (2022). A New Method for Long-Term River Discharge Estimation of Small- and Medium-Scale Rivers by Using Multisource Remote Sensing and RSHS: Application and Validation. Remote Sensing, 14(8), 1798. https://doi.org/10.3390/rs14081798






