Mapping Soil Properties with Fixed Rank Kriging of Proximally Sensed Soil Data Fused with Sentinel-2 Biophysical Parameter
Abstract
1. Introduction
2. Materials and Methods
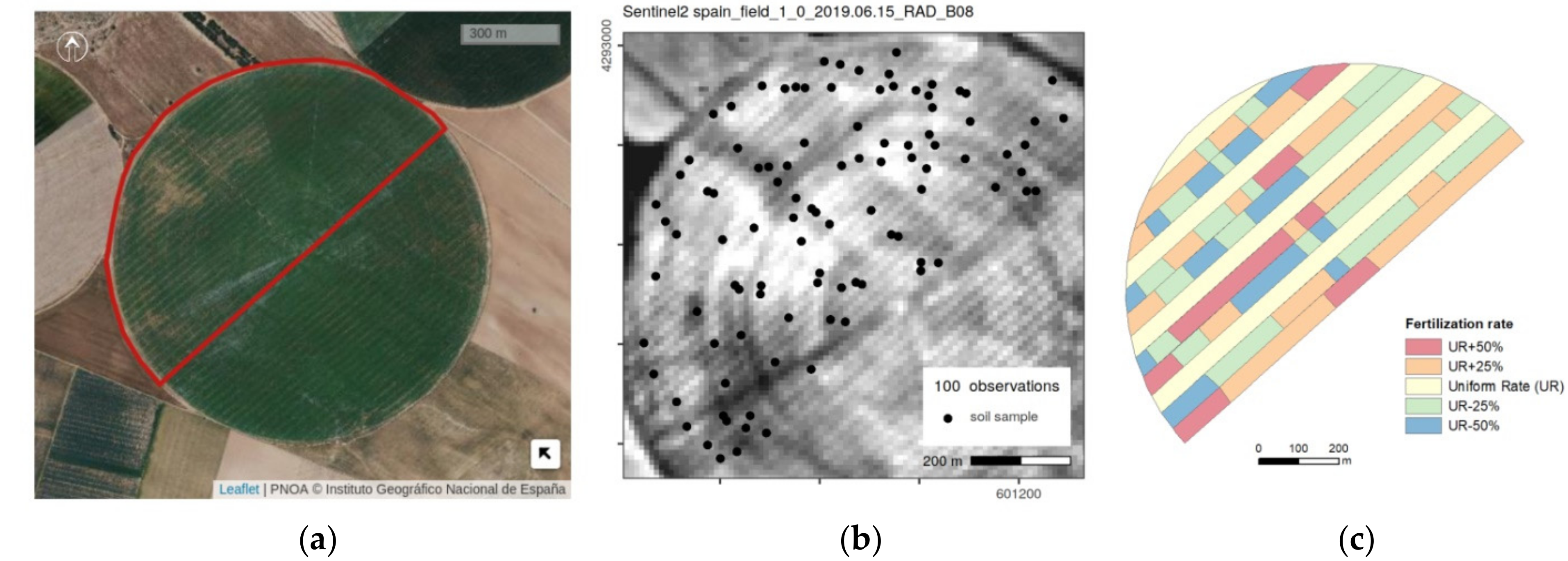
2.1. Study Area
2.2. Soil—VNIR Data
2.3. Earth Observation Data
2.4. Auxiliary Variables as Covariates
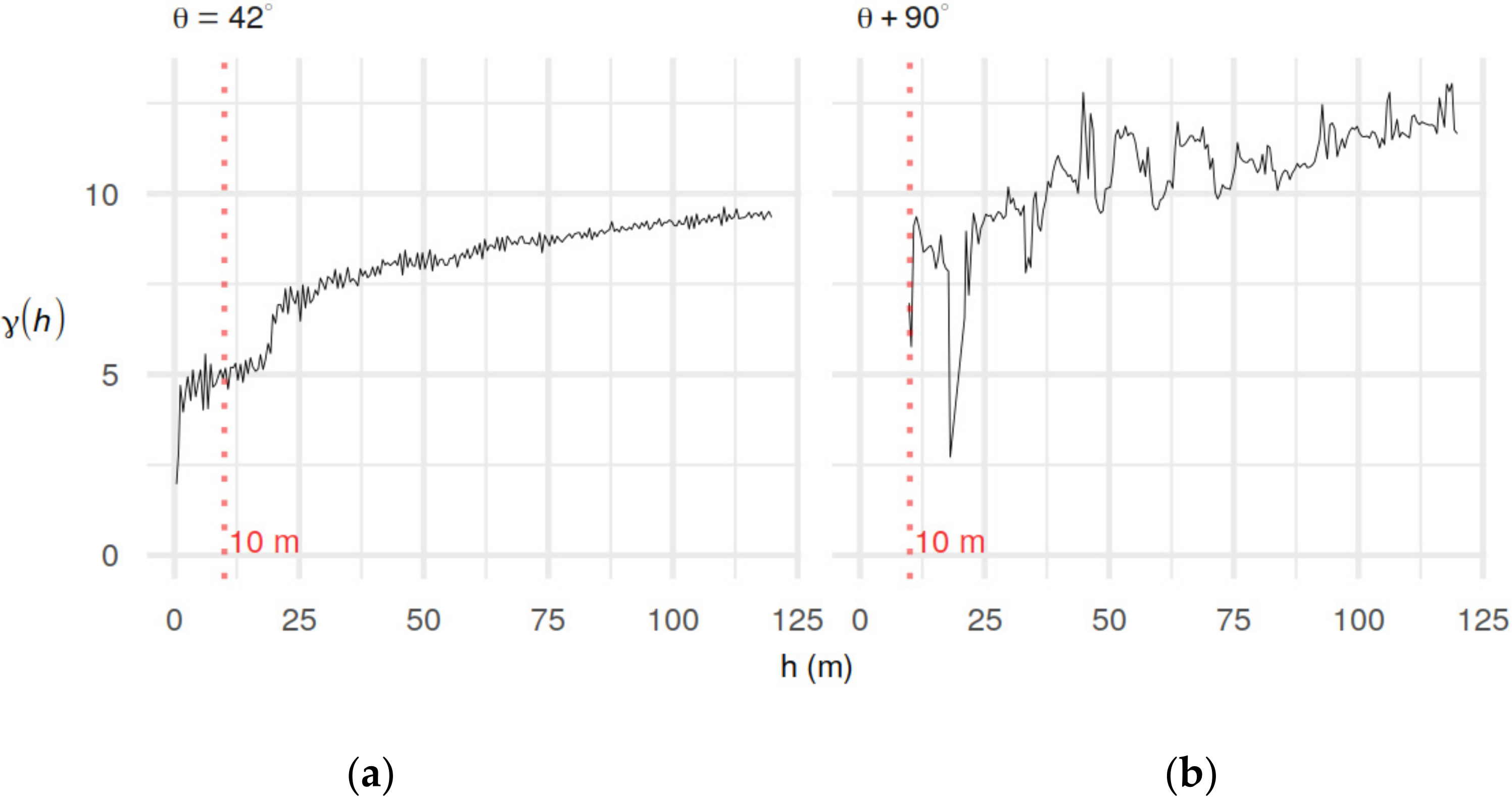
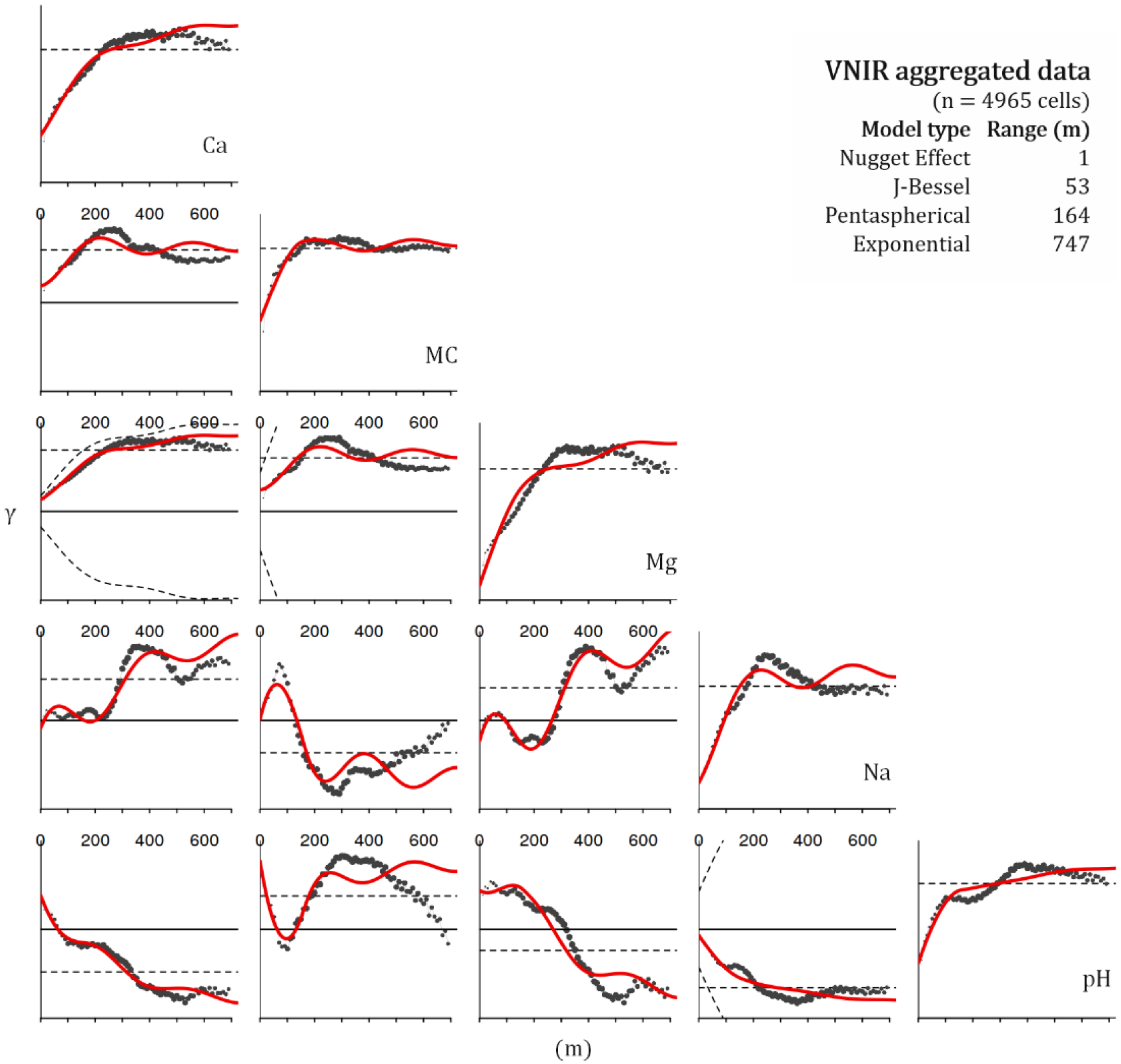
2.5. Variogram Analysis
2.6. Ordinary Kriging
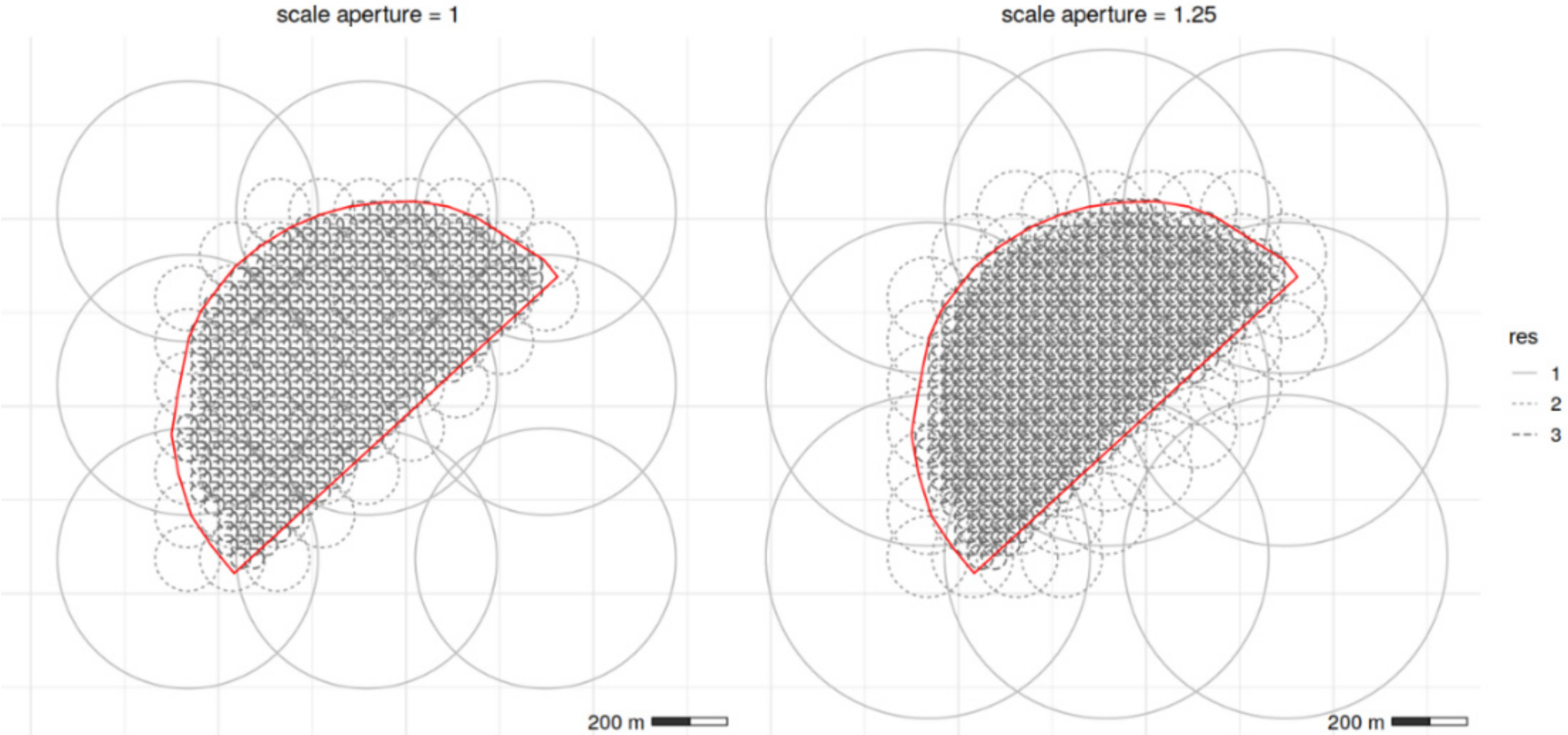
2.7. Fixed-Rank Kriging
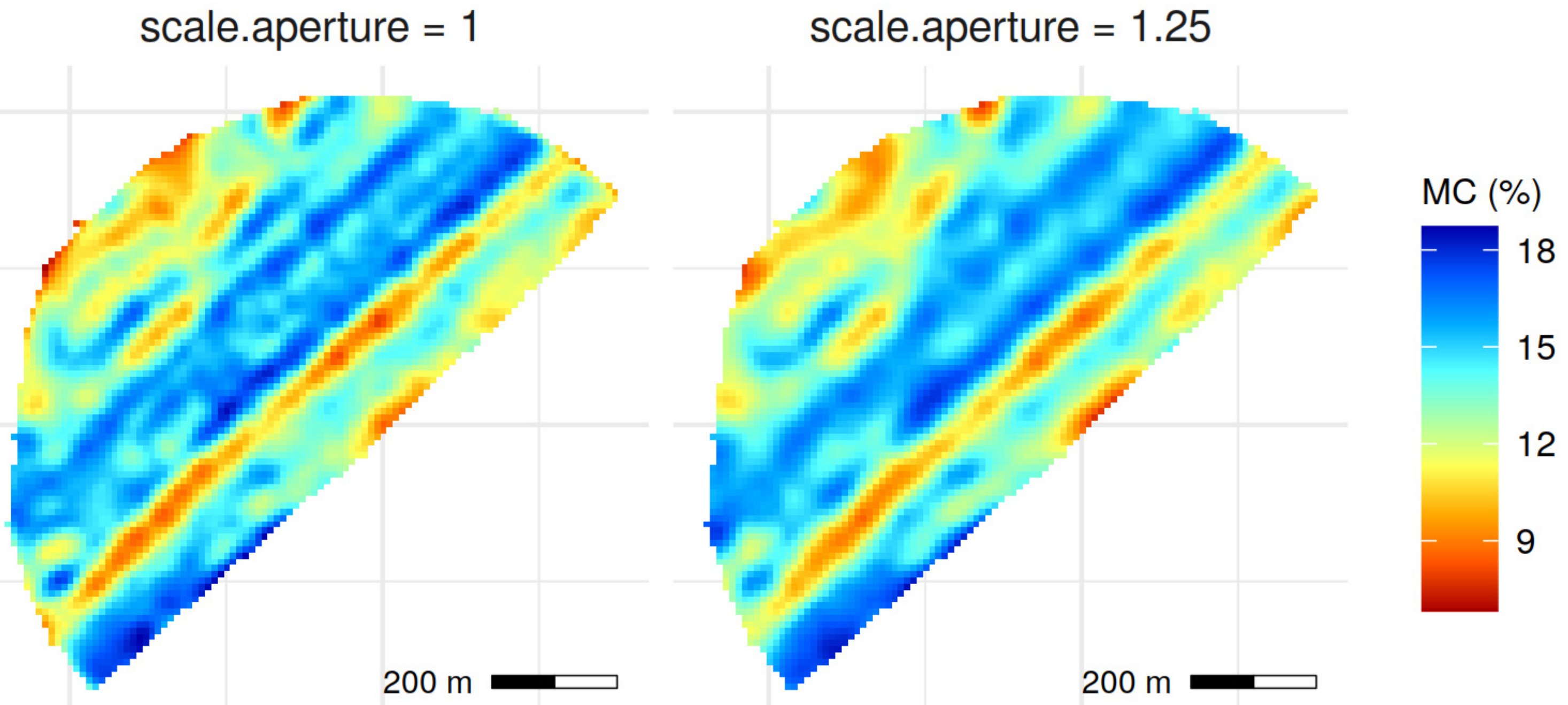
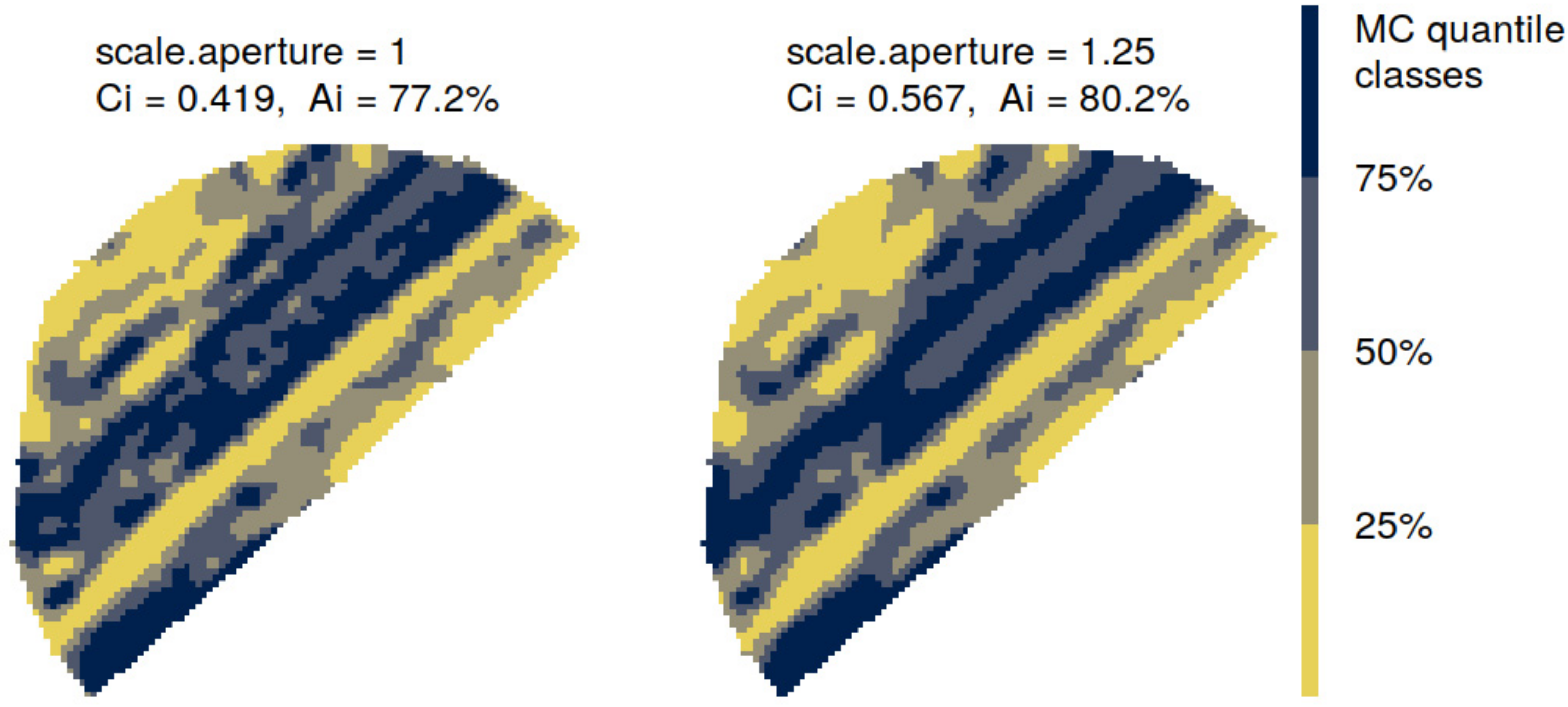
- Scale aperture = 1, almost matched the detected spatial structures from variogram analysis, by distributing a variable number of bisquare basis functions at resolutions of 53, 174 and 696 m, approximately, according to each VNIR soil variable.
- Scale aperture = 1.25, yielded a distribution of a variable number of bisquare basis functions at resolutions of 66, 217 and 869 m, approximately, according to each VNIR soil variable. The target resolutions overlap the detected spatial structures from variogram analysis, and were adopted in order to assess the effect of the spatial covariance function magnitude on the filtering performance of the interpolator.
2.8. Metrics for Evaluation
3. Results
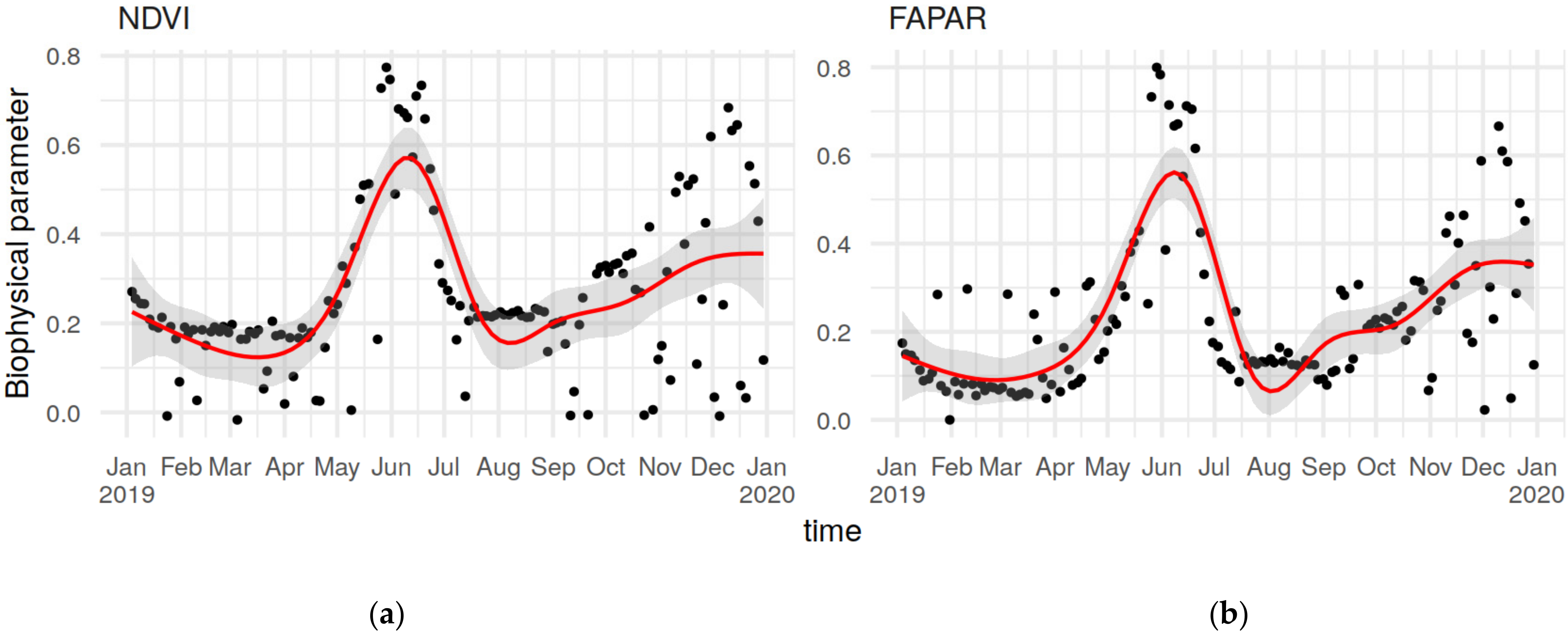
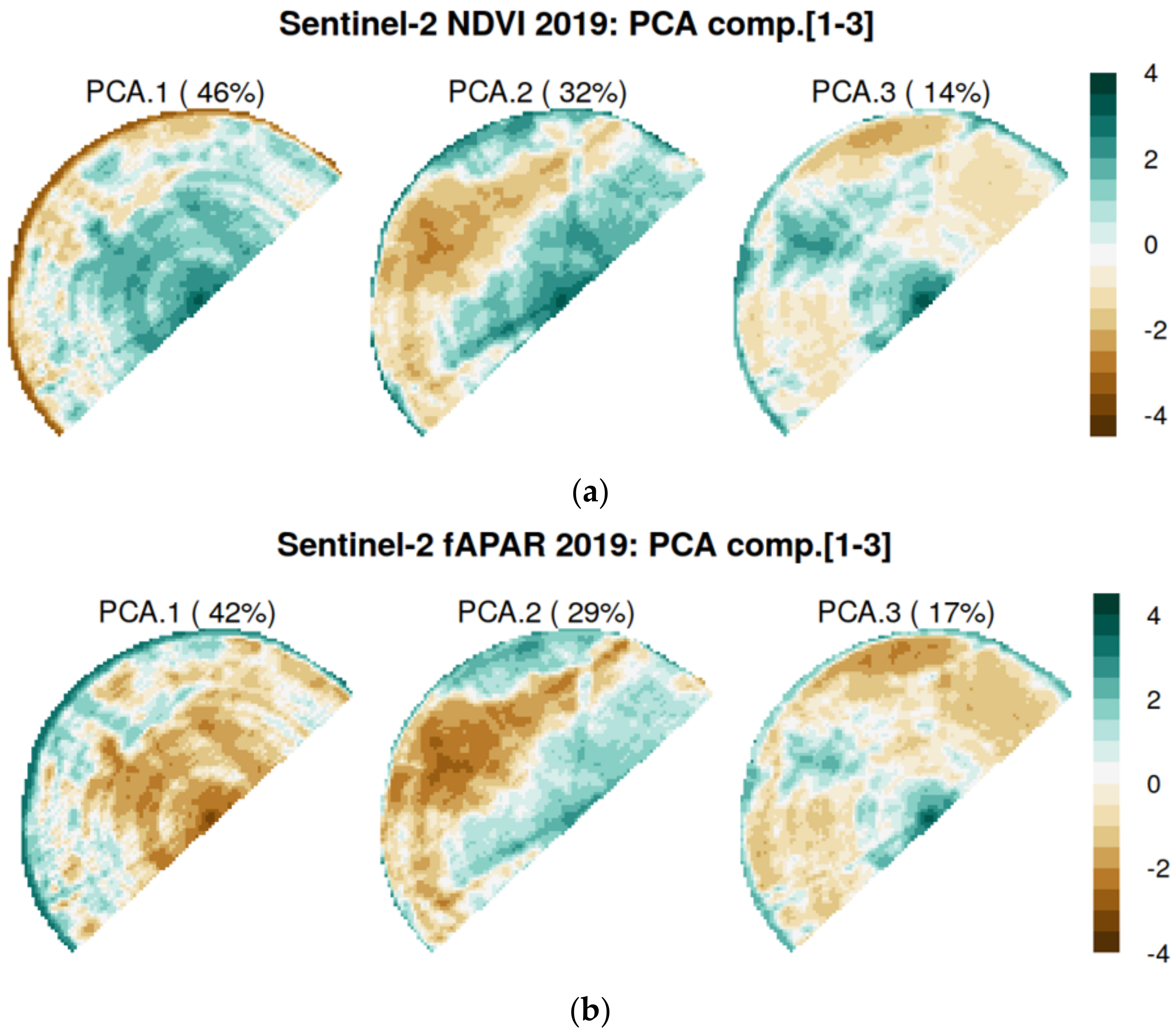
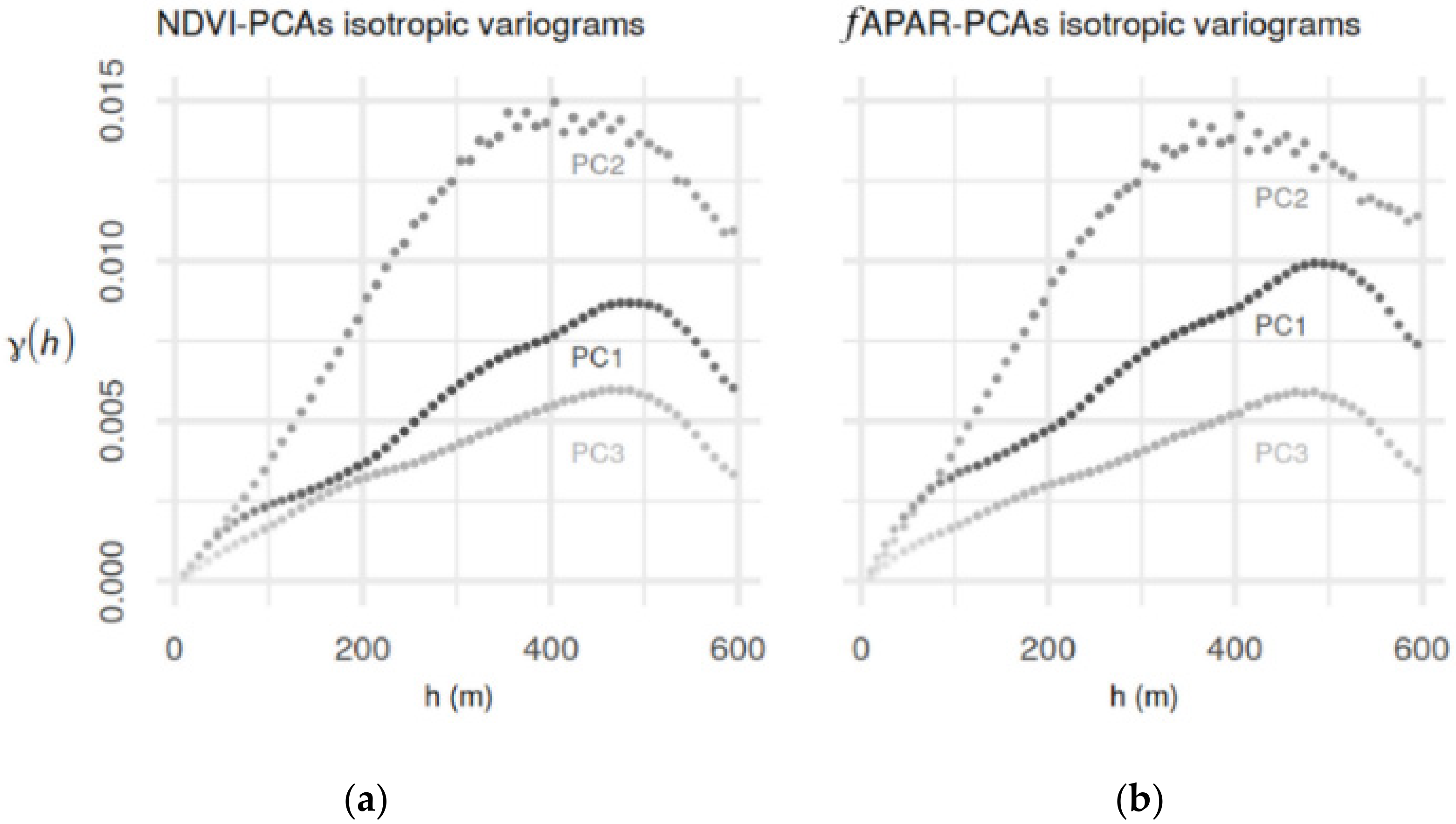
3.1. Soil-Biophysical Parameter Relationship
3.2. Ordinary Kriging Predictions
3.3. Fixed Rank Kriging Predictions
3.4. Performance Assessment and Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Auernhammer, H. Precision farming—the environmental challenge. Comput. Electron. Agric. 2001, 30, 31–43. [Google Scholar] [CrossRef]
- Řezník, T.; Lukas, V.; Charvát, K.; Charvát, K., Jr.; Horáková, Š.; Křivánek, Z.; Hermana, L. Monitoring of in-field variability for site specific crop management through open geospatial information. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 1023–1028. [Google Scholar] [CrossRef]
- Castrignanò, A.; Buttafuoco, G.; Quarto, R.; Parisi, D.; Rossel, R.V.; Terribile, F.; Langella, G.; Venezia, A. A geostatistical sensor data fusion approach for delineating homogeneous management zones in Precision Agriculture. Catena 2018, 167, 293–304. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.; Chappell, A.; De Caritat, P.; McKenzie, N. On the soil information content of visible–near infrared reflectance spectra. Eur. J. Soil Sci. 2011, 62, 442–453. [Google Scholar] [CrossRef]
- Kuang, B.; Mahmood, H.S.; Quraishi, M.Z.; Hoogmoed, W.B.; Mouazen, A.M.; Van Henten, E.J. Sensing soil properties in the laboratory, in situ, and on-line: A review. Adv. Agron. 2012, 114, 155–223. [Google Scholar]
- Mouazen, A.M.; Alexandridis, T.; Buddenbaum, H.; Cohen, Y.; Moshou, D.; Mulla, D.; Nawar, S.; Sudduth, K.A. Chapter 2—Monitoring. In Agricultural Internet of Things and Decision Support for Precision Smart Farming; Castrignanò, A., Buttafuoco, G., Khosla, R., Mouazen, A.M., Moshou, D., Naud, O., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 35–138. [Google Scholar]
- Mouazen, A.M.; Maleki, M.; Cockx, L.; Van Meirvenne, M.; Van Holm, L.; Merckx, R.; De Baerdemaeker, J.; Ramon, H. Optimum three-point linkage set up for improving the quality of soil spectra and the accuracy of soil phosphorus measured using an on-line visible and near infrared sensor. Soil Tillage Res. 2009, 103, 144–152. [Google Scholar] [CrossRef]
- Munnaf, M.A.; Nawar, S.; Mouazen, A.M. Estimation of secondary soil properties by fusion of laboratory and on-line measured Vis–NIR spectra. Remote Sens. 2019, 11, 2819. [Google Scholar] [CrossRef]
- Cressie, N.; Johannesson, G. Fixed rank kriging for very large spatial data sets. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2008, 70, 209–226. [Google Scholar] [CrossRef]
- Cressie, N.; Shi, T.; Kang, E.L. Fixed rank filtering for spatio-temporal data. J. Comput. Graph. Stat. 2010, 19, 724–745. [Google Scholar] [CrossRef]
- Sun, W.; Minasny, B.; McBratney, A. Analysis and prediction of soil properties using local regression-kriging. Geoderma 2012, 171, 16–23. [Google Scholar] [CrossRef]
- Van der Meer, F. Remote-sensing image analysis and geostatistics. Int. J. Remote Sens. 2012, 33, 5644–5676. [Google Scholar] [CrossRef]
- Walter, C.; McBratney, A.B.; Douaoui, A.; Minasny, B. Spatial prediction of topsoil salinity in the Chelif Valley, Algeria, using local ordinary kriging with local variograms versus whole-area variogram. Soil Res. 2001, 39, 259–272. [Google Scholar] [CrossRef][Green Version]
- Khosla, R.; Westfall, D.; Reich, R.; Mahal, J.; Gangloff, W. Spatial variation and site-specific management zones. In Geostatistical Applications for Precision Agriculture; Springer: Berlin/Heidelberg, Germany, 2010; pp. 195–219. [Google Scholar]
- Lal, R.; Stewart, B.A. Soil-Specific Farming: Precision Agriculture; CRC Press: Boca Raton, FL, USA, 2015; Volume 22. [Google Scholar]
- Nawar, S.; Corstanje, R.; Halcro, G.; Mulla, D.; Mouazen, A.M. Delineation of soil management zones for variable-rate fertilization: A review. Adv. Agron. 2017, 143, 175–245. [Google Scholar]
- Shaddad, S.; Madrau, S.; Castrignanò, A.; Mouazen, A. Data fusion techniques for delineation of site-specific management zones in a field in UK. Precis. Agric. 2016, 17, 200–217. [Google Scholar] [CrossRef]
- Bevington, J.; Scudiero, E.; Teatini, P.; Vellidis, G.; Morari, F. Factorial kriging analysis leverages soil physical properties and exhaustive data to predict distinguished zones of hydraulic properties. Comput. Electron. Agric. 2019, 156, 426–438. [Google Scholar] [CrossRef]
- Keskin, H.; Grunwald, S. Regression kriging as a workhorse in the digital soil mapper’s toolbox. Geoderma 2018, 326, 22–41. [Google Scholar] [CrossRef]
- Casa, R.; Castaldi, F.; Pascucci, S.; Basso, B.; Pignatti, S. Geophysical and hyperspectral data fusion techniques for in-field estimation of soil properties. Vadose Zone J. 2013, 12, 1–10. [Google Scholar] [CrossRef]
- Nguyen, H.; Cressie, N.; Braverman, A. Spatial statistical data fusion for remote sensing applications. J. Am. Stat. Assoc. 2012, 107, 1004–1018. [Google Scholar] [CrossRef]
- Wulf, H.; Mulder, T.; Schaepman, M.E.; Keller, A.; Jörg, P.C. Remote Sensing of Soils; University of Zurich: Zurich, Switzerland, 2015; pp. 1–71. [Google Scholar]
- Mulder, V.; De Bruin, S.; Weyermann, J.; Kokaly, R.F.; Schaepman, M.E. Characterizing regional soil mineral composition using spectroscopy and geostatistics. Remote Sens. Environ. 2013, 139, 415–429. [Google Scholar] [CrossRef]
- Cressie, N.; Kang, E.L. High-resolution digital soil mapping: Kriging for very large datasets. In Proximal Soil Sensing; Springer: Berlin/Heidelberg, Germany, 2010; pp. 49–63. [Google Scholar]
- Campos, I.; González-Gómez, L.; Villodre, J.; Calera, M.; Campoy, J.; Jiménez, N.; Plaza, C.; Sánchez-Prieto, S.; Calera, A. Mapping within-field variability in wheat yield and biomass using remote sensing vegetation indices. Precis. Agric. 2019, 20, 214–236. [Google Scholar] [CrossRef]
- Mouazen, A. Soil Survey Device. International Publication Published under the Patent Cooperation Treaty (PCT); World Intellectual Property Organization, International Bureau: Geneva, Switzerland, 2006. [Google Scholar]
- Weiss, M.; Baret, F. ATBD S2ToolBox Level 2 Products: LAI, FAPAR, FCOVER (Version 1.1). 2016. Available online: http://step.esa.int/docs/extra/ATBD_S2ToolBox_L2B_V1.1.pdf (accessed on 27 February 2022).
- Gobin, A.; Campling, P.; Deckers, J.; Feyen, J. Quantifying soil morphology in tropical environments methods and application in soil classification. Soil Sci. Soc. Am. J. 2000, 64, 1423–1433. [Google Scholar] [CrossRef]
- Gobin, A.; Campling, P.; Feyen, J. Soil-landscape modelling to quantify spatial variability of soil texture. Phys. Chem. Earth Part B: Hydrol. Ocean. Atmos. 2001, 26, 41–45. [Google Scholar] [CrossRef]
- Hengl, T.; Toomanian, N.; Reuter, H.I.; Malakouti, M.J. Methods to interpolate soil categorical variables from profile observations: Lessons from Iran. Geoderma 2007, 140, 417–427. [Google Scholar] [CrossRef]
- Xu, Y.; Smith, S.E.; Grunwald, S.; Abd-Elrahman, A.; Wani, S.P. Incorporation of satellite remote sensing pan-sharpened imagery into digital soil prediction and mapping models to characterize soil property variability in small agricultural fields. ISPRS J. Photogramm. Remote Sens. 2017, 123, 1–19. [Google Scholar] [CrossRef]
- Heuvelink, G.B.; Pebesma, E.J. Spatial aggregation and soil process modelling. Geoderma 1999, 89, 47–65. [Google Scholar] [CrossRef]
- Duffera, M.; White, J.G.; Weisz, R. Spatial variability of Southeastern US Coastal Plain soil physical properties: Implications for site-specific management. Geoderma 2007, 137, 327–339. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical tools for characterizing the spatial variability of microbiological and physico-chemical soil properties. Biol. Fertil. Soils 1998, 27, 315–334. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Zammit-Mangion, A.; Cressie, N. FRK: An R package for spatial and spatio-temporal prediction with large datasets. J. Stat. Softw. 2021, 98, 1–48. [Google Scholar] [CrossRef]
- Katzfuss, M.; Cressie, N. Spatio-temporal smoothing and EM estimation for massive remote-sensing data sets. J. Time Ser. Anal. 2011, 32, 430–446. [Google Scholar] [CrossRef]
- Kang, E.L.; Liu, D.; Cressie, N. Statistical analysis of small-area data based on independence, spatial, non-hierarchical, and hierarchical models. Comput. Stat. Data Anal. 2009, 53, 3016–3032. [Google Scholar] [CrossRef]
- Nychka, D.; Wikle, C.; Royle, J.A. Multiresolution models for nonstationary spatial covariance functions. Stat. Model. 2002, 2, 315–331. [Google Scholar] [CrossRef]
- Janssen, P.; Heuberger, P. Calibration of process-oriented models. Ecol. Model. 1995, 83, 55–66. [Google Scholar] [CrossRef]
- Wang, B.; Waters, C.; Orgill, S.; Gray, J.; Cowie, A.; Clark, A.; Li Liu, D. High resolution mapping of soil organic carbon stocks using remote sensing variables in the semi-arid rangelands of eastern Australia. Sci. Total Environ. 2018, 630, 367–378. [Google Scholar] [CrossRef] [PubMed]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.-M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Řezník, T.; Herman, L.; Trojanová, K.; Pavelka, T.; Leitgeb, Š. Interpolation of data measured by field harvesters: Deployment, comparison and verification. In Proceedings of the International Symposium on Environmental Software Systems, Wageningen, The Netherlands, 5–7 February 2020; pp. 258–270. [Google Scholar]
- McGarigal, K. FRAGSTATS: Spatial Pattern Analysis Program for Quantifying Landscape Structure; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, Oregon, USA, 1995; Volume 351. [Google Scholar]
- Hesselbarth, M.H.; Sciaini, M.; With, K.A.; Wiegand, K.; Nowosad, J. landscapemetrics: An open-source R tool to calculate landscape metrics. Ecography 2019, 42, 1648–1657. [Google Scholar] [CrossRef]
- Huete, A.; Miura, T.; Yoshioka, H.; Ratana, P.; Broich, M. Indices of vegetation activity. In Biophysical Applications of Satellite Remote Sensing; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–41. [Google Scholar]
- Jiang, Z.; Huete, A.R.; Li, J.; Chen, Y. An analysis of angle-based with ratio-based vegetation indices. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2506–2513. [Google Scholar] [CrossRef]
- Miller, B.A.; Koszinski, S.; Wehrhan, M.; Sommer, M. Impact of multi-scale predictor selection for modeling soil properties. Geoderma 2015, 239, 97–106. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1. [Google Scholar] [CrossRef]
- Royston, J.P. An extension of Shapiro and Wilk’s W test for normality to large samples. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1982, 31, 115–124. [Google Scholar] [CrossRef]
- Mouazen, A.; Maleki, M.; De Baerdemaeker, J.; Ramon, H. On-line measurement of some selected soil properties using a VIS–NIR sensor. Soil Tillage Res. 2007, 93, 13–27. [Google Scholar] [CrossRef]
| Soil Variables | Total Points | Prediction Points | NN Min 1 | NN Max 1 | NN Mean 1 | Min | 1st Qu | Mean | 3rd Qu | Max | SD | CV% | Kurtosis | Skewness |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ca (meq/100 g) | 33,659 | 31,874 | 0.15 | 11.3 | 1.14 | 23.53 | 35.39 | 38.86 | 41.13 | 85.89 | 4.142 | 10.88 | 2.5445 | −0.0937 |
| MC (%) | 29,444 | 29,444 | 0.24 | 13.1 | 1.18 | 6.333 | 11.56 | 14.06 | 16.67 | 21.5 | 3.487 | 24.79 | 2.8964 | −0.1803 |
| Mg (meq/100 g) | 32,071 | 31,380 | 0.15 | 11.8 | 1.16 | 2.50 | 4.971 | 5.765 | 6.467 | 14.96 | 1.075 | 18.86 | 2.3110 | 0.1633 |
| Na (meq/100 g) | 33,032 | 32,668 | 0.15 | 11.3 | 1.14 | 0.004 | 0.306 | 0.415 | 0.520 | 1.14 | 0.154 | 37.86 | 2.9403 | −0.2632 |
| pH | 28,035 | 28,035 | 0.15 | 33.7 | 1.19 | 7.93 | 8.313 | 8.439 | 8.579 | 8.8 | 0.186 | 2.21 | 2.7543 | −0.2855 |
| Soil Variables | Min. | 1st Qu | Median | Mean | 3rd Qu | Max. | Stand Dev | CV% |
|---|---|---|---|---|---|---|---|---|
| Ca (meq/100 g) | 26.37 | 35.3 | 38.93 | 39.1 | 42.54 | 83.15 | 7.003 | 17.91 |
| MC (%) | 7.027 | 10.9 | 12.88 | 13.18 | 15.45 | 20.81 | 2.883 | 21.88 |
| Mg (meq/100 g) | 3.076 | 4.812 | 5.575 | 5.878 | 6.756 | 14.42 | 1.686 | 28.68 |
| Na (meq/100 g) | 0.004307 | 0.1828 | 0.3533 | 0.3839 | 0.5536 | 1.09 | 0.2513 | 65.44 |
| pH | 7.97 | 8.394 | 8.48 | 8.459 | 8.56 | 8.765 | 0.1331 | 1.574 |
| Soil Variable | Model/Direction | Nugget | Partial Sill | Sill | Nugget/Sill | Range (m) | Lag Size (m) | Cut-Off (m) | Prediction Neighbors | Cross-Validation RMSE |
|---|---|---|---|---|---|---|---|---|---|---|
| Ca | stable/isotropic | 0.0171602 | 33 | 33.01716 | 0.000520 | 112 | 14 | 168 | 200 | 2.844 |
| MC | stable/isotropic | 0.2366 | 0.808 | 1.0446 | 0.226498 | 180 | 15 | 180 | 200 | 2.397 |
| Mg | spherical/isotropic | 0.0011571 | 2.5345 | 2.535657 | 0.000456 | 112 | 14 | 168 | 200 | 0.603 |
| Na | stable/isotropic | 0.01095 | 0.01588 | 0.02683 | 0.408125 | 244 | 18 | 360 | 200 | 0.1037 |
| pH | stable/isotropic | 0.4913 | 0.4721 | 0.9634 | 0.509965 | 135 | 17 | 204 | 200 | 0.1421 |
| VNIR Soil | Scale Aperture: 1 | Scale Aperture: 1.25 | ||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Res.1 | Res.2 | Res.3 | Total count | Res.1 | Res.2 | Res.3 | Total Count |
| Ca | 52.68 | 173.88 | 695.52 | 480 | 66.09 | 217.34 | 869.74 | 472 |
| MC | 52.80 | 173.96 | 695.85 | 477 | 66.10 | 217.59 | 870.34 | 468 |
| Mg | 52.92 | 173.64 | 694.55 | 480 | 66.13 | 216.93 | 867.74 | 467 |
| Na | 52.89 | 173.44 | 693.75 | 483 | 66.23 | 217.06 | 868.25 | 471 |
| pH | 52.73 | 173.64 | 694.58 | 482 | 66.09 | 217.16 | 868.64 | 470 |
| Aggregated Data on 10 m Grid | PC1.NDVI | PC2.NDVI | PC3.NDVI | PC1.fAPAR | PC2. fAPAR | PC3. fAPAR |
|---|---|---|---|---|---|---|
| Ca | 0.21 *** | −0.52 *** | 0.07 *** | 0.14 *** | −0.47 *** | −0.07 *** |
| MC | 0.07 *** | −0.17 *** | 0.04 ** | −0.08 *** | −0.19 *** | −0.02 |
| Mg | −0.24 *** | −0.56 *** | 0.06 *** | 0.15 *** | −0.51 *** | −0.08 *** |
| Na | −0.26 *** | −0.14 *** | 0.08 *** | 0.22 *** | −0.06 *** | 0.06 *** |
| pH | 0.14 *** | 0.14 *** | 0.02 | −0.11 *** | 0.09 *** | 0.04 ** |
| Aggregated VNIR Soil Variable | RMSE | R2 | Lambda |
|---|---|---|---|
| Ca | 3.063 | 0.245 | 0.169 |
| MC | 2.869 | 0.043 | 0.048 |
| Mg | 0.815 | 0.316 | 0.053 |
| Na | 0.126 | 0.034 | 0.002 |
| pH | 0.149 | 0.033 | 0.002 |
| Soil Var | Method | Covariates | ML Estim. | Number of Iterations | Basis Functions | Estimation Cells | Mean obs. Variance at Cell | Elapsed Time (s) |
|---|---|---|---|---|---|---|---|---|
| Ca | FRK | EM | 21 | 476 | 5086 | 5.8437 | 308.2 | |
| FRK-BioPAR | PC1n,PC2n,PC1f,PC2f | EM | 111 | 472 | 5113 | 5.8437 | 1618.1 | |
| MC | FRK | EM | 14 | 468 | 5086 | 4.1921 | 182.7 | |
| FRK-BioPAR | PC1n,PC2n,PC1f,PC2f | EM | 26 | 470 | 5096 | 4.1921 | 333.9 | |
| Mg | FRK | EM | 16 | 472 | 5086 | 0.2363 | 216.2 | |
| FRK-BioPAR | PC1n,PC2n,PC1f,PC2f | EM | 107 | 467 | 5112 | 0.2363 | 1452.2 | |
| Na | FRK | EM | 19 | 471 | 5086 | 0.0076 | 250.3 | |
| FRK-BioPAR | PC1n,PC2n,PC1f,PC2f | EM | 27 | 473 | 5119 | 0.0076 | 361.4 | |
| pH | FRK | EM | 24 | 471 | 5086 | 0.0152 | 276.4 | |
| FRK-BioPAR | PC1n,PC2n,PC1f,PC2f | EM | 38 | 470 | 5086 | 0.0152 | 444.3 |
| Soil Variable | Ordinary Kriging | Fixed Rank Kriging | Fixed Rank Kriging with BioPAR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | RPIQ | MAE | RMSE | RPIQ | RI % | RI*% | MAE | RMSE | RPIQ | RI % | RI*% | |
| Ca (meq/100 g) | 4.118 | 6.242 | 1.16 | 4.005 | 6.118 | 1.176 | 1.99 | (1.19) | 4.037 | 6.124 | 1.175 | 1.89 | (1.22) |
| MC (%) | 2.594 | 3.149 | 1.445 | 2.436 | 2.933 | 1.527 | 6.86 | (4.00) | 2.432 | 2.921 | 1.533 | 7.24 | (4.00) |
| Mg (meq/100 g) | 1.022 | 1.457 | 1.334 | 0.9833 | 1.399 | 1.402 | 3.98 | (4.26) | 0.9912 | 1.404 | 1.397 | 3.64 | (3.91) |
| Na (meq/100 g) | 0.157 | 0.201 | 1.846 | 0.1565 | 0.1995 | 1.819 | 0.75 | (0.15) | 0.1559 | 0.1995 | 1.819 | 0.75 | (0.50) |
| pH | 0.104 | 0.144 | 1.153 | 0.1035 | 0.139 | 1.196 | 3.47 | (5.00) | 0.1039 | 0.1392 | 1.194 | 3.33 | (5.00) |
| Soil | dv Quantiles | Noise Statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | Method | 2% | 25% | 50% | 75% | 98% | MSEn | MSE*n | Mean | St. Dev | W-Test |
| Ca (meq/100 g) | OK | −9.41 | −1.518 | 0 | 1.39 | 6.47 | 1.5 | (1.5) | −4.08 × 10−2 | 1.22 | 0.93 |
| FRK | −16.86 | −2.755 | 0.2539 | 2.893 | 9.61 | 4.21 | (3.95) | −1.44 × 10−2 | 2.05 | 0.952 | |
| FRK-BioPAR | −16.82 | −2.811 | 0.2847 | 2.928 | 9.59 | 4.27 | (4.04) | −1.91 × 10−2 | 2.07 | 0.955 | |
| MC (%) | OK | −30.14 | −4.068 | 0 | 3.232 | 14.13 | 1.22 | (1.22) | −7.11 × 10−2 | 1.1 | 0.938 |
| FRK | −52.65 | −10.182 | 0.35 | 8.431 | 22.99 | 4.11 | (3.74) | −2.96 × 10−2 | 2.03 | 0.99 | |
| FRK-BioPAR | −53 | −10.062 | 0.6773 | 8.855 | 24.25 | 4.21 | (3.84) | −3.02 × 10−3 | 2.05 | 0.992 | |
| Mg (meq/100 g) | OK | −15.73 | −2.953 | 0 | 1.822 | 10.11 | 0.0881 | (0.0881) | −2.26 × 10−2 | 0.296 | 0.925 |
| FRK | −30.14 | −4.91 | 0.6942 | 5.521 | 16.98 | 0.283 | (0.273) | 1.62 × 10−2 | 0.532 | 0.977 | |
| FRK-BioPAR | −31.71 | −5.11 | 0.6782 | 5.563 | 17.49 | 0.292 | (0.28) | 1.54 × 10−2 | 0.54 | 0.975 | |
| Na (meq/100 g) | OK | −49.8 | −4.537 | 0 | 3.853 | 21.37 | 0.0017 | (0.0017) | 1.51 × 10−4 | 0.0412 | 0.912 |
| FRK | −93.27 | −9.493 | 0.0997 | 8.208 | 29.48 | 0.00424 | (0.00406) | −1.99 × 10−4 | 0.0651 | 0.962 | |
| FRK-BioPAR | −93.15 | −9.965 | −0.2347 | 8.062 | 29.57 | 0.00426 | (0.00407) | −1.14 × 10−3 | 0.0653 | 0.966 | |
| pH | OK | −2.07 | −0.362 | 0 | 0.298 | 1.62 | 0.0044 | (0.0044) | −4.49 × 10−3 | 0.0662 | 0.925 |
| FRK | −2.81 | −0.667 | 0.0612 | 0.75 | 2.47 | 0.0107 | (0.0102) | 9.10 × 10−4 | 0.103 | 0.985 | |
| FRK-BioPAR | −2.83 | −0.661 | 0.0842 | 0.791 | 2.55 | 0.011 | (0.0104) | 2.79 × 10−3 | 0.105 | 0.988 | |
| Method | Ca | MC | Mg | Na | pH | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ci Avg. | Ai % | Ci Avg. | Ai % | Ci Avg. | Ai % | Ci Avg. | Ai % | Ci avg. | Ai % | |
| OK | 0.1665 | 66.93 | 0.1696 | 61.2 | 0.1402 | 68.23 | 0.1779 | 74.56 | 0.1909 | 64.21 |
| FRK | 0.4783 | 85.23 | 0.5891 | 80.74 | 0.5886 | 89.43 | 0.6601 | 87.31 | 0.511 | 81.7 |
| FRK-BioPAR | 0.414 | 84.37 | 0.487 | 79.89 | 0.4527 | 88.72 | 0.5529 | 86.69 | 0.4198 | 80.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karapetsas, N.; Alexandridis, T.K.; Bilas, G.; Munnaf, M.A.; Guerrero, A.P.; Calera, M.; Osann, A.; Gobin, A.; Rezník, T.; Moshou, D.; et al. Mapping Soil Properties with Fixed Rank Kriging of Proximally Sensed Soil Data Fused with Sentinel-2 Biophysical Parameter. Remote Sens. 2022, 14, 1639. https://doi.org/10.3390/rs14071639
Karapetsas N, Alexandridis TK, Bilas G, Munnaf MA, Guerrero AP, Calera M, Osann A, Gobin A, Rezník T, Moshou D, et al. Mapping Soil Properties with Fixed Rank Kriging of Proximally Sensed Soil Data Fused with Sentinel-2 Biophysical Parameter. Remote Sensing. 2022; 14(7):1639. https://doi.org/10.3390/rs14071639
Chicago/Turabian StyleKarapetsas, Nikolaos, Thomas K. Alexandridis, George Bilas, Muhammad Abdul Munnaf, Angela P. Guerrero, Maria Calera, Anna Osann, Anne Gobin, Tomáš Rezník, Dimitrios Moshou, and et al. 2022. "Mapping Soil Properties with Fixed Rank Kriging of Proximally Sensed Soil Data Fused with Sentinel-2 Biophysical Parameter" Remote Sensing 14, no. 7: 1639. https://doi.org/10.3390/rs14071639
APA StyleKarapetsas, N., Alexandridis, T. K., Bilas, G., Munnaf, M. A., Guerrero, A. P., Calera, M., Osann, A., Gobin, A., Rezník, T., Moshou, D., & Mouazen, A. M. (2022). Mapping Soil Properties with Fixed Rank Kriging of Proximally Sensed Soil Data Fused with Sentinel-2 Biophysical Parameter. Remote Sensing, 14(7), 1639. https://doi.org/10.3390/rs14071639












