Optical Design of a Common-Aperture Camera for Infrared Guided Polarization Imaging
Abstract
:1. Introduction
2. Principle and Imaging Mode
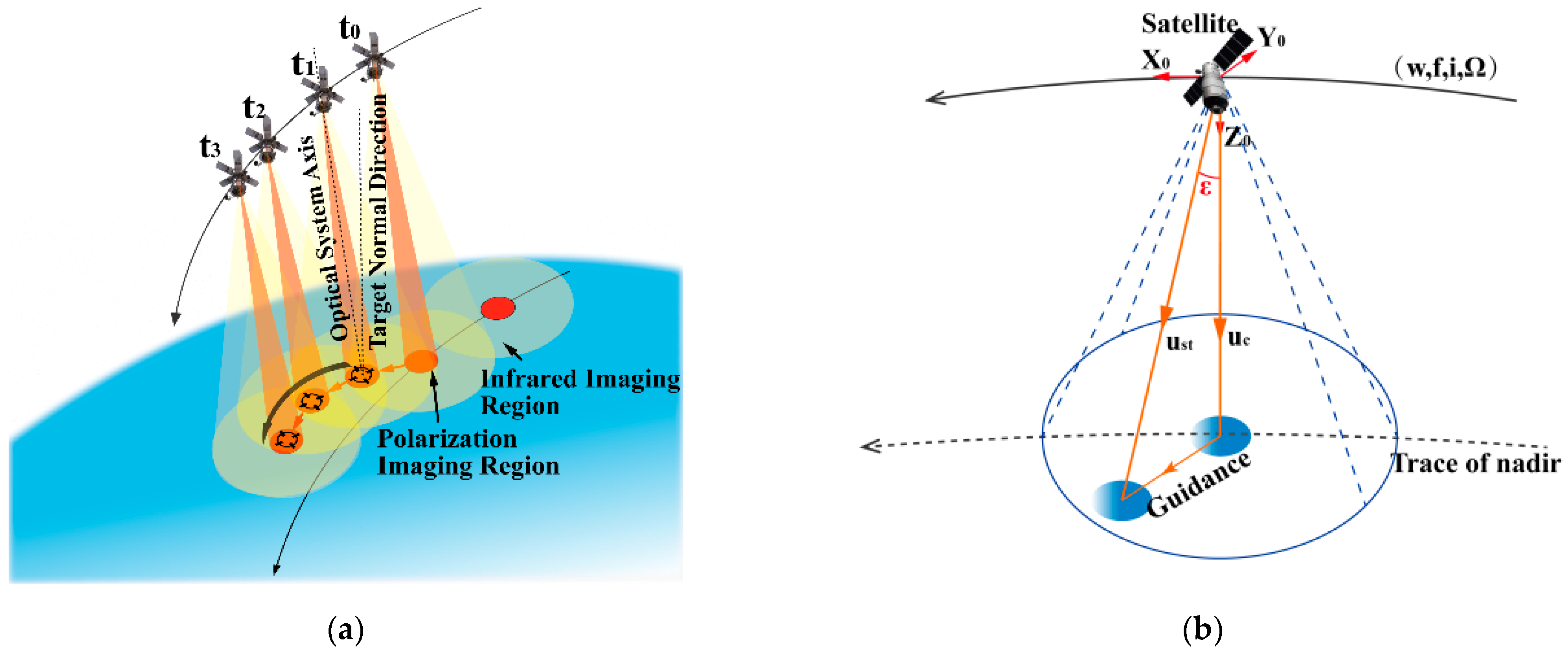
2.1. IGP Imaging Model
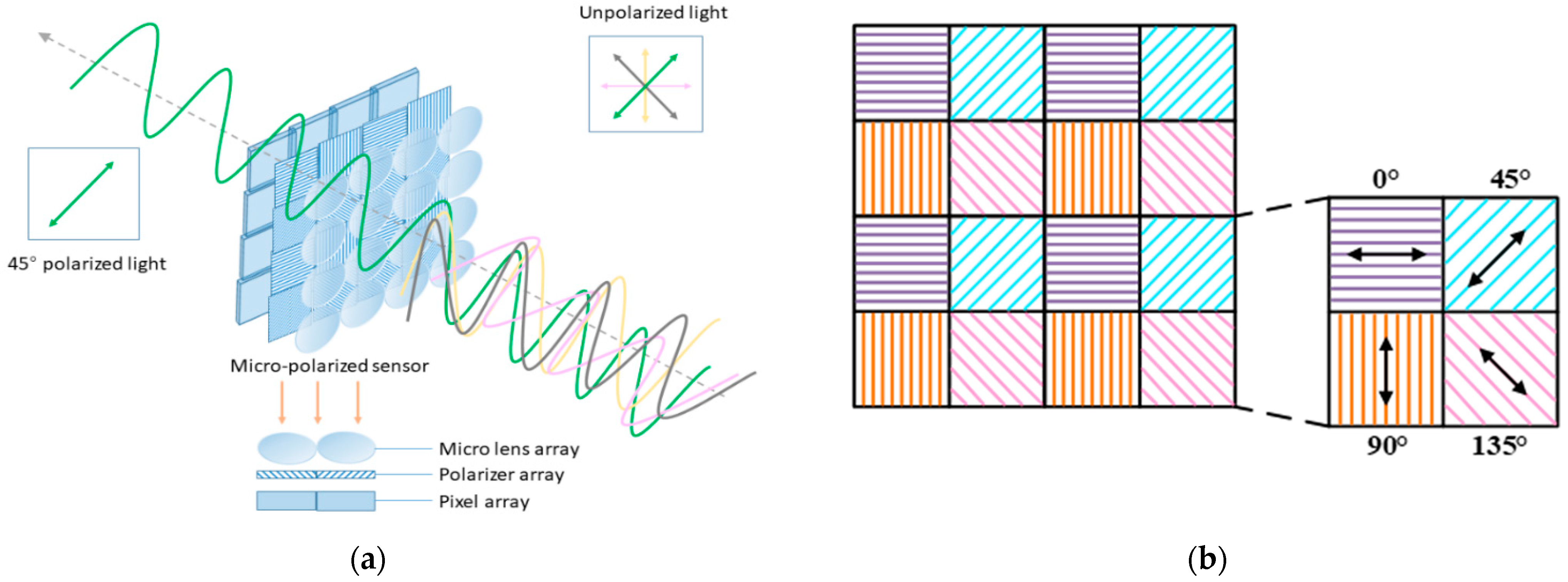
2.2. Pixel-Level Polarization Sensor
3. Optical Design and Analysis
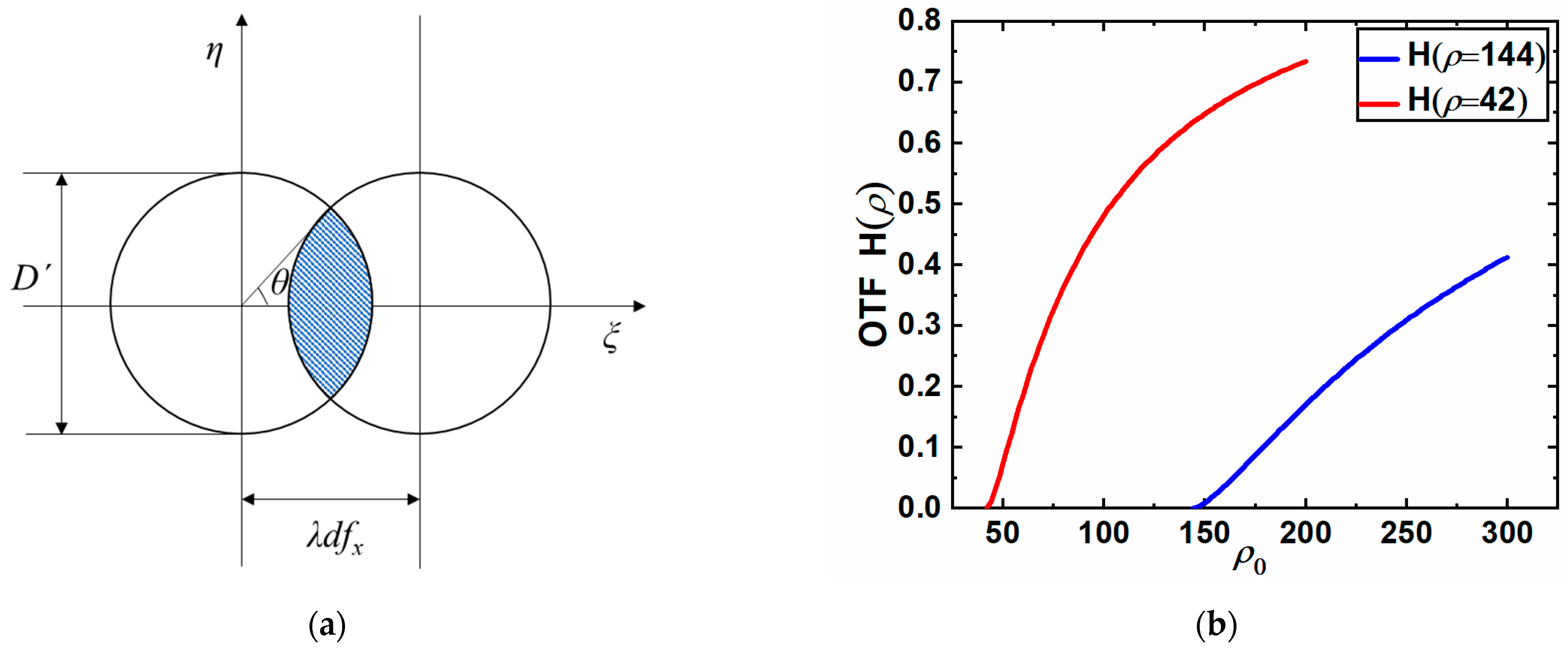
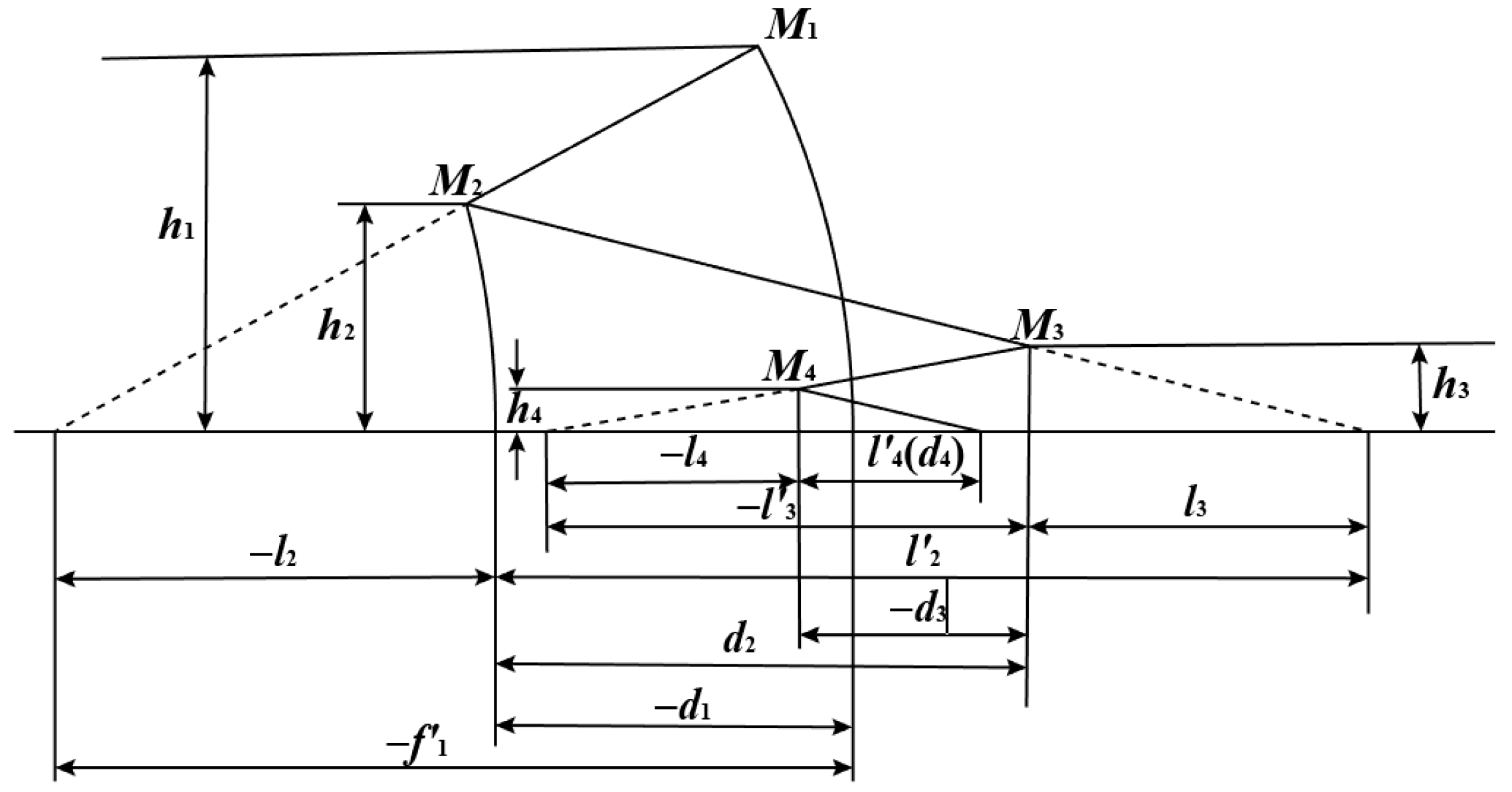
3.1. Calculation of Optical Parameter
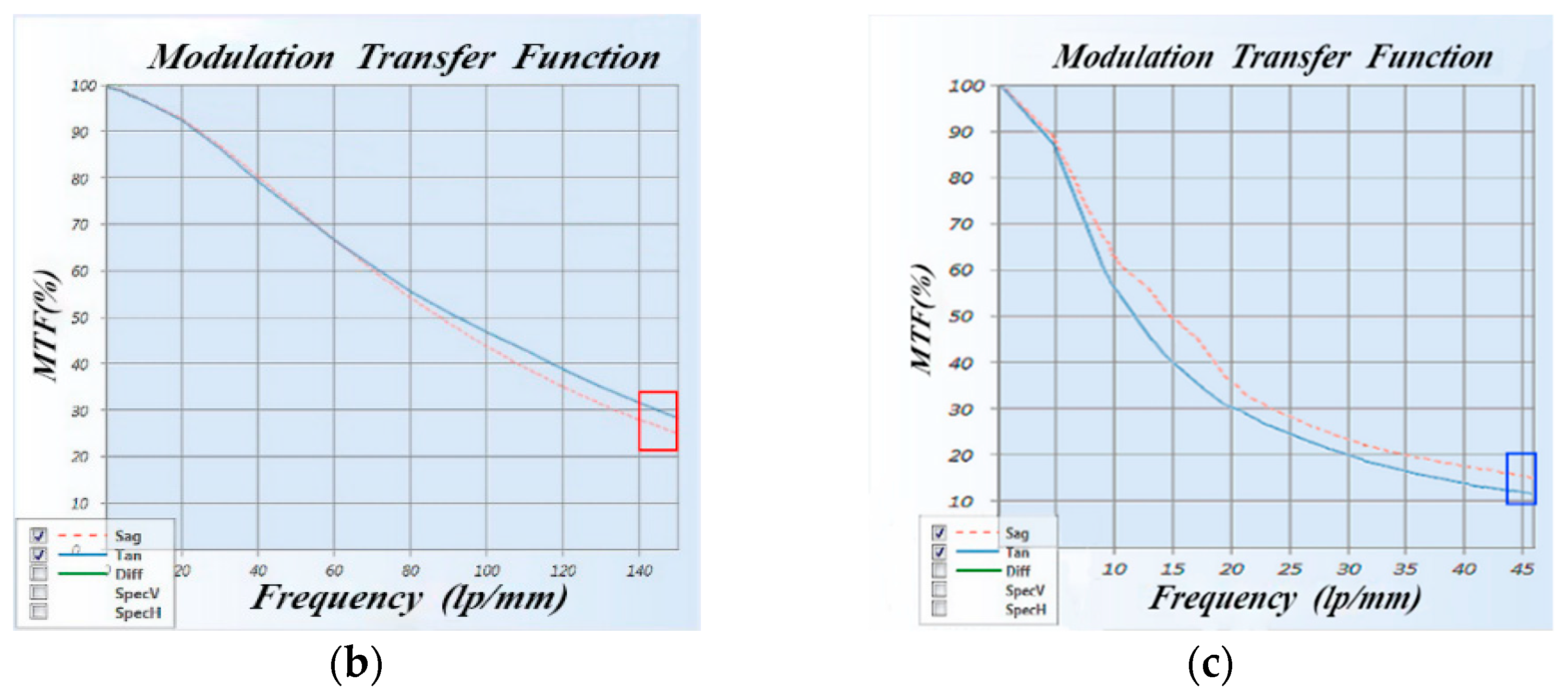
3.2. Fore-Infrared System
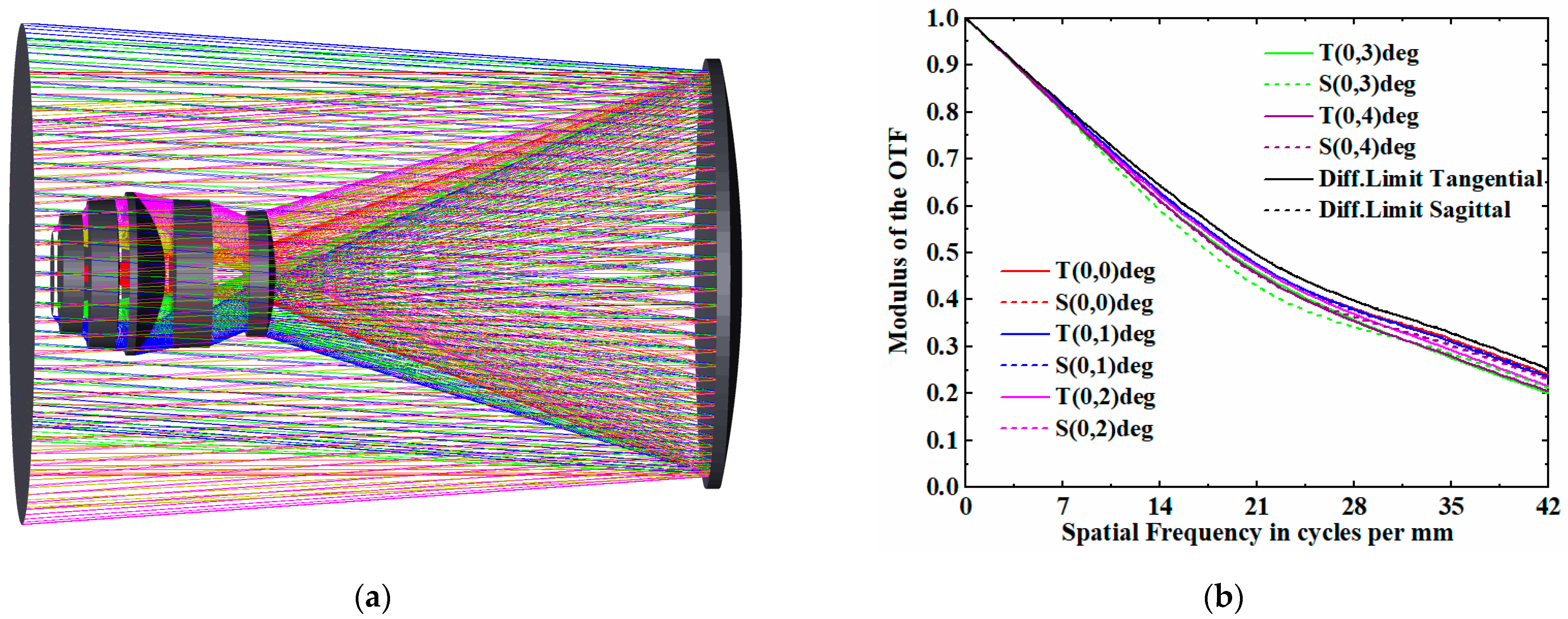
3.3. Rear-Polarization System
3.4. Overall Optical System
4. Ground Imaging Experiment
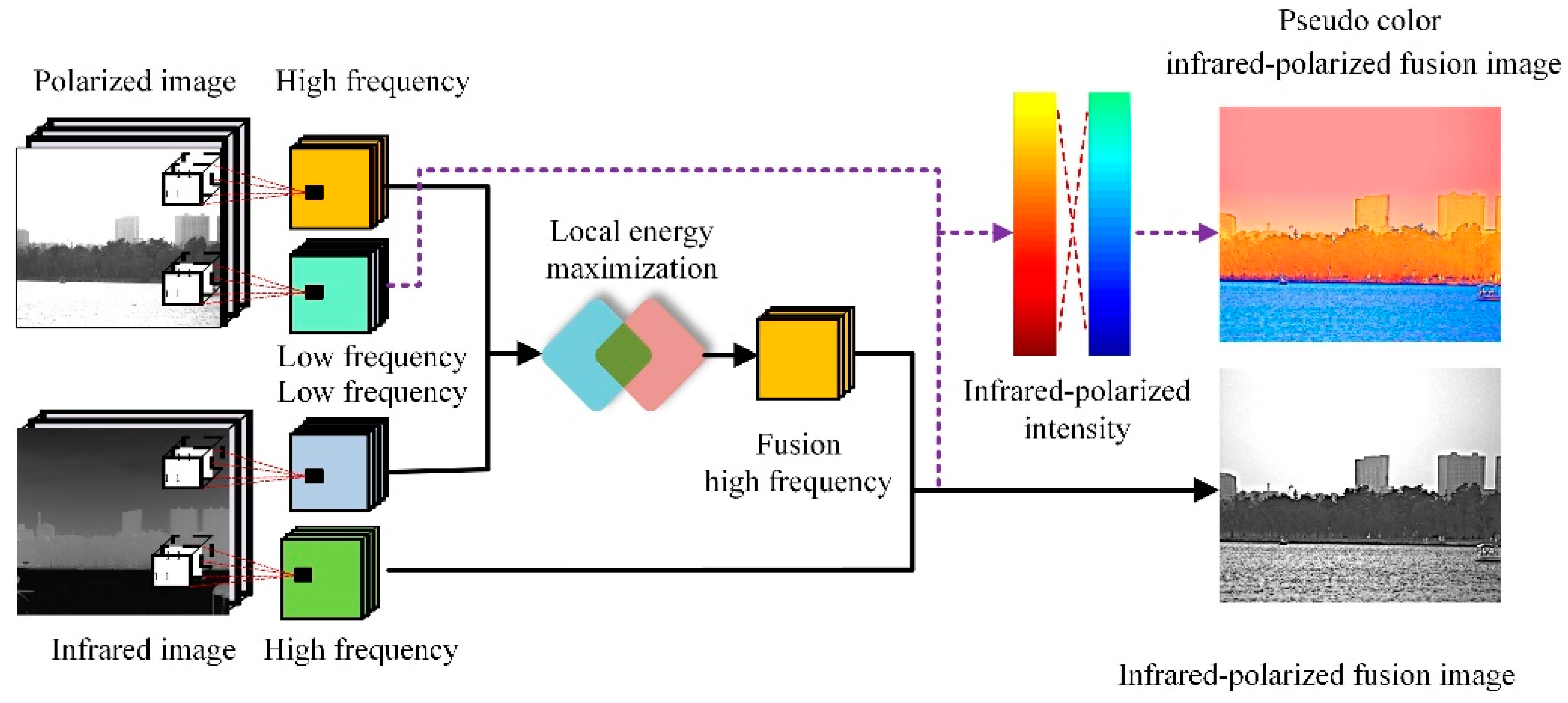
Outfield Imaging Experiment and Image Fusion
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, M.; Xu, W.; Sun, Z.; Wu, H.; Tian, Y.; Li, L. Mid-wave infrared polarization imaging system for detecting moving scene. Opt. Lett. 2020, 45, 5884–5887. [Google Scholar] [CrossRef] [PubMed]
- Bowles, J.H.; Korwan, D.R.; Montes, M.J.; Gray, D.J.; Gillis, D.B.; Lamela, G.M.; Miller, W.D. Airborne system for multispectral, multiangle polarimetric imaging. Appl. Opt. 2015, 54, F256–F267. [Google Scholar] [CrossRef] [PubMed]
- Miyata, M.; Nakajima, M.; Hashimoto, T. Compound-eye metasurface optics enabling a high-sensitivity, ultra-thin polarization camera. Opt. Express 2020, 28, 9996–10014. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Yan, R.; Zhang, J.; Xu, Y.; Chen, P.; Shi, L.; Wang, J.; Zhong, S.; Zhang, X. Arctic Sea Ice Classification Based on CFOSAT SWIM Data at Multiple Small Incidence Angles. Remote Sens. 2021, 14, 91. [Google Scholar] [CrossRef]
- Touzi, R. Target Scattering Decomposition in Terms of Roll-Invariant Target Parameters. IEEE Trans. Geosci. Remote Sens. 2006, 45, 73–84. [Google Scholar] [CrossRef]
- Muhuri, A.; Manickam, S.; Bhattacharya, A. Scattering Mechanism Based Snow Cover Mapping Using RADARSAT-2 C-Band Polarimetric SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3213–3224. [Google Scholar] [CrossRef]
- Mura, A.; Adriani, A.; Sordini, R.; Sindoni, G.; Plainaki, C.; Tosi, F.; Filacchione, G.; Bolton, S.; Zambon, F.; Hansen, C.J.; et al. Infrared Observations of Ganymede from the Jovian InfraRed Auroral Mapper on Juno. J. Geophys. Res. Planets 2020, 125, e2020JE006508. [Google Scholar] [CrossRef]
- Vizgaitis, J.N.; Hastings, A. Dual band infrared picture-in-picture systems. Opt. Eng. 2013, 52, 061306. [Google Scholar] [CrossRef]
- Ohno, H. Multi-angle-view monocular camera using a polarization image sensor. Appl. Opt. 2019, 58, 4036–4041. [Google Scholar] [CrossRef]
- Ding, Z.; Sun, C.; Han, H.; Ma, L.; Zhao, Y. Calibration Method for Division-of-Focal-Plane Polarimeters Using Nonuniform Light. IEEE Photonics J. 2021, 13, 3900309. [Google Scholar] [CrossRef]
- Ratliff, B.M.; LeMaster, D.A.; Mack, R.T.; Villeneuve, P.V.; Weinheimer, J.J.; Middendorf, J.R. Detection and tracking of RC model aircraft in LWIR microgrid polarimeter data. Proc. SPIE-Int. Soc. Opt. Eng. 2011, 8160, 25–31. [Google Scholar]
- Baumann, B.; Götzinger, E.; Pircher, M.; Hitzenberger, C.K. Single camera based spectral domain polarization sensitive optical coherence tomography. Opt. Express 2007, 15, 1054–1063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fei, H.; Li, F.-M.; Chen, W.-C.; Zhang, R.; Chen, C.-S. Calibration method for division of focal plane polarimeters. Appl. Opt. 2018, 57, 4992–4996. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Zhao, Y.; Pan, Q.; Kong, S.G. Demosaicking DoFP images using Newton’s polynomial interpolation and polarization difference model. Opt. Express 2019, 27, 1376–1391. [Google Scholar] [CrossRef]
- Yang, T.; Jin, G.-F.; Zhu, J. Automated design of freeform imaging systems. Light. Sci. Appl. 2017, 6, e17081. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, W.; Ren, L.; Ju, H.; Qu, E. Polarimetric dehazing method for visibility improvement based on visible and infrared image fusion. Appl. Opt. 2016, 55, 8221. [Google Scholar] [CrossRef]
- Fang, S.; Xia, X.; Huo, X.; Chen, C. Image dehazing using polarization effects of objects and airlight. Opt. Express 2014, 22, 19523–19537. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, K.; You, Z.; Huang, K. Real-time polarization imaging algorithm for camera-based polarization navi-gation sensors. Appl. Opt. 2017, 56, 3199–3205. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, K.; Wang, X.; You, Z.; Huang, K. Real-time Imaging Orientation Determination System to Verify Imaging Polarization Navigation Algorithm. Sensors 2016, 16, 144. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.; Yang, X. Study on Enlarging the Searching Scope of Staring Area and Tracking Imaging of Dynamic Targets by Optical Satellites. IEEE Sens. J. 2021, 21, 5349–5358. [Google Scholar] [CrossRef]
- Tangpattanakul, P.; Jozefowiez, N.; Lopez, P. A multi-objective local search heuristic for scheduling Earth observations taken by an agile satellite. Eur. J. Oper. Res. 2015, 245, 542–554. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Chang, Y.; Xiang, G.; Han, L.; Chen, F.; Luo, D.; Li, S.; Sun, L.; Tu, B.; Meng, B.; et al. Polarization measurement accuracy analysis and improvement methods for the directional polarimetric camera. Opt. Express 2020, 28, 38638–38666. [Google Scholar] [CrossRef] [PubMed]
- Huang, E.; Ma, Q.; Liu, Z. Ultrafast Imaging using Spectral Resonance Modulation. Sci. Rep. 2016, 6, 25240. [Google Scholar] [CrossRef]
- Brueckner, A.; Duparré, J.; Leitel, R.; Dannberg, P.; Bräuer, A.; Tünnermann, A. Thin wafer-level camera lenses inspired by insect compound eyes. Opt. Express 2010, 18, 24379–24394. [Google Scholar] [CrossRef]
- Gong, T.; Jin, G.; Zhu, J. Point-by-point design method for mixed-surface-type off-axis reflective imaging systems with spherical, aspheric, and freeform surfaces. Opt. Express 2017, 25, 10663. [Google Scholar] [CrossRef]
- Xu, T.; Yang, X.; Xu, C.; Chang, L.; Zhu, L. Study of satellite imaging with pitch motion compensation to increase SNR. Optik 2019, 192, 162933. [Google Scholar] [CrossRef]
- Nieke, J.; Solbrig, M.; Neumann, A. Noise contributions for imaging spectrometers. Appl. Opt. 1999, 38, 5191–5194. [Google Scholar] [CrossRef]
- Issa, V.; Daya, Z.A. Modeling the ship white water wake in the midwave infrared. Appl. Opt. 2018, 57, 10125–10134. [Google Scholar] [CrossRef] [PubMed]
- Shuai, T.; Sun, K.; Wu, X.N.; Zhang, X.; Shi, B.H. A ship target automatic detection method for high-resolution remote sensing. In Proceedings of the IGARSS 2016—2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 1258–1261. [Google Scholar]
- Han, J.; Moradi, S.; Faramarzi, I.; Liu, C.; Zhang, H.; Zhao, Q. A Local Contrast Method for Infrared Small-Target Detection Utilizing a Tri-Layer Window. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1822–1826. [Google Scholar] [CrossRef]
- Li, G.; Lin, Y.; Qu, X. An infrared and visible image fusion method based on multi-scale transformation and norm optimization. Inf. Fusion 2021, 71, 109–129. [Google Scholar] [CrossRef]
- Stokes, G.G. On the Composition and Resolution of Streams of Polarized Light from different Sources. Trans. Camb. Philos. Soc. 1851, 9, 399. [Google Scholar]
- Bhattacharya, A.; De, S.; Muhuri, A.; Surendar, M.; Venkataraman, G.; Das, A. A new compact polarimetric SAR decomposition technique. Remote Sens. Lett. 2015, 6, 914–923. [Google Scholar] [CrossRef]
- Chen, G.; Li, L.; Jin, W.; Zhu, J.; Shi, F. Weighted sparse representation multi-scale transform fusion algorithm for high dynamic range imaging with a low-light dual-channel camera. Opt. Express 2019, 27, 10564–10579. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wang, L.; Sun, Z.B.; Jiang, Y.D.; Zhai, G.J. Fusion of color microscopic images based on bidimensional empirical mode decomposition. Opt. Express 2010, 18, 21757–21769. [Google Scholar] [CrossRef] [PubMed]
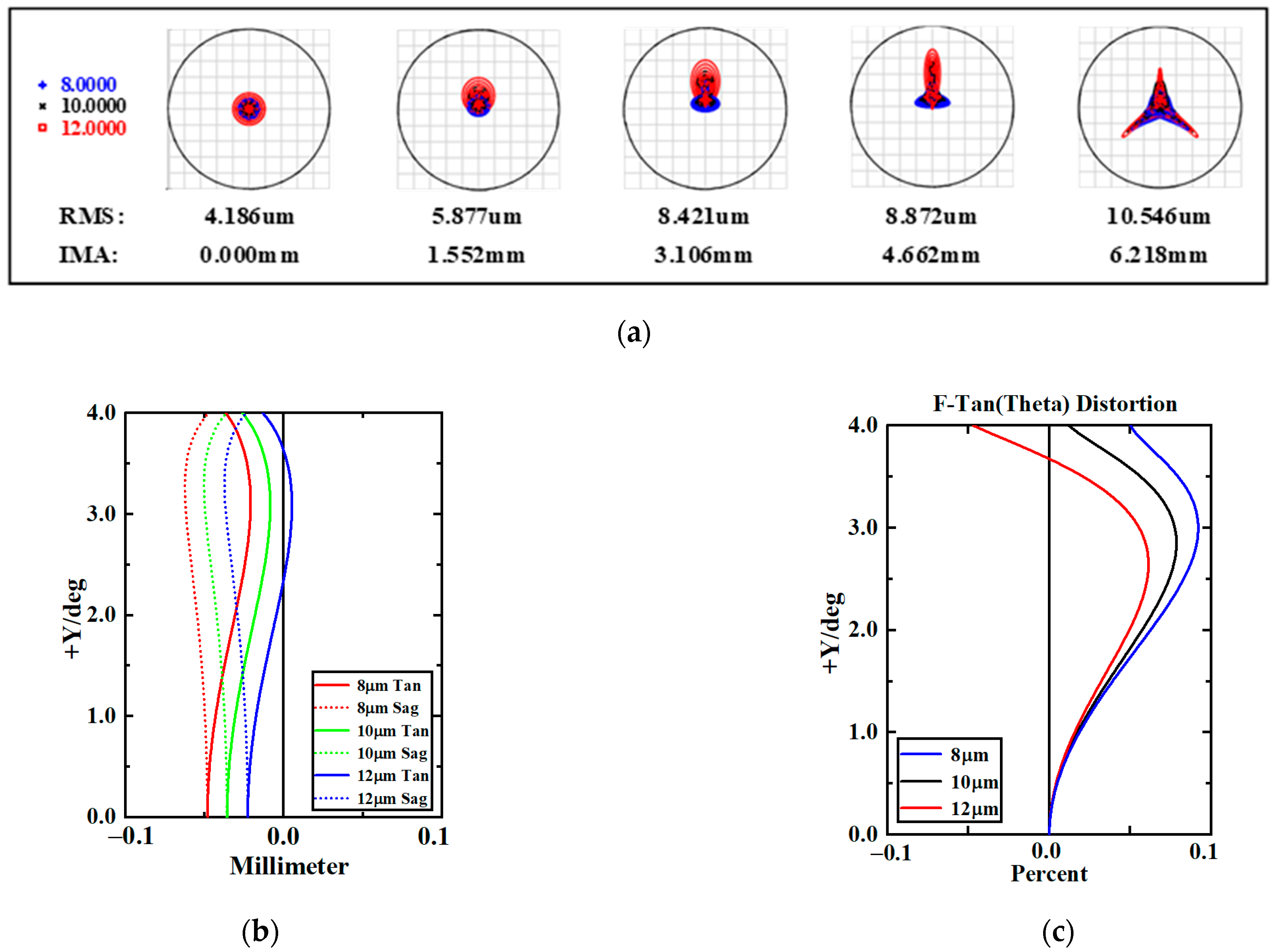
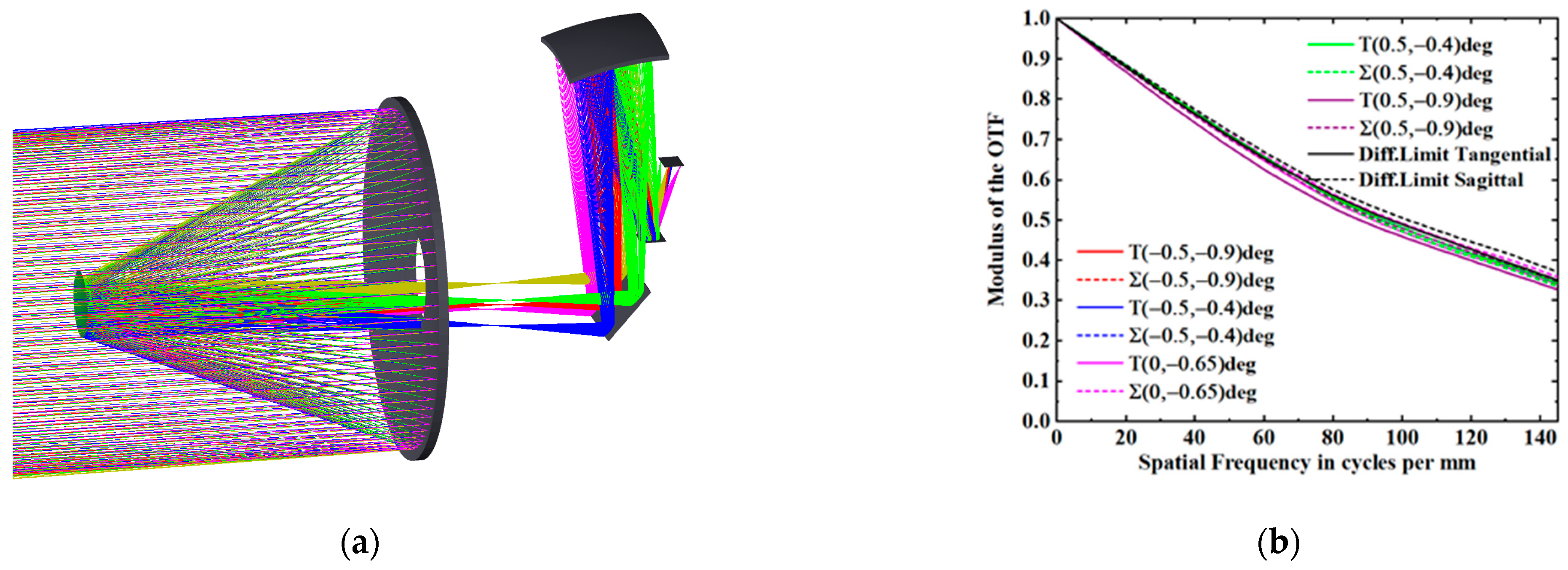
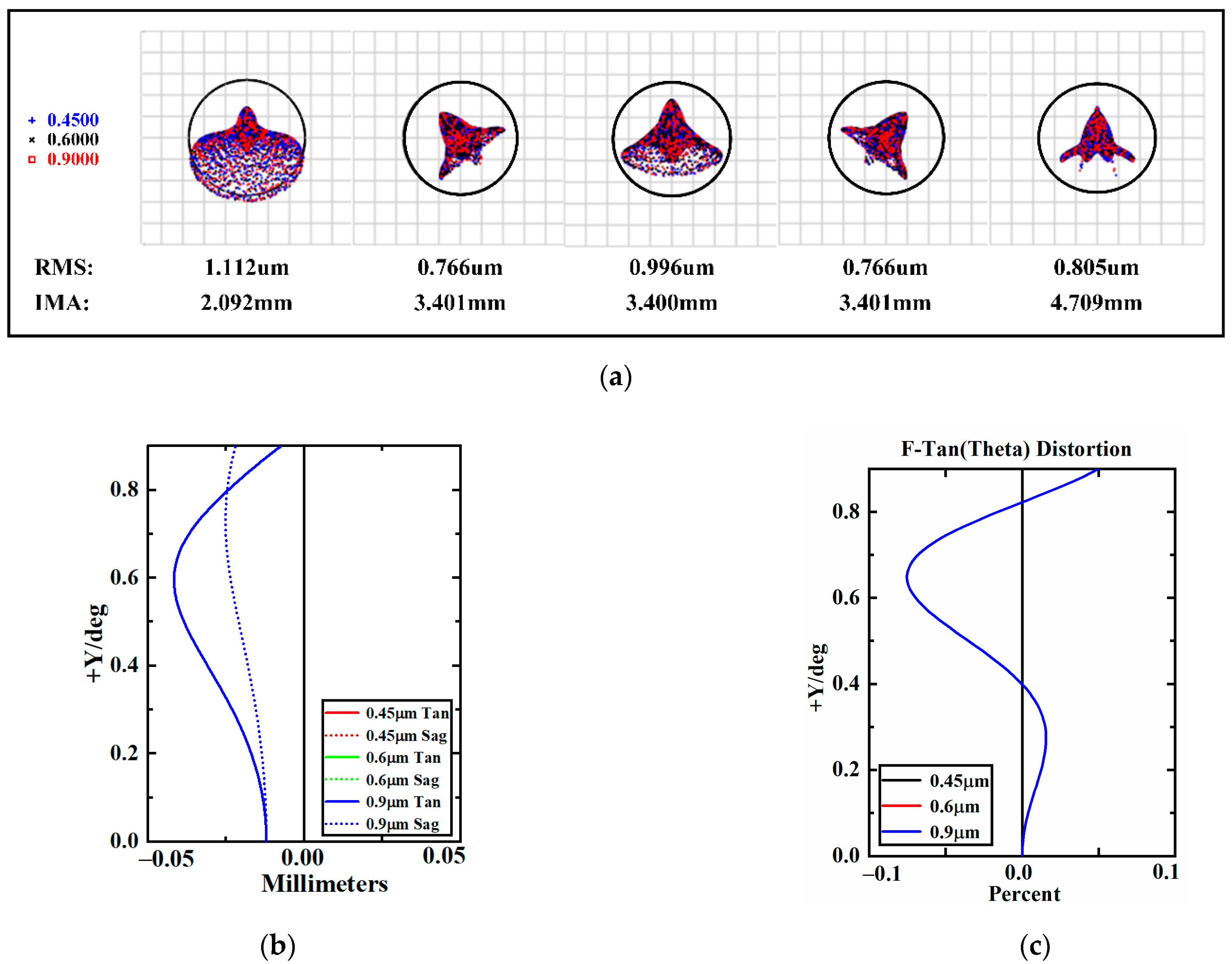




| Imaging Parameters | Fore-Infrared System | Rear Polarization System |
|---|---|---|
| Full field of view/° | 8 | 2 |
| Focal length/mm | 60 | 300 |
| GSD/m | 114 | 11.5 |
| Width/km | 70 | 9 |
| Surface | Radius/mm | Thickness/mm | Conic |
|---|---|---|---|
| Primary mirror | −160.45 | 67.23 | −0.99 |
| 1st lens | −28.92 | 2.21 | −1.66 |
| 2nd lens | −214.73 | 5.76 | 0 |
| 3rd lens | 18.87 | 3.90 | 0 |
| 4th lens | −122.87 | 4.59 | 0 |
| 5th lens | −4.28 | 3.09 | 0 |
| Surface | Radius/mm | Thickness/mm | Conic |
|---|---|---|---|
| Primary mirror | −160.45 | 67.23 | −0.99 |
| Secondary mirror | −28.92 | 104.16 | −1.66 |
| Tertiary mirror | 65.41 | 35.00 | −1.48 |
| fourth mirror | −80.25 | 16.38 | 1.24 |
| Parameters | IE | SD | AG |
|---|---|---|---|
| I0 | 6.03 | 88.96 | 6.44 |
| I45 | 6.70 | 83.67 | 7.32 |
| I90 | 6.62 | 79.58 | 7.35 |
| I135 | 6.70 | 82.46 | 7.20 |
| IV | 6.82 | 66.21 | 6.07 |
| IR | 6.08 | 55.71 | 4.10 |
| F | 7.53 | 55.03 | 12.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, W.; Jiang, L.; Yang, X.; Gao, S.; Xie, Y.; Xu, T. Optical Design of a Common-Aperture Camera for Infrared Guided Polarization Imaging. Remote Sens. 2022, 14, 1620. https://doi.org/10.3390/rs14071620
Yue W, Jiang L, Yang X, Gao S, Xie Y, Xu T. Optical Design of a Common-Aperture Camera for Infrared Guided Polarization Imaging. Remote Sensing. 2022; 14(7):1620. https://doi.org/10.3390/rs14071620
Chicago/Turabian StyleYue, Wei, Li Jiang, Xiubin Yang, Suining Gao, Yunqiang Xie, and Tingting Xu. 2022. "Optical Design of a Common-Aperture Camera for Infrared Guided Polarization Imaging" Remote Sensing 14, no. 7: 1620. https://doi.org/10.3390/rs14071620
APA StyleYue, W., Jiang, L., Yang, X., Gao, S., Xie, Y., & Xu, T. (2022). Optical Design of a Common-Aperture Camera for Infrared Guided Polarization Imaging. Remote Sensing, 14(7), 1620. https://doi.org/10.3390/rs14071620





