Nowcasting System Based on Sky Camera Images to Predict the Solar Flux on the Receiver of a Concentrated Solar Plant
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
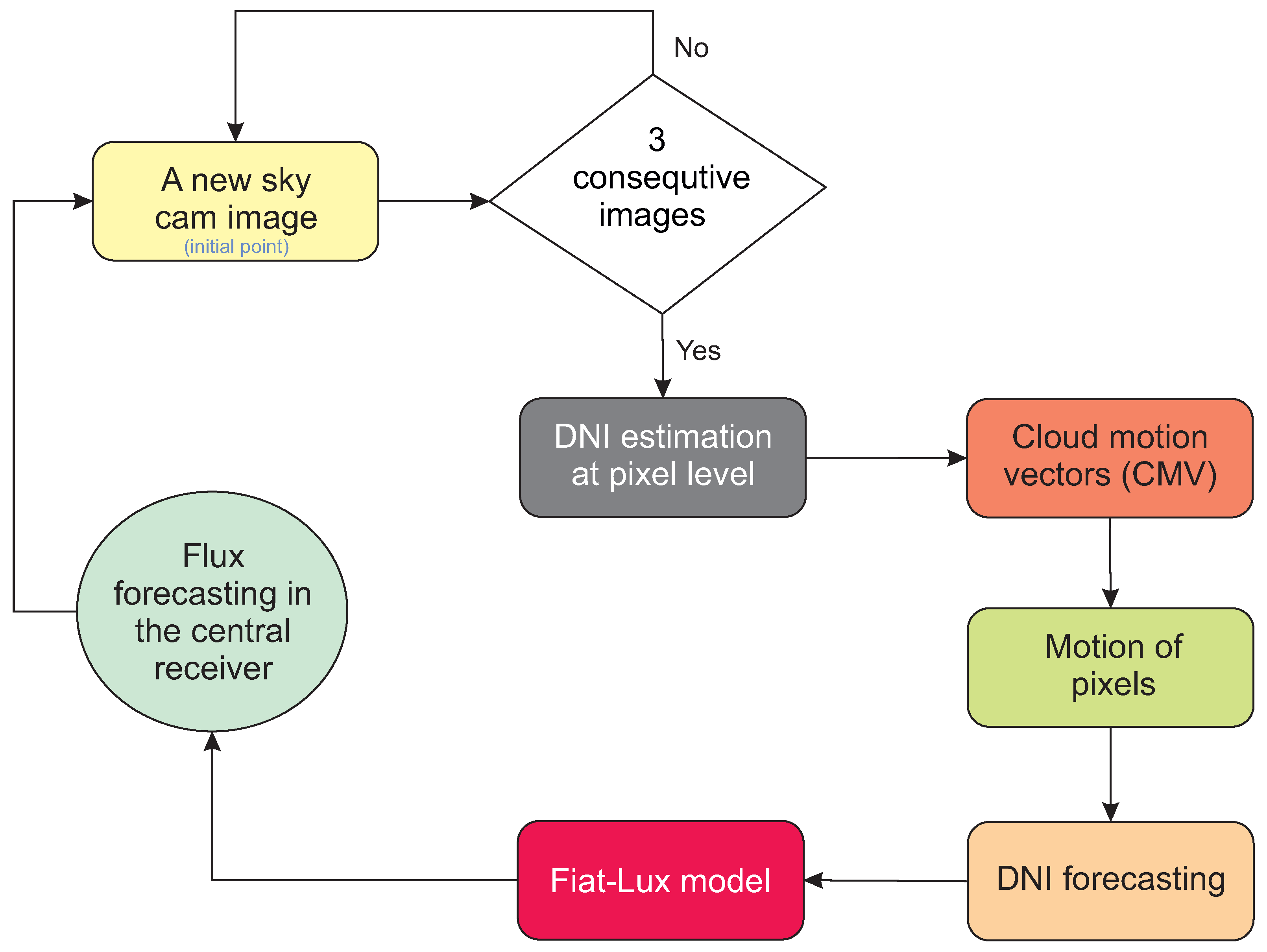
2.2. DNI Forecasting Approach
2.3. DNI Estimation at the Pixel Level
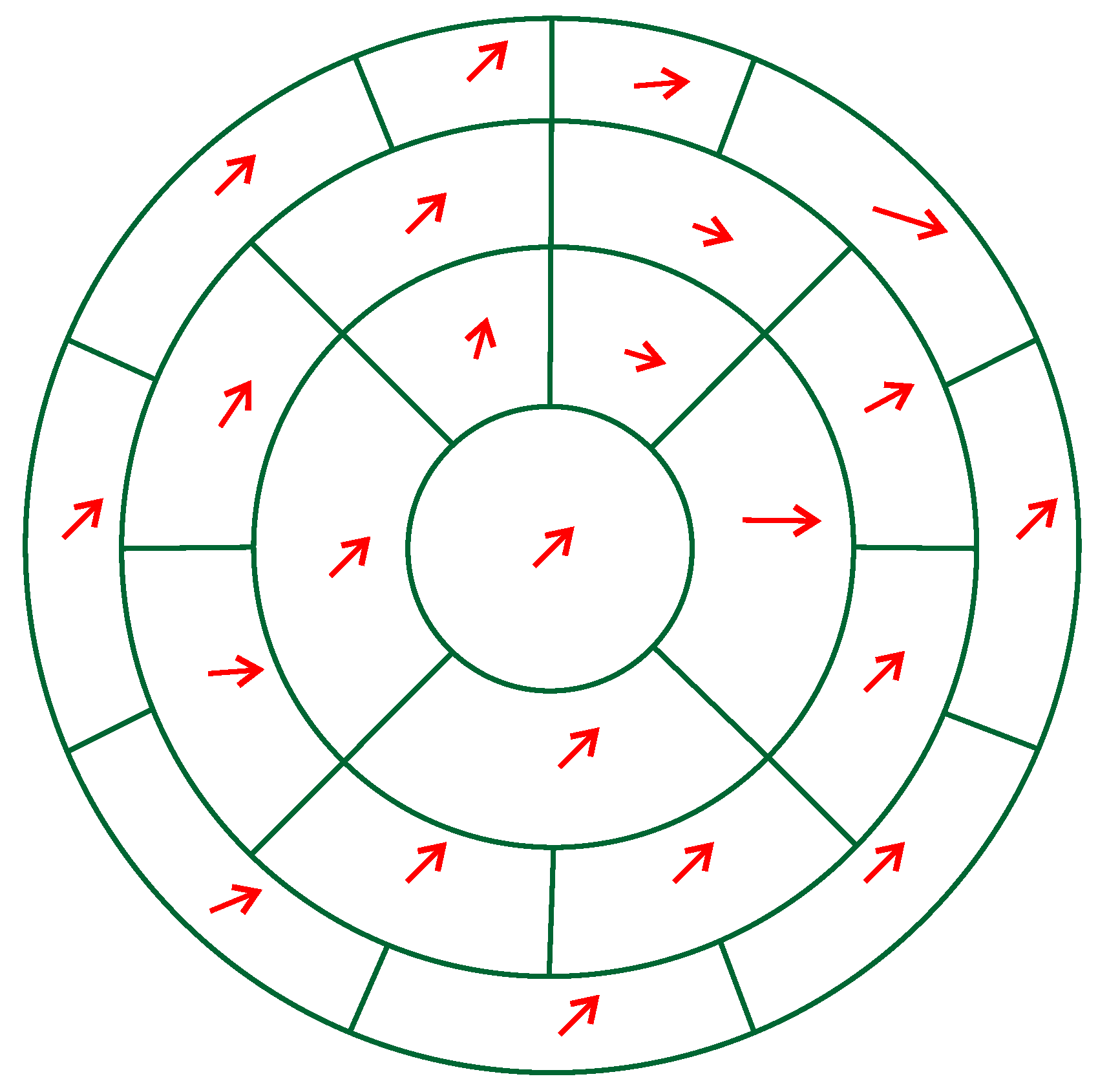
2.4. Determination of the Cloud Motion Vectors (CMV)
2.5. Motion of Pixels and DNI Forecasting
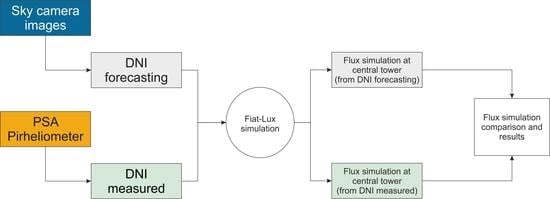
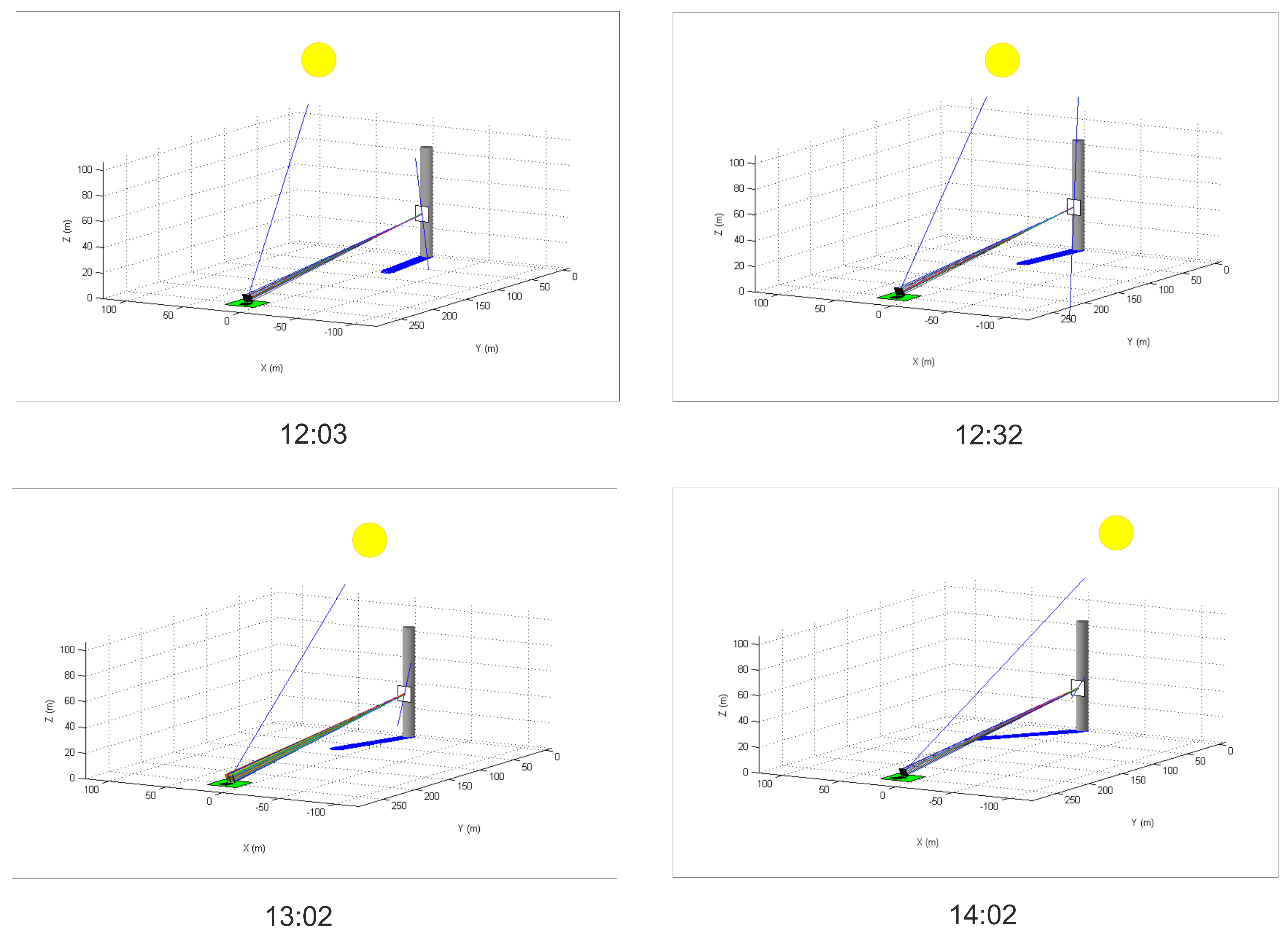
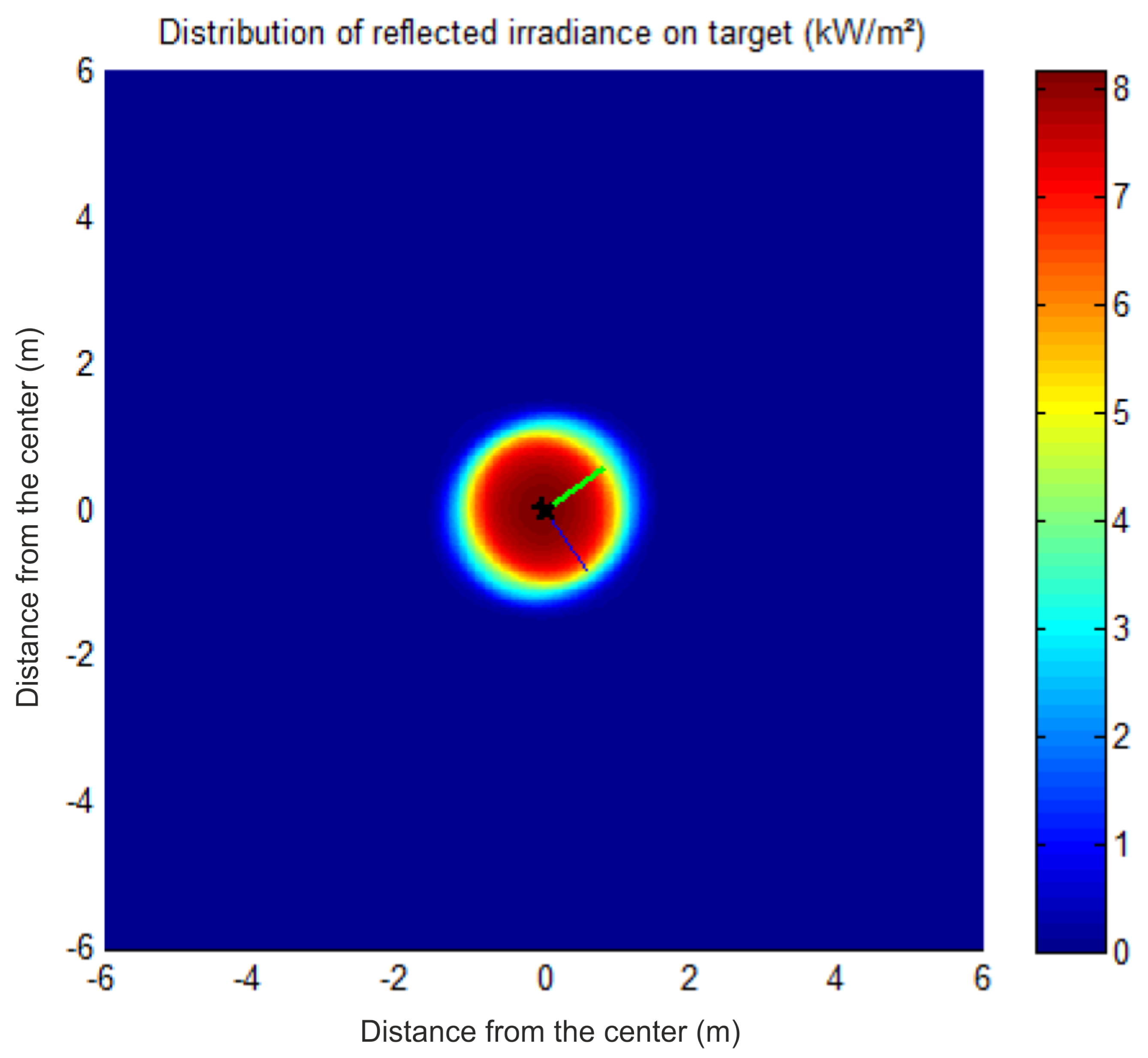
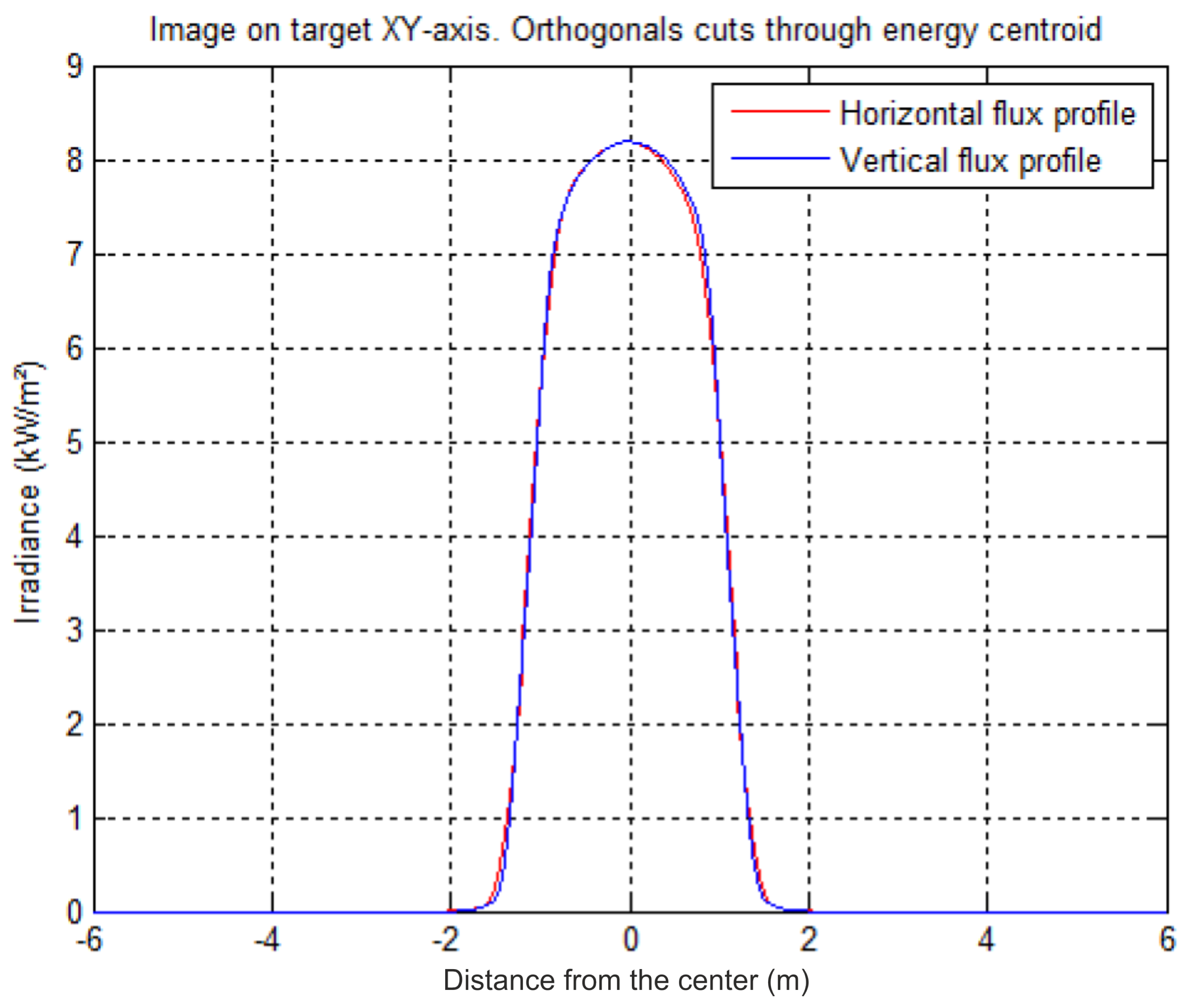
2.6. Fiat-Lux Simulation
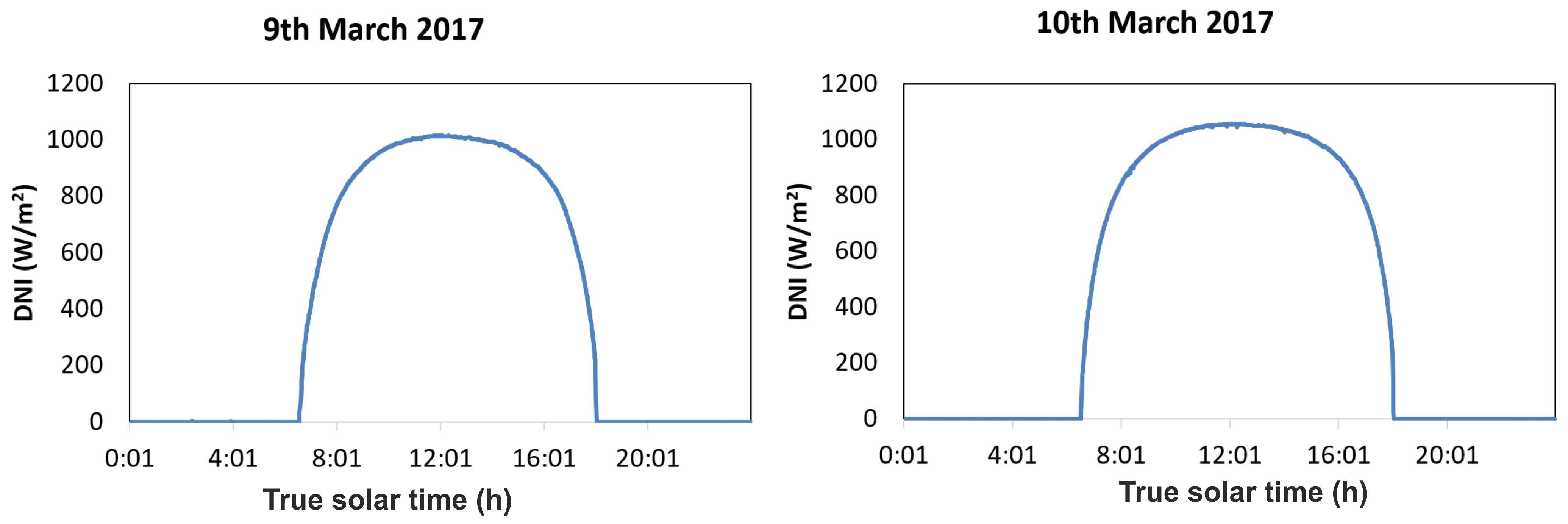
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chapman, A.J.; McLellan, B.C.; Tezuka, T. Prioritizing mitigation efforts considering co-benefits, equity and energy justice: Fossil fuel to renewable energy transition pathways. Appl. Energy 2018, 219, 187–198. [Google Scholar] [CrossRef]
- Li, H.; Edwards, D.; Hosseini, M.; Costin, G. A review on renewable energy transition in Australia: An updated depiction. J. Clean. Prod. 2020, 242, 118475. [Google Scholar] [CrossRef]
- Lovegrove, K.; Stein, W. Concentrating Solar Power Technology: Principles, Developments and Applications; Woodhead Publishing: Sawston, UK, 2012; pp. 1–674. [Google Scholar]
- Petrík, T.; Daneček, M.; Uhlíř, I.; Poulek, V.; Libra, M. Distribution Grid Stability—Influence of Inertia Moment of Synchronous Machines. Appl. Sci. 2020, 10, 9075. [Google Scholar] [CrossRef]
- Ferro, G.; Robba, M.; Sacile, R. A Model Predictive Control Strategy for Distribution Grids: Voltage and Frequency Regulation for Islanded Mode Operation. Energies 2020, 13, 2637. [Google Scholar] [CrossRef]
- Lubkoll, M.; Erasmus, D.; Harms, T.; von Backström, T.; Kröger, D. Performance characteristics of the Spiky Central Receiver Air Pre-heater (SCRAP). Sol. Energy 2020, 201, 773–786. [Google Scholar] [CrossRef] [Green Version]
- Ballestrín, J.; Marzo, A. Solar radiation attenuation in solar tower plants. Sol. Energy 2012, 86, 388–392. [Google Scholar] [CrossRef]
- Hanrieder, N.; Wilbert, S.; Pitz-Paal, R.; Emde, C.; Gasteiger, J.; Mayer, B.; Polo, J. Atmospheric extinction in solar tower plants: Absorption and broadband correction for MOR measurements. Atmos. Meas. Tech. 2015, 8, 3467–3480. [Google Scholar] [CrossRef] [Green Version]
- López, G.; Gueymard, C.A.; Bosch, J.L.; Rapp-Arrarás, I.; Alonso-Montesinos, J.; Pulido-Calvo, I.; Ballestrín, J.; Polo, J.; Barbero, J. Modelling water vapor impact on the solar energy reaching the receiver of a solar tower plant by means of artificial neural networks. Sol. Energy 2016, 165, 34–39. [Google Scholar]
- Blanco, M.J.; Mutuberria, A.; Martínez, D. Experimental validation of Tonatiuh using the Plataforma Solar de Almería secondary concentrator test campaign data. In Proceedings of the 16th Annual SolarPACES Symposium, Perpignan, France, 21–24 September 2010. [Google Scholar]
- Polo, J.; Ballestrín, J.; Carra, E. Sensitivity study for modelling atmospheric attenuation of solar radiation with radiative transfer models and the impact in solar tower plant production. Sol. Energy 2016, 134, 219–227. [Google Scholar] [CrossRef]
- Mondragón, R.; Alonso-Montesinos, J.; Riveros-Rosas, D.; Bonifaz, R. Determination of cloud motion applying the Lucas-Kanade method to sky cam imagery. Remote Sens. 2020, 12, 2643. [Google Scholar] [CrossRef]
- Masuda, R.; Iwabuchi, H.; Schmidt, K.; Damiani, A.; Kudo, R. Retrieval of cloud optical thickness from sky-view camera images using a deep convolutional neural network based on three-dimensional radiative transfer. Remote Sens. 2019, 11, 1962. [Google Scholar] [CrossRef] [Green Version]
- Alonso, J.; Batlles, F.J. The use of a sky camera for solar radiation estimation based on digital image processing. Energy 2015, 90, 377–386. [Google Scholar] [CrossRef]
- Mommert, M. Cloud Identification from All-sky Camera Data with Machine Learning. Astron. J. 2020, 159, 4. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J. Real-time automatic cloud detection using a low-cost sky camera. Remote Sens. 2020, 12, 1382. [Google Scholar] [CrossRef]
- Ballestrín, J.; Monterreal, R.; Carra, M.; Fernández-Reche, J.; Polo, J.; Enrique, R.; Rodríguez, J.; Casanova, M.; Barbero, F.; Alonso-Montesinos, J.; et al. Solar extinction measurement system based on digital cameras. Application to solar tower plants. Renew. Energy 2018, 125, 648–654. [Google Scholar] [CrossRef]
- Alonso, J.; Batlles, F.J.; López, G.; Ternero, A. Sky camera imagery processing based on a sky classification using radiometric data. Energy 2014, 68, 599–608. [Google Scholar] [CrossRef]
- Chu, Y.; Li, M.; Coimbra, C. Sun-tracking imaging system for intra-hour DNI forecasts. Renew. Energy 2016, 96, 792–799. [Google Scholar] [CrossRef]
- Dev, S.; Savoy, F.; Hui Lee, Y.; Winkler, S. Estimating solar irradiance using sky imagers. Atmos. Meas. Tech. 2019, 12, 5417–5429. [Google Scholar] [CrossRef] [Green Version]
- Rajagukguk, R.A.; Kamil, R.; Lee, H.J. A Deep Learning Model to Forecast Solar Irradiance Using a Sky Camera. Appl. Sci. 2021, 11, 5049. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J.; Batlles, F.; Portillo, C. Solar irradiance forecasting at one-minute intervals for different sky conditions using sky camera images. Energy Convers. Manag. 2015, 105, 1166–1177. [Google Scholar] [CrossRef]
- Bone, V.; Pidgeon, J.; Kearney, M.; Veeraragavan, A. Intra-hour direct normal irradiance forecasting through adaptive clear-sky modelling and cloud tracking. Sol. Energy 2018, 159, 852–867. [Google Scholar] [CrossRef]
- Alonso, J.; Batlles, F.J.; Villarroel, C.; Ayala, R.; Burgaleta, J.I. Determination of the sun area in sky camera images using radiometric data. Energy Convers. Manag. 2014, 78, 24–31. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J.; Batlles, F.J. Short and medium-term cloudiness forecasting using remote sensing techniques and sky camera imagery. Energy 2014, 73, 890–897. [Google Scholar] [CrossRef]
- Sánchez-González, A.; Santana, D. Solar flux distribution on central receivers: A projection method from analytic function. Renew. Energy 2015, 74, 576–587. [Google Scholar] [CrossRef]
- He, C.; Zhao, H.; He, Q.; Zhao, Y.; Feng, J. Analytical radiative flux model via convolution integral and image plane mapping. Energy 2021, 222, 119937. [Google Scholar] [CrossRef]
- Monterreal, R. A new computer code for solar concentrating optics simulation. J. Phys. 1999, 9, 77–82. [Google Scholar] [CrossRef]



| Area 1 | ||
|---|---|---|
| Sky Condition | Digital Level (ND) | |
| Area 1 | Cloudless | (GR/RD) sin() |
| Overcast | (V/RD) sin() | |
| Sky Condition | Coefficients (a, b, c, d, e, f, g) | |
|---|---|---|
| Area 1 | Cloudless | −2.35, 4.37, 5.86, 14.39, −83.44, 120.70, 805.70 |
| Overcast | 0.32, −3.63, 6.37, 24.92, −17.14, 20.86, 116.40 |
| Forecast Time | nMBE (%) | nRMSE (%) | r |
|---|---|---|---|
| 1 min | −10.73 | 14.63 | 0.92 |
| 30 min | −9.62 | 15.74 | 0.87 |
| 60 min | −7.70 | 17.52 | 0.77 |
| 120 min | −2.68 | 21.60 | 0.54 |
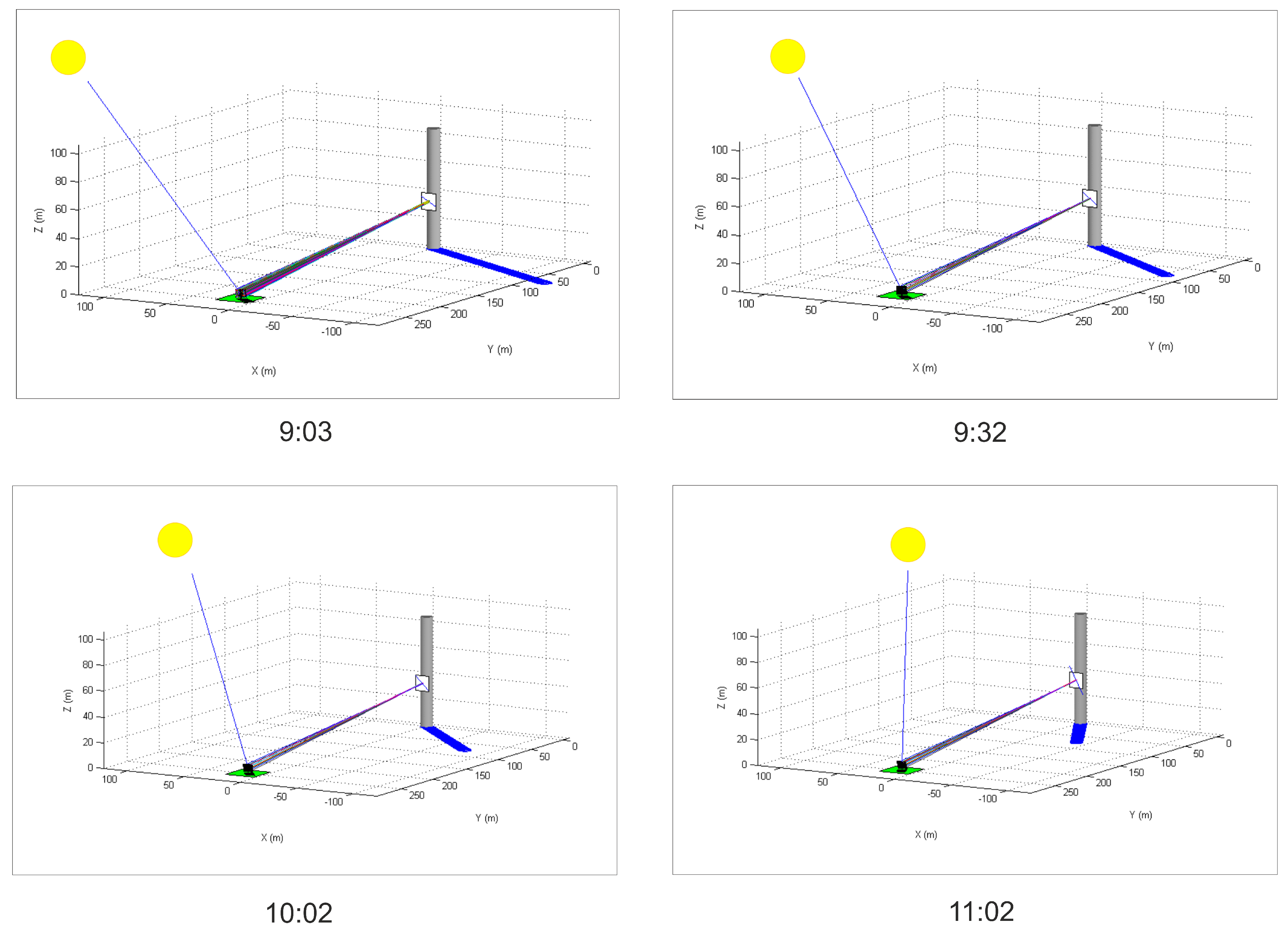
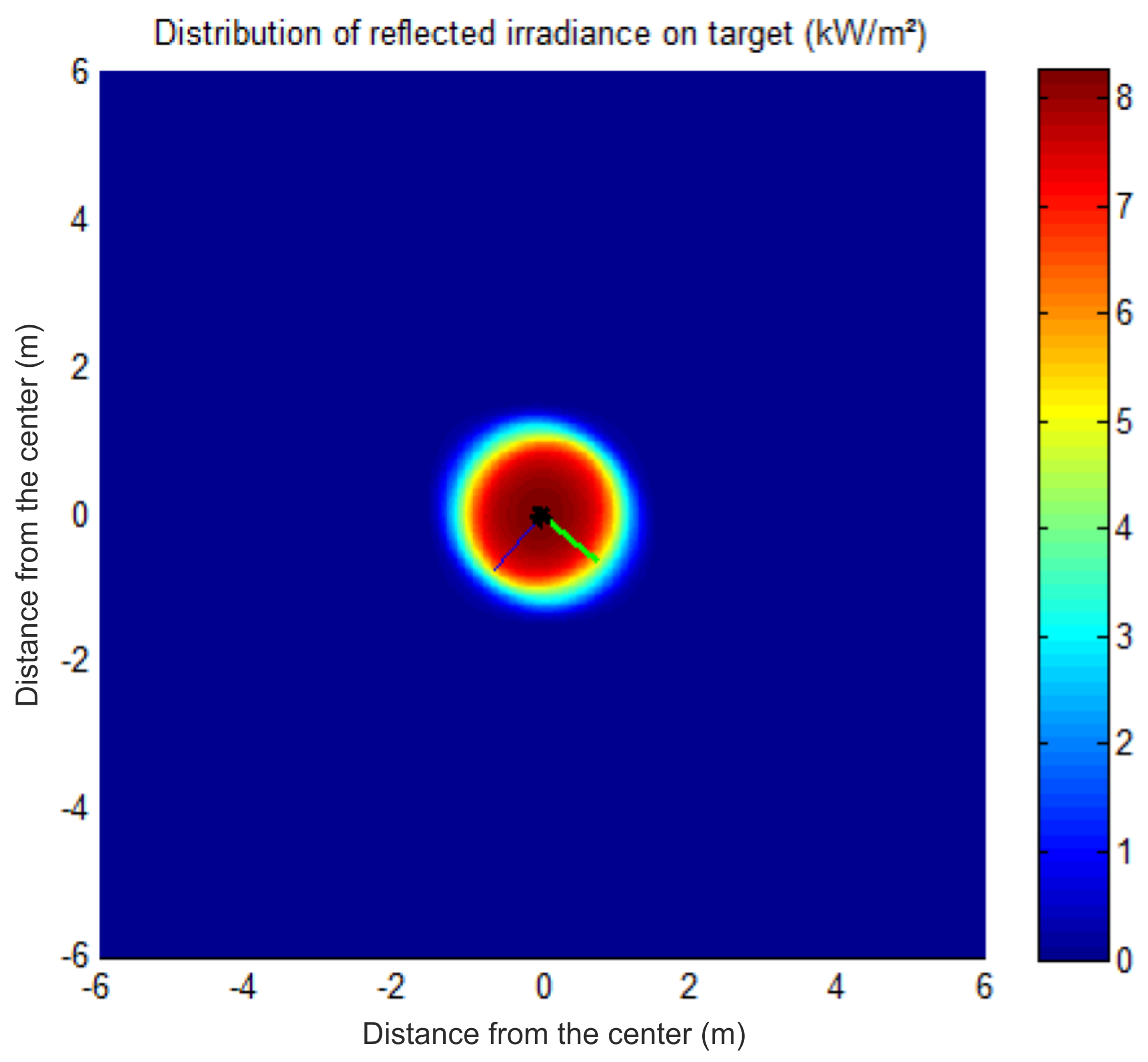
| Date of Prediction | Forecast Time (UTC) | DNI Predicted (W/m) | DNI Measured (W/m) | PTAP (kW) | RTAP (kW) | PTPT (kW) | RTPT (kW) | ACF | PIP (kW/m) | RIP (kW/m) |
|---|---|---|---|---|---|---|---|---|---|---|
| 9 March | 1 min | 849.9 | 912.0 | 33.7 | 36.7 | 28.9 | 31.1 | 0.86 | 7.5 | 8.1 |
| 2017 | 30 min | 848.0 | 949.0 | 33.6 | 37.6 | 29.5 | 33.0 | 0.88 | 7.7 | 8.6 |
| 9:02 | 60 min | 846.0 | 975.0 | 33.6 | 38.7 | 30.0 | 34.6 | 0.89 | 8.9 | 9.1 |
| 120 min | 845.5 | 1004.0 | 33.5 | 39.8 | 31.0 | 36.6 | 0.92 | 8.1 | 9.7 | |
| 9 March | 1 min | 862.0 | 1015.0 | 34.2 | 40.3 | 31.9 | 37.5 | 0.93 | 8.4 | 9.9 |
| 2017 | 30 min | 861.0 | 1013.0 | 34.2 | 40.2 | 31.9 | 37.5 | 0.93 | 8.4 | 9.9 |
| 12:02 | 60 min | 860.9 | 1008.0 | 34.2 | 39.9 | 31.8 | 37.2 | 0.93 | 8.4 | 9.8 |
| 120 min | 861.0 | 993.0 | 34.5 | 39.4 | 31.4 | 36.2 | 0.92 | 8.3 | 9.5 | |
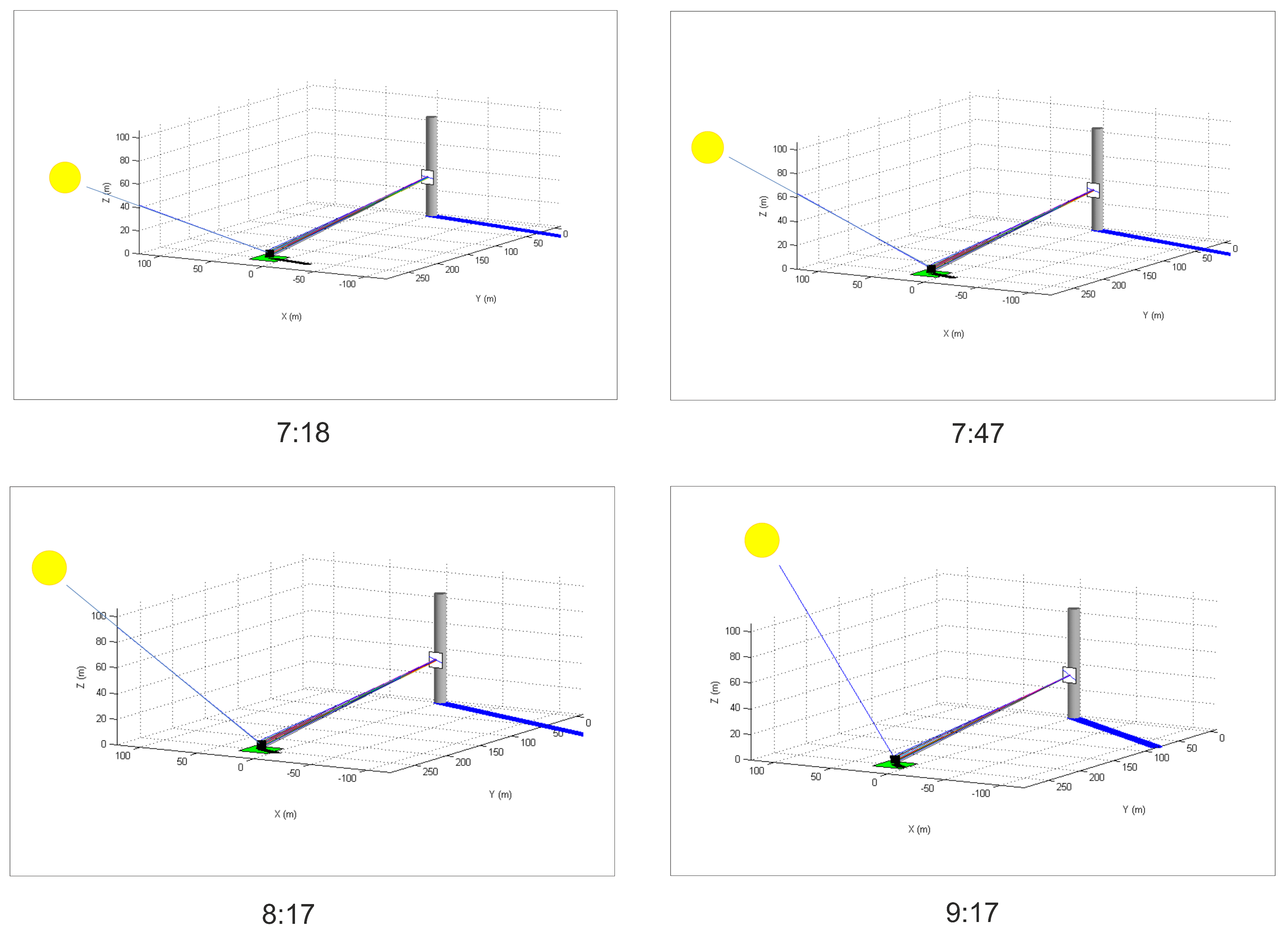
| 10 March | 1 min | 826.0 | 659.0 | 32.8 | 26.1 | 25.3 | 20.2 | 0.78 | 6.3 | 5.0 |
| 2017 | 30 min | 826.3 | 798.2 | 32.8 | 31.7 | 26.2 | 25.3 | 0.80 | 6.6 | 6.4 |
| 7:17 | 60 min | 826.0 | 881.0 | 32.8 | 35.0 | 27.0 | 28.8 | 0.82 | 6.9 | 7.4 |
| 120 min | 826.0 | 983.0 | 32.8 | 39.0 | 28.4 | 33.8 | 0.87 | 7.4 | 8.8 | |
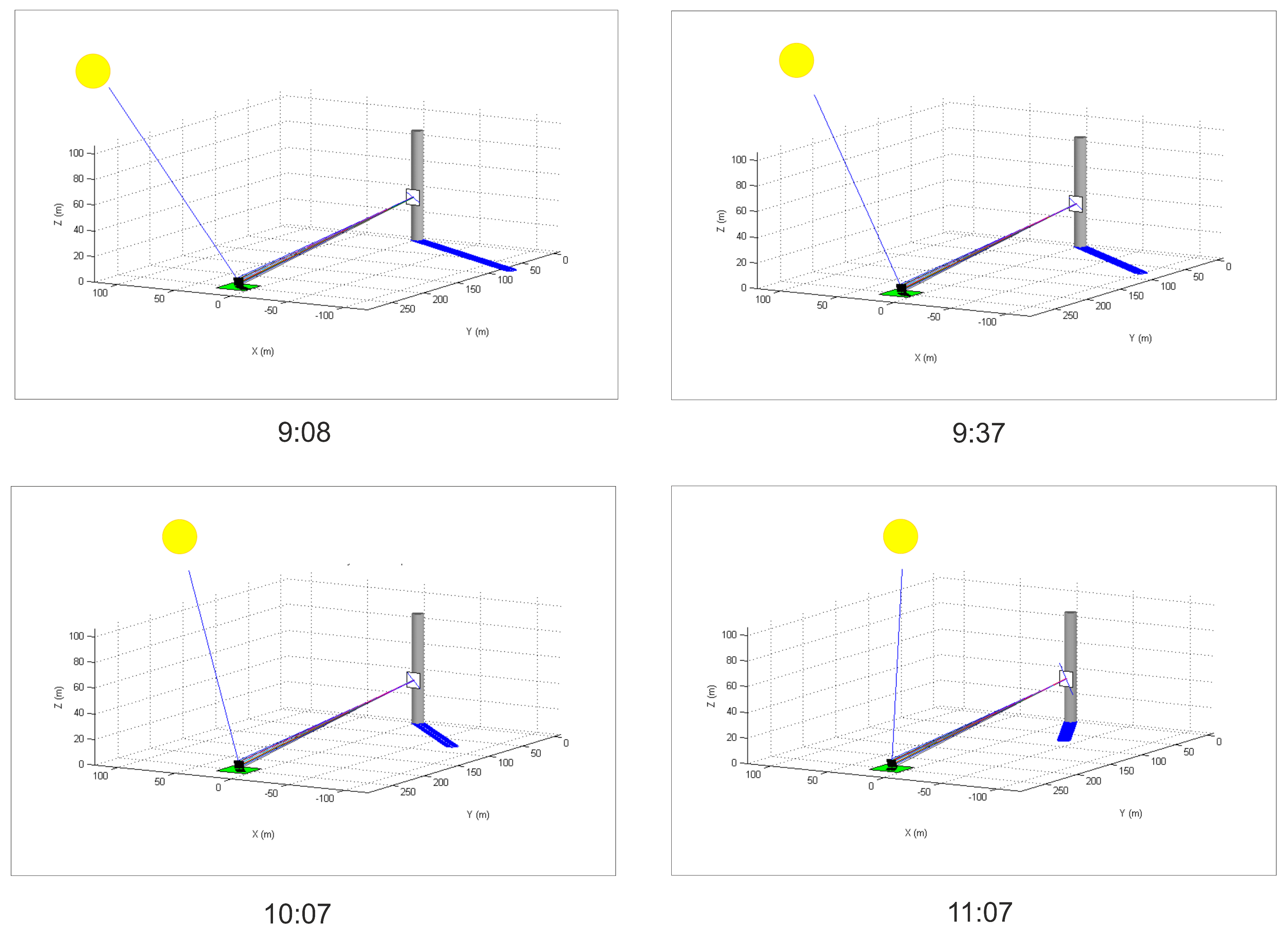
| 10 March | 1 min | 851.8 | 973.0 | 33.8 | 38.6 | 29.1 | 33.2 | 0.86 | 7.6 | 8.6 |
| 2017 | 30 min | 851.8 | 1002.0 | 33.8 | 39.8 | 29.7 | 35.0 | 0.88 | 7.8 | 9.1 |
| 7:17 | 60 min | 851.8 | 1024.0 | 33.8 | 40.6 | 30.3 | 36.4 | 0.90 | 7.9 | 9.5 |
| 120 min | 851.8 | 1051.0 | 33.8 | 41.7 | 31.1 | 38.3 | 0.92 | 8.2 | 10.1 | |
| 10 March | 1 min | 863.6 | 1057.0 | 34.3 | 41.9 | 31.9 | 39.0 | 0.93 | 8.4 | 10.3 |
| 2017 | 30 min | 863.6 | 1056.0 | 34.3 | 41.9 | 31.9 | 39.0 | 0.93 | 8.4 | 10.3 |
| 7:17 | 60 min | 863.6 | 1052.0 | 34.3 | 41.7 | 31.9 | 38.8 | 0.93 | 8.4 | 10.2 |
| 120 min | 863.6 | 1028.0 | 34.3 | 40.8 | 31.4 | 37.4 | 0.92 | 8.3 | 9.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso-Montesinos, J.; Monterreal, R.; Fernandez-Reche, J.; Ballestrín, J.; López, G.; Polo, J.; Barbero, F.J.; Marzo, A.; Portillo, C.; Batlles, F.J. Nowcasting System Based on Sky Camera Images to Predict the Solar Flux on the Receiver of a Concentrated Solar Plant. Remote Sens. 2022, 14, 1602. https://doi.org/10.3390/rs14071602
Alonso-Montesinos J, Monterreal R, Fernandez-Reche J, Ballestrín J, López G, Polo J, Barbero FJ, Marzo A, Portillo C, Batlles FJ. Nowcasting System Based on Sky Camera Images to Predict the Solar Flux on the Receiver of a Concentrated Solar Plant. Remote Sensing. 2022; 14(7):1602. https://doi.org/10.3390/rs14071602
Chicago/Turabian StyleAlonso-Montesinos, Joaquín, Rafael Monterreal, Jesus Fernandez-Reche, Jesús Ballestrín, Gabriel López, Jesús Polo, Francisco Javier Barbero, Aitor Marzo, Carlos Portillo, and Francisco Javier Batlles. 2022. "Nowcasting System Based on Sky Camera Images to Predict the Solar Flux on the Receiver of a Concentrated Solar Plant" Remote Sensing 14, no. 7: 1602. https://doi.org/10.3390/rs14071602
APA StyleAlonso-Montesinos, J., Monterreal, R., Fernandez-Reche, J., Ballestrín, J., López, G., Polo, J., Barbero, F. J., Marzo, A., Portillo, C., & Batlles, F. J. (2022). Nowcasting System Based on Sky Camera Images to Predict the Solar Flux on the Receiver of a Concentrated Solar Plant. Remote Sensing, 14(7), 1602. https://doi.org/10.3390/rs14071602