A Proposed Satellite-Based Crop Insurance System for Smallholder Maize Farming
Abstract
1. Introduction
2. Materials and Methods
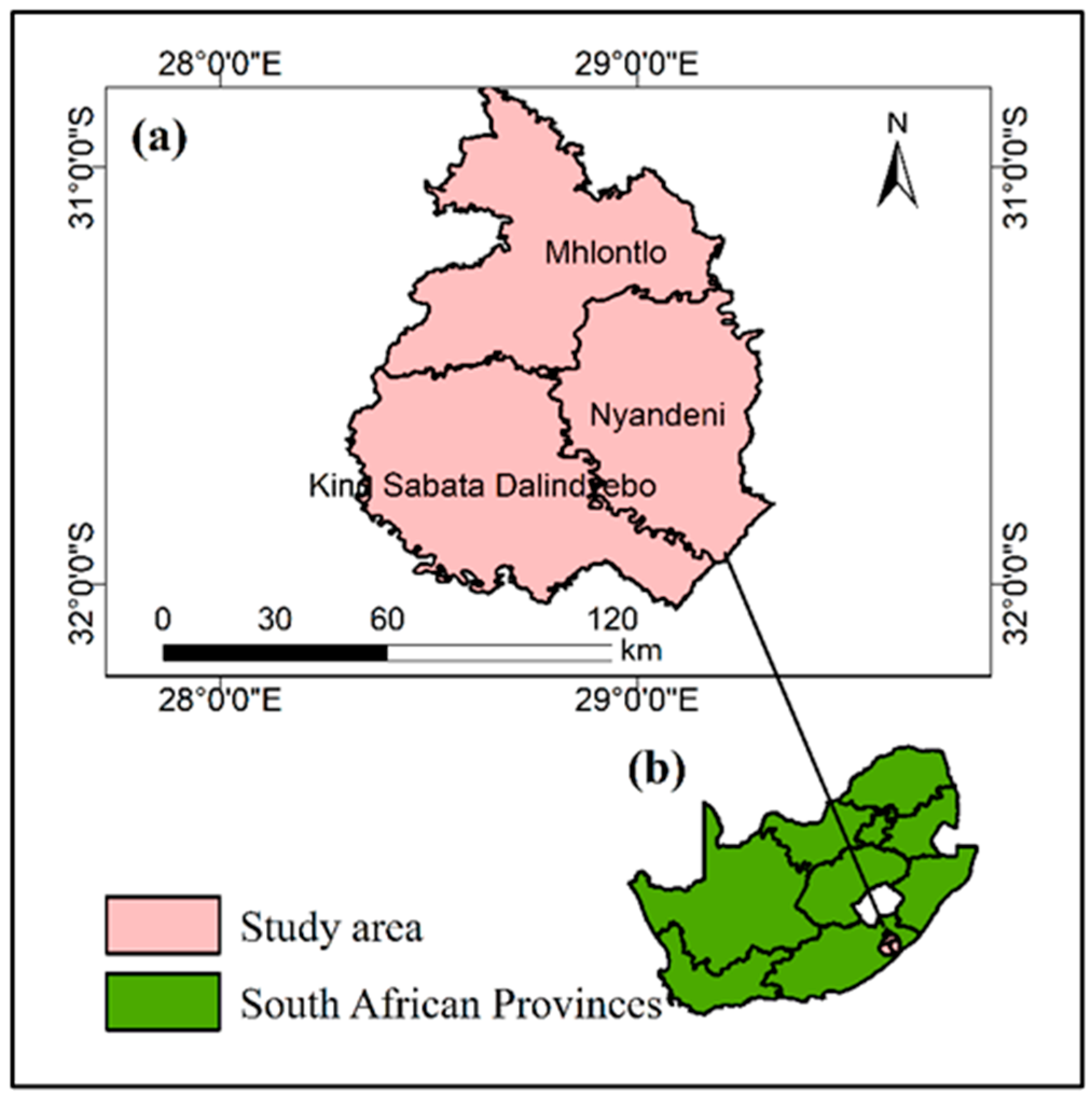
2.1. Study Area
2.2. Data
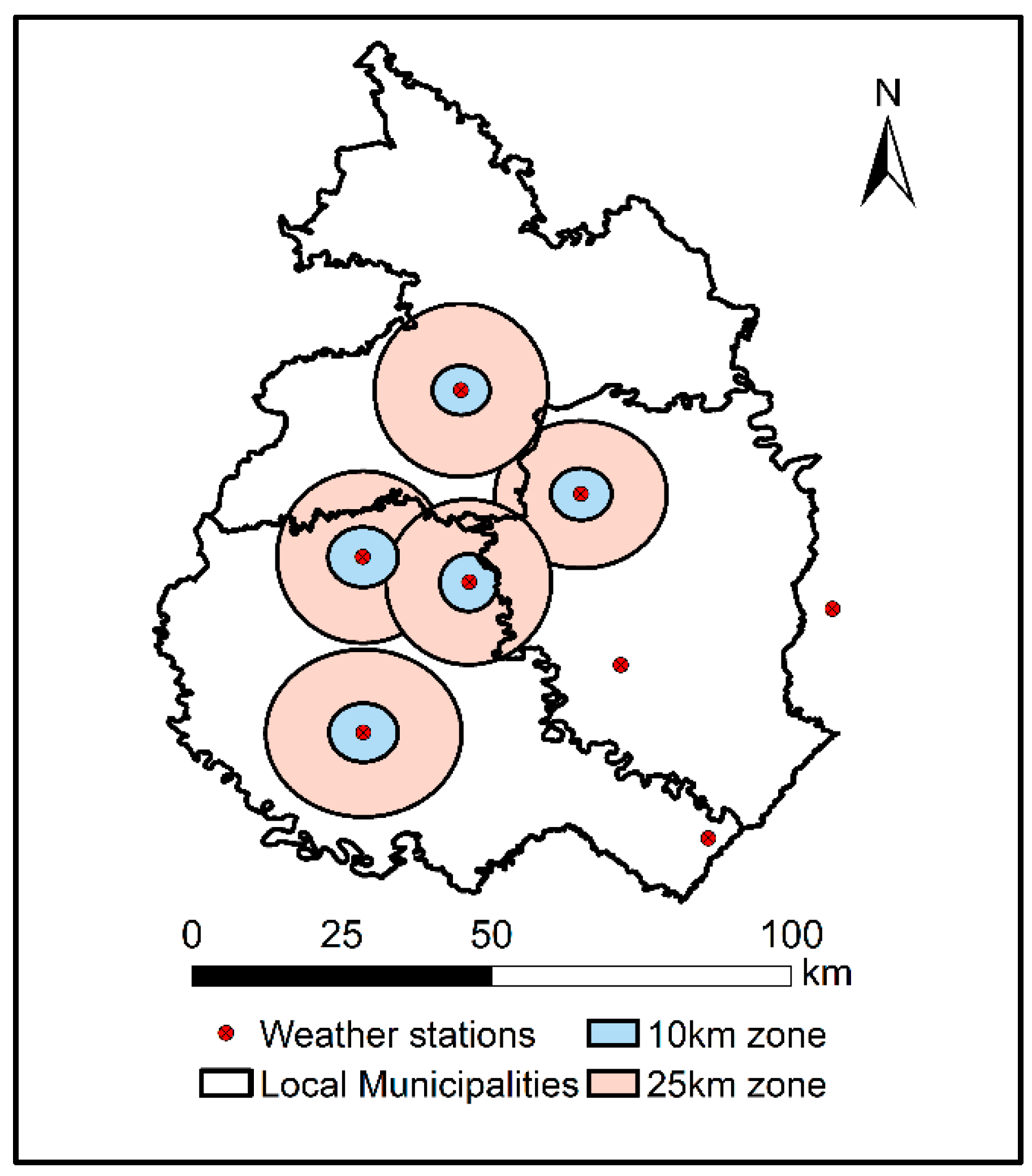
2.2.1. In-Situ Rainfall Data
2.2.2. TAMSAT
2.2.3. CHIRPS
2.2.4. Climate Data Used for Calculating CWR
2.3. Data Preprocessing and Analysis
2.3.1. Preprocessing of In-Situ Rainfall Data
2.3.2. Preprocessing of SRFEs
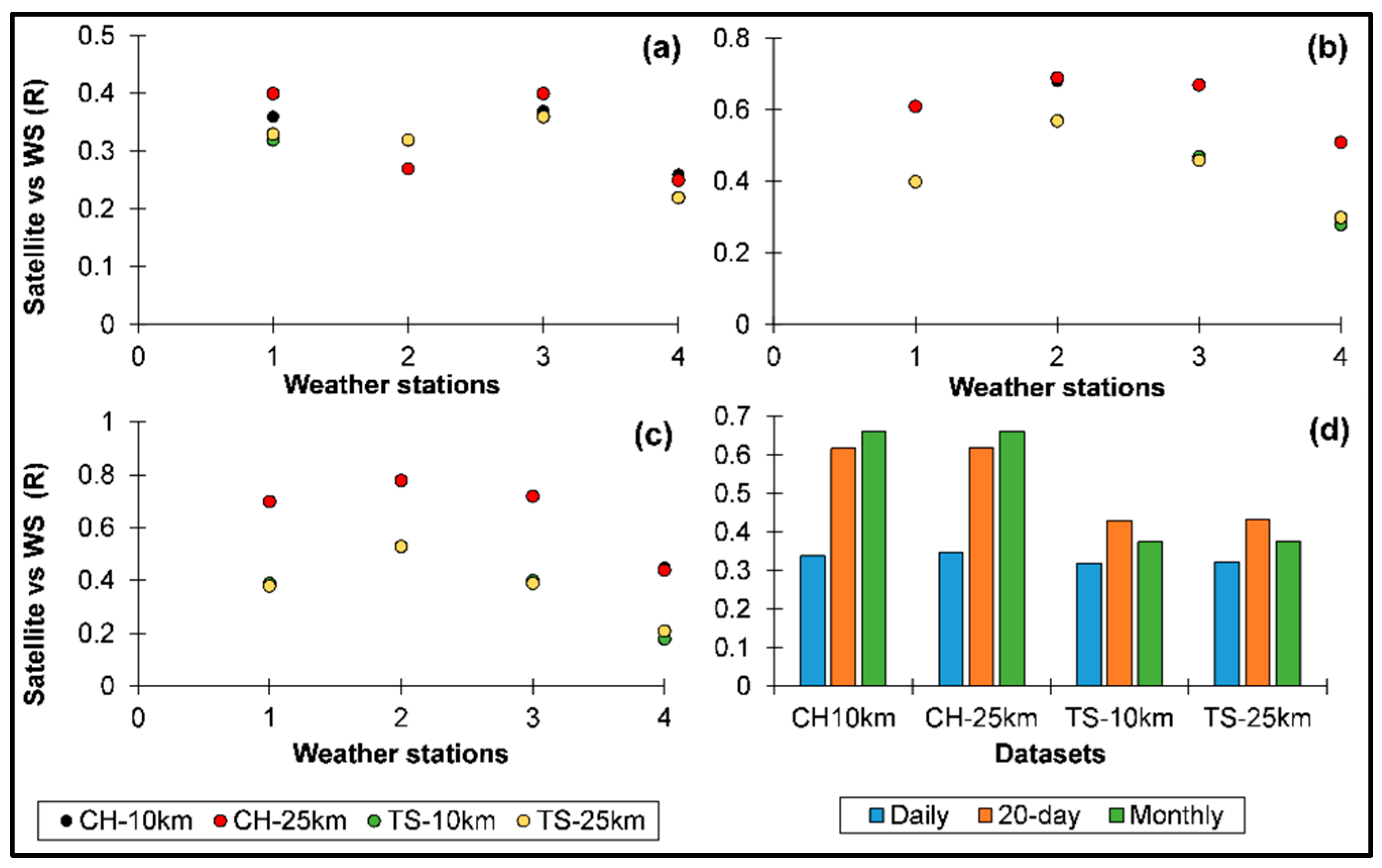
2.3.3. Evaluating TAMSAT and CHIRPS against In-Situ Rainfall Data
2.3.4. Crop Water Requirements
2.3.5. IBCI Development and Payout Thresholds
- is the insured amount for growth stage , which is a portion of the costs spent on inputs (seeds, fertilizers, pesticides, herbicides, land preparations, etc.) [17],
- is the actual index value of growth stage ,
- is the trigger point at which payout starts, and
- is the exit threshold at which full payout is given.
3. Results
3.1. Correlations between Satellite and WS Data at Different Spatial and Temporal Scales
3.2. Crop Water Requirements Based on Different Planting Dates
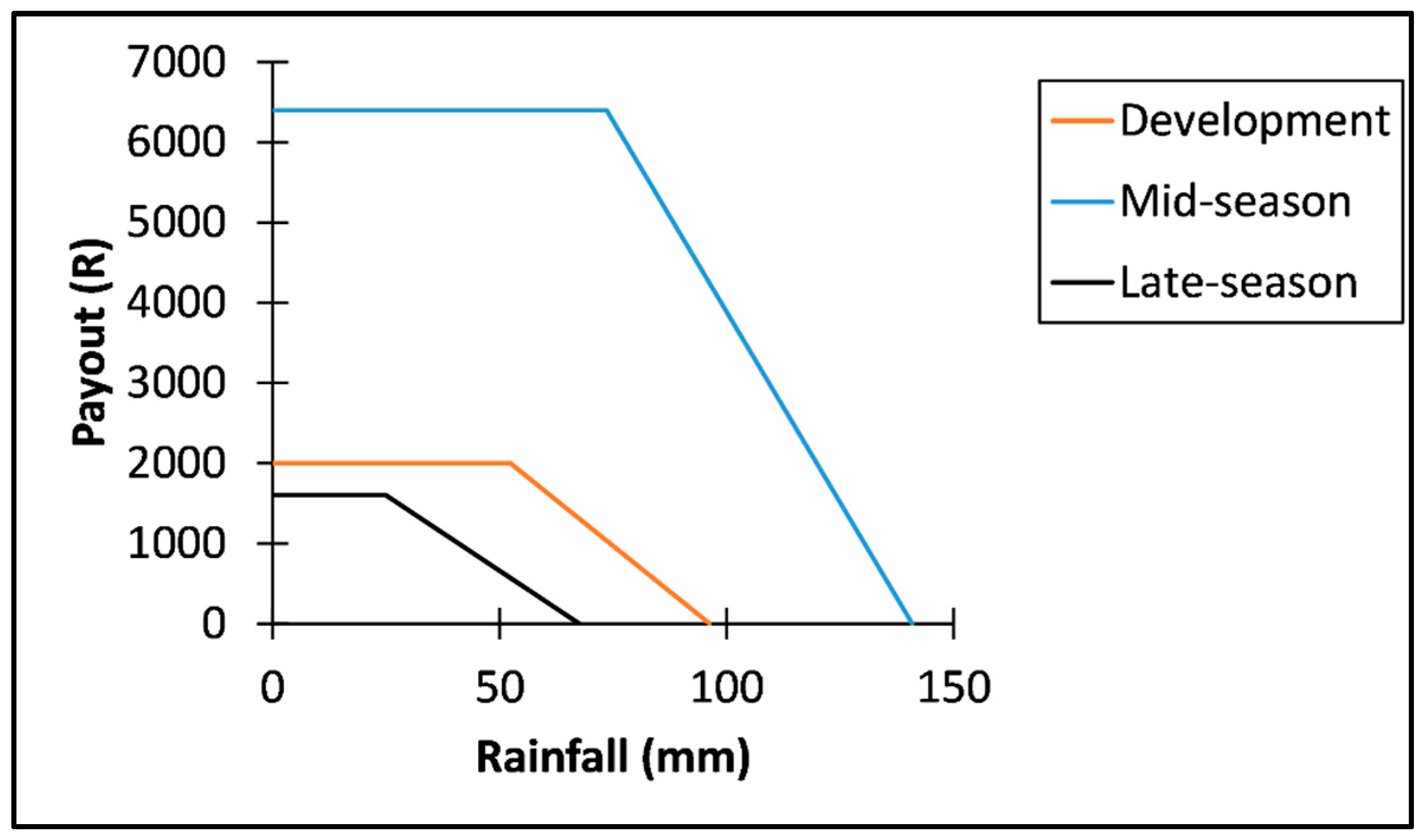
3.3. Insurance Threshold Values
- First, we observed that total seasonal and mid-season CWR decrease with delayed planting. In other words, planting on 21 December results in less CWR than planting on 11 December, 1 December, and 21 November;
- Second, total seasonal and mid-season RD also decrease with delayed planting. In other words, planting on 21 December results in less RD than planting earlier;
- Third, the mid-season stage is given more weight because it has the highest CWR and RD, and it is the most water-sensitive growth stage;
- Fourth, a planting date that evenly and proportionately distributes CWR and RD across multiple stages is less risky;
- Fifth, the farmers’ experiences and historical planting dates were considered.
4. Discussions and Conclusions
4.1. Satellite Data for IBCI Design
4.2. Maize Water Requirements and IBCI Design
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Langyintuo, A. Smallholder farmers’ access to inputs and finance in Africa. In The Role of Smallholder Farms in Food and Nutrition Security; Paloma, S., Riesgo, L., Louhichi, K., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 133–152. [Google Scholar] [CrossRef]
- Akinnagbe, O.M.; Irohibe, I.J. Agricultural adaptation strategies to climate change impacts in Africa: A review. Bangladesh J. Agric. 2014, 39, 407–418. [Google Scholar] [CrossRef]
- Sultan, B.; Defrance, D.; Iizumi, T. Evidence of crop production losses in West Africa due to historical global warming in two crop models. Sci. Rep. 2019, 9, 1–15. [Google Scholar] [CrossRef]
- Buhaug, H.; Benaminsen, T.A.; Sjaastad, E.; Magnus Theisen, O. Climate variability, food production shocks, and violent conflict in Sub-Saharan Africa. Environ. Res. Lett. 2015, 10, 125015. [Google Scholar] [CrossRef]
- Gebremeskel, G.; Tang, Q.; Sun, S.; Huang, Z.; Zhang, X.; Liu, X. Droughts in East Africa: Causes, impacts and resilience. Earth-Sci. Rev. 2019, 193, 146–161. [Google Scholar] [CrossRef]
- ACRE. 3-D Client Value Assessment for ACRE Rwanda Maize & Livestock Insurance Products; ACRE: Nairobi, Kenya, 2020; Available online: https://acreafrica.com/ (accessed on 26 May 2021).
- WFP. R4 Rural Resilience Initiative: Annual Report; WFP: Rome, Italy, 2020; Available online: https://www.wfp.org/publications/r4-rural-resilience-initiative-2020-annual-report (accessed on 4 February 2021).
- Sharoff, J.; Diro, R.L.; McCarney, G.; Norton, M. R4 Rural Resilience Initiative in Ethiopia. Clim. Serv. Partnersh. 2015, 1–7. Available online: https://www.climate-services.org/wp-content/uploads/2015/09/R4_Ethiopia_Case_Study.pdf (accessed on 18 January 2021).
- ARC. Africa RiskView: End of Season Report|Malawi (2020/21 Season); ARC: Johannesburg, South Africa, 2020. [Google Scholar]
- Hernandez, E.; Goslinga, R.; Wang, V. Using Satellite Data to Scale Smallholder Agricultural Insurance; CGAP: Washington, DC, USA, 2018; Available online: https://www.cgap.org/sites/default/files/Brief-Using-Satellite-Data-Smallholder-Agricultural-Insurance-Aug-2018.pdf (accessed on 18 June 2019).
- Barnett, B.J.; Mahul, O. Weather index insurance for agriculture and rural areas in lower-income countries. Am. J. Agric. Econ. 2007, 89, 1241–1247. [Google Scholar] [CrossRef]
- Ntukamazina, N.; Onwonga, R.N.; Sommer, R.; Rubyogo, J.C.; Mukankusi, C.M.; Mburu, J.; Kariuki, R. Index-based agricultural insurance products: Challenges, opportunities and prospects for uptake in sub-Sahara Africa. J. Agric. Rural Dev. Trop. Subtrop. 2017, 118, 171–185. Available online: https://www.jarts.info/index.php/jarts/article/view/2017042052372 (accessed on 13 May 2019).
- Tadesse, M.A.; Shiferaw, B.A.; Erenstein, O. Weather index insurance for managing drought risk in smallholder agriculture: Lessons and policy implications for sub-Saharan Africa. Agric. Food Econ. 2015, 3, 1–21. [Google Scholar] [CrossRef]
- Clement, K.Y.; Wouter Botzen, W.J.; Brouwer, R.; Aerts, J.C.J.H. A global review of the impact of basis risk on the functioning of and demand for index insurance. Int. J. Disaster Risk Reduct. 2018, 28, 845–853. [Google Scholar] [CrossRef]
- Choudhury, A.; Jones, J.; Okine, A.; Choudhury, R.L. Drought-triggered index insurance using cluster analysis of rainfall affected by climate change. J. Insur. Issues 2016, 39, 169–186. Available online: https://www.jstor.org/stable/43921956 (accessed on 16 February 2020).
- Enenkel, M.; Osgood, D.; Anderson, M.; Powell, B.; McCarty, J.; Neigh, C.; Carroll, M.; Wooten, M.; Husak, G.; Hain, C.; et al. Exploiting the convergence of evidence in satellite data for advanced weather index insurance design. Weather Clim. Soc. 2019, 11, 65–93. [Google Scholar] [CrossRef]
- Eze, E.; Girma, A.; Zenebe, A.A.; Zenebe, G. Feasible crop insurance indexes for drought risk management in Northern Ethiopia. Int. J. Disaster Risk Reduct. 2020, 47, 101544. [Google Scholar] [CrossRef]
- Masiza, W.; Chirima, J.; Hamandawana, H.; Kalumba, A.M.; Magagula, H.B. Linking agricultural index insurance with factors that influence maize yield in rain-fed smallholder farming systems. Sustainability 2021, 13, 5176. [Google Scholar] [CrossRef]
- Gornott, C.; Hattermann, F.; Wechsung, F. Yield gap analysis for Tanzania—The impacts of climate, management, and socio-economic impacts on maize yields. Procedia Environ. Sci. 2015, 29, 231. [Google Scholar] [CrossRef]
- Kihara, J.; Tamene, L.D.; Massawe, P.; Bekunda, M. Agronomic survey to assess crop yield, controlling factors and management implications: A case-study of Babati in northern Tanzania. Nutr. Cycl. Agroecosyst. 2015, 102, 5–16. [Google Scholar] [CrossRef]
- Beza, E.; Silva, J.V.; Kooistra, L.; Reidsma, P. Review of yield gap explaining factors and opportunities for alternative data collection approaches. Eur. J. Agron. 2017, 82, 206–222. [Google Scholar] [CrossRef]
- MacCarthy, D.S.; Adiku, S.G.; Freduah, B.S.; Kamara, A.Y.; Narh, S.; Abdulai, A.L. Evaluating maize yield variability and gaps in two agroecologies in northern Ghana using a crop simulation model. S. Afr. J. Plant Soil 2018, 35, 137–147. [Google Scholar] [CrossRef]
- Assefa, B.T.; Chamberlin, J.; Reidsma, P.; Silva, J.V.; van Ittersum, M.K. Unravelling the variability and causes of smallholder maize yield gaps in Ethiopia. Food Secur. 2020, 12, 489–490. [Google Scholar] [CrossRef]
- Dutta, S.; Chakraborty, S.; Goswami, R.; Banerjee, H.; Majumdar, K.; Li, B.; Jat, M.L. Maize yield in smallholder agriculture system—An approach integrating socio-economic and crop management factors. PLoS ONE 2020, 15, e0229100. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, H.; Goswami, R.; Chakraborty, S.; Dutta, S.; Majumdar, K.; Satyanarayana, T.; Jat, M.L.; Zingore, S. Understanding biophysical and socio-economic determinants of maize (Zea mays L.) yield variability in eastern India. NJAS-Wagening. J. Life Sci. 2014, 70, 79–93. [Google Scholar] [CrossRef]
- Masiza, W.; Chirima, G.J.; Hamandawana, H.; Kalumba, A.M.; Magagula, H.B. Do satellite data correlate with in-situ rainfall and smallholder crop yields? Implications for crop insurance. Sustainability 2022, 14, 1670. [Google Scholar] [CrossRef]
- Carletto, C.; Jolliffe, D.; Banerjee, R. The Emperor Has No Data! Agricultural Statistics in Sub-Saharan Africa. World Bank Working Paper. 2013. Available online: http://mortenjerven.com/wp-content/uploads/2013/04/Panel-3-Carletto.pdf (accessed on 16 March 2018).
- Djurfeldt, G.; Hall, O.; Jirström, M.; Archila Bustos, M.; Holmquist, B.; Nasrin, S. Using panel survey and remote sensing data to explain yield gaps for maize in sub-Saharan Africa. J. Land Use Sci. 2018, 13, 344–357. [Google Scholar] [CrossRef]
- Osgood, D.; Powell, B.; Diro, R.; Farah, C.; Enenkel, M.; Brown, M.E.; Husak, G.; Blakeley, L.; Hoffman, L.; McCarty, J.L. Farmer perception, recollection, and remote sensing in weather index insurance: An Ethiopia case study. Remote Sens. 2018, 10, 1887. [Google Scholar] [CrossRef]
- Pereira, L.S.; Alves, I. Crop. Water Requirements; Elsevier Inc.: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Wani, S.P.; Sreedevi, T.K.; Rockström, J.; Ramakrishna, Y.S. Rainfed agriculture—Past trends and future prospects. In Rainfed Agriculture: Unlocking the Potential; Wani, S.P., Sreedevi, T.K., Rockström, J., Ramakrishna, Y.S., Eds.; CABI: Wallingford, UK, 2009; pp. 1–35. [Google Scholar] [CrossRef]
- Worldbank. Weather Index Insurance for Agriculture: Guidance for Development Practitioners; Worldbank: Washington, DC, USA, 2011; Available online: https://documents1.worldbank.org/curated/en/590721468155130451/pdf/662740NWP0Box30or0Ag020110final0web.pdf (accessed on 11 February 2022).
- Belissa, T.; Bulte, E.; Cecchi, F.; Gangopadhyay, S.; Lensink, R. Liquidity constraints, informal institutions, and the adoption of weather insurance: A randomized controlled trial in Ethiopia. J. Dev. Econ. 2019, 140, 269–278. [Google Scholar] [CrossRef]
- Alcaide, K.D.R.; Buncag, M.J.J.; Mendoza, R.E.S.; Santos, L.B.U. Developing a Rainfall-Based Index for Corn Crop Insurance in Isabela, Philippines. Int. J. Sci. Manag. Stud. 2019, 2, 77–84. [Google Scholar] [CrossRef]
- Butts-Wilmsmeyer, C.J.; Seebauer, J.R.; Singleton, L.; Below, F.E. Weather during key growth stages explains grain quality and yield of maize. Agronomy 2019, 9, 16. [Google Scholar] [CrossRef]
- Çakir, R. Effect of water stress at different development stages on vegetative and reproductive growth of corn. F. Crop. Res. 2004, 89, 1–16. [Google Scholar] [CrossRef]
- Song, L.; Jin, J.; He, J. Effects of severe water stress on maize growth processes in the field. Sustainability 2019, 11, 5086. [Google Scholar] [CrossRef]
- Le Coz, C.; Van De Giesen, N. Comparison of rainfall products over sub-saharan africa. J. Hydrometeorol. 2020, 21, 553–596. [Google Scholar] [CrossRef]
- Gebremicael, T.; Mohamed, Y.; van der Zaag, P.; Berhe, A.G.; Haile, G.G.; Hagos, E.Y.; Hagos, M.K. Comparison and validation of eight satellite rainfall products over the rugged topography of Tekeze-Atbara Basin at different spatial and temporal scales. Hydrol. Earth Syst. Sci. Discuss. 2017, 1–31, preprint. [Google Scholar] [CrossRef]
- Jordaan, A.; Makate, D.; Mashego, T.; Mdungela, N.; Phatudi-Mphahlele, B.; Mashimbye, C.; Mlambo, D. Vulnerability Adaptation to and Coping with Drought: The Case of Commercial and Subsistence Rain Fed Farming in the Eastern Cape; Water Research Commission: Pretoria, South Africa, 2017; Available online: www.wrc.org.za (accessed on 6 June 2018).
- Eta, N.E.; Grace, G. Investigation of some physicochemical charactyeristics/prperties of geophagic soil in the Oliver Tambo District Munucipality in the Eastern cape. Acad. J. Sci. 2013, 2, 465–471. [Google Scholar]
- Sibanda, M.; Mushunje, A.; Mutengwa, C.S. An evaluation on the profitability of growing improved maize open pollinated varieties in the Eastern Cape Province, South Africa. J. Dev. Agric. Econ. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- DALRRD. Trends in the Agricultural Sector; DALRRD: Pretoria, South Africa, 2018. Available online: https://www.dalrrd.gov.za (accessed on 15 November 2018).
- Chimonyo, V.G.P.; Mutengwa, C.; Chiduza, C.; Tandzi, L. Participatory variety selection of maize genotypes in the Eastern cape province of South Africa. S. Afr. J. Agric. Ext. 2019, 47, 103–117. [Google Scholar] [CrossRef]
- Chimonyo, V.G.P.; Mutengwa, C.; Chiduza, C.; Tandzi, L. Characteristics of maize growing farmers, varietal use, and constraints to increase productivity in selected villages in the Eastern Cape province of South Africa. S. Afr. J. Agric. Ext. 2020, 48, 71–77. [Google Scholar] [CrossRef]
- NAMC. Agripreneur: Agriculture Insurance; NAMC: Pretoria, South Africa, 2020; Available online: https://www.namc.co.za/wp-content/uploads/2020/04/Agrepreneur-Issue-20-March-2020.pdf (accessed on 13 February 2022).
- Partridge, A.G.; Wagner, N.J. Risky business: Agricultural insurance in the face of climate change: Elsenburg journal. Agriprobe 2016, 13, 49–53. [Google Scholar] [CrossRef]
- Elum, Z.A.; Modise, D.M.; Marr, A. Farmer’s perception of climate change and responsive strategies in three selected provinces of South Africa. Clim. Risk Manag. 2017, 16, 246–257. [Google Scholar] [CrossRef]
- Nyandeni Local Municipality. Nyandeni Local Municipality: Local Economic Development Strategy Review; Nyandeni Local Municipality: Libode, South Africa, 2018. Available online: https://www.nyandenilm.gov.za/wp-content/uploads/2019/08/Final-Nyandeni-LM-LED-Strategy-Review-pdf (accessed on 18 November 2020).
- Maidment, R.; Black, E.; Greatrex, H.; Young, M. TAMSAT. In Satellite Precipitation Measurement; Levizzani, V., Kidd, C., Kirschbaum, D., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, S.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data. 2015, 2, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.; Kivumbi, D.; Heng, L. Use of the FAO CROPWAT Model in Deficit Irrigation Studies; FAO: Rome, Italy, 2002; pp. 17–27. Available online: https://agris.fao.org/agris-search/search.do?recordID=XF2002407869 (accessed on 6 February 2019).
- Muhammad, N. Simulation of maize crop under irrigated and rainfed conditions with CROPWAT model. J. Agric. Biol. Sci. 2009, 4, 68–73. Available online: http://www.arpnjournals.com/jabs/research_papers/rp_2009/jabs_0309_123.pdf (accessed on 18 November 2021).
- Nyambo, P.; Wakindiki, I.I.C. Water footprint of growing vegetables in selected smallholder irrigation schemes in South Africa. Water SA 2015, 41, 571–578. [Google Scholar] [CrossRef]
- Worldbank. Actual Crop. Water Use in Project Countries—A Synthesis at the Regional Level; Worldbank: Washington, DC, USA, 2007; Volume 4288, Available online: https://elibrary.worldbank.org/doi/abs/10.1596/1813-9450-4288 (accessed on 10 February 2022).
- Singo, L.R.; Kundu, P.; Mathivha, F. Spatial variation of reference evapotranspiration and its influence on the hydrology of Luvuvhu River Catchment. Res. J. Agric. Environ. Manag. 2016, 5, 187–196. Available online: https://univendspace.univen.ac.za/handle/11602/1265 (accessed on 10 February 2022).
- Dabrowski, J.M.; Murray, K.; Ashton, P.J.; Leaner, J.J. Agricultural impacts on water quality and implications for virtual water trading decisions. Ecol. Econ. 2009, 68, 1074–1082. [Google Scholar] [CrossRef]
- du Plessis, J. Maize Production; DALRRD: Pretoria, South Africa, 2003. [Google Scholar] [CrossRef]
- Frost, C.; Thiebaut, N.; Newby, T. Evaluating Terra MODIS satellite sensor data products for maize yield estimation in South Africa. S. Afr. J. Geomat. 2013, 2, 106–119. [Google Scholar]
- Masupha, T.E.; Moeletsi, M.E. The use of Water Requirement Satisfaction Index for assessing agricultural drought on rain-fed maize, in the Luvuvhu River catchment, South Africa. Agric. Water Manag. 2020, 237, 106142. [Google Scholar] [CrossRef]
- Ali, M.; Mubarak, S. Effective rainfall calculation methods for field crops: An overview, analysis and new formulation. Asian Res. J. Agric. 2017, 7, 1–12. [Google Scholar] [CrossRef]
- Bokke, A.S.; Shoro, K.E. Impact of effective rainfall on net irrigation water requirement: The case of Ethiopia. Water Sci. 2020, 34, 155–163. [Google Scholar] [CrossRef]
- Chen, W.; Hohl, R.; Tiong, L.K. Rainfall index insurance for corn farmers in Shandong based on high-resolution weather and yield data. Agric. Financ. Rev. 2017, 77, 337–354. [Google Scholar] [CrossRef]
- Masiza, W.; Chirima, J.; Hamandawana, H.; Pillay, R. Enhanced mapping of a smallholder crop farming landscape through image fusion and model stacking. Int. J. Remote Sens. 2020, 41, 8739–8756. [Google Scholar] [CrossRef]
- Mashaba-Munghemezulu, Z.; Chirima, G.J.; Munghemezulu, C. Delineating smallholder maize farms from sentinel-1 coupled with sentinel-2 data using machine learning. Sustainability 2021, 13, 4728. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Kimani, M.W.; Hoedjes, J.C.B.; Su, Z. An assessment of satellite-derived rainfall products relative to ground observations over East Africa. Remote Sens. 2017, 9, 430. [Google Scholar] [CrossRef]
- Tarnavsky, E.; Chavez, E.; Boogaard, H. Agro-meteorological risks to maize production in Tanzania: Sensitivity of an adapted Water Requirements Satisfaction Index (WRSI) model to rainfall. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 77–87. [Google Scholar] [CrossRef]
- DuPlessis, K.; Kibii, J. Applicability of CHIRPS-based satellite rainfall estimates for South Africa. J. S. Afr. Inst. Civ. Eng. 2021, 63, 43–54. [Google Scholar] [CrossRef]
- Mahlalela, P.T.; Blamey, R.C.; Hart, N.C.G.; Reason, C.J.C. Drought in the Eastern Cape region of South Africa and trends in rainfall characteristics. Clim. Dyn. 2020, 55, 2743–2759. [Google Scholar] [CrossRef] [PubMed]
- Enenkel, M.; Osgood, D.; Powell, B. The added value of satellite soil moisture for agricultural index insurance. In Remote Sensing of Hydrometeorological Hazards; Petropoulos, G.P., Islam, T., Eds.; CRS Press: Boca Raton, FL, USA, 2017; pp. 69–83. [Google Scholar] [CrossRef]
- Enenkel, M.; Farah, C.; Hain, C.; White, A.; Anderson, M.; You, L.; Wagner, W.; Osgood, D. What rainfall does not tell us—enhancing financial instruments with satellite-derived soil moisture and evaporative stress. Remote Sens. 2018, 10, 1819. [Google Scholar] [CrossRef]
- Arce, C. Comparative Assessment of Weather Index Insurance Strategies in Sub-Saharan Africa; Vuna Africa: Pretoria, South Africa, 2016; Available online: http://www.vuna-africa.com (accessed on 19 August 2019).
- Sibanda, M.; Mushunje, A.; Mutengwa, C. Factors influencing the demand for improved maize open pollinated varieties (OPVs) by smallholder farmers in the Eastern Cape Province, South Africa. J. Cereals Oilseeds 2016, 7, 14–26. [Google Scholar] [CrossRef][Green Version]
- Osgood, D.; Mclaurin, M.; Carriquiry, M.; Mishra, A.; Fiondella, F.; Hansen, J.W.; Peterson, N.; Ward, M.N. Designing Weather Insurance Contracts for Farmers in Malawi, Tanzania, and Kenya; International Research Institute for Climate and Society (IRI), Columbia University: New York, NY, USA, 2007; Available online: https://iri.columbia.edu/~deo/IRI-CRMG-Africa-Insurance-Report-6-2007/IRI-CRMG-Kenya-Tanzania-Malawi-Insurance-Report-6-2007.pdf (accessed on 15 March 2018).
- Masupha, T.E.; Moeletsi, M.E. Use of standardized precipitation evapotranspiration index to investigate drought relative to maize, in the Luvuvhu River catchment area, South Africa. Phys. Chem. Earth. 2017, 102, 1–9. [Google Scholar] [CrossRef]
- Udom, B.E.; Kamalu, O.J. Crop water requirements during growth period of maize (Zea mays L.) in a moderate permeability soil on coastal Plain sands. Int. J. Plant. Res. 2019, 2019, 1–7. [Google Scholar] [CrossRef]
| Station Name | Latitude | Longitude |
|---|---|---|
| Tsolo | −31.2923 | 28.7627 |
| Libode | −31.4481 | 28.9430 |
| Ross Mission | −31.5427 | 28.6153 |
| Qunu | −31.8060 | 28.6161 |
| Mthatha | −31.5803 | 28.7754 |
| Planting Date | Stage | Days | CWR | ER * | RD | MR * | MMR * |
|---|---|---|---|---|---|---|---|
| 21 November | Initial | 20 | 25.20 | 50.40 | 0.00 | 67.07 | 37.79 |
| Development | 30 | 102.30 | 83.70 | 18.60 | 90.22 | 63.92 | |
| Mid-season | 40 | 201.00 | 115.10 | 85.90 | 141.98 | 109.63 | |
| Late season | 30 | 73.50 | 86.40 | 0.00 | 94.58 | 26.84 | |
| Total | 120 | 402.00 | 335.60 | 104.50 | 393.82 | 238.18 | |
| 1 December | Initial | 20 | 25.20 | 52.80 | 0.00 | 62.23 | 47.76 |
| Development | 30 | 103.20 | 86.50 | 16.70 | 92.03 | 66.59 | |
| Mid-season | 40 | 184.20 | 113.10 | 71.10 | 146.74 | 108.17 | |
| Late season | 30 | 78.20 | 81.30 | 0.00 | 96.45 | 75.74 | |
| Total | 120 | 390.80 | 333.70 | 87.80 | 397.45 | 298.26 | |
| 11 December | Initial | 20 | 26.80 | 54.80 | 0.00 | 54.51 | 26.60 |
| Development | 30 | 105.30 | 87.90 | 17.40 | 100.62 | 84.21 | |
| Mid-season | 40 | 170.70 | 112.90 | 57.80 | 137.10 | 109.03 | |
| Late season | 30 | 74.20 | 72.10 | 2.10 | 87.88 | 25.93 | |
| Total | 120 | 377.00 | 327.70 | 77.30 | 380.11 | 245.77 | |
| 21 December | Initial | 20 | 27.20 | 56.70 | 0.00 | 65.22 | 26.53 |
| Development | 30 | 102.40 | 87.30 | 15.10 | 96.27 | 52.40 | |
| Mid-season | 40 | 163.00 | 114.20 | 48.80 | 140.87 | 73.55 | |
| Late season | 30 | 70.30 | 58.20 | 12.10 | 67.52 | 24.94 | |
| Total | 120 | 362.90 | 316.40 | 76.00 | 369.88 | 177.42 |
| Growth Stages | Trigger (mm) | Exit (mm) | Tick (R/mm) | Weight | Amount (R) |
|---|---|---|---|---|---|
| Development | 96.27 | 52.40 | 45.59 | 0.20 | 2000 |
| Mid-season | 140.87 | 73.55 | 95.07 | 0.64 | 6400 |
| Late-season | 67.52 | 24.94 | 37.58 | 0.16 | 1600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masiza, W.; Chirima, J.G.; Hamandawana, H.; Kalumba, A.M.; Magagula, H.B. A Proposed Satellite-Based Crop Insurance System for Smallholder Maize Farming. Remote Sens. 2022, 14, 1512. https://doi.org/10.3390/rs14061512
Masiza W, Chirima JG, Hamandawana H, Kalumba AM, Magagula HB. A Proposed Satellite-Based Crop Insurance System for Smallholder Maize Farming. Remote Sensing. 2022; 14(6):1512. https://doi.org/10.3390/rs14061512
Chicago/Turabian StyleMasiza, Wonga, Johannes George Chirima, Hamisai Hamandawana, Ahmed Mukalazi Kalumba, and Hezekiel Bheki Magagula. 2022. "A Proposed Satellite-Based Crop Insurance System for Smallholder Maize Farming" Remote Sensing 14, no. 6: 1512. https://doi.org/10.3390/rs14061512
APA StyleMasiza, W., Chirima, J. G., Hamandawana, H., Kalumba, A. M., & Magagula, H. B. (2022). A Proposed Satellite-Based Crop Insurance System for Smallholder Maize Farming. Remote Sensing, 14(6), 1512. https://doi.org/10.3390/rs14061512







