Sea Surface Skin Temperature Retrieval from FY-3C/VIRR
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collections
2.1.1. FY-3C/VIRR L1B Data
2.1.2. TERRA/MODIS L1B Data
2.1.3. Metop-A/AVHRR SSTskin Data
2.1.4. Buoy Data
2.1.5. ERA-Interim Data
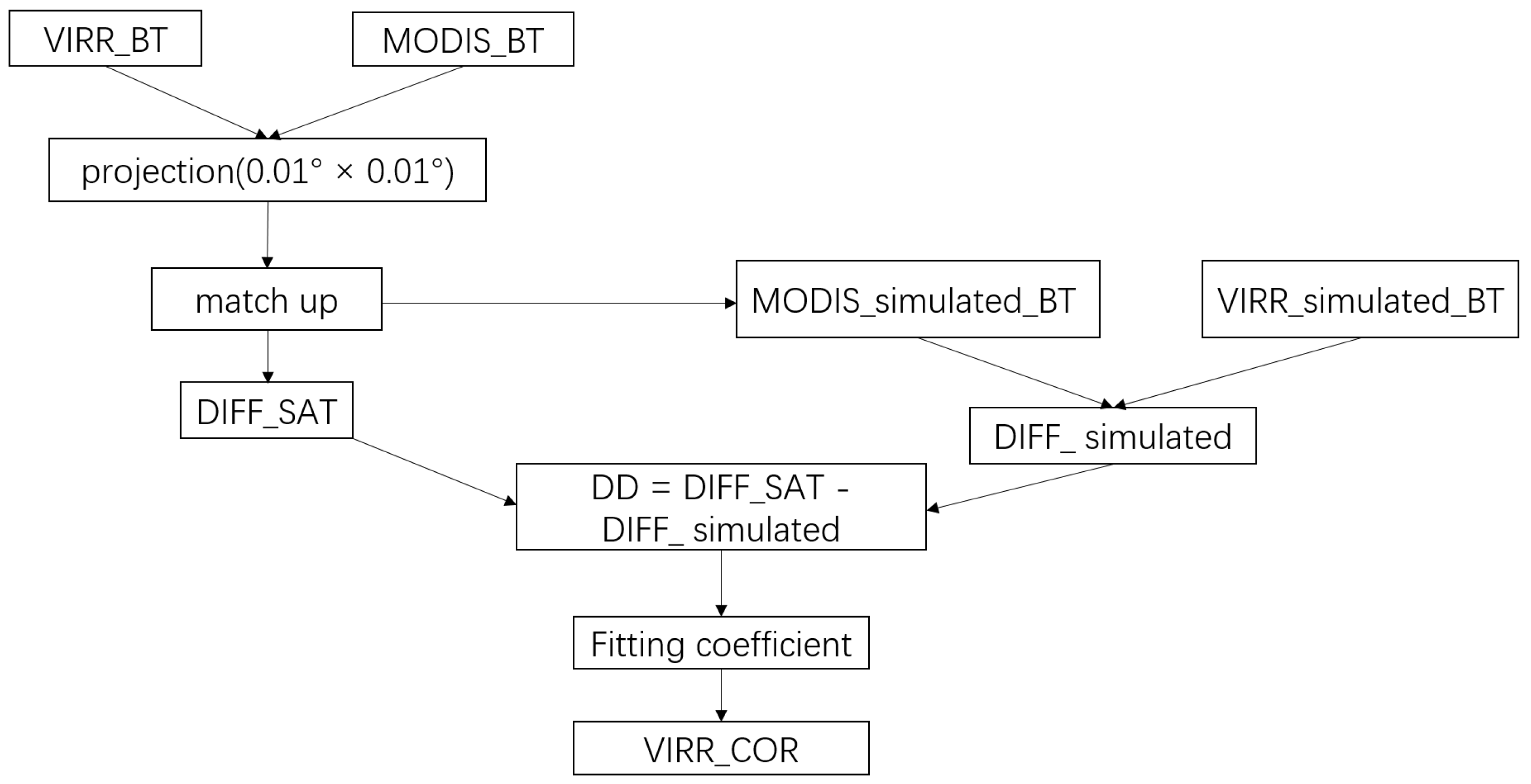
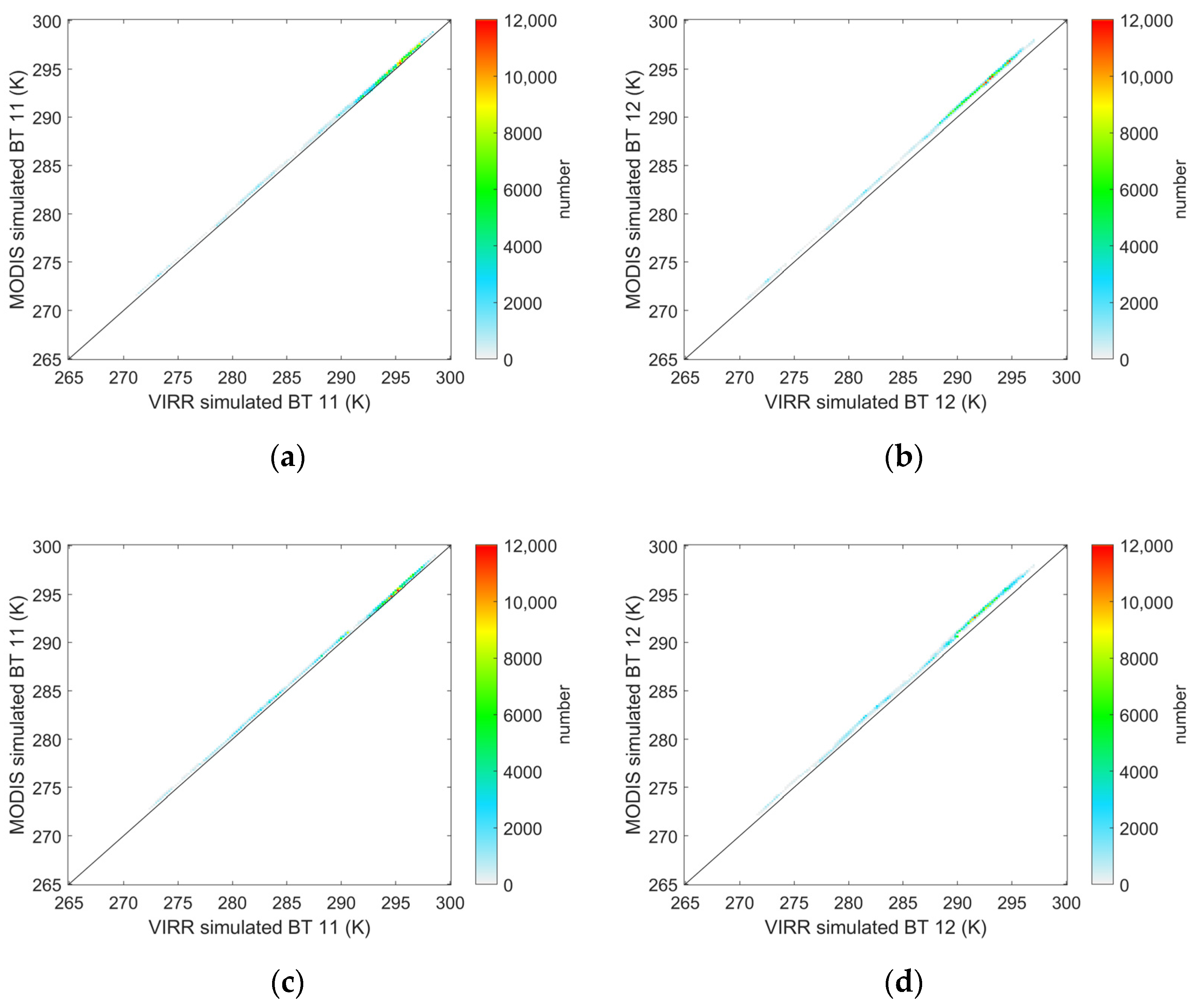
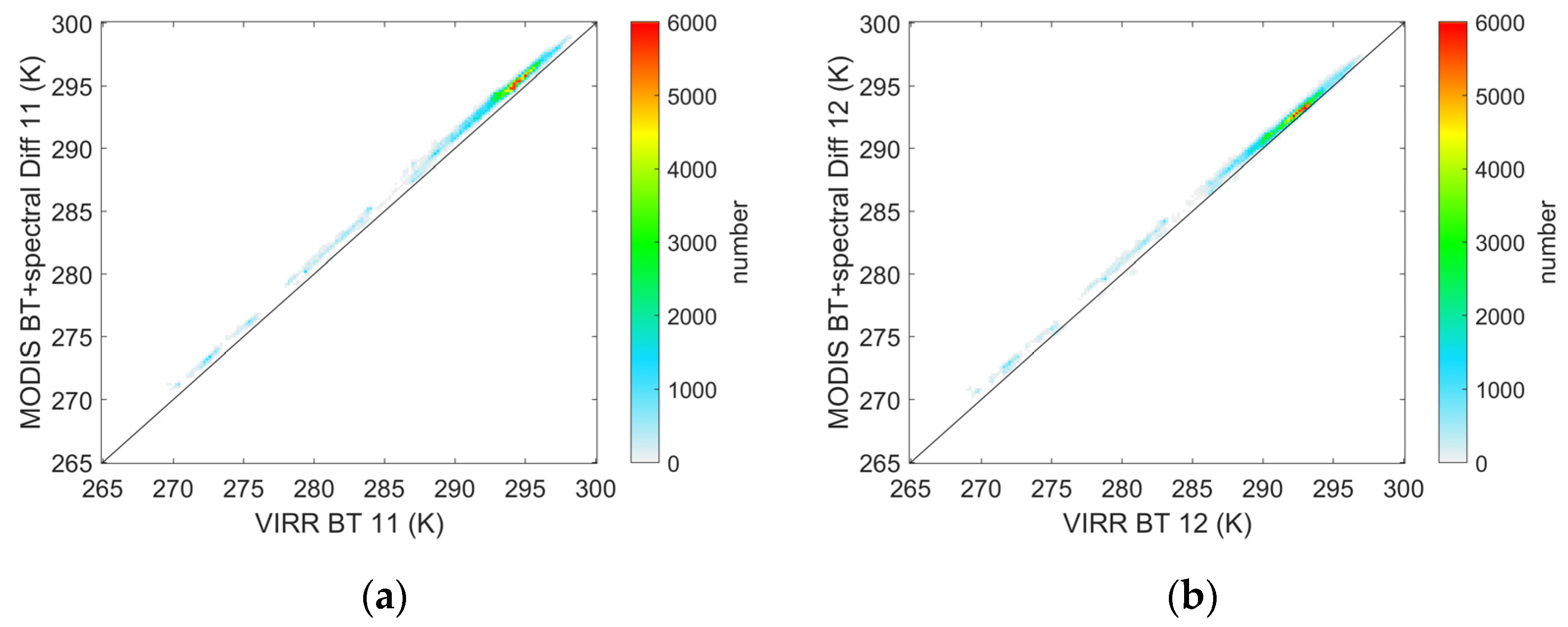
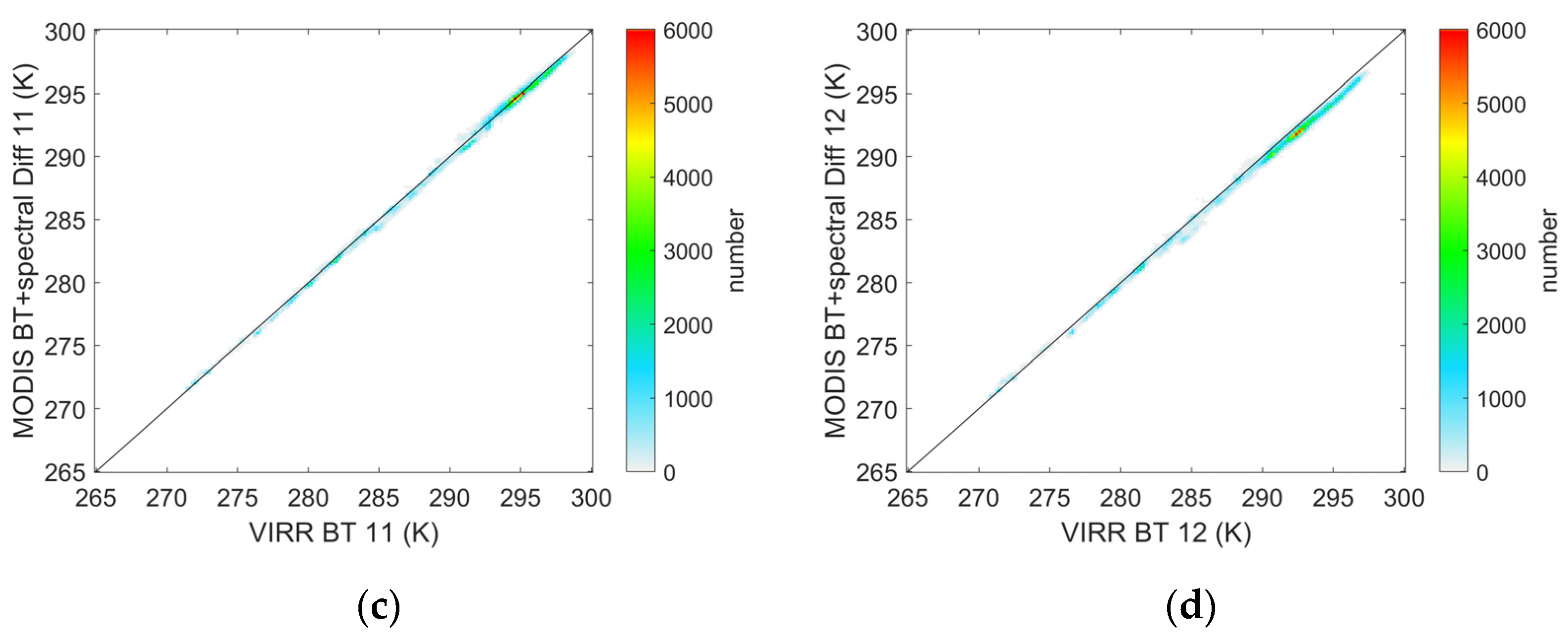
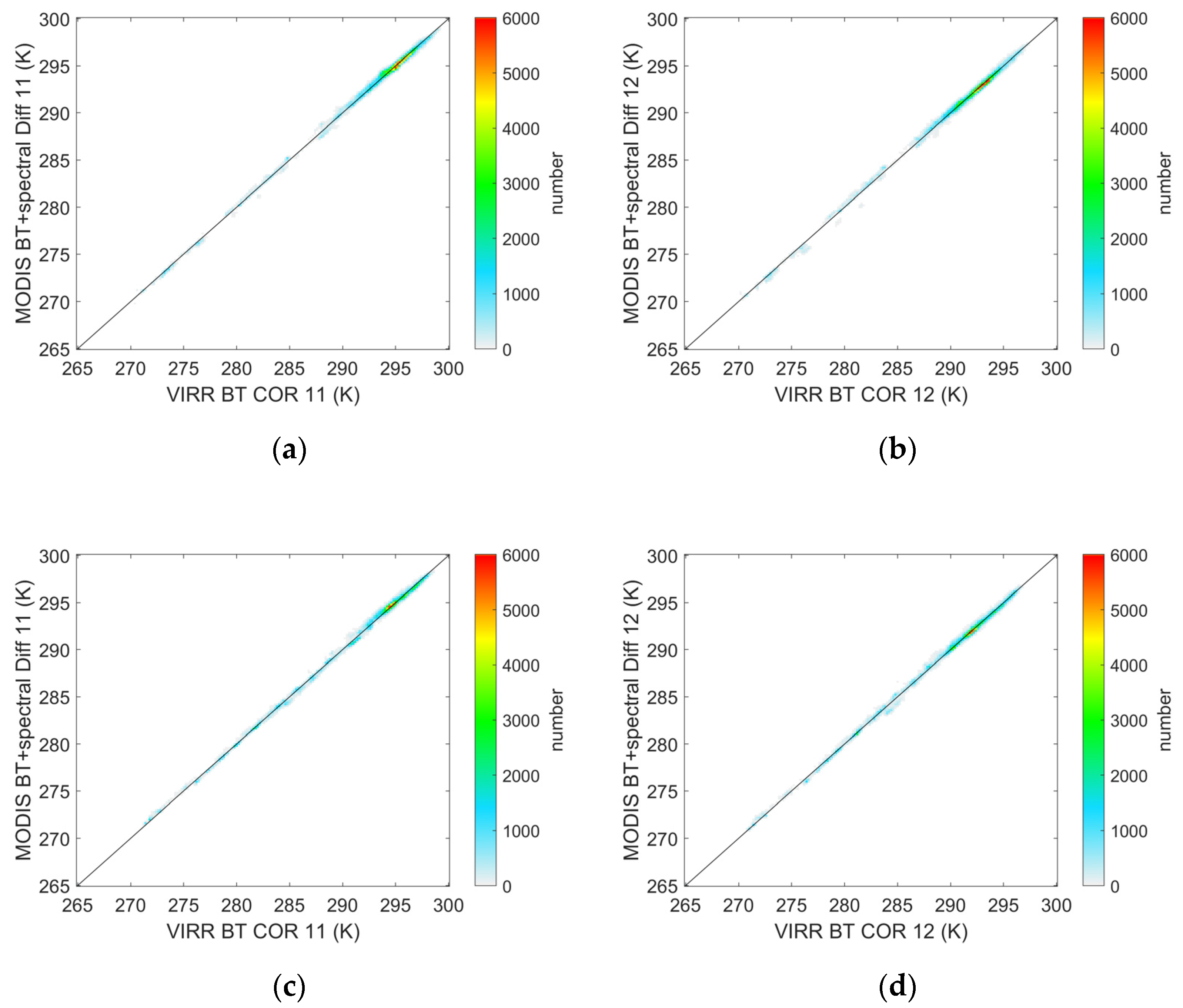
2.2. Inter-Calibration with MODIS L1B BT Data
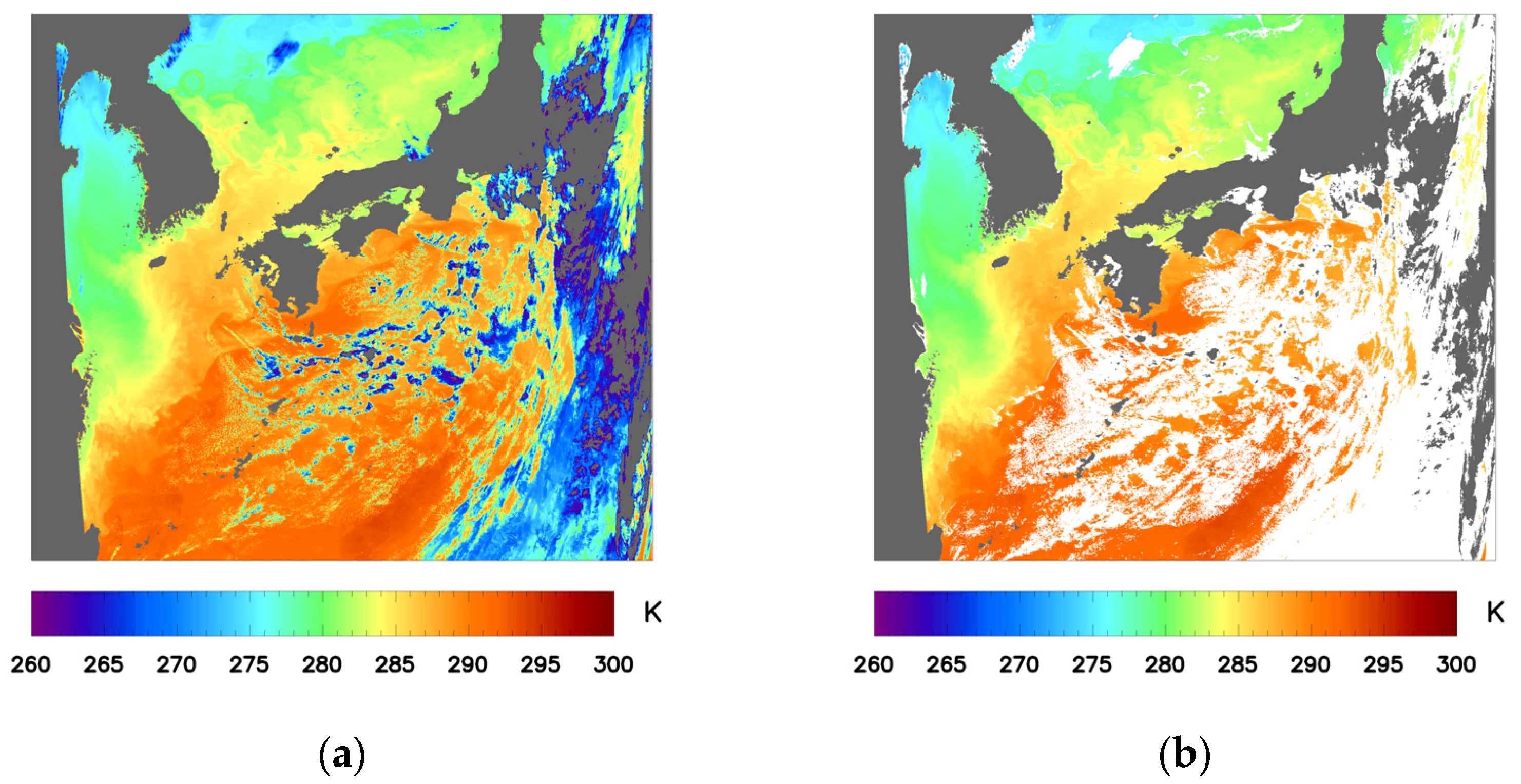
2.3. Cloud Detection
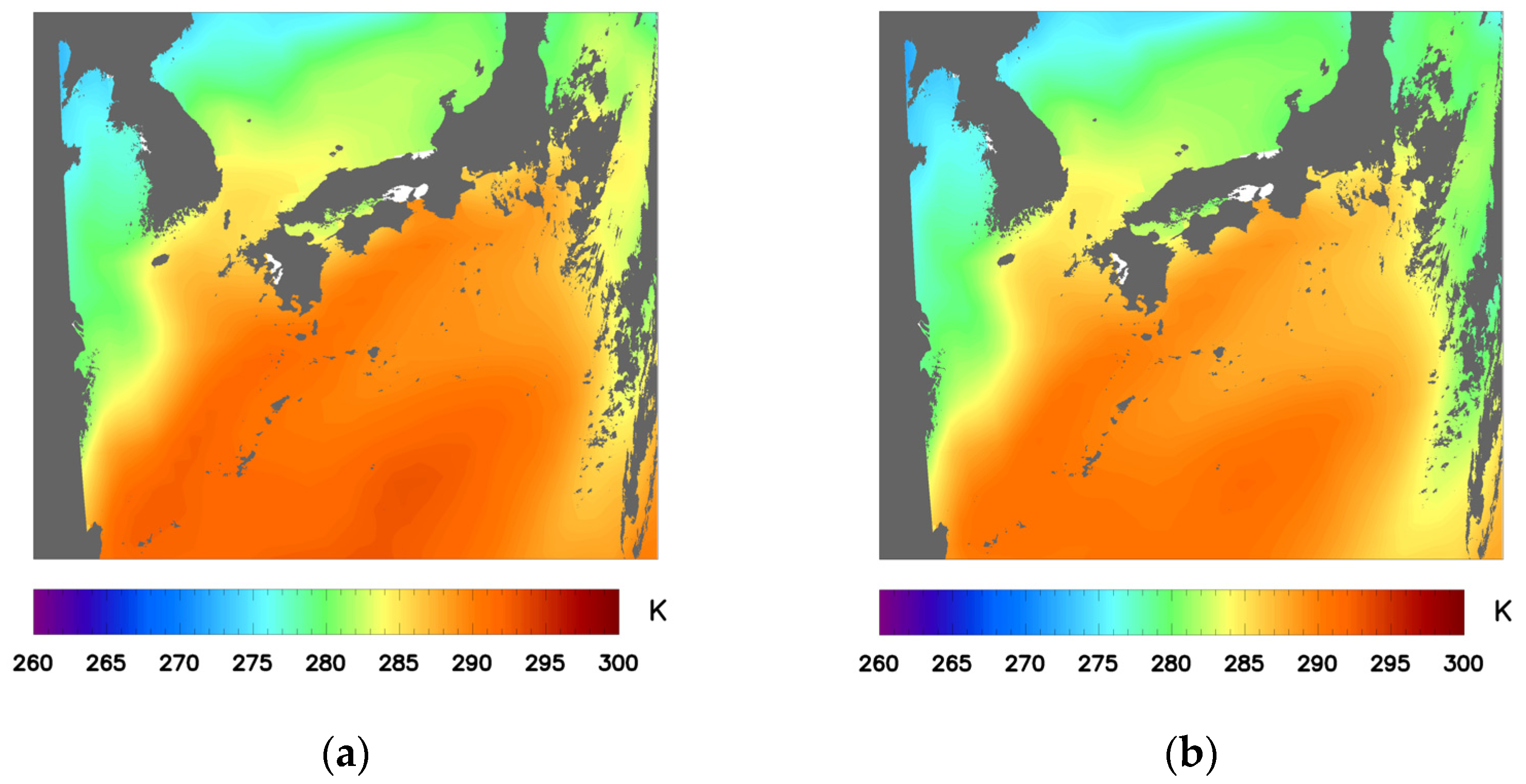
2.4. SST Retrieval
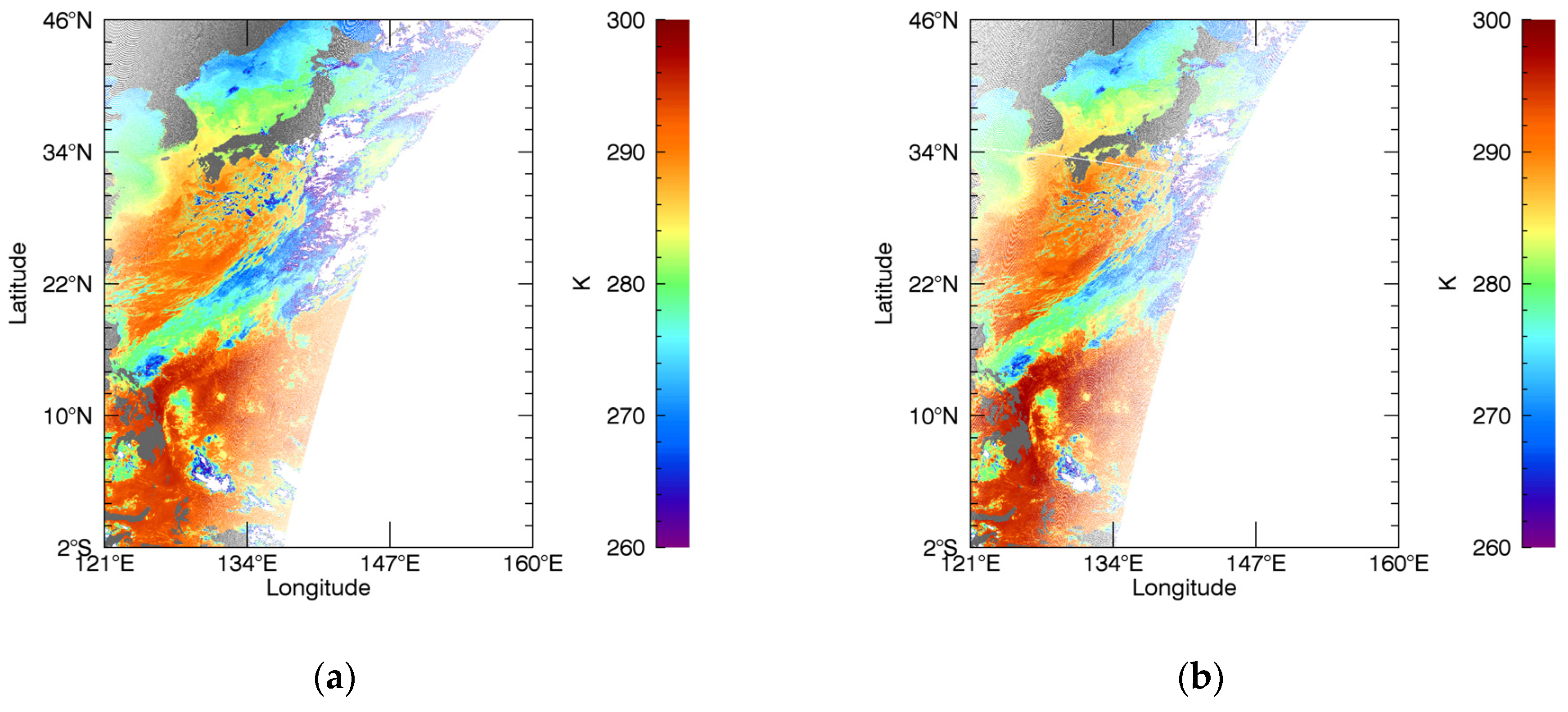
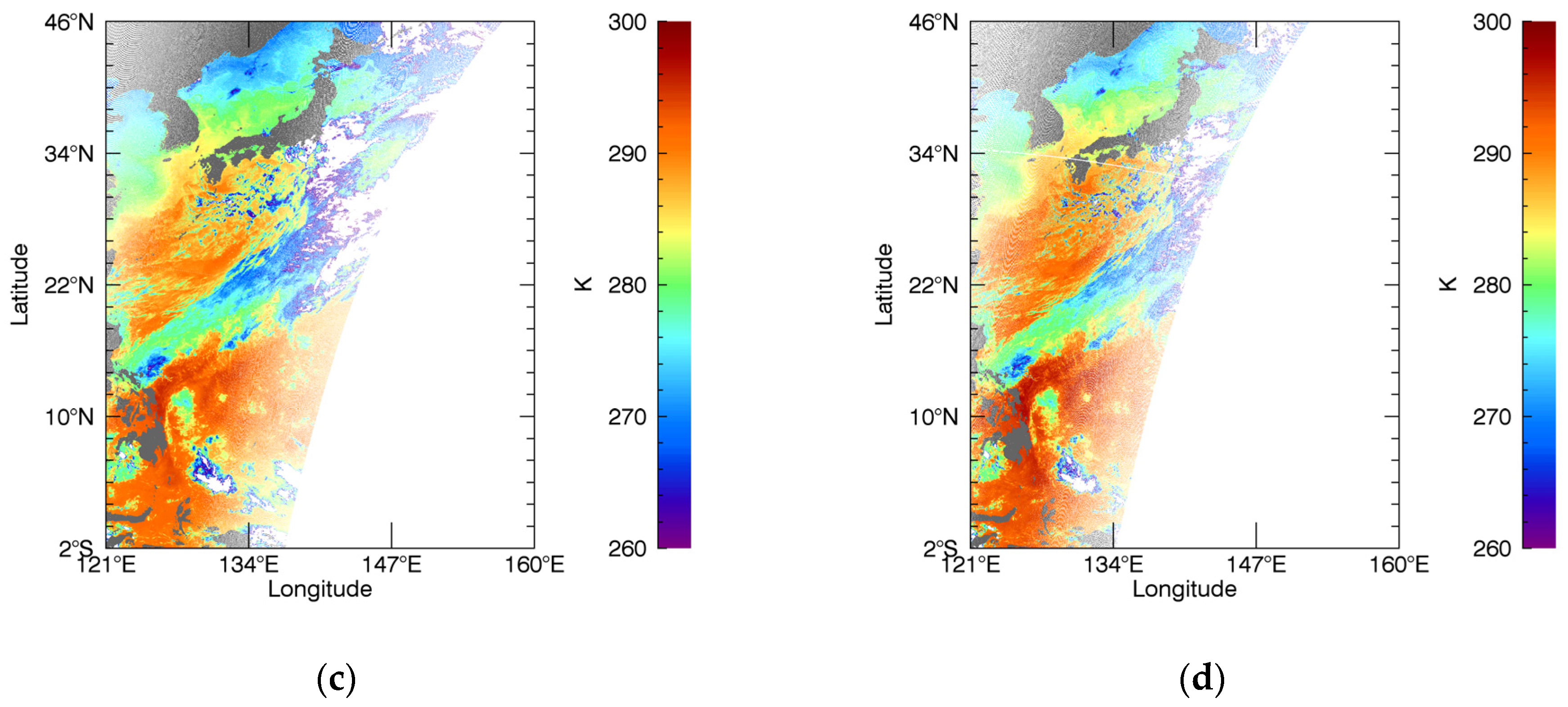
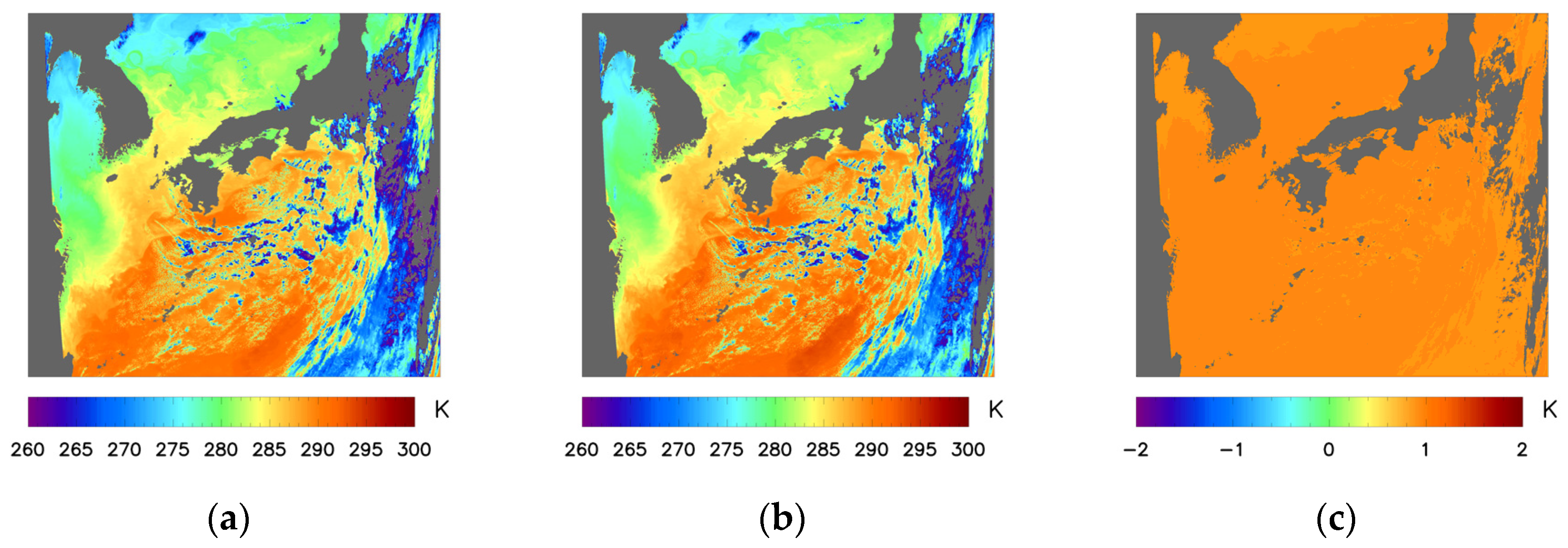
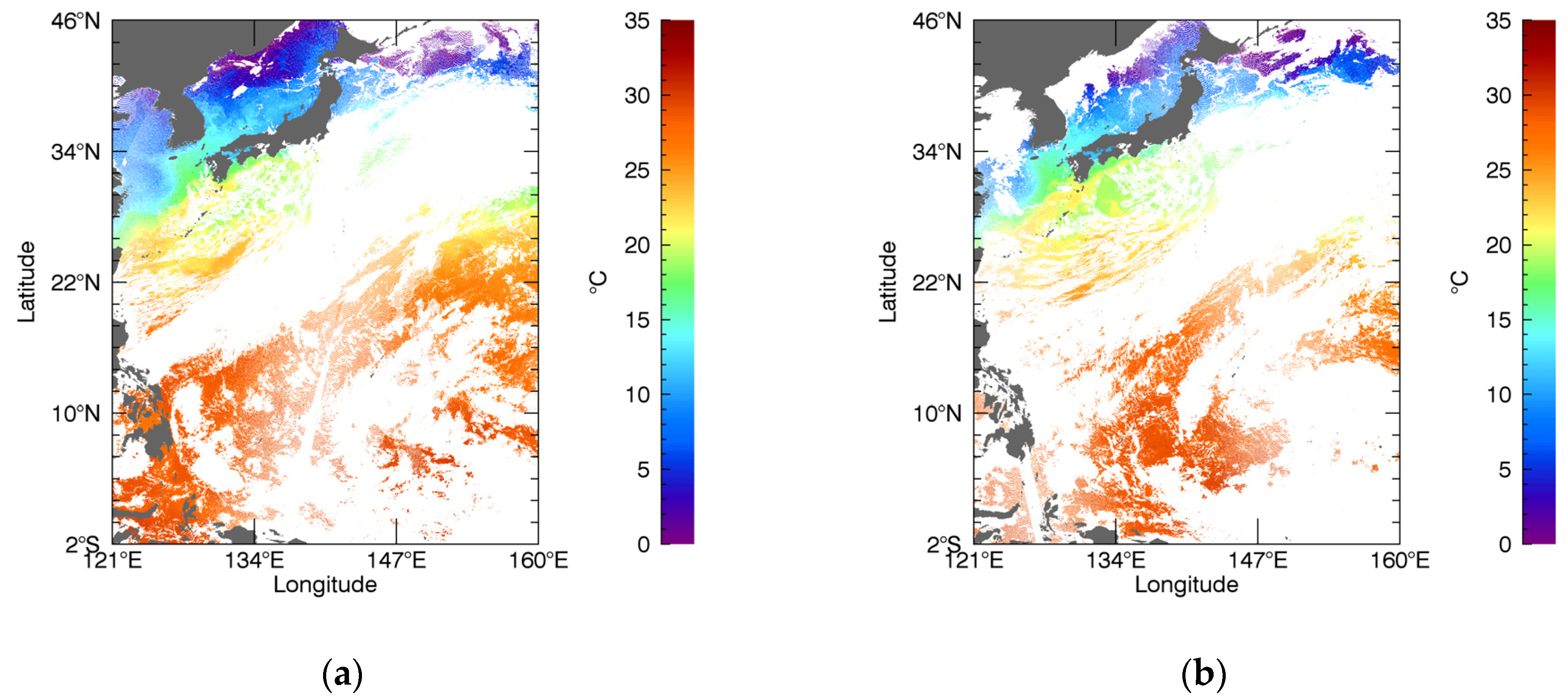
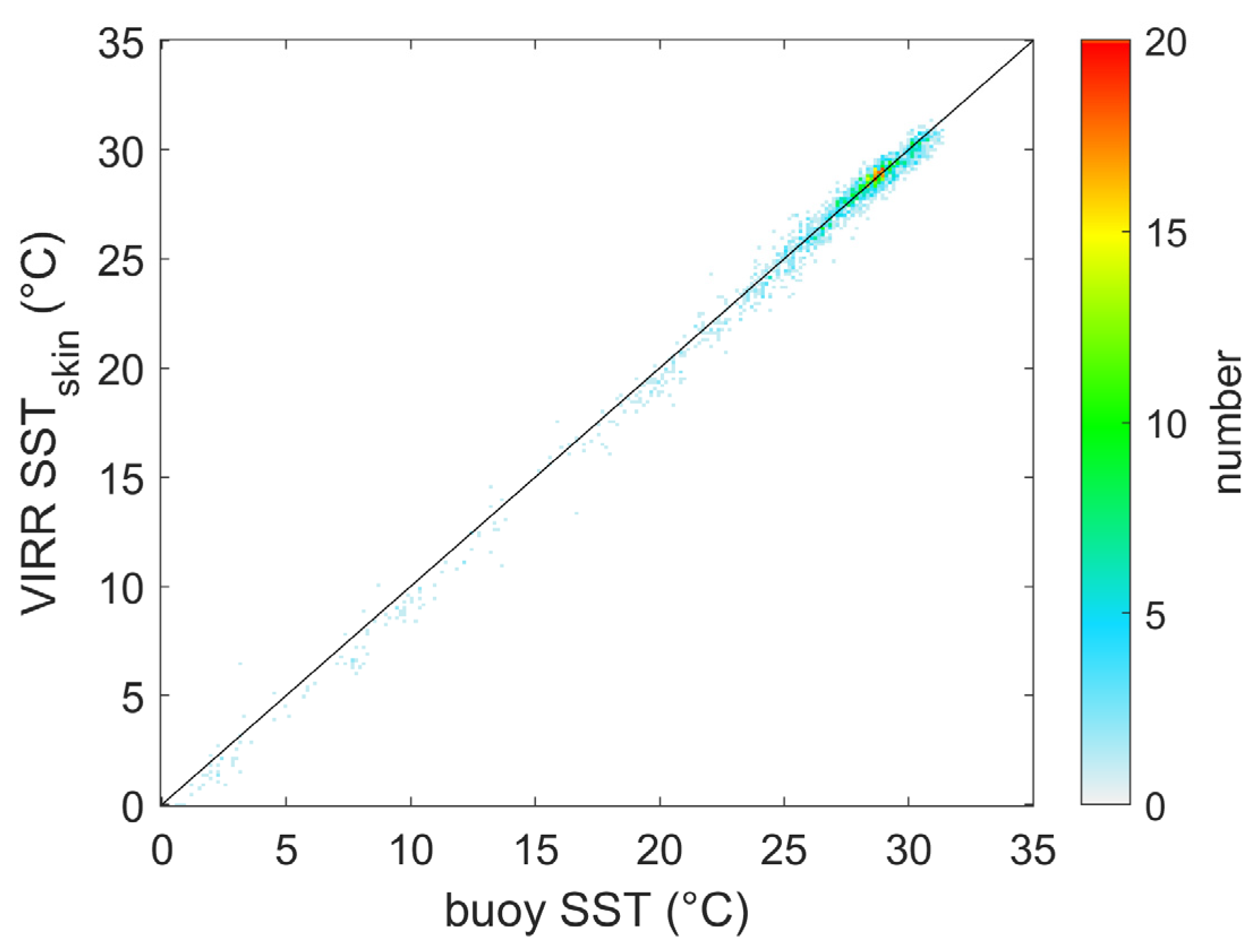
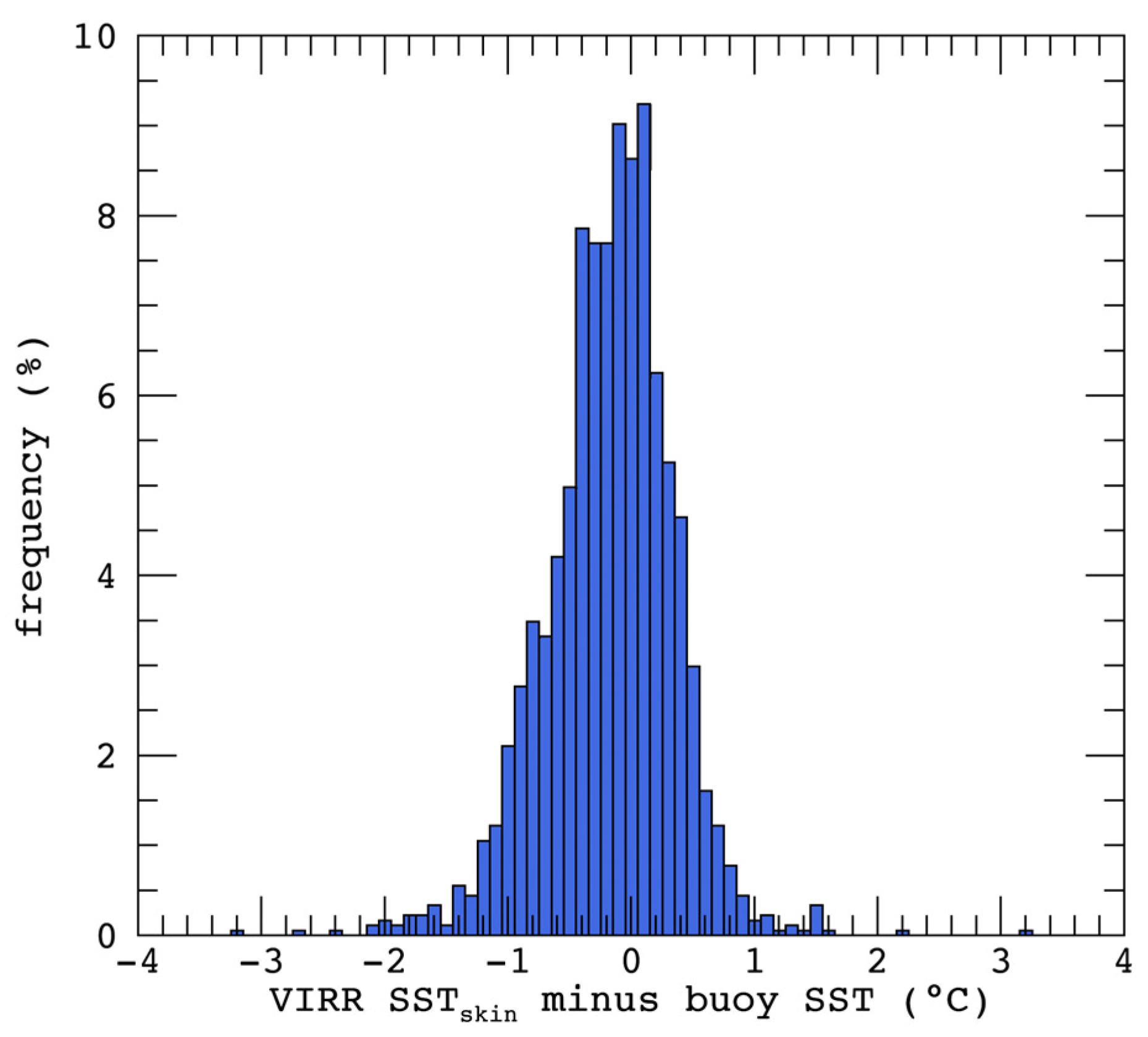
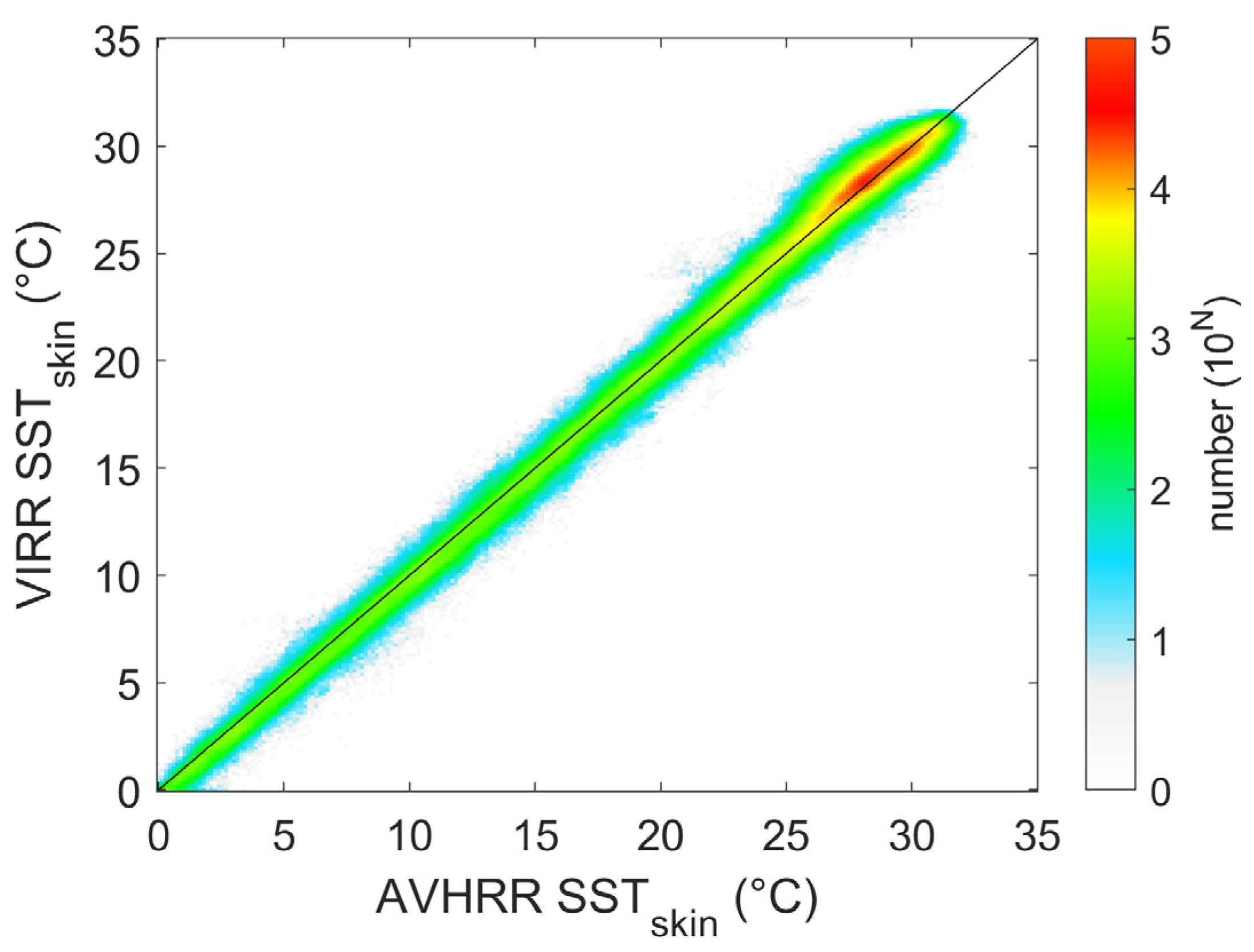
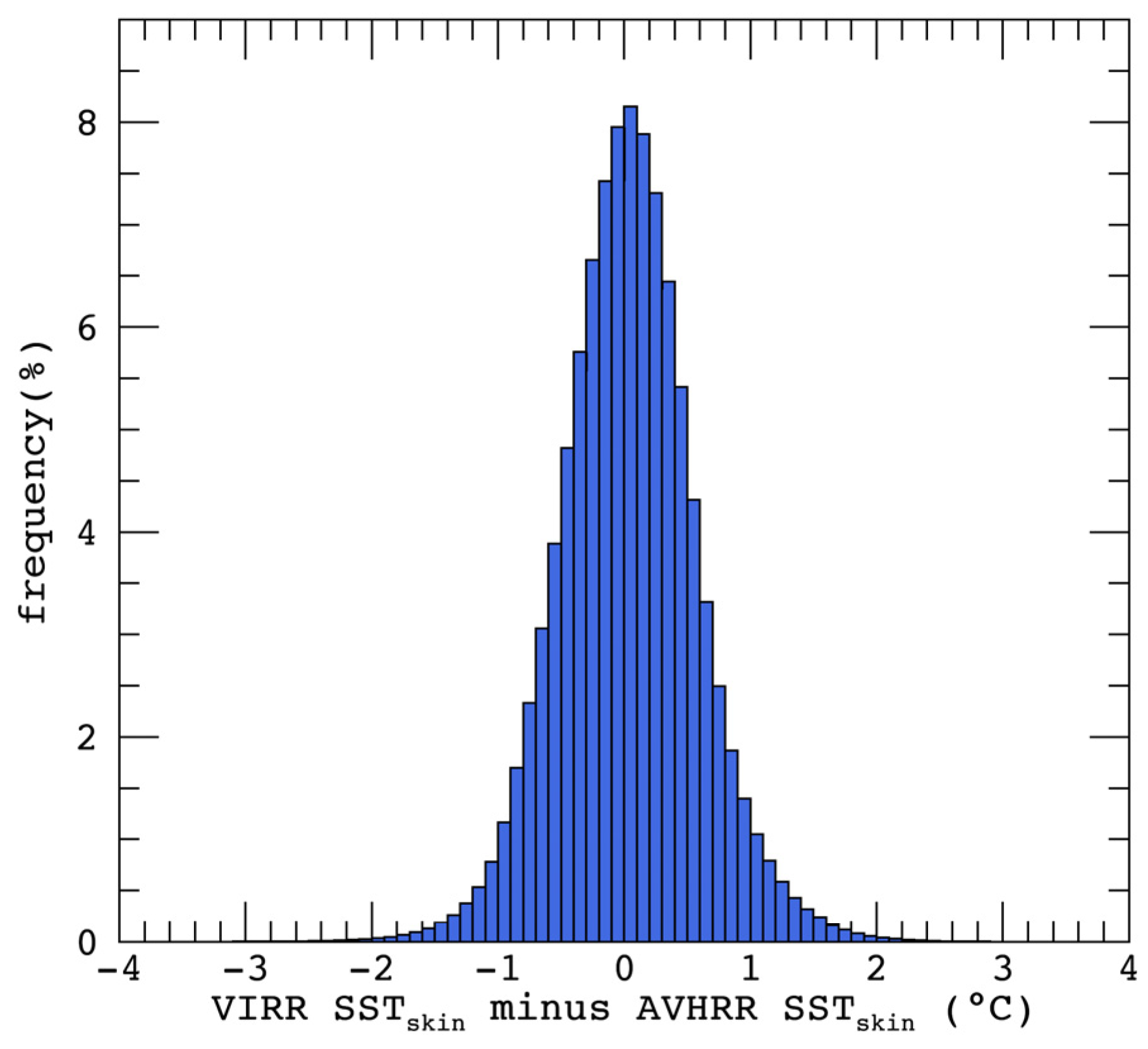
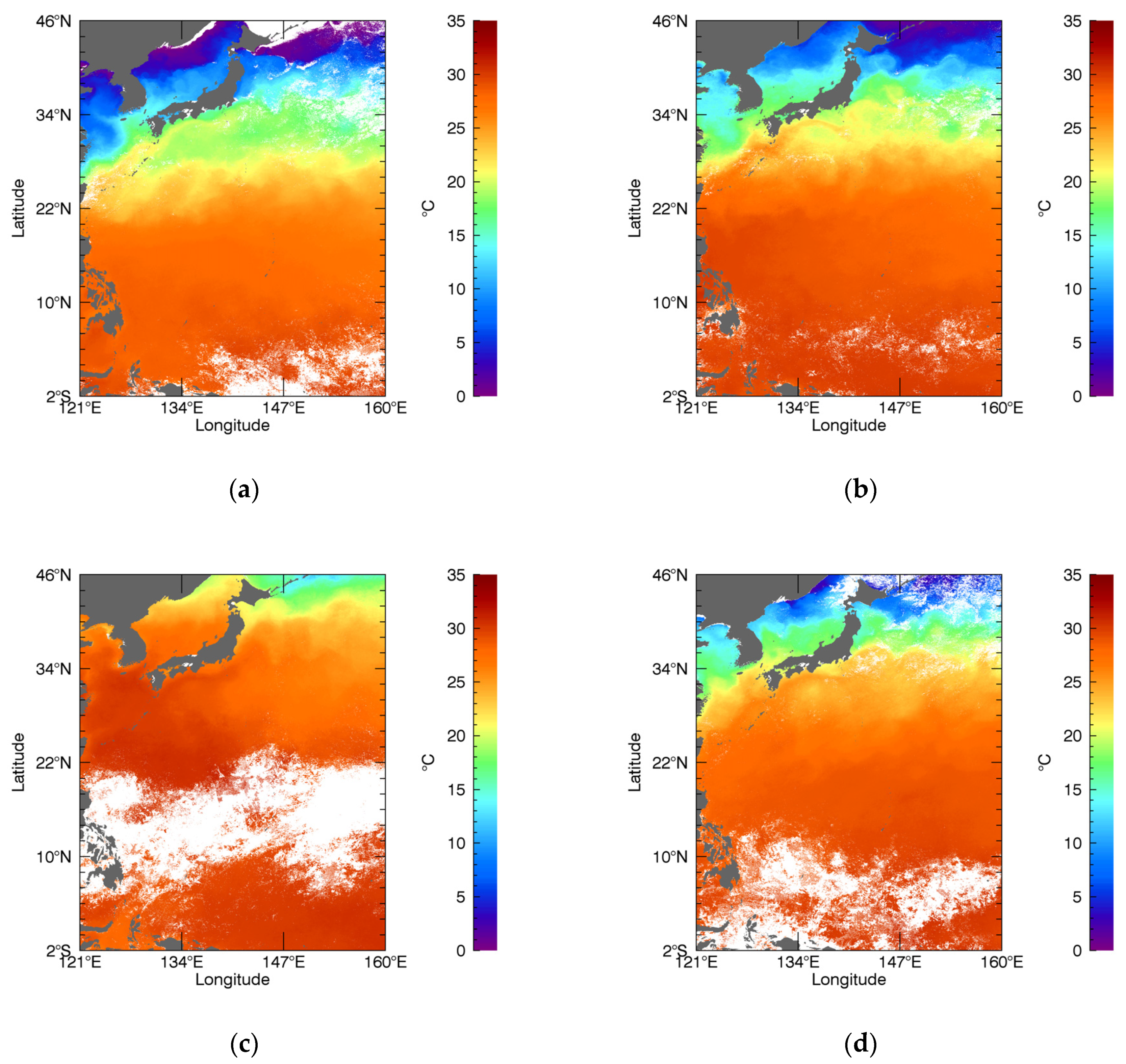
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barnett, T.P.; Graham, N.; Pazan, S.; White, W.; Latif, M.; Flügel, M. ENSO and ENSO-related Predictability. Part I: Prediction of Equatorial Pacific Sea Surface Temperature with a Hybrid Coupled Ocean–Atmosphere Model. J. Clim. 1993, 6, 1545–1566. [Google Scholar] [CrossRef] [Green Version]
- Dai, A. Future Warming Patterns Linked to Today’s Climate Variability. Sci. Rep. 2016, 6, 19110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ward, M.N.; Folland, C.K. Prediction of seasonal rainfall in the north nordeste of Brazil using eigenvectors of sea-surface temperature. Int. J. Climatol. 1991, 11, 711–743. [Google Scholar] [CrossRef]
- Aydoğdu, A.; Pinardi, N.; Pistoia, J.; Martinelli, M.; Belardinelli, A.; Sparnocchia, S. Assimilation experiments for the Fishery Observing System in the Adriatic Sea. J. Mar. Syst. 2016, 162, 126–136. [Google Scholar] [CrossRef]
- Harries, J.E.; Llewellyn-Jones, D.T.; Minnett, P.J.; Saunders, R.W.; Zavody, A.M.; Wadhams, P.; Taylor, P.K.; Houghton, J.T. Observations of Sea-Surface Temperature for Climate Research and Discussion. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1983, 309, 381–395. [Google Scholar]
- Ohring, G.; Wielicki, B.; Spencer, R. Satellite Instrument Calibration for Measuring Global Climate Change: Report of a Workshop. Bull. Am. Meteorol. Soc. 2004, 86, 1303–1313. [Google Scholar] [CrossRef]
- Casey, K.S.; Brandon, T.B.; Cornillon, P.; Evans, R. The Past, Present, and Future of the AVHRR Pathfinder SST Program. In Oceanography from Space; Springer: Dordrecht, The Netherland, 2010; pp. 273–287. [Google Scholar] [CrossRef]
- Borgne, P.L.; Legendre, G.; Marsouin, A. Operational SST Retrieval from Metop/AVHRR. In Proceedings of the 2007 EUMETSAT Conference, Amsterdam, The Netherlands, 24–28 September 2007. [Google Scholar]
- Minnett, P.J.; Brown, O.B.; Evans, R.H.; Key, E.L.; Kearns, E.J.; Kilpatrick, K.; Kumar, A.; Maillet, K.A.; Szczodrak, G. Sea-surface temperature measurements from the Moderate-Resolution Imaging Spectroradiometer (MODIS) on Aqua and Terra. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004. [Google Scholar]
- Gentemann, C.L. Three way validation of MODIS and AMSR-E sea surface temperatures. J. Geophys. Res. Ocean. 2014, 119, 2583–2598. [Google Scholar] [CrossRef]
- Godin, R. Joint Polar Satellite System (JPSS) Operational Algorithm Description (OAD) Document for VIIRS Sea Surface Temperature (SST) Environmental Data Record (EDR) Software; National Polar-Orbiting Operational Environmental Satellite System: Washington, DC, USA, 2017. [Google Scholar]
- Dash, P.; Ignatov, A.; Kihai, Y.; Sapper, J. The SST quality monitor (SQUAM). J. Atmos. Ocean. Technol. 2010, 27, 1899–1917. [Google Scholar] [CrossRef]
- Petrenko, B.; Ignatov, A.; Kihai, Y.; Stroup, J.; Dash, P. Evaluation and selection of SST regression algorithms for JPSS VIIRS. J. Geophys. Res. Atmos. 2014, 119, 4580–4599. [Google Scholar] [CrossRef]
- Tsamalis, C.; Saunders, R. Quality Assessment of Sea Surface Temperature from ATSRs of the Climate Change Initiative (Phase 1). Remote Sens. 2018, 10, 497. [Google Scholar] [CrossRef] [Green Version]
- Luo, B.; Minnett, P.J.; Szczodrak, M.; Kilpatrick, K.; Izaguirre, M. Validation of Sentinel-3A SLSTR derived Sea-Surface Skin Temperatures with those of the shipborne M-AERI. Remote Sens. Environ. 2020, 244, 111826. [Google Scholar] [CrossRef]
- Martin, S. An Introduction to Ocean Remote Sensing; Cambridge University Press: Cambridge, UK, 2014; p. 8. [Google Scholar]
- Wang, S.; Cui, P.; Zhang, P.; Ran, M.; Lu, F.; Wang, W. FY-3C/VIRR SST algorithm and cal/val activities at NSMC/CMA. SPIE Proc. 2014, 9261, 92610G. [Google Scholar] [CrossRef]
- Wang, S.J.; Cui, P.; Zhang, P.; Yang, Z.D.; Ran, M.N.; Xiu-Qing, H.U.; Feng, L.U.; Liu, J. Progress of VIRR Sea Surface Temperature Product of FY-3 Satellite. Aerospace Shanghai 2017, 34, 79–84. [Google Scholar]
- Wang, S.J.; Cui, P.; Zhang, P.; Yang, Z.D.; Xiu-Qing, H.U.; Ran, M.N.; Liu, J.; Lin, M.Y.; Qiu, H. FY-3C/VIRR SST Sea Surface Temperature Products and Quality Validation. J. Appl. Meteorol. Sci. 2020, 31, 729–739. [Google Scholar] [CrossRef]
- Yang, H.; Wang, S.J.; Liu, M.K.; Guan, L. Evaluation of sea surface temperature from FY-3C/VIRR observations in the Northwest Pacific. Period. Ocean. China 2020, 50, 151–159. [Google Scholar] [CrossRef]
- Wong, E.W.; Minnett, P.J. The Response of the Ocean Thermal Skin Layer to Variations in Incident Infrared Radiation. J. Geophys. Res. Ocean. 2018, 123, 2475–2493. [Google Scholar] [CrossRef]
- Soloviev, A.V.; Lukas, R. The Near-Surface Layer of the Ocean: Structure, Dynamics, and Applications, 2nd ed.; Springer: Dordrecht, The Netherland, 2014; p. 71. [Google Scholar]
- Minnett, P.J.; Kaiser-Weiss, A.K. Group for High Resolution Sea-Surface Temperature Discussion Document: Near-Surface Oceanic Temperature Gradients. 2012. Available online: https://www.ghrsst.org/wp-content/uploads/2021/04/SSTDefinitionsDiscussion.pdf (accessed on 6 September 2020).
- Merchant, C.J.; Le Borgne, P.; Marsouin, A.; Roquet, H. Optimal estimation of sea surface temperature from split-window observations. Remote Sens. Environ. 2008, 112, 2469–2484. [Google Scholar] [CrossRef]
- Fengyun Satellite Remote Sensing Data Service Network. Available online: http://satellite.nsmc.org.cn/PortalSite/StaticContent/DeviceIntro_FY3_VIRR.aspx (accessed on 13 February 2019).
- NASA MODIS. Available online: https://modis.gsfc.nasa.gov/about/specifications.php (accessed on 6 June 2020).
- Merchant, C.J.; Embury, O.; Bulgin, C.E.; Block, T.; Corlett, G.K.; Fiedler, E.; Good, S.A.; Mittaz, J.; Rayner, N.A.; Berry, D.; et al. Satellite-based time-series of sea-surface temperature since 1981 for climate applications. Sci. Data 2019, 6, 223. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Ignatov, A. In situ SST Quality Monitor (iQuam). J. Atmos. Ocean. Technol. 2014, 31, 164–180. [Google Scholar] [CrossRef]
- Berrisford, P.; Dee, D.P.; Fielding, M.; Fuentes, M.; Kållberg, P.W.; Kobayashi, S.; Uppala, S. The ERA-Interim Archive; ECMWF: Reading, UK, 2009; p. 16. [Google Scholar]
- Xiong, X.; Chiang, K.; Sun, J.; Barnes, W.L.; Guenther, B.; Salomonson, V.V. NASA EOS Terra and Aqua MODIS on-orbit performance. Adv. Space Res. 2009, 43, 413–422. [Google Scholar] [CrossRef]
- Qin, Y.; McVicar, T.R. Spectral band unification and inter-calibration of Himawari AHI with MODIS and VIIRS: Constructing virtual dual-view remote sensors from geostationary and low-Earth-orbiting sensors. Remote Sens. Environ. 2018, 209, 540–550. [Google Scholar] [CrossRef]
- Voss, S.; Merchant, C.; Maccallum, S. Generalized Bayesian Cloud Screening (GBCS); School of Geosciences: Edinburgh, UK, 2008. [Google Scholar]
- SST CCI Auxiliary Datasets. Available online: https://zenodo.org/record/2586714#.YGWWWa8zaUk (accessed on 7 April 2021).
- Merchant, C.J.; Harris, A.R.; Maturi, E.; Maccallum, S. Probabilistic physically based cloud screening of satellite infrared imagery for operational sea surface temperature retrieval. Q. J. R. Meteorol. Soc. 2005, 131, 2735–2755. [Google Scholar] [CrossRef] [Green Version]
- Merchant, C.J.; Le Borgne, P.; Roquet, H.; Marsouin, A. Sea surface temperature from a geostationary satellite by optimal estimation. Remote Sens. Environ. 2009, 113, 445–457. [Google Scholar] [CrossRef]
- Merchant, C.J.; Le Borgne, P.; Roquet, H.; Legendre, G. Extended optimal estimation techniques for sea surface temperature from the Spinning Enhanced Visible and Infra-Red Imager (SEVIRI). Remote Sens. Environ. 2013, 131, 287–297. [Google Scholar] [CrossRef]
- Donlon, C.; Minnett, P.; Gentemann, C.; Nightingale, T.; Barton, I.; Ward, B.; Murray, J. Toward Improved Validation of Satellite Sea Surface Skin Temperature Measurements for Climate Research. J. Clim. 2002, 14, 353–369. [Google Scholar] [CrossRef] [Green Version]
- Minnett, P.J.; Alvera-Azcárate, A.; Chin, T.M. Half a century of satellite remote sensing of sea-surface temperature. Remote Sens. Environ. 2019, 233, 111366. [Google Scholar] [CrossRef]
| Channel | Band Range (μm) | Noise Equivalent Reflectivity ρ(%) Noise Equivalent Temperature Difference (300 K) | Dynamic Range |
|---|---|---|---|
| 1 | 0.58–0.68 | 0.10% | 0–100% |
| 2 | 0.84–0.89 | 0.10% | 0–100% |
| 3 | 3.55–3.93 | 0.3 K | 180–350 K |
| 4 | 10.3–11.3 | 0.2 K | 180–330 K |
| 5 | 11.5–12.5 | 0.2 K | 180–330 K |
| 6 | 1.55–1.64 | 0.15% | 0–90% |
| 7 | 0.43–0.48 | 0.05% | 0–50% |
| 8 | 0.48–0.53 | 0.05% | 0–50% |
| 9 | 0.53–0.58 | 0.05% | 0–50% |
| 10 | 1.325–1.395 | 0.19% | 0–90% |
| 11 μm | 12 μm | ||||||
| Mean (K) | Std Dev (K) | R | Mean (K) | Std Dev (K) | R | Number | |
| D | −0.31 | 0.10 | 0.9999 | −0.97 | 0.15 | 0.9999 | 411,100 |
| N | −0.33 | 0.10 | 0.9999 | −0.86 | 0.21 | 0.9997 | 397,902 |
| 11 μm | 12 μm | ||||||
| Mean (K) | Std Dev (K) | R | Mean (K) | Std Dev (K) | R | Number | |
| D | −0.93 | 0.27 | 0.9989 | −0.53 | 0.31 | 0.9985 | 411,100 |
| N | 0.13 | 0.28 | 0.9991 | 0.44 | 0.32 | 0.9989 | 397,902 |
| 11 μm | 12 μm | ||||||
| Mean (K) | Std Dev (K) | R | Mean (K) | Std Dev (K) | R | Number | |
| D | −0.31 | 0.25 | 0.9990 | −0.97 | 0.32 | 0.9985 | 411,100 |
| N | −0.34 | 0.25 | 0.9993 | −0.86 | 0.34 | 0.9987 | 397,902 |
| 11 μm | 12 μm | ||||||
| Mean (K) | Std Dev (K) | R | Mean (K) | Std Dev (K) | R | Number | |
| D | 0.00 | 0.27 | 0.9989 | 0.00 | 0.29 | 0.9991 | 411,100 |
| N | −0.01 | 0.28 | 0.9985 | 0.01 | 0.28 | 0.9989 | 397,902 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Liu, M.; Wang, S.; Qu, L.; Guan, L. Sea Surface Skin Temperature Retrieval from FY-3C/VIRR. Remote Sens. 2022, 14, 1451. https://doi.org/10.3390/rs14061451
Li Z, Liu M, Wang S, Qu L, Guan L. Sea Surface Skin Temperature Retrieval from FY-3C/VIRR. Remote Sensing. 2022; 14(6):1451. https://doi.org/10.3390/rs14061451
Chicago/Turabian StyleLi, Zhuomin, Mingkun Liu, Sujuan Wang, Liqin Qu, and Lei Guan. 2022. "Sea Surface Skin Temperature Retrieval from FY-3C/VIRR" Remote Sensing 14, no. 6: 1451. https://doi.org/10.3390/rs14061451
APA StyleLi, Z., Liu, M., Wang, S., Qu, L., & Guan, L. (2022). Sea Surface Skin Temperature Retrieval from FY-3C/VIRR. Remote Sensing, 14(6), 1451. https://doi.org/10.3390/rs14061451






