An Algorithm to Bias-Correct and Transform Arctic SMAP-Derived Skin Salinities into Bulk Surface Salinities
Abstract
1. Introduction
2. Data and Methods
2.1. Satellite Data
2.2. In-Situ Data
2.3. OAFlux Air-Sea Forcing/Flux Data
2.4. Generalized Additive Model
3. Results
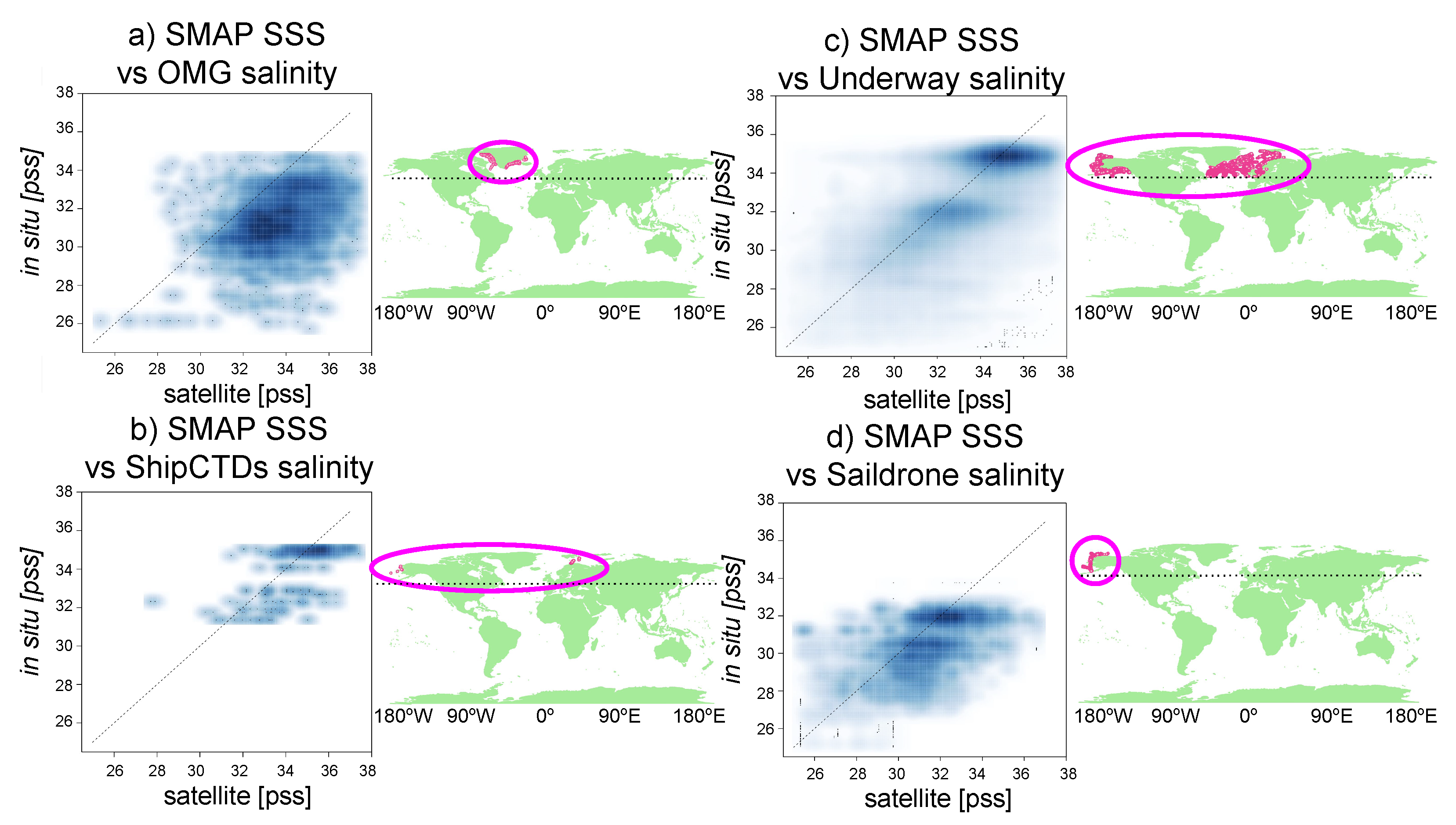
3.1. Satellite SSS and In-Situ Salinity Comparisons
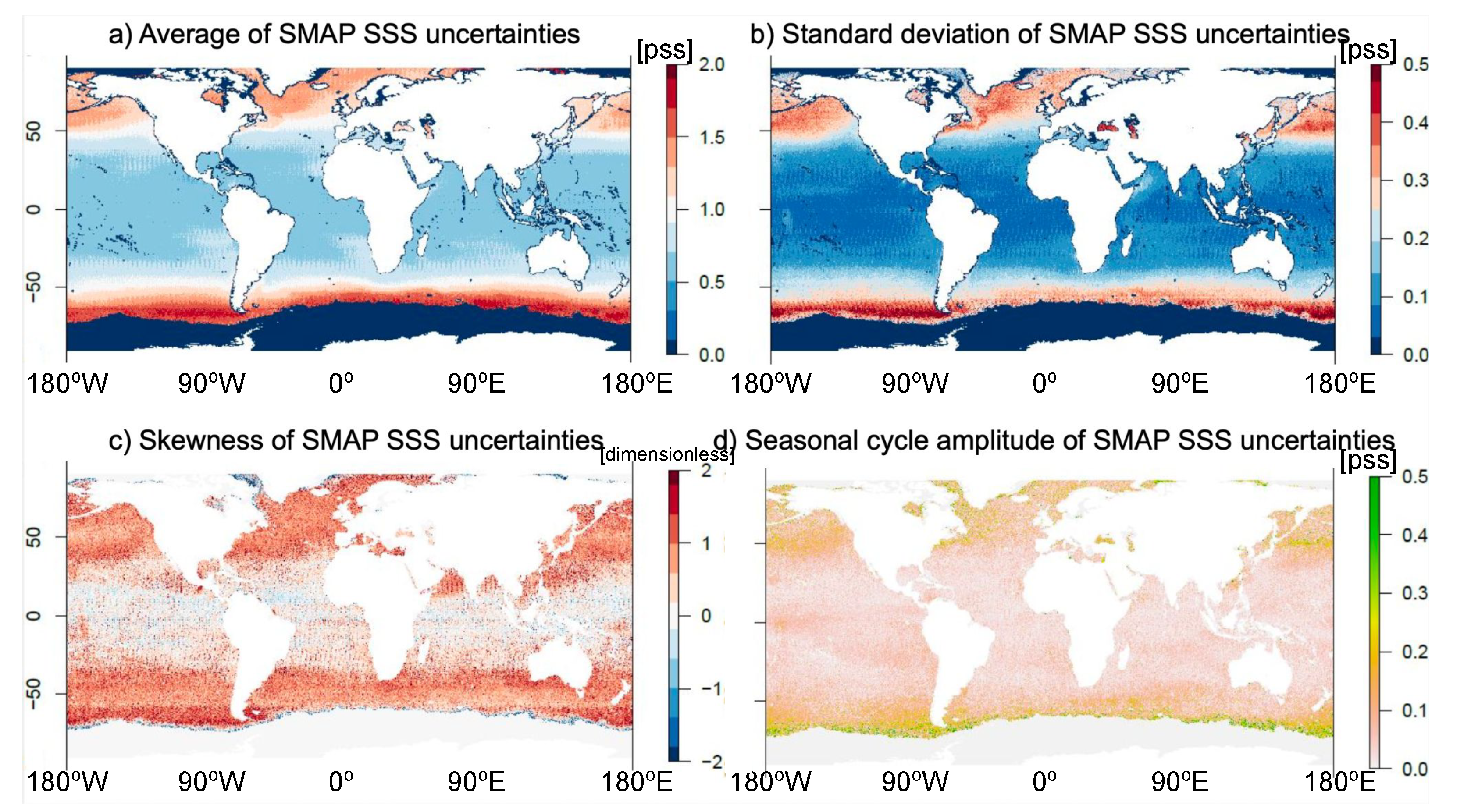
3.2. Temporal Statistics of Arctic SSS
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, T. Consistency of Aquarius sea surface salinity with Argo products on various spatial and temporal scales. Geophys. Res. Lett. 2016, 43, 3857–3864. [Google Scholar] [CrossRef]
- Reul, N.; Grodsky, S.A.; Arias, M.; Boutin, J.; Catany, R.; Chapron, B.; D’Amico, F.; Dinnat, E.; Donlon, C.; Fore, A.; et al. Sea surface salinity estimates from spaceborne L-band radiometers: An overview of the first decade of observation (2010–2019). Remote Sens. Environ. 2020, 242, 111769. [Google Scholar] [CrossRef]
- Tang, W.; Yueh, S.; Yang, D.; Fore, A.; Hayashi, A.; Lee, T.; Fournier, S.; Holt, B. The potential and challenges of using soil moisture active passive (SMAP) sea surface salinity to monitor Arctic ocean freshwater changes. Remote Sens. 2018, 10, 869. [Google Scholar] [CrossRef]
- Yu, L. Variability and uncertainty of satellite sea surface salinity in the subpolar North Atlantic (2010–2019). Remote Sens. 2020, 12, 2092. [Google Scholar] [CrossRef]
- Supply, A.; Boutina, J.; Vergely, J.-L.; Kolodziejczyk, N.; Reverdin, G.; Reul, N.; Tarasenko, A. New insights into SMOS sea surface salinity retrievals in the Arctic Ocean. Remote Sens. Environ. 2020, 249, 112027. [Google Scholar] [CrossRef]
- Dong, S.; Volkov, D.; Goni, G.; Lumpkin, R.; Foltz, G.R. Near-surface salinity and temperature structure observed with dual-sensor drifters in the subtropical South Pacific. J. Geophys. Res. Oceans 2017, 122, 5952–5969. [Google Scholar] [CrossRef]
- Anderson, J.E.; Riser, S.C. Near-surface variability of temperature and salinity in the near-tropical ocean: Observations from profiling floats. J. Geophys. Res. Oceans 2014, 119, 7433–7448. [Google Scholar] [CrossRef]
- Bingham, F.M.; Tsontos, V.; de Charon, A.; Lauter, C.J.; Taylor, L. The SPURS-2 eastern tropical Pacific field campaign data collection. Oceanography 2019, 32, 142–149. [Google Scholar] [CrossRef]
- Saunders, P. The temperature at the ocean-air interface. J. Atmos. Sci. 1967, 24, 267–273. [Google Scholar] [CrossRef]
- Yu, L. On sea surface salinity skin effect induced by evaporation and implications for remote sensing of ocean salinity. J. Phys. Oceanogr. 2010, 40, 85–102. [Google Scholar] [CrossRef]
- Polyakov, I.V.; Pnyushkov, A.V.; Alkire, M.B.; Ashik, I.M.; Baumann, T.M.; Carmack, E.C.; Coszczko, I.; Guthrie, J.; Ivanov, V.V.; Kanzow, T.; et al. Greater role for Atlantic inflows on sea-ice loss in the Eurasian Basin of the Arctic Ocean. Science 2017, 356, 285–291. [Google Scholar] [CrossRef] [PubMed]
- Polyakov, I.V.; Rippeth, T.P.; Fer, I.; Alkire, M.B.; Baumann, T.M.; Carmack, E.C.; Ingvaldsen, R.; Ivanov, V.V.; Janout, M.; Lind, S.; et al. Weakening of cold halocline layer exposes sea ice to oceanic heat in the eastern Arctic Ocean. J. Clim. 2020, 33, 8107–8123. [Google Scholar] [CrossRef]
- Davis, P.E.D.; Lique, C.; Johnson, H.L.; Guthrie, J.D. Competing effects of elevated vertical mixing and increased freshwater input on the stratification and sea ice cover in a changing Arctic Ocean. J. Phys. Oceanogr. 2016, 46, 1531–1553. [Google Scholar] [CrossRef]
- Halloran, P.R.; Hall, I.R.; Menary, M.; Reynolds, D.J.; Scourse, J.D.; Screen, J.A.; Bozzo, A.; Dunstone, N.; Phipps, S.; Schurer, A.P.; et al. Natural drivers of multidecadal Arctic sea ice variability over the last millennium. Nat. Sci. Rep. 2020, 10, 688. [Google Scholar] [CrossRef] [PubMed]
- Jahn, A.; Holland, M.M. Implications of Arctic sea ice changes for North Atlantic deep convection and the meridional overturning circulation in CCSM4-CMIP5 simulations. Geophys. Res. Lett. 2013, 40, 1206–1211. [Google Scholar] [CrossRef]
- Liu, W.; Fedorov, A.; Sévellec, F. The mechanisms of the Atlantic meridional overturning circulation slowdown induced by arctic sea ice decline. J. Clim. 2019, 32, 977–996. [Google Scholar] [CrossRef]
- Stouffer, R.J.; Yin, J.; Gregory, J.M.; Dixon, K.W.; Spelman, M.J.; Hurlin, W.; Weaver, A.J.; Eby, M.; Flato, G.M.; Hasumi, H.; et al. Investigating the causes of the response of the thermohaline circulation to past and future climate changes. J. Clim. 2006, 19, 1365–1387. [Google Scholar] [CrossRef]
- Doddridge, E.W.; Meneghello, G.; Marshall, J.; Scott, J.; Lique, C. A three-way balance in the Beaufort Gyre: The ice-ocean governor, wind stress, and eddy diffusivity. J. Geophys. Res. Ocean. 2019, 124, 3107–3124. [Google Scholar] [CrossRef]
- Haine, T.W.N. A conceptual model of polar overturning circulations. J. Phys. Oceanogr. 2021, 51, 727–744. [Google Scholar] [CrossRef]
- Jensen, M.F.; Nilsson, J.; Nisancioglu, K.H. The interaction between sea ice and salinity-dominated ocean circulation: Implications for halocline stability and rapid changes of sea ice cover. Clim. Dyn. 2021, 47, 3301–3317. [Google Scholar] [CrossRef]
- Meneghello, G.; Marshall, J.C.; Timmermans, M.-L.; Scott, J. Observations of seasonal upwelling and downwelling in the Beaufort Sea mediated by sea ice. J. Phys. Oceanogr. 2018, 48, 795–805. [Google Scholar] [CrossRef]
- Proshutinsky, A.; Krishfield, R.; Timmermans, M.-L.; Toole, J.; Carmack, E.; McLaughlin, F.; Williams, W.J.; Zimmermann, S.; Itoh, M.; Shimada, K. Beaufort Gyre freshwater reservoir: State and variability from observations. J. Geophys. Res. 2009, 114, C00A10. [Google Scholar] [CrossRef]
- Sedláček, J.; Knutti, R.; Martius, O.; Beyerle, U. Impact of a reduced Arctic sea ice cover on ocean and atmospheric properties. J. Clim. 2012, 25, 307–319. [Google Scholar] [CrossRef]
- Kolodziejczyk, N.; Hamon, M.; Boutin, J.; Vergely, J.-L.; Reverdin, G.; Supply, A.; Reul, N. Objective Analysis of SMOS and SMAP Sea Surface Salinity to Reduce Large-Scale and Time-Dependent Biases from Low to High Latitudes. J. Atmos. Ocean. Technol. 2021, 38, 405–421. [Google Scholar] [CrossRef]
- Mecklenburg, S.; Drusch, M.; Kaleschke, L.; Rodriguez-Fernandez, N.; Reul, N.; Kerr, Y.; Font, J.; Martin-Neira, M.; Oliva, R.; Daganzo-Eusebio, E.; et al. ESA’s Soil Moisture and Ocean Salinity mission: From science to operational applications. Remote Sens. Environ. 2016, 180, 3–18. [Google Scholar] [CrossRef]
- Vinogradova, N.; Lee, T.; Boutin, J.; Drushka, K.; Fournier, S.; Sabia, R.; Stammer, D.; Bayler, E.; Reul, N.; Arnold, G.; et al. Satellite salinity observing system: Recent discoveries and the way forward. Front. Mar. Sci. 2019, 6, 243. [Google Scholar] [CrossRef]
- Fore, A.G.; Yueh, S.H.; Tang, W.; Stiles, B.W.; Hayashi, A.K. Combined Active/Passive Retrievals of Ocean Vector Wind and Sea Surface Salinity With SMAP. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7396–7404. [Google Scholar] [CrossRef]
- Cole, S.T.; Wortham, C.; Kunze, E.; Owens, W.B. Eddy stirring and horizontal diffusivity from Argo float observations: Geographic and depth variability. Geophys. Res. Lett. 2015, 42, 3989–3997. [Google Scholar] [CrossRef]
- Mordy, C.W.; Cokelet, E.D.; De Robertis, A.; Jenkins, R.; Kuhn, C.E.; Lawrence-Slavas, N.; Berchok, C.L.; Crance, J.L.; Sterling, J.T.; Cross, J.N.; et al. Advances in ecosystem research: Saildrone surveys of oceanography, fish, and marine mammals in the Bering Sea. Oceanography 2017, 30, 113–115. [Google Scholar] [CrossRef]
- Fenty, I.; Willis, J.K.; Khazendar, A.; Dinardo, S.; Forsberg, R.; Fukumori, I.; Holland, D.; Jakobsson, M.; Moller, D.; Morison, J.; et al. Oceans Melting Greenland: Early results from NASA’s ocean-ice mission in Greenland. Oceanography 2016, 29, 72–83. [Google Scholar] [CrossRef]
- Yu, L.; Jin, X.; Weller, A. Multidecade Global Flux Datasets from the Objectively Analyzed Air-Sea Fluxes (OAFlux) Project: Latent and Sensible Heat Fluxes, Ocean Evaporation, and Related Surface Meteorological Variables; WHOI OAFlux Project Technical Report (OA-2008-01); WHOI OAFlux: Falmouth, MA, USA, 2008. [Google Scholar]
- Yu, L.; Jin, X. Satellite-Based Global Ocean Vector Wind Analysis by the Objectively Analyzed Air-Sea Fluxes (OAFlux) Project: Establishing Consistent Vector Wind Time Series from July 1987 Onward through Synergizing Microwave Radiometers and Scatterometers; WHOI OAFlux Project Technical Report; WHOI OAFlux: Falmouth, MA, USA, 2010. [Google Scholar]
- Yu, L.; Jin, X. Insights on the OAFlux ocean surface vector wind analysis merged from scatterometers and passive microwave radiometers (1987 onward). J. Geophys. Res. Ocean. 2014, 119, 5244–5269. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Jin, X.; Yu, L. Assessing high-resolution analysis of surface heat fluxes in the Gulf Stream region. J. Geophys. Res. Ocean. 2013, 118, 5353–5375. [Google Scholar] [CrossRef][Green Version]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Busalacchi, A.J.; Cheney, R.; Donguy, J.-R.; Gage, K.S.; Halpern, D.; Ji, M.; Julian, P.; Meyers, G.; Mitchum, G.T.; et al. The Tropical Ocean-Global Atmosphere observing system: A decade of progress. J. Geophys. Res. 1998, 103, 14169–14240. [Google Scholar] [CrossRef]
- Colbo, K.; Weller, R.A. The accuracy of the IMET sensor package in the subtropics. J. Atmos. Ocean. Technol. 2009, 26, 1867–1890. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Daley, R. Atmospheric Data Analysis; Cambridge Univ. Press: Cambridge, UK, 1991; 457p. [Google Scholar]
- Talagrand, O. Assimilation of observations, an introduction. J. Meteorol. Soc. Jpn. 1997, 75, 191–209. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin, Germany, 2001. [Google Scholar]
- McDougall, T.J.; Barker, P.M. Getting Started with TEOS-10 and the Gibbs Seawater (GSW) Oceanographic Toolbox; WG127; SCOR/IAPSO: Paris, France, 2011. [Google Scholar]
- Sharqawy, M.H.; Lienhard, V.J.H.; Zubair, S.M. Thermophysical properties of seawater: A review of existing correlations and data. Desalin. Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]
- Martínez, J.; Gabarró, C.; Turiel, A. Arctic Sea Surface Salinity L2 Orbits and L3 Maps (v.3.1) [Dataset]. DIGITAL.CSIC 2019. Available online: http://hdl.handle.net/10261/229624 (accessed on 1 January 2021).
- Olmedo, E.; Gabarró, C.; González-Gambau, V.; Martínez, J.; Ballabrera-Poy, J.; Turiel, A.; Portabella, M.; Fournier, S.; Lee, T. Seven years of SMOS sea surface salinity at high latitudes: Variability in Arctic and sub-Arctic regions. Remote Sens. 2018, 10, 1772. [Google Scholar] [CrossRef]
- Fournier, S.; Lee, T.; Wang, X.; Armitage, T.W.K.; Wang, O.; Fukumori, I.; Kwok, R. Sea surface salinity as a proxy for Arctic ocean freshwater changes. J. Geophys. Res. Ocean. 2020, 125, e2020JC016110. [Google Scholar] [CrossRef]
- Schanze, J.J.; Le Vine, D.M.; Dinnat, E.P.; Kao, H.-Y. Comparing satellite salinity retrievals with in-situ measurements: A recommendation for Aquarius and SMAP. Zenodo 2020. [Google Scholar] [CrossRef]
- Roquet, F.; Williams, G.; Hindell, M.A.; Harcourt, R.; McMahon, C.; Guinet, C.; Charrassin, J.-B.; Reverdin, G.; Boehme, L.; Lovell, P.; et al. A Southern Indian Ocean database of hydrographic profiles obtained with instrumented elephant seals. Nat. Sci. Data 2014, 1, 140028. [Google Scholar] [CrossRef] [PubMed]
- Treasure, A.M.; Roquet, F.; Ansorge, I.J.; Bester, M.N.; Boehme, L.; Bornemann, H.; Charrassin, J.-B.; Chevallier, D.; Costa, D.P.; Fedak, M.A.; et al. Marine mammals exploring the oceans pole to pole: A review of the MEOP consortium. Oceanography 2017, 30, 132–138. [Google Scholar] [CrossRef]
- Fournier, S.; Lee, T.; Tang, W.; Steele, M.; Olmedo, E. Evaluation and Intercomparison of SMOS, Aquarius, and SMAP Sea Surface Salinity Products in the Arctic Ocean. Remote Sens. 2019, 11, 3043. [Google Scholar] [CrossRef]
- Manucharyan, G.E.; Thompson, A.F. Submesoscale sea ice-ocean interactions in marginal ice zones. J. Geophys. Res. Ocean. 2017, 122, 9455–9475. [Google Scholar] [CrossRef]
- Brucker, L.; Dinnat, E.P.; Koenig, L.S. Weekly Gridded Aquarius L-band Radiometer/Scatterometer Observations and Salinity Retrievals Over the Polar Regions—Part 1: Product Description. Cryosphere 2014, 8, 905–913. [Google Scholar] [CrossRef]
- Brucker, L.; Dinnat, E.P.; Koenig, L.S. Weekly Gridded Aquarius L-band Radiometer/Scatterometer Observations and Salinity Retrievals Over the Polar Regions—Part 2: Initial Product Analysis. Cryosphere 2014, 8, 915–930. [Google Scholar] [CrossRef]
- Liu, C.; Liang, X.; Chambers, D.P.; Ponte, R.M. Global patterns of spatial and temporal variability in salinity from multiple gridded Argo products. J. Clim. 2020, 33, 8751–8766. [Google Scholar] [CrossRef]
- Meissner, T.; Manaster, A. SMAP salinity retrievals near the sea-ice edge using multi-channel AMSR2 brightness temperatures. Remote Sens. 2021, 13, 5120. [Google Scholar] [CrossRef] [PubMed]
- Gentemann, C.L.; Clayson, C.A.; Brown, S.; Lee, T.; Parfitt, R.; Farrar, J.T.; Bourassa, M.; Minnett, P.J.; Seo, H.; Gille, S.T.; et al. Fluxsat: Measuring the ocean–atmosphere turbulent exchange of heat and moisture from space. Remote Sens. 2020, 12, 1796. [Google Scholar] [CrossRef]





| Term | Description |
|---|---|
| Smoother functions for | |
| Tensor product of pairwise variables | |
| Satellite-derived SSS from | |
| t | Julian day relative to January 1 of 1970 |
| z | Depth of the in-situ observations |
| an empirical coefficient as in [10] | |
| Sensible heat flux from OAFlux [31] | |
| Latent heat flux from OAFlux [31] | |
| Sea-surface temperature in Celsius from OAFlux [31] | |
| Latent heat of evaporation calculated using TEOS-10 [45] | |
| Thermal expansion coefficient calculated using TEOS-10 [45] | |
| Haline contraction coefficient calculated using TEOS-10 [45] | |
| Specific heat of seawater calculated using TEOS-10 [45] | |
| is the kinematic viscosity of seawater | |
| p | Pressure |
| k | |
| thermal conductivity of seawater [46] (in W m K) | |
| g | m s is the acceleration due to gravity |
| wind stress from OAFlux [32] | |
| in-situ density calculated using TEOS-10 [45] | |
| is a function of the inverse wind stress | |
| E | Evaporation from OAFlux [31] |
| Near-surface humidity from OAFlux [31] | |
| bias correction, with proportionality constant [10]; | |
| is determined with the GAM |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trossman, D.; Bayler, E. An Algorithm to Bias-Correct and Transform Arctic SMAP-Derived Skin Salinities into Bulk Surface Salinities. Remote Sens. 2022, 14, 1418. https://doi.org/10.3390/rs14061418
Trossman D, Bayler E. An Algorithm to Bias-Correct and Transform Arctic SMAP-Derived Skin Salinities into Bulk Surface Salinities. Remote Sensing. 2022; 14(6):1418. https://doi.org/10.3390/rs14061418
Chicago/Turabian StyleTrossman, David, and Eric Bayler. 2022. "An Algorithm to Bias-Correct and Transform Arctic SMAP-Derived Skin Salinities into Bulk Surface Salinities" Remote Sensing 14, no. 6: 1418. https://doi.org/10.3390/rs14061418
APA StyleTrossman, D., & Bayler, E. (2022). An Algorithm to Bias-Correct and Transform Arctic SMAP-Derived Skin Salinities into Bulk Surface Salinities. Remote Sensing, 14(6), 1418. https://doi.org/10.3390/rs14061418






