Assessing Obukhov Length and Friction Velocity from Floating Lidar Observations: A Data Screening and Sensitivity Computation Approach
Abstract
:1. Introduction
2. Materials
3. Methods
3.1. Wind Notation Conventions
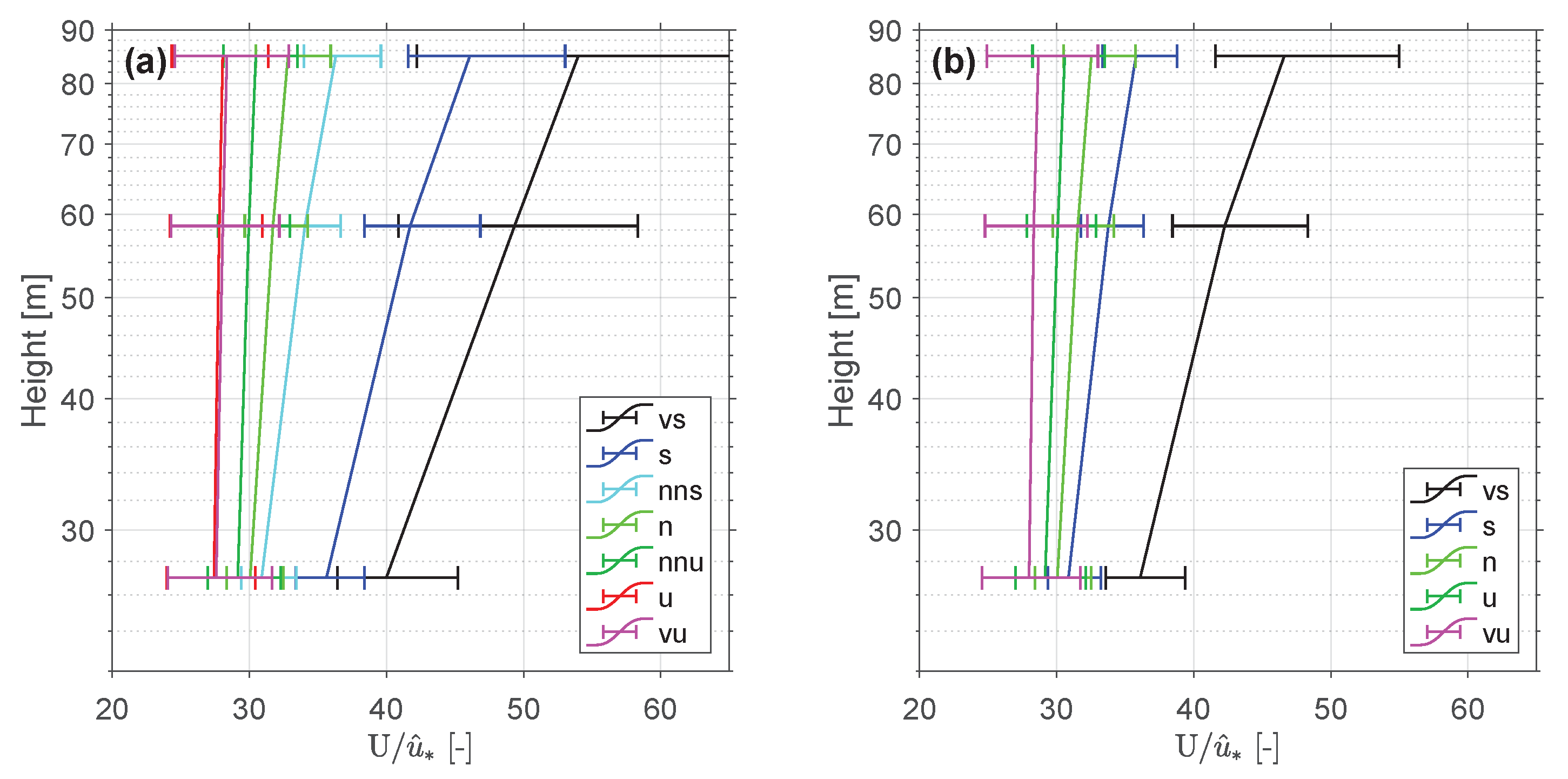
3.2. Surface-Layer theory
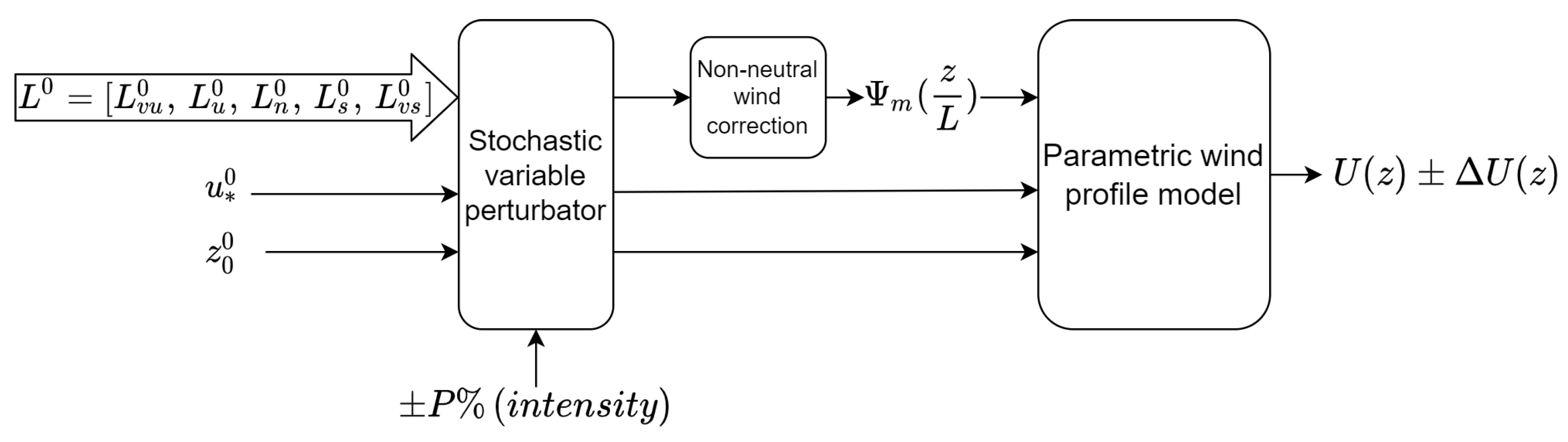
3.3. Parametric Wind Model Estimation
- m,
- m/s, and
- m.
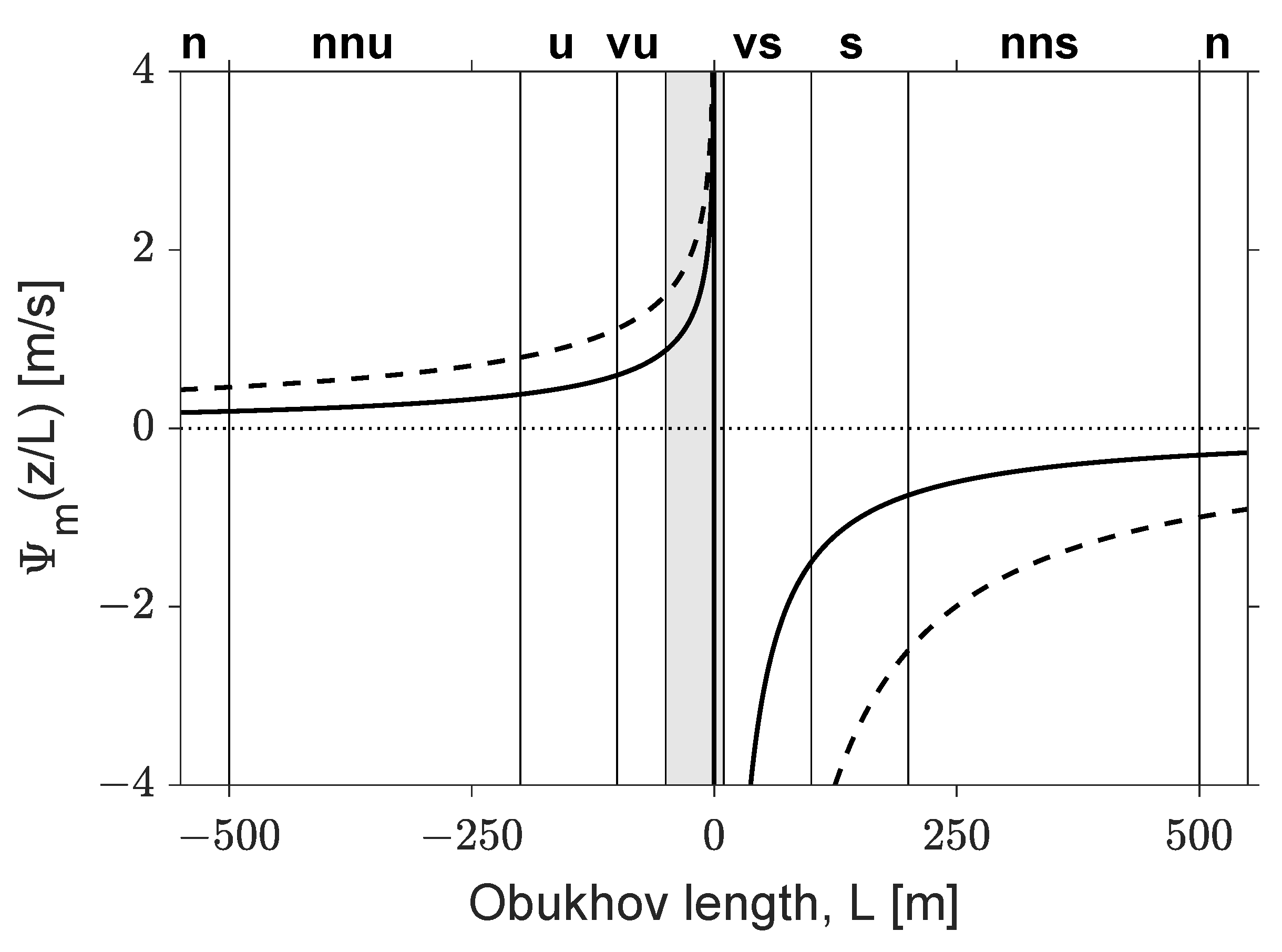
3.4. Reference Measurements: Atmospheric Stability
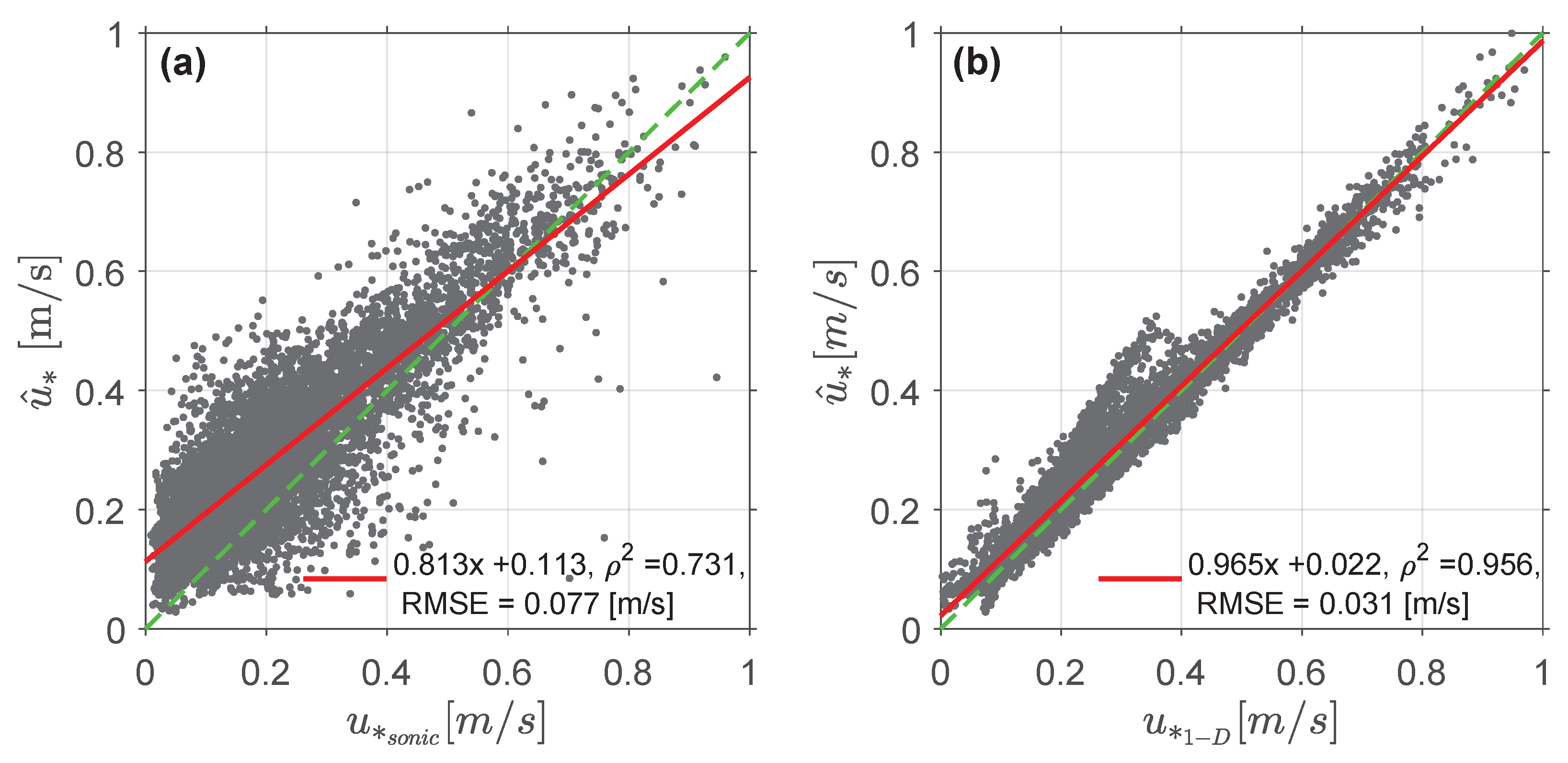
3.5. Reference Measurements: Friction Velocity
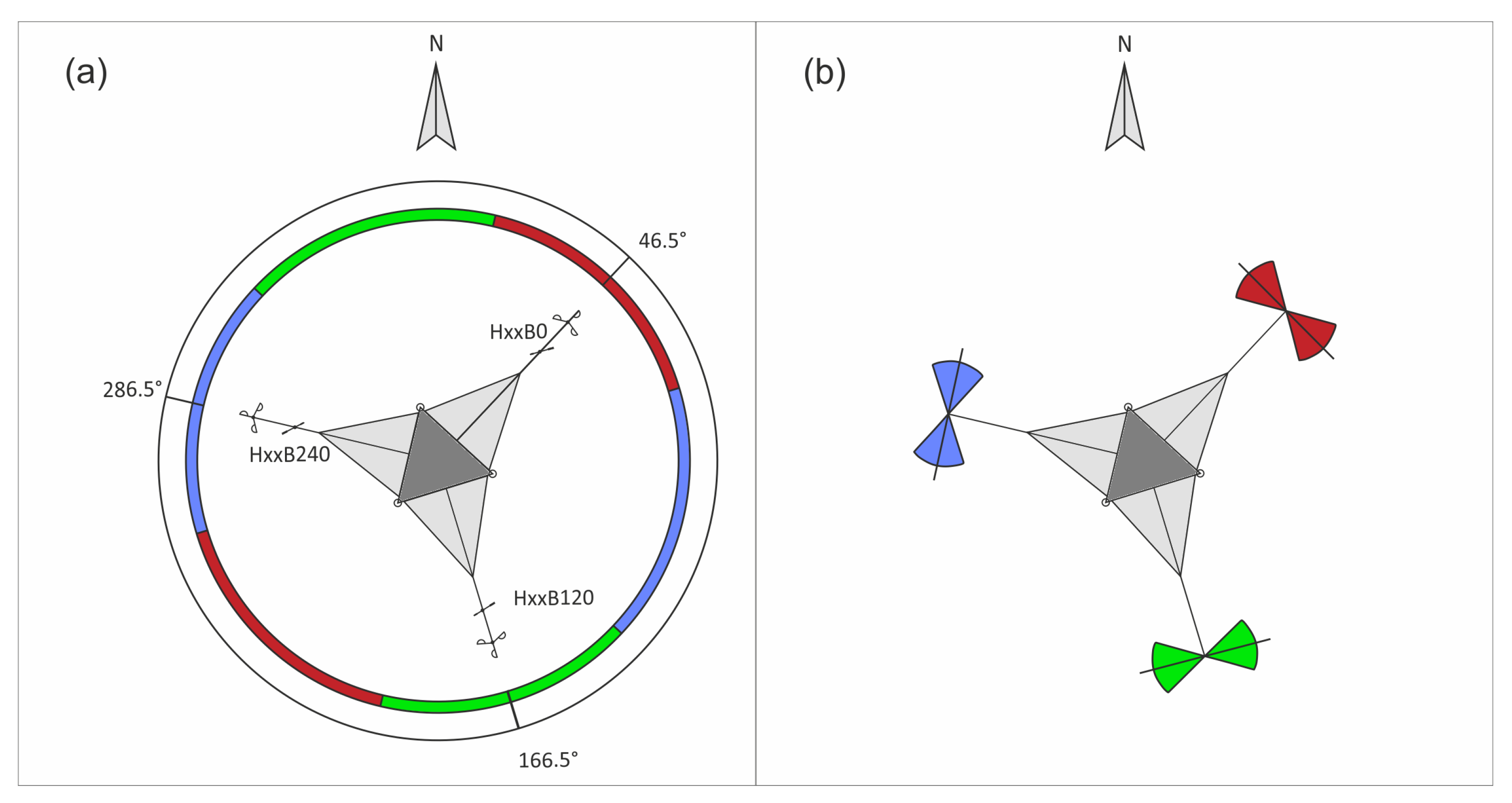
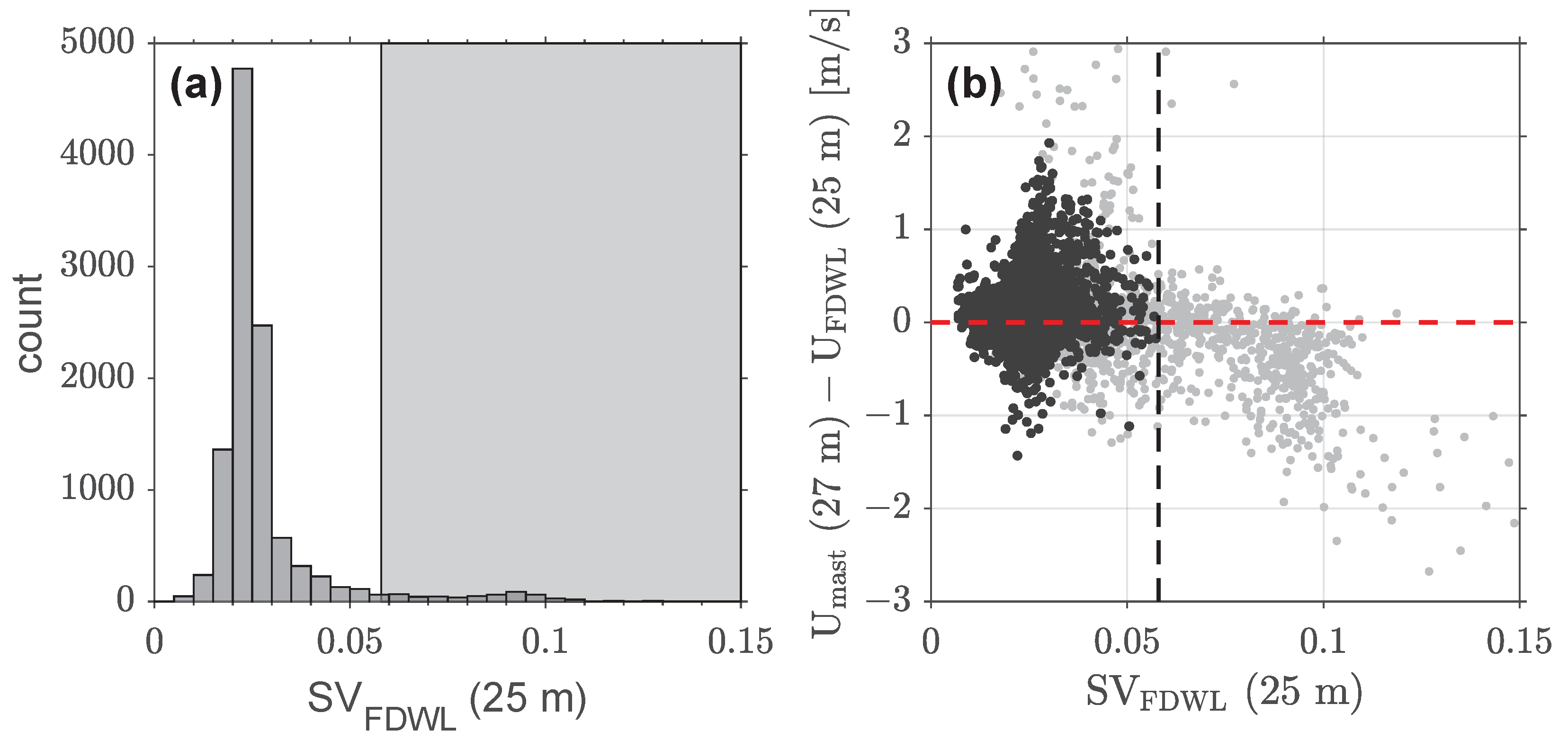
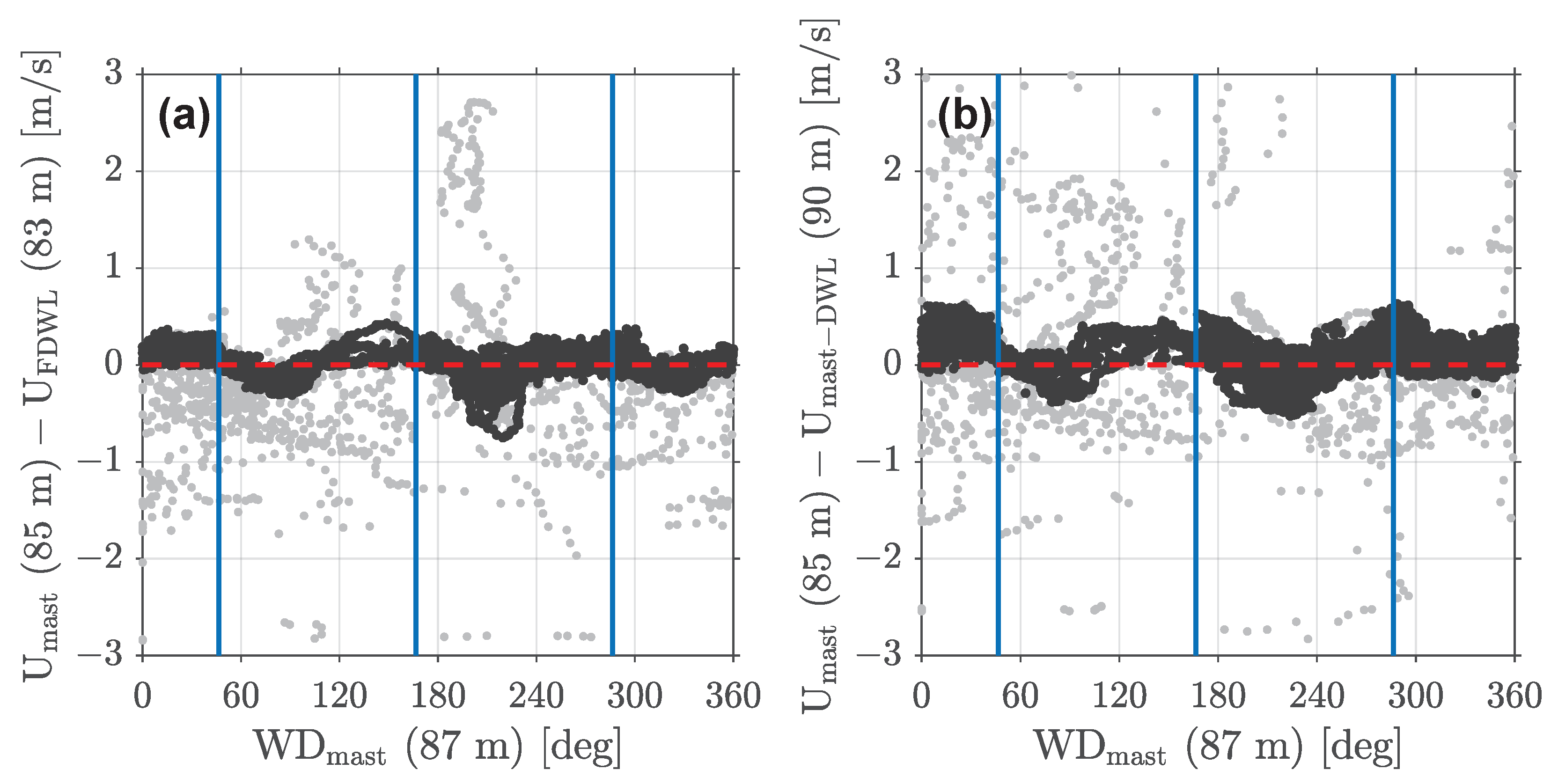
3.6. Data Screening
- If the MWD lay on the red crown, the TWD was computed as the mean WD between vanes HxxB240 and HxxB120,
- If (…) on the blue crown, (…) between vanes HxxB0 and HxxB120, and
- If (…) on the green crown, (…) between vanes HxxB240 and HxxB0.
- (i)
- HWS < 2 m/s or HWS > 70 m/s,
- (ii)
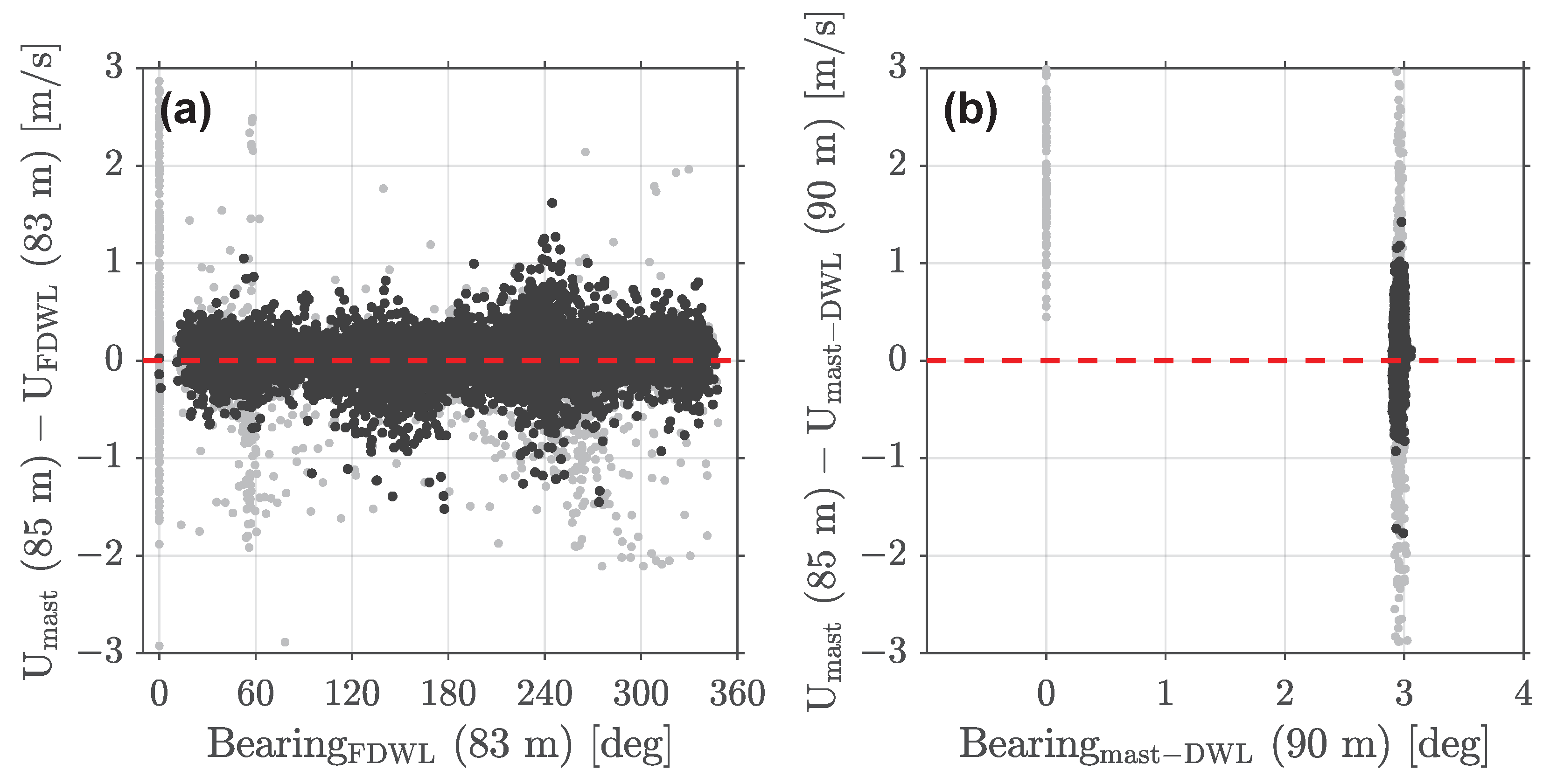
- bearing = 0 (FDWL compass issue, see Section 4.1), and
- (iii)
- 95th percentile spatial-variation threshold.
4. Results and Discussion
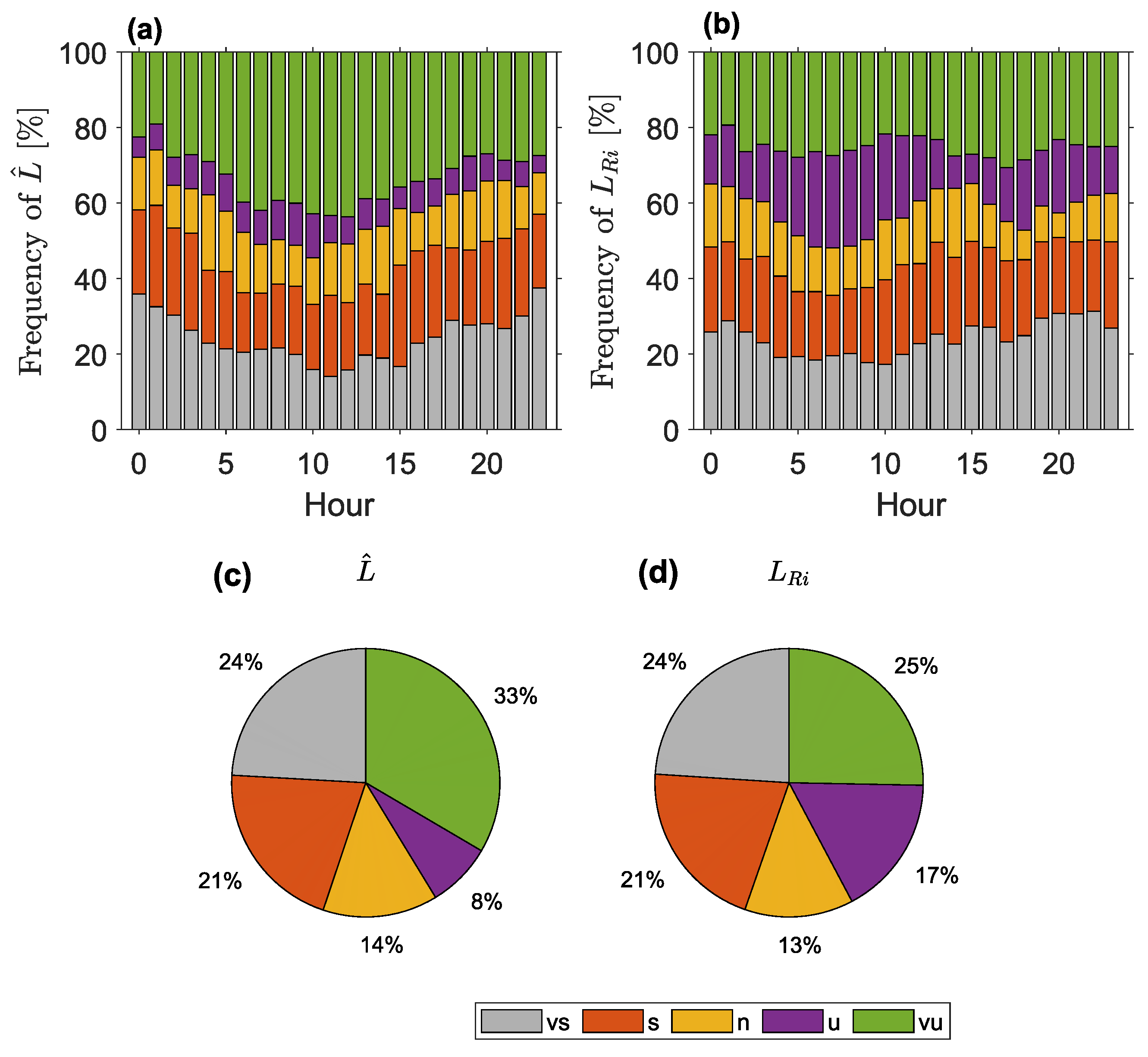
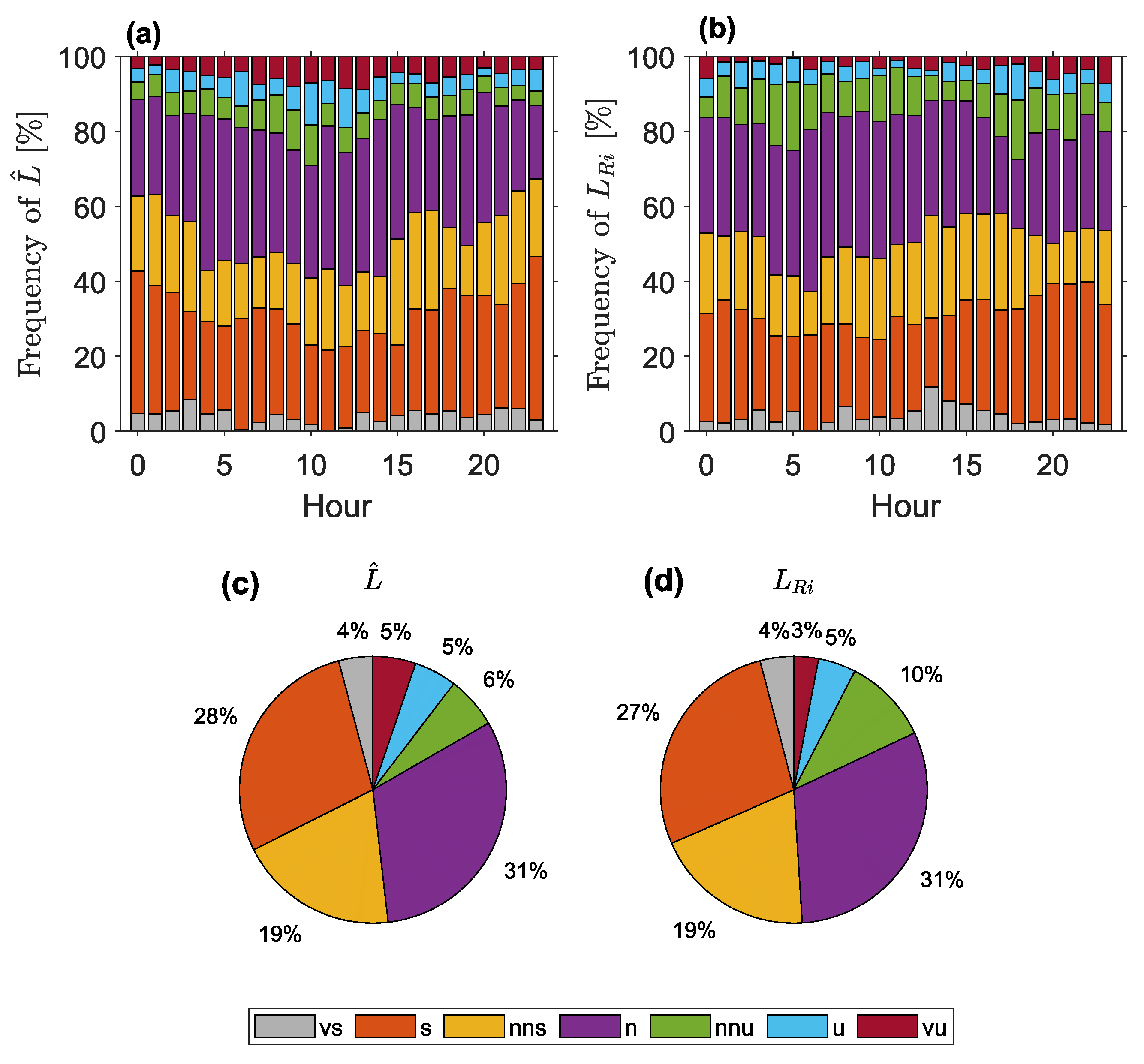
4.1. Data Screening and Quality Assurance
4.2. Sensitivity to the Wind Model Parameters
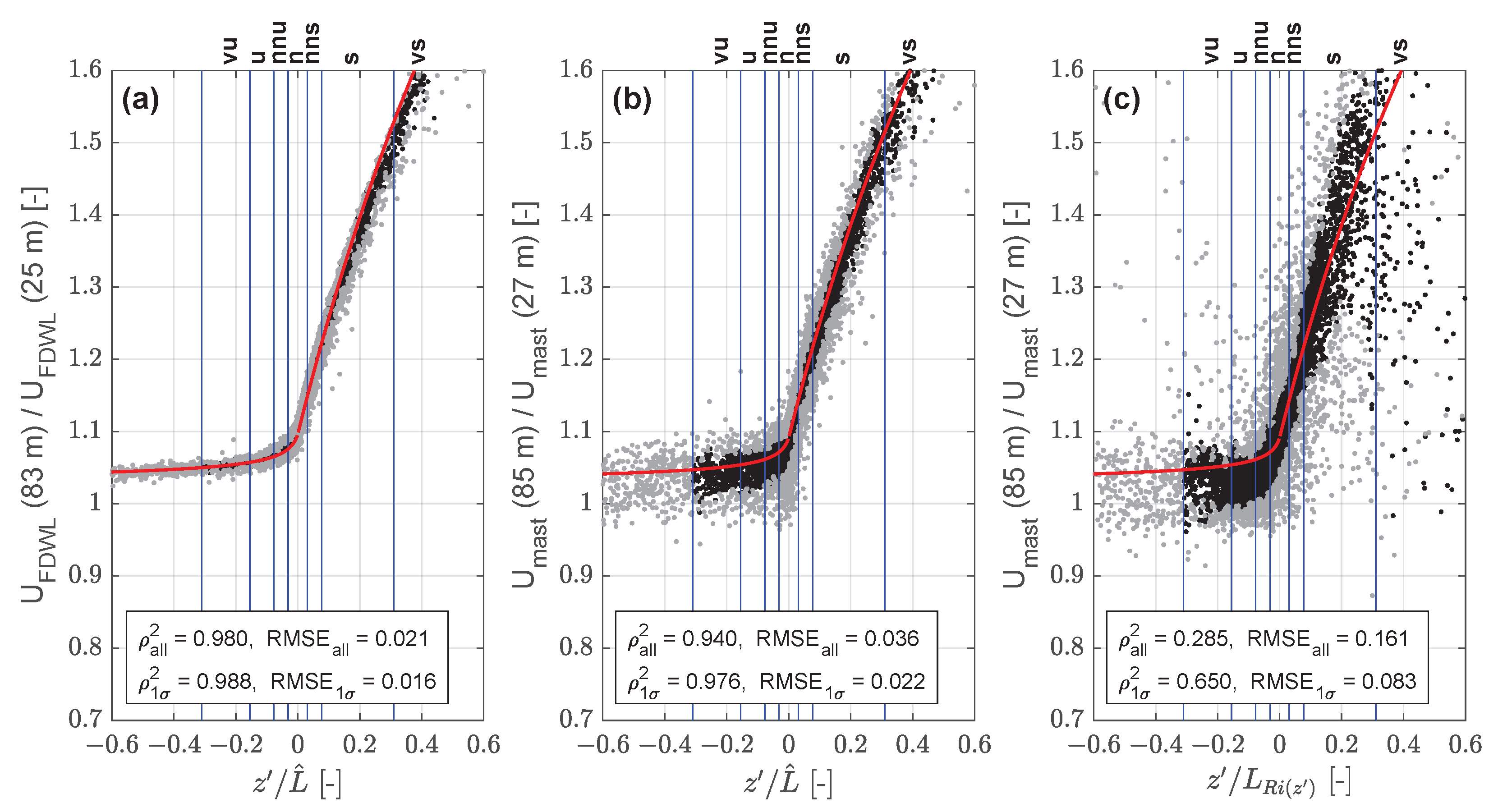
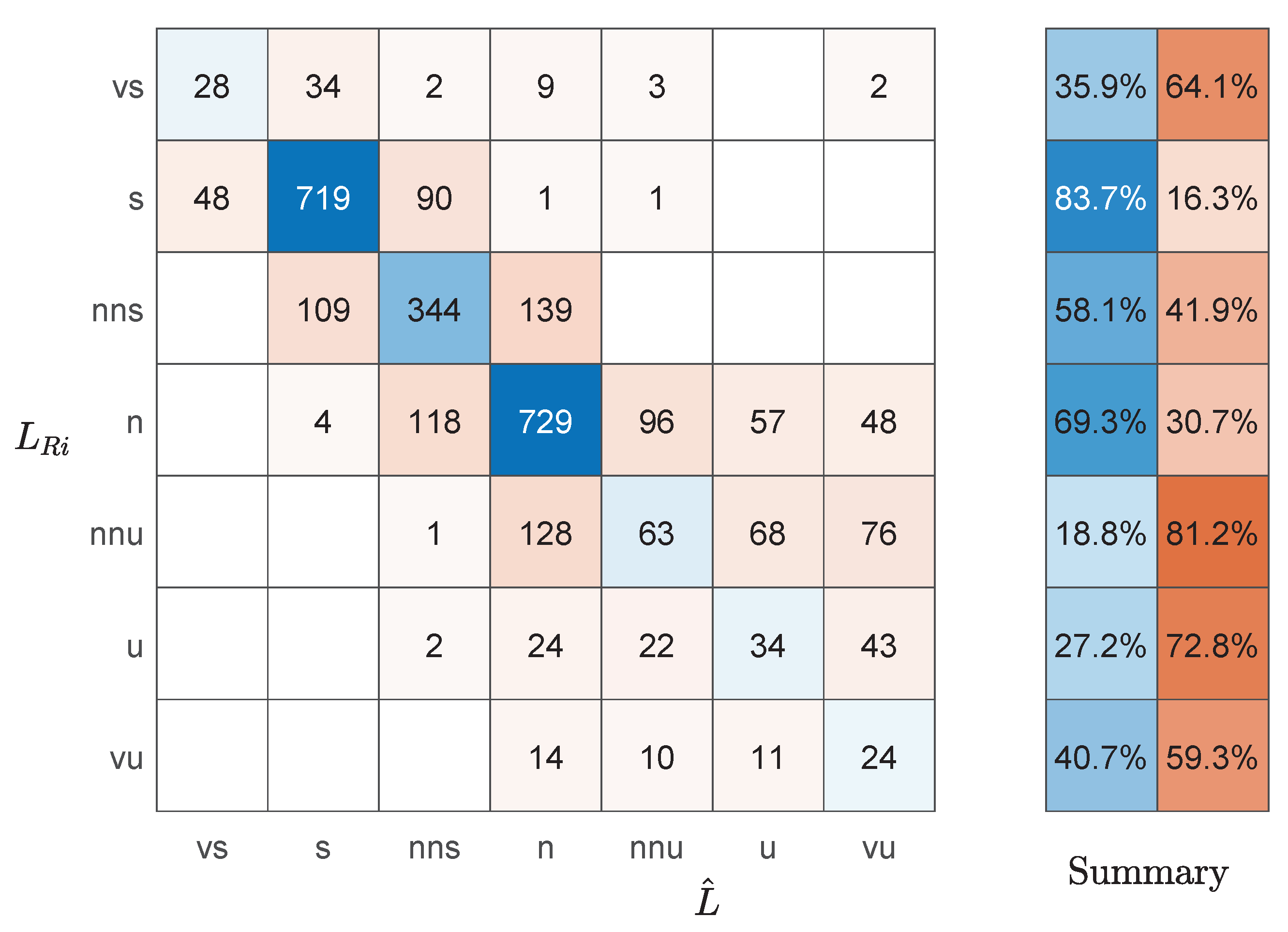
4.3. Wind Shear Dependence on Dimensionless Stability
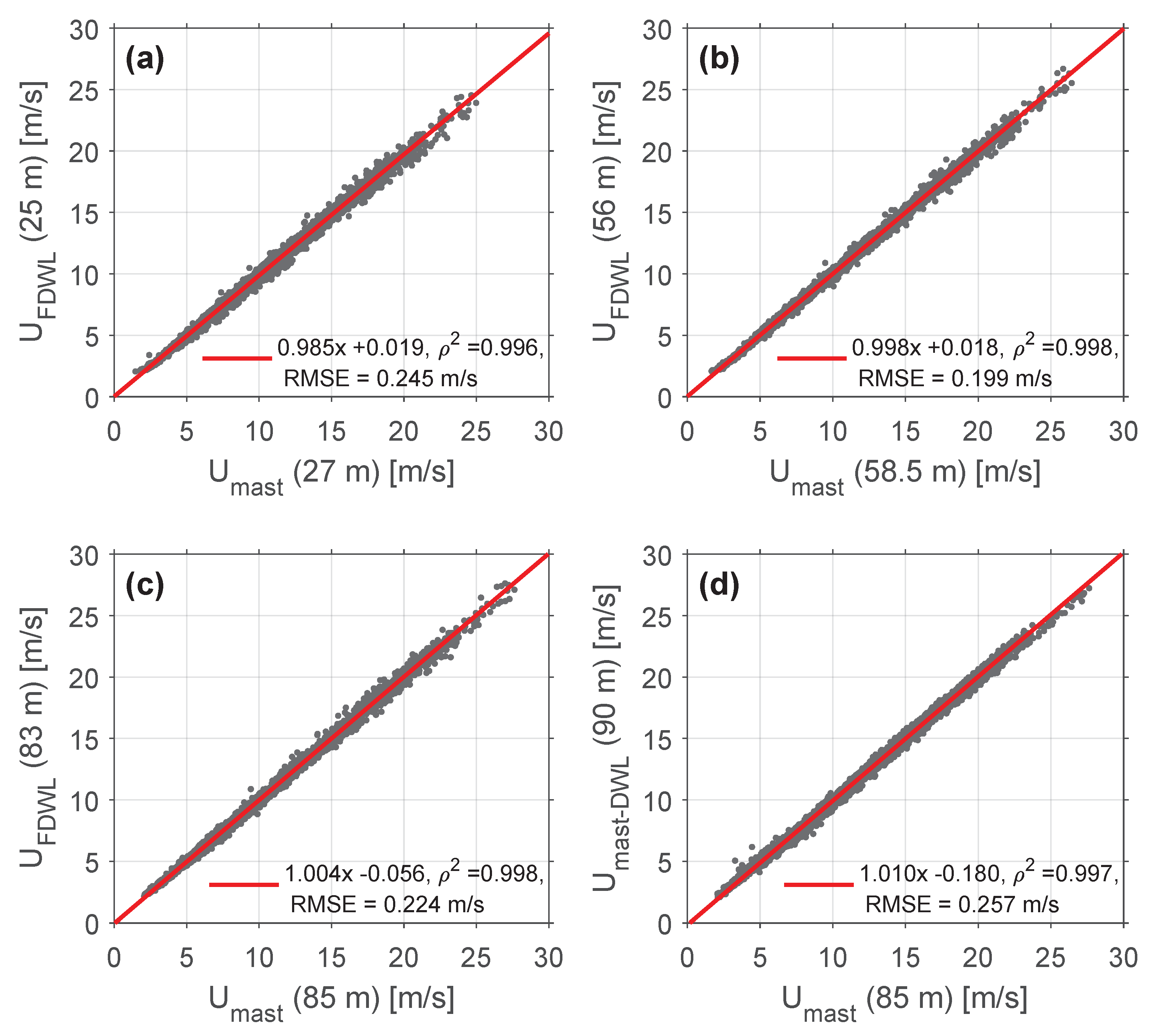
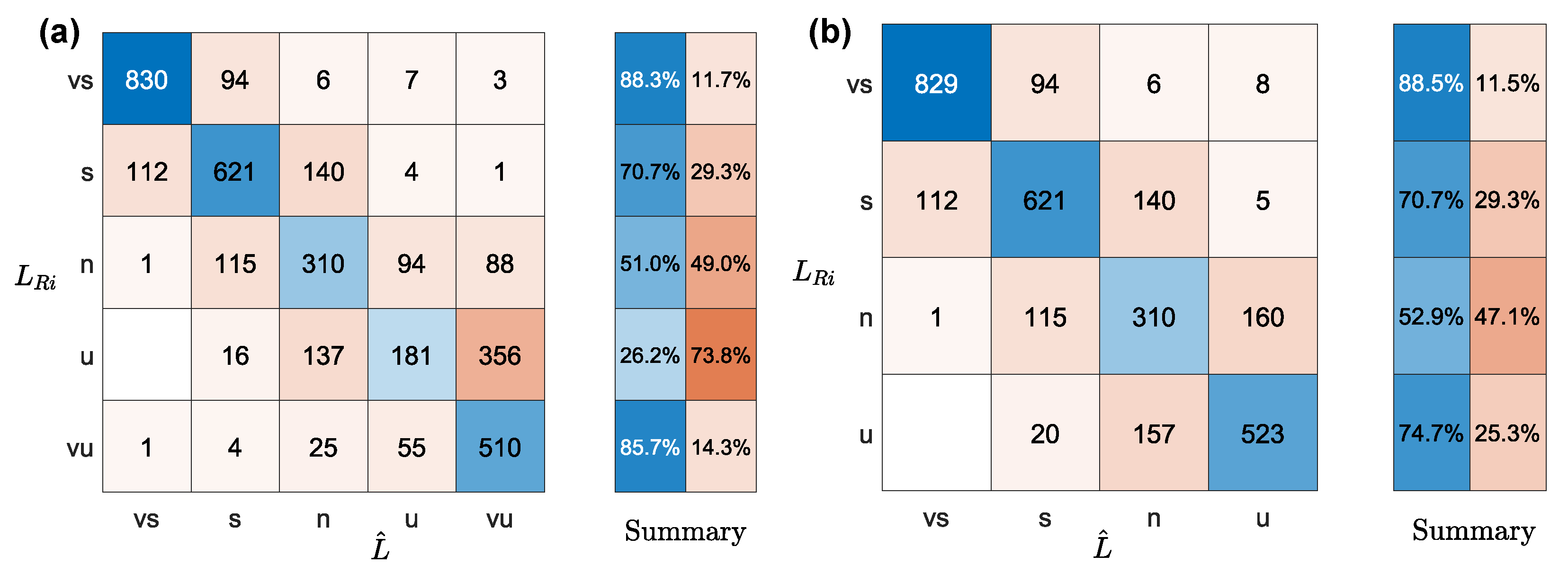
4.4. Performance Statistics: Friction Velocity and Stability
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DWL | Doppler Wind lidar |
| FDWL | Floating Doppler Wind lidar |
| HR | Hit Rate |
| KPI | Key Performance Indicator |
| HWS | Horizontal Wind Speed |
| LAT | Lowest Astronomical Tide |
| LoS | Line of Sight |
| LR | Linear Regression |
| metmast | Meteorological Mast |
| MOST | Monin-Obukhov Similarity Theory |
| NLSQ | Non-Linear Least Squares |
| OWEZ | Offshore Wind Farm Egmond aan Zee |
| RMSE | Root-Mean-Squared Error |
| TWD | True-Wind Direction |
| VAD | Velocity Azimuth Display |
| WD | Wind Direction |
| WE | Wind Energy |
References
- Council, G.W.E. Global Wind Report 2018; Technical Report; Global Wind Energy Council: Brussels, Belgium, 2019. [Google Scholar]
- Gutiérrez Antuñano, M. Doppler Wind LIDAR Systems Data Processing and Applications: An Overview towards Developing the New Generation of Wind Remote Sensing Sensors for Offshore wind Farms. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2019. [Google Scholar]
- Global Wind Energy Council. Global Wind Energy Outlook 2016; Technical Report; Global Wind Energy Council: Brussels, Belgium, 2016. [Google Scholar]
- Carbon-Trust. Offshore Wind Accelerator Roadmap for the Commercial Acceptance of Floating LIDAR Technology; Technical Report; Carbon Trust: London, UK, 2018. [Google Scholar]
- Hevia-Koch, P.; Jacobsen, H. Comparing offshore and onshore wind development considering acceptance costs. Energy Policy 2019, 125, 9–19. [Google Scholar] [CrossRef]
- IRENA. Future of Wind: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects; Technical Report; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Sathe, A.; Mann, J. A review of turbulence measurements using ground-based wind lidars. Atmos. Meas. Tech. 2013, 6, 3147–3167. [Google Scholar] [CrossRef] [Green Version]
- WindPower. Do We Still Need Met Masts? 2018. Available online: https://www.windpowermonthly.com/article/1458018/need-met-masts (accessed on 6 April 2021).
- Gottschall, J.; Wolken-Möhlmann, G.; Lange, B. About offshore resource assessment with floating lidars with special respect to turbulence and extreme events. J. Phys. Conf. Ser. 2014, 555, 12–43. [Google Scholar] [CrossRef]
- Nicholls-Lee, R. A low motion floating platform for offshore wind resource assessment using Lidars. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Nantes, France, 9–14 June 2013; Volume 55423, p. 008. [Google Scholar]
- Peña, A.; Hasager, C.; Lange, J.; Anger, J.; Badger, M.; Bingöl, F.; Bischoff, O.; Cariou, J.P.; Dunne, F.; Emeis, S.; et al. Remote Sensing for Wind Energy; DTU Wind Energy: Roskilde, Denmark, 2013. [Google Scholar]
- Pichugina, Y.; Banta, R.; Brewer, W.; Sandberg, S.; Hardesty, R. Doppler Lidar–Based Wind-Profile Measurement System for Offshore Wind-Energy and Other Marine Boundary Layer Applications. J. Appl. Meteorol. Climatol. 2012, 51, 327–349. [Google Scholar] [CrossRef]
- Salcedo-Bosch, A.; Rocadenbosch, F.; Gutiérrez-Antuñano, M.A.; Tiana-Alsina, J. Estimation of Wave Period from Pitch and Roll of a Lidar Buoy. Sensors 2021, 21, 1310. [Google Scholar] [CrossRef] [PubMed]
- Salcedo-Bosch, A.; Farré-Guarné, J.; Sala-Álvarez, J.; Villares-Piera, J.; Rocadenbosch, F.; Tanamachi, R.L. Floating Doppler wind lidar simulator for horizontal wind speed measurement error assessment. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium (IGARSS-2021), Brussels, Belgium, 11–16 July 2021. [Google Scholar]
- Tiana-Alsina, J.; Rocadenbosch, F.; Gutierrez-Antunano, M.A. Vertical Azimuth Display simulator for wind-Doppler lidar error assessment. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1614–1617. [Google Scholar] [CrossRef] [Green Version]
- Kelberlau, F.; Neshaug, V.; Lønseth, L.; Bracchi, T.; Mann, J. Taking the Motion out of Floating Lidar: Turbulence Intensity Estimates with a Continuous-Wave Wind Lidar. Remote Sens. 2020, 12, 898. [Google Scholar] [CrossRef] [Green Version]
- Gutiérrez, M.A.; Tiana-Alsina, J.; Bischoff, O.; Cateura, J.; Rocadenbosch, F. Performance evaluation of a floating doppler wind lidar buoy in mediterranean near-shore conditions. In Proceedings of the Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015. [Google Scholar]
- Gutierrez-Antunano, M.A.; Tiana-Alsina, J.; Rocadenbosch, F.; Sospedra, J.; Aghabi, R.; Gonzalez-Marco, D. A wind-lidar buoy for offshore wind measurements: First commissioning test-phase results. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS-2017), Fort Worth, TX, USA, 23–28 July 2017; pp. 1607–1610. [Google Scholar] [CrossRef]
- Schuon, F.; González, D.; Rocadenbosch, F.; Bischoff, O.; Jané, R. KIC InnoEnergy Project Neptune: Development of a Floating LiDAR Buoy for Wind, Wave and Current Measurements. In Proceedings of the DEWEK 2012 German Wind Energy Conference, Bremen, Germany, 7–8 November 2012. [Google Scholar]
- Mathisen, J.P. Measurement of wind profile with a buoy mounted lidar. Energy Procedia 2013, 12, 145. [Google Scholar]
- Gutiérrez-Antu nano, M.; Tiana-Alsina, J.; Salcedo, A.; Rocadenbosch, F. Estimation of the Motion-Induced Horizontal-Wind-Speed Standard Deviation in an Offshore Doppler Lidar. Remote Sens. 2018, 10, 2037. [Google Scholar] [CrossRef] [Green Version]
- Scientific, C. ZephIR 300; Technical Report; Campbell Scientific: Edmonton, AB, Canada, 2016. [Google Scholar]
- Subramanian, B.; Chokani, N.; Abhari, R.S. Impact of atmospheric stability on wind turbine wake evolution. J. Wind. Eng. Ind. Aerodyn. 2018, 176, 174–182. [Google Scholar] [CrossRef]
- Machefaux, E.; Larsen, G.C.; Koblitz, T.; Troldborg, N.; Kelly, M.C.; Chougule, A.; Hansen, K.S.; Rodrigo, J.S. An experimental and numerical study of the atmospheric stability impact on wind turbine wakes. Wind. Energy 2016, 19, 1785–1805. [Google Scholar] [CrossRef]
- Kim, D.Y.; Kim, Y.H.; Kim, B.S. Changes in wind turbine power characteristics and annual energy production due to atmospheric stability, turbulence intensity, and wind shear. Energy 2021, 214, 119051. [Google Scholar] [CrossRef]
- Ghaisas, N.S.; Archer, C.L.; Xie, S.; Wu, S.; Maguire, E. Evaluation of layout and atmospheric stability effects in wind farms using large-eddy simulation. Wind Energy 2017, 20, 1227–1240. [Google Scholar] [CrossRef]
- Alblas, L.; Bierbooms, W.; Veldkamp, D. Power output of offshore wind farms in relation to atmospheric stability. J. Phys. 2014, 555, 012004. [Google Scholar] [CrossRef] [Green Version]
- Sathe, A.; Mann, J.; Barlas, T.; Bierbooms, W.A.A.M.; Van Bussel, G.J.W. Influence of atmospheric stability on wind turbine loads. Wind Energy 2013, 16, 1013–1032. [Google Scholar] [CrossRef]
- Kretschmer, M.; Schwede, F.; Guzmán, R.F.; Lott, S.; Cheng, P. Influence of atmospheric stability on the load spectra of wind turbines at alpha ventus. J. Phys. 2018, 1037, 052009. [Google Scholar] [CrossRef] [Green Version]
- Holtslag, M.C.; Bierbooms, W.A.A.M.; Van Bussel, G.J.W. Wind turbine fatigue loads as a function of atmospheric conditions offshore. Wind Energy 2016, 19, 1917–1932. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 1954, 151, e187. [Google Scholar]
- Barthelmie, R. The effects of atmospheric stability on coastal wind climates. Meteorol. Appl. J. Forecast. Pract. Appl. Train. Tech. Model. 1999, 6, 39–47. [Google Scholar] [CrossRef]
- Holtslag, M.C.; Bierbooms, W.A.A.M.; Van Bussel, G.J.W. Validation of surface layer similarity theory to describe far offshore marine conditions in the Dutch North Sea in scope of wind energy research. J. Wind. Eng. Ind. Aerodyn. 2015, 136, 180–191. [Google Scholar] [CrossRef]
- Sathe, A.; Gryning, S.E.; Peña, A. Comparison of the atmospheric stability and wind profiles at two wind farm sites over a long marine fetch in the North Sea. Wind Energy 2011, 14, 767–780. [Google Scholar] [CrossRef]
- Beljaars, A.C.M.; Holtslag, A.; Van Westrhenen, R. Description of a Software Library for the Calculation of Surface Fluxes; KNMI: De Bilt, The Netherlands, 1989. [Google Scholar]
- Motta, M.; Barthelmie, R.J.; Vølund, P. The influence of non-logarithmic wind speed profiles on potential power output at Danish offshore sites. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2005, 8, 219–236. [Google Scholar] [CrossRef]
- Holtslag, M.C.; Bierbooms, W.A.A.M.; Van Bussel, G.J.W. Estimating atmospheric stability from observations and correcting wind shear models accordingly. J. Phys. 2014, 555, 012052. [Google Scholar] [CrossRef]
- Basu, S. A simple recipe for estimating atmospheric stability solely based on surface-layer wind speed profile. Wind Energy 2018, 21, 937–941. [Google Scholar] [CrossRef] [Green Version]
- Salcedo-Bosch, A.; Rocadenbosch, F.; Sospedra, J. A Robust Adaptive Unscented Kalman Filter for Floating Doppler Wind-LiDAR Motion Correction. Remote Sens. 2021, 13, 4167. [Google Scholar] [CrossRef]
- Werkhoven, E.J.; Verhoef, J.P. Offshore Meteorological Mast IJmuiden: Abstract of Instrumentation Report; Technical Report; Energy Research Centre of the Netherlands (ECN): Petten, The Netherlands, 2012. [Google Scholar]
- Panofsky, H.A. Tower Micrometeorogy. In Workshop on Micrometeorolgy; Haugeb, D.A., Ed.; American Meteorology Society: Boston, MA, USA, 1973; pp. 151–176. [Google Scholar]
- Peña, A.; Gryning, S.E.; Hasager, C.B. Measurements and modelling of the wind speed profile in the marine atmospheric boundary layer. Bound.-Layer Meteorol. 2008, 129, 479–495. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science & Business Media: Dordrecht, The Netherlands, 1988; Volume 13. [Google Scholar]
- Peña, A.; Gryning, S.E. Charnock’s roughness length model and non-dimensional wind profiles over the sea. Bound.-Layer Meteorol. 2008, 128, 191–203. [Google Scholar] [CrossRef]
- Charnock, H. Wind stress on a water surface. Q. J. R. Meteorol. Soc. 1955, 81, 639–640. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Dyer, A.J. A review of flux-profile relationships. Bound.-Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Högström, U. Non-dimensional wind and temperature profiles in the atmospheric surface layer: A re-evaluation. In Topics in Micrometeorology. A Festschrift for Arch Dyer; Springer: Berlin/Heidelberg, Germany, 1988; pp. 55–78. [Google Scholar]
- Lange, B.; Larsen, S.; Højstrup, J.; Barthelmie, R. Importance of thermal effects and sea surface roughness for offshore wind resource assessment. J. Wind. Eng. Ind. Aerodyn. 2004, 92, 959–988. [Google Scholar] [CrossRef] [Green Version]
- Van Wijk, A.; Beljaars, A.; Holtslag, A.; Turkenburg, W. Evaluation of stability corrections in wind speed profiles over the North Sea. J. Wind. Eng. Ind. Aerodyn. 1990, 33, 551–566. [Google Scholar] [CrossRef]
- Gryning, S.E.; Batchvarova, E.; Brümmer, B.; Jørgensen, H.; Larsen, S. On the extension of the wind profile over homogeneous terrain beyond the surface boundary layer. Bound.-Layer Meteorol. 2007, 124, 251–268. [Google Scholar] [CrossRef]
- Golbazi, M.; Archer, C.L. Methods to Estimate Surface Roughness Length for Offshore Wind Energy. Adv. Meteorol. 2019, 2019, 5695481. [Google Scholar] [CrossRef] [Green Version]
- Emeis, S.; Türk, M. Wind-driven wave heights in the German Bight. Ocean. Dyn. 2009, 59, 463–475. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L.; Andreas, E.L. Formulation of the Sea Surface Friction Velocity in Terms of the Mean Wind and Bulk Stability. J. Appl. Meteorol. Climatol. 2015, 54, 691–703. [Google Scholar] [CrossRef]
- Grachev, A.; Fairall, C. Dependence of the Monin—Obukhov stability parameter on the bulk Richardson number over the ocean. J. Appl. Meteorol. 1997, 36, 406–414. [Google Scholar] [CrossRef]
- Borvarán, D.; Peña, A.; Gandoin, R. Characterization of offshore vertical wind shear conditions in Southern New England. Wind Energy 2021, 24, 465–480. [Google Scholar] [CrossRef]
- Wallace, J.M.; Hobbs, P.V. 3—Atmospheric Thermodynamics. In Atmospheric Science, 2nd ed.; Wallace, J.M., Hobbs, P.V., Eds.; Academic Press: San Diego, CA, USA, 2006; p. 78. [Google Scholar] [CrossRef]
- MacIsaac, C.; Naeth, S. TRIAXYS Next Wave II Directional Wave Sensor The evolution of wave measurements. In Proceedings of the 2013 OCEANS—San Diego, San Diego, CA, USA, 23–27 September 2013; pp. 1–8. [Google Scholar]
- Fritsch, F.N.; Carlson, R.E. Monotone piecewise cubic interpolation. SIAM J. Numer. Anal. 1980, 17, 238–246. [Google Scholar] [CrossRef]
- Kahaner, D.; Moler, C.; Nash, S. Numerical Methods and Software; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1989. [Google Scholar]
- Salcedo-Bosch, A.; Gutierrez-Antunano, M.A.; Tiana-Alsina, J.; Rocadenbosch, F. Floating Doppler Wind Lidar Measurement of Wind Turbulence: A Cluster Analysis. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium (IGARSS-2020), Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar]
- Gutiérrez-Antu nano, M.A.; Tiana-Alsina, J.; Rocadenbosch, F. Performance evaluation of a floating lidar buoy in nearshore conditions. Wind Energy 2017, 20, 1711–1726. [Google Scholar] [CrossRef] [Green Version]
- Arranz, P.G. D6.6.2 Measurements in Complex Terrain Using a Lidar; Technical Report; CENER: Navarra, Spain, 2011. [Google Scholar]
- Wagner, R.; Mikkelsen, T.; Courtney, M. Investigation of Turbulence Measurements with a Continuous Wave, Conically Scanning LiDAR; Technical Report; DTU: Lyngby, Denmark, 2009. [Google Scholar]
- Cheynet, E.; Jakobsen, J.B.; Obhrai, C. Spectral characteristics of surface-layer turbulence in the North Sea. Energy Procedia 2017, 137, 414–427. [Google Scholar] [CrossRef]
- Kelly, M. Direct Solution of Various Micrometeorological Problems via the Lambert-W Function. Bound.-Layer Meteorol. 2021, 179, 163–168. [Google Scholar] [CrossRef]
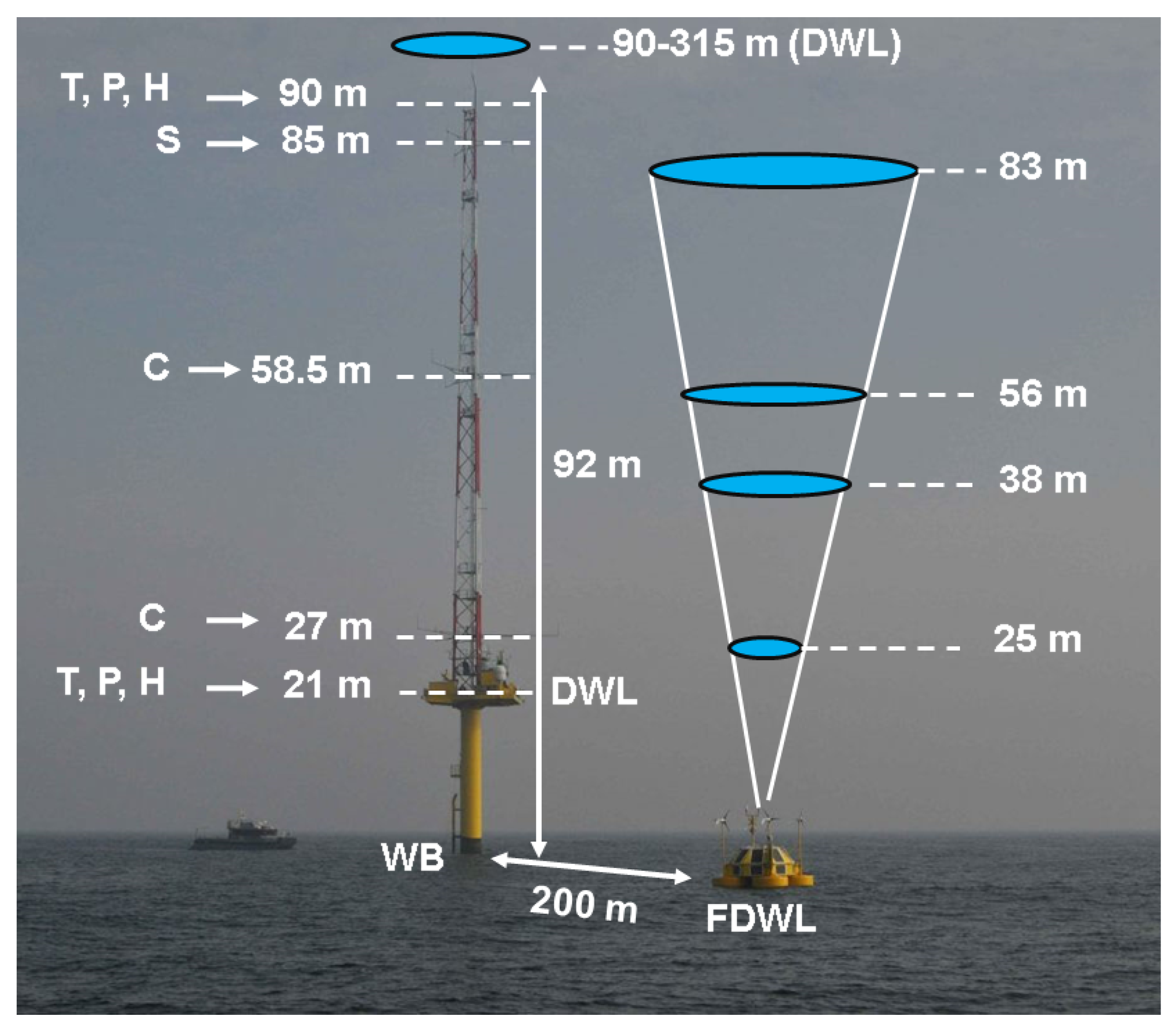
| Sensor | Parameter | Unit | Sampling Rate | Height (1) | Orientation |
|---|---|---|---|---|---|
| 3 × Metek USA-1 Sonic Anemometer | Wind speed | m/s | 4 Hz | 85 m | 46.5, 166.5 and 286.5 |
| 6 × Thies First Class Advanced Anemometer | Wind Speed | m/s | 4 Hz | 27 and 58.5 m | |
| 9 × First Class Wind Vane | Wind Direction | deg | 4 Hz | 26.2, 57.7 and 87 m | |
| 2 × Vaisala PTB210 | Air pressure | hPa | 4 Hz | 21 and 90 m | N (21 m) and N-E (90 m) |
| 2 × Vaisala HMP155D | Air temperature | C | 4 Hz | 21 and 90 m | N (21 m) and N-W (90 m) |
| Relative humidity | % | 4 Hz | |||
| TRYAXIS wave buoy | Water temperature | C | 60 min | sea level | |
| 2 × ZephIR 300 | Wind speed | m/s | 1 Hz (2) | 90-315 m, every 25 m (mast-DWL) | S-W |
| (mast-DWL and FDWL) | 25, 38, 56 and 83 m (FDWL) | 200-m from the mast |
| Atmospheric Stability | Obukhov Length Range (m) |
|---|---|
| Very Stable—vs | |
| Stable—s | |
| Neutral—n | |
| Unstable—u | |
| Very Unstable—vu |
| Atmospheric Stability | Obukhov Length Range (m) |
|---|---|
| Very Stable—vs | |
| Stable—s | |
| Near-Neutral Stable—nns | |
| Neutral—n | |
| Near-Neutral Unstable—nnu | |
| Unstable—u | |
| Very Unstable—vu |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Araújo da Silva, M.P.; Rocadenbosch, F.; Farré-Guarné, J.; Salcedo-Bosch, A.; González-Marco, D.; Peña, A. Assessing Obukhov Length and Friction Velocity from Floating Lidar Observations: A Data Screening and Sensitivity Computation Approach. Remote Sens. 2022, 14, 1394. https://doi.org/10.3390/rs14061394
Araújo da Silva MP, Rocadenbosch F, Farré-Guarné J, Salcedo-Bosch A, González-Marco D, Peña A. Assessing Obukhov Length and Friction Velocity from Floating Lidar Observations: A Data Screening and Sensitivity Computation Approach. Remote Sensing. 2022; 14(6):1394. https://doi.org/10.3390/rs14061394
Chicago/Turabian StyleAraújo da Silva, Marcos Paulo, Francesc Rocadenbosch, Joan Farré-Guarné, Andreu Salcedo-Bosch, Daniel González-Marco, and Alfredo Peña. 2022. "Assessing Obukhov Length and Friction Velocity from Floating Lidar Observations: A Data Screening and Sensitivity Computation Approach" Remote Sensing 14, no. 6: 1394. https://doi.org/10.3390/rs14061394
APA StyleAraújo da Silva, M. P., Rocadenbosch, F., Farré-Guarné, J., Salcedo-Bosch, A., González-Marco, D., & Peña, A. (2022). Assessing Obukhov Length and Friction Velocity from Floating Lidar Observations: A Data Screening and Sensitivity Computation Approach. Remote Sensing, 14(6), 1394. https://doi.org/10.3390/rs14061394







