Analysis of Precise Orbit Determination for the HY2D Satellite Using Onboard GPS/BDS Observations
Abstract
:1. Introduction
2. Materials
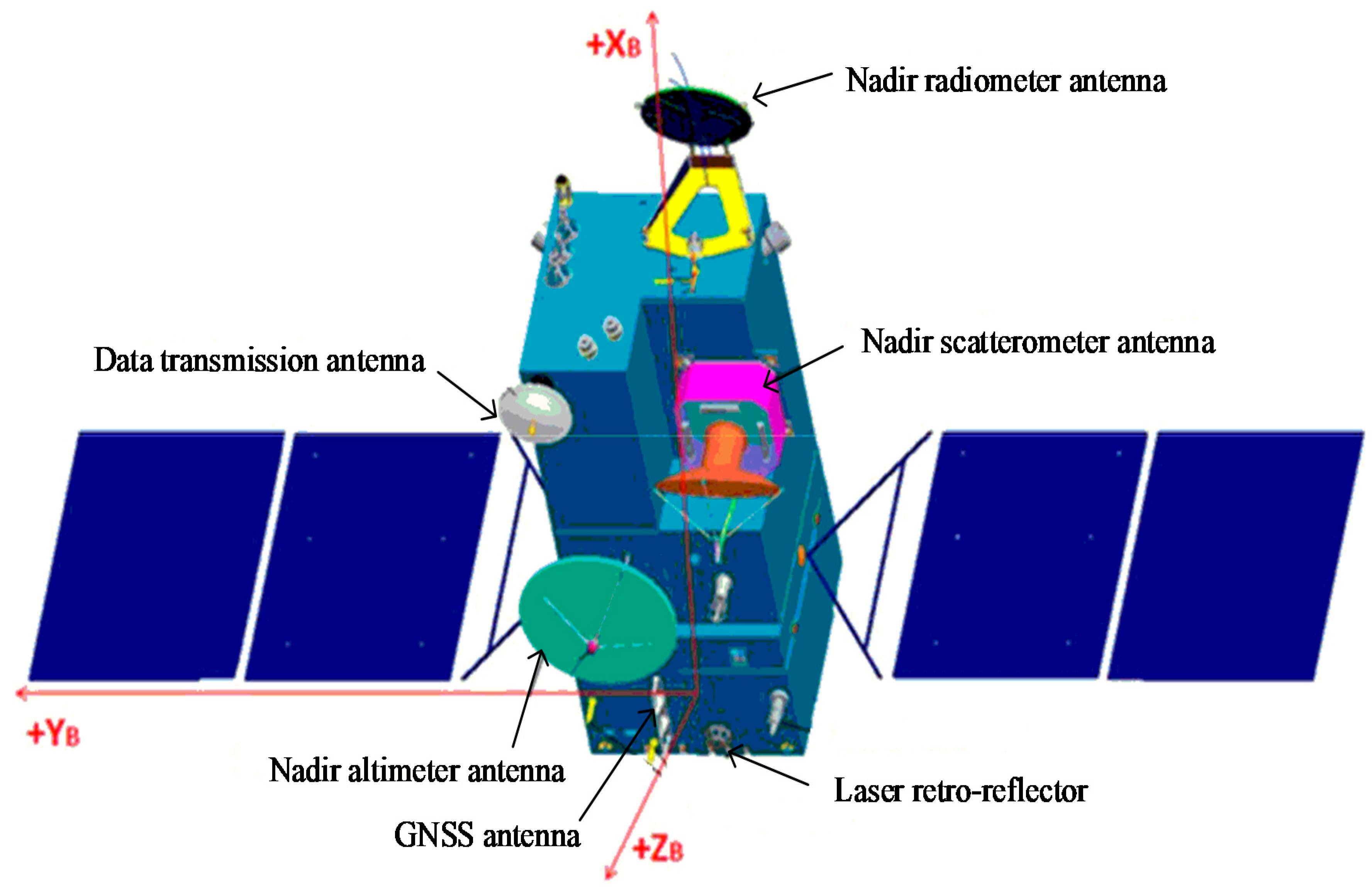
2.1. HY2D Spacecraft
2.2. Data Collection
3. POD Method and Strategies
3.1. Observation Model
3.2. Dynamic Model
4. Results and Discussion
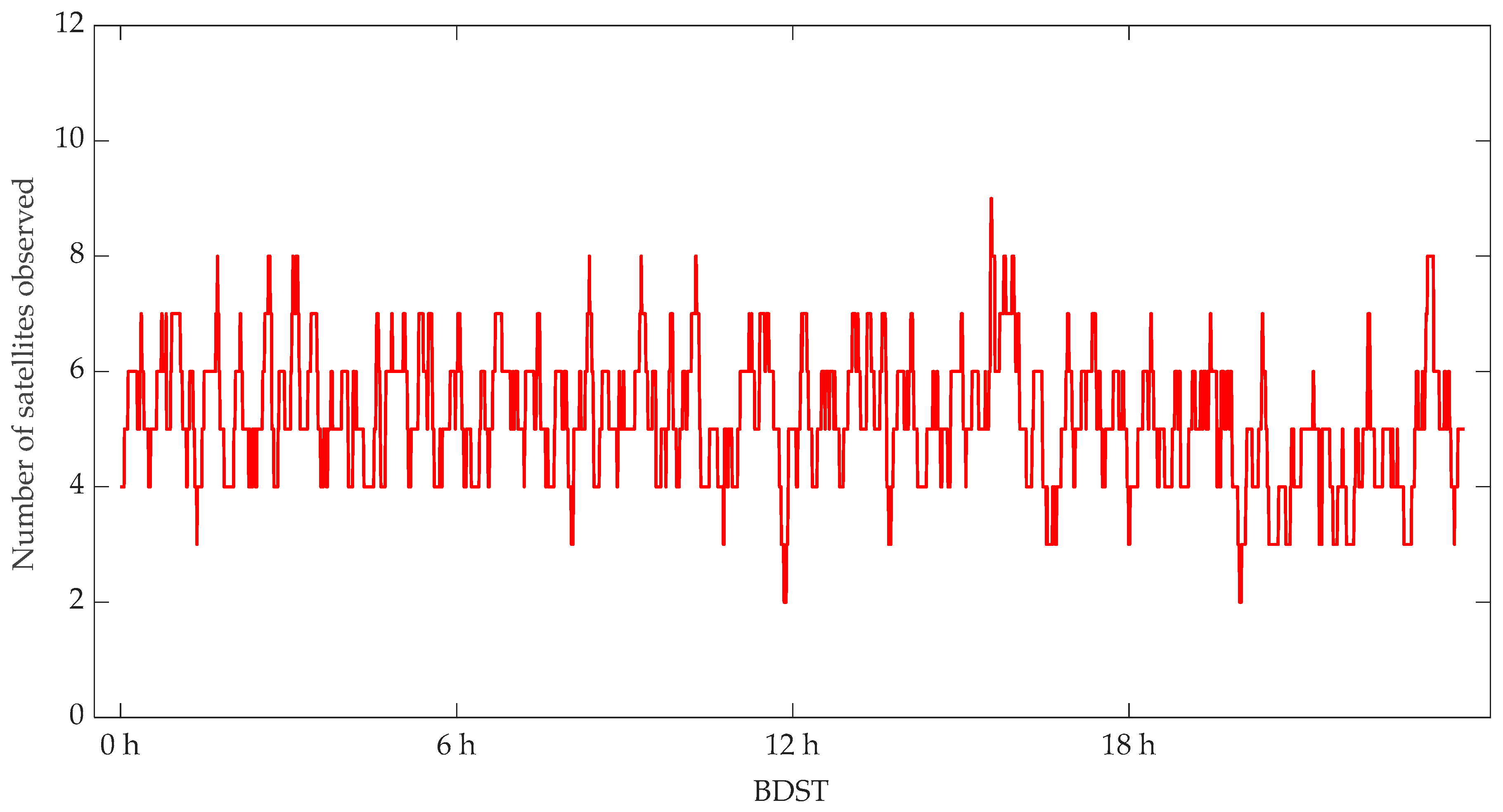
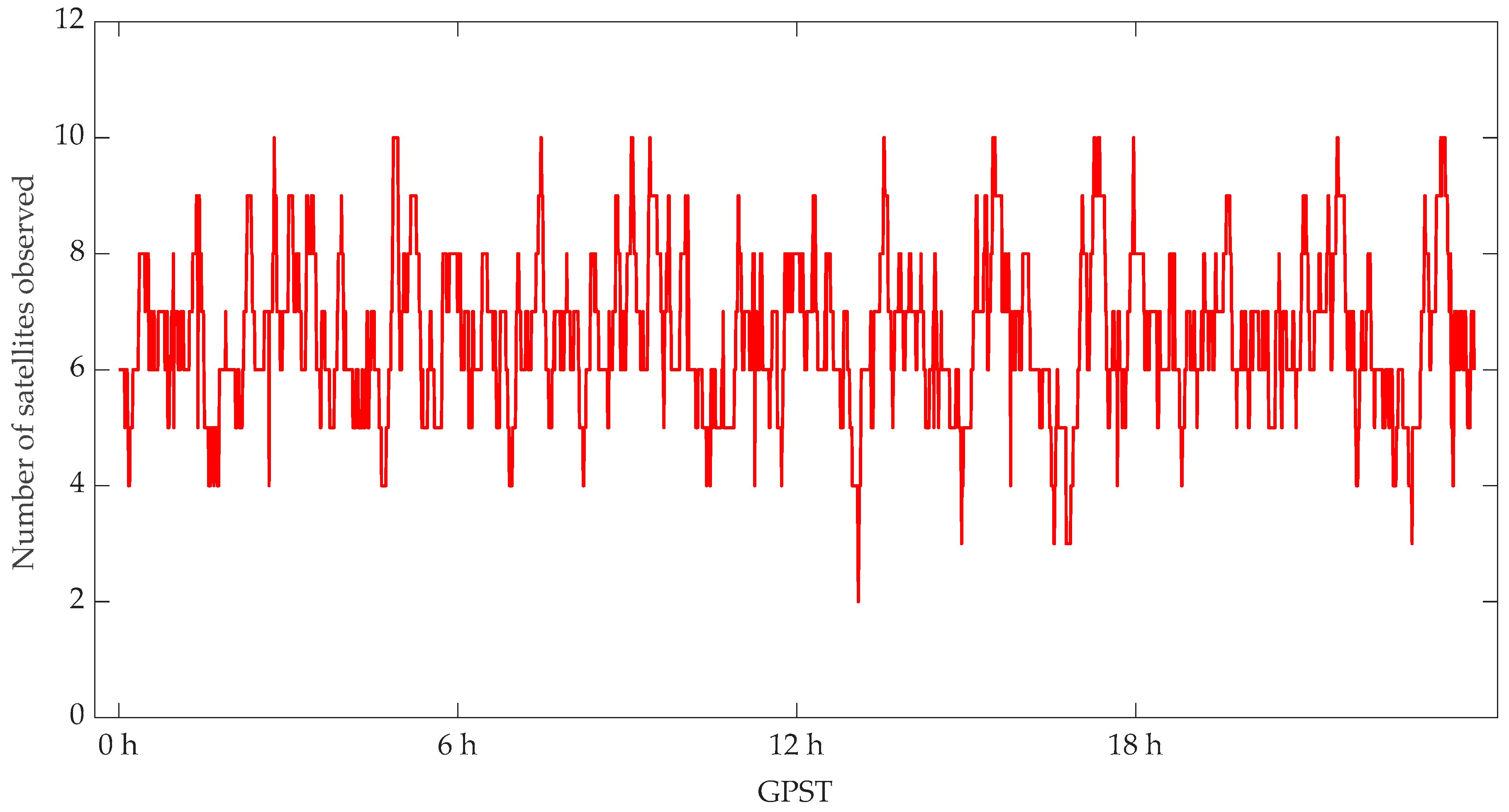
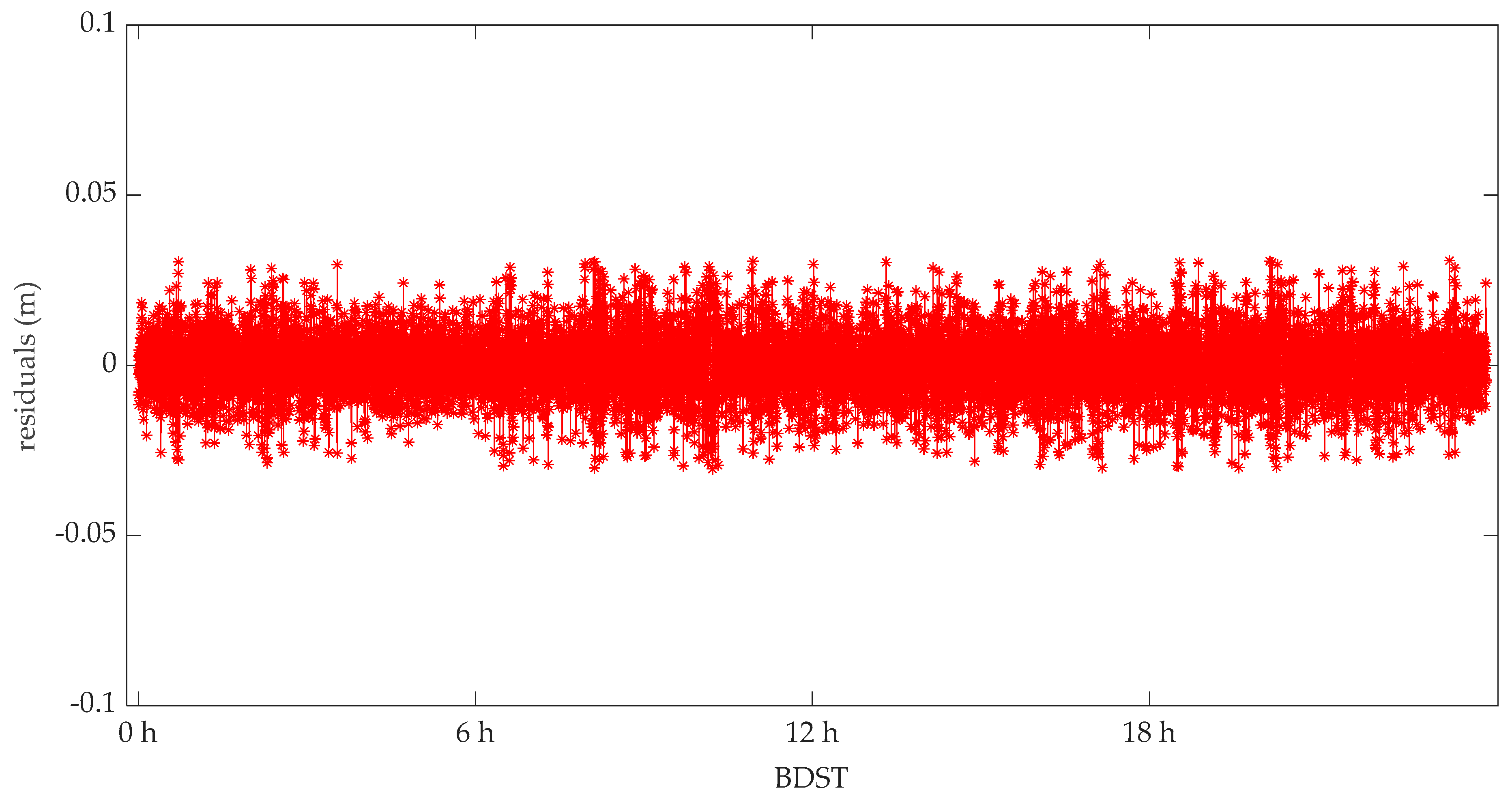
4.1. POD Residuals Analysis
4.2. POD Precision Analysis for HY2D
4.3. SLR Validation for the POD of HY2D
5. Conclusions
- (1)
- The standard deviation of the POD residuals based on spaceborne BDS and GPS data are, respectively, 9.12 mm and 8.53 mm, and these residual variations show no significant deviations or systematic errors.
- (2)
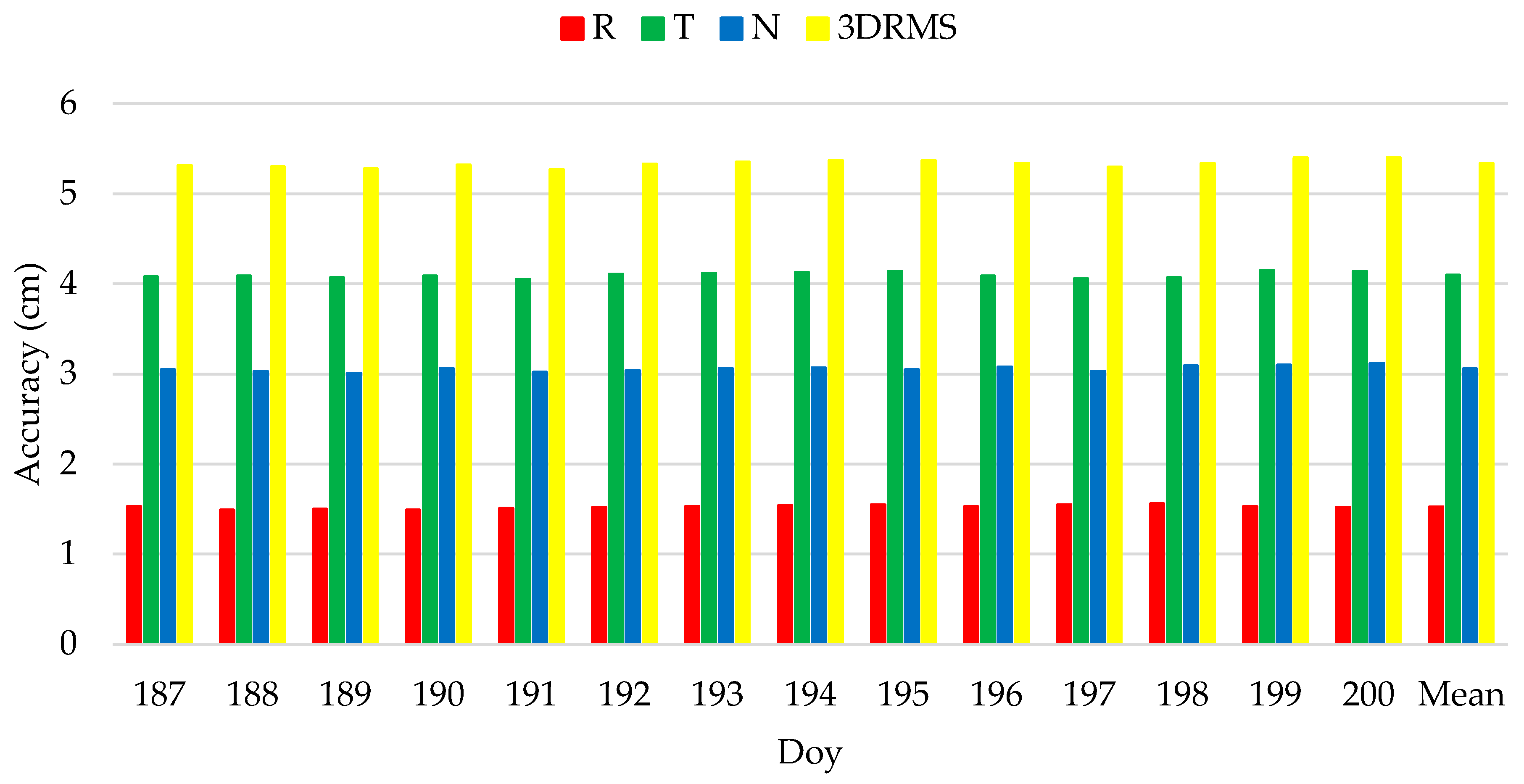
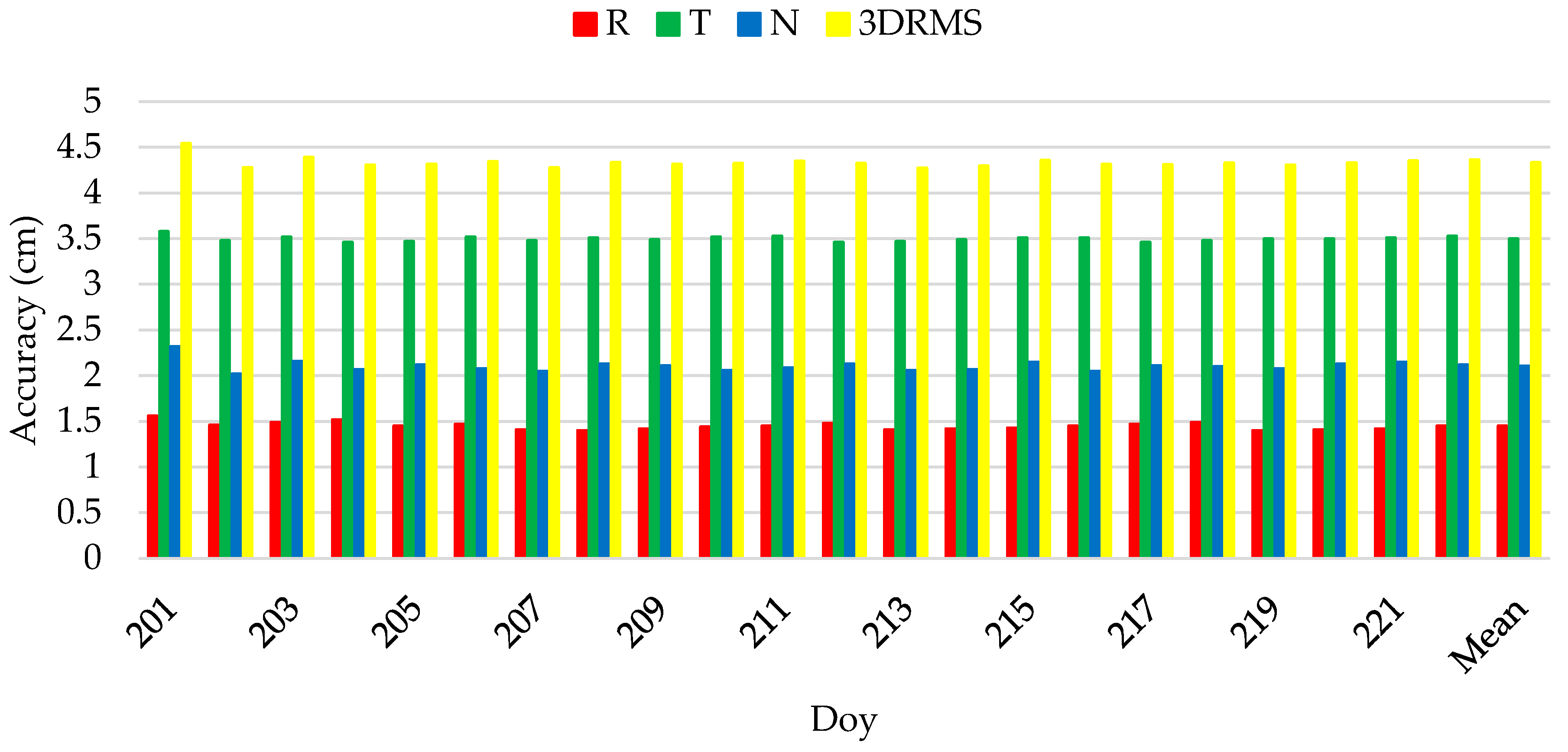
- The comparison results with DORIS-derived orbits show that the average radial RMS value of spaceborne BDS and GPS are 1.5 cm and 1.4 cm, respectively, and the corresponding 3D RMS accuracy are 5.3 cm and 4.3 cm, respectively. Overall, these results indicate that the POD processing of the HY2D satellite using spaceborne BDS and GPS data can achieve 1 cm radial precision and satisfy the current high-precision altimetry applications.
- (3)
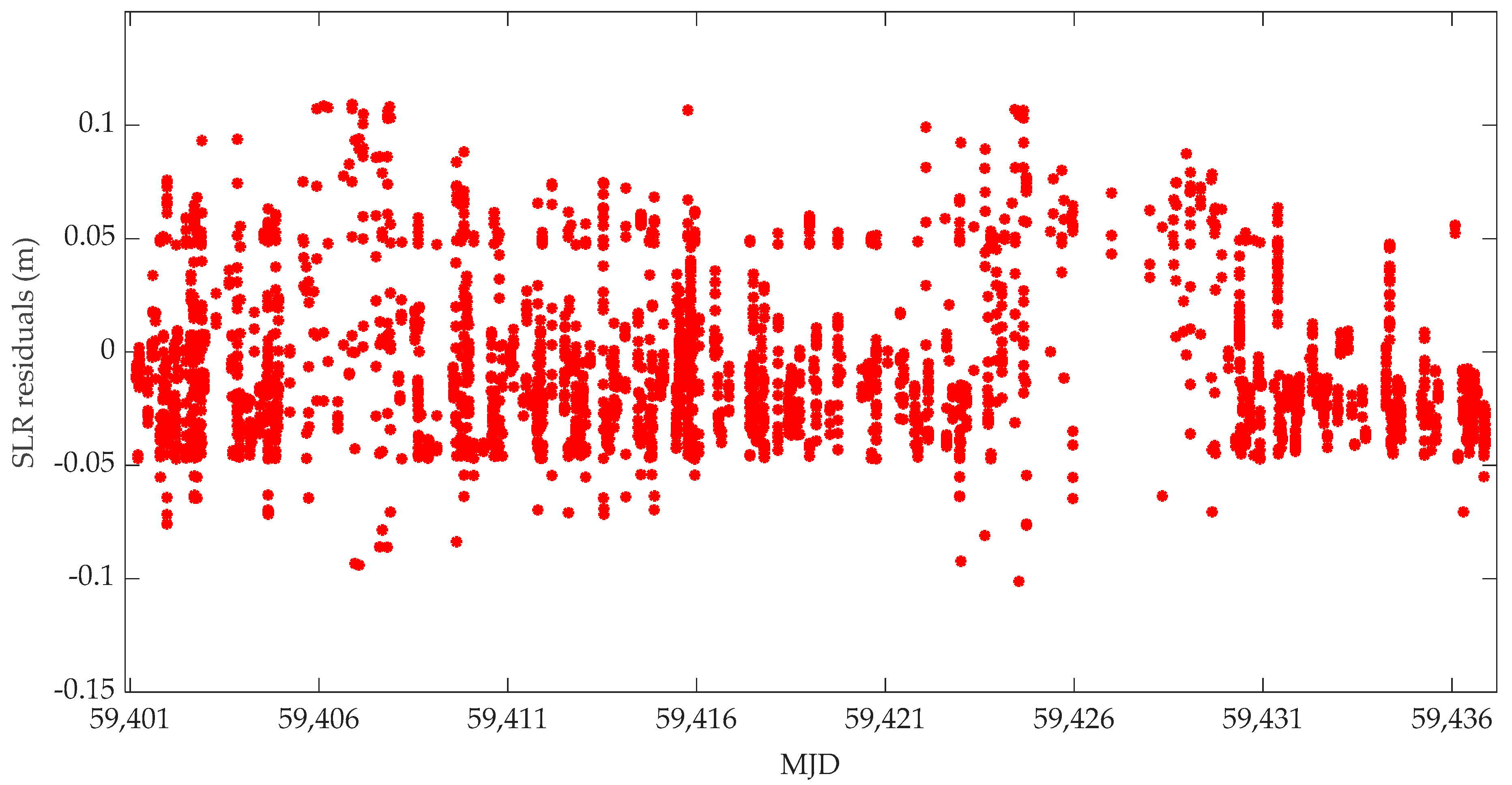
- According to the SLR validation results, it is shown that the standard deviation of residuals is 3.3 cm, which indicates that the orbital accuracy of the HY2D satellite is approximately 3.3 cm, and the used model strategy is also reliable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cerri, L.; Berthias, J.P.; Bertiger, W.I.; Haines, B.J.; Lemoine, F.G.; Mercier, F.; Ries, J.C.; Willis, P.; Zelensky, N.P.; Ziebart, M. Precision Orbit Determination Standards for the Jason Series of Altimeter Missions. Mar. Geodesy 2010, 33, 379–418. [Google Scholar] [CrossRef]
- D’Amico, S.; Ardaens, J.-S.; Larsson, R. Spaceborne Autonomous Formation-Flying Experiment on the PRISMA Mission. J. Guid. Control. Dyn. 2012, 35, 834–850. [Google Scholar] [CrossRef]
- Zhang, Y.; Vincent, T. HY2-ICD-0-00009-CNES. Technical Document for HY2A Ground Segment. 2011.
- Kang, Z.; Tapley, B.; Bettadpur, S.; Ries, J.; Nagel, P.; Pastor, R. Precise orbit determination for the GRACE mission using only GPS data. J. Geodesy 2006, 80, 322–331. [Google Scholar] [CrossRef]
- Bock, H.; Jäggi, A.; Meyer, U.; Visser, P.; Ijssel, J.V.D.; van Helleputte, T.; Heinze, M.; Hugentobler, U. GPS-derived orbits for the GOCE satellite. J. Geodesy 2011, 85, 807–818. [Google Scholar] [CrossRef] [Green Version]
- Bock, H.; Jäggi, A.; Švehla, D.; Beutler, G.; Hugentobler, U.; Visser, P. Precise orbit determination for the GOCE satellite using GPS. Adv. Space Res. 2007, 39, 1638–1647. [Google Scholar] [CrossRef]
- Ijssel, J.V.D.; da Encarnacao, J.T.; Doornbos, E.; Visser, P. Precise science orbits for the Swarm satellite constellation. Adv. Space Res. 2015, 56, 1042–1055. [Google Scholar] [CrossRef]
- Tapley, B.; Ries, J.C.; Davis, G.W.; Eanes, R.J.; Schutz, B.E.; Shum, C.K.; Watkins, M.M.; Marshall, J.A.; Nerem, R.S.; Putney, B.H.; et al. Precision orbit determination for TOPEX/POSEIDON. J. Geophys. Res. Earth Surf. 1994, 99, 24383–24404. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, X.; Zhao, G.; Peng, H.; Wu, B. The Precise Orbit Determination for HY2A Satellite Using GPS, DORIS and SLR Data. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 1000–1005. [Google Scholar]
- Gao, F.; Peng, B.; Zhang, Y.; Evariste, N.H.; Liu, J.; Wang, X.; Zhong, M.; Lin, M.; Wang, N.; Chen, R.; et al. Analysis of HY2A precise orbit determination using DORIS. Adv. Space Res. 2015, 55, 1394–1404. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, Q.; Guo, X.; Liu, X.; Liu, J.; Zhou, Q. Quality assessment of onboard GPS receiver and its combination with DORIS and SLR for Haiyang 2A precise orbit determination. Sci. China Earth Sci. 2014, 58, 138–150. [Google Scholar] [CrossRef]
- Haines, B.; Bar-Sever, Y.; Bertiger, W.; Desai, S.; Willis, P. One-Centimeter Orbit Determination for Jason-1: New GPS-Based Strategies. Mar. Geodesy 2004, 27, 299–318. [Google Scholar] [CrossRef]
- Lemoine, F.G.; Zelensky, N.; Chinn, D.; Pavlis, D.; Rowlands, D.; Beckley, B.; Luthcke, S.; Willis, P.; Ziebart, M.; Sibthorpe, A.; et al. Towards development of a consistent orbit series for TOPEX, Jason-1, and Jason-2. Adv. Space Res. 2010, 46, 1513–1540. [Google Scholar] [CrossRef]
- Liu, M.; Yuan, Y.; Ou, J.; Chai, Y. Research on Attitude Models and Antenna Phase Center Correction for Jason-3 Satellite Orbit Determination. Sensors 2019, 19, 2408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, S.C.; Yunck, T.P.; Thornton, C.L. Reduced-dynamic technique for precise orbit determination of low earth satellites. J. Guid. Control. Dyn. 1991, 14, 24–30. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Jiang, K.; Li, W.; Zhao, Q.; Peng, H.; Lin, M. Precise orbit determination of the Haiyang 2C altimetry satellite using attitude modeling. GPS Solutions 2022, 26, 1–14. [Google Scholar] [CrossRef]
- Min, L.; Qu, L.; Zhao, Q.; Jing, G.; Xing, S.; Li, X. Precise Point Positioning with the BeiDou Navigation Satellite System. Sensors 2014, 14, 927–943. [Google Scholar]
- Li, M.; Li, W.; Shi, C.; Jiang, K.; Guo, X.; Dai, X.; Meng, X.; Yang, Z.; Yang, G.; Liao, M. Precise orbit determination of the Fengyun-3C satellite using onboard GPS and BDS observations. J. Geodesy 2017, 91, 1313–1327. [Google Scholar] [CrossRef] [Green Version]
- Xiong, C.; Lu, C.; Zhu, J.; Ding, H. Orbit determination using real tracking data from FY3C-GNOS. Adv. Space Res. 2017, 60, 543–556. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, C.; Guo, J.; Yang, G.; Liao, M.; Ma, H.; Liu, J. Enhanced orbit determination for BeiDou satellites with FengYun-3C onboard GNSS data. GPS Solutions 2017, 21, 1179–1190. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhang, K.; Meng, X.; Zhang, W.; Zhang, Q.; Zhang, X.; Li, X. Precise Orbit Determination for the FY-3C Satellite Using Onboard BDS and GPS Observations from 2013, 2015, and 2017. Engineering 2019, 6, 904–912. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, X.; Qu, L.; Zhao, Q. Precise Orbit Determination of FY-3C with Calibration of Orbit Biases in BeiDou GEO Satellites. Remote Sens. 2018, 10, 382. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Zhou, S.; Ci, Y.; Hu, X.; Cao, J.; Chang, Z.; Tang, C.; Guo, D.; Guo, K.; Liao, M. High-precision orbit determination for a LEO nanosatellite using BDS-3. GPS Solutions 2020, 24, 1–14. [Google Scholar] [CrossRef]
- The General Information of HY-2 Satellites. Available online: https://ilrs.gsfc.nasa.gov/missions/satellite_missions/current_missions/hy2d_general.html (accessed on 10 February 2022).
- Montenbruck, O.; Gill, E.; Lutze, F. Satellite Orbits: Models, Methods, and Applications. Appl. Mech. Rev. 2002, 55, B27–B28. [Google Scholar] [CrossRef]
- Rim, H.; Kang, Z.; Nagel, P.; Yoon, S.; Bettadpur, S.; Schutz, B.; Tapley, B. CHAMP precision orbit determination. Advances in the Astronautical Sciences. 2002.
- Rim, H.J.; Yoon, S.P.; Schutz, R.E. Effect of GPS orbit accuracy on CHAMP precision orbit determination. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, San Antonio, TX, USA, 27–30 January 2002; 2002; 2, pp. 1411–1418. [Google Scholar]
- Zhao, Q. Research on Precision Orbit Determination Theory and Software of both GPS Navigation Constellation and LEO Satellites; Wuhan University: Wuhan, China, 2004. [Google Scholar]
- Lemoine, J.M.; Biancale, R.; Reinquin, F.; Bourgogne, S.; Gégout, P. CNES/GRGS RL04 Earth gravity field models, from GRACE and SLR data. GFZ Data Serv. 2019. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisions and scientific issues. J. Geophys. Res. 2002, 107, SIA15-1–SIA15-16. [Google Scholar] [CrossRef]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P. Adjustable box-wing model for solar radiation pressure impacting GPS satellites. Adv. Space Res. 2012, 49, 1113–1128. [Google Scholar] [CrossRef]
- Standish, E.M. JPL Planetary and Lunar Ephemerides, DE405/LE405, Jet Propulsion Laboratory Interoffice Memoran-Dum. 312.F-98-048. 1998. [Google Scholar]
- Knocke, P.; Ries, J.; Tapley, B. Earth radiation pressure effects on satellites. In Proceedings of the Astrodynamics Conference, Stowe, Vermont, 15–17 August 1988. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS conventions. IERS Technical Note No.36; IERS Convention Centre, 2010. Available online: https://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn36.html (accessed on 10 February 2022).
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Bizouard, C.; Lambert, S.; Gattano, C.; Becker, O.; Richard, J.-Y. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014. J. Geodesy 2018, 93, 621–633. [Google Scholar] [CrossRef]
- Mendes, V.B.; Pavlis, E.C. High-accuracy zenith delay prediction at optical wavelengths. Geophys. Res. Lett. 2004, 31, 189–207. [Google Scholar] [CrossRef] [Green Version]
- Pearlman, M.; Degnan, J.; Bosworth, J. The International Laser Ranging Service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]

| X (mm) | Y (mm) | Z (mm) | |
|---|---|---|---|
| Center of mass | 1319.4 | −4.7 | 5.7 |
| GPS phase center (L1) | 347.2 | −181.9 | −1377.5 |
| GPS phase center (L2) | 347.4 | −181.0 | −1396.1 |
| BDS phase center (B1) | 427.4 | 177.7 | −1378.5 |
| BDS phase center (B2) | 427.7 | 177.9 | −1397.3 |
| LRA spherical center | 311.7 | −215.5 | 1060.8 |
| X+ | X− | Y+ | Y− | Z+ | Z− | SA+ | SA− | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Spacecraft surfaces | Projected area (m2) | 3.62 | 3.92 | 5.17 | 5.46 | 3.06 | 6.22 | - | - | |
| Visible | Specular | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | - | - | |
| Diffuse | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||||
| Absorbed | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | - | - | ||
| Infra-red | Specular | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | - | - | |
| Diffuse | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | ||||
| Absorbed | 0.69 | 0.69 | 0.69 | 0.69 | 0.69 | 0.69 | - | - | ||
| Radiators and solar arrays | Projected area (m2) | 0.33 | 0.37 | 2.61 | 2.33 | 4.88 | 1.72 | 18.12 | 18.12 | |
| Visible | Specular | 0.87 | 0.87 | 0.87 | 0.87 | 0.00 | 0.87 | 0.10 | 0.00 | |
| Diffuse | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.00 | 0.00 | 0.10 | ||
| Absorbed | 0.13 | 0.13 | 0.13 | 0.13 | 0.85 | 0.13 | 0.90 | 0.90 | ||
| Infra-red | Specular | 0.22 | 0.22 | 0.22 | 0.22 | 0.00 | 0.22 | 0.08 | 0.00 | |
| Diffuse | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.00 | 0.00 | 0.10 | ||
| Absorbed | 0.78 | 0.78 | 0.78 | 0.78 | 0.85 | 0.78 | 0.92 | 0.90 | ||
| Date (Year/Month/Day) | Time (Hour/Minute/Second) | Roll (deg.) | Pitch (deg.) | Yaw (deg.) |
|---|---|---|---|---|
| 2021/7/10 | 19:20:56.322 | −0.0770 | −0.0385 | +88.0330 |
| 2021/7/10 | 19:20:57.346 | −0.0770 | −0.0385 | +88.1155 |
| 2021/7/10 | 19:20:58.370 | −0.0770 | −0.0385 | +88.1980 |
| 2021/7/10 | 19:20:59.394 | −0.0770 | −0.0385 | +88.2805 |
| 2021/7/10 | 19:21:00.418 | −0.0770 | −0.0385 | +88.3630 |
| 2021/7/10 | 19:21:01.442 | −0.0770 | −0.0385 | +88.4455 |
| 2021/7/10 | 19:21:02.466 | −0.0825 | −0.0385 | +88.5225 |
| 2021/7/10 | 19:21:03.490 | −0.0825 | −0.0385 | +88.6050 |
| 2021/7/10 | 19:21:04.514 | −0.0825 | −0.0385 | +88.6875 |
| 2021/7/10 | 19:21:05.538 | −0.0825 | −0.0385 | +88.7700 |
| … | … | … | … | … |
| 2021/7/10 | 19:30:47.425 | −0.1650 | +0.0165 | +133.0285 |
| 2021/7/10 | 19:30:48.449 | −0.1650 | +0.0165 | +133.1000 |
| 2021/7/10 | 19:30:49.473 | −0.1650 | +0.0165 | +133.1715 |
| 2021/7/10 | 19:30:50.497 | −0.1650 | +0.0165 | +133.2375 |
| 2021/7/10 | 19:30:51.521 | −0.1650 | +0.0165 | +133.3090 |
| 2021/7/10 | 19:30:52.545 | −0.1650 | +0.0165 | +133.3750 |
| 2021/7/10 | 19:30:53.313 | −0.1650 | +0.0165 | +133.4300 |
| 2021/7/10 | 19:30:54.337 | −0.1650 | +0.0165 | +133.4960 |
| Project | Selection/Description |
|---|---|
| Dynamic model | |
| Gravity model | EIGEN-GRGS.RL04. MEAN-FIELD 120 × 120 [29] |
| Atmosphere drag | MSIS00 density model [30] |
| Solar radiation pressure | Box-Wing model [31] |
| Sun and moon ephemeris | JPL DE405 [32] |
| Earth radiation pressure | Knocke-Ries-Tapley model [33] |
| Empirical force model | RTN perturbation |
| Ocean tide [34] | FES2004 [35] |
| Solid Earth tide [34] | TIDE2000 [34] |
| Earth orientation parameter | IERS EOP 14 C04 [36], IAU2000A model |
| Observation model | |
| Data type | Code and phase observation of ionosphere-free combination |
| Data interval | 30 s |
| Elevation cutoff | 7° |
| HY2D satellite attitude | Quaternion data |
| GPS and BDS phase model | IGS14.atx |
| Orbit determination arc length and integration step | 24 h arc dynamic solution, 30 s integral step |
| GPS and BDS satellite ephemeris and clock | CODE precise products |
| Atmospheric drag coefficient estimation | Cd/6 h |
| Solar radiation pressure coefficient estimation | Cr/24 h |
| RTN perturbation estimation | Tangential and normal/24 h |
| Receiver clock error estimation | Gaussian white noise |
| Ambiguities | Float solutions of ionosphere-free combination |
| SLR validation for the calculated HY2D orbit | |
| Cut-off angle | 20° |
| SLR station coordinate | SLRF2014 |
| Troposphere delay correction | Mendes-Pavlis delay model [37] |
| Relativity correction (propagation path) | IERS Conventions 2010 [34] |
| Mean | RMS | ||
|---|---|---|---|
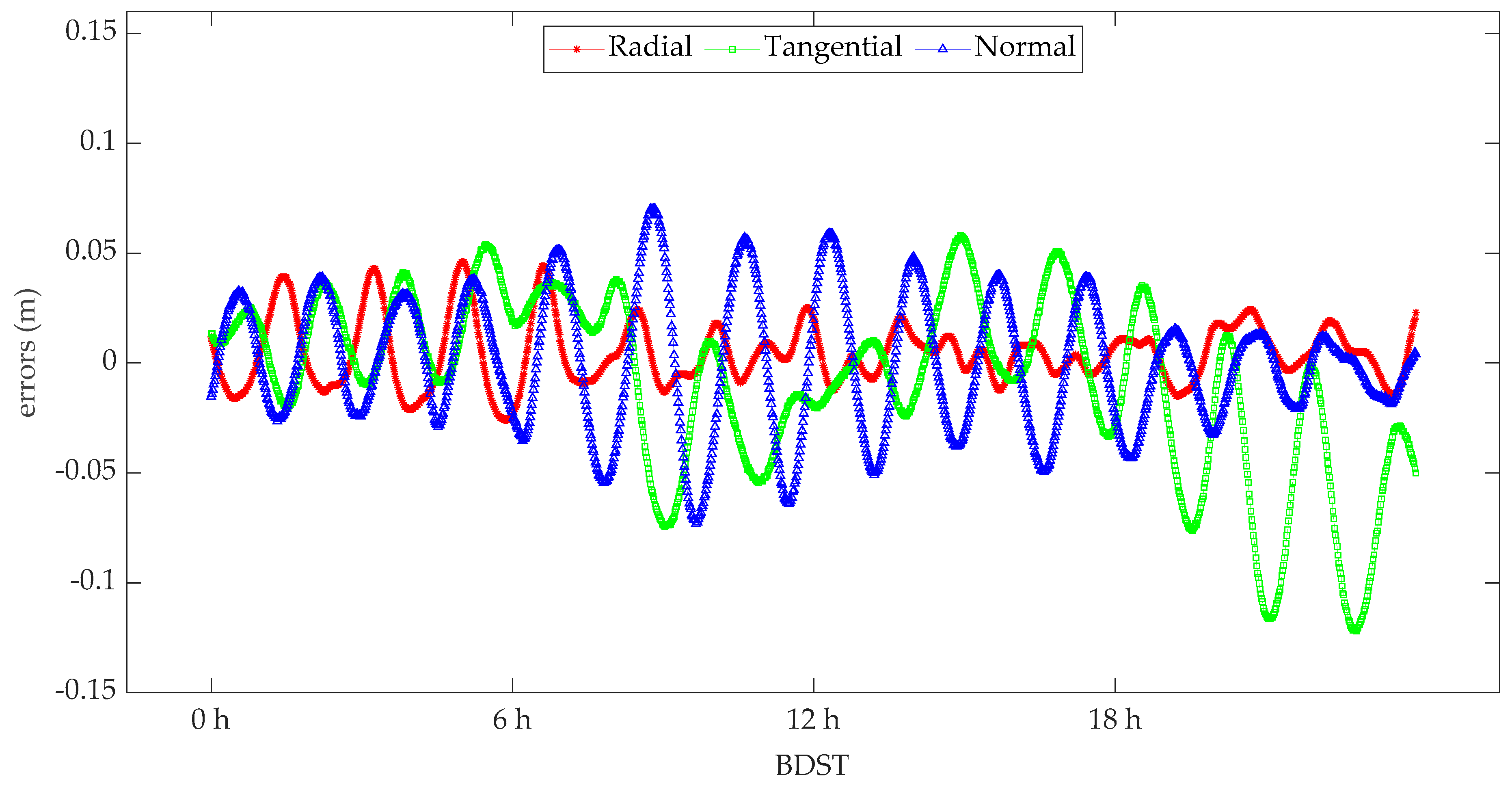
| BDS | Radial | 0.4 | 1.5 |
| Tangential | −0.8 | 4.1 | |
| Normal | 0.1 | 3.0 | |
| 3DRMS | 5.3 | ||
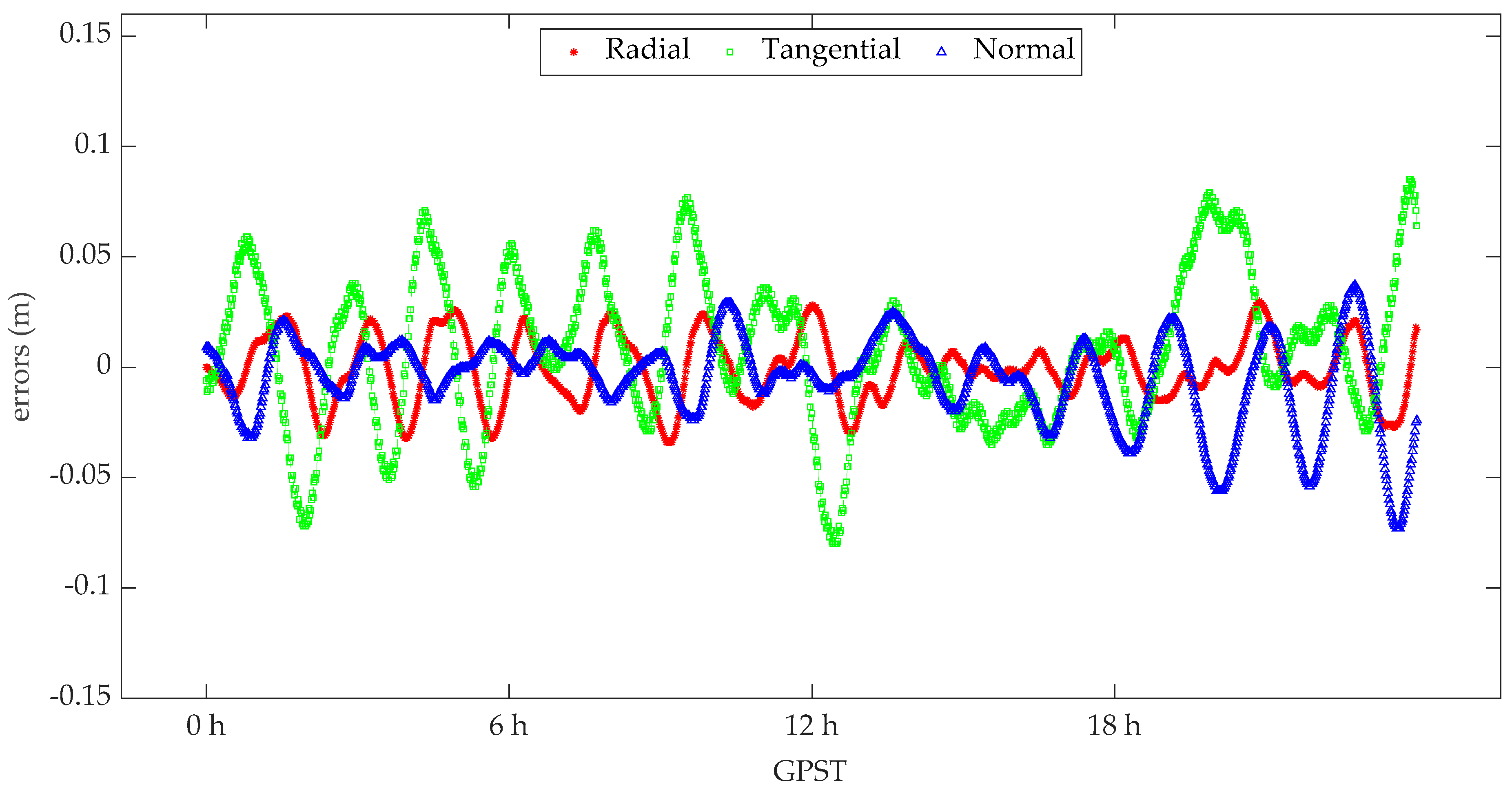
| GPS | Radial | −0.1 | 1.5 |
| Tangential | 0.8 | 3.5 | |
| Normal | −0.5 | 2.0 | |
| 3DRMS | 4.3 | ||
| Doy | R | T | N | 3DRMS |
|---|---|---|---|---|
| 187 | 1.5 | 4.1 | 3.1 | 5.3 |
| 188 | 1.5 | 4.1 | 3.0 | 5.3 |
| 189 | 1.5 | 4.1 | 3.0 | 5.3 |
| 190 | 1.5 | 4.1 | 3.1 | 5.3 |
| 191 | 1.5 | 4.1 | 3.0 | 5.3 |
| 192 | 1.5 | 4.1 | 3.0 | 5.3 |
| 193 | 1.5 | 4.1 | 3.1 | 5.4 |
| 194 | 1.5 | 4.1 | 3.1 | 5.4 |
| 195 | 1.6 | 4.1 | 3.1 | 5.4 |
| 196 | 1.5 | 4.1 | 3.1 | 5.3 |
| 197 | 1.5 | 4.1 | 3.1 | 5.3 |
| 198 | 1.6 | 4.1 | 3.1 | 5.3 |
| 199 | 1.5 | 4.2 | 3.1 | 5.4 |
| 200 | 1.5 | 4.1 | 3.1 | 5.4 |
| Mean | 1.5 | 4.1 | 3.1 | 5.4 |
| Doy | R | T | N | 3DRMS |
|---|---|---|---|---|
| 201 | 1.6 | 3.6 | 2.3 | 4.5 |
| 202 | 1.5 | 3.5 | 2.0 | 4.3 |
| 203 | 1.5 | 3.5 | 2.2 | 4.4 |
| 204 | 1.5 | 3.5 | 2.1 | 4.3 |
| 205 | 1.5 | 3.5 | 2.1 | 4.3 |
| 206 | 1.5 | 3.5 | 2.1 | 4.3 |
| 207 | 1.4 | 3.5 | 2.1 | 4.3 |
| 208 | 1.4 | 3.5 | 2.1 | 4.3 |
| 209 | 1.4 | 3.5 | 2.1 | 4.3 |
| 210 | 1.4 | 3.5 | 2.1 | 4.3 |
| 211 | 1.5 | 3.5 | 2.1 | 4.4 |
| 212 | 1.5 | 3.5 | 2.1 | 4.3 |
| 213 | 1.4 | 3.5 | 2.1 | 4.3 |
| 214 | 1.4 | 3.5 | 2.1 | 4.3 |
| 215 | 1.4 | 3.5 | 2.2 | 4.4 |
| 216 | 1.5 | 3.5 | 2.1 | 4.3 |
| 217 | 1.5 | 3.5 | 2.1 | 4.3 |
| 218 | 1.5 | 3.5 | 2.1 | 4.3 |
| 219 | 1.4 | 3.5 | 2.1 | 4.3 |
| 220 | 1.4 | 3.5 | 2.1 | 4.3 |
| 221 | 1.4 | 3.5 | 2.1 | 4.4 |
| 222 | 1.5 | 3.5 | 2.1 | 4.4 |
| Mean | 1.4 | 3.5 | 2.1 | 4.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, H.; Zhou, C.; Zhong, S.; Peng, B.; Zhou, X.; Yan, H.; Zhang, J.; Han, J.; Guo, F.; Chen, R. Analysis of Precise Orbit Determination for the HY2D Satellite Using Onboard GPS/BDS Observations. Remote Sens. 2022, 14, 1390. https://doi.org/10.3390/rs14061390
Peng H, Zhou C, Zhong S, Peng B, Zhou X, Yan H, Zhang J, Han J, Guo F, Chen R. Analysis of Precise Orbit Determination for the HY2D Satellite Using Onboard GPS/BDS Observations. Remote Sensing. 2022; 14(6):1390. https://doi.org/10.3390/rs14061390
Chicago/Turabian StylePeng, Hailong, Chongchong Zhou, Shiming Zhong, Bibo Peng, Xuhua Zhou, Haoming Yan, Jie Zhang, Jinyang Han, Fengcheng Guo, and Runjing Chen. 2022. "Analysis of Precise Orbit Determination for the HY2D Satellite Using Onboard GPS/BDS Observations" Remote Sensing 14, no. 6: 1390. https://doi.org/10.3390/rs14061390
APA StylePeng, H., Zhou, C., Zhong, S., Peng, B., Zhou, X., Yan, H., Zhang, J., Han, J., Guo, F., & Chen, R. (2022). Analysis of Precise Orbit Determination for the HY2D Satellite Using Onboard GPS/BDS Observations. Remote Sensing, 14(6), 1390. https://doi.org/10.3390/rs14061390






