High-Rate One-Hourly Updated Ultra-Rapid Multi-GNSS Satellite Clock Offsets Estimation and Its Application in Real-Time Precise Point Positioning
Abstract
:1. Introduction
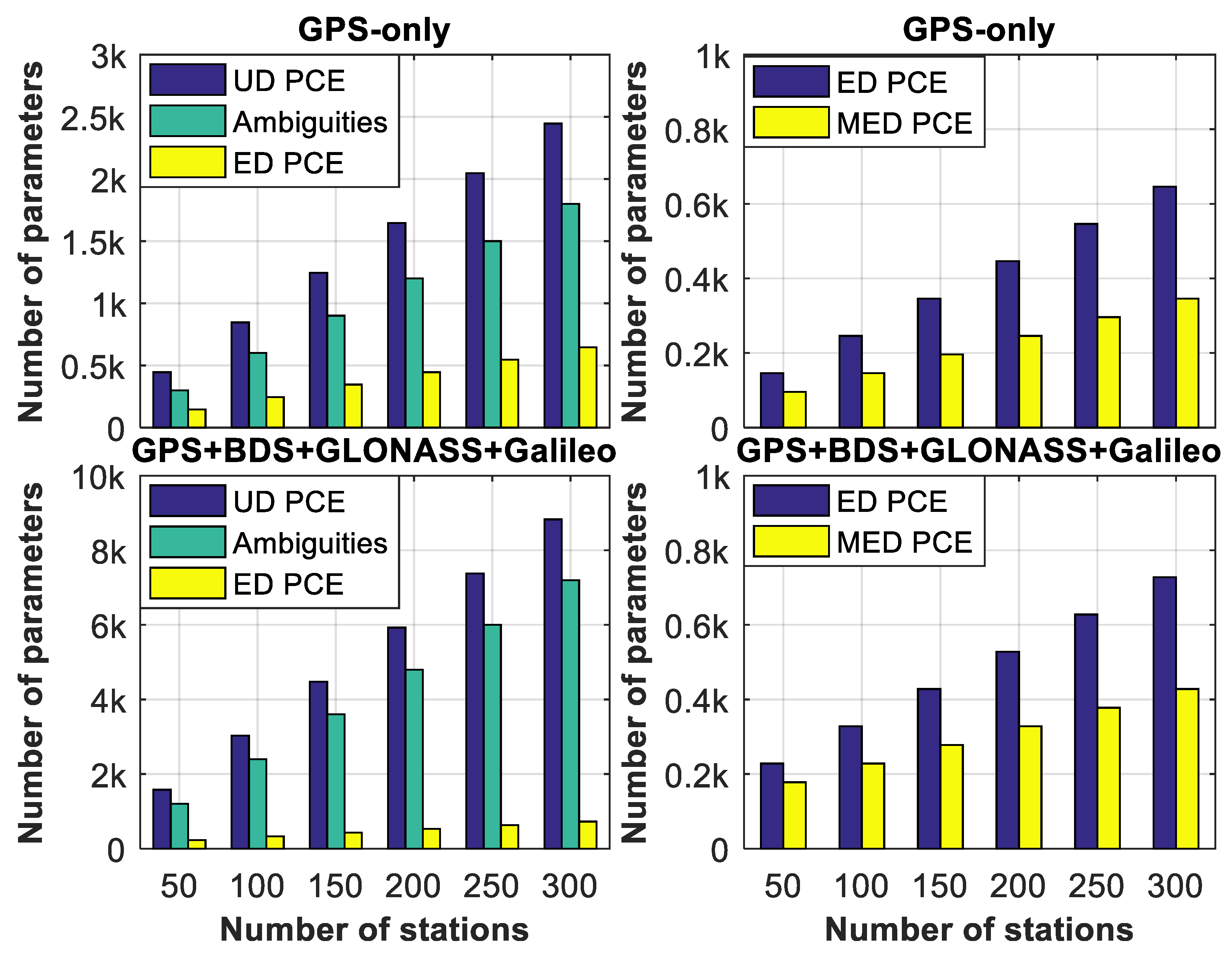
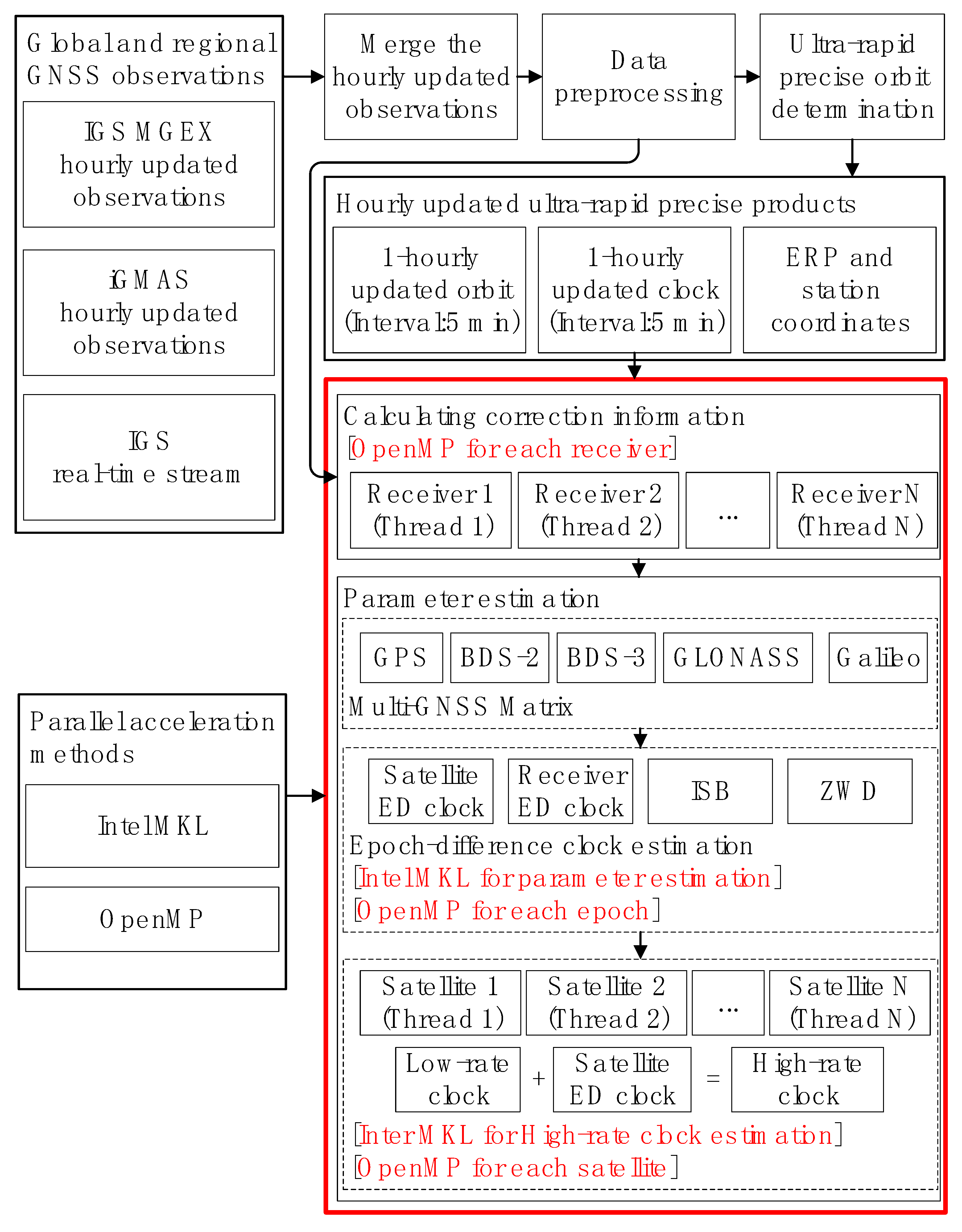
2. Methods
3. Datasets and Processing Strategies
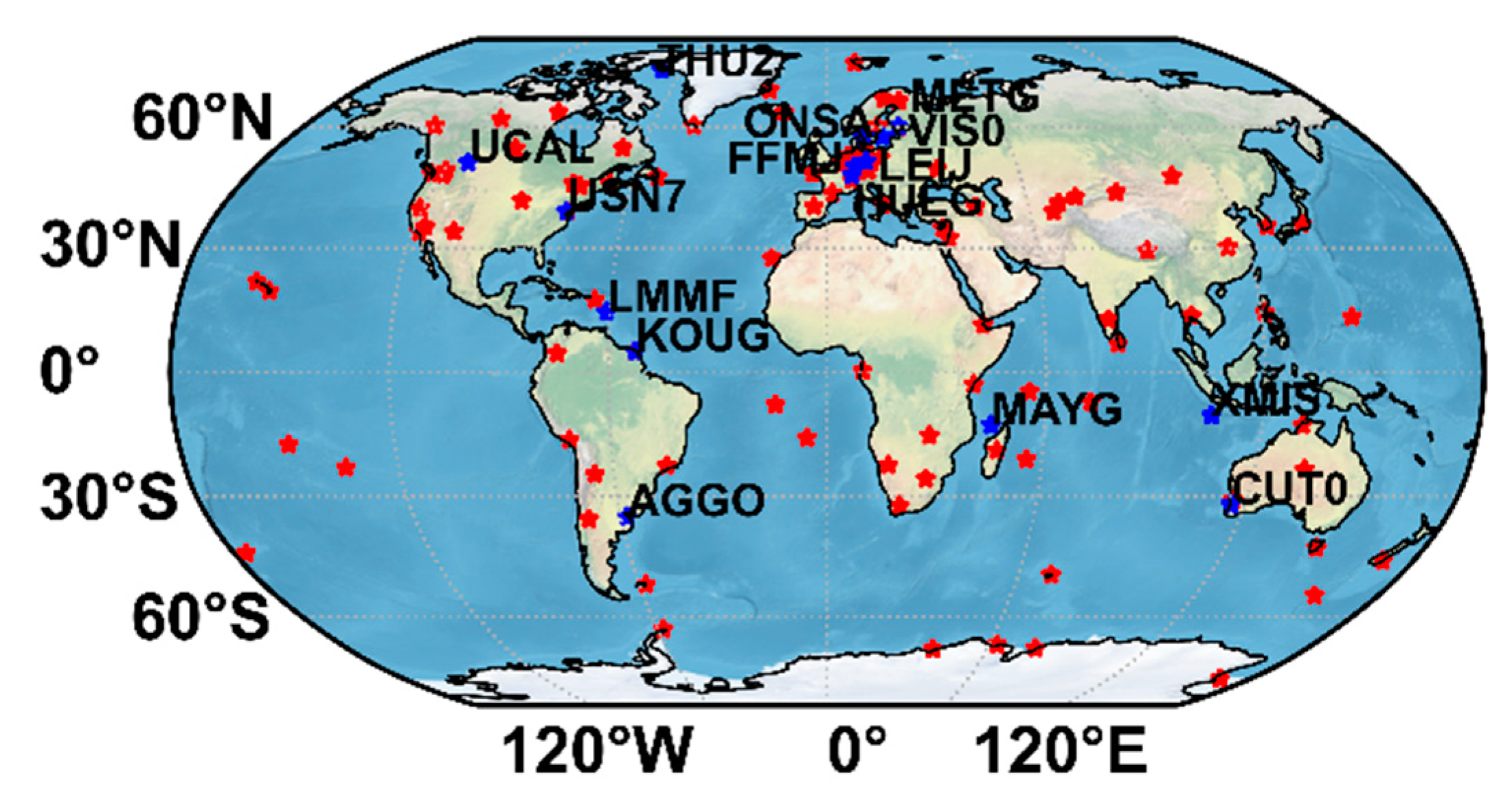
3.1. Datasets
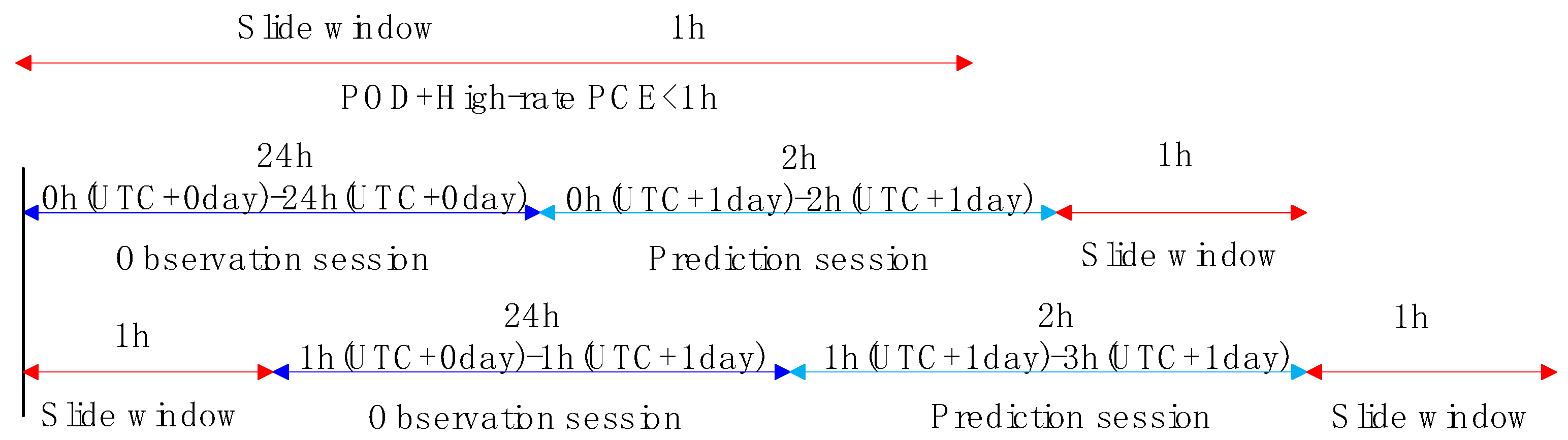
3.2. Processing Strategies
4. Validation and Results
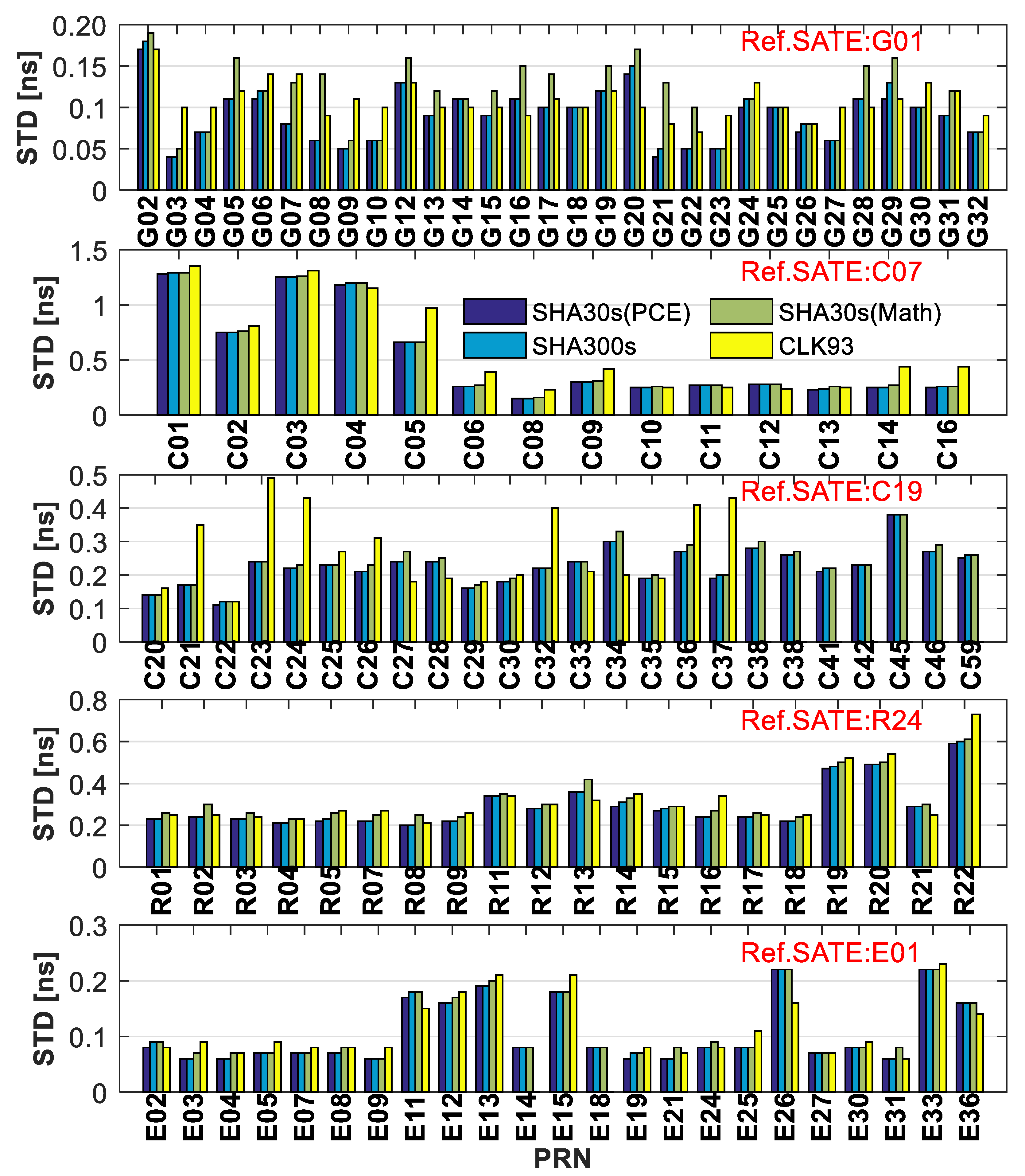
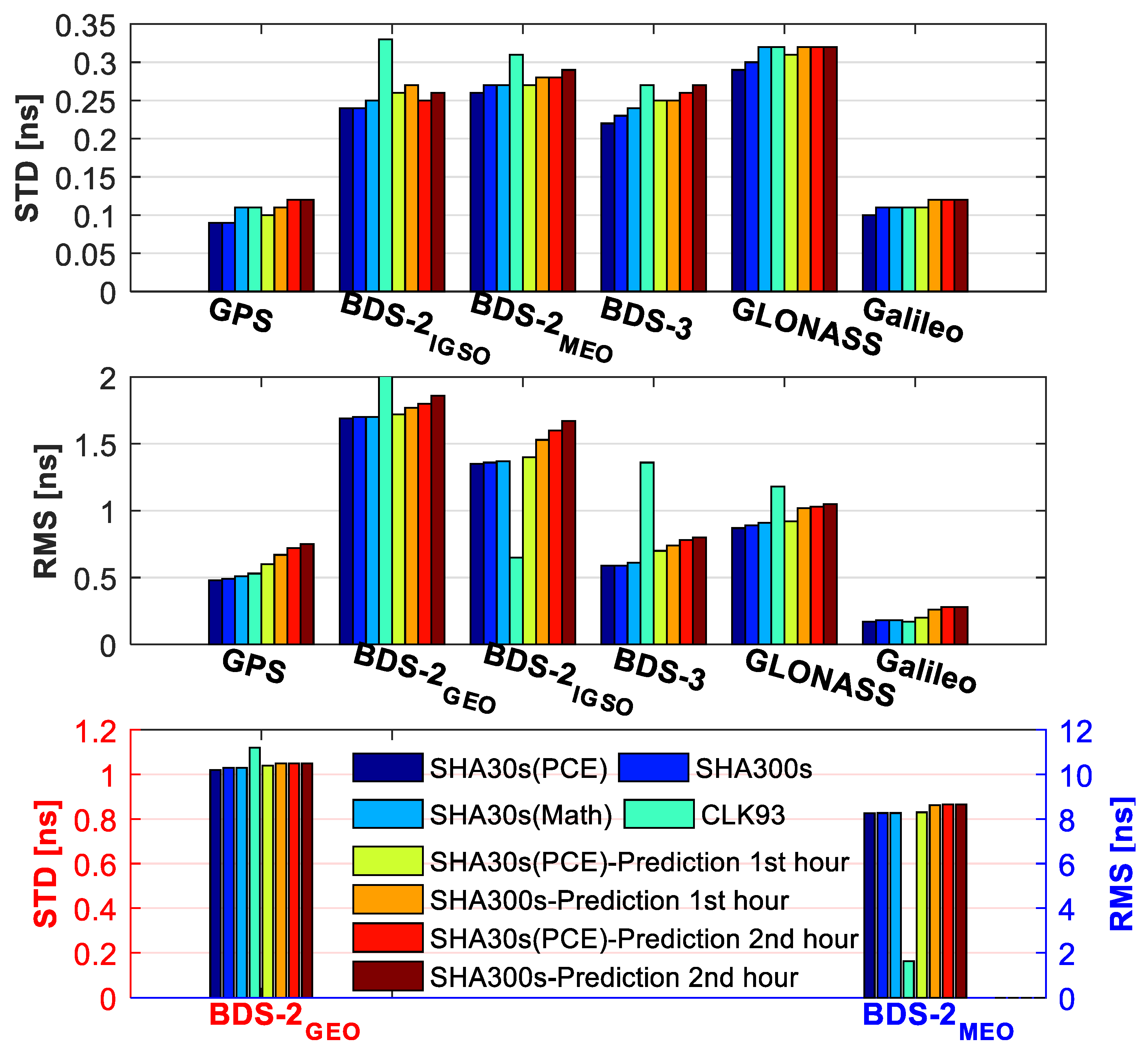
4.1. The ED Clock Offsets
4.2. The Absolute Clock Offsets
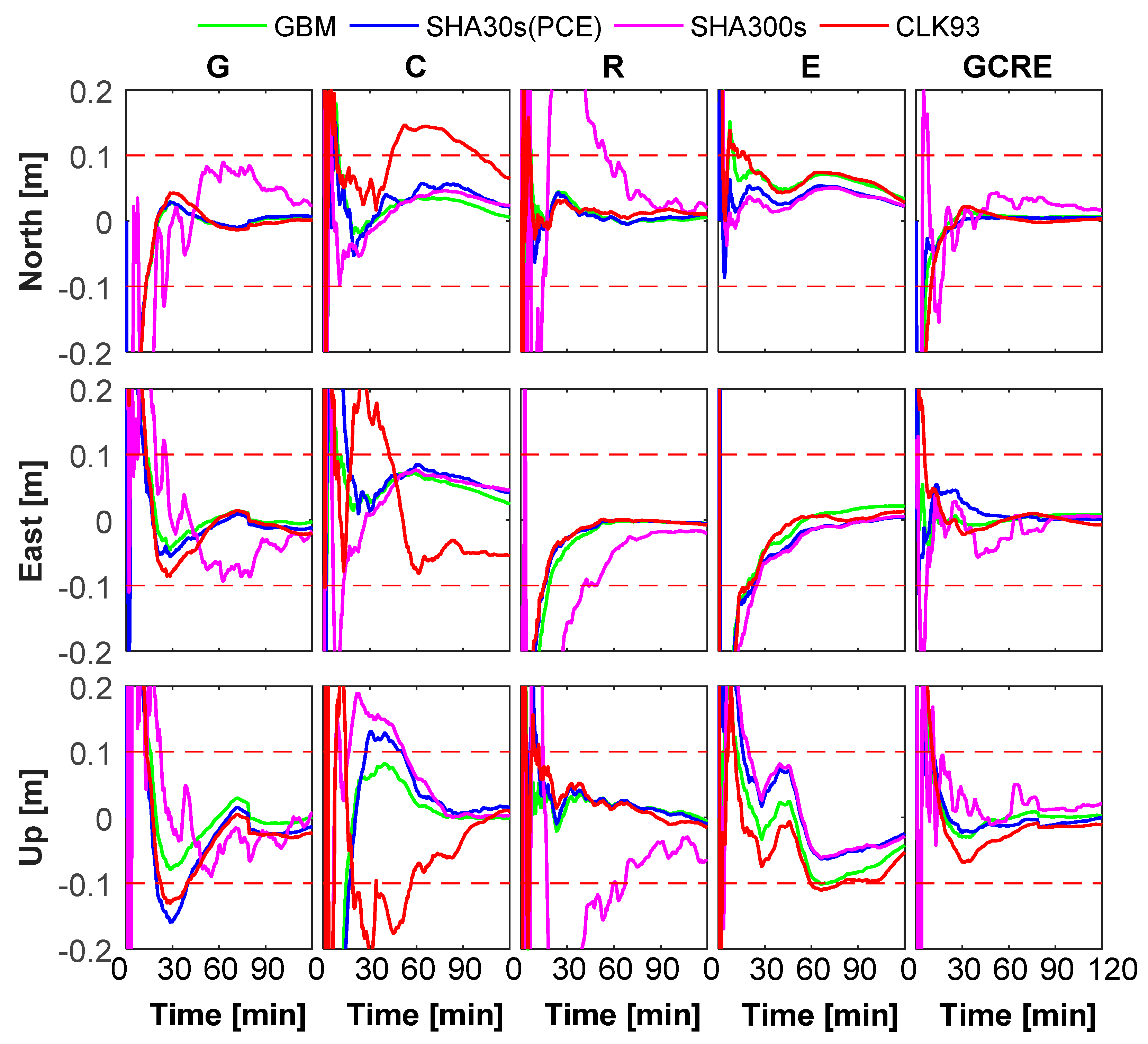
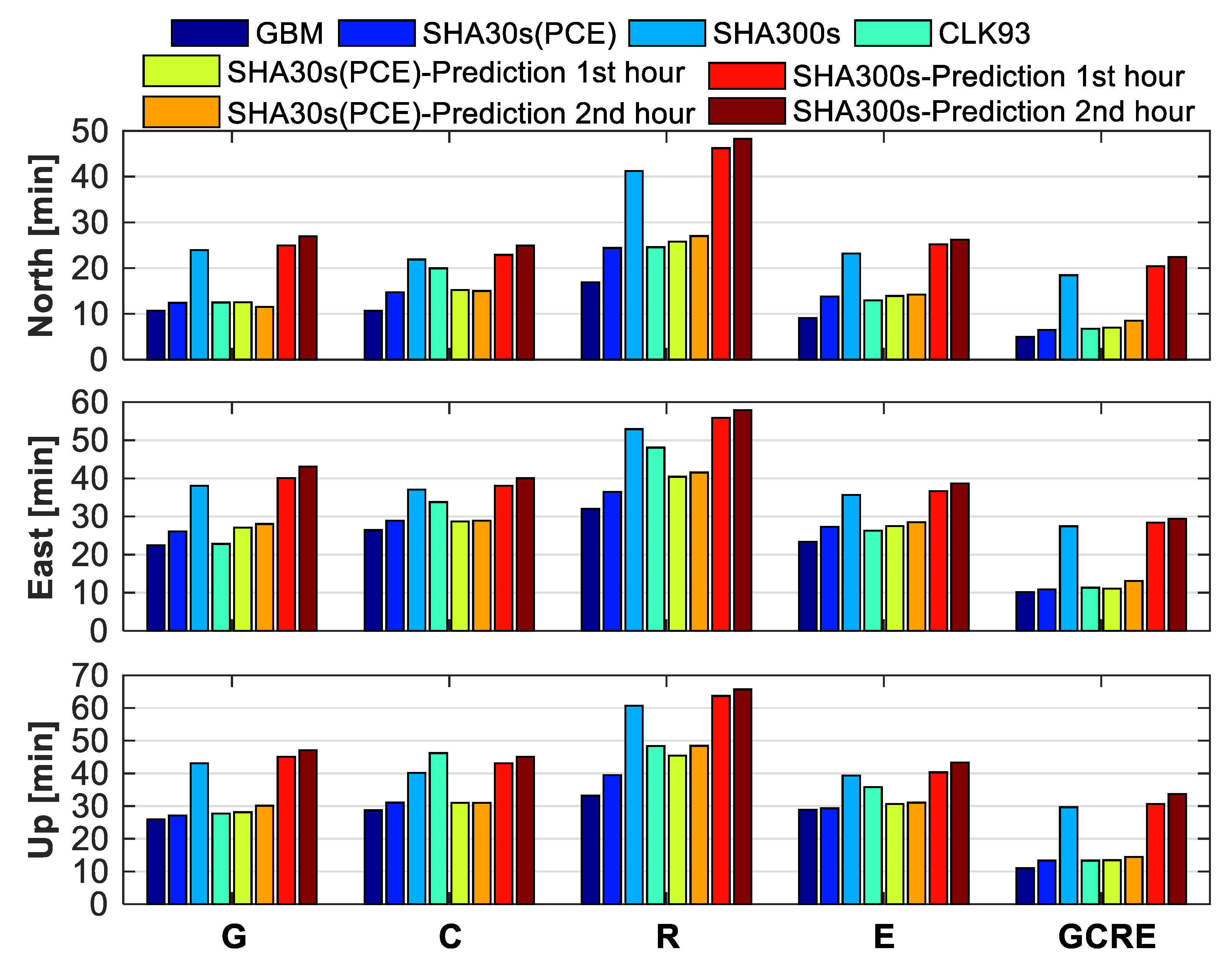
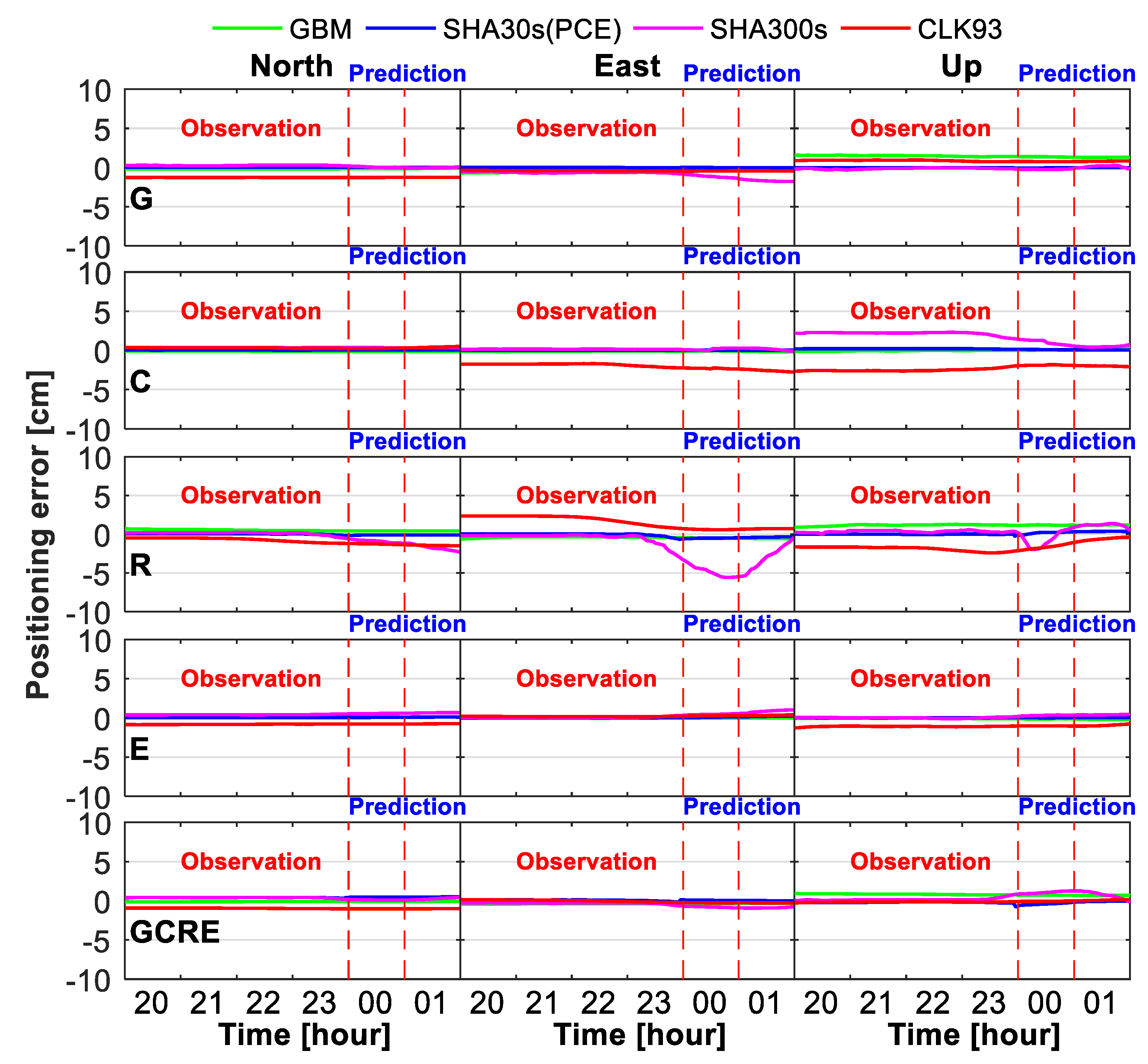
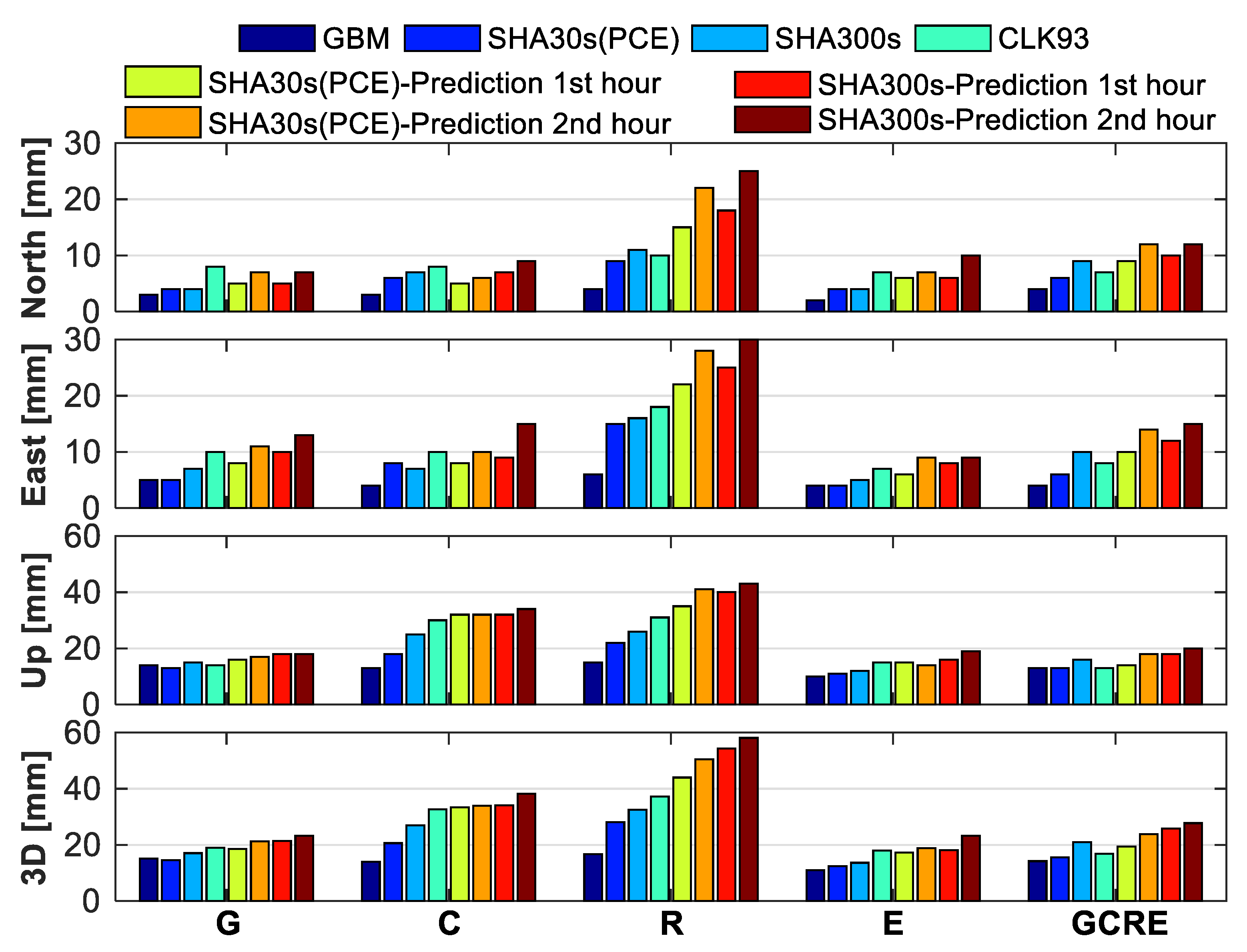
4.3. Real-Time PPP Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products; Jet Propulsion Laboratory: Pasadena, CA, USA, 2009; p. 34. Available online: http://igscb.jpl.nasa.gov/igscb/resource/pubs/GuidetoUsingIGSProducts.pdf (accessed on 1 March 2022).
- Dow, J.M.; Neilan, R.E.; Rizos, C. The International GNSS Service in a changing landscape of Global Navigation Satellite Systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Choi, K.K.; Ray, J.; Griffiths, J.; Bae, T.-S. Evaluation of GPS orbit prediction strategies for the IGS Ultra-rapid products. GPS Solut. 2012, 17, 403–412. [Google Scholar] [CrossRef]
- Lutz, S.; Beutler, G.; Schaer, S.; Dach, R.; Jäggi, A. CODE’s new ultra-rapid orbit and ERP products for the IGS. GPS Solut. 2014, 20, 239–250. [Google Scholar] [CrossRef] [Green Version]
- Elsobeiey, M.; Al-Harbi, S. Performance of real-time Precise Point Positioning using IGS real-time service. GPS Solut. 2015, 20, 565–571. [Google Scholar] [CrossRef]
- Laurichesse, D.; Cerri, L.; Berthias, J.P.; Mercier, F. Real Time Precise GPS Constellation and Clocks Estimation by Means of a Kalman Filter. In Proceedings of the 26th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS + 2013), Nashville, TN, USA, 16–20 September 2013; pp. 1155–1163. [Google Scholar]
- Ge, M.; Chen, J.; Douša, J.; Gendt, G.; Wickert, J. A computationally efficient approach for estimating high-rate satellite clock corrections in realtime. GPS Solut. 2011, 16, 9–17. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.P.; Rothacher, M. A New Data Processing Strategy for Huge GNSS Global Networks. J. Geod. 2006, 80, 199–203. [Google Scholar] [CrossRef]
- Zuo, X.; Jiang, X.; Li, P.; Wang, J.; Ge, M.; Schuh, H. A square root information filter for multi-GNSS real-time precise clock estimation. Satell. Navig. 2021, 2, 28. [Google Scholar] [CrossRef]
- Li, X.; Chen, X.; Ge, M.; Schuh, H. Improving multi-GNSS ultra-rapid orbit determination for real-time precise point positioning. J. Geod. 2018, 93, 45–64. [Google Scholar] [CrossRef]
- Chen, Q.; Song, S.; Zhou, W. Accuracy Analysis of GNSS Hourly Ultra-Rapid Orbit and Clock Products from SHAO AC of iGMAS. Remote Sens. 2021, 13, 1022. [Google Scholar] [CrossRef]
- Guo, J.; Xu, X.; Zhao, Q.; Liu, J. Precise orbit determination for quad-constellation satellites at Wuhan University: Strategy, result validation, and comparison. J. Geod. 2015, 90, 143–159. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, Q.; Xu, X. A New Method and Strategy for Precise Ultra-Rapid Orbit Determination. In Proceedings of the China Satellite Navigation Conference (CSNC), Shanghai, China, 23–25 May 2017; Lecture Notes in Electrical Engineering. Springer: Singapore, 2017; pp. 191–205. [Google Scholar]
- Guo, F.; Zhang, X.; Li, X.; Cai, S. Impact of sampling rate of IGS satellite clock on precise point positioning. Geo-Spat. Inf. Sci. 2010, 13, 150–156. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Guo, F. Satellite clock estimation at 1 Hz for realtime kinematic PPP applications. GPS Solut. 2010, 15, 315–324. [Google Scholar] [CrossRef]
- Hein, G.W. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 22. [Google Scholar] [CrossRef] [PubMed]
- Bahadur, B.; Nohutcu, M. Comparative analysis of MGEX products for post-processing multi-GNSS PPP. Measurement 2019, 145, 361–369. [Google Scholar] [CrossRef]
- Bock, H.; Dach, R.; Jäggi, A.; Beutler, G. High-rate GPS clock corrections from CODE: Support of 1 Hz applications. J. Geod. 2009, 83, 1083–1094. [Google Scholar] [CrossRef] [Green Version]
- Ye, S.; Zhao, L.; Song, J.; Chen, D.; Jiang, W. Analysis of estimated satellite clock biases and their effects on precise point positioning. GPS Solut. 2017, 22, 16. [Google Scholar] [CrossRef]
- Zhang, W.; Lou, Y.; Gu, S.; Shi, C.; Haase, J.S.; Liu, J. Joint estimation of GPS/BDS real-time clocks and initial results. GPS Solut. 2015, 20, 665–676. [Google Scholar] [CrossRef]
- Zhang, Q.; Moore, P.; Hanley, J.; Martin, S. Auto-BAHN: Software for near real-time GPS orbit and clock computations. Adv. Space Res. 2007, 39, 1531–1538. [Google Scholar] [CrossRef]
- Landskron, D.; Bohm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Rebischung, P.; Schmid, R. IGS14/igs14.atx: A new framework for the IGS products. In Proceedings of the AGU Fall Meeting 2016, San Francisco, CA, USA, 12–16 December 2016; Volume 121, pp. 6109–6131. [Google Scholar]
- Wu, J.-T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. In Proceedings of the Astrodynamics 1991, San Diego, CA, USA, 19–22 August 1991; pp. 1647–1660. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions(2010); IERS Technical Note No. 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Zhou, W.; Huang, C.; Song, S.; Chen, Q.; Liu, Z. Characteristic Analysis and Short-Term Prediction of GPS/BDS Satellite Clock Correction. In Proceedings of the China Satellite Navigation Conference (CSNC) 2016 Proceedings: Volume III, Changsha, China, 27 April 2016; pp. 187–200. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Shen, J.; Dai, X. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system. Sci. China Earth Sci. 2013, 57, 144–152. [Google Scholar] [CrossRef]
- Deng, Z.; Ge, M.; Uhlemann, M.; Zhao, Q. Precise orbit determination of BeiDou satellites at GFZ. In Proceedings of the IGS Workshop, Vienna, Austria, 2 May 2014; pp. 23–27. [Google Scholar]
- Yao, Y.; He, Y.; Yi, W.; Song, W.; Cao, C.; Chen, M. Method for evaluating real-time GNSS satellite clock offset products. GPS Solut. 2017, 21, 1417–1425. [Google Scholar] [CrossRef]
- Uhlemann, M.; Gendt, G.; Ramatschi, M.; Deng, Z. GFZ global multi-GNSS network and data processing results. In IAG 150 Years; Springer: Berlin/Heidelberg, Germany, 2015; pp. 673–679. [Google Scholar]




| Items | Strategies | ||||
|---|---|---|---|---|---|
| System | GPS | GLONASS | Galileo | BDS-2 | BDS-3 |
| Frequency | L1/L2 | G1/G2 | E1/E5a | B1I/B3I | B1I/B3I |
| Observations | Pseudorange and carrier phase observations | ||||
| Elevation cutoff | 7 degrees | ||||
| Observation weighting | Elevation weight [sin(elevation)] | ||||
| Satellite orbit | Fixed by SHAO one-hourly updated ultra-rapid precise orbit products | ||||
| Satellite ED clock offsets | Estimated | ||||
| Satellite absolute clock offsets | Estimated by using satellite ED clock offsets and low-rate absolute clock offsets | ||||
| Receiver coordinate | Fixed by SHAO station coordinates | ||||
| Reference clock | Receiver clock | ||||
| Receiver ED clock | Ordinary station: EstimatedReference station: Fixed | ||||
| Tropospheric delay | SHA1: Modified Hopfield for dry and wet part SHA2: Modified Hopfield for dry part and estimated for wet part (10−9 m2/s) | ||||
| Ionospheric delay | Eliminated first order by IF observations | ||||
| Satellite antenna | IGS MGEX values | BDS official | |||
| Receiver antenna | IGS MGEX values | ||||
| Phase windup effect | Corrected [25] | ||||
| Relativistic effect | Corrected [26] | ||||
| Earth rotation | Corrected [26] | ||||
| Tide effect | Solid Earth, Pole, and Ocean tide | ||||
| Ambiguity | Eliminated by ED model | ||||
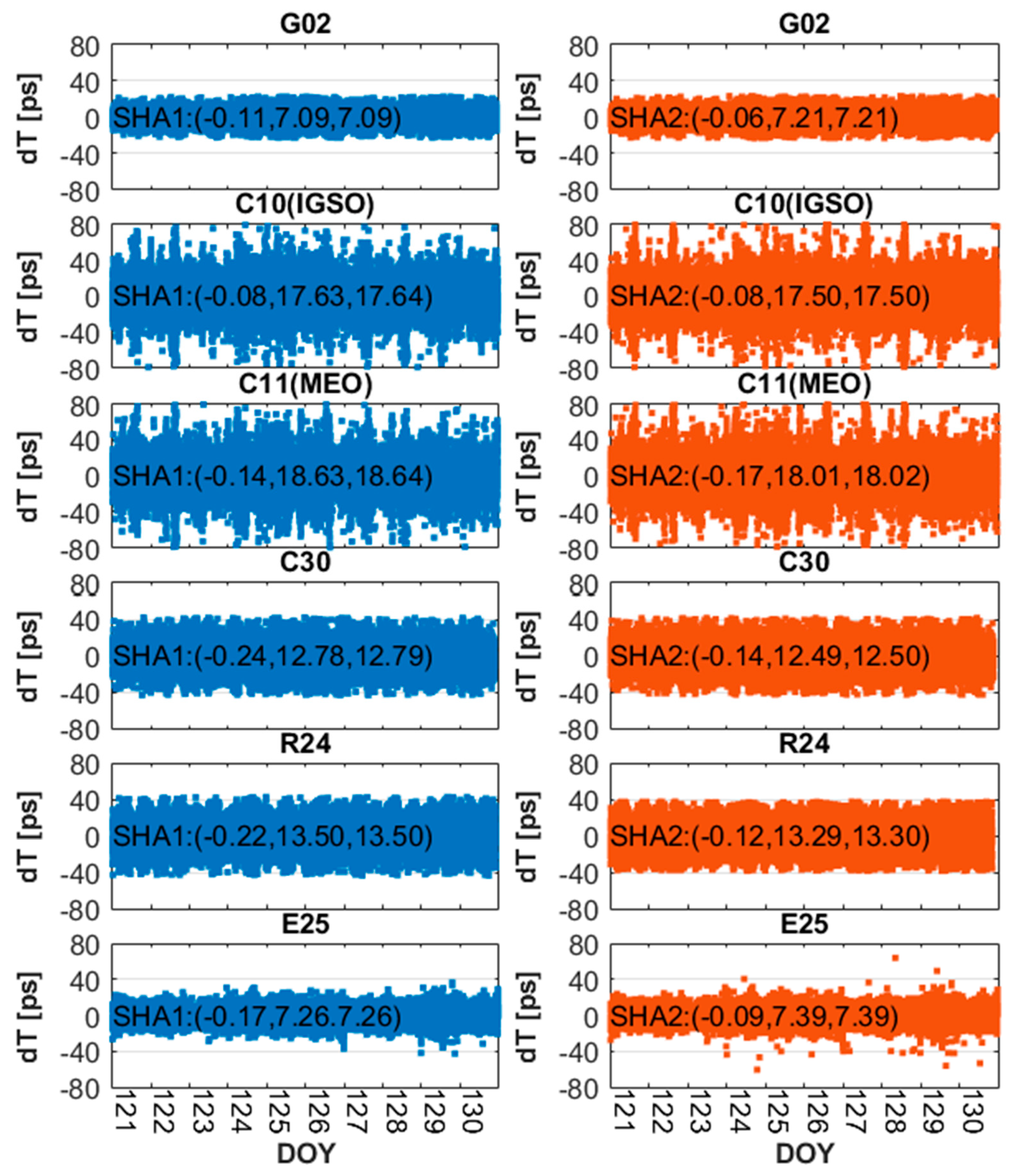
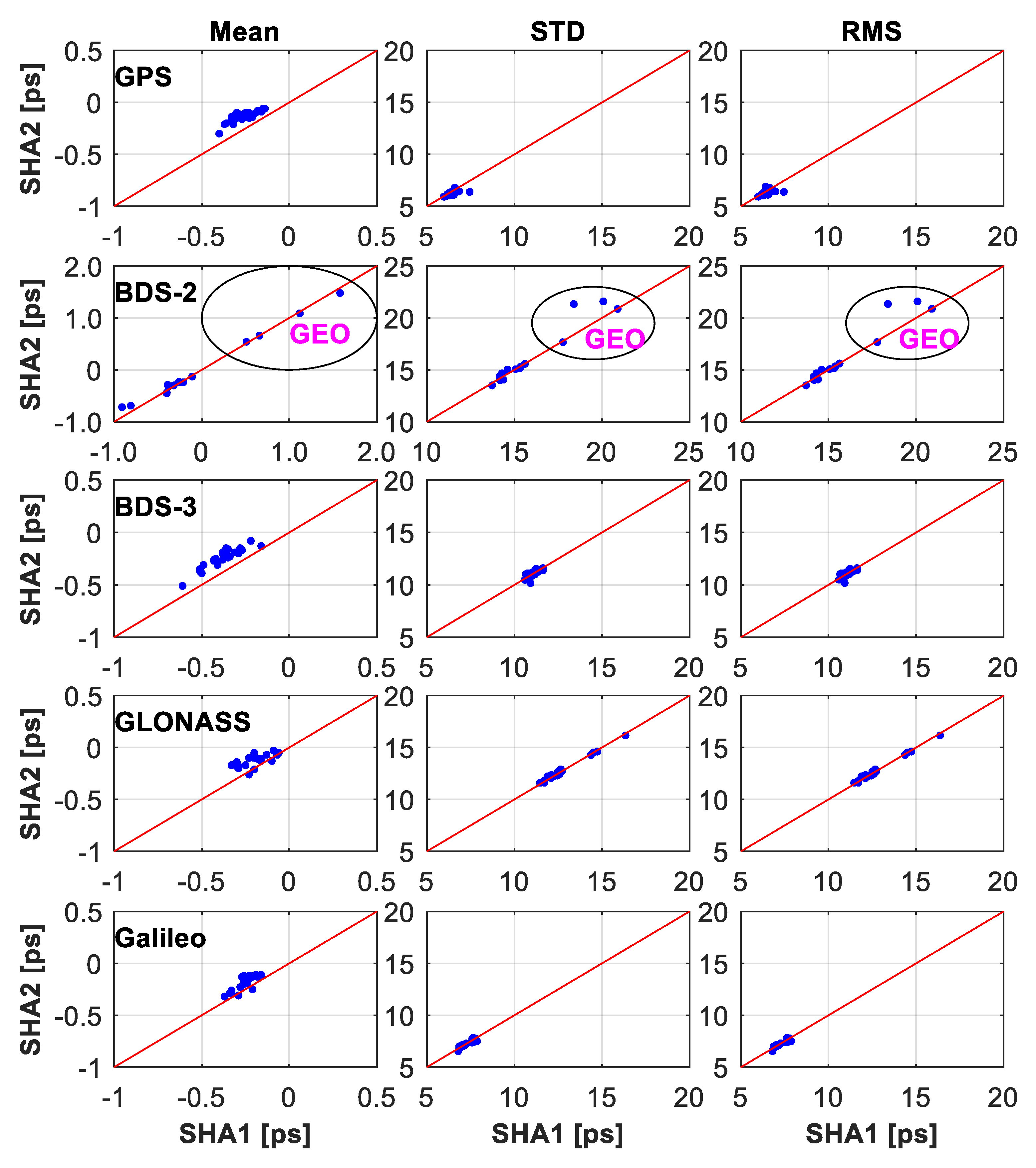
| System | GPS | BDS-2 (GEO) | BDS-2 (IGSO) | BDS-2 (MEO) | BDS-3 | GLONASS | Galileo | |
|---|---|---|---|---|---|---|---|---|
| Type | ||||||||
| SHA1 (GBM) | Mean | −0.26 | 0.96 | −0.47 | −0.30 | −0.37 | −0.20 | −0.25 |
| STD | 6.45 | 21.31 | 15.19 | 14.36 | 11.04 | 12.64 | 7.17 | |
| RMS | 6.46 | 21.33 | 15.20 | 14.36 | 11.05 | 12.65 | 7.17 | |
| SHA2 (GBM) | Mean | −0.13 | 0.94 | −0.43 | −0.25 | −0.24 | −0.13 | −0.18 |
| STD | 6.29 | 21.25 | 15.54 | 14.56 | 11.03 | 12.71 | 7.16 | |
| RMS | 6.32 | 21.27 | 15.55 | 14.57 | 11.03 | 12.71 | 7.16 | |
| SHA1 (COD) | Mean | −0.21 | Non | −0.27 | −0.22 | −0.25 | −0.11 | −0.22 |
| STD | 6.73 | Non | 14.93 | 14.50 | 11.22 | 12.61 | 6.87 | |
| RMS | 6.82 | Non | 15.01 | 14.52 | 11.24 | 12.71 | 6.90 | |
| SHA2 (COD) | Mean | −0.09 | Non | −0.15 | −0.17 | −0.13 | −0.03 | −0.12 |
| STD | 6.54 | Non | 15.46 | 13.90 | 11.46 | 13.26 | 7.32 | |
| RMS | 6.57 | Non | 15.50 | 14.00 | 11.48 | 13.30 | 7.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, G.; Song, S. High-Rate One-Hourly Updated Ultra-Rapid Multi-GNSS Satellite Clock Offsets Estimation and Its Application in Real-Time Precise Point Positioning. Remote Sens. 2022, 14, 1257. https://doi.org/10.3390/rs14051257
Jiao G, Song S. High-Rate One-Hourly Updated Ultra-Rapid Multi-GNSS Satellite Clock Offsets Estimation and Its Application in Real-Time Precise Point Positioning. Remote Sensing. 2022; 14(5):1257. https://doi.org/10.3390/rs14051257
Chicago/Turabian StyleJiao, Guoqiang, and Shuli Song. 2022. "High-Rate One-Hourly Updated Ultra-Rapid Multi-GNSS Satellite Clock Offsets Estimation and Its Application in Real-Time Precise Point Positioning" Remote Sensing 14, no. 5: 1257. https://doi.org/10.3390/rs14051257
APA StyleJiao, G., & Song, S. (2022). High-Rate One-Hourly Updated Ultra-Rapid Multi-GNSS Satellite Clock Offsets Estimation and Its Application in Real-Time Precise Point Positioning. Remote Sensing, 14(5), 1257. https://doi.org/10.3390/rs14051257







