2.2. The NNGIM Forecasting Algorithm
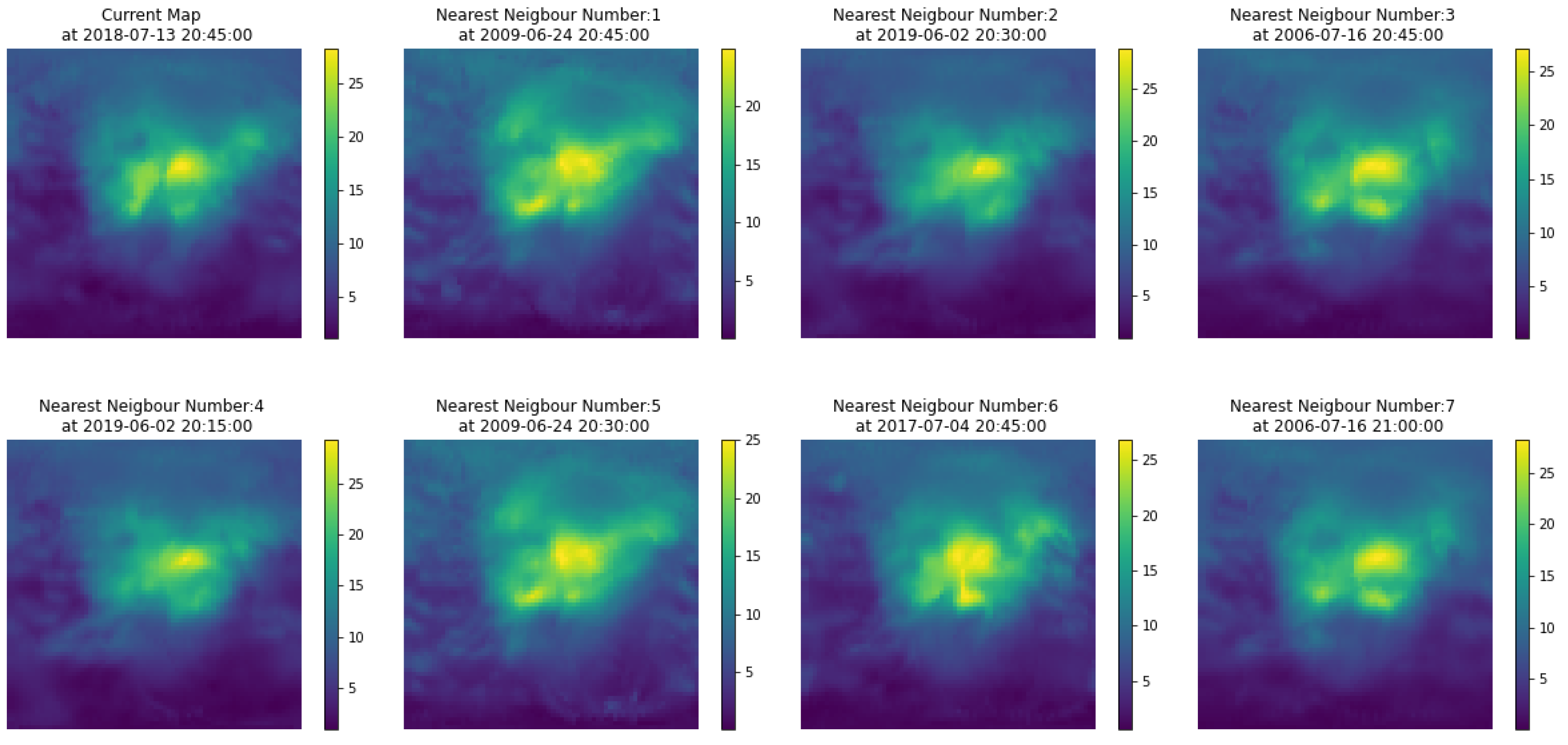
In this section, we will describe the Nearest Neighbour GIM (NNGIM) algorithm. This algorithm consists of searching for the N maps closest (in Euclidean metric) to the current one in the database of past maps (more than one solar cycle). Then, from these maps, the GIMs with an offset equal to the prediction horizon are retrieved and averaged.
The assumption underlying the NNGIM algorithm is that in a database that encompasses more than one solar cycle, a small number of maps with the property of being the closest in Euclidean distance to the current one can be found, and that have ionosphere conditions in common with the current one, might characterize the maps at a time shift equal to the forecast horizon. Although each ionosphere condition is unique, it is assumed that in the past there have been conditions with a similar composition of external features and that the average of all of them will reflect the specific features of the current one. The set of similar maps therefore take into account the cyclical aspects that influence the overall distribution of TEC along with the various external influences. That is, if we select a set of future map values closer to the current one when averaging, common values in subsets of the future maps will be retained, while non-common conditions will be attenuated. Note that the idea behind the assumption is that there will be subsets of maps representing similar ionospheric conditions, and the overall composition of these parts will allow us to approximate previously unseen situations. We assume that these previously unseen situations are composed of subgroups that characterize part of the previous conditions common to the current situation.
The UPC-IonSat GIMs database, which spans over two solar cycles and consists of more than
maps, was used to implement the method (see [
19] for details).
In the algorithm diagram, Algorithm 1, we present the summary of the NNGIM algorithm. A detailed explanation of the algorithm is given below, also defining the variables involved.
The input of the algorithm consists of a database spanning more than two solar cycles (). Note that for consistency in the computation of the distance between maps at different moments, the database and the current map are transformed to sun-fixed geomagnetic coordinates. After the forecast, the inverse transform is performed.
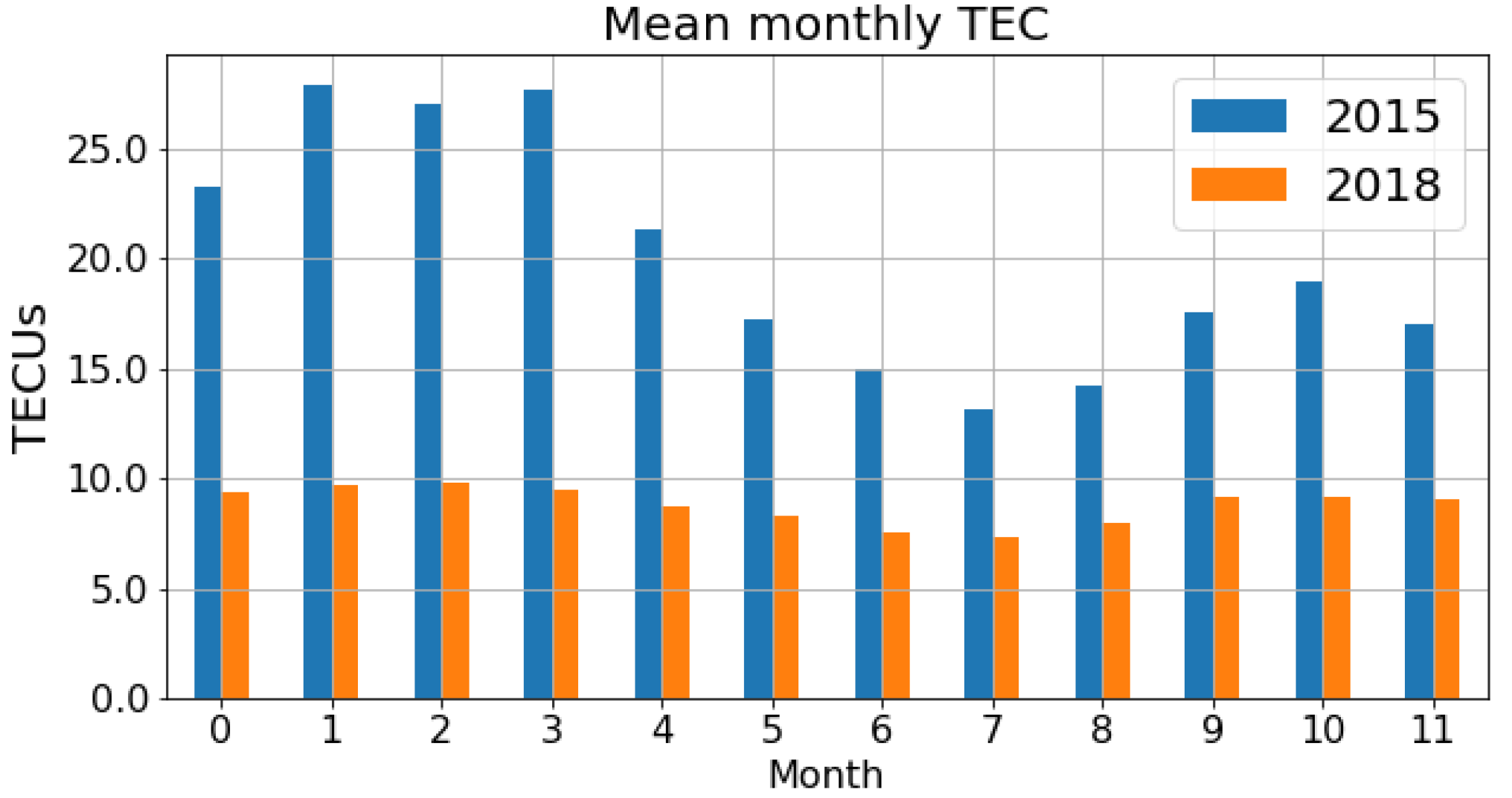
Since the maps have a seasonal component with a mean TEC value that depends on the season of the year (see
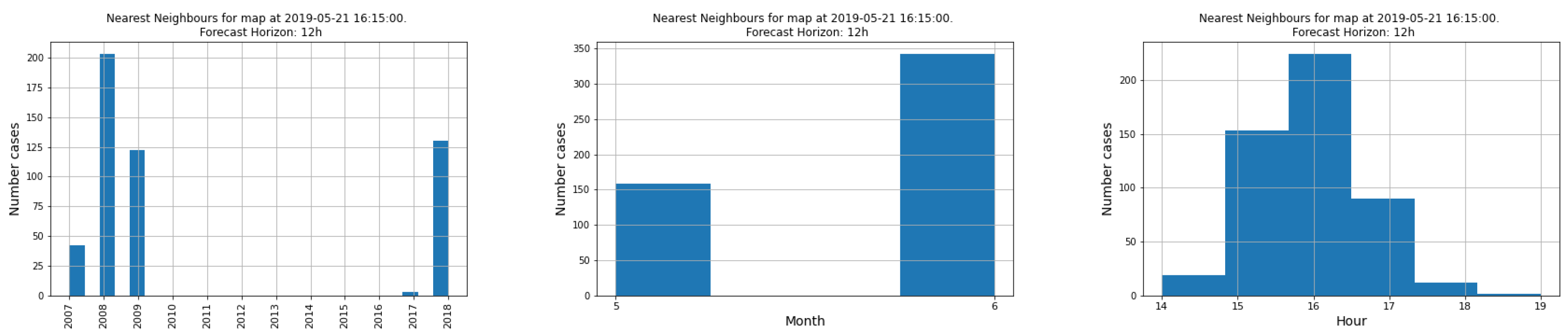
Figure 1), the search for the nearest map will be carried out in the vicinity of the current month. Therefore, given the date of the current map
, the month is extracted (
), and maps the current month and a window of
months are selected from the database. In the experiments, a neighbourhood of
was taken. Other parameters are the forecast horizon in hours (
) and the number of nearest neighbours (
). The next step is to construct a second database (
), which will consist of the maps with the current map month and the neighbouring months for all years. The Euclidean distance between the current map
and the maps in the
database is then calculated (lines 3 to 7 of the Algorithm 1). The vector of distances is then sorted from smallest to largest (line 8 of the Algorithm 1) and assigned to the vector of indices
.
We define as the number of maps to be used for prediction estimation. The Algorithm 1, lines 9 to 15 describe the process for generating the prediction. For the nearest maps, we find the corresponding index and the associated date . Next, we add the offset to generate the date associated with each of the maps. The maps associated with each date are combined to generate the future map .
Finally, from the maps of the horizon shift, the standard deviation at the pixel level is calculated, as shown in line 17.
| Algorithm 1: The NNGIM algorithm. |
![Remotesensing 14 01361 i001]() |
Various strategies for combining the maps were tested, such as a simple average, a distance-weighted average, or weight that diminishes with the time difference. We also tried a trim mean, defined as the average of the values of each specific pixel in the maps, using only the values between the 25th percentile and the 75th percentile. The median of the pixels of the nearest maps was also tested. The combination that gave the best results was a simple average of the maps.
One parameter to be adjusted is the number used to calculate the forecast. This value depends on the forecast horizon and the month of the year. For all experiments we chose a value = 500. The choice was made based on the performance during June 2019 and was explored for values between 1 and 1000. The rationale for the choice of date was to have a date in a cycle (C24) different from the cycle in which the results are presented (C23), and also at a season of low activity. The experiments showed that for this month and horizons between 3 h and 48 h the optimum value was between 150 and 700. In the real-time implementation, a look-up table will be used in which the month and horizon will be related to the value.
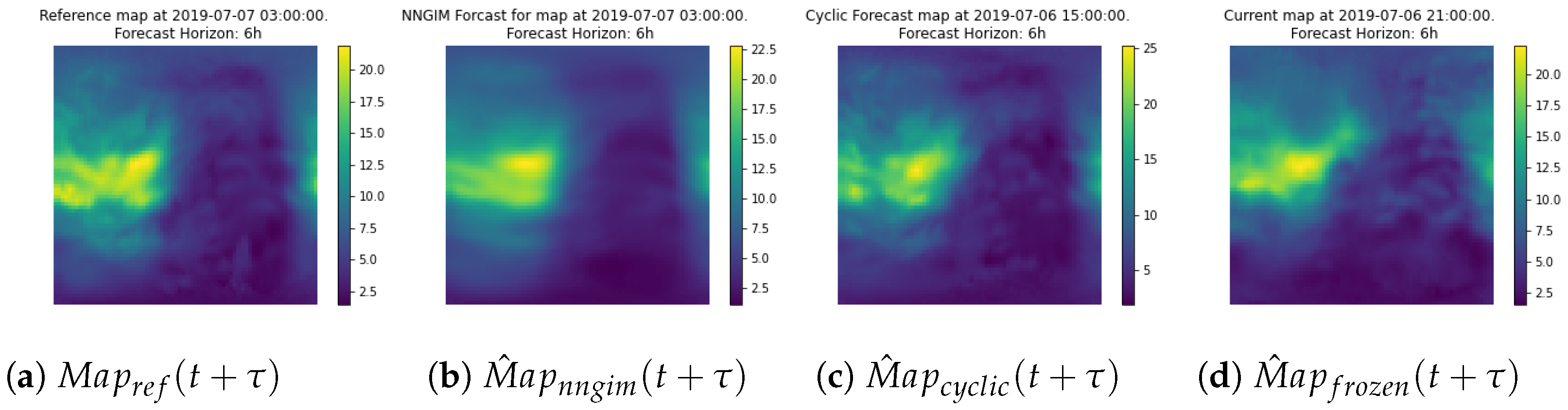
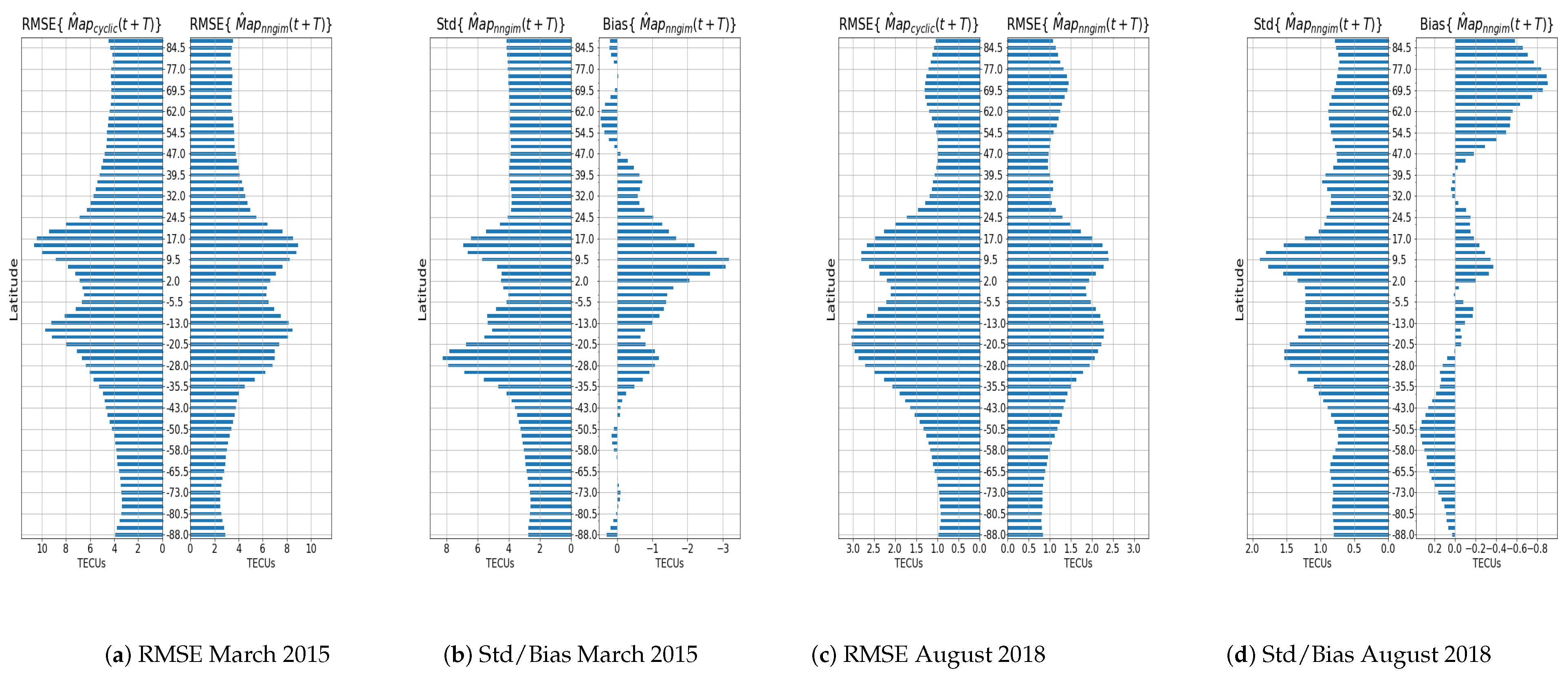
An interesting result is that using only the nearest neighbour, i.e., = 1 provided results with a quality equal to using the cyclic version of the map, (defined as ). The performance did not improve until using a number of greater than 50. This leads us to think that the use of a large number of maps allows us to create a representation of the possible contributions of the factors that affect ionisation. The explanation is that the combination of external factors is larger than the number of examples in the database. The underlying assumption is that the current combination of factors affecting ionisation can be expressed as a linear combination of similar situations in the past.
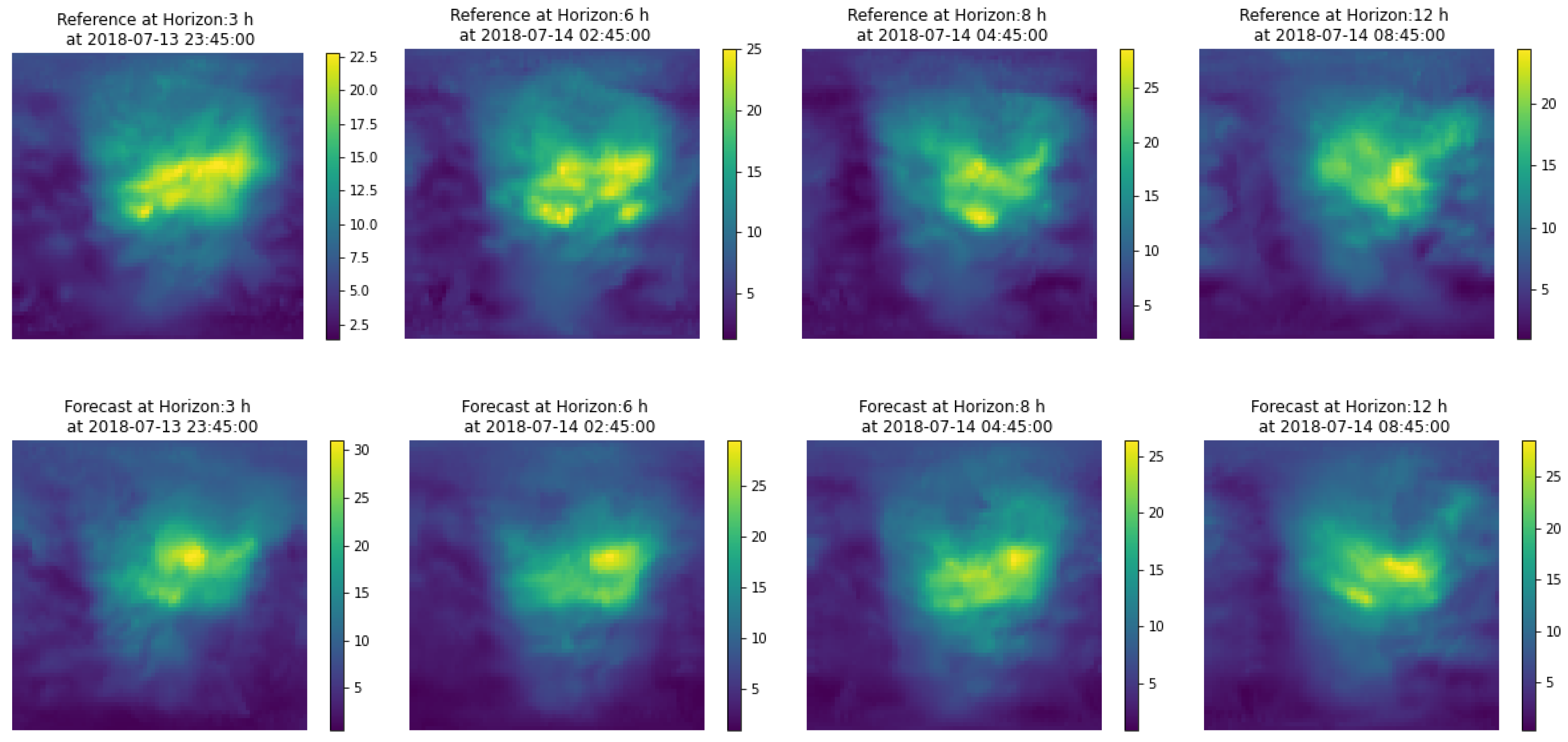
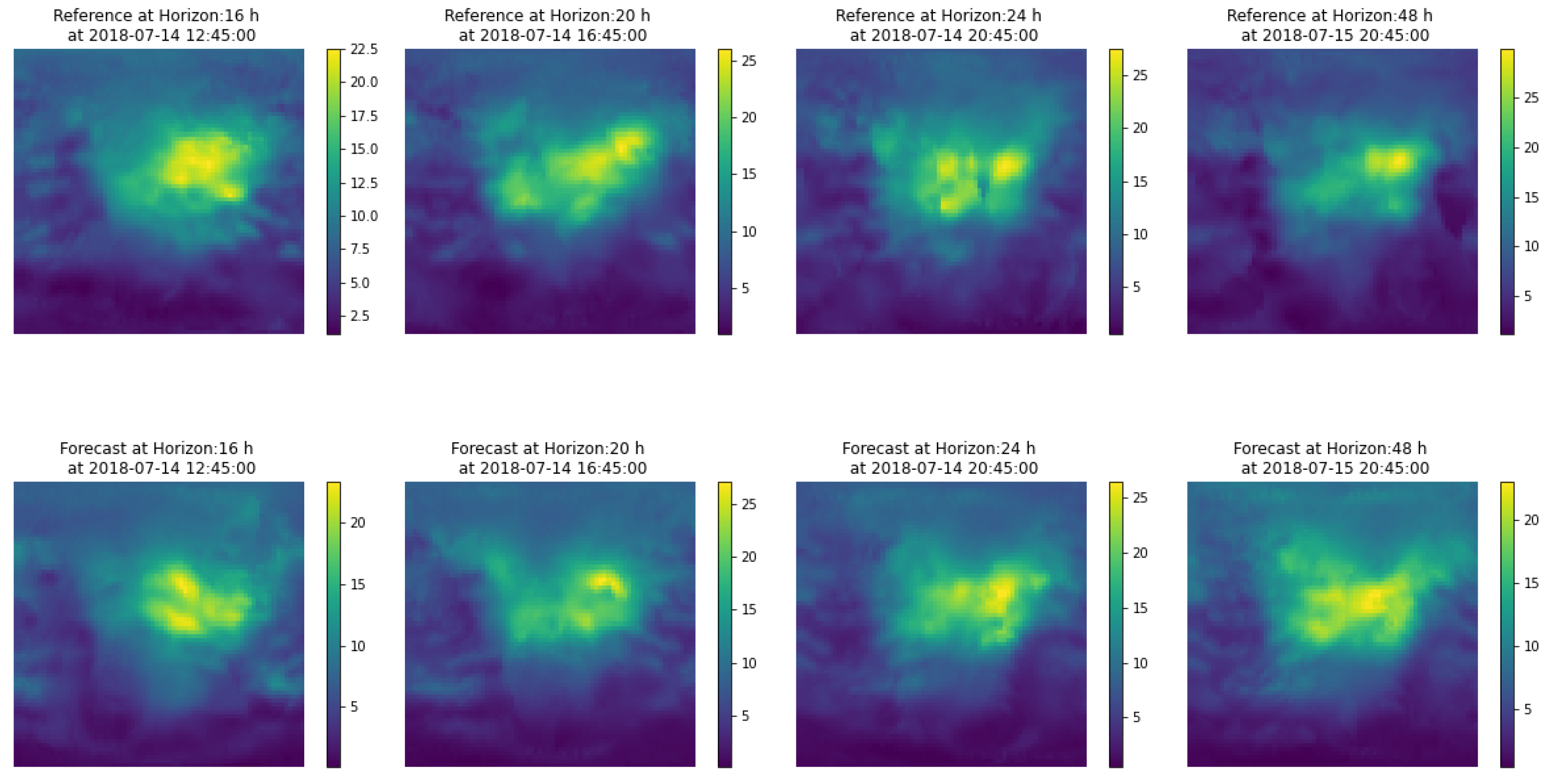
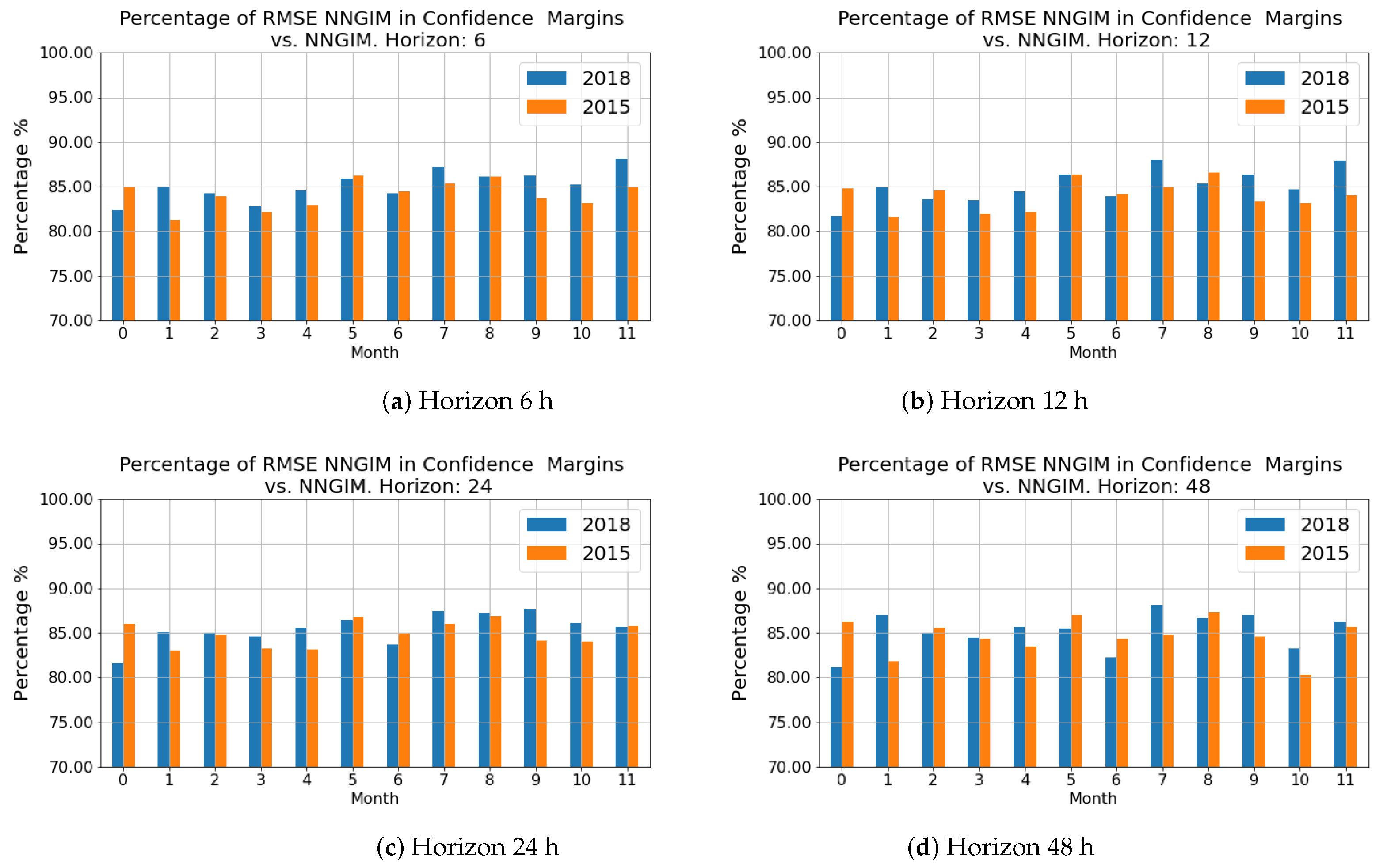
A product of this algorithm is that it can provide confidence intervals for the GIMs, i.e., the local standard deviation of the ionisation values. The estimation of confidence intervals can be done directly, as a collection of several hundred maps is available. One of the features of the maps from which the prediction is constructed is the variability around a central value, as shown in
Figure 2. Therefore from the set of maps used to generate the prediction, one can estimate a standard deviation
at a pixel level, defining this standard deviation as the deviation of the maps from the mean value of the prediction
. One point that we show in
Section 4.1 is that the prediction covers most of the area of the reference map
, so we can consider that this variance provides us with an adequate measure of uncertainty for the prediction.
Parameter setting. The algorithm has two parameters to be adjusted, which are the window in months to select maps, denoted as and the number of elements to calculate the mean value of the nearest neighbors, denoted as . The criterion to adjust the parameters was to fit on a subset of the training base (the test was not used at any time for adjustment). In the case of , which corresponds to the neighboring months, it was observed that due to the variation of the algorithm itself, examples were always selected either from the current month or from the neighboring months. In order to limit the calculation needs, the calculation of distances was limited to the intervals determined by this variable. As for the variable, the result is different from the normal application of the Nearest Neighbour (NN) algorithm, in the sense that in order to compensate for the specific variability of each example used for the prediction, the number of neighbors to be used is much higher than in normal applications of the NN. In our case, the prediction error decreased monotonically until reaching a NumNNN value of about 500, producing a plateau of error with small oscillations of the error until reaching about 1500, and at this point the error starts to increase. Note that the fraction of elements used is small with respect to the total number of examples which exceeds one million.
To see the effects of adjusting these parameters, see illustration of how the algorithm works (
Section 2.3) and example of forecasts at several horizons (
Section 2.4).
Improvements: The improvements we envisage in the next step are to change the average distance, using a metric on the manifold in which the map is located. This is the distance defined in [
20] in which coefficients of the angle between coordinates
are used to weight the Euclidean distance. The advantage of using this distance is that it allows considering in the similarity measure between maps, distortions such as shifts, rotations, etc. The reason why it has not been used in this implementation is that it requires a computational load proportional to the square of the number of map elements. With the current hardware capabilities at 2021, the computation of
took about ten minutes, so it was not implemented in the final prototype.
Another improvement is to use a heuristic that decreases the computational needs to determine the nearest neighbors. That is, an algorithm with a suitable heuristic for the dimensionality of the maps and with a lower search cost, as is the case of [
21]. The fact that the GIMs have the ionisation levels distributed in clear and distinct regions makes this algorithm efficient. This might allow implementing a distance with higher computational cost as the nearest neighbour search cost can be decreased.
The computational cost on an iMac i7 using one core of applying the algorithm was as follows. The Euclidean distance from a map to the database consisting of the current month and the two neighbouring months (with 170,000 maps) was of the order of 135 ms, and the cost of sorting the distances of 9 ms, the calculation of the average map , was less than 1 ms.
The format of the maps consisted of TEC values measured with a resolution of 2.5 degrees in latitude and 5 degrees in longitude, resulting in maps represented as a 72 × 71 array of floats. Each map occupied 40 k bytes on disk (the float represented in ascii format had only one decimal place), while in memory it occupied 164 k bytes with a float-32 bit representation. For more information see
Section 2.1The most time-consuming part of the algorithm is the loading into memory of the pre-computed database , which occupies 2 gigabytes. The time cost on an SSD is in the order of 2 s. However, in a real-time application, the database can be kept permanently in memory.
The real-time prediction of the implementation of this algorithm can be found at the following URL: [
22], with the following naming convention:
The three regions where the forecast was done: Global Forecast (un*g), North-Pole Forecast (un*n), South-Pole Forecast (un*s) And the different horizons that were implemented in real time:
- 1
un0g/un0n/un0s: 1 h Forecast
- 2
un1g/un1n/un1s: 6 h Forecast
- 3
un2g/un2n/un2s: 12 h Forecast
- 4
un3g/un3n/un3s: 18 h Forecast
- 5
un4g/un4n/un4s: 24 h Forecast
- 6
un8g/un8n/un8s: 48 h Forecast
The polar predictions consist of segments of the global map clipped at 45 degrees of latitude.