Combining Crop Modeling with Remote Sensing Data Using a Particle Filtering Technique to Produce Real-Time Forecasts of Winter Wheat Yields under Uncertain Boundary Conditions
Abstract
:1. Introduction
- Determining state variables of crops from remote sensing signals is not straightforward. This is mainly due to image resolution (spatial, temporal, and radiometric), the background soil effect, signal sensitivity saturation, and atmospheric effects [14,25]. In the early growing season, the soil and soil moisture state blur the signals, while in the mid-late growing season the signals become less sensitive to LAI because of leaf overlapping. The latter is called the saturation phenomenon. Systematic errors in the estimated variables will force the crop model to produce unrealistic predictions [2]. It remains to be clarified, how accurate remote sensing data should be to improve yield prediction. To mitigate deficiencies in the satellite signals, researchers have developed various empirical and mechanistic models. In general, mechanistic approaches provide better results but require more input [11], which is typically unavailable on large scale. Among the empirical remote sensing approaches, the Choudhury model [26] converts satellite signals to LAI using a parameter related to the leaf geometry in the canopy. Therefore, it can be adjusted to erectophile and planophile canopies. Provided that the number of evaluated remote sensing images is high Thorp et al. [5] showed that the Choudhury model performs as good as the mechanistic model PROSAIL. However, fine-resolution, cloud-free data from optical sensors are not always available at regular intervals due to unfavorable atmospheric conditions, especially in areas with high cloud coverage during the growing season.
- Another part of uncertainty comes from incompletely resolved system information including explanatory variables (inputs and forcing data). Spatial differences in agronomic practices, mainly sowing date, fertilizer application, and crop genotype, are major contributors to input uncertainty [27]. This information is crucial for running crop models, but it is rarely available on a large scale mainly since data acquisition is too costly. They somehow can be estimated either directly or indirectly by satellite observations. Jégo et al. [28] reduced the yield prediction uncertainty associated with crop management by assimilating remote sensing LAI. Seasonal and yearly variation in weather data that control crop phenology, water availability, and photosynthesis have been recognized as the main sources for inter-annual yield variability [29]. Bias and uncertainty of the weather data may be large, but this is often neglected in the literature [30,31]. The real aim of data assimilation is real-time prediction, requiring generated or forecasted weather data. Most research in this field, however, has used data assimilation for hindcasting with measured or gridded deterministic weather data [7,27].
- The third large source of uncertainty lies in the structure of crop models and the parameters relating the assimilated state variable to the target variable, in our case grain yield. Data assimilation may significantly improve the prediction of the assimilated variables but not necessarily the prediction of grain yield. The model structural link between LAI and biomass, for example, is commonly strong, but this is less so for grain yield [32]. Also, the time at which LAI information is available, relative to harvest, has an impact. For example, soil moisture and LAI available during the early growing season may be less important for yield forecast accuracy than data available in the mid or late growing season. A weak correlation between assimilated variables and yield, which may be the result of model structure or parameterization or both, does not lead to improved yield prediction even if the uncertainties previously mentioned are fully accounted for. In other words, the crop variable used for data assimilation should contain information about the uncertainty of the parameters and affect the yield [33]. Model structure is also important since the input uncertainty propagates to yield prediction through crop model equations and parameters. Complex, process-based models can explain many processes in detail and provide the dynamics of many state variables, provided that the required inputs are available. However, in the absence of large-scale agronomic and soil data, simple models with fewer parameters may be more useful, e.g., the PILOTE model [34,35], which we will employ here, or others such as SAFY [36]. PILOTE simulates LAI as a function of temperature and soil water balance using empirical equations. It then computes biomass from LAI, incoming radiation, and radiation use efficiency.
2. Materials and Methods
2.1. Study Location and Data
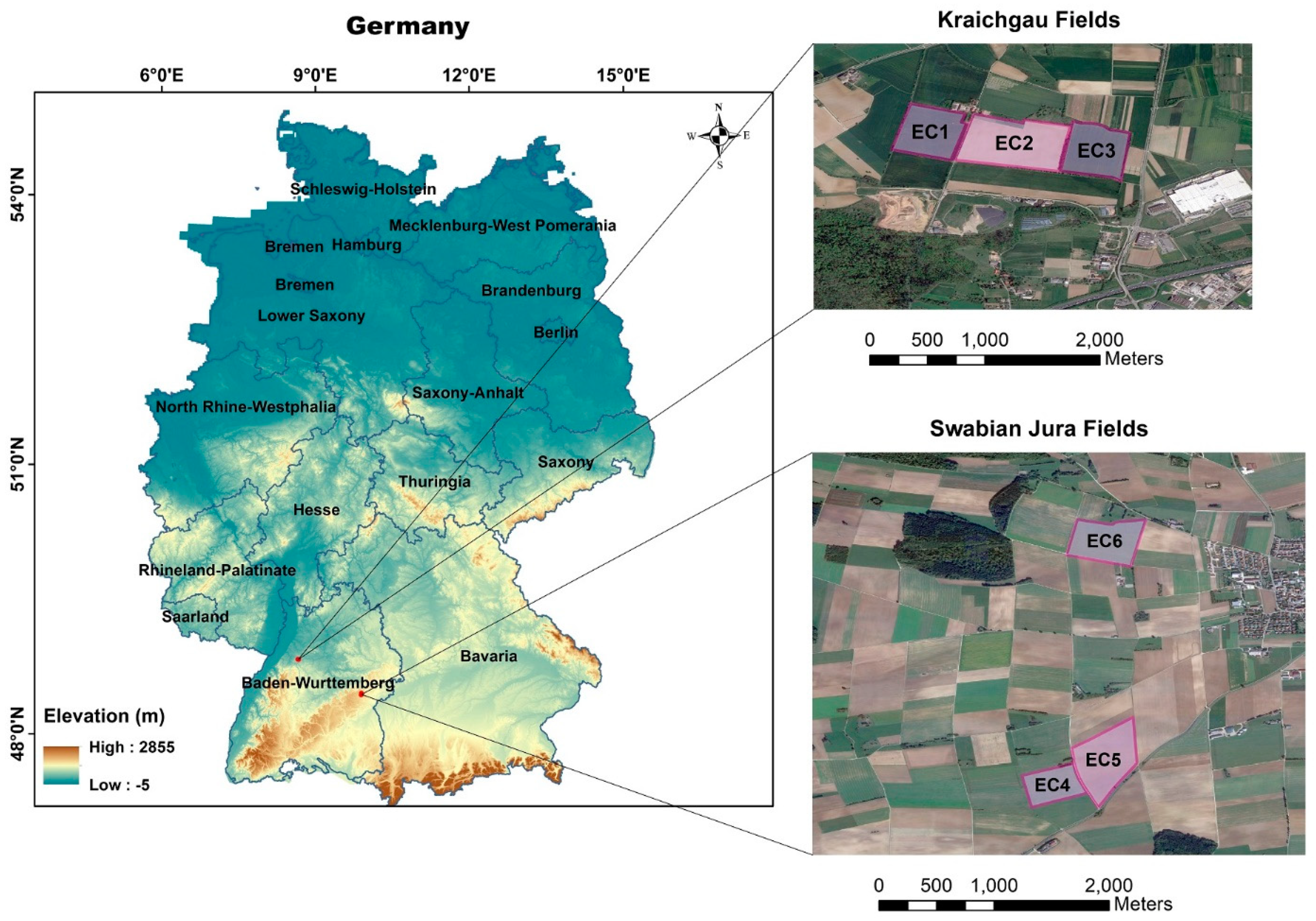
2.1.1. Study Sites
2.1.2. Weather Generator
2.1.3. Remote Sensing Data
2.2. Data Assimilation Methodology
2.2.1. The Recursive Bayesian State Estimator
2.2.2. Particle Filtering Method
2.3. Particle Filtering Implementation
2.3.1. Prediction Model and Driving Uncertainties
2.3.2. Observation Model and Likelihood
2.4. Data Assimilation Setup
2.5. Testing against Monte-Carlo Simulations
3. Results
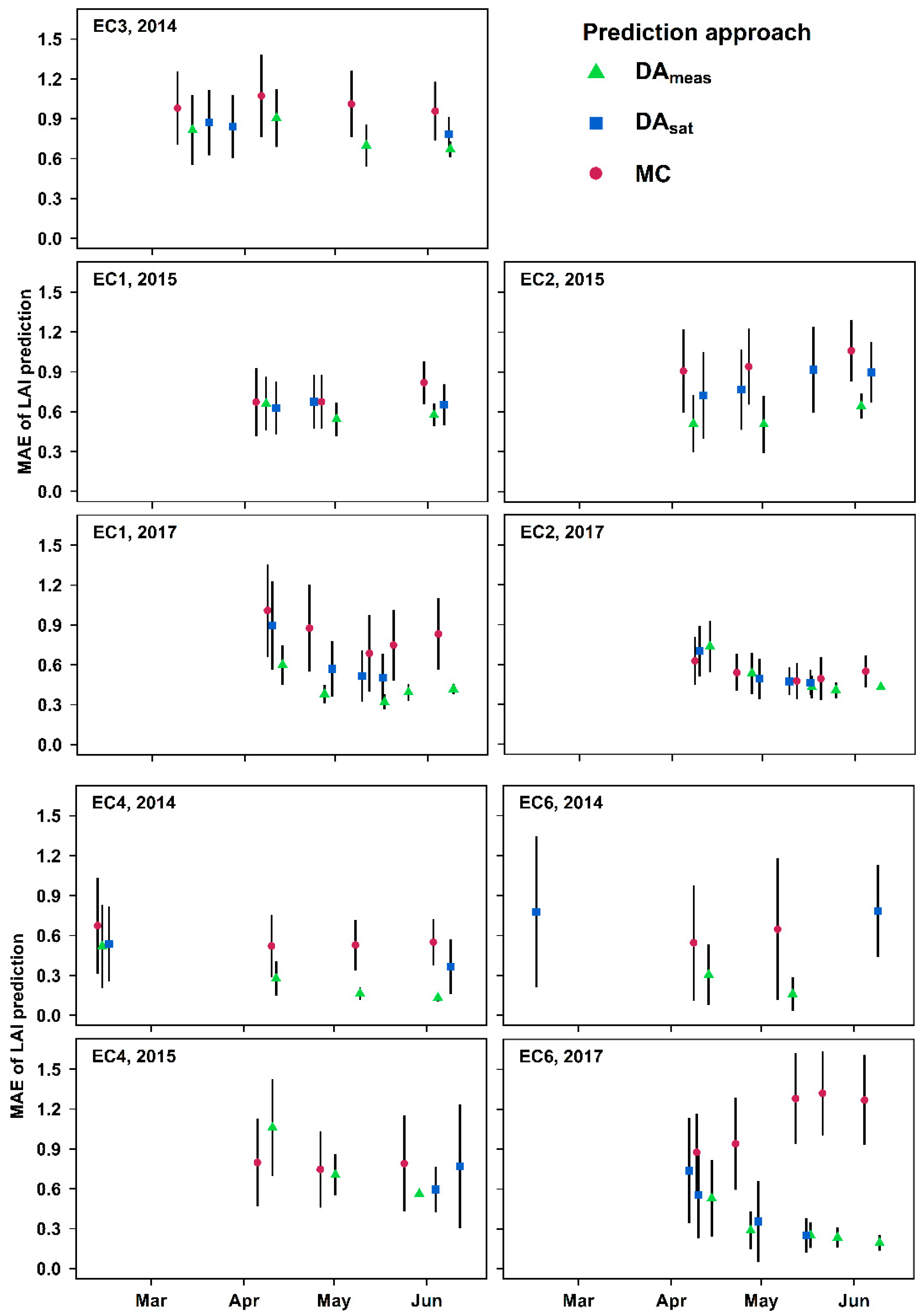
3.1. Real-Time LAI Prediction
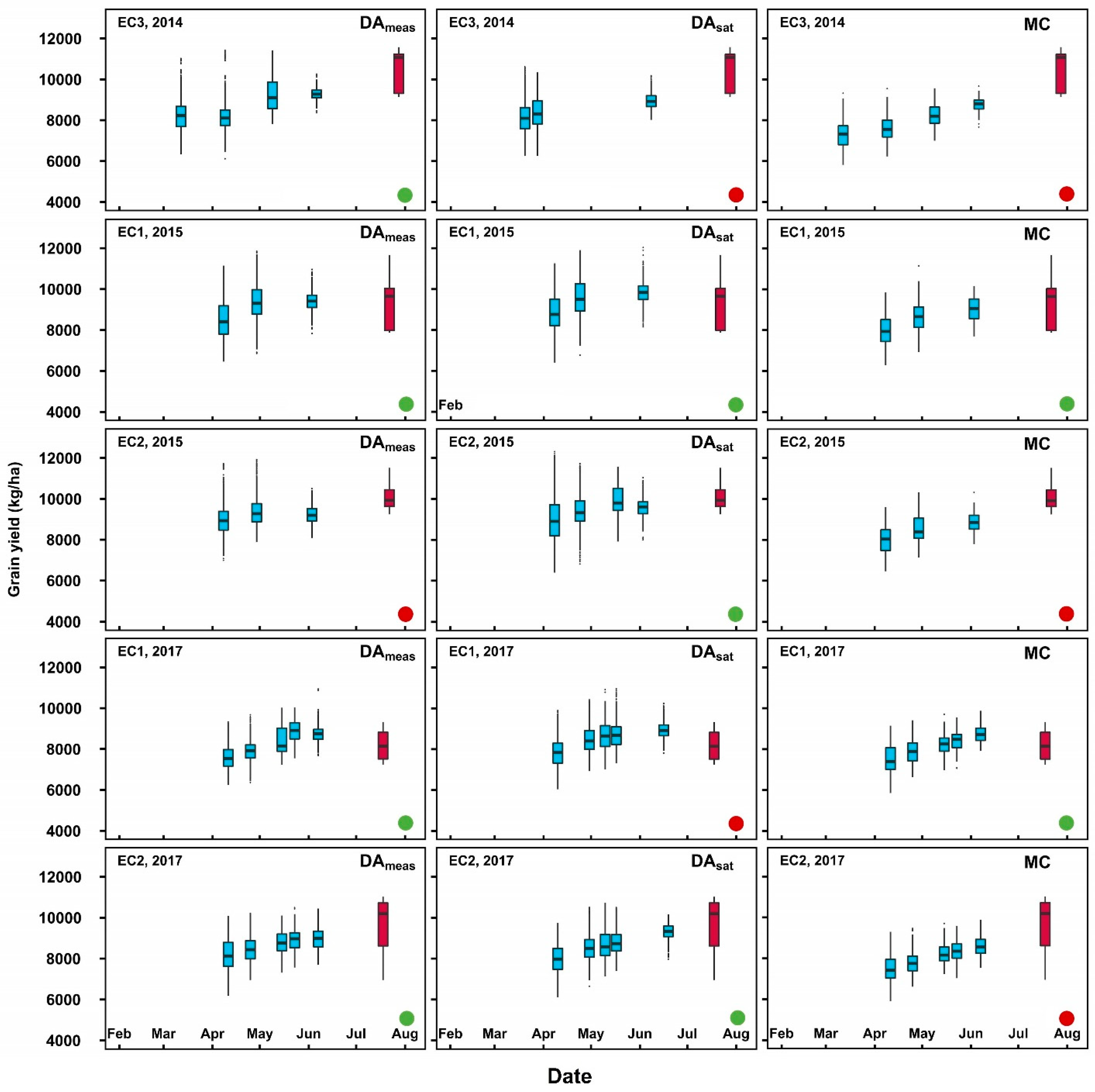
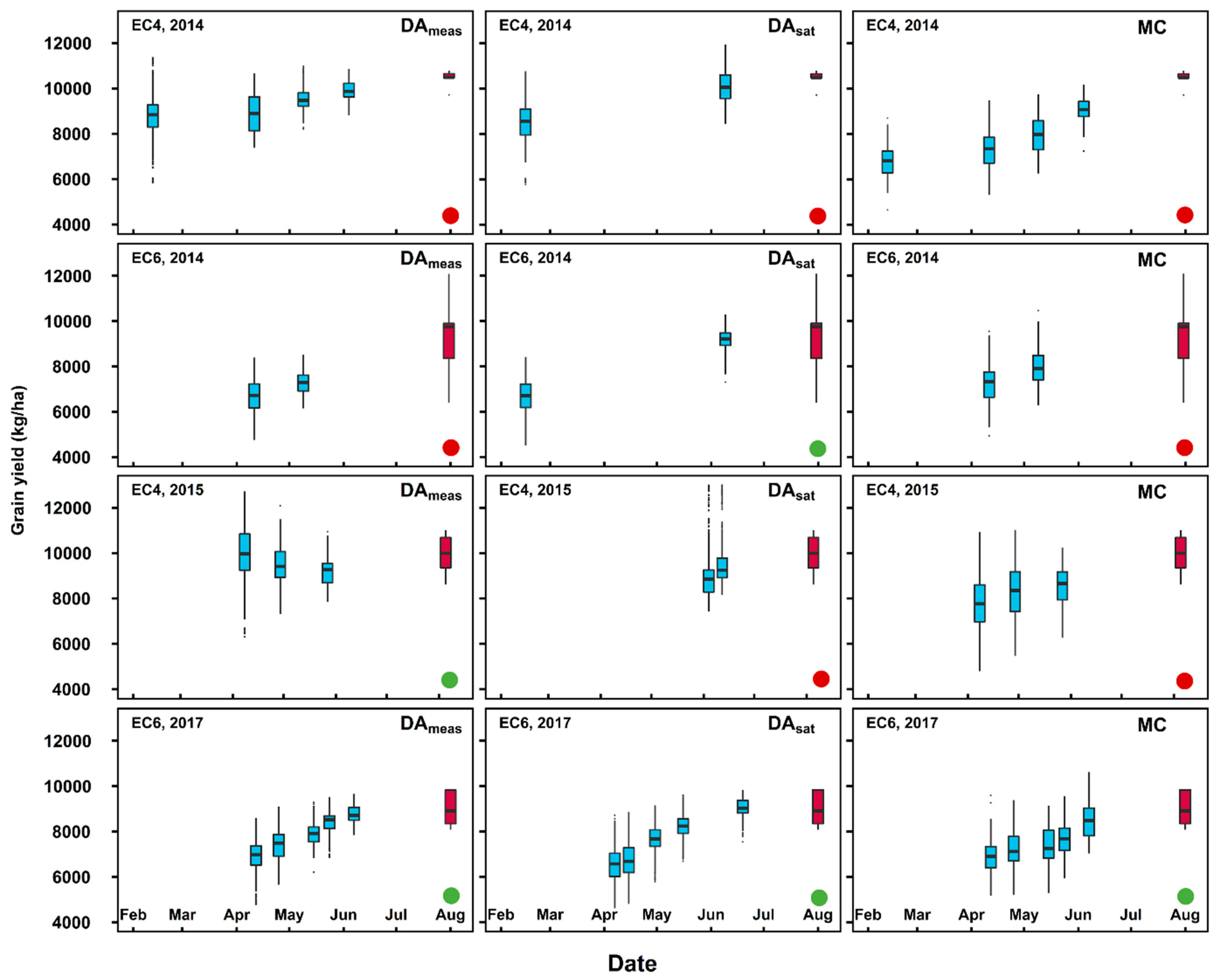
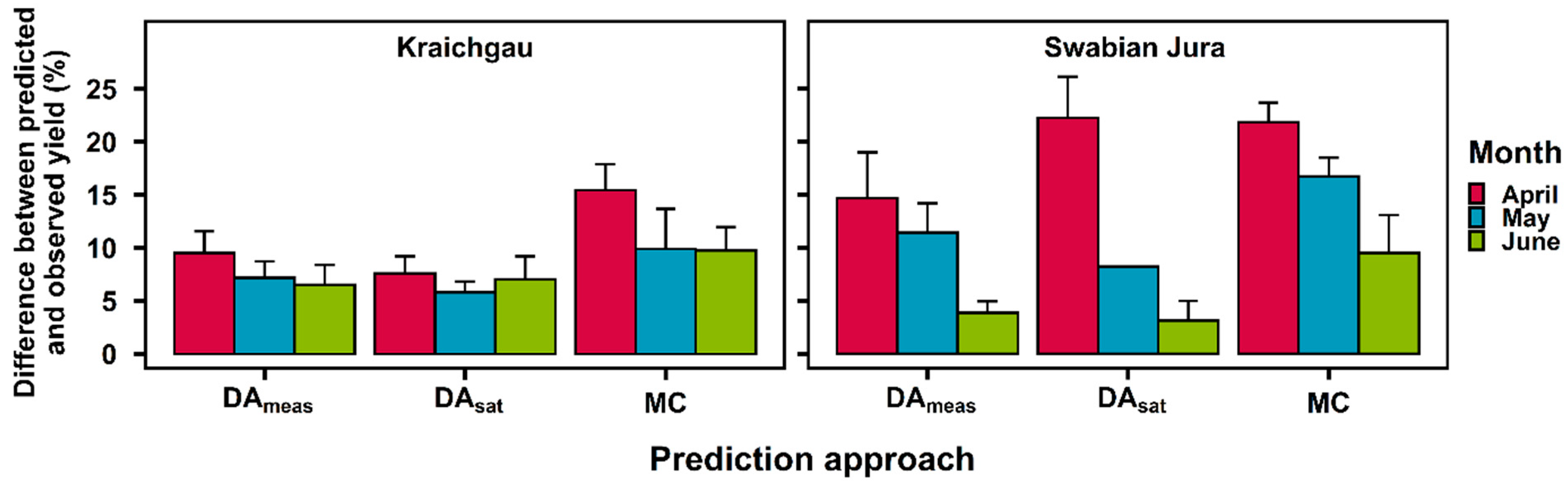
3.2. Real-time Grain Yield Prediction
4. Discussion
4.1. Error in the Assimilation Protocol and Observation Data
4.2. Uncertainty from the Model Inputs
4.3. Impact of Model Errors
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. The PILOTE Model
Appendix A.2. Model Calibration and Evaluation Method
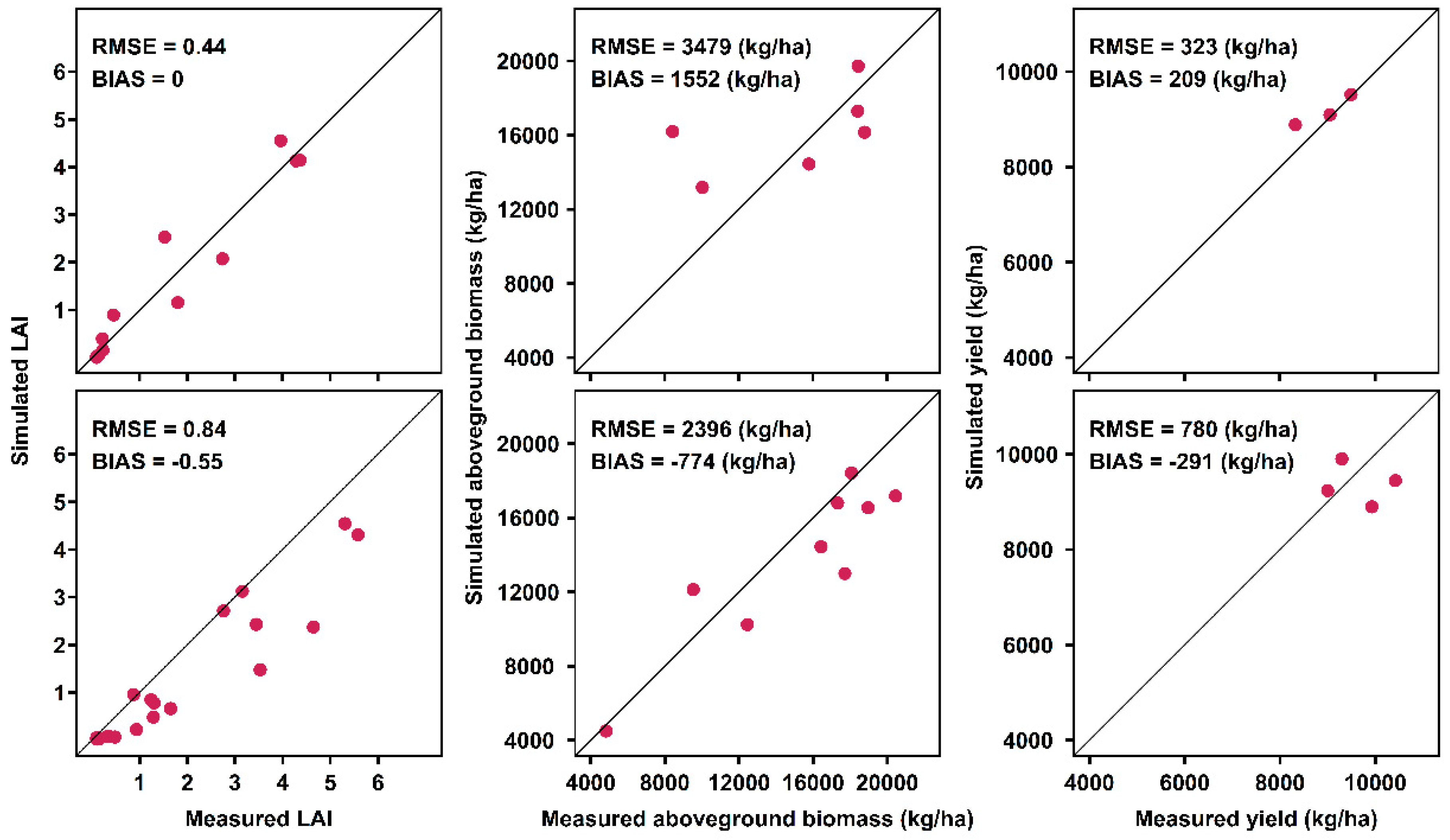
Appendix A.3. Model Calibration and Evaluation Result
Appendix A.3.1. PILOTE
| Parameter | Units | Optimized Value | |
|---|---|---|---|
| Kraichgau | Swabian Jura | ||
| °C | 1220 | 1120 | |
| m2/m2 | 5.50 | 5.10 | |
| - | 0.45 | 0.30 | |
| g/MJ | 1.15 | 1.05 | |
| °C | 1500 | 1200 | |
| m2/m2 | 3.85 | 4.80 | |
| - | −0.15 | −0.80 | |


Appendix A.3.2. Choudhury
Appendix B

References
- Iizumi, T.; Shin, Y.; Kim, W.; Kim, M.; Choi, J. Global crop yield forecasting using seasonal climate information from a multi-model ensemble. Clim. Serv. 2018, 11, 13–23. [Google Scholar] [CrossRef]
- Curnel, Y.; de Wit, A.J.W.; Duveiller, G.; Defourny, P. Potential performances of remotely sensed LAI assimilation in WOFOST model based on an OSS Experiment. Agric. For. Meteorol. 2011, 151, 1843–1855. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F. Improving regional winter wheat yield estimation through assimilation of phenology and leaf area index from remote sensing data. Eur. J. Agron. 2018, 101, 163–173. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Thorp, K.R.; Wang, G.; West, A.L.; Moran, M.S.; Bronson, K.F.; White, J.W.; Mon, J. Estimating crop biophysical properties from remote sensing data by inverting linked radiative transfer and ecophysiological models. Remote Sens. Environ. 2012, 124, 224–233. [Google Scholar] [CrossRef] [Green Version]
- Silvestro, P.; Pignatti, S.; Pascucci, S.; Yang, H.; Li, Z.; Yang, G.; Huang, W.; Casa, R. Estimating Wheat Yield in China at the Field and District Scale from the Assimilation of Satellite Data into the Aquacrop and Simple Algorithm for Yield (SAFY) Models. Remote Sens. 2017, 9, 509. [Google Scholar] [CrossRef] [Green Version]
- Ines, A.V.M.; Das, N.N.; Hansen, J.W.; Njoku, E.G. Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction. Remote Sens. Environ. 2013, 138, 149–164. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.-L.; Diao, W.-Y.; Xiao, C.-H.; Wang, F.-Y.; Chen, B.; Wang, K.-R.; Li, S.-K. Estimation of wheat agronomic parameters using new spectral indices. PLoS ONE 2013, 8, e72736. [Google Scholar] [CrossRef] [Green Version]
- Eitel, J.U.H.; Long, D.S.; Gessler, P.E.; Smith, A.M.S. Using in-situ measurements to evaluate the new RapidEye ™ satellite series for prediction of wheat nitrogen status. Int. J. Remote Sens. 2007, 28, 4183–4190. [Google Scholar] [CrossRef]
- Nasrallah, A.; Baghdadi, N.; El Hajj, M.; Darwish, T.; Belhouchette, H.; Faour, G.; Darwich, S.; Mhawej, M. Sentinel-1 Data for Winter Wheat Phenology Monitoring and Mapping. Remote Sens. 2019, 11, 2228. [Google Scholar] [CrossRef] [Green Version]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Ma, G.; Huang, J.; Wu, W.; Fan, J.; Zou, J.; Wu, S. Assimilation of MODIS-LAI into the WOFOST model for forecasting regional winter wheat yield. Math. Comput. Model. 2013, 58, 634–643. [Google Scholar] [CrossRef]
- Feng, W.; Wu, Y.; He, L.; Ren, X.; Wang, Y.; Hou, G.; Wang, Y.; Liu, W.; Guo, T. An optimized non-linear vegetation index for estimating leaf area index in winter wheat. Precis. Agric. 2019, 20, 1157–1176. [Google Scholar] [CrossRef] [Green Version]
- Silvestro, P.C.; Casa, R.; Hanuš, J.; Koetz, B.; Rascher, U.; Schuettemeyer, D.; Siegmann, B.; Skokovic, D.; Sobrino, J.; Tudoroiu, M. Synergistic Use of Multispectral Data and Crop Growth Modelling for Spatial and Temporal Evapotranspiration Estimations. Remote Sens. 2021, 13, 2138. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, Z.; Chen, J.; Ren, J.; Li, Z.; Sun, L. The Estimation of Regional Crop Yield Using Ensemble-Based Four-Dimensional Variational Data Assimilation. Remote Sens. 2014, 6, 2664–2681. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Chen, Z.; Chen, J.; Liu, J.; Ren, J.; Li, Z.; Sun, L.; Li, H. Application of Crop Model Data Assimilation With a Particle Filter for Estimating Regional Winter Wheat Yields. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4422–4431. [Google Scholar] [CrossRef]
- De Bernardis, C.; Vicente-Guijalba, F.; Martinez-Marin, T.; Lopez-Sanchez, J. Particle Filter Approach for Real-Time Estimation of Crop Phenological States Using Time Series of NDVI Images. Remote Sens. 2016, 8, 610. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Li, Z.; Yang, G.; Yang, H.; Feng, H.; Xu, X.; Wang, J.; Li, X.; Luo, J. Winter wheat yield estimation based on multi-source medium resolution optical and radar imaging data and the AquaCrop model using the particle swarm optimization algorithm. ISPRS J. Photogramm. Remote Sens. 2017, 126, 24–37. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, P.; Sun, H.; Zhang, S.; Li, L. Assimilation of Leaf Area Index and Surface Soil Moisture With the CERES-Wheat Model for Winter Wheat Yield Estimation Using a Particle Filter Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1303–1316. [Google Scholar] [CrossRef]
- Tian, X.; Xie, Z.; Sun, Q. A POD-based ensemble four-dimensional variational assimilation method. Tellus A Dyn. Meteorol. Oceanogr. 2011, 63, 805–816. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z.; Liu, G.; Jiang, Z.; Huang, C. Improving Winter Wheat Yield Estimation from the CERES-Wheat Model to Assimilate Leaf Area Index with Different Assimilation Methods and Spatio-Temporal Scales. Remote Sens. 2017, 9, 190. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Cournède, P.-H. Data assimilation to reduce uncertainty of crop model prediction with Convolution Particle Filtering. Ecol. Model. 2014, 290, 165–177. [Google Scholar] [CrossRef] [Green Version]
- Ling, X.-L.; Fu, C.-B.; Yang, Z.-L.; Guo, W.-D. Comparison of different sequential assimilation algorithms for satellite-derived leaf area index using the Data Assimilation Research Testbed (version Lanai). Geosci. Model. Dev. 2019, 12, 3119–3133. [Google Scholar] [CrossRef] [Green Version]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Kang, Y.; Özdoğan, M. Field-level crop yield mapping with Landsat using a hierarchical data assimilation approach. Remote Sens. Environ. 2019, 228, 144–163. [Google Scholar] [CrossRef]
- Jégo, G.; Pattey, E.; Mesbah, S.M.; Liu, J.; Duchesne, I. Impact of the spatial resolution of climatic data and soil physical properties on regional corn yield predictions using the STICS crop model. Int. J. Appl. Earth Obs. Geoinf. 2015, 41, 11–22. [Google Scholar] [CrossRef]
- Ceglar, A.; Toreti, A.; Lecerf, R.; van der Velde, M.; Dentener, F. Impact of meteorological drivers on regional inter-annual crop yield variability in France. Agric. For. Meteorol. 2016, 216, 58–67. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, C.; Zhang, Y. Uncertainties in the Effects of Climate Change on Maize Yield Simulation in Jilin Province: A Case Study. J. Meteorol. Res. 2019, 33, 777–783. [Google Scholar] [CrossRef]
- Tao, F.; Rötter, R.P.; Palosuo, T.; Gregorio Hernández Díaz-Ambrona, C.; Mínguez, M.I.; Semenov, M.A.; Kersebaum, K.C.; Nendel, C.; Specka, X.; Hoffmann, H.; et al. Contribution of crop model structure, parameters and climate projections to uncertainty in climate change impact assessments. Glob. Chang. Biol. 2018, 24, 1291–1307. [Google Scholar] [CrossRef] [PubMed]
- Wallach, D.; Makowski, D.; Jones, J.W.; Brun, F. Working with Dynamic Crop Models: Methods, Tools and Examples for Agriculture and Environment, 3rd ed.; Elsevier Science & Technology: San Diego, CA, USA, 2018; ISBN 9780128117569. [Google Scholar]
- LeBauer, D.S.; Wang, D.; Richter, K.T.; Davidson, C.C.; Dietze, M.C. Facilitating feedbacks between field measurements and ecosystem models. Ecol. Monogr. 2013, 83, 133–154. [Google Scholar] [CrossRef]
- Mailhol, J.C.; Olufayo, A.A.; Ruelle, P. Sorghum and sunflower evapotranspiration and yield from simulated leaf area index. Agric. Water Manag. 1997, 35, 167–182. [Google Scholar] [CrossRef]
- Khaledian, M.R.; Mailhol, J.C.; Ruelle, P.; Rosique, P. Adapting PILOTE model for water and yield management under direct seeding system: The case of corn and durum wheat in a Mediterranean context. Agric. Water Manag. 2009, 96, 757–770. [Google Scholar] [CrossRef] [Green Version]
- Duchemin, B.; Maisongrande, P.; Boulet, G.; Benhadj, I. A simple algorithm for yield estimates: Evaluation for semi-arid irrigated winter wheat monitored with green leaf area index. Environ. Model. Softw. 2008, 23, 876–892. [Google Scholar] [CrossRef] [Green Version]
- Ingwersen, J.; Högy, P.; Wizemann, H.D.; Warrach-Sagi, K.; Streck, T. Coupling the land surface model Noah-MP with the generic crop growth model Gecros: Model description, calibration and validation. Agric. For. Meteorol. 2018, 262, 322–339. [Google Scholar] [CrossRef]
- Wizemann, H.-D.; Ingwersen, J.; Högy, P.; Warrach-Sagi, K.; Streck, T.; Wulfmeyer, V. Three year observations of water vapor and energy fluxes over agricultural crops in two regional climates of Southwest Germany. Metz 2015, 24, 39–59. [Google Scholar] [CrossRef]
- Google Maps. Available online: https://www.google.com (accessed on 17 June 2020).
- Meier, U. Growth Stages of Mono- and Dicotyledonous Plants: BBCH Monograph; Open Agrar Repositorium: Quedlinburg, Germany, 2018. [Google Scholar]
- Weber, T.K.D.; Ingwersen, J.; Högy, P.; Poyda, A.; Wizemann, H.-D.; Demyan, M.S.; Bohm, K.; Eshonkulov, R.; Gayler, S.; Kremer, P.; et al. Multi-Site, Multi-Crop Measurements in the Soil-Vegetation-Atmosphere Continuum: A Comprehensive Dataset from Two Climatically Contrasting Regions in South West Germany for the Period 2009–2018. Earth Syst. Sci. Data Discuss. 2021, 1–32. [Google Scholar] [CrossRef]
- Högy, P.; Wieser, H.; Köhler, P.; Schwadorf, K.; Breuer, J.; Franzaring, J.; Muntifering, R.; Fangmeier, A. Effects of elevated CO2 on grain yield and quality of wheat: Results from a 3-year free-air CO2 enrichment experiment. Plant Biol. 2009, 11 (Suppl. 1), 60–69. [Google Scholar] [CrossRef]
- Eshonkulov, R.; Poyda, A.; Ingwersen, J.; Pulatov, A.; Streck, T. Improving the energy balance closure over a winter wheat field by accounting for minor storage terms. Agric. For. Meteorol. 2019, 264, 283–296. [Google Scholar] [CrossRef]
- Eshonkulov, R.; Poyda, A.; Ingwersen, J.; Wizemann, H.-D.; Weber, T.K.D.; Kremer, P.; Högy, P.; Pulatov, A.; Streck, T. Evaluating multi-year, multi-site data on the energy balance closure of eddy-covariance flux measurements at cropland sites in southwestern Germany. Biogeosciences 2019, 16, 521–540. [Google Scholar] [CrossRef] [Green Version]
- Poyda, A.; Wizemann, H.-D.; Ingwersen, J.; Eshonkulov, R.; Högy, P.; Demyan, M.S.; Kremer, P.; Wulfmeyer, V.; Streck, T. Carbon fluxes and budgets of intensive crop rotations in two regional climates of southwest Germany. Agric. Ecosyst. Environ. 2019, 276, 31–46. [Google Scholar] [CrossRef]
- Jones, P.G.; Thornton, P.K. Generating downscaled weather data from a suite of climate models for agricultural modelling applications. Agric. Syst. 2013, 114, 1–5. [Google Scholar] [CrossRef]
- U.S. Geological Survey. Available online: https://earthexplorer.usgs.gov/ (accessed on 12 December 2018).
- Copernicus Open Access Hub. Available online: https://www.copernicus.eu/en (accessed on 8 September 2020).
- Congedo, L. Semi-Automatic Classification Plugin for QGIS; Sapienza University: Rome, Italy, 2013. [Google Scholar]
- Kriegler, F.J.; Malila, W.A.; Nalepka, R.F.; Richardson, W. Preprocessing Transformations and Their Effects on Multispectral Recognition. In Proceedings of the 6th International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 14–16 October 1969. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches/Dan Simon; Wiley [Chichester]; John Wiley: Hoboken, NJ, USA, 2006; ISBN 0471708585. [Google Scholar]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Mailhol, J.-C.; Albasha, R.; Cheviron, B.; Lopez, J.-M.; Ruelle, P.; Dejean, C. The PILOTE-N model for improving water and nitrogen management practices: Application in a Mediterranean context. Agric. Water Manag. 2018, 204, 162–179. [Google Scholar] [CrossRef]
- Guo, D.; Westra, S.; Maier, H.R. An R package for modelling actual, potential and reference evapotranspiration. Environ. Model. Softw. 2016, 78, 216–224. [Google Scholar] [CrossRef]
- Soetaert, K.; Petzoldt, T. Inverse Modelling, Sensitivity and Monte Carlo Analysis in R Using Package FME. J. Stat. Soft. 2010, 33, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Zambrano-Bigiarini, M. hydroGOF: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series. R Package Version. 2020. Available online: https://hzambran.github.io/hydroGOF/ (accessed on 15 January 2022).
- Hijmans, R.J. Geographic Data Analysis and Modeling [R Package Raster Version 3.0-7]. Comprehensive R Archive Network (CRAN). 2019. Available online: https://rspatial.github.io/raster/ (accessed on 15 January 2022).
- Pebesma, E. Simple Features for R: Standardized Support for Spatial Vector Data. R J. 2018, 10, 439. [Google Scholar] [CrossRef] [Green Version]
- Pellenq, J.; Boulet, G. A methodology to test the pertinence of remote-sensing data assimilation into vegetation models for water and energy exchange at the land surface. Agronomie 2004, 24, 197–204. [Google Scholar] [CrossRef] [Green Version]
- Waha, K.; Huth, N.; Carberry, P.; Wang, E. How model and input uncertainty impact maize yield simulations in West Africa. Environ. Res. Lett. 2015, 10, 24017. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.-H.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019, 276, 107609. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Allen, R.G., Ed.; FAO: Rome, Italy, 1998; ISBN 9251042195. [Google Scholar]
- Zhang, T.; Su, J.; Liu, C.; Chen, W.-H. Bayesian Calibration of AquaCrop Model. In Proceedings of the 37th Chinese Control Conference, Wuhan, China, 25–27 July 2018; Chen, X., Zhao, Q., Eds.; IEEE: Piscataway, NJ, USA, 2018; pp. 10334–10339. ISBN 978-988-15639-5-8. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Choudhury, B.J. A sensitivity analysis of the radiation use efficiency for gross photosynthesis and net carbon accumulation by wheat. Agric. For. Meteorol. 2000, 101, 217–234. [Google Scholar] [CrossRef]
- Lafitte, H.R.; Edmeades, G.O. Temperature effects on radiation use and biomass partitioning in diverse tropical maize cultivars. Field Crops Res. 1997, 49, 231–247. [Google Scholar] [CrossRef]


| Year of Growing Season | EC1 | EC2 | EC3 | EC4 | EC5 | EC6 |
|---|---|---|---|---|---|---|
| 2009–2010 | CUL: Cubus SD: 22-Oct HD: 5-Aug | CUL: Pamier SD: 18-Sep HD: 26-Aug | ||||
| 2010–2011 | CUL: Akteur SD: 19-Oct HD: 28-Jul | CUL: Akteur SD: 11-Oct HD: 29-Jul | CUL: Akteur SD: 22-Sep HD: 20-Aug | CUL: Hermann SD: 13-Oct HD: 22-Aug | ||
| 2011–2012 | CUL: Akteur SD: 18-Oct HD: 1-Aug | |||||
| 2012–2013 | CUL: Akteur SD: 17-Oct HD: 4-Aug | CUL: Akteur SD: 26-Oct HD: 5-Aug | ||||
| 2013–2014 | CUL: JB Asano SD: 25-Oct HD: 4-Aug | CUL: Orcas SD: 8-Oct HD: 23-Aug | CUL: Pamier SD: 9-Oct HD: 20-Aug | |||
| 2014–2015 | CUL: Sokal SD: 23-Oct HD: 20-Jul | CUL: Akteur SD: 28-Oct HD: 24-Jul | CUL: Arezzo SD: 14-Oct HD: 12-Aug | |||
| 2015–2016 | CUL: Estivus, Pamier, Ferrum SD: 24-Oct HD: 30-Jul | |||||
| 2016–2017 | CUL: Patras SD: 14-Nov HD: 30-Jul | CUL: Sokal SD: 12-Oct HD: 18-Jul | CUL: Elixer SD: 4-Oct HD: 14-Aug |
| Year | Kraichgau | Swabian Jura | ||
|---|---|---|---|---|
| Date | Satellite | Date | Satellite | |
| 2014 | 20-Mar | Landsat 8 | 29-Mar | Landsat 7 |
| 28-Mar | Landsat 7 | 9-Jun | Landsat 7 | |
| 8-Jun | Landsat 8 | |||
| 2015 | 4-Apr | Landsat 8 | 4-Jun | Landsat 8 |
| 24-Apr | Landsat 8 | 12-Jun | Landsat 7 | |
| 18-May | Landsat 7 | |||
| 3-Jun | Landsat 7 | |||
| 2017 | 21-Apr | Landsat 7 | 10-Apr | Sentinel-2 |
| 10-May | Sentinel-2 | 30-Apr | Landsat 7 | |
| 17-May | Sentinel-2 | 10-May | Sentinel-2 | |
| 23-May | Landsat 7 | 17-May | Sentinel-2 | |
| 16-Jun | Landsat 8 | 19-Jun | Sentinel-2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zare, H.; Weber, T.K.D.; Ingwersen, J.; Nowak, W.; Gayler, S.; Streck, T. Combining Crop Modeling with Remote Sensing Data Using a Particle Filtering Technique to Produce Real-Time Forecasts of Winter Wheat Yields under Uncertain Boundary Conditions. Remote Sens. 2022, 14, 1360. https://doi.org/10.3390/rs14061360
Zare H, Weber TKD, Ingwersen J, Nowak W, Gayler S, Streck T. Combining Crop Modeling with Remote Sensing Data Using a Particle Filtering Technique to Produce Real-Time Forecasts of Winter Wheat Yields under Uncertain Boundary Conditions. Remote Sensing. 2022; 14(6):1360. https://doi.org/10.3390/rs14061360
Chicago/Turabian StyleZare, Hossein, Tobias K. D. Weber, Joachim Ingwersen, Wolfgang Nowak, Sebastian Gayler, and Thilo Streck. 2022. "Combining Crop Modeling with Remote Sensing Data Using a Particle Filtering Technique to Produce Real-Time Forecasts of Winter Wheat Yields under Uncertain Boundary Conditions" Remote Sensing 14, no. 6: 1360. https://doi.org/10.3390/rs14061360
APA StyleZare, H., Weber, T. K. D., Ingwersen, J., Nowak, W., Gayler, S., & Streck, T. (2022). Combining Crop Modeling with Remote Sensing Data Using a Particle Filtering Technique to Produce Real-Time Forecasts of Winter Wheat Yields under Uncertain Boundary Conditions. Remote Sensing, 14(6), 1360. https://doi.org/10.3390/rs14061360






