Abstract
It is of great significance for emergency rescue to rapidly assess damage of buildings after an earthquake. Some previous methods are time-consuming, data are difficult to obtain, or there is lack of regional damage assessment. We proposed a novel way to rapidly assess building damage by comprehensively utilizing earth observation-derived data and field investigation to alleviate the above problems. These data are related to hazard-causing factors, hazard-formative environment, and hazard-affected body. Specifically, predicted ground motion parameters are used to reflect hazard-causing factors, e.g., peak ground velocity (PGV), peak ground acceleration (PGA), and pseudo-spectral acceleration (PSA). The hazard-formative environment is denoted by the underground 30 m shear wave velocity. Vulnerability of buildings is reflected by their structure type, age, and height. We take the April 2015 Nepal earthquake as a case study, and building damage data interpreted from satellite images are used to validate the effectiveness of the proposed method. Based on the gradient boosting machine, this paper rapidly assesses building damage from two different spatial levels, i.e., pixel and microzone, and obtains the potentially affected position and regional damage rate. Compared with the method of fragility function, the machine learning method provide a better estimation of the building damage rate. Compared with the assessment method based on remote sensing image, the method in this paper is very efficient since spatial distribution of hazard-causing factors, e.g., PGA, can be quickly predicted shortly after an earthquake. The comparison of experiment with and without vulnerability data of buildings shows that data on the vulnerability of buildings are very important to improve the assessment accuracy of building damage.
1. Introduction
Since the building is the most important place of human activity, it is very important for emergency rescue to obtain building damage information shortly after an earthquake. The location and state of each damaged building can be accurately obtained by investigation after an earthquake [1,2]. However, this would be a lengthy and resource intensive process that is not sufficient to support emergency response and early recovery plans. Although the timeliness is poor, these field investigations are actually very important because they can provide relatively accurate research data and valuable experience for subsequent earthquake research. Leaving aside the most primitive way, it is a subject worthy of research to rapid assess building damage after an earthquake.
1.1. Previous Related Work
Data are the basis of research. According to the data, we can divide the building damage assessment methods into two categories. The first category uses data that can be seen directly. This method category is mainly remote sensing method. Remote sensing is an advanced method widely used in earthquake damage assessment [3,4,5,6,7,8,9]. As one of the important hazard-affected bodies, a building is a complex object because of the diversity of materials and the differences in geographic regions. The seismic damage caused by structural damage is difficult to extract from the image. The acquisition of remote sensing images after an earthquake has a lag, and differences in data sources will also lead to a poor model transfer capability [10]. Therefore, we did not use remote sensing images to extract earthquake damage. Remote sensing products of historical earthquake damage combined with manual interpretation are used as verification data. Damaged pixels made by SAR or interpreted by optical images are used as the ground truth or verification data of damaged buildings, which are described in detail below.
The data used in the second category methods cannot be seen directly and need to be observed, investigated, or predicted. In this method category, the traditional method fragility function plays a vital role in understanding the regional risk of seismic active areas. The fragility function describes the probability of reaching or exceeding a given damage state under the action of a given ground motion. The empirical method is the most widely used when large databases are available because real-time building damage can be expressed as a function of any ground motion parameter. Due to the low frequency of destructive earthquakes in seismic active areas, most of the existing empirical fragility curves are constructed using limited databases, which is one of the salient features of empirical fragility curves. In the past few decades, the number of fragility functions using various methods has increased significantly around the world [11,12]. However, the fragility functions basically use a single influencing factor, ignoring a large number of relevant factors or available data, such as PGA, PGV, PSA, slope, and site effect factor. There are also methods to comprehensively use a variety of factors for building damage assessment. ShakeMap [13,14] and ShakeCast [15] developed by USGS are feasible in providing timely information of impact on buildings after earthquake. ShakeMap combines ground motion records with seismic information, such as magnitude, location, and fault type, as well as the geological conditions (i.e., shear wave velocity of 30 m underground) of the affected area, to automatically generate seismic intensity maps. ShakeCast was developed as a supplement to ShakeMap, which can assess the damage to the infrastructure in real time. With the advancement of contemporary information technology, the availability and access to data related to building damage have increased. After the Gurkha earthquake in 2015, the government carried out detailed damage assessment activities. Some scholars formulated the fragility function and curve based on the collected building damage cases [16,17]. At the same time, after the earthquake in Nepal, a large amount of accessible building data were generated, including building structure, age, height, and other information. These developments have made it possible to explore how to timely assess building damage by using machine learning from available data [18,19]. Machine learning methods can solve the problem of multi-inputs and difficult fitting of the model and make comprehensive use of a variety of factors. Related machine learning methods include fuzzy logic [20], multi-layer perceptron [21], support vector machine [22], tree model [23], and deep neural networks [24]. These machine learning models are basically for the damage assessment of single buildings and use a lot of detail data of building structure, which are difficult to obtain. In the earthquake emergency rescue, the regional building damage is often used to provide information for dispatching rescue forces.
Above all, the first category of methods is similar to visual interpretation, and the assessment is closer to identifying building damage. The second category of methods is closer to predicting building damage, which predicts the building damage unseen according to some parameters. The first category needs to mobilize satellites after an earthquake, and the second category is easier to assess rapidly. However, some of the second category methods use a single factor, and some methods focus on the damage assessment of single buildings and use the data difficult to be obtained, which makes it difficult to assess rapidly. We try to solve these problems by building regional assessment models, using multi factors, shortening the data acquisition time, and improving the quality of assessment data.
1.2. Overview of Research Process
We explored a novel way shown in Figure 1 to rapidly assess building damage by comprehensively utilizing multi-source data concerning hazard-causing factors, hazard-formative environment, and hazard-affected body. Among them, the hazard-formative environment and the hazard-affected body can be regarded as the prior information before the earthquake. The hazard-formative environment includes site conditions and terrain slope. As the analysis object of this paper, the building is the main hazard-affected body, and its structure, age, height, density, and distribution are the factors affecting the vulnerability of the hazard-affected body. The hazard-causing factors in our analysis are mainly the ground motion parameters, including PGV, PGA, and PSA, which can be observed or predicted after an earthquake to further assess building damage. According to previous studies, these parameters can reflect the impact of ground motion on buildings [25,26,27,28]. Among them, PSA contains the values of three periods of 0.3 s, 1.0 s, and 3.0 s. These three periods are also the three periods used by the pseudo-spectral acceleration output by ShakeMap. The corresponding PSA (0.3 s, 1.0 s and 3.0 s) can also be obtained through ShakeMap when quickly assessing the damage of regional buildings after the earthquake, which can reduce the limitations of the method proposed in this paper and help the model to be used and evaluated by others. The above data are all observation-derived or field investigated and used for analysis at two levels. Pixel-level classification is to distinguish damaged pixels, and microzone-level regression is to construct a model of the relationship between the damage rate and factors to estimate the proportion of damaged buildings with different damage levels. The whole method framework uses a variety of influencing factors to assess building damage from the regional level (pixels can also be regarded as areas of a certain size). According to the method framework, the relevant models can be built in advance. After the earthquake, the relevant data including ground motion parameters can be quickly obtained or predicted after the earthquake, so as to achieve the purpose of rapid assessment.
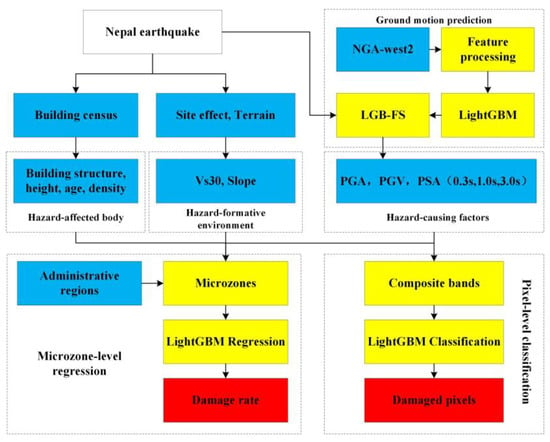
Figure 1.
Technical flow chart. The blue rectangles represent data, the yellow rectangles represent method or processing operations, and the red rectangles represent the desired result.
2. Multi-Source Data of the 2015 Nepal Earthquake
The Mw 7.8 earthquake in Nepal is used as a case for research. The earthquake occurred on 25 April 2015 and caused casualties and serious damage to houses. The epicenter was 77 km northwest of Kathmandu [29]. The microzone-level analysis area is located in the red wireframe in Figure 2, covering all administrative districts with building structure information. The green areas in subplot 2(b) shows the administrative districts with structural information in detail. There are still some administrative districts without structural information, such as Kathmandu. The pixel-level analysis area is located in the green wireframe in Figure 3, covering Kathmandu and some surrounding areas. The longer yellow line in Figure 2 and Figure 3 is the Himalayan fault zone with roughly the same extension direction as microzones distribution. The deep slope (MHT) of the main Himalayan fault has a strike of 295°, a dip angle of 11°, and a forward dip of 103°. It is the seismogenic structure of the Nepal main shock [30].
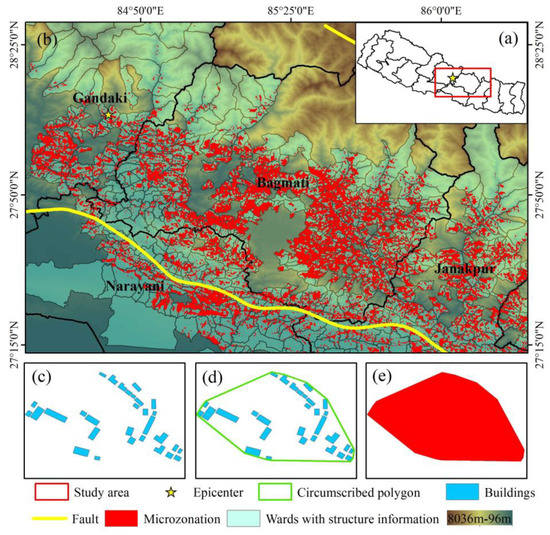
Figure 2.
Distribution of building regions with structural information and refined building regions. Subplot (a) shows the geographical location of all microzones. Subplot (b) shows the distribution of all microzones. The background is terrain, and the light green regions are the administrative wards with building structure information. The longer yellow line in subplot b represents the seismogenic fault. Subplots (c–e) show the refinement process of the building regions, transforming the building regions from wards to microzones. The Green wireframe is the circumscribed polygon of blue buildings in subplot (d); the red parts are building regions after refinement named microzones, and the red polygon in subplot (e) is one of the microzones.
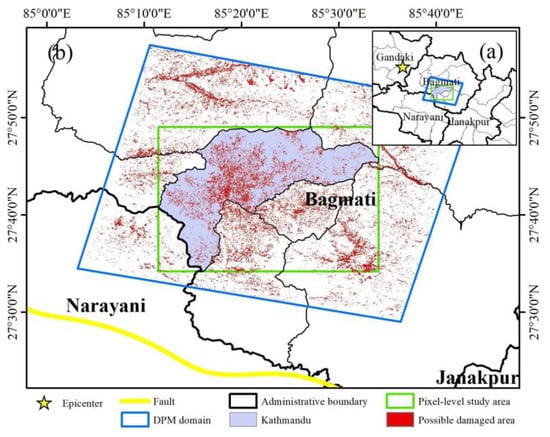
Figure 3.
(a,b) Damage proxy map and pixel-level study area. The green box is the analysis area at the pixel level, including Kathmandu. The red position indicates where there may be building damage. The yellow line indicates the seismogenic fault.
2.1. Observation-Derived Data and Field Investigation
According to the technical flow chart in Figure 1, the data used are observation-derived or investigated, divided into three categories, i.e., hazard-formative environment, hazard-causing factors, and hazard-affected body. The hazard-formative environment consists of both the DEM data of Nepal with a spatial resolution 30 m and the global Vs30 product data with a spatial resolution 1000 m (i.e., the shear wave velocity of 30 m underground, which is widely used to reflect the site conditions) [31]. The slope data of the study area can be calculated based on DEM. The hazard-causing factors include PGA, PGV, and PSA (0.3 s, 1.0 s, and 3.0 s), which are predicted based on the observed seismic information. The data of the hazard-affected body are composed of building attributes, i.e., vectorized footprint, structure, height, and age, which are from the survey of building damage done by the National Planning Commission (NPC) of Nepal after the earthquake [32]. Based on the vector data of buildings from OSM [33], the building density can be calculated, which represents the number of buildings distributed per unit area. Table 1 lists all the data and their sources. Among these data, some are made (i.e., DEM and Vs30) or predicted (i.e., PGA, PGV, and PSA) based on earth observation data, and some are from field investigation (i.e., building attributes).

Table 1.
Different categories of data and applied analysis levels.
2.2. Data Processing for Microzone-Level Regression
When assessing the damage pattern of buildings at microzone level, the analysis units are transformed from single buildings into building regions. We used the field investigation of more than 760,000 houses obtained by the NPC of Nepal after the earthquake as basic building data. A total of 832 small building regions are obtained through statistical analysis of the basic building data based on the smallest administrative unit “ward” in Nepal. However, these 832 building regions are still divided on the basis of administrative districts. Many regions have a small number of buildings, and most of the locations have no building. The total area of 832 wards is 20,634 km2, and the total area of buildings is 47 km2, accounting for 0.23%. Figure 2 shows that most of the locations without buildings are mountain. The entire region is considered when calculating the average value of each feature, which will inevitably cause errors. In order to reduce the errors, we refined the building regions. The method is to delineate the outer polygon of the building group as an independent building region, as shown in subplot 2(d). Two separate building regions are generated where the distance between buildings exceeds 500 m. After refined processing, a total of 2439 building regions called microzones are finally formed as the red fragmented parts in subplot 2(b). The average scale of these microzones is 1.64 km2. As for each microzone, the building attributes (e.g., structure, age, height) are obtained through the regionalized statistics of the buildings, while the other features are the average values of the coverage of each microzone.
2.3. Data Processing for Pixel-Level Classification
After obtaining the basic data, the data need to be processed differently according to different purposes. When assessing building damage patterns at pixel level, we transformed this problem into a pixel-level classification. A damage proxy map (DPM) is used as the ground truth for result evaluation. As shown in Figure 3, the damage proxy map covers the area around Kathmandu and was processed by ARIA, an advanced rapid imaging analysis team from JPL and California Institute of Technology, using X-band interferometric synthetic aperture radar data from the COSMO-SkyMed satellite [34]. The technology uses prototype algorithms to quickly monitor changes in the surface caused by natural or man-made destruction. Assessment techniques are most sensitive to damage to the built environment. The multi-temporal radar data span is from 24 November 2014 to 29 April 2015. DPM is raster data with a spatial resolution of 30 m.
We use a 9-bands feature map for classification. The 9 bands are the distribution of buildings, the shear wave velocity of 30 m underground, terrain slope data, building density, PGA, PGV, PSA0.3 s, PSA1.0 s, and PSA3.0 s. The raster data of the building distribution are transformed from vector data with a spatial resolution of 100 m. The original spatial resolution of the Vs30 data is 1000 m, and here, we upsample it to 100 m. Correspondingly, slope data and building density data are also adjusted to 100 m resolution. The ground motion raster data can be obtained from USGS, and their original resolution is 5000 m, which is much larger than 100 m. Here we use a machine learning method to predict the distribution of ground motions, instead of using the same up-sampling method to avoid the “different objects have the same spectrum” as much as possible. According to previous studies, ground motion parameters are functions of both distance and magnitude and many scholars have developed a variety of GMPEs based on this combined with other parameters [35,36,37,38,39,40]. Based on the global ground motion database NGA-west2, we used a gradient boosting tree method to build a prediction model of ground motion parameters and predicted the ground motion of Nepal earthquake with a spatial resolution of 100 m.
2.4. Classification System of Building Damage
It is critical to determine the damage classification system of buildings before building damage assessment. At present, there are many damage classification standards in the world, where both EMS-98 [41] and FEMA-273 [42] are often adopted in practice. In Nepal, 90% of buildings can be roughly divided into reinforced concrete, stone masonry, and bamboo and wood structures. The National Housing and Census of Nepal emphasizes that 9.94% of buildings are reinforced concrete structures, and most of the buildings are stone masonry structures [43]. Therefore, stone masonry buildings are also the main building structures analyzed in Nepal earthquake cases. Dipendra et al. [16,17] proposed a modified damage system based on the standard proposed by Grunthal [41], which is also the standard used by the fragility function of stone masonry structure in this paper. The NPC standard mainly considers the structural damage of buildings and mainly for single buildings. It is a comprehensive damage system, which divides the building damage into 5 levels. In this study, the microzone-level analysis adopts the same standard as NPC but takes the proportions of buildings with different damage levels in each microzone as its damage rates. The pixel-level analysis adopts two damage levels, namely, damaged and intact. The different classification systems are shown in Table 2.

Table 2.
Different damage classification systems for Nepal’s buildings.
3. Methodology
The light gradient boosting machine (LightGBM) [44] used in this paper is an ensemble of learning methods, and a decision tree is used as basic learner. LightGBM can be used for regression and classification problems, suitable for the task of building damage assessment.
3.1. LightGBM
The Boosting algorithm based on the tree model uses a pre-sorting algorithm for feature selection and tree splitting, but this consumes more space and time resources. As shown in Figure 4, LightGBM uses a histogram algorithm to discretize continuous eigenvalues into k discrete values and constructs a histogram of width k according to the segmentation point. The next step is to traverse all the data and count the cumulative statistics of each segmentation point in the histogram. When selecting features, the histogram is traversed, and the best segmentation point can be found according to the discrete value of the histogram, which can greatly save time and space resources. Due to its regularization effect, it can also effectively prevent over-fitting of the model and improve accuracy. After the histogram is processed, the feature values are input into the decision tree for regression or classification. LightGBM uses a leaf-wise growth strategy with depth restrictions instead of the level-wise strategy currently used by most GBDT algorithms. Based on the level-wise strategy, the leaves of the same layer can be divided at the same time to control the complexity of the model so that the model is not easy to overfit. However, the level-wise is an inefficient strategy because it treats leaves of the same layer indiscriminately, which will cause a lot of unnecessary calculations. In fact, there is no need to search and segment many leaves because the segmentation gain is very low. The leaf-wise strategy is a more effective strategy. Each segmentation needs to find the leaf with the largest segmentation gain from all current leaves [44]. LightGBM is an ensemble model based on the CART tree, which connects multiple decision tree models in series to make classification decisions together.
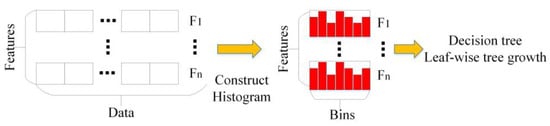
Figure 4.
Histogram-based decision tree algorithm. The left part of the figure represents the organization form of the original data, and the middle part of the figure represents the histogram data.
3.2. Ground Motion Prediction
In addition to ground motion prediction equations (GMPEs) [35,36,37,38,39,40], there have also been many studies using machine learning methods for ground motion prediction in recent years [45,46,47]. Ground motion parameters are mainly functions of both magnitude and distance, and many ground motion equations also use these two factors as the main influencing factors. In addition, factors such as the location of the epicenter, the location of the target point, the fault related parameters (e.g., rake, strike, dip), and site effect will also have an impact on ground motion. We use LightGBM, a tree model method under the framework of gradient boosting tree, to build a model combined with the strong motion database NGA-West2, predicting the distribution of ground motion parameters, i.e., PGA, PGV, and PSA. A total of 305 earthquakes and 12,892 strong motion data records are used for model construction and verification. The magnitudes of 305 historical earthquake cases range between Mw 3.2 and Mw 7.9. In the process of model construction, the features mentioned above are used as regression parameters. The resolution of the predicted ground motion distribution can reach to 100 m and is used for the regression of microzone-level damage rate and pixel-level classification. The ground motion prediction method carried out features selection and transformation, and the method LGB-FS is introduced in detail in another paper [48]. We use mean absolute error (MAE), root mean squared error (RMSE), and coefficient of determination (R2) [49] as evaluation indicators. MAE can reflect the average error level of the predicted results. RMSE actually describes dispersion, which can be understood as stability of errors. The smaller the RMSE, the more stable the errors of the predicted values, and the larger the RMSE, the more unstable and fluctuating the predicted errors. R2 is the fitting coefficient in linear regression. The closer to 1, the better the fit of the regression.
As shown in Table 3 by Chen et al. [48], compared with other methods, the ground motion parameters obtained by this method are more accurate. The results evaluation of PGA and PGV are listed in the table. Compared with GMPEs and ShakeMap, the predicted ground motion parameters are closer to the observed values. Based on the constructed ground motion prediction model, the distribution of ground motion can be quickly predicted when the basic parameters of the earthquake are quickly obtained after an earthquake. Because the ground motion of Nepal is used in this paper, we validate the ground motion prediction model with the Nepal earthquake case. The ground motion data used in the verification are from five seismic stations [50], and the relevant data can be obtained from https://www.strongmotioncenter.org/ (accessed on 10 September 2021). The ground motion distribution given by ShakeMap is based on GMPEs and corrected with the observation data of some seismic stations. As shown in Table 4, the PGA predicted by LGB-FS model is closer to the observation data of the five seismic stations than ShakeMap. AE in the table represents absolute error.

Table 3.
Performance comparison of the LGB-FS for ground motion prediction with other methods.

Table 4.
Performance comparison of the LGB-FS for PGA prediction with ShakeMap after Nepal earthquake.
The ground motion prediction model seems to be a black box model, but it can be explained. LightGBM model is a tree-based model. In the process of building the model, we built 2000 trees to fit the model. If it is unrealistic to show these trees, we choose one of them as an example. The target of each fitting of the model is the residual between the fitting result of the previous tree and the final regression target. For example, the fitting target bit is 10, the fitting result of the first tree is 8, and the fitting target of the second tree is 2. Therefore, it can be deduced that the final predicted value of the model is the sum of the predicted values of each tree. Figure 5 shows a tree of the fitted PGA prediction model. The output value of each leaf node is the average value of the samples falling into the leaf node. Mag represents the magnitude of the earthquake, and EpiD represents the epicentral distance. Sx and Sy respectively represent the Cartesian coordinates X and Y values of the target point. The following trees will fit the residual between the predicted value and the actual value on the basis of this tree.
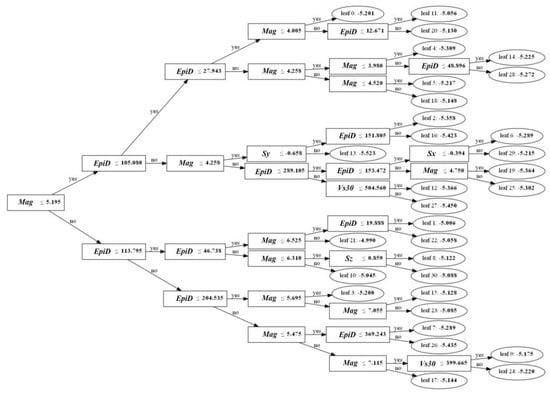
Figure 5.
A tree of PGA prediction model. Rectangles represent feature segmentation nodes, and ellipses represent leaf nodes.
3.3. Regression of Microzone-Level Damage Rate
The LightGBM is used to regress and estimate damage rates of each microzone. There are up to 13 features for regression in each microzone, including ground motion parameters PGA, PGV, PSA (0.3 s, 1.0 s, and 3.0 s), terrain slope, site effect, building density, the proportion of stone masonry buildings, the proportion of bamboo and wood buildings, the proportion of reinforced concrete (RC) buildings, and the age and height of buildings. The proportions of several building structures mentioned above can be defined and calculated by the following formula:
where P represents the proportion of a certain type of buildings, and N represents the total number of such buildings in a microzone. i is 1 for stone masonry buildings, i is 2 for bamboo wood structure buildings, i is 3 for RC structure buildings, and i is 4 for other structure buildings.
Ground motion parameters can be quickly predicted after the earthquake, or the results of USGS can be used as a substitute. The terrain slope can be calculated based on DEM data. The site effect is the product data already available. However, data of vulnerability of buildings, e.g., structure, age, and height, may not be quickly obtained after the earthquake. Therefore, two kinds of feature combinations will be analyzed according to data availability, which is terms as “EASY” and “HARD” mode. These two modes will be elaborated in detail later.
3.4. Classification of Pixel-Level Damaged Buildings
The assessment of damaged pixels is reformulated as a dichotomous classification problem. Specifically, the values of pixels with the distribution of damaged buildings are 1, and the values of pixels without damaged buildings are 0. We use a trained LightGBM model to accomplish this task. The feature dimension used for classification is 9, including five ground motion parameters (i.e., PGA, PGV, PSA0.3s, PSA1.0s, and PSA3.0s), building distribution, building density, terrain slope, and site effect. During model training, we can fit a binary classification model through the histogram algorithm and the leaf-wise tree growth strategy. In the model fitting process, each tree is used to estimate the error of all previous trees, and the fitting is performed with the goal of reducing the error. After the model is trained and fitted, we need to input each 1 × 1 × 9 pixel into the fitted tree for classification.
When classifying the damage state of the pixel, we use recall, precision, and F1 Score as evaluation indicators, which can be calculated by the confusion matrix. We calculate the above indicators on the test set to evaluate the classification effect of the model.
3.5. Comparison of Methods
In the classification of damaged pixels in Nepal, we also try to use other machine learning methods and compare them with the LightGBM method used in this paper. The data used for method comparison are located in the green box in Figure 2. In this area, the training set and the test set are randomly selected according to the ratio of 7:3, and the methods are compared on the test set. As shown in Figure 6a, LightGBM has the highest accuracy in the test data, and its several evaluation indexes including recall, precision, and F1 score are the highest among several methods. In terms of the classification performance, the effect of random forest is closest to LightGBM. On the other hand, the algorithms are compared by using true positive rate and false positive rate. As shown in Figure 6b, when the classification threshold is 0.5, different points represent the performance of different algorithms. The closer the point is to (0, 1), the better the performance of the model. Among them, the red dot is closest to (0, 1), which represents the best performance of LightGBM.
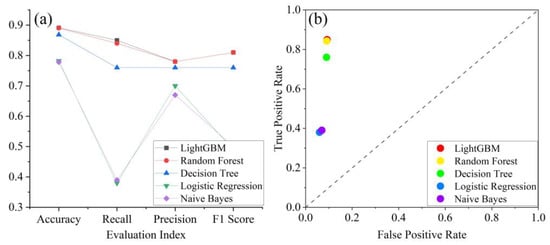
Figure 6.
Performance comparison of classification methods. Subplot (a) shows the accuracy, recall, precision, and F1 score of several machine learning methods. Subplot (b) shows the FPR and TPR classified by several methods with a classification threshold of 0.5.
4. Results and Discussion
Based on the building census data, we analyzed the building vulnerability after the Nepal earthquake. Then we perform microzone-level regression and pixel-level classification on building damage and establish the corresponding regression and classification models to quickly assess building damage after the Nepal earthquake. The detailed analysis results and discussion are as follows.
4.1. Analysis of Building Vulnerability
As the most important hazard-affected body in an earthquake, the building and its attributes will inevitably affect the severity of damage. In the case of the Nepal earthquake, the attributes of buildings include structure, age, and height. We analyze the damage of buildings in different attribute intervals and explore the impact of attribute changes on building damage. Most of the buildings in Nepal are stone masonry buildings. Buildings with different structures in each microzone have their corresponding proportion. Subplot 7(c) shows the distribution of the proportion of buildings with different structures. It can be seen from subplot 7(c) that in the census of housing damage conducted by the government after the earthquake, stone masonry buildings accounted for more than 90% in most building regions, while bamboo and wood structure buildings and RC structure buildings accounted for very little, and the two types of buildings in most building regions did not exceed 10%. Since stone masonry is the main building structure in Nepal, we analyzed damage to building regions with different proportions of stone masonry. For the building regions with damage levels 5 and 4, as the proportion of stone masonry increases, the damage rate shows an upward trend, especially the damage rate of regions with damage level 5.
The height and structure of buildings are also closely related to the vulnerability of buildings. When a major earthquake occurred in 2015, the overall height of buildings in Nepal was not high, which was related to the structures of the local buildings. As shown in Figure 7b, the average height of most building regions is less than 25 feet, of which the building regions around 15 feet are the most, and the average height of the regions basically conforms to the normal distribution. According to the research of Takai et al. [50], the natural vibration period of high-rise buildings in Nepal is between 3 and 5 s, and for low-rise buildings, the natural vibration period is less than 3 s. Most of the research areas in this paper are rural areas in the middle and high mountainous areas, and the main types of buildings are stone masonry structures, which account for the largest proportion. Stone masonry buildings are non-engineering buildings and do not meet any seismic requirements, especially toughness requirements. The large number of damaged stone masonry buildings in each earthquake in Nepal’s history also proves this point. According to NPC records, in the 2015 earthquake, buildings in 31 administrative regions of Nepal were damaged, of which 84.2% were stone masonry structures in the wild, 5.4% were masonry structures, 4.1% were reinforced concrete structures, and 5.8% are bamboo and wood structures. As can be seen from subplot 7(e), the severe damage rate will increase as the height increases for buildings under 20 feet. This is also caused by the majority of stone masonry buildings, and the height of stone masonry buildings is usually not too high.
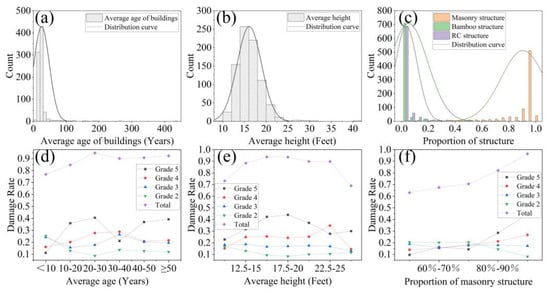
Figure 7.
Damage rate curves of different damage levels and distribution of building attributes. Subplot (a), the building age distribution; subplot (d), the damage rate curves of different age; subplot (b), the building height distribution; subplot (e), the damage rate curves of different height; subplot (c), the distribution of different building structures; subplot (f) shows the effect of different stone masonry proportions on the damage rate.
The construction period of the building has a certain impact on the damage of the building after an earthquake. Generally, the older the building, the worse the quality, and the greater the possibility of earthquake damage. The ages of buildings in the study area are basically distributed within 50 years, and buildings with a construction period of 10–30 years occupy the main body. As can be seen from Figure 7d, with the increase of building age, the proportion of each damage level shows an upward trend, but there are some fluctuations. The total damage rate of buildings in 30–40 years will decline, which is due to the decline of the proportion of stone masonry buildings in this age group. At this time, the impact of structure exceeds that of building age. Within 10 years, the proportions of bamboo wood structure and RC structure will increase a lot, so the proportion of severely damaged buildings will be smaller.
4.2. Damage Assessment at Microzone Level
The research objects in this section are 2439 microzones, 2000 of which are randomly selected as training data, and the rest are as test data. The features that affect the building damage include ground motion parameters, building attribute (density and structure), site effect (Vs30), and terrain slope. Each microzone has the above-mentioned features, and feature values are the average values of each microzone. Actually, not all data can be obtained quickly after the earthquake. Therefore, we have considered two feature combinations according to the difficulty of data acquisition, i.e., EASY and HARD mode. In the EASY mode, there are 8 features, including PGA, PGV, PSA (0.3 s, 1.0 s, and 3.0 s), building density, terrain slope, and Vs30. In the HARD mode, five additional features are included, which are closely related to vulnerability of buildings, e.g., structure, age, and height of buildings. The building structure information includes the proportion of stone masonry structure, the proportion of bamboo and wood structure, and the proportion of RC structure. The corresponding feature combinations are used to perform regression learning on the damage rates of different damage levels, and the models obtained are evaluated on the test set. The evaluation results are shown in the Table 5. The assessment accuracy of the regression models is significantly improved due to the addition of features related to vulnerability of buildings. When the damage level is 5, the MAE of estimated damage rate is 0.07, while it is 0.05 for the damage level 4. It can be understood that the error ranges of estimating the severe damage rates reach ±7% and ±5%, respectively.

Table 5.
Evaluation of microzone-level building damage assessment with different feature combinations.
The importance of a feature is calculated based on the total information gain generated when it is used as a feature of tree splitting [53]. After calculating and normalizing the feature importance of the models with different feature combinations as Figure 8, it can be found that the most important features are related to the building structures, especially the proportion of stone masonry and bamboo and wood structure. The attributes of hazard-affected body are more important to the model than the ground motion parameters. Building structure, age, and height can be obtained through building census before earthquake to build a basic information database. On the premise of using the above data, a better regression model can be constructed to assess damage of building regions in Nepal. The feature importance ranking shown in Figure 8 is only for the study area of the Nepal earthquake, from which we can see the importance of different features in the model construction, which is not necessarily applicable to all earthquakes in the world.
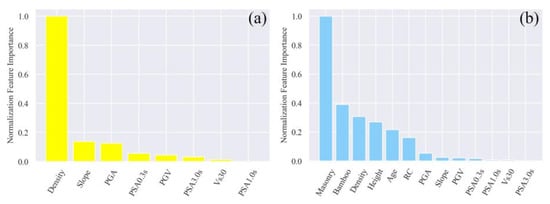
Figure 8.
Feature importance of different feature combinations. Subplot (a) represents the EASY mode, and subplot (b) represents the HARD mode.
In order to better measure the pros and cons of the regional building damage assessment methods, we use the traditional empirical fragility function method to assess regional damage. Dipendra et al. constructed the fragility curve of buildings in Nepal based on the building damage cases collected after earthquake by the Nepal government [8]. He used the two-parameter Gaussian distribution function to derive the fragility curves. The estimation of Gaussian parameters from building damage data can be found firstly in the studies of Shinozuka et al. [54] and Porter et al. [55]. The Figure 9 shows the fragility curves of stone masonry buildings in Nepal. PGA and PSA0.3s are used as indicators to measure the intensity of ground motion. According to the fragility curves, the probability of buildings reaching each damage level can be calculated under different intensity levels.
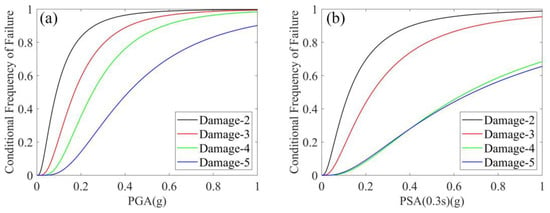
Figure 9.
(a,b) Empirical fragility curves for stone masonry buildings in Nepal considering PGA and PSA0.3s as intensity measures.
The building structures in the test area are mainly stone masonry, so that the fragility functions of stone masonry building can be used. We select the building regions where the stone masonry structure buildings account for more than 90% to compare the two methods. As shown in Table 6, it is obvious that the regression method using multiple data is better than the general fragility function, especially for the damage rate estimation of severe damage levels. When the damage level is 5, the estimation error of the fragility functions reaches 33.8%, while the worst of the regression models is 18.6%; when the damage level is 4, the estimation error of the fragility functions is 14.1%, and the worst of the regression model is 11.2%. Most of the current empirical fragility functions are the relationships between ground motion parameters and building damage constructed using historical seismic damage data. They all use a single influencing factor to build an empirical model, which may lead to worse results than the multi-factor regression model.

Table 6.
Results comparison of fragility curves and assessment model in microzones where the stone masonry is the main building structure (MAE).
As mentioned earlier, when the structure, age, and height of the building are used in the regression model, the estimated regional building damage rates would achieve the highest accuracy. As shown in Figure 10, subplots (a)–(d) respectively show the correlation between damage rates of the four damage levels estimated using 13 features and the true damage rates. The R-squares between the estimated damage rates and the true damage rates of the four levels are relatively high on the test set. The linear regression coefficients are basically about 1. The MAE below 0.1 means that the estimation error is within ±10 %. In summary, the estimated results of the regression models are better than damage estimated results using fragility functions. Taking the Nepal earthquake as an example, the method can be transferred to other regions. The regional damage assessment model based on different regional building information can quickly give the damage ratios after an earthquake, which is helpful for earthquake emergency and loss assessment. This is also the transfer idea of the method.
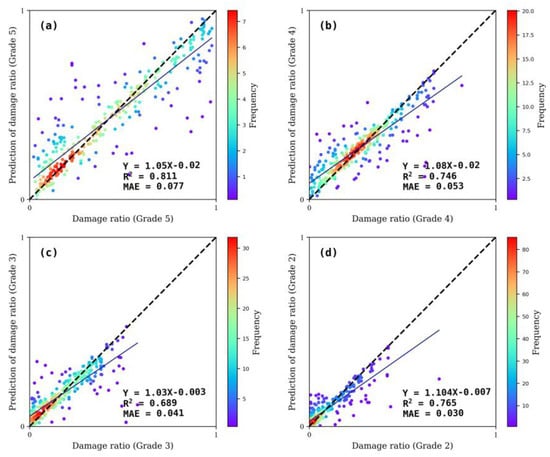
Figure 10.
Evaluation of the assessment results of the best-performing (considering building attributes) regression model for different damage grades on test data. Subplots (a–d) represent evaluation of the best-performing model for damage grades 5-2, respectively.
4.3. Damage Assessment at Pixel Level
When assessing the building damage at pixel level, the study area is a 269 × 410 area including Kathmandu. After many trials, we have adopted a sampling strategy to separate the regions of training and test data. We re-segmented the training area and the test area. The training area is 269 × 301 pixels as the subplot Figure 11a, and the test area is 269 × 108 pixels as the subplot Figure 11b. Buildings are mainly distributed in low terrain locations and less in mountainous areas. The pixels containing damaged buildings are positive samples, and the pixels without damaged buildings are negative samples. The positive samples are selected from the pixels with both buildings and damage information, and the negative samples are selected from the pixels without damage information. In DPM, the damaged pixels without buildings are not selected to be negative samples, because some of the damage pixels in ground truth are not caused by building damage. Subplot Figure 11c is the assessment result. The orange pixels represent the damaged pixels classified correctly (true positive), and the green pixels represent the damaged pixels classified incorrectly (false positive). Subplot Figure 11e shows the details of the assessment results. Red pixels indicate that the damaged pixels are incorrectly classified as non-damaged pixels, and green pixels indicate the redundant classified damaged pixels. Finally, the recall of damaged pixels classification is 0.80, the precision is 0.56, and the F1 score is 0.65 on the test set.
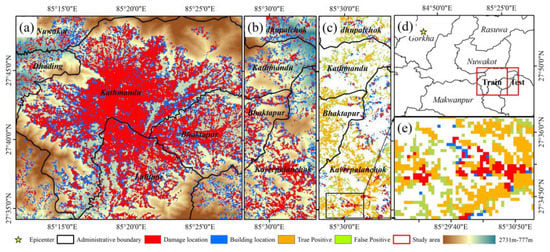
Figure 11.
Map of building damage assessment in Kathmandu. Subplot (a), terrain, building, and damage information of the training area; subplot (b), terrain, building, and damage information of the test area; subplot (c), the damage assessment in test area; subplot (d), the epicenter, the training area, and test area; subplot (e), detailed display of the classified result in the black box. Orange pixels represent damaged pixels classified correctly, and green pixels represent damaged pixels classified incorrectly.
Figure 12 shows the ranges of influencing factors in the classification of damaged pixels. Blue and red represent the training set and test set, respectively. It can be seen from the figure that the data distribution on the test set is basically distributed within the coverage of the value range of the training set. However, the data ranges of some factors are different between the training set and the test set, such as PGV and PSA0.3s, PSA3.0s, which could make the classified results on the test set different from the ground truth.
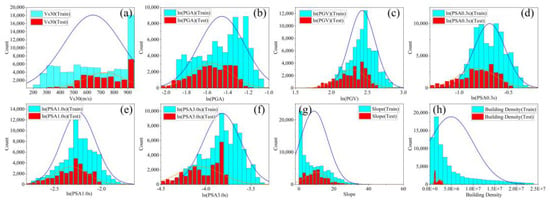
Figure 12.
Ranges of influencing factors of Nepal earthquake. Subplots (a–h) represent the value distribution of Vs30, PGA, PGV, PSA0.3s, PSA1.0s, PSA3.0s, slope, building density, and other factors. The blue histogram and curve represent the distribution of values on the training set, and the red histogram and curve represent the distribution of values on the test set.
As shown in Figure 13, we used optical remote sensing image data to verify the classified results of damaged pixels. The optical image verification data used is the damaged building data produced by the UNOSAT (United Nations Satellite) project of UNITAR (United Nations Institute for Training and Research). These interpretation data based on optical images are not available in all locations. UNITAR has only conducted visual interpretation at individual locations shown as the red and orange pixels in subplot (a). We only verify pixels where there is damage information interpreted by UNITAR. The damaged information was interpreted based on Worldview3 images. There are 49 pixels with damage information in UNOSAT data. Our model classified 44 of the 49 damaged pixels correctly, with an accuracy of nearly 90%. Subplots (b1)–(c1) and (c2)–(c2) are optical images at several red pixels in subplot (a) before and after earthquake. At the locations of red pixels, the model could not correctly classify the damaged pixels and wrongly classified them as non-damaged pixels, called false negatives. Subplots (d1)–(g1) and (d2)–(g2) are optical images at several orange pixels in subplot (a) before and after earthquake. At the locations of orange pixels, the model correctly classified the damaged pixels as true positives. The damage of buildings can be reflected in the boxes of subplots. It can be seen that the damage of buildings on true positive pixels is more serious than that of those on false negative pixels, and even many buildings outside orange dash boxes have undergone severe deformation, which leads to the misclassification of the model at false negative pixels.

Figure 13.
Validation of classified results of damaged pixels on remote sensing images. Remote sensing validation data were produced by UNOSAT project of UNITAR. The selected verification pixels are distributed in the blue box of the thumbnail (part of the test area). In subplot (a), the yellow pixels represent the classified damaged pixels, the red pixels represent the damaged locations interpreted from optical image, and the orange pixels represent the correctly classified damaged pixels (true positive). The sampling pixels b to g are marked in subplot (a) in blue font. Subplots (b1,c1) and (b2,c2) are optical images at the positions of red pixels (false negative) before and after earthquake, respectively. Subplots (d1–g1) and (d2–g2) are optical images at the positions of orange pixels (true positive) before and after earthquake, respectively. The red and orange dash boxes indicate the locations of the damaged buildings.
5. Conclusions
The paper takes the Nepal earthquake in April 2015 as a research case. Aiming at solving the problem that a single source data cannot correctly extract building damage, we use machine learning methods to assess building damage from both pixel and microzone levels by combining multi-source data such as hazard-formative environment, hazard-affected body, and hazard-causing factors. The assessment results include possible damaged locations and damage rate. The main contributions are as follows, which can be referenced by emergency departments or teams to improve the efficiency of emergency rescue after earthquakes.
- (1)
- We comprehensively use multiple factors such as ground motion parameters, building distribution and attributes, terrain slope, site effects, etc., to provide a new idea for building damage assessment after earthquakes.
- (2)
- Compared with remote sensing methods, the assessment method at pixel level in this paper considers the physical causes of building damage. Therefore, it has a better transfer capability and overcomes the deficiencies of data source differences and difficulty in data acquisition.
- (3)
- We discussed the building damage with different attributes at microzone level. It can be seen that the structural information of the building has the greatest impact on the results combined with experiments. Compared with the fragility function, the application of multiple factors can better promote the construction of a regional damage assessment model, with better accuracy and transfer capability.
- (4)
- Building damage at both levels can be assessed rapidly based on data that can be quickly obtained or predicted after earthquake. The assessment mode can be selected according to the availability of data.
We have done some exploratory work on earthquake damage assessment, but there are still many problems that need to be resolved. The resolution of different data is different in pixel classification. The problem of “different objects having the same spectrum” remains unavoidable after using the resampling method. The damage assessment of building regions mostly considers the area near the epicenter, where the difference of ground motion is small, and the building structure is the main influencing factor. The Nepal earthquake case cannot clearly reflect the impact of ground motion on building damage so that other earthquake cases need to be introduced for further exploration.
Author Contributions
Conceptualization, H.T.; methodology, J.C.; data curation, J.C. and J.G.; experiment and validation, J.C. and J.G.; visualization, J.C.; writing—original draft, J.C.; writing—review and editing, H.T. and Y.P.; supervision, H.T.; funding acquisition, Y.P. and H.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by the National Key R&D Program of China (grant no. 2018YFC1504603) and the National Natural Science Foundation of China (grant no. 42192584).
Data Availability Statement
The NGA-west2 data used in the article can be obtained from the following link as http://peer.berkeley.edu/ngawest2/databases/ (accessed on 10 September 2021). Building census data comes from the National Planning Commission of Nepal, which can be obtained at http://eq2015.npc.gov.np/ (accessed on 10 September 2021). Building vector data are available at https://www.openhistoricalmap.org/ (accessed on 10 September 2021). Damage Proxy Map is produced by JPL and available at https://aria-share.jpl.nasa.gov/ (accessed on 10 September 2021).
Acknowledgments
In this research, the results are obtained by programming in Python. The figures are performed using the ArcGIS, Origin, and Python.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following symbols and abbreviated terms are used in this paper.
| PGV | Peak ground velocity |
| PGA | Peak ground acceleration |
| PSA | Pseudo-spectral acceleration |
| SAR | Synthetic Aperture Radar |
| OSM | Open street map |
| NPC | National Planning Commission |
| DPM | Damage proxy map |
| JPL | Jet Propulsion Laboratory |
| NGA-west2 | Enhancement of Next Generation Attenuation Relationships for Western US |
| LightGBM | Light gradient boosting machine |
| GMPEs | Ground motion prediction equations |
| MAE | Mean absolute error |
| RMSE | Root mean squared error |
References
- Boatwright, J.; Blair, J.L.; Aagaard, B.T.; Wallis, K. The distribution of red and yellow tags in the City of Napa. Seismol. Res. Lett. 2015, 86, 361–368. [Google Scholar] [CrossRef]
- Ohsumi, T.; Mukai, Y.; Fujitani, H. Investigation of Damage in and around Kathmandu Valley Related to the 2015 Gorkha, Nepal Earthquake and Beyond. Geotech. Geol. Eng. 2016, 34, 1223–1245. [Google Scholar] [CrossRef][Green Version]
- Shohei, N.; Hiromitsu, T.; Yuji, M.; Takeshi, N.; Naokazu, M.; Hiromitsu, N.; Hiroyuki, F.; Gaku, S. Building-Damage detection method based on machine learning utilizing aerial photographs of the Kumamoto earthquake. Earthq. Spectra 2020, 36, 1166–1187. [Google Scholar] [CrossRef]
- Yanbing, B.; Bruno, A.; Erick, M.; Hideomi, G.; Shunichi, K. Object-based building damage assessment methodology using only post event ALOS-2/PALSAR-2 dual polarimetric SAR intensity images. J. Disaster Res. 2017, 12, 259–271. [Google Scholar] [CrossRef]
- Cooner, A.J.; Shao, Y.; Campbell, J.B. Detection of Urban Damage Using Remote Sensing and Machine Learning Algorithms: Revisiting the 2010 Haiti Earthquake. Remote Sens. 2016, 8, 868. [Google Scholar] [CrossRef]
- Bai, Y.; Hu, J.; Su, J.; Liu, X.; Liu, H.; He, X.; Meng, S.; Mas, E.; Koshimura, S. Pyramid Pooling Module-Based Semi-Siamese Network: A Benchmark Model for Assessing Building Damage from xBD Satellite Imagery Datasets. Remote Sens. 2020, 12, 4055. [Google Scholar] [CrossRef]
- Dongmei, S.; Xuan, T.; Bin, W.; Ling, Z.; Xinjian, S.; Jianyong, C. Integration of super-pixel segmentation and deep-learning methods for evaluation earthquake-damaged buildings using single-phase remote sensing imagery. Int. J. Remote Sens. 2020, 41, 1040–1066. [Google Scholar] [CrossRef]
- James, B.; Thomas, O.; Umaa, R.; Eugene, L. Object-based classification of earthquake damage from high-resolution optical imagery using machine learning. J. Appl. Remote Sens. 2016, 10, 036025. [Google Scholar] [CrossRef]
- Dell’Acqua, F.; Gamba, P. Remote Sensing and Earthquake Damage Assessment: Experiences, Limits, and Perspectives. Proc. IEEE 2012, 100, 2876–2890. [Google Scholar] [CrossRef]
- Yanbing, B.; Bruno, A.; Erick, M.; Shunichi, K. Building damage assessment in the 2015 Gorkha, Nepal, earthquake using only post-event dual polarization synthetic aperture radar imagery. Earthq. Spectra 2017, 33, 185–195. [Google Scholar] [CrossRef]
- Rosti, A.; Rota, M.; Penna, A. Empirical fragility curves for Italian URM buildings. Bull. Earthq. Eng. 2021, 19, 3057–3076. [Google Scholar] [CrossRef]
- Rosti, A.; Del Gaudio, C.; Rota, M.; Ricci, P.; Ludovico, M.D.; Penna, A.; Verderame, G.M. Empirical fragility curves for Italian residential RC buildings. Bull. Earthq. Eng. 2020, 19, 3165–3183. [Google Scholar] [CrossRef]
- Wald, D.J.; Quitoriano, V.; Heaton, T.H.; Kanamori, H.; Scrivner, C.W.; Worden, C.B. TriNet “ShakeMaps”: Rapid generation of peak ground motion and intensity maps for earthquakes in southern California. Earthq. Spectra 1999, 15, 537–555. [Google Scholar] [CrossRef]
- Wald, D.J.; Worden, B.C.; Quitoriano, V.; Pankow, K.L. ShakeMap Manual: Technical Manual, User’s Guide, and Software Guide; USGS: Golden, CO, USA, 2005. [Google Scholar]
- Wald, D.J.; Lin, K.; Porter, K.; Turner, L. ShakeCast: Automating and improving the use of ShakeMap for post-earthquake decision-making and response. Earthq. Spectra 2008, 24, 533–553. [Google Scholar] [CrossRef]
- Dipendra, G. Observational fragility functions for residential stone masonry buildings in Nepal. Bull. Earthq. Eng. 2018, 16, 4661–4673. [Google Scholar] [CrossRef]
- Dipendra, G.; Giovanni, F.; Filippo, S.M. Derive empirical fragility functions for Nepali residential buildings. Eng. Struct. 2018, 171, 617–628. [Google Scholar] [CrossRef]
- Sujith, M.; Han, S.; Chukwuebuka, C.N.; Zhengxiang, Y.; Henry, V.B. Classifying earthquake damage to buildings using machine learning. Earthq. Spectra 2020, 36, 183–208. [Google Scholar] [CrossRef]
- Samuel, R.; Quincy, M.; Hugon, J.; Alonso, G.; Joerg, W.; Liam, W. A machine learning damage prediction model for the 2017 Puebla-Morelos, Mexico, earthquake. Earthq. Spectra 2020, 36, 314–339. [Google Scholar] [CrossRef]
- Harirchian, E.; Lahmer, T. Improved Rapid Visual Earthquake Hazard Safety Evaluation of Existing Buildings Using a Type-2 Fuzzy Logic Model. Appl. Sci. 2020, 10, 2375. [Google Scholar] [CrossRef]
- Jaewon, Y.; Seokgyeong, H.; Jaehun, A. Seismic ground response prediction based on multilayer perceptron. Appl. Sci. 2021, 11, 2088. [Google Scholar] [CrossRef]
- Harirchian, E.; Kumari, V.; Jadhav, K.; Rasulzade, S.; Lahmer, T.; Raj Das, R. A Synthesized Study Based on Machine Learning Approaches for Rapid Classifying Earthquake Damage Grades to RC Buildings. Appl. Sci. 2021, 11, 7540. [Google Scholar] [CrossRef]
- Yerlikaya-Özkurt, F.; Askan, A. Prediction of potential seismic damage using classification and regression trees: A case study on earthquake damage databases from Turkey. Nat. Hazards 2020, 103, 3163–3180. [Google Scholar] [CrossRef]
- Jinke, L.; Zheng, H.; Xuefeng, Z. A data-driven building’s seismic response estimation method using a deep convolutional neural network. IEEE Access 2021, 9, 50061–50077. [Google Scholar] [CrossRef]
- Yamazaki, F.; Murao, O. Vulnerability Functions for Japanese Buildings Based on Damage Data from the 1995 Kobe Earthquake. In Implications of Recent Earthquakes on Seismic Risk; Imperial College Press: London, UK, 2000; Volume 2. [Google Scholar]
- Yamaguchi, N.; Yamazaki, F. Fragility curves for buildings in Japan based on damage surveys after the 1995 Kobe earthquake. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; p. 2451. [Google Scholar]
- Horie, K.; Hayashi, H.; Okimura, T.; Tanaka, S.; Maki, N.; Torii, N. Development of seismic risk assessment method reflecting building damage levels, fragility functions for complete collapse of wooden buildings. In Proceedings of the 13th World Conference Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; p. 2240. [Google Scholar]
- Luis, M.; Erick, M.; Shunichi, K.; Fumio, Y. Synthetic building damage scenarios using empirical fragility functions: A case study of the 2016 Kumamoto earthquake. Int. J. Disast. Risk Reduct. 2018, 31, 76–84. [Google Scholar] [CrossRef]
- Hossain, A.S.M.F.; Adhikari, T.L.; Ansary, M.A.; Bari, Q.H. Characteristics and consequence of Nepal earthquake 2015: A review. Geotech. Eng. J. SEAGS AGSSFA 2015, 46, 114–120. [Google Scholar]
- Lifen, Z.; Jinggang, L.; Wulin, L.; Qiuliang, W. Source rupture process of the 2015 Gorkha, Nepal Mw7.9 earthquake and its tectonic implications. Geod. Geodyn. 2016, 7, 124–131. [Google Scholar] [CrossRef]
- Heath, D.; Wald, D.J.; Worden, C.B.; Thompson, E.M.; Scmocyk, G. A Global Hybrid Vs30 Map with a Topographic-Slope-Based Default and Regional Map Insets. Earthq. Spectra 2020, 36, 1570–1584. [Google Scholar] [CrossRef]
- 2015 Nepal Earthquake: Open Data Portal. Available online: http://eq2015.npc.gov.np/ (accessed on 10 September 2021).
- OpenStreetMap. Available online: https://www.openhistoricalmap.org/ (accessed on 10 September 2021).
- Damage Proxy Maps. Jet Propulsion Laboratory; California Institute Technology. Available online: https://aria-share.jpl.nasa.gov/ (accessed on 10 September 2021).
- Abrahamson, N.A.; Silva, W.J. Summary of the Abrahamson & Silva NGA ground motion relations. Earthq. Spectra 2008, 24, 67–97. [Google Scholar] [CrossRef]
- Boore, D.M.; Stewart, J.P.; Seyhan, E.; Atkinson, G.A. NGA-West2 Equations for Predicting Response Spectral Accelerations for Shallow Crustal Earthquakes; PEER Report No. 2013/05; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2013. [Google Scholar]
- Idriss, I.M. NGA-West2 Model for Estimating Average Horizontal Values of Pseudo-Absolute Spectral Accelerations Generated by Crustal Earthquakes; PEER Report No. 2013/08; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2013. [Google Scholar]
- Abrahamson, N.A.; Silva, W.J.; Kamai, R. Summary of the ASK14 ground-motion relation for active crustal regions. Earthq. Spectra 2014, 30, 1025–1055. [Google Scholar] [CrossRef]
- Campbell, K.W.; Bozorgnia, Y. NGA-West2 ground motion model for the average Horizontal components of PGA, PGV, and 5%-damped linear Response Spectra. Earthq. Spectra 2014, 30, 1087–1115. [Google Scholar] [CrossRef]
- Chiou, B.S.J.; Youngs, R.R. Update of the Chiou and Youngs NGA ground motion model for average horizontal component of peak ground motion and response spectra. Earthq. Spectra 2014, 30, 1117–1153. [Google Scholar] [CrossRef]
- Grunthal, G. (Ed.) European Macroseismic Scale 1998 (EMS-98); European Seismological Commission (ESC): Luxemburg, 1998. [Google Scholar]
- Federal Emergency Management Agency (FEMA). NEHRP Guidelines for Seismic Rehabilitation of Buildings; Federal Emergency Management Agency Report: FEMA-273; FEMA: Washington, DC, USA, 1997.
- Central Bureau of Statistics (CBS). National Population and Housing Census (National Report); Government of Nepal: Kathmandu, Nepal, 2011; p. 2012.
- Ke, G.L.; Meng, Q.; Finley, T.; Wang, T.F.; Chen, W.; Ma, W.D.; Ye, Q.W.; Liu, T.Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), New York, NY, USA, 4–9 December 2017; pp. 3146–3154. [Google Scholar]
- Gandomi, A.H.; Alavi, A.H.; Mousavi, M.; Tabatabaei, S.M. A hybrid computational approach to derive new ground-motion prediction equations. Eng. Appl. Artif. Intell. 2011, 24, 717–732. [Google Scholar] [CrossRef]
- Alavi, A.H.; Gandomi, A.H. Prediction of principal ground-motion parameters using a hybrid method coupling artificial neural networks and simulated annealing. Comput. Struct. 2011, 89, 2176–2194. [Google Scholar] [CrossRef]
- Derakhshani, A.; Foruzan, A.H. Predicting the principal strong ground motion parameters: A deep learning approach. Appl. Soft Comput. 2019, 80, 192–201. [Google Scholar] [CrossRef]
- Jin, C.; Hong, T.; Wenkai, C.; Naisen, Y. A prediction method of ground motion for regions without available observation data (LGB-FS) and its application to both Yangbi and Maduo earthquakes in 2021. J. Earth Sci. 2021. (in press). Available online: http://en.earth-science.net/en/article/doi/10.1007/s12583-021-1560-6 (accessed on 10 September 2021).
- Nagelkerke, N.J.D. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 148–151. [Google Scholar] [CrossRef]
- Takai, N.; Shigefuji, M.; Rajaure, S.; Bijukchhen, S.; Ichiyanagi, M.; Dhital, M.R.; Tsutomu, S. Strong ground motion in the Kathmandu Valley during the 2015 Gorkha, Nepal, earthquake. Earth Planets Space 2016, 68, 10. [Google Scholar] [CrossRef]
- Alavi, A.H.; Gandomi, A.H.; Modaresnezhad, M.; Mousavi, M. New ground-motion prediction equations using multi expression programing. J. Earthq. Eng. 2011, 15, 511–536. [Google Scholar] [CrossRef]
- Mohammadnejad, A.K.; Mousavi, S.M.; Torabi, M.; Mousavi, M.; Alavi, A.H. Robust attenuation relations for peak time-domain parameters of strong ground motions. Environ. Earth Sci. 2012, 67, 53–70. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees (CART). Biometrics 1984, 40, 358. [Google Scholar] [CrossRef]
- Shinozuka, M.; Feng, M.; Lee, J.; Naganuma, T. Statistical analysis of fragility curves. J. Eng. Mech. 2000, 126, 1224–1231. [Google Scholar] [CrossRef]
- Porter, K.; Kennedy, R.; Bachman, R. Creating fragility functions for performance-based earthquake engineering. Earthq. Spectra 2007, 23, 471–489. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).