Efficient Depth Fusion Transformer for Aerial Image Semantic Segmentation
Abstract
:1. Introduction
- Differing from conventional two-stream networks of the same two branches, in order to improve the computational efficiency, our network adopts two different branches, which includes a novel depth branch of four downsampling convolution layers.
- Two kinds of self-attention module are proposed to mitigate the gap caused by teh difference between two branches and two modalities. We validate their capability and flexibility on the problem of multi-modal feature fusion.
- With the above two designs and the backbone transformer, we propose a more efficient network for RGB-D semantic segmentation task: Efficient Depth Fusion Transformer (EDFT).
2. Related Works
2.1. Acquiring Long-Range Dependency
2.2. RGB-D Segmentation by Deep Learning
2.3. Attention for RGB-D Fusion
3. Method
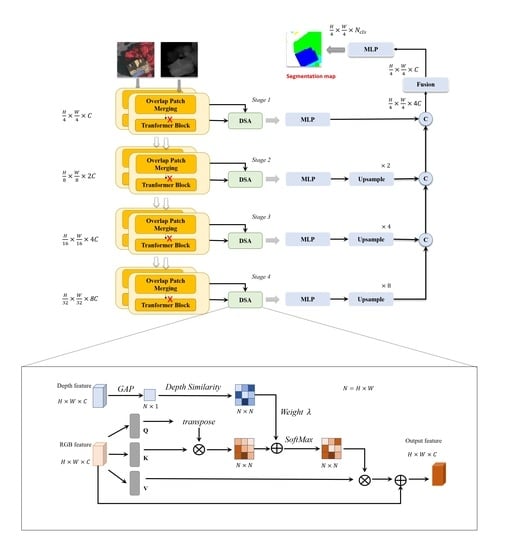
3.1. Network Architecture
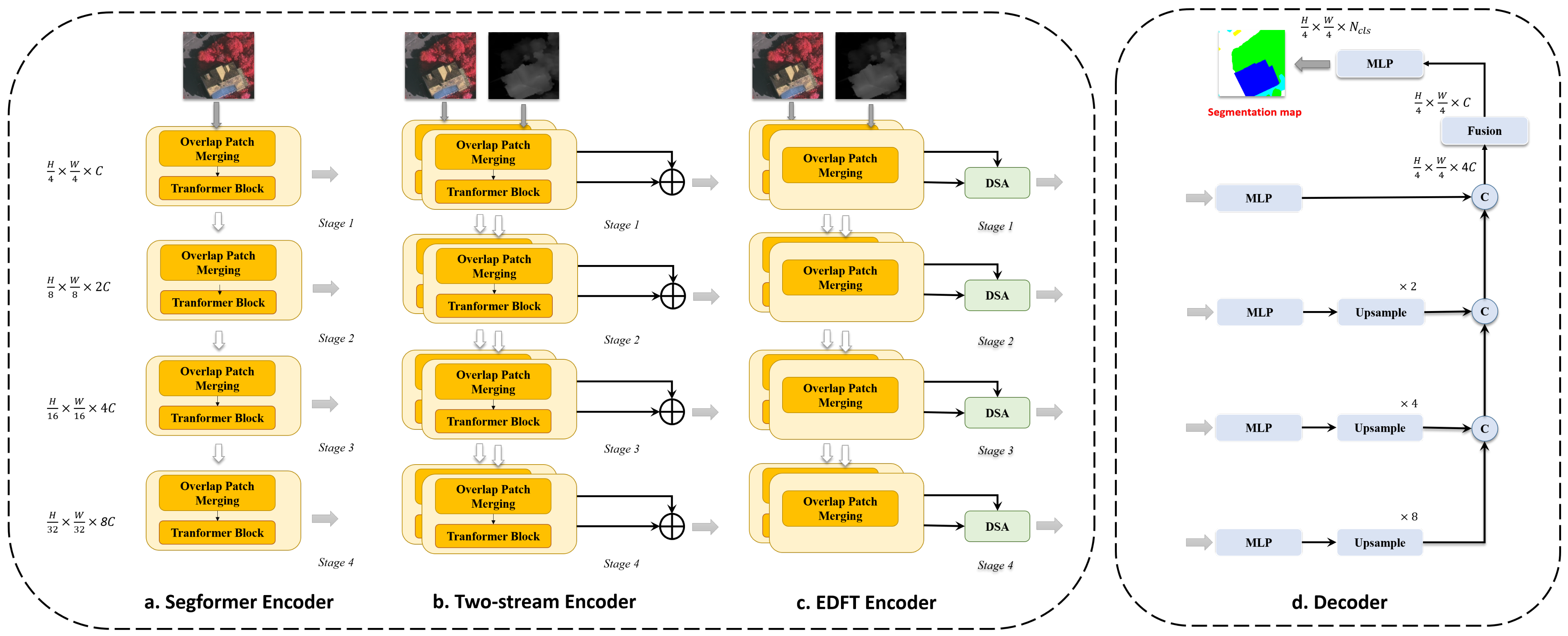
3.1.1. Segformer Network
3.1.2. Conventional Two-Stream Scheme
3.1.3. EDFT Network
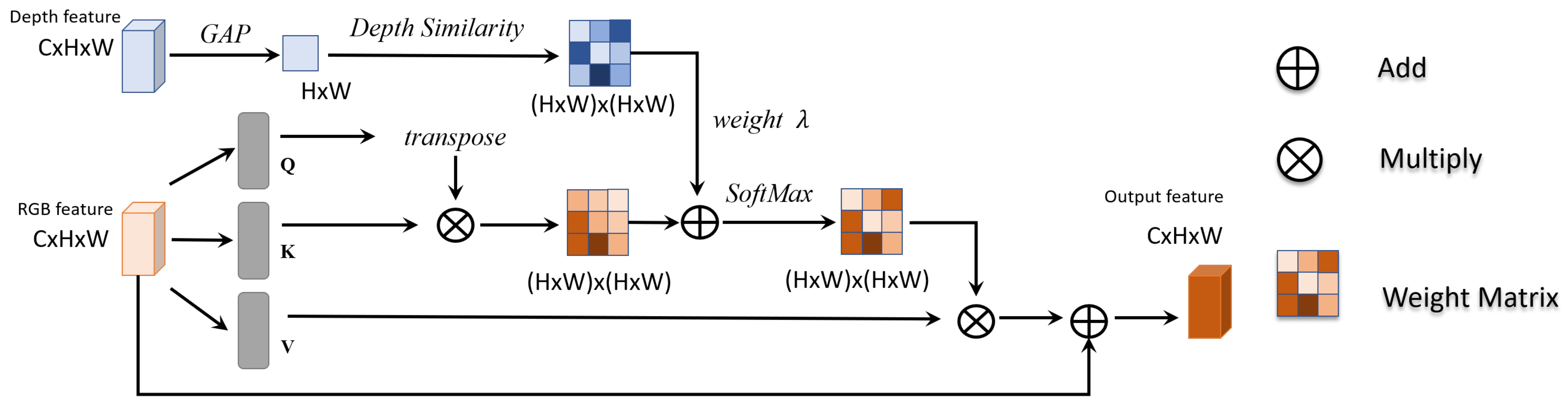
3.2. Depth-Aware Self-Attention Module
3.2.1. Computation of Self-Attention
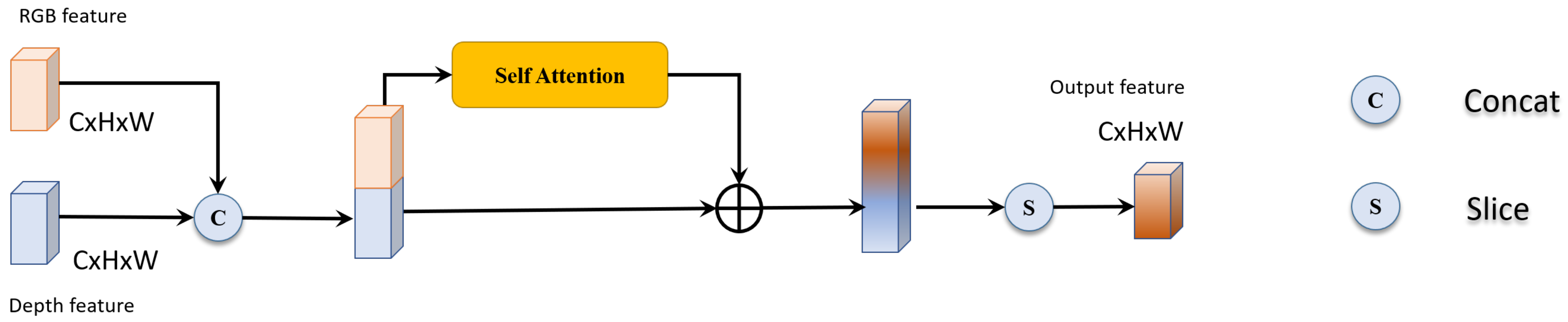
3.2.2. Fusing Depth in a Concat Mode
3.2.3. Fusing Depth in an Addition Mode
4. Experiments
4.1. Experimental Settings
4.1.1. DataSets
4.1.2. Metrics
4.1.3. Implementation Details
4.2. Compare to the State-of-the-Art
4.2.1. Efficiency Contrast
4.2.2. Results on Vaihingen and Potsdam
4.2.3. Visual Comparison
4.2.4. Confusion Matrices
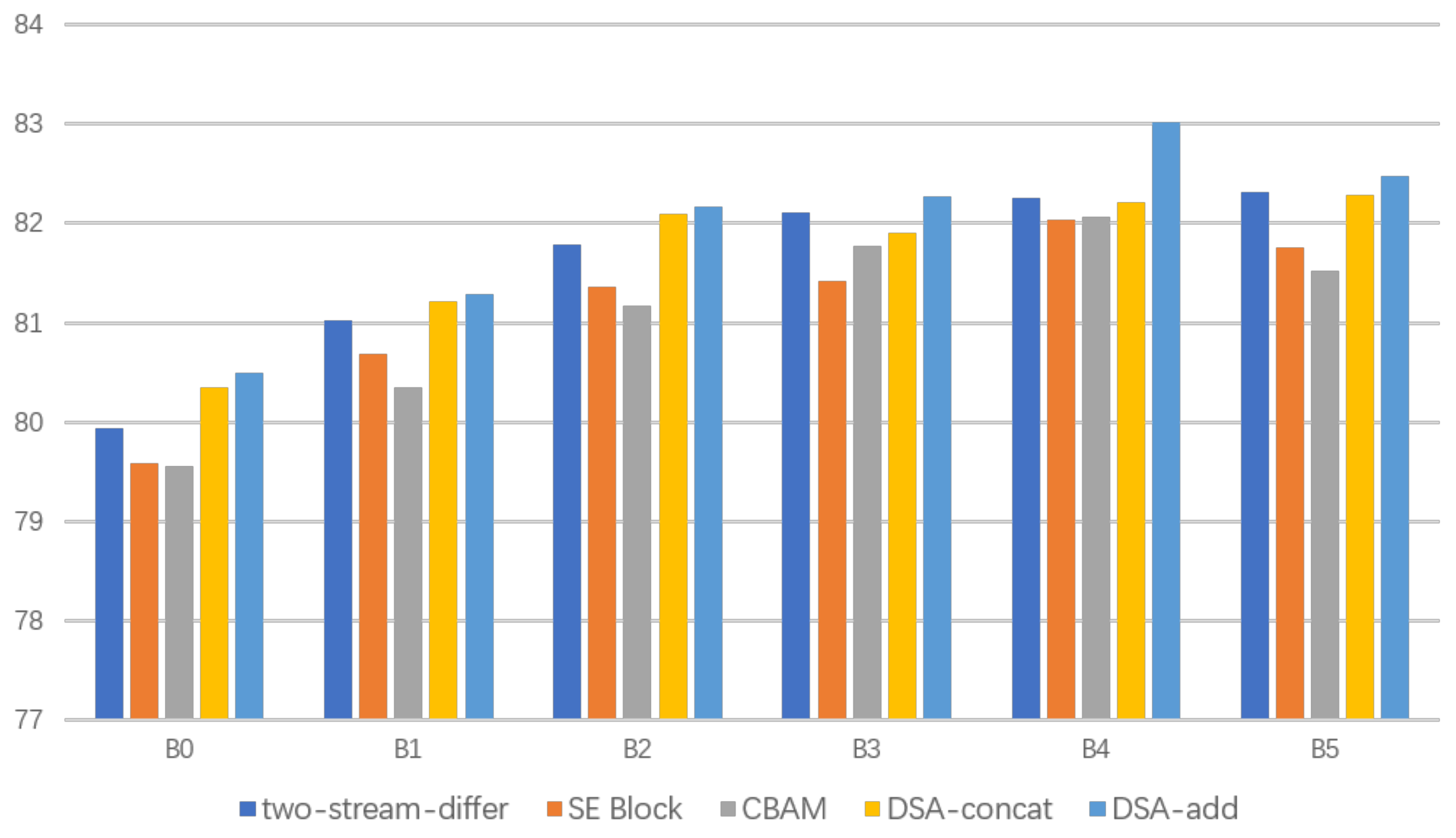
4.3. Ablation Study
4.3.1. Downsample Scheme
4.3.2. Attention Type
4.3.3. Weight Parameter
5. Discussion
6. Conclusions
- Depth feature acquired by simple downsampling on the original depth map are also beneficial to segmentation. Identical branches in two-stream network are not necessary;
- Addition fusion ignores the gap between two modalities and two branches. Applying attention in the fusion problem to decide which feature is more reliable achieves better performance;
- Computing attention on multi-modal data by combining similarities can obtain better results than concatenating data in the input phase.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations (ICLR), Online, 3–7 May 2021. [Google Scholar]
- Kampffmeyer, M.; Salberg, A.B.; Jenssen, R. Semantic Segmentation of Small Objects and Modeling of Uncertainty in Urban Remote Sensing Images Using Deep Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 680–688. [Google Scholar]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Semantic Segmentation of Earth Observation Data Using Multimodal and Multi-scale Deep Networks. In Proceedings of the Asian Conference on Computer Vision (ACCV), Taipei, Taiwan, 20–24 November 2016; pp. 180–196. [Google Scholar]
- Zhang, W.; Huang, H.; Schmitz, M.; Sun, X.; Wang, H.; Mayer, H. Effective Fusion of Multi-Modal Remote Sensing Data in a Fully Convolutional Network for Semantic Labeling. Remote Sens. 2018, 10, 52. [Google Scholar] [CrossRef] [Green Version]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Beyond RGB: Very high resolution urban remote sensing with multimodal deep networks. ISPRS J. Photogramm. Remote Sens. 2018, 140, 20–32. [Google Scholar] [CrossRef] [Green Version]
- Hazirbas, C.; Ma, L.; Domokos, C.; Cremers, D. FuseNet: Incorporating Depth into Semantic Segmentation via Fusion-Based CNN Architecture. In Proceedings of the Asian Conference on Computer Vision (ACCV), Taipei, Taiwan, 20–24 November 2016; pp. 213–228. [Google Scholar]
- Hu, X.; Yang, K.; Fei, L.; Wang, K. ACNET: Attention Based Network to Exploit Complementary Features for RGBD Semantic Segmentation. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1440–1444. [Google Scholar]
- Chen, X.; Lin, K.Y.; Wang, J.; Wu, W.; Qian, C.; Li, H.; Zeng, G. Bi-directional Cross-Modality Feature Propagation with Separation-and-Aggregation Gate for RGB-D Semantic Segmentation. In Proceedings of the European Conference on Computer Cision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 561–577. [Google Scholar]
- Luo, H.; Chen, C.; Fang, L.; Zhu, X.; Lu, L. High-Resolution Aerial Images Semantic Segmentation Using Deep Fully Convolutional Network With Channel Attention Mechanism. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3492–3507. [Google Scholar] [CrossRef]
- Cheng, Y.; Cai, R.; Li, Z.; Zhao, X.; Huang, K. Locality-Sensitive Deconvolution Networks with Gated Fusion for RGB-D Indoor Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1475–1483. [Google Scholar]
- Liu, H.; Wu, W.; Wang, X.; Qian, Y. RGB-D joint modelling with scene geometric information for indoor semantic segmentation. Multimed. Tools Appl. 2018, 77, 22475–22488. [Google Scholar] [CrossRef]
- Wang, W.; Ulrich, N. Depth-Aware CNN for RGB-D Segmentation. In Proceedings of the European Conference on Computer Cision (ECCV), Munich, Germany, 8–14 September 2018; pp. 144–161. [Google Scholar]
- Xing, Y.; Wang, J.; Chen, X.; Zeng, G. 2.5D Convolution for RGB-D Semantic Segmentation. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1410–1414.
- Xing, Y.; Wang, J.; Zeng, G. Malleable 2.5D Convolution: Learning Receptive Fields along the Depth-axis for RGB-D Scene Parsing. In Proceedings of the European Conference on Computer Cision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 555–571. [Google Scholar]
- Chen, R.; Zhang, F.L.; Rhee, T. Edge-Aware Convolution for RGB-D Image Segmentation. In Proceedings of the 35th International Conference on Image and Vision Computing New Zealand (IVCNZ), Wellington, New Zealand, 25–27 November 2020; pp. 1–6. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Online, 11–17 October 2021. [Google Scholar]
- Sun, Y.; Tian, Y.; Xu, Y. Problems of encoder-decoder frameworks for high-resolution remote sensing image segmentation: Structural stereotype and insufficient learning. Neurocomputing 2019, 330, 297–304. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mou, L.; Hua, Y.; Zhu, X.X. A Relation-Augmented Fully Convolutional Network for Semantic Segmentation in Aerial Scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12408–12417. [Google Scholar]
- Niu, R.; Sun, X.; Tian, Y.; Diao, W.; Chen, K.; Fu, K. Hybrid Multiple Attention Network for Semantic Segmentation in Aerial Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Duan, C.; Su, J.; Zhang, C. Multistage Attention ResU-Net for Semantic Segmentation of Fine-Resolution Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, L.; Li, R.; Duan, C.; Zhang, C.; Meng, X.; Fang, S. A Novel Transformer based Semantic Segmentation Scheme for Fine-Resolution Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2022, 19. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, W.; Zhang, T.; Yang, Z.; Li, J. Efficient Transformer for Remote Sensing Image Segmentation. Remote Sens. 2021, 13, 3585. [Google Scholar] [CrossRef]
- Fooladgar, F.; Kasaei, S. A survey on indoor RGB-D semantic segmentation: From hand-crafted features to deep convolutional neural networks. Multimed. Tools Appl. 2020, 79, 4499–4524. [Google Scholar] [CrossRef]
- Chen, K.; Fu, K.; Gao, X.; Yan, M.; Zhang, W.; Zhang, Y.; Sun, X. Effective Fusion of Multi-Modal Data with Group Convolutions for Semantic Segmentation of Aerial Imagery. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 3911–3914. [Google Scholar]
- Volpi, M.; Tuia, D. Dense Semantic Labeling of Subdecimeter Resolution Images With Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 881–893. [Google Scholar] [CrossRef] [Green Version]
- Marcos, D.; Volpi, M.; Kellenberger, B.; Tuia, D. Land cover mapping at very high resolution with rotation equivariant CNNs: Towards small yet accurate models. ISPRS J. Photogramm. Remote Sens. 2018, 145, 96–107. [Google Scholar] [CrossRef] [Green Version]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. High-Resolution Aerial Image Labeling With Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7092–7103. [Google Scholar] [CrossRef] [Green Version]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Lvarez, J.E.M.A.; Luo, P. SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Online, 6–14 December 2021. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Zhao, H.; Jia, J.; Koltun, V. Exploring Self-Attention for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 10073–10082. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11531–11539. [Google Scholar]
- Marmanis, D.; Schindler, K.; Wegner, J.D.; Galliani, S.; Datcu, M.; Stilla, U. Classification with an edge: Improving semantic image segmentation with boundary detection. ISPRS J. Photogramm. Remote Sens. 2018, 135, 158–172. [Google Scholar] [CrossRef] [Green Version]
- Gerke, M. Use of the Stair Vision Library within the ISPRS 2D Semantic Labeling Benchmark (Vaihingen); ResearcheGate: Berlin, Germany, 2015. [Google Scholar] [CrossRef]
- Yue, K.; Yang, L.; Li, R.; Hu, W.; Zhang, F.; Li, W. TreeUNet: Adaptive Tree convolutional neural networks for subdecimeter aerial image segmentation. ISPRS J. Photogramm. Remote Sens. 2019, 156, 1–13. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, B.; Wang, L.; Bai, J.; Xiang, S.; Pan, C. Semantic labeling in very high resolution images via a self-cascaded convolutional neural network. ISPRS J. Photogramm. Remote Sens. 2018, 145, 78–95. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wen, C.; Wang, L.; Fang, Y. Geometry-Aware Segmentation of Remote Sensing Images via Joint Height Estimation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Xiao, T.; Liu, Y.; Zhou, B.; Jiang, Y.; Sun, J. Unified Perceptual Parsing for Scene Understanding. In Proceedings of the European Conference on Computer Cision (ECCV), Munich, Germany, 8–14 September 2018; pp. 432–448. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Cision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
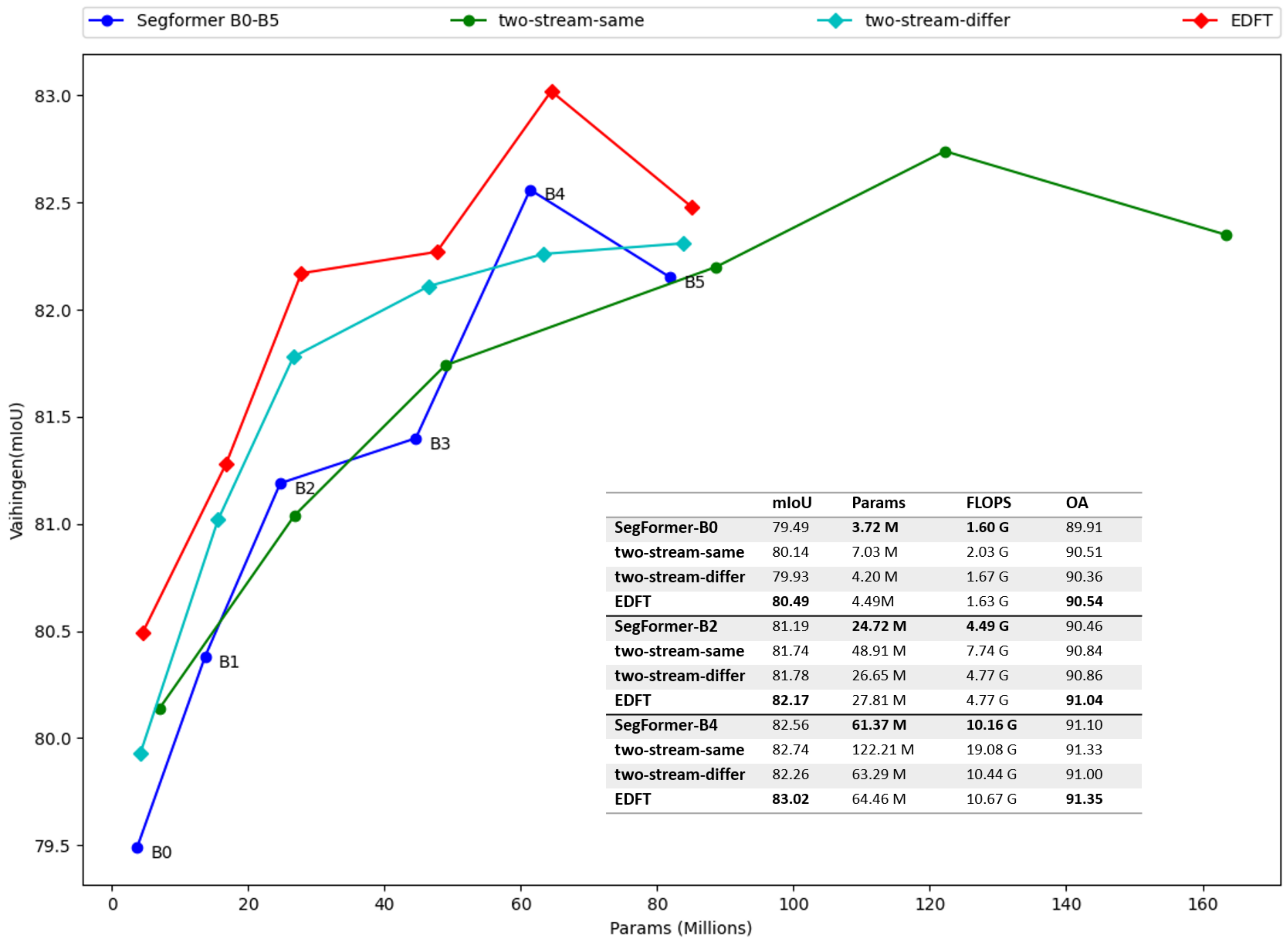


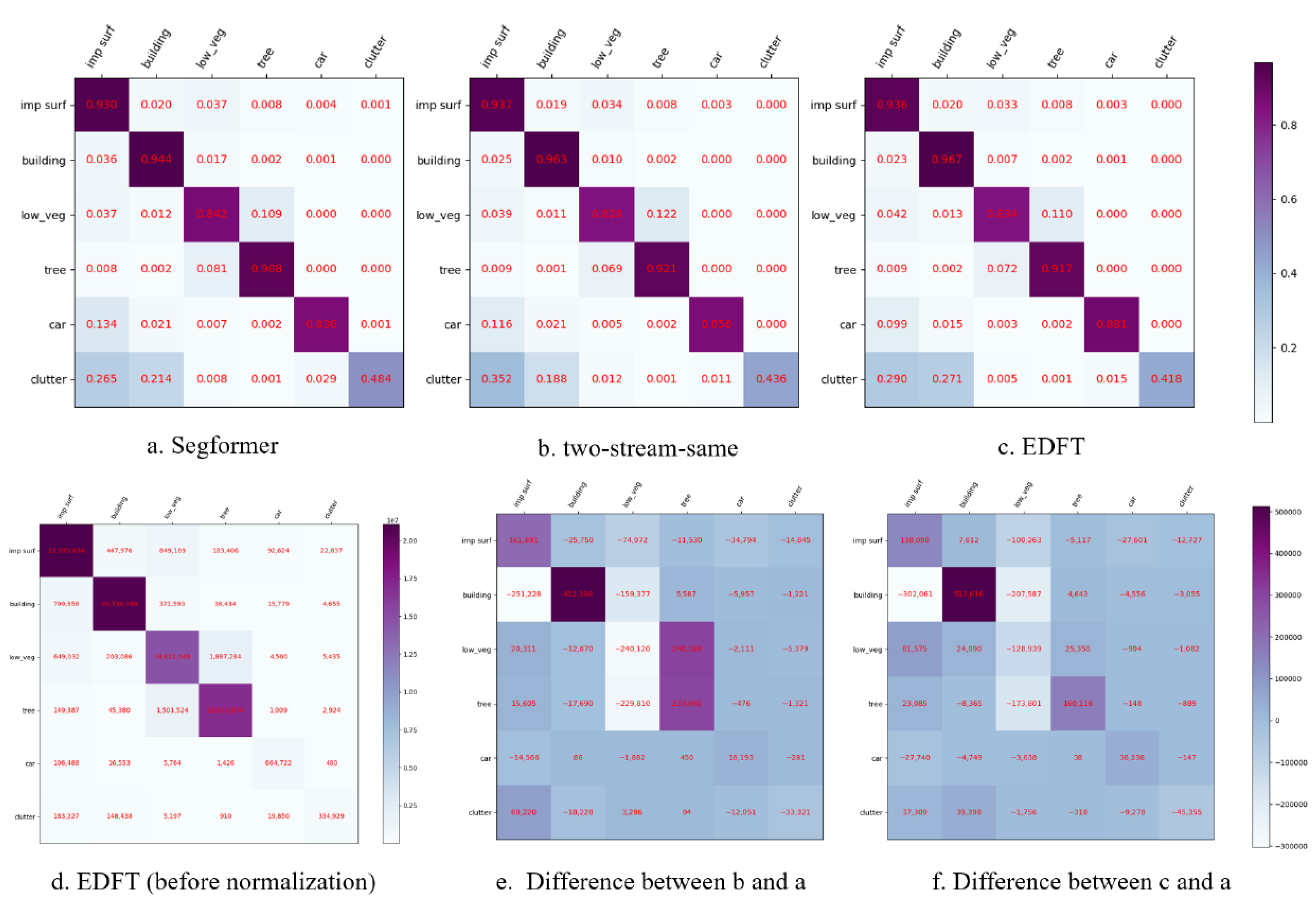
| Method | Backbone | Imp.surf. | Building | Low Veg. | Tree | Car | Mean F1 | OA (%) | mIoU (%) |
|---|---|---|---|---|---|---|---|---|---|
| UZ_1 * [29] | CNN-FPL | 89.20 | 92.50 | 81.60 | 86.90 | 57.30 | 81.50 | 87.30 | - |
| Maggiori et al. * [31] | FCN | 91.69 | 95.24 | 79.44 | 88.12 | 78.42 | 86.58 | 88.92 | - |
| S-RA-FCN [22] | VGG-16 | 91.47 | 94.97 | 80.63 | 88.57 | 87.05 | 88.54 | 89.23 | 79.76 |
| V-FuseNet * [8] | VGG-16 | 91.00 | 94.40 | 84.50 | 89.90 | 86.30 | 89.22 | 90.00 | - |
| TreeUNet * [39] | VGG-16 | 92.50 | 94.90 | 83.60 | 89.60 | 85.90 | 89.30 | 90.40 | - |
| VIT [4] | Vit-L ** | 92.7 | 95.32 | 84.36 | 89.73 | 82.28 | 88.88 | 90.67 | 80.33 |
| UperNet [42] | ResNet-101 | 92.37 | 95.62 | 84.44 | 89.97 | 87.92 | 90.06 | 90.71 | 82.14 |
| CASIA [40] | ResNet-101 | 93.20 | 96.00 | 84.70 | 89.90 | 86.70 | 90.10 | 91.10 | - |
| Swin [19] | Swin-S ** | 93.21 | 95.97 | 84.9 | 90.21 | 87.74 | 90.41 | 91.26 | 82.73 |
| GANet * [41] | ResNet-101 | 93.10 | 95.90 | 84.60 | 90.10 | 88.40 | 90.42 | 91.30 | - |
| HUSTW [20] | ResegNet | 93.30 | 96.10 | 86.40 | 90.80 | 74.60 | 88.24 | 91.60 | - |
| HMANet [23] | ResNet-101 | 93.50 | 95.86 | 85.41 | 90.40 | 89.63 | 90.96 | 91.44 | 83.49 |
| Segformer [32] | MiT-B4 ** | 93.49 | 96.27 | 85.09 | 90.31 | 89.63 | 90.96 | 91.51 | 83.63 |
| EDFT (ours) * | MiT-B4 ** | 93.40 | 96.35 | 85.52 | 90.57 | 89.55 | 91.08 | 91.65 | 83.82 |
| Method | Backbone | Imp.surf. | Building | Low Veg. | Tree | Car | Mean F1 | OA (%) | mIoU (%) |
|---|---|---|---|---|---|---|---|---|---|
| UZ_1 * [29] | CNN-FPL | 89.30 | 95.40 | 81.80 | 80.50 | 86.50 | 86.70 | 85.80 | - |
| Maggiori et al. * [31] | FCN | 89.31 | 94.37 | 84.83 | 81.10 | 93.56 | 86.62 | 87.02 | - |
| S-RA-FCN [22] | VGG-16 | 91.33 | 94.70 | 86.81 | 83.47 | 94.52 | 90.17 | 88.59 | 82.38 |
| VIT [4] | Vit-L ** | 93.17 | 95.90 | 87.11 | 88.04 | 94.88 | 91.82 | 90.42 | 85.08 |
| UperNet [42] | Resnet-101 | 93.27 | 96.78 | 86.82 | 88.62 | 96.07 | 92.31 | 90.42 | 85.97 |
| V-FuseNet * [8] | VGG-16 | 92.70 | 96.30 | 87.30 | 88.50 | 95.40 | 92.04 | 90.60 | - |
| TreeUNet * [39] | VGG-16 | 93.10 | 97.30 | 86.60 | 87.10 | 95.80 | 91.98 | 90.70 | - |
| CASIA [40] | ResNet-101 | 93.40 | 96.80 | 87.60 | 88.30 | 96.10 | 92.44 | 91.00 | - |
| GANet * [41] | ResNet-101 | 93.00 | 97.30 | 88.20 | 89.50 | 96.80 | 92.96 | 91.30 | - |
| HUSTW [20] | ResegNet | 93.60 | 97.60 | 88.50 | 88.80 | 94.60 | 92.62 | 91.60 | - |
| Swin [19] | Swin-S ** | 94.02 | 97.24 | 88.39 | 89.08 | 96.32 | 93.01 | 91.70 | 87.15 |
| Segformer [32] | MiT-B4 ** | 94.27 | 97.43 | 88.28 | 89.09 | 96.25 | 93.07 | 91.78 | 87.26 |
| HMANet [23] | ResNet101 | 93.85 | 97.56 | 88.65 | 89.12 | 96.84 | 93.20 | 92.21 | 87.28 |
| EDFT (ours) * | MiT-B4 ** | 94.08 | 97.31 | 88.63 | 89.29 | 96.53 | 93.17 | 91.85 | 87.43 |
| Method | Decoder | Imp.surf. | Building | Low Veg. | Tree | Car | Mean F1 | OA (%) | mIoU (%) |
|---|---|---|---|---|---|---|---|---|---|
| Segformer [32] | ALL-MLP | 94.27 | 97.43 | 88.28 | 89.09 | 96.25 | 93.07 | 91.78 | 87.26 |
| Segformer [32] | Uperhead | 94.33 | 97.48 | 88.38 | 89.24 | 96.27 | 93.14 | 91.87 | 87.38 |
| EDFT (ours) | ALL-MLP | 94.08 | 97.31 | 88.63 | 89.29 | 96.53 | 93.17 | 91.85 | 87.43 |
| EDFT (ours) | Uperhead | 94.17 | 97.50 | 88.64 | 89.66 | 96.42 | 93.28 | 91.91 | 87.61 |
| Overlap | Embedding | mIoU (%) | OA (%) |
|---|---|---|---|
| 82.39 | 91.02 | ||
| 82.47 | 91.12 | ||
| 82.16 | 90.96 | ||
| 82.26 | 91.21 |
| Model | Weight | Mean F1 | OA (%) | mIoU (%) |
|---|---|---|---|---|
| B0 | 0.5 | 89.00 | 90.53 | 80.49 |
| B1 | 0.4 | 89.49 | 90.81 | 81.28 |
| B2 | 0.9 | 90.05 | 91.09 | 82.17 |
| B3 | 0.7 | 90.11 | 91.23 | 82.27 |
| B4 | 0.8 | 90.58 | 91.35 | 83.02 |
| B5 | 1.4 | 90.25 | 91.12 | 82.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Huang, J.; Xie, H.; Wei, P.; Gao, Z. Efficient Depth Fusion Transformer for Aerial Image Semantic Segmentation. Remote Sens. 2022, 14, 1294. https://doi.org/10.3390/rs14051294
Yan L, Huang J, Xie H, Wei P, Gao Z. Efficient Depth Fusion Transformer for Aerial Image Semantic Segmentation. Remote Sensing. 2022; 14(5):1294. https://doi.org/10.3390/rs14051294
Chicago/Turabian StyleYan, Li, Jianming Huang, Hong Xie, Pengcheng Wei, and Zhao Gao. 2022. "Efficient Depth Fusion Transformer for Aerial Image Semantic Segmentation" Remote Sensing 14, no. 5: 1294. https://doi.org/10.3390/rs14051294
APA StyleYan, L., Huang, J., Xie, H., Wei, P., & Gao, Z. (2022). Efficient Depth Fusion Transformer for Aerial Image Semantic Segmentation. Remote Sensing, 14(5), 1294. https://doi.org/10.3390/rs14051294