Abstract
The directional polarimetric camera (DPC) is a Chinese satellite sensor with a large field of view (FOV) (±50° both along-track and cross-track) and a high spatial resolution (about 3.3 km at nadir) that operates in a sun-synchronous orbit. It is a difficult task to calibrate the in-flight relative radiometric variation of the sensors with such a wide FOV. In this study, a new method based on Rayleigh scattering over the ocean is developed to estimate the radiometric sensitivity variation over the whole FOV of DPC. Firstly, the theoretical uncertainty of the method is analyzed to calibrate the relative radiometric response. The calibration uncertainties are about 2–6.9% (depending on the wavelength) when the view zenith angle (VZA) is 0° and decrease to about 1–3.8% when VZA increases to 70°. Then, the method is applied to evaluate the long-term radiometric drift of the DPC. It is found that the radiometric response of DPC/GaoFen-5 over the whole FOV is progressively drifting over time. The sensitivity at shorter bands decreases more strongly than longer bands, and at the central part of the optics decreases more strongly than the marginal part. During the 14 months (from March 2019 to April 2020) of operational running in-orbit, the DPC radiometric responses of 443 nm, 490 nm, 565 nm, and 670 nm bands drifted by about 4.44–23.08%, 4.75–16.22%, 3.86–9.81%, and 4.7–16.86%, respectively, from the marginal to the central part of the FOV. The radiometric sensitivity has become more stable since January 2020. The monthly radiometric drift is separated into the relative radiometric part and the absolute radiometric part. The relative radiometric drift of DPC is found to be smoothly varying with VZA, which can be parameterized as a polynomial function via VZA. At last, the temporal radiometric drift of DPC/GaoFen-5 is corrected by combining the relative and absolute radiometric coefficients. The correction is convincing by cross calibration with MODIS/Aqua observation over the desert sites and improving the aerosol retrievals. The Rayleigh method in this study is efficient for the radiometric sensitivity calibration of wide FOV satellite sensors.
1. Introduction
The reliable in-flight radiometric calibration of optical satellite sensors is essential for quantitative remote sensing applications [1]. For example, estimating the climate forcing of aerosol and cloud accurately requires satellite observation of the earth–atmosphere system with high accuracy [2]. The in-flight radiometric calibration of satellite sensors consists of absolute and relative response parts. The absolute radiometric response part represents the radiometric response of the sensor at the reference part of the optics corresponding to a unit of the incident light. Meanwhile, the relative radiometric response part represents the relative response variations of the sensor at the other part of the optics. The in-flight relative radiometric drift of the optical device is different from the scanning mode of the sensors. The images of whisk broom and push-broom sensors may have stripe noise due to the differences in detector’ responses. However, for the sensors of a charge coupled device (CCD) matrix, it is difficult to visually identify the relative difference from images since the signals may be coupled with multiple sources, including the optics and detectors. The relative radiometric response should be corrected prior to its absolute radiometric calibration to avoid uncertainties caused by the relative radiometric variation.
The in-flight relative radiometric calibration is usually performed by using the on-board calibration method [3,4], statistical method [5,6], yaw calibration method [7,8], and uniform site-based method [9,10]. The onboard calibration method relies on the expensive onboard calibration device that is usually equipped with an onboard calibration lamb or a solar diffuser. The statistical calibration method is based on the probability statistics law of the detector’s response with massive remote sensing images. The yaw calibration method requires that the sensor axis rotates 90° in yaw relative to the normal acquisitions so that each detector can acquire the same target. This method is generally applied to push-broom sensors, which have a control ability of the yaw angle. The uniform site-based method is mainly encountered on spatially homogeneous sites that provide nearly invariant brightness. Furthermore, the site should be large enough to cover the whole field of view (FOV) of the sensor [11].
The directional polarimetric camera (DPC) is a Chinese satellite sensor with a large field of view (±50° both along-track and cross-track) and a high spatial resolution (about 3.3 km at nadir) operated in a sun-synchronous orbit. DPC shares many similarities in the instrument design with satellite sensors of the Polarization and Directionality of the Earth’s Reflectance (POLDER) series [12]. The relative response variation of DPC reflects the response inconsistency of different FOV to the same incident radiation. It is mainly contributed by the transmission non-uniformity of optics and filters (known as the low-frequency part), as well as the sensitivity variation of detectors within the CCD (known as the high-frequency part). For the temporal evolution of radiometric sensitivity of the sensors with a wide FOV such as POLDER, the dominant contributing factor is the aging of the optics rather than the detectors [13,14,15]. Therefore, this research mainly focuses on monitoring the aging of the optics of DPC.
For the multi-angular camera with a wide FOV, such as DPC and POLDER, it is necessary to evaluate the in-flight relative response, which determines the accuracy of the multi-angular measurements. The in-flight absolute calibration is also strongly dependent on the relative radiometric calibration [14]. As it is difficult to build an on-board calibration device that can cover the entire FOV of this type of sensor, a method based on a desert target was proposed to calibrate the low-frequency part of the relative response of POLDER [15]. Several spatially homogeneous desert sites (with a size of 100 × 100 km) in North Africa and the Arabian Desert were selected, and bidirectional measurements were used to characterize the bidirectional reflectance distribution function (BRDF) of the surface to derive the directional variations of their top-of-atmosphere (TOA) precisely. Chen et al. [16] used a desert field method and Rayleigh method to validate the in-flight radiometric deviation of DPC on-board GaoFen-5.
As it is costly to conduct field experiments to measure the BRDF of natural targets like desert sites and it is hard to cover the whole FOV of the sensor required by the in-flight relative radiometric calibration, new calibration methods based on natural targets are developed. The Rayleigh scattering over an ocean area is widely used for the absolute calibration at short visible bands. An accuracy of 2–5% can be achieved by the Rayleigh calibration method by selecting a very clear ocean site [17,18]. More importantly, the Rayleigh method has the advantages of not being geographically or geo-physically limited in the deep ocean and a large number of observations can be obtained. An in-flight calibration approach based on the Rayleigh scattering statistics is proposed to monitor the temporal relative radiometric and absolute radiometric drift of DPC in this study. The main instrumental characteristics of DPC are introduced briefly in Section 2. Then, the in-flight absolute and relative radiometric calibration method of DPC is introduced with an error budget in Section 3. The temporal radiometric sensitivity results of the DPC onboard GaoFen-5 are analyzed in Section 4. In Section 5, the DPC calibration results are validated in three ways, i.e., a self-consistency test with the corrected, a cross-calibration with the MODIS/Aqua L1 reflectance data over the desert, and the improvement of AOD retrievals using the corrected data. The conclusion is given in Section 6.
2. DPC Instrument
The DPC, developed by Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Science, is a satellite sensor that aims to observe the polarization and directionality of the earth’s reflectance and detect global atmospheric aerosol and cloud properties. As shown in Figure 1, DPC’s optical system consists of a telecentric optic with wide FOV, a rotating wheel module carrying spectral filters and polarizers, and a bidimensional CCD detector array with 512 × 512 detectors. (1) The wide FOV optic is consist of an inverse Galileo telescope and a focusing group, with a diaphragm aperture placed between them. The inverse Galileo is designed to reduce the angle between the beam and the optical axis, and to eliminate astigmatism and distortion of the system. The focusing group is used to balance the residual astigmatism, distortion, and other aberrations of the inverse Galileo telescope and focus the beam. The diaphragm aperture is designed to make the lens telecentric in image space. It has a FOV of ±50° both along-track and cross-track, under a swath width of about 1850 km. (2) The rotating wheel rotates steadily and carries the interference filters and polarizers to observe different spectral bands and polarization directions quasi-simultaneously. It carries 15 slots, including an opaque filter to measure the dark current, and the other 14 slots carry five non-polarized and nine polarized filters (three bands each has three polarization directions). To compensate for satellite motion during the lag and to geometrically register the three polarized measurements, a small angle wedge prism is used in each polarizing assembly. Thus, DPC acquires 5 non-polarized band (443, 565, 763, 765, and 910 nm) measurements and 3 polarized bands (490, 670 and 865 nm). (3) The CCD sensor array is composed of 512 × 512 effective pixels from 544 × 512 useful pixels, realizing a high spatial resolution of 3.3 km at the nadir of the sun-synchronous orbit. Due to the design of the wide two-dimensional FOV with along-track migration at satellite velocity, multi-angular viewing of the same surface target in more than 9 angles is possible due to the over-riding of the successive images along the satellite track [19,20].
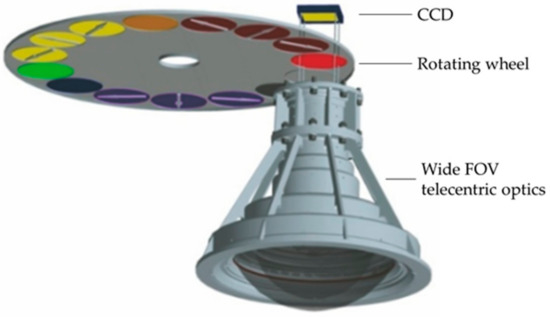
Figure 1.
The optics of the DPC.
The intensity of light on the pixel is linearly correlated to the output digital number (DN) value. The radiometric model of the non-polarized bands of the DPC can be expressed as
where is the electronic relative gain referred to the nominal gain ( = 1), is the exposure time referred to the original exposure time ( = 1). is the absolute calibration coefficient of the spectral band k which is determined on a reference pixel at the center of the CCD, represents the relative response variation of a pixel , and denotes the dark current, represents the intensity of the illumination onto the CCD, represents the intensity of linear polarization perpendicular or parallel to the reference plane, and represents the pixel coordinate on CCD. The DNs of the different pixels are related to different CCD detectors and then the corresponding position of instrumental FOV. The radiometric model of the polarized bands of the DPC can be expressed as
where , and are the polarization effect parameters of the optical system. represents the polarization rate of the optics. represents the relative azimuth angle between the polarizer and the local reference frame of the pixel. indicates the intensity of linear polarization at an angle of 45 degrees with the reference plane. Systematic and complete preflight radiometric calibration of DPC would be proposed before launch. A two-dimensional turntable and integrating sphere are taken to calibrate the relative radiometric variation in the laboratory with an accuracy of 0.3%, and the nominal absolute calibration accuracy is 5% pre-launch [19].
The first DPC sensor onboard the Chinese GaoFen-5 satellite, which was successfully launched on 9 May 2018, provides multi-angle polarized observation of the earth-atmosphere system. The local overpass time is 1:30 p.m. with the orbital regressive period of 51 days and node period of 98.925 min. The in-orbit testing phase of DPC/GaoFen-5 ended on 1 March 2019, and the official Level 1 products were published after that. The data acquisition ended on 10 April 2020,due to satellite faults. The Level 1 reflectance product is reconstructed using multi-angle data in the sinusoidal projection with HDF5 format. In this study, the Level 1 reflectance data of the sensor are used to evaluate the radiometric response drift over the whole DPC FOV during its life cycle.
3. Methods
3.1. Absolute Calibration Using Rayleigh Scattering
Rayleigh scattering may contribute up to 70% of the satellite observation at the TOA over a clear deep ocean region [17]. Therefore, the apparent reflectance observed by satellite can be accurately simulated using a radiative transfer model (RTM) [20], which can be approximately expressed as follows,
where is the contribution of Rayleigh scattering of atmospheric molecules, is the contribution of aerosol scattering. and are the contributions of water-leaving reflectance and the whitecap reflectance respectively. represents the reflectance of direct sunlight on the ocean surface. M is the air mass, and δ is the total optical thickness of the atmosphere. All the contributions and the coupling terms between them can be calculated by using the 6SV model [21]. Assuming that the in-flight polarization effect parameters of the optical system are stable and accurately accorded, then the in-flight/preflight variation of the satellite absolute radiometric coefficient is obtained through the Formulas (1)–(3), and (5),
where is the in-flight absolute calibration coefficient. is the preflight absolute calibration coefficient. is the radiance calculated with pre-flight calibration coefficients at band k, via Formula (1) at non-polarized bands and Formulas (2) and (3) at polarized bands, which is obtained directly in the official Level 1 product. The is the theoretical radiance that should be observed by the satellite sensor at the TOA, which is simulated by the RTM by inputting the sun-viewing geometry and the atmospheric and oceanic parameters.
The Rayleigh scattering calibration samples are selected based on strict criteria (i.e., satellite observations in clear ocean area, with low aerosol content and low chlorophyll content, away from the clouds and sunglint, and with low surface wind speed) to reduce the uncertainties caused by the atmospheric and oceanic parameters. The accuracy of the Rayleigh calibration method is about 2–5% at the short visible bands [22,23] and decreases with wavelength since the Rayleigh scattering signal decreases rapidly with wavelength.
3.2. Relative Radiometric Calibration by Rayleigh Samples Statistics
The relative radiometric calibration of DPC is defined as estimating the inconsistency sensitivity at different positions of the FOV to the same incident radiation, which are dimensionless functions related to the spectral band [19]. The relative response calibration usually consists in having the instrument look at a spatially uniform source, which can be an integrating sphere in the laboratory or uniform natural targets on the earth. It is difficult to calibrate the in-flight relative radiometric variation of the sensor over the whole wide field of view (FOV) of DPC because a continuous uniform natural target, as large as several thousand kilometers, does not exist. However, the response variation with the instrumental viewing geometry (i.e., the position of FOV) can be checked by carefully examining the behavior of the total response calibration results as a function of the viewing angles. Suppose that the directional variations of the TOA reflectance of Rayleigh calibration samples were well characterized, then the relative radiometric calibration of DPC can be achieved by fitting the as a function of the viewing angles. Of course, large amounts of samples are required to cover the whole FOV of DPC and to reduce the uncertainty caused by the samples’ random error at a specified position of the FOV. As it is easy to obtain the ocean targets for satellite and thanks to the multi-angular observation of DPC, the Rayleigh method seems to be appropriate for the relative radiometric calibration of DPC.
The evolution of the relative response coefficients is defined as the ratio of the in-flight/pre-flight relative response variation coefficients,
For DPC, the pixel’s VZA at the geocentric coordinate system is positively correlated with the instrumental viewing angle at the radial direction. Therefore, the relative radiometric calibration coefficient of the sensor could be represented as the relationship between the radiometric response and the VZA. By using the Rayleigh scattering method, can be calculated using the ratio of and ,
where the and are the in-flight/preflight variation coefficient at a specified viewing zenith angle (VZA) of and a reference VZA of (the central part of the FOV, usually represents a VAZ of 0°), respectively. Here, the and are derived with pre-flight calibration of . Here, the azimuthal inconsistency sensitivity in the FOV is neglected as the optical devices of axial symmetry [20].
3.3. Error Budget
Theoretical error at different VZA for Rayleigh radiometric calibration is simulated to estimate the reliability of relative radiometric calibration by using the Rayleigh method. The theoretical relative error of Rayleigh radiometric calibration is defined as the relative variation in the simulated reflectance caused by the atmospheric and water surface parameter uncertainties (wind speed, aerosol optical depth (AOD), chlorophyll concentration, ozone column concentration and surface pressure). These errors are simulated at different VZA by using the 6SV model. As listed in Table 1, typical uncertainties for the input parameters are considered in the simulation, with a wind speed error of 2 m/s, an AOD error of 0.01, a chlorophyll concentration error of 41%, an ozone column concentration error of 5%, and a surface pressure error of 100 Pa. To cover the entire observation geometry of DPC, the simulation value of VZA is set to 0–70° with the step of 10°, the solar zenith angle (SZA) is set to 0–70° with the step of 10°, and the sun–satellite relative azimuth angle (RAA) is set to 0–180° with the step of 20°. The radiometric calibration relative errors of each parameter are represented by the average simulation error at these solar and viewing angles.

Table 1.
The parameters setting for the error budget of the Rayleigh scattering method.
The theoretical Rayleigh radiometric calibration relative errors are displayed as the function of VZA in Figure 2. As shown, the AOD and wind speed error contribute most of the radiometric calibration relative error, and both the errors increase with wavelength. The theoretical calibration relative errors, caused by the surface wind speed chlorophyll content error, and surface pressure decrease with VZA, while that of AOD and ozone slightly increase with VZA.
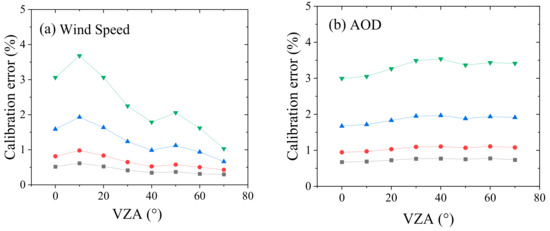
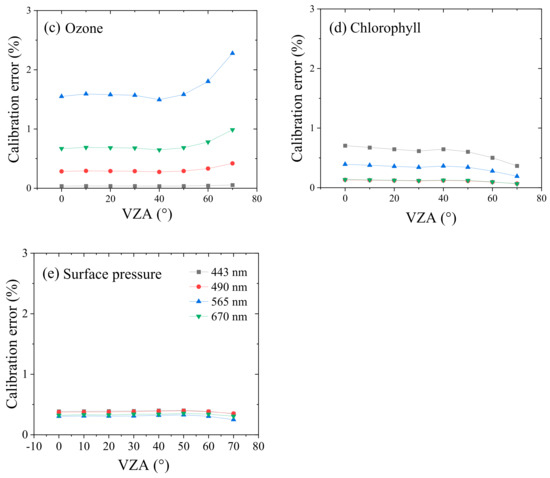
Figure 2.
Theoretical Rayleigh radiometric calibration relative errors caused by the input parameter uncertainties plotted as a function of VZA at four visible bands of DPC (i.e., 443, 490, 565, 670 nm) in which that (a) wind speed, (b) AOD, (c) ozone column concentration, (d) chlorophyll concentration and (e) surface pressure, respectively. The calibration relative error is the average value at different solar and viewing zenith angles of 0–70° and relative azimuth angle of 0–180° when the sunglint angle is greater than 40°.
The total theoretical radiometric calibration relative error is given by the mean quadratic sum of the five independent errors and is displayed as the function of VZA, as shown in Figure 3. These errors show a decreasing trend with the VZA, especially for the 670 nm and 565 nm bands. The theoretical errors of the Rayleigh scattering method are about 6.9% and 4% when VZA = 0°, and decrease to about 3.8% and 3.1% when VZA = 70° for the 670 nm and 565 nm bands. The errors decrease slightly from about 2% to 1% at 443 nm and 490 nm bands when VZA increases from 0° to 70°. This indicates that the absolute calibration uncertainties increase for the central part of the FOV of DPC, and the uncertainty may transfer to the relative calibration coefficients. However, note that, as the calibration errors caused by the input parameters errors represent random noise to some degree, they may be reduced by averaging a large volume of samples.
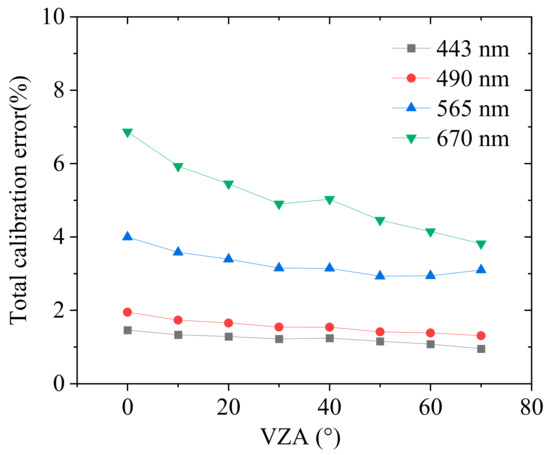
Figure 3.
Total Rayleigh calibration error varying with the view zenith angle of DPC at four visible bands (i.e., 443, 490, 565, 670 nm).
4. Results
4.1. Data
In this research, the Rayleigh scattering method is used to monitor the in-flight relative radiometric variation of DPC/GaoFen-5 from March 2019 to April 2020. As shown in Figure 4, six non-equipped sites located in the deep ocean are selected following Fougine et al. [24]. Firstly, the cloud mask procedure identifies a pixel as a clear sample that satisfies the threshold in five bands simultaneously ( _443 < 0.55, _490 < 0.55, _670 < 0.2, _763 < 0.2 and _765 < 0.2), where ρ represents the measured reflectance of the DPC. Only clear pixels are retained for calibration. The cloud mask algorithm is described in detail and the result is validated by Hou et al. [25]. Then, the auxiliary atmospheric and oceanic data from satellite products or reanalysis products are used as the input of RTM. The source of auxiliary data used for simulation and the criteria for data screening are listed in Table 2 [22,26]. After cloud masking and the matching of auxiliary atmospheric and oceanic data, 577,170 samples are selected from original pixels, which is about 1% of the gathered data (the samples always represent ozone of 0.3° × 0.3° which pixels has almost the same reflectance). The AOD is provided by MODIS/Aqua level 2 product MYD04 with a spatial resolution of 3 km [1]. As the MODIS AOD product has been cloud masked strictly, it enhances the DPC cloud masks, because their imaging times are close (the overpass time of MODIS/Aqua is 1:30 p.m.). Ozone column concentration is obtained from the ozone monitoring instrument (OMI) product OMTO3, which is a daily dataset inversion from the total ozone mapping spectrometer algorithm with a spatial resolution of 0.25 × 0.25° and uncertainty of 5% [27]. Chlorophyll a concentration is taken from the daily VIIRS/S-NPP level 2 chlorophyll data with a spatial resolution of 1 km [28]. Wind speed, wind direction, and surface pressure are obtained from the National Center for Environmental Prediction (NCEP) reanalysis dataset with a spatial resolution of 0.33 × 1° and uncertainty of about 2 m/s [29].

Figure 4.
Location of global radiometric calibration ocean sites for Rayleigh scattering calibration and the desert sites for cross-calibration with MODIS/Aqua.

Table 2.
The auxiliary data source and the sample selecting criteria for Rayleigh scattering calibration.
4.2. Temporal Evolution of DPC Radiometric Sensitivity
4.2.1. Temporal Drift of the Total Radiometric Response over the FOV
To show the temporal drift of DPC/GaoFen-5, the monthly results of the , from March 2018 to April 2019 are presented in Figure 5. Further, three-month results of in 2018 are added as the reference relative radiometric response at the early in-flight period of DPC. As shown, the are near to 1.0 at the early stage (i.e., June 2018, August 2018) of DPC in orbit, indicating the reliable pre-flight calibration of the DPC radiometric response. However, the appears a gradual drift process along time at the four visible bands of DPC, which not only exists in the absolute value of , but also in the curve via the VZA. This indicates that both the absolute and the relative radiometric responses of DPC drift along time. The short wavelength drifts more strongly than the longer wavelength, which is consistent with the drift regulation of the optics. Another phenomenon is that the at small VZA (i.e., 0–10°) drifts more aggressively than the large VZA area (i.e., 50–70°), and a “valley” appears at the VZA between 30° and 40°. This indicates that the center part of the optic systems drifts to a greater extent than the margin part, which may relate to the optical lens material aging process. The radiometric response drift, from the marginal to the central part of the FOV, is about 4.44–23.08%, 4.75–16.22%, 3.86–9.81%, and 4.7–16.86% for 443 nm, 490 nm, 565 nm, and 670 nm, respectively. The of VZA 0–20° in 670 nm in early months seems to be in larger uncertainty may be caused by the limited samples at the center FOV and insufficient stray light correction. In addition, the evaluation of calibration results in different azimuth angles indicates that the azimuthal inconsistency is about 2%, which is less than the accuracy of the Rayleigh scattering method.
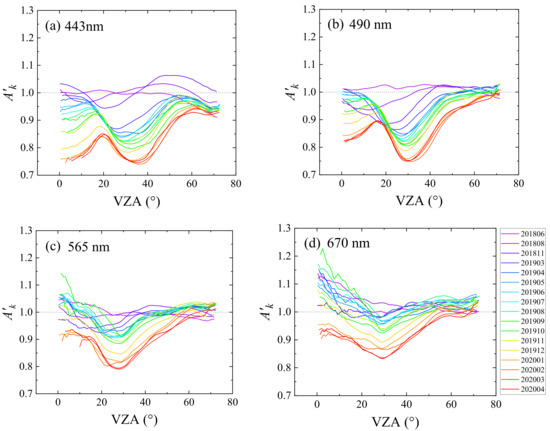
Figure 5.
The monthly average results of Rayleigh scattering calibration vary with VZA from March 2019 to April 2020 for (a) 443 nm, (b) 490 nm, (c) 565 nm and (d) 670 nm bands of DPC/GaoFen-5.
4.2.2. Temporal Drift of the Relative Radiometric Response over the FOV
To separate the drift of the optical transmittance of the optical system, the radiometric calibration result of each month is separated as and , which represents the relative radiometric calibration coefficient and the absolute calibration coefficient, respectively. Here, the is defined as the average value of the for VZA less than 10°. The monthly , dated from March 2019 to April 2020, at the four visible bands of DPC are shown in Figure 6. As shown, the relative radiometric response drifts more aggressively at shorter wavelength bands than at longer wavelength bands. The monthly indicates a “single valley” pattern with the valley located around 30°, except for that at 443 nm and 490 nm bands after November 2019, where a “peak-valley-peak” pattern appeared. The first peak appears at about 15°–20° of VZA, while the second peak appears at about 60°. This indicates that the transmittance of the optical system of DPC drifts asynchronously along with the radial direction of the FOV and the strongest drift appears at about VZA = 30° of the FOV.
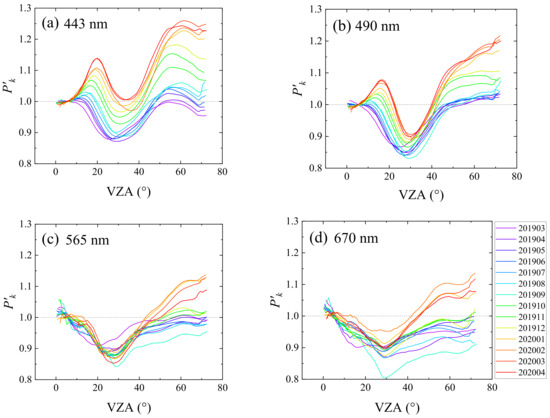
Figure 6.
The relative radiometric calibration results of varing with the VZA, from March 2019 to April 2020 for (a) 443 nm, (b) 490 nm, (c) 565 nm and (d) 670 nm bands of DPC/GaoFen-5. The is normalized by the average for VZA less than 10°.
As the temporal drift of DPC’s relative response varies smoothly with the VZA, is fitted as polynomial functions of , represented as
Therefore, the measured radiance of DPC after correction, , is represented as
The monthly polynomial fitting coefficients – at the four bands are listed in Table A1. Most of the polynomial fitting correlation coefficients R2 are larger than 0.93. The model fitting is best at the 443 nm band and degrades a little at longer bands because the smoothness of the curve at longer bands degrade to some degree, as shown in Figure 6c,d. So, the relative radiometric drift of DPC can be corrected by Formula (9).
4.2.3. Temporal Drift of the Absolute Radiometric Coefficients
The pre-launch absolute calibration coefficient of DPC is defined as the radiometric response at the center of FOV. In this study, the absolute calibration coefficient is defined as the average at the central part of the FOV, with VZA less than 10°, to guarantee enough calibration samples. The temporal drift of the average is displayed in Figure 7, and the error bar means the standard deviation of . As shown, the absolute radiometric coefficients decrease with time at all four bands, and this decrease is aggressive in the early months but becomes more stable after January 2020. The radiometric sensitivity degrades more strongly when the bands are shorter. This trend is consistent with that of the relative radiometric coefficients. The uncertainty of the calibration coefficient increases with wavelength, as determined by the uncertainty of the Rayleigh method. Figure 7 shows that the absolute coefficient at the central part of DPC drifted about 1.64% per month at the 443 nm band, 1.2% at 490 nm band, 0.7% at 565 nm band, and 1.2% at 670 nm band.
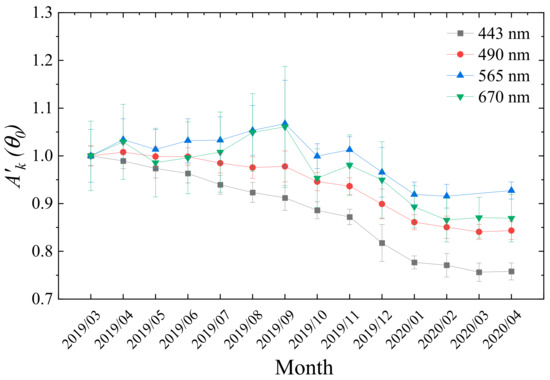
Figure 7.
Temporal evolution of the absolute coefficient from March 2019 to April 2020 for bands 443 nm, 490 nm, 565 nm and 670 nm of DPC/GaoFen-5. The results are normalized to the of the view zenith angle smaller than 10° at March 2019.
5. Validation of the Results
The absolute and relative radiometric drift correction of DPC Level 1 data is performed by using the monthly calibration coefficients listed in Table 3, Appendix A (Table A1), and Formula (9). The effectiveness of this correction is verified in three ways, i.e., the self-consistency validation of the relative radiometric response adjustment, cross comparison with the MODIS/Aqua observations over the African and Arabian desert sites, and improving the AOD retrievals over land.

Table 3.
Monthly absolute calibration coefficient from March 2019 to April 2020 for four visible bands of DPC/GaoFen-5.
5.1. Self-Consistency Validation
The absolute and relative radiometric calibration results in Section 4.2 are used to correct all the Rayleigh scattering samples to validate the self-consistency of both calibration coefficients. If it is self-consistent, the of the scatters after correction should distribute around 1.0 at all VZA. The scatters for the samples via the VZA before and after the correction are shown in Figure 8a,b, respectively. As shown, the biased curvatures of with VZA in Figure 8a are corrected successfully in Figure 8b, and the corrected values of highly coincide with the reference line. The temporal drift of the absolute and relative radiometric response of DPC/GaoFen-5 can be corrected effectively by the calibration coefficients. The corrections are validated to be self-consistent for the Rayleigh calibration samples.
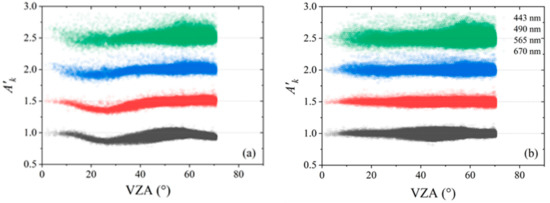
Figure 8.
Comparison of the scatters of via VZA for the Rayleigh calibration samples of DPC/GaoFen-5, before (a) and after (b) the temporal drift correction of the absolute and relative radiometric response. The plus 0, 0.5, 1.0, and 1.5 for the 443 nm (black points), 490 nm (red points), 565 nm (blue points), and 670 nm (green points) bands, respectively, to make the scatters plots clear.
5.2. Verification by Cross Calibration with MODIS over Desert Sites
It is necessary to validate the radiometric calibration results of DPC/GaoFen-5 with the independent data source. MODIS is a high accuracy in-flight satellite payload that is equipped with an onboard calibration device and provides a well-calibrated radiance product with an uncertainty of 2% [30]. The MODIS L1B dataset contains the calibrated and geolocated at-aperture radiance for 36 bands. It is widely used for cross-calibration for other satellite sensors (e.g., Sentinel 2A/2B [31]). MODIS/Aqua has a passing time of about 1:30 pm, which is almost the same as DPC/GaoFen-5. Moreover, as shown in Figure 9, the spectral response function at two bands of MODIS, central at 443 and 488 nm, is close to that of DPC’s 443 and 490 nm bands. The MODIS/Aqua L1B product is selected to validate the radiometric correction of DPC Level 1 data by using a cross-calibration method over desert sites.
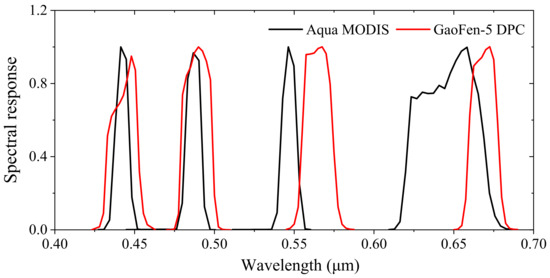
Figure 9.
Comparison of the Spectral Response Function of the MODIS/Aqua and DPC/GaoFen-5 at several visible bands.
The pseudo-invariant calibration sites (PICS) located in African and Arabian Desert sites are selected for the cross-calibration, as shown in Figure 4. They have been proven to accommodate high brightness and a spatial variation coefficient lower than 3% [32,33], which are appropriate natural targets for satellite cross-calibration [33,34]. The steps for the cross-calibration are as follows. Firstly, a temporal and geometrical coupling of MODIS and DPC measurements is performed to obtain the cross-calibration samples. The pairs of measurements with similar observing time and viewing and solar geometries over the desert sites are selected. A viewing and solar geometries difference window is defined as listed in Table 4. A total of 10,970 pairs of cross-calibration samples are obtained from January 2020 to April 2020. Second, the MODIS AOD product (MYD04_L2 [1,35]) and VIIRS BRDF product (VNP43 [36]) (three weighting parameters of Ross-Li model) are input into the 6SV model to correct the atmospheric scattering and surface direction reflection effect, respectively. An AOD threshold of 0.4 is set to reduce the uncertainty of calculating radiance at TOA caused by aerosols. At last, a spectral interpolation method is performed to derive the MODIS-transferred reference reflectance at the DPC observation geometry [33]. The data source and the thresholds for cross-calibration sample selection are listed in Table 4.

Table 4.
Sample selecting principle for cross-calibration of DPC/GaoFen-5 via MODIS/Aqua. The δVZ, δSZ, δRAA means the difference of the VZA, SZA and RAA respectively between two sensors.
The cross-calibration results of DPC/GaoFen-5 versus MODIS/Aqua by using the DPC measurements before and after the radiometric correction are shown in Figure 10. As shown, the trend of via VZA before cross correction is similar to that of the Rayleigh scattering calibration, a similar “single valley” pattern with the valley located around 30° appears. After correction, the of cross calibration displays obvious promotion, especially for the VZA around 30°. Here, the mean bias of is promoted form 0.17 to 0.05 and from 0.13 to 0.05, and RMSE is promoted from 0.18 to 0.06 and from 0.15 to 0.05, for 443 nm and 490 nm bands, respectively. This means that the radiometric correction of DPC data is proved to be efficient. However, the after correction still shows a visible bias of 0.05. That is partly attributed to the method error between two methods, and another possible reason may be the DPC radiometric correction error caused by neglecting the azimuthal inconsistency sensitivity in the FOV of DPC. Because the degradation of DPC optics may not be azimuthal consistent at specific directions, further research is necessary in future work.
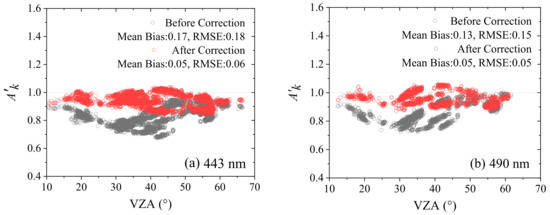
Figure 10.
The cross-calibration results of DPC/GaoFen-5 via MODIS/Aqua by using the DPC measurements before and after the radiometric correction. (a) 443 nm; (b) 490 nm. The mean bias and RMSE represents the difference between of samples and = 1.
5.3. Verification by Improving the AOD Product
An application of the radiometric corrected DPC data to improve the AOD retrievals is performed to prove the efficiency of the correction. An aerosol retrieval algorithm based on the inter-band surface reflectance relationship of the 443, 490, and 670 nm bands is used to retrieve the AOD at 550 nm [37,38]. The AOD products of AERONET and SONET [39,40], which are produced by the ground-based Sun-sky radiometer observation, are used to validate the AOD retrievals.
The DPC data dated from January 2020 to April 2020 are used for the retrieval. The comparison of AOD retrievals with the ground-based observations by using the DPC measurements before and after the radiometric correction is shown in Figure 11. As shown, the AOD retrieved from the original DPC measurements is systematically lower than the observation of sun-photometer with a linear fitting slope of 0.6, indicating an underestimation of AOD. The AOD retrievals from the corrected DPC measurements are distinctly improved with a linear fitting slope of 1.06. The linear fitting correlation coefficient improved from 0.88 to 0.91, too. The root mean square error (RMSE) between the AOD retrieval and ground-based observation and a good fraction (Gfrac) of the scatters falling within the expected error (EE = ±(0.05 + 20%) are estimated too. As shown, the RMSE of the AOD retrieval after correction decreases from 0.31 to 0.21, and the Gfrac increases from 50.4% to 59.8%. All of this indicates an improvement of the AOD retrieval by using the radiometrically corrected data.
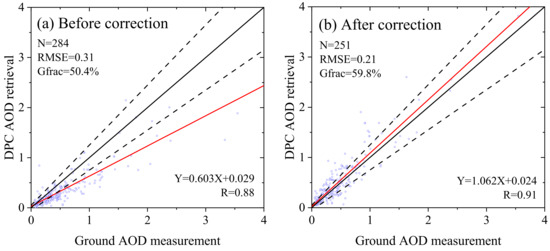
Figure 11.
The comparison of AOD retrievals with the ground-based observations at 550nm by using (a) the original DPC data and (b) the radiometric corrected DPC data. Black solid, dashed lines and red lines are the 1:1 lines, EE envelope lines and fit lines, respectively.
6. Conclusions
The DPC is a Chinese satellite sensor with a large FOV and a high spatial resolution. The aging of the sensor is inevitable, even though the systematic radiometric calibration was performed in the laboratory before launch. A relative radiometric calibration method based on Rayleigh scattering is proposed to monitor the temporal drift of DPC’s whole FOV.
Firstly, the error budget of the method is estimated by theoretical simulation with the RTM. The calibration uncertainties decrease with the VZA. For the 670 nm and 565 nm bands, the calibration errors are about 6.9% and 4% when VZA = 0°, and decrease to about 3.8% and 3.1% when VZA = 70°. For the 443 nm and 490 nm bands, the errors decrease slightly from about 2% to 1% when VZA increases from 0° to 70°. Then, the method is applied to evaluate the long-term radiometric drift of the DPC onboard the GaoFen-5 satellite. The calibration results show that the optic system is degraded progressively along time at all four visible bands. The radiometric sensitivity of the 443 nm and 490 nm bands drifts more strongly than the 565 nm and 670 nm bands, and the margin part of the optics is more stable than the central part. During the 14 months (from March 2019 to April 2020) of operational running in-orbit, the DPC radiometric response drifted about 4.44–23.08%, 4.75–16.22%, 3.86–9.81%, and 4.7–16.86% for 443 nm, 490 nm, 565 nm, and 670 nm bands, respectively. This drift trend becomes gentler after January 2020. The monthly radiometric drift is separated into the absolute radiometric part and the relative radiometric part, which is parameterized as a polynomial function via VZA. At last, the temporal radiometric drift correction of DPC/GaoFen-5 based on these two parts is proven to be effective by cross comparing with the MODIS/Aqua observations over the desert sites and improving the aerosol retrievals. The Rayleigh method is proven to be efficient for the radiometric sensitivity calibration for the wide FOV satellites sensors, expected to be used for the long-term in-flight monitoring of DPC-II on-board the GaoFen-5(02) satellite. It is noted that, in this study, the Rayleigh method accounted for the so-called low-frequency part of the relative response drift of DPC, which is caused by the aging of the optics, and the high-frequency part dominated by the evaluation of detectors also demands assessment in future work adopting the statistical power of a large number of cloud pixels.
Author Contributions
This work was carried out in collaboration with all the authors. Conceptualization, S.Z., Z.L. and L.Q.; methodology, S.Z. and L.Q.; writing—original draft, S.Z., Z.L., L.Q., H.X., B.G., Y.X. (Yisong Xie), R.Q., Y.X. (Yanqing Xie), J.H., B.M., B.T. and F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Finance science and technology project of Hainan province (Science and technology cooperation project, Key R&D plan of Hainan Province, ZDYF2020206), the National Outstanding Youth Foundation of China (Grant No. 41925019), and the National Natural Science Foundation of China (Grant No. 42175148, Grant No. 42175147).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used in this study can be downloaded for free. DPC/GF-5 data can be downloaded from the High Resolution Earth Observation System Grid Platform/Chinese National Space Administration Earth Observation and Data Center website (https://www.cheosgrid.org.cn/, accessed on 15 April 2021). MODIS L1 data can be downloaded from the website of NASA (https://ladsweb.modaps.eosdis.nasa.gov/, accessed on 25 February 2021).
Acknowledgments
The authors would like to thank the Chinese National Space Administration Earth Observation and Data Center for providing the DPC/GF-5 data, and NASA for providing the MODIS L1 data.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The relative calibration coefficients of the polynomial fitting model function (8) at four visible bands of DPC/GaoFen-5.
Table A1.
The relative calibration coefficients of the polynomial fitting model function (8) at four visible bands of DPC/GaoFen-5.
| Band | Month | B0(E-01) | B1(E-02) | B2(E-03) | B3(E-05) | B4(E-07) | B5(E-08) | B6(E-10) |
|---|---|---|---|---|---|---|---|---|
| 443 nm | 2019/03 | 9.6639 | 1.5350 | −1.4400 | 2.2013 | 6.1170 | −1.7493 | 1.1166 |
| 2019/04 | 9.7453 | 1.1020 | −0.6462 | −2.7131 | 19.5955 | −3.4302 | 1.8965 | |
| 2019/05 | 9.7502 | 1.0750 | −0.5746 | −3.2068 | 21.0176 | −3.6076 | 1.9753 | |
| 2019/06 | 9.8363 | 0.3620 | 0.6601 | −10.4115 | 39.6778 | −5.8323 | 2.9745 | |
| 2019/07 | 9.8893 | −0.2630 | 1.8000 | −17.1225 | 57.4140 | −8.0078 | 3.9858 | |
| 2019/08 | 9.9466 | −0.6450 | 2.3900 | −20.1063 | 63.8235 | −8.6143 | 4.1908 | |
| 2019/09 | 10.0670 | −1.3260 | 3.3100 | −24.2876 | 72.2820 | −9.3691 | 4.4184 | |
| 2019/10 | 9.9804 | −1.2080 | 3.4700 | −25.7637 | 77.0388 | −10.0258 | 4.7445 | |
| 2019/11 | 10.0723 | −1.9270 | 4.6900 | −32.8372 | 95.8306 | −12.3572 | 5.8386 | |
| 2019/12 | 10.2969 | −2.9530 | 5.8200 | −37.8952 | 106.9370 | −13.5305 | 6.3167 | |
| 2020/01 | 10.2640 | −3.2500 | 6.4200 | −40.2411 | 108.8190 | −13.2205 | 5.9452 | |
| 2020/02 | 10.6663 | −5.0440 | 8.6200 | −50.8551 | 133.2590 | −15.9164 | 7.0921 | |
| 2020/03 | 10.6436 | −4.9440 | 8.5400 | −50.4991 | 132.6210 | −15.8723 | 7.0849 | |
| 2020/04 | 10.5217 | −4.3580 | 7.8600 | −47.5064 | 126.7420 | −15.3559 | 6.9203 | |
| 490 nm | 2019/03 | 9.7715 | 1.9670 | −3.0100 | 12.9375 | −23.2533 | 1.8139 | −0.4771 |
| 2019/04 | 9.6730 | 2.3200 | −3.1100 | 12.1584 | −18.9917 | 1.1227 | −0.1081 | |
| 2019/05 | 9.6635 | 2.3670 | −3.1200 | 11.9071 | −17.7142 | 0.9106 | 0.0083 | |
| 2019/06 | 9.6947 | 1.9610 | −2.2500 | 6.0098 | −0.9373 | −1.2313 | 1.0217 | |
| 2019/07 | 9.5101 | 2.4940 | −2.5800 | 7.0270 | −2.9429 | −0.9880 | 0.8950 | |
| 2019/08 | 9.5269 | 2.2400 | −2.0400 | 3.6803 | 5.7921 | −2.0184 | 1.3506 | |
| 2019/09 | 9.5336 | 1.7750 | −1.0500 | −2.4981 | 22.8231 | −4.1639 | 2.3596 | |
| 2019/10 | 9.6888 | 1.1500 | −0.1368 | −7.4012 | 35.2836 | −5.6579 | 3.0376 | |
| 2019/11 | 9.6859 | 0.9360 | 0.4382 | −11.1619 | 45.8123 | −6.9971 | 3.6738 | |
| 2019/12 | 9.6134 | 0.9530 | 0.5195 | −11.7803 | 47.5799 | −7.2204 | 3.7794 | |
| 2020/01 | 9.7351 | 0.0386 | 2.0200 | −19.7973 | 65.9922 | −9.0999 | 4.4793 | |
| 2020/02 | 9.6997 | −0.0920 | 2.5400 | −23.2691 | 75.4733 | −10.2709 | 5.0202 | |
| 2020/03 | 9.6732 | 0.0957 | 2.2800 | −21.9549 | 72.5307 | −9.9750 | 4.9115 | |
| 2020/04 | 9.2962 | 1.6170 | 0.4575 | −12.8336 | 50.8436 | −7.5213 | 3.8441 | |
| 565 nm | 2019/03 | 10.5619 | −0.8320 | −0.8383 | 7.6900 | −21.7704 | 2.6529 | −1.1958 |
| 2019/04 | 10.0140 | 1.0590 | −2.1700 | 10.5964 | −22.0062 | 2.0932 | −0.7502 | |
| 2019/05 | 10.0418 | 0.9780 | −2.0300 | 9.6084 | −18.9396 | 1.6722 | −0.5401 | |
| 2019/06 | 10.1014 | 0.6220 | −1.4200 | 5.6972 | −7.8270 | 0.2350 | 0.1522 | |
| 2019/07 | 9.8543 | 1.5510 | −2.3800 | 10.1655 | −18.5332 | 1.5041 | −0.4333 | |
| 2019/08 | 10.2167 | 0.3810 | −1.3700 | 6.3378 | −11.5477 | 0.9073 | −0.2449 | |
| 2019/09 | 10.0578 | 1.1460 | −2.4000 | 10.9869 | −20.9131 | 1.7825 | −0.5526 | |
| 2019/10 | 9.8873 | 1.1990 | −1.8000 | 6.7803 | −9.2663 | 0.3376 | 0.1141 | |
| 2019/11 | 9.9139 | 1.1580 | −1.6900 | 5.7335 | −5.7305 | −0.1552 | 0.3557 | |
| 2019/12 | 9.6085 | 2.2390 | −2.8300 | 10.7984 | −16.6471 | 0.9946 | −0.1201 | |
| 2020/01 | 9.6194 | 2.2440 | −2.8700 | 11.6022 | −20.2395 | 1.6082 | −0.4733 | |
| 2020/02 | 8.6279 | 5.2320 | −5.4700 | 21.4538 | −38.8702 | 3.3287 | −1.0892 | |
| 2020/03 | 7.8343 | 6.5590 | −6.4700 | 25.0900 | −45.7703 | 3.9853 | −1.3350 | |
| 2020/04 | 6.8971 | 9.1380 | −8.9100 | 35.8502 | −69.6268 | 6.5565 | −2.4095 | |
| 670 nm | 2019/03 | 11.0199 | −3.0330 | 1.9800 | −7.3261 | 15.3412 | −1.6382 | 0.6884 |
| 2019/04 | 10.3899 | −1.0990 | 0.7239 | −4.1420 | 12.6602 | −1.7396 | 0.8683 | |
| 2019/05 | 10.3432 | −0.8860 | 0.5659 | −3.8563 | 13.2152 | −1.9357 | 1.0056 | |
| 2019/06 | 10.3466 | −1.0100 | 1.0000 | −7.3694 | 24.3504 | −3.4743 | 1.7784 | |
| 2019/07 | 10.3241 | −0.8080 | 0.6400 | −5.0342 | 17.3024 | −2.4938 | 1.2721 | |
| 2019/08 | 10.4927 | −1.2730 | 0.8747 | −5.7385 | 18.3070 | −2.5422 | 1.2680 | |
| 2019/09 | 10.4829 | −1.0820 | 0.3574 | −2.1194 | 8.6613 | −1.4289 | 0.8010 | |
| 2019/10 | 10.4079 | −1.1860 | 0.7206 | −4.1144 | 13.3273 | −1.9300 | 1.0027 | |
| 2019/11 | 10.2380 | −0.6380 | 0.3846 | −4.0810 | 16.8243 | −2.6873 | 1.4698 | |
| 2019/12 | 10.1484 | −0.3330 | 0.1849 | −4.1750 | 19.6457 | −3.2837 | 1.8404 | |
| 2020/01 | 10.1481 | −0.5790 | 0.7103 | −6.1315 | 21.4229 | −3.0841 | 1.5653 | |
| 2020/02 | 10.0271 | −0.0794 | 0.2909 | −5.0614 | 21.0868 | −3.2612 | 1.7234 | |
| 2020/03 | 9.9585 | 0.2910 | −0.1911 | −2.6749 | 15.5124 | −2.6457 | 1.4648 | |
| 2020/04 | 9.5060 | 2.1790 | −2.3900 | 8.3306 | −11.2585 | 0.4806 | 0.0591 |
References
- Levy, R.C.; Mattoo, S.; Munchak, L.A.; Remer, L.A.; Hsu, N.C. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar] [CrossRef] [Green Version]
- Solomon, S.D.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Avery, K.B.; Tignor, M.; Miller, H.L. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Helder, D.L. Comparison of MSS relative radiometric calibration methods. Proc. SPIE—Int. Soc. Opt. Eng. 1993, 1938, 46–55. [Google Scholar]
- Xiong, X.; Chiang, K.; Esposito, J.; Guenther, B.; Barnes, W. MODIS on-orbit calibration and characterization. Metrologia 2003, 40, S89. [Google Scholar] [CrossRef]
- Meygret, A.; Dinguirard, M.C.; Henry, P.J.; Poutier, L.; Hazane, P. SPOT Histogram data base. Proc. SPIE—Int. Soc. Opt. Eng. 1997, 2957, 322–331. [Google Scholar]
- Horn, B.; Woodham, R.J. Destriping LANDSAT MSS images by histogram modification. Comput. Graph. Image Processing 1979, 10, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Chen, C.; Pan, J.; Zhu, Y.; Chang, X. A Relative Radiometric Calibration Method Based on the Histogram of Side-Slither Data for High-Resolution Optical Satellite Imagery. Remote Sens. 2018, 10, 381. [Google Scholar] [CrossRef] [Green Version]
- Henderson, B.G.; Krause, K.S. Relative radiometric correction of QuickBird imagery using the side-slither technique on orbit. Proc. SPIE—Int. Soc. Opt. Eng. 2004, 5542, 426–436. [Google Scholar]
- Pagnutti, M.; Ryan, R.E.; Kelly, M.; Holekamp, K.; Zanoni, V.; Thome, K.; Schiller, S. Radiometric characterization of IKONOS multispectral imagery. Remote Sens. Environ. 2003, 88, 53–68. [Google Scholar] [CrossRef] [Green Version]
- Bindschadler, R.; Choi, H. Characterizing and correcting Hyperion detectors using ice-sheet images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1189–1193. [Google Scholar] [CrossRef]
- Butler, J.J.; Krause, K.S.; Xiong, J. QuickBird relative radiometric performance and on-orbit long term trending. In Proceedings of the Earth Observing Systems XI, San Diego, CA, USA, 7 September 2006. [Google Scholar]
- Deschamps, P.Y.; Breon, F.M.; Leroy, M.; Podaire, A.; Bricaud, A.; Buriez, J.C.; Seze, G. The POLDER mission: Instrument characteristics and scientific objectives. IEEE Trans. Geosci. Remote Sens. 1994, 32, 598–615. [Google Scholar] [CrossRef]
- Fougnie, B. Improvement of the PARASOL Radiometric In-Flight Calibration Based on Synergy Between Various Methods Using Natural Targets. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2140–2152. [Google Scholar] [CrossRef]
- Fougnie, B.; Henry, P.J.; Cabot, F.; Meygret, A.; Laubies, M.-C. Vegetation: In-flight multiangular calibration. In Proceedings of the Earth Observing Systems V, San Diego, CA, USA, 15 November 2000; pp. 331–338. [Google Scholar]
- Cosnefroy, H.; Soule, P.; Briottet, X.; Hagolle, O.; Cabot, F. POLDER multiangular calibration using desert sites: Method and performances. Proc. SPIE—Int. Soc. Opt. Eng. 1997, 3221, 141–148. [Google Scholar]
- Chen, F.; Luo, D.; Li, S.; Yang, B.; Sun, L.; Ge, S.; Hong, J. The Operational Inflight Radiometric Uniform Calibration of a Directional Polarimetric Camera. Remote Sens. 2021, 13, 3823. [Google Scholar] [CrossRef]
- Vermote, E.; Santer, R.; Deschamps, P.Y.; Herman, M. In-flight calibration of large field of view sensors at short wavelengths using Rayleigh scattering. Int. J. Remote Sens. 1992, 13, 3409–3429. [Google Scholar] [CrossRef]
- Hagolle, O.; Goloub, P.; Deschamps, P.Y.; Cosnefroy, H.; Briottet, X.; Bailleul, T.; Nicolas, J.M.; Parol, F.; Lafrance, B.; Herman, M. Results of POLDER in-flight calibration. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1550–1566. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Xiang, G.; Chang, Y.; Han, L.; Zhang, M.; Li, S.; Tu, B.; Meng, B.; Hong, J. Pre-flight calibration of a multi-angle polarimetric satellite sensor directional polarimetric camera. Opt Express 2020, 28, 13187–13215. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Xing, J.; Liu, L.; Li, Z.; Mei, X.; Fu, Q.; Xie, Y.; Ge, B.; Li, K.; Xu, H. In-Flight Calibration of GF-1/WFV Visible Channels Using Rayleigh Scattering. Remote Sens. 2017, 9, 513. [Google Scholar] [CrossRef] [Green Version]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.-J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef] [Green Version]
- Qie, L.; Li, Z.; Zhu, S.; Xu, H.; Xie, Y.; Qiao, R.; Hong, J.; Tu, B. In-flight radiometric and polarimetric calibration of the Directional Polarimetric Camera onboard the GaoFen-5 satellite over the ocean. Appl. Opt. 2021, 60, 7186–7199. [Google Scholar] [CrossRef]
- Frouin, R. In-Flight Calibration of Satellite Ocean-Colour Sensors; Reports of the International Ocean-Colour Coordinating Group; International Ocean-Colour Coordinating Group: Dartmouth, NS, Canada, 2013. [Google Scholar]
- Fougnie, B.; Llido, J.; Gross-Colzy, L.; Henry, P.; Blumstein, D. Climatology of oceanic zones suitable for in-flight calibration of space sensors. In Proceedings of the Earth Observing Systems XV, San Diego, CA, USA, 27 August 2010; p. 78070S. [Google Scholar]
- Hou, M.L.Z.; Xie, Y.; Rui, Q.; Xie, Y.; Qie, L.; Shi, Z. Research on Spectral Feature Cloud Detection Method of Directional Polarimetric Camera on Chinese Satellite. J. Atmos. Environ. Opt. 2022, accepted. [Google Scholar]
- Zhu, S.; Chen, X.; Liu, L.; Qie, L.; Li, Z.; Ma, J.; Ge, S.; Hong, J.; Li, X.; Gao, H. Evaluation of radiometric performance of MODIS visible bands using the Rayleigh scattering method. J. Appl. Remote Sens. 2019, 13. [Google Scholar] [CrossRef]
- Antón, M.; López, M.; Vilaplana, J.M.; Kroon, M.; Mcpeters, R.; Bañón, M.; Serrano, A. Validation of OMI-TOMS and OMI-DOAS total ozone column using five Brewer spectroradiometers at the Iberian peninsula. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Werdell, P.J.; Bailey, S.W. An improved bio-optical data set for ocean color algorithm development and satellite data product variation. Remote Sens. Environ. 2005, 98, 122–140. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Toller, G.; Chiang, V.; Sun, J.; Esposito, J.; Barnes, W. MODIS Level 1B Algorithm Theoretical Basis Document; NASA MODIS Characterization Support Team: Washington, DC, USA, 2005. [Google Scholar]
- Angal, A.; Xiong, X.; Shrestha, A. Cross-Calibration of MODIS Reflective Solar Bands With Sentinel 2A/2B MSI Instruments. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5000–5007. [Google Scholar] [CrossRef]
- Cosnefroy, H.; Leroy, M.; Briottet, X. Selection and characterization of Saharan and Arabian desert sites for the calibration of optical satellite sensors. Remote Sens. Environ. 1996, 58, 101–114. [Google Scholar] [CrossRef]
- Lacherade, S.; Fougnie, B.; Henry, P.; Gamet, P. Cross Calibration Over Desert Sites: Description, Methodology, and Operational Implementation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1098–1113. [Google Scholar] [CrossRef]
- Angal, A.; Xiong, X.; Wu, A.; Changler, G.; Choi, T. Multitemporal Cross-Calibration of the Terra MODIS and Landsat 7 ETM+ Reflective Solar Bands. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1870–1882. [Google Scholar] [CrossRef]
- Hsu, N.C.; Jeong, M.J.; Bettenhausen, C.; Sayer, A.M.; Tsay, S.C. Enhanced Deep Blue aerosol retrieval algorithm: The second generation. J. Geophys. Res. Atmos. 2013, 118, 9296–9315. [Google Scholar] [CrossRef]
- Roujean, J.L.; Leroy, M.; Deschamps, P.Y. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Ge, B.; Li, Z.; Liu, L.; Yang, L.; Chen, X.; Hou, W.; Zhang, Y.; Li, D.; Li, L.; Qie, L. A dark target method for Himawari-8/AHI aerosol retrieval: Application and validation. IEEE Trans. Geosci. Remote Sens. 2018, 57, 381–394. [Google Scholar] [CrossRef]
- Ge, B.; Mei, X.; Li, Z.; Hou, W.; Xie, Y.; Zhang, Y.; Xu, H.; Li, K.; Wei, Y. An improved algorithm for retrieving high resolution fine-mode aerosol based on polarized satellite data: Application and validation for POLDER-3. Remote Sens. Environ. 2020, 247, 111894. [Google Scholar] [CrossRef]
- Li, Z.; Xu, H.; Li, K.; Li, D.; Xie, Y.; Li, L.; Zhang, Y.; Gu, X.; Zhao, W.; Tian, Q. Comprehensive study of optical, physical, chemical, and radiative properties of total columnar atmospheric aerosols over China: An overview of Sun–Sky Radiometer Observation Network (SONET) measurements. Bull. Am. Meteorol. Soc. 2018, 99, 739–755. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Li, K.; Xu, H.; Chen, X.; Chen, C.; Xie, Y.; Li, L.; Li, L.; Li, W. Sun-sky radiometer observation network with the extension of multi-wavelength polarization measurements. J. Remote Sens. 2015, 19, 495–519. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).