Abstract
Grassland vegetation typically comprises the species groups grasses, herbs, and legumes. These species groups provide different functional traits and feed values. Therefore, knowledge of the botanical composition of grasslands can enable improved site-specific management and livestock feeding. A systematic approach was developed to analyze vegetation of managed permanent grassland using hyperspectral imaging in a laboratory setting. In the first step, hyperspectral images of typical grassland plants were recorded, annotated, and classified according to species group and plant parts, that is, flowers, leaves, and stems. In the second step, three different machine learning model types—multilayer perceptron (MLP), random forest (RF), and partial least squares discriminant analysis (PLS-DA)—were trained with pixel-wise spectral information to discriminate different species groups and plant parts in individual models. The influence of radiometric data calibration and specific data preprocessing steps on the overall model performance was also investigated. While the influence of proper radiometric calibration was negligible in our setting, specific preprocessing variants, including smoothening and derivation of the spectrum, were found to be beneficial for classification accuracy. Compared to extensively preprocessed data, raw spectral data yielded no statistically decreased performance in most cases. Overall, the MLP models outperformed the PLS-DA and RF models and reached cross-validation accuracies of 96.8% for species group and 88.6% for plant part classification. The obtained insights provide an essential basis for future data acquisition and data analysis of grassland vegetation.
1. Introduction
Grasslands provide forage for ruminant livestock to produce meat, milk, wool, and hide [1] and for biogas production. Permanent grasslands are the predominant type of grassland in topographically and climatically disadvantaged regions, such as mountainous areas [2]. In contrast with the intensively utilized grasslands that occur in agriculturally more favorable areas, and which usually consist of only a few plant species, the permanent grasslands in mountainous and alpine regions provide species-rich vegetation and are utilized under moderate management regimes [3]. Grassland vegetation typically comprises grasses, herbs, and legumes. These species groups and plant species represent different functional traits [4] and feed values; knowledge of their relative proportions, therefore, offers advantages for site-specific management and livestock feeding. Grass–legume mixtures generally outperform pure grass stands in yield, resilience, and nitrogen efficiency because of leguminous nitrogen fixation in symbiosis with the soil bacteria rhizobia, weed suppression, and forage quality [5,6,7,8,9]. Rasmussen et al. [10] observed more than 300 /ha per year of N2-fixation by Trifolium pratense L. and Medicago sativa L. with Lolium perenne L. as companion grass species. This allows a substantial reduction in the mineral nitrogen fertilizer input and thus a reduction in CO2 emissions from nitrogen fertilizer production [11]. Another advantage of grass–clover mixtures is their increased feeding efficiency due to their high nutritional value. In particular, high crude protein content helps to meet the increasing demand for proteins [7]. Because of spatio-temporal variability in species groups and species composition, comprehensive mapping of the grassland sward can contribute substantially to improvement of site-specific management, especially with respect to fertilization and feed efficiency.
As proposed by Peratoner and Pötsch [12], estimating species groups and species composition is laborious, time-consuming, and requires advanced botanical and agronomic knowledge. Remote sensing is a promising alternative for assessing botanical composition, yield, and forage quality. It is non-destructive and can be used for the reproducible sensing of large areas in a very efficient manner [13]. Sensors for grassland monitoring can be based on the technical principles of photography, spectrometry, spectral imaging, synthetic aperture radar, light detection and ranging, and ultrasound [13].
Besides the high number of different technical principles and their possible combinations, the number of applications in grassland itself is also high. The large number of recent publications concerning remote sensing in grassland emphasizes the importance of this area. Common applications include modeling of grassland successional stages [14], forage quality parameters [15], biomass [16,17,18,19], legume N-fixation [17], chlorophyll content [20], species richness [21,22], leaf area index [23,24], and (species) classification [25,26,27,28,29,30]. Next to the vast number of applications, there is a large variability of grassland types due to local and regional factors [18,26,27,30]. In particular, grassland species and their composition vary by management type and site conditions. Opportunities for comparability between different studies are limited, and therefore an exclusive focus is set on managed permanent grassland in Austria, which is representative for many areas in the European alpine arc. Concerning grassland species classification, traditional computer vision approaches using morphological operators, such as those implemented by Bonesmo et al. [31] for mapping white clover in pastures, led to systems with a high sensitivity to adjustments and, thus, a small generalization ability. More recently, Bateman et al. [32], Skovsen et al. [33], and Sun et al. [34] developed species distribution mapping systems for grass–clover mixtures using RGB images and convolutional neural networks. However, their systems were trained on a forage ley, which has limited comparability to permanent grasslands. Compared to such broadband sensors, hyperspectral sensors with narrow and near-continuous spectra facilitate better granularity [13]. Furthermore, multispectral and hyperspectral sensors often extend the spectral range from the visible spectrum (VIS) to the near-infrared region (NIR). Taken together, these methods might enable the detection of even subtle differences in plants.
In principle, the usage of spatial information can be beneficial for practical grassland classification applications. In an ideal scenario however, without any spectral mixing of multiple plants, spectral information might be sufficient to train machine learning models to analyze the species composition. Therefore, an exclusive use of spectral information would allow simpler sensor systems and reduced machine learning effort to obtain satisfactory models. Combining spectral and spatial information could further increase classification quality for field applications.
Conti et al. [21] successfully used a six-channel multispectral camera and a spatial resolution of approximately 3 to assess the link between species diversity and spectral characteristics for permanent grassland biodiversity. The work and results of Suzuki et al. [29] are promising for spectral-based classification of grassland. They used hyperspectral data to analyze the botanical composition of Japanese grassland concerning the classes perennial ryegrass, white clover and other plants. They reached an overall accuracy of 80.3% based on linear discriminant analysis models. However, in their work only three classes were differentiated and today there are many new and optimized machine learning frameworks such as CatBoost [35] for gradient boosting and PyTorch [36] for neural networks available.
Analysis of species groups and species composition of managed permanent grasslands based on spectral data in the visible and near-infrared range has not been covered in detail so far.
Spectral signatures may vary, depending not only on the species groups but also on the plant parts captured (flower, leaf, and stem). The latter can even be absent at certain times (e.g., flowers) or show different characteristics over the course of the vegetation period due to species-specific differences in phenology and development, but also due to certain environmental conditions such as drought (e.g., leaf structure). Further, including information on the plant part composition might reveal insights into sward structures. The authors are not aware of any other investigations or publications regarding species group and plant part classification of managed, species-rich permanent grasslands.
Vegetation indices can be used with comparably low effort [37] as no training is necessary compared to machine learning and they allow for estimating plant functional traits [38]. However, many indices only utilize few spectral channels [37] and hence might exclude substantial information. Furthermore, indices might be affected by saturation problems [39]. Machine learning models based on hyperspectral data might overcome these limitations by using all available information at the same time.
Partial least squares discriminant analysis (PLS-DA) and random forest (RF) are popular classification algorithms, and neither system suffers from the multicollinearity usually present in high-dimensional spectral data [17]. A powerful alternative might be multilayer perceptron (MLP). This feedforward neural network type can characterize and learn features for prediction purposes [40]. For omics data [41] and weed and grass discrimination [42], MLP classification outperformed various other machine learning algorithms. Independent of the algorithm utilized, the quantity and quality of data are of utmost importance for a reliable analysis. This depends on thorough data acquisition with an accurate calibration process for spectral data, but biases and uncertainties remain [43]. As for data acquisition, image quality is mainly affected by consistent illumination and sufficient spatial resolution. While adjusting these parameters in on-field applications can be challenging [44], a laboratory setting provides a controlled environment assuring constant data quality with the added possibility of radiometric calibration.
Dark and bright reflection standards are commonly used for calibration purposes [45] to consider the sensor-specific dark current and the light source’s heterogeneous spectrum. Because parameters such as plant height and light conditions influence spectral signals and may render calibration techniques unsuccessful, laboratory conditions are advantageous. Further, data preprocessing might be a substantial step in enhancing the model performance. The use of derivatives with spectral data is a common technique [30,46]. It removes background signals and visualizes spectral curve shape differences that might not be evident in the spectra [47]. Smoothing operations such as Savitzky–Golay filtering are frequently applied [16,45] as well as data standardization or normalization.
A first step towards spectral-based classification of permanent grassland vegetation is to examine spectral properties under laboratory conditions, thereby enabling reproducible results to be obtained by minimizing the effects of influencing factors such as changing illumination or spatial distance variations. Only a systematic review under such conditions can reveal the influence of the vast number of data processing variants in combination with machine learning on the classification accuracy of grassland plants. Accordingly, the objectives of this study to lay a foundation for the development of spectral-based managed permanent grassland applications are as follows:
- Determine the spectral-based classification potential of grassland plants with respect to species group and plant part, and
- perform a systematic analysis regarding the influence of model type, calibration variant, and data preprocessing on classification accuracy.
2. Materials and Methods
2.1. Measurement Setup
An in-house hyperspectral imaging setup was used for measurements under standardized laboratory conditions (Figure 1a). It consists of a line scanning hyperspectral camera Fx10 (Specim, Spectral Imaging Ltd., Oulu, Finland) with a 12 Cinegon 1.4/12-0906 camera lens (Schneider Kreuznach, Bad Kreuznach, Germany). Resolutions were 1024 pixels and 224 spectral bands in the range of 400 to 1000 (full width at half maximum: 2.6 to 2.8 ). Illumination was provided by four 50 , 3000 halogen light sources “GX5,3 DECOSTAR” (OSRAM GmbH, Munich, Germany). The sample stage had a size of × 25 , and was mounted onto a linear axis SHT12 with a 250 mm driving path (igus Inc., East Providence, Rumford, RI, USA) and driven by a stepper motor PD4-C5918L4204-E-08 (Nanotec Electronic GmbH & Co. KG, Feldkirchen, Germany). The camera was positioned in a nadir position at a distance of 20 between the camera lens and the sample stage. A black shading box was used to exclude extraneous light. The system was operated with an in-house C++ software using the LUMO SpecSensor SDK 1.1 provided by the camera manufacturer and Qt 5.14.2 (Qt Group Plc, Helsinki, Finland) and OpenCV 4.10 (OpenCV, Great Lakes, OH, USA).
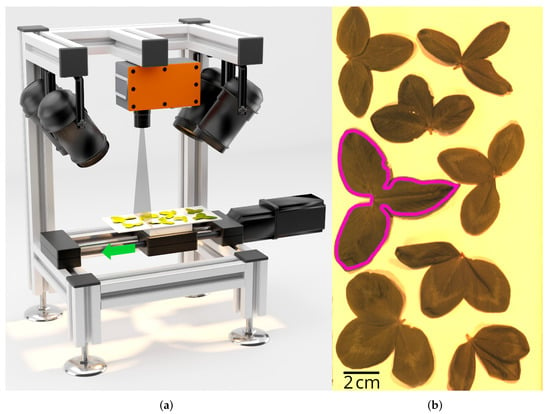
Figure 1.
Hyperspectral data acquisition. (a) Illustration of the measurement setup. Here, the slider moves the sample stage with specimens through the camera’s scanning line, illuminated using halogen lamps. (b) RGB image of the representative hyperspectral imaging data. An acquisition with eight samples of clover leaves is shown. Manually processed polygon annotation for one sample is shown in pink.
2.2. Sampling Locations
Plant samples were acquired at two grassland sites, each of which was harvested three times per year. The first location was the experimental field at the “Agricultural Research and Education Centre Raumberg-Gumpenstein” (Irdning, Austria, coordinates: 47.495° N, 14.100° E). Numerous grassland species were grown here in monoculture (pure grass and legume stands). The second location was the “VetFarm” of the University of Veterinary Medicine, Vienna, located in Pottenstein, Austria, where three different grassland types were selected; first, an intensively used grass–clover mixture (k1: flat and moist area, coordinates: 47.960° N, 16.138° E), and second, a more extensively used permanent grassland (k2: flat and relatively dry area, coordinates: 47.960° N, 16.139° E), both located in a forest. The third site in Kremesberg was a quite extensively used meadow (k3: a relatively dry and hilly area, coordinates: 47.956° N, 16.116° E). Grass samples were taken at typical harvest times between the vegetation stages of “stem elongation” (E) and “anther emergence/anthesis” (R4) according to the definitions by Moore et al. [48]. Legumes were sampled at the vegetation stage of “inflorescence emergence/1st spikelet visible” to “anther emergence, anthesis” (R1–R4). Further details regarding the dataset are provided in Table S1.
2.3. Sampling Procedure and Data Acquisition
Plant samples were manually picked from randomly selected positions within the sampling area and processed immediately. Stems were cut a few centimeters above the ground level. Samples that did not fit the sample stage were cut into smaller pieces and considered a single sample. Each sample was derived from an individual plant, except for the creeping plant species where repeated sampling might have occurred. Samples were classified according to species group (grass, herb, or legume) and plant part (flower, leaf, or stem) (Table 1 and Table S1) and placed on the sample stage with the upper surface facing the camera lens (Figure 1a). In total, 5768 samples of at least 19 grass, 6 herb, and 5 legume species were acquired and processed (Table 2). By sampling all individual growths, species-specific differences in phenology and development over the course of the vegetation period could be well recorded and taken into account.

Table 1.
Number of samples with respect to class membership, location, and seasonal cut. Each plant part (flower, leaf, or stem) from a different plant per seasonal cut is considered a sample.

Table 2.
Species respectively species groups definitely included in the dataset. For herbs only the genus was determined. At VetFarm additional species might have been sampled.
Dark calibration acquisitions were obtained by covering the lens with a lightproof lens cap using the same exposure time as the sample acquisitions. A calibrated reflection standard Zenith Lite with approximately 90% reflection (250 to 2450 ) (SphereOptics GmbH, Herrsching, Germany) was used for bright calibration acquisitions. Here, shorter exposure times compared to sample acquisitions were used to prevent overexposure of the camera chip. Dark and bright calibration acquisitions were obtained separately for each date.
2.4. Data Processing
The acquired data were processed before machine learning (Figure 2). For this, an RGB representation of each acquisition was used to manually annotate each flower, leaf, or stem with polygons (Figure 1b) using the software Computer Vision Annotation Tool (CVAT) (version: server 1.1, core 2.0.1, canvas 2.0.1, UI 1.2.0) [49]. A minimal distance was kept from the outer edges of the samples during annotation to exclude background information and rule out border effects. Metainformation regarding the species group, plant part, location, and the seasonal cut was assigned to each polygon. Pixels with intensity values of 0 or 4095 (12-bit detector) were disregarded.

Figure 2.
Schematic data processing workflow from data acquisition to model training. Inputs and outputs are denoted with rounded and processes with sharp box edges, respectively.
Next, the dark and bright calibration median lines were calculated. Defective camera sensor pixels were excluded using the 1st and 99th percentiles of the calibration medians with an interquartile range standard multiplication factor of 1.5 for bright calibration and a more preserving factor of 5 for dark calibration. Starting from uncalibrated reflectance data , dark calibrated reflectance and radiometrically calibrated reflectance for each pixel x and each wavelength were calculated according to
where D is the dark calibration median, B is the bright calibration median, and C is a specific correction factor of the reflectance standard provided by the manufacturer. Bright calibration reflectance values were corrected using a scaling factor for the differences in exposure time. Otherwise, all exposure times were identical.
The 16 lowest and highest spectral bands were removed for cleanup because of the low quantum efficiency of the sensor and the low light intensity at the border areas, resulting in an effective spectral range from 440.43 to 957.9 and 192 spectral channels. Next, outliers from each sample were removed by carrying out a robust principal component analysis with two main components (function PcaHubert from R package rrcov 1.5.5 [50]).
Next, subsampling using hierarchical clustering with the function hclust from R package fastcluster 1.2.3 [51] with complete linkage based on a Euclidean dissimilarity matrix was performed. The generated cluster tree was cut down to 10 clusters. Then, for each polygon, a total of 100 pixels were drawn randomly stratified from the clusters. In the case of 100 or fewer pixels available in total, all the pixels were drawn. However, polygons consisting of less than 95 pixels were disregarded. For species group and plant part classes separately, all polygons were grouped based on their class membership, and then randomly stratified and assigned a chunk number in the range of 1 to 5. Polygon selection and chunk assignments from the RC dataset were used for all calibration variants.
These variants were further preprocessed using different combinations of Savitzky–Golay smoothening (function savgol with a filter length of 5 and quadratic filter from R package pracma 2.3.3 [52]), derivation, and Z-standardization (Table 3). Eighty-one different dataset variants (3 calibration and 27 preprocessing variants) were generated for two groups (species group and plant part).

Table 3.
Preprocessing variants generated on top of each calibration variant. Processing steps are denoted from top to bottom. O = original data, D = derivative, S = Savitzky–Golay filter, Z = Z-standardization.
2.5. Machine Learning
MLP, RF, and PLS-DA models were trained for the species group and plant part classifications, respectively. The class weights were normalized by the number of samples per class to compensate for the unbalanced classes. Final training was performed 5-fold cross-validated, and performance metrics were calculated based on the validation parts not used for training.
Training and analysis for PLS-DA and RF and statistical analyses were conducted using R 4.0.1 [53]. Specifically, data processing was conducted using the R packages data.table 1.14.0 [54], dtplyr 1.1.0 [55], and tidyverse 1.3.1 [56]. Statistical significance was computed using an ANOVA using the function “aov” included in R followed by a Tukey test using the function “HSD.test” (package agricolae 1-3.5 [57]) with a significance level ( = 5%). All parameters not explicitly mentioned were set to default values.
2.5.1. Multi-Layer Perceptron (MLP)
MLP networks were trained using Python 3.8.1, PyTorch 1.7.0 [36], Tune [58] included in Ray 1.0.1 [59] and hyperopt 0.2.5 [60].
The network architecture started with a fully connected layer, connecting the inputs, that is, all spectral channels, with the first hidden layer followed by batch normalization and a rectified linear unit activation function (ReLU). After another fully connected layer with a ReLU, the final layer is connected to the three output classes. Cross-entropy loss with class weights was used as a loss function together with a stochastic gradient descent optimizer. A softmax function was used during inference to convert the raw MLP output into probabilities.
Hyperparameters for each variant were searched using an “AsyncSuccessiveHalvingAlgorithm” (ASHA) included in Ray Tune as a scheduler together with the hyperopt search algorithm. Each hyperparameter combination, selected by hyperopt out of the search space (Table 4), was trained for 100 epochs or early stopped by ASHA which was configured with one grace period and a reduction factor of 4. In total, 100 hyperparameter combinations per dataset variant and group were evaluated using the dataset chunks 1 to 4 as the training dataset and chunk 5 for validation. The five hyperparameter combinations, having achieved the highest accuracy per dataset variant and group, were retrained with 5-fold cross-validation for 120 epochs. The model with the highest cross-validated accuracy among the five models found at any epoch is depicted in the results. More details about the hyperparameters used in the final models are given in Table S2.

Table 4.
Hyperparameter search space used to find hyperparameter combinations for high model accuracies. l1 and l2 = number of nodes in the first respectively second hidden layer. lr = learning rate.
2.5.2. Random Forest (RF)
The RFs were trained using the function ranger from the ranger package 0.12.1 [61] with the parameter “respect.unordered.factors” set to “order”. The calculated class weights were supplied to the parameter “case.weights”. Simplified training was conducted to identify suitable hyperparameters. A model was trained for every dataset variant and group (chunks 1–4) with 20 trees. The number of randomly sampled predictors (mtry) was in the range of 25 to 45 with increments of 5 and validated on chunk 5 (Table S3). The variant RC O-S-D-S-Z achieved the highest accuracy for species group and plant part and was therefore chosen exclusively for further hyperparameter selection tests to decrease the computation time of hyperparameter determination. With this dataset variant, models for species group and plant part were trained cross-validated for mtry values of 10 to 90 with increments of 10. After these trials, a mtry value of 40 was selected for final training to compromise accuracy and computation time (Table S4).
To select the sample fraction, that is the percentage of rows to randomly sample from per tree, as well as the number of trees to train, models with sample fraction values of 0.5, 0.75, and 1 were trained for a number of 100 trees to 500 trees in increments of 100 trees (Table S5). An sample fraction value of 1 and a number of 400 trees was chosen, resulting in reasonable accuracy with acceptable computation time for final training.
2.5.3. Partial Least Squares Discriminant Analysis (PLS-DA)
PLS regression was performed using the cppls function from the pls package 2.7.3 [62] with 64 components, class weights set, and no data centering or scaling. Subsequently, linear DAs with the lda function from MASS package 7.3–54 [63] were performed, including up to all 64 PLS components. The model with the best cross-validated accuracy found at any number of PLS components is indicated in the results (see also Table S2).
3. Results
3.1. Species Group Classification
The evaluation of the mean species group classification accuracy across all calibration and preprocessing variants showed that, on average, MLP provided the highest accuracy, followed by PLS-DA and RF, with the best representative models showing a classification accuracy of 95.7%, 88.1%, and 84.1%, respectively (Figure 3). On the other hand, PLS-DA provided the smallest standard deviation, followed by MLP and RF. Of all 81 different dataset variants, the best not significantly different models per model type included 67 MLP, 66 PLS-DA and 6 RF models. Furthermore, variants differing only in subsequent Z-standardization showed significant differences solely for two variant pairs, namely MLP: RC O-S(-Z) and PLS-DA: RC O-D-D(-Z). Interestingly, some individual models for specific dataset variants outperformed model types that performed well on average, as can be seen for some RC RF models that outperformed the PLS-DA models.

Figure 3.
Mean species group classification accuracy based on the preprocessing variant for multilayer perceptron (MLP), partial least squares discriminant analysis (PLS-DA) and random forest (RF) models for dark calibrated (DC), radiometrically calibrated (RC), and uncalibrated (UC) datasets. X-axis abbreviations (preprocessing steps from bottom to top): O = original data, D = derivative, S = Savitzky–Golay filter, Z = Z-standardization. MLP and RF values are shown with a slight x-axis offset for better visualization. Error bars indicate standard deviation, 5-fold cross-validated.
While all model types showed significant differences compared to each other, no significant differences in the calibration variant could be detected (Table 5 and Table S6). Independent of the calibration variant, similar trends in classification accuracy could be observed depending on the preprocessing variant (Table 6). In particular, for RF and other model types, variants containing a derivation (D) without prior Savitzky–Golay filter (S) mainly performed worse than variants with a combination of S and D. For MLP and PLS-DA, even the original dataset variant (O) generated models that were not significantly different from the best statistical model, except for the RC variant for MLP.

Table 5.
Mean validation accuracy of species group classification across all preprocessing variants based on calibration variant and model type. Different characters denote a significant difference (). Values are presented with standard deviation, 5-fold cross-validated.

Table 6.
Top 5 MLP, PLS-DA, and RF model results based on total validation accuracy for the classification of species groups with statistical significance and accuracy. Different characters denote a significant difference ( = 5%). Values are presented with standard deviation, 5-fold cross-validated.
The focus was on the five best performing models for each model type for species group classification to compare different dataset variants (Table 6). For these dataset variants, it can be observed that most preprocessing variants consist of at least one D and one S. Out of the top five variants per model, all MLP variants contained the preprocessing combination S-D. In contrast, for RF and PLS-DA, only four and two variants contained this combination, respectively. Interestingly, no preprocessing combinations contained a second D. The validation accuracy for MLP was approximately 97% and nearly identical for all five best performing variants. The same was applicable to the PLS-DA with an accuracy of approximately 89%. In contrast, RF showed a slightly higher accuracy spread (88–90%). As for the influence of the calibration variant in the best performing models, PLS-DA achieved the best results with UC and RF with RC datasets. However, no such trend was observed for the MLP models.
Comparisons of species group accuracies showed that grass classification always gave the best performance, followed by legumes and herbs (Table 6). MLP performed best for grasses, followed by PLS-DA and RF with the best models resulting in classification accuracies of 98.9%, 96.4%, and 95.7%, respectively. The same ranking was found for the herbs, with MLP performing best, followed by PLS-DA and RF, with classification accuracies of 86%, 55.3%, and 46.7%, respectively, for the best performing models. For legumes, MLP performed best with an accuracy of 94.7% for the best model. However, RF outperformed PLS-DA with an accuracy of 84.2% compared to 79.5% for the best models of the respective model type.
While grass and legume classification gave accurate results, the major misclassification in all model types occurred for herbs (Figure 4). With MLP 13.4%, with PLS-DA 39.5%, and with RF 42.2% of herbs were classified as legumes. Misclassification of herbs as grasses was minor for all model types, although it was above 10% for RF. The second noteworthy misclassification occurred in the legumes with PLS-DA classifying 14.2% and RF 12.9% as grass. All other misclassifications of legumes were <10%.

Figure 4.
Confusion matrices of MLP, PLS-DA, and RF models with the highest species group classification accuracy. Values with standard deviation, 5-fold cross-validated.
3.2. Plant Part Classification
The evaluation of the mean plant part classification accuracy across all calibration and preprocessing variants showed that, on average, MLP performed best, followed by PLS-DA and RF, with the best model having a classification accuracy of 86.7%, 78.9%, and 77.8%, respectively (Figure 5). MLP showed the smallest standard deviation followed by RF and PLS-DA. Of the 81 different dataset variants, the best not significantly different models per model type included 60 MLP, 72 PLS-DA, and 28 RF models. Interestingly, for all model types, the O variant was included in these groups. Furthermore, variants differing only in subsequent Z-standardization showed no significant differences. As with the species group result, some individual models for specific dataset variants outperformed model types that performed well on average.
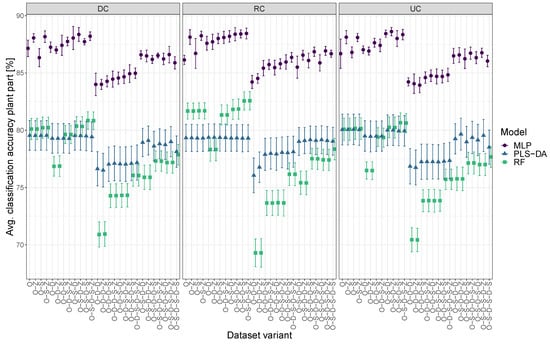
Figure 5.
Mean plant part classification accuracy based on the preprocessing variant for MLP-, PLS-DA- and RF-models for DC, RC, and UC. X-axis abbreviations (preprocessing steps from bottom to top): O = original data, D = derivative, S = Savitzky–Golay filter, Z = Z-standardization. MLP and RF values are shown with a slight x-axis offset for better visualization. Error bars indicate standard deviation, 5-fold cross-validated.
MLP results were significantly different from the PLS-DA and RF results. However, there was no significant difference between PLS-DA and RF, except for the UC calibration variant (Table 7 and Table S7). Upon examining each model type individually, no significant differences in the calibration variants could be detected. Independent of the calibration variant, similar trends in classification accuracy could be observed depending on the preprocessing variant. Furthermore, previously observed tendencies from the species group classification were also held for the plant part classification.

Table 7.
Mean validation accuracy of plant part classification across all preprocessing variants. Different characters denote a significant difference ( = 5%). Values are presented with standard deviation, 5-fold cross-validated.
The focus was on the five best-performing models for each model type for plant part classification to compare different dataset variants (Table 8). As for the dataset variants, all top five MLP models contained the preprocessing S-D, whereas, in the case of PLS-DA, only one variant contained this combination, and in the case of RF only four variants contained this combination. Interestingly, none of the combinations contained a second D. The validation accuracy for the MLP was nearly identical for all five best-performing variants and was approximately 88%. The same was true for PLS-DA, with an accuracy of approximately 80%, whereas RF showed a slightly higher accuracy spread (81.7–82.6%). As for the influence of the calibration variant on the best-performing models, MLP achieved the best results with UC and RC calibration variants, whereas PLS-DA achieved the best results with UC and RF performed best with RC datasets.

Table 8.
Top 5 MLP, PLS-DA, and RF model results based on total validation accuracy for the classification of plant parts with statistical significance and accuracy. Different characters denote a significant difference ( = 5%). Values are presented with standard deviation, 5-fold cross-validated.
With respect to plant part accuracies, the classification of leaves always gave the best performance, followed by flowers and stems, except for flowers and leaves for RF RC O-S (Table 8). MLP performed best for flowers, followed by RF and PLS-DA with the best models resulting in the classification accuracy of 90.3%, 85.8%, and 73.1%, respectively. The same was true for the stems with MLP performing best, followed by RF and PLS-DA, with classification accuracies of 83.7%, 72.7%, and 66% for the best performing models, respectively. Concerning leaves, MLP gave the best classification accuracy (92.7% for the best case), but in contrast with the previously mentioned classes, it is followed by PLS-DA and then RF with 91.3% and 87.3% accuracies in the best case, respectively.
While leaf and flower classifications showed relatively accurate results, the significant misclassification for all model types occurred for stems (Figure 6). With MLP 10.3%, with PLS-DA 27.9%, and RF 20.1% of stems were classified as leaves. The misclassification percentages of stems as flowers remained relatively constant for all model types, with values ranging from 6.1–7.8%. The second biggest misclassification occurred for the flowers. However, flower classification accuracy was similar to leaf classification accuracy with the different model types, except with PLS-DA. In this case, 13.1% and 13.7% of all flowers were classified as stems and leaves, respectively. The leaves had the lowest misclassification rate. With all model types, leaves were rather classified as stems (6.2–9.8%), and only a low number was predicted as flowers (1.6–2.8%).

Figure 6.
Confusion matrices of MLP-, PLS-DA-, and RF-models with the highest plant part classification accuracy. Values with standard deviation, 5-fold cross-validated.
4. Discussion
For both species group and plant part, MLP showed the highest classification accuracies. These were 96.8% for species group and 88.6% for plant part for the best models. Similar results using hyperspectral imaging data from a pot experiment to discriminate between three weed and one grass species using PLS-DA, SVM, and MLP led to a superior MLP model with 89.1% accuracy [42]. However, the classification of individual species is not directly comparable to the classification of species groups. In other areas, MLP also demonstrated powerful classification abilities. Research conducted by de Castro et al. [64] classifying cruciferous weeds, wheat, and broad beans under field conditions yielded an MLP model with nearly 100% accuracy. However, these results are hardly comparable to those presented here, mainly because of different methods, research objects, and exogenous conditions.
Next to the best performing MLP models, typical model types of PLS-DA and RF were investigated. The common attribute between all the three model types is that hyperparameters influence their reachable accuracies. However, for PLS-DA and RF, it is unlikely that unsuitable hyperparameters is the reason for their lower performance compared with MLP. For PLS-DA, the number of components included (ncomp) is the standard parameter that is tuned. It is usually tuned over the entire possible range up to the number of spectral channels. However, as the spectral dataset used is highly colinear, high ncomp values cannot be realized. Because of this collinearity and the typical decline in accuracy increment per increased ncomp step, the maximum ncomp value was set to 64 (approximately of available predictors). PLS-DA model accuracies were on average steeply increasing up to approximately 30 and 60 components for plant part and species group, respectively. The results based on the top five models for species groups and plant part show that only one model for species groups used all available 64 components. Furthermore, for the last five ncomp steps, the absolute average accuracy changes were only % for species groups and % for plant part. Therefore, no significant gain with higher ncomp values is expected.
Several hyperparameters could be tuned using the ranger RF package. According to Probst et al. [65], the two most essential hyperparameters are the sample fraction and mtry, which were tuned in our analysis. However, tunability within the ranger is generally low [65]. During the hyperparameter search for a representative variant, the accuracy was already stable with 400 trees; no further accuracy gain with additional tuning was expected.
For MLP an assessment of further tunability is virtually impossible as, for neural networks, even random variables such as the weights for network initialization may have a noticeable effect on model quality [66]. In addition, other search spaces or even different model architectures could significantly affect model accuracy. The accuracies achieved by our models indicate that the chosen parameters are acceptable. In comparison, Adagbasa et al. [25] used a similar MLP design to classify grass species based on Sentinel-2 MSI data. For their purposes, they proposed 3–5 hidden layers with a learning rate of 0.001, a weight decay of 1 × 10 and the usage of the ADAM optimizer, which is similar to our configuration. Interestingly, their trained MLP outperformed other machine learning algorithms, including RF.
Independent of the algorithm used, data quality is of the utmost importance to achieve high-performance machine learning models. When dealing with spectral data, the covered spectral range is a crucial parameter. The observed spectral range in our case was 440.43 to 957.9 . Asner [67] determined that plant tissue properties are wavelength-dependent. In the case of green leaves, the smallest variation occurs in the VIS region. At the same time, it is more significant in the NIR region. Therefore, for foliar chemistry, the NIR region provided the best link. The studies of Yu et al. [30] underline the importance of this to discriminate different grassland species, where NIR and SWIR performed better than VIS alone. Furthermore, Basinger et al. [68] and Pfitzner et al. [28] indicate that utilizing the spectral range VIS-SWIR could benefit species discrimination. Therefore, considering this range could potentially lead to improved model performance.
Spatial resolution is another important parameter in addition to spectral resolution. As individual grassland samples show spectral variations, a low spatial resolution leads to averaging effects [69]. The high spatial resolution of approximately 60 pixel/ in the deployed measurement system circumvents this issue. It allows the capture of spectral signatures for distinct sample regions. Consequently, with the usage of a high spatial sampling resolution, manual averaging or algorithms with high generalization ability are mandatory to achieve high model accuracies.
Biological characteristics that result in similar reflection properties can give rise to misclassifications. Here, leaf sheaths covering the stems might have introduced these misclassifications for stems. In terms of accuracy, herb classification was underperformed compared to grass and legume classification. This might be because the sample number of herbs was small compared to the other classes and because of the potential for a greater amount of variability within the herb species group.
Parameters such as spectral and spatial resolutions are commonly determined by the equipment used. However, different calibration and data processing methods are applicable independently of this constraint. According to Dao et al. [45], proper calibration of airborne hyperspectral imaging data is mandatory to detect slight differences in spectral curve changes, especially in vegetation such as grassland. Here, it seems that for certain model types, specific calibration variants result in better-performing models. However, all calibration variants were present in similar fractions in the best statistically non-significant different groups, except for RF in the species group classification. Further, our results show, on average, no statistically significant difference between the calibration variants UC, DC, and RC for each model type for species group and plant part. This does not translate to the UC variant being sufficient because light conditions, although changing between measurement days due to variations in lamp positioning, were kept relatively constant compared to realistic field conditions. The 3D canopy structure can significantly impact reflection behavior [45,67] with plant height differences and light scattering effects making a physically correct radiometric calibration unfeasible. Nevertheless, our results suggest that calibration does not influence the model performance under nearly constant light and three-dimensional conditions.
MLP and PLS-DA performed well with a wide range of preprocessing variants, but this was not the case with RF. The main reason for this is that RF usually uses only a few predictors at the tree level to form a decision boundary [70], which makes it more sensitive to data variations than MLP and PLS-DA. Thus, MLP and PLS-DA show a high generalization ability with respect to preprocessing variants compared to RF. Preprocessing variants, including a Savitzky–Golay filter before a derivation, work particularly well for data with low spectral band distances. In this case, differences between successive spectral channels may be slight compared to random noise [47]. Other variants can also benefit from Savitzky–Golay filtering employed as a noise reduction technique. Interesting preprocessing variants that performed well, independent of the model and calibration type, included the combination S-D without a second D. These variants were present in the best statistically non-significant groups. However, for RF this holds only for RC data variants and for species group classification. This is the only calibration variant present in the best group. This underlines the usefulness of spectral gradients in combination with smoothing for machine learning applications. Independent of model type and calibration, Z-standardization showed no significant differences on average. Preprocessing steps that do not lead to increased accuracy, such as Z-standardization, should be avoided for the sake of simplicity.
5. Conclusions
The vegetation composition of grasslands with respect to species group and plant part could be determined under laboratory conditions with high accuracy. The exclusive use of spectral information seems to be sufficient for grassland classification according to these criteria. In particular, MLP outperformed PLS-DA and RF and, thus, can be recommended for further research and applications. Interestingly, calibration on average under laboratory conditions did not influence the classification accuracy for all tested model types. Although raw spectral data variants led to acceptable classification accuracies, further data preprocessing before model training can improve the classification performance. In particular, variants including Savitzky–Golay smoothing and a subsequent derivation seem beneficial with respect to classification quality. In contrast, data processing, including two derivations, seems to be detrimental. The presented results provide an essential basis for the comprehensive mapping of grassland species group distribution to aid site-specific management and feed efficiency. However, these findings do not directly apply to field-like conditions, as in this case the system complexity increases. While seasonal and local canopy structure effects were implicitly included in the presented results, effects of the 3D structure were not considered. Here, further research, e.g., with potted plants could be a next step. Still, this work can contribute to existing sensor systems and it demonstrates the potential for future precision farming applications in general. In particular for grassland management, an automatized, non-destructive discrimination of species groups and plant parts would be beneficial to adapt management strategies and increase process sustainability. However, other aspects and challenges such as location influence, species differentiation, illumination, 3D sward structure, spectrally mixed pixels, and identification of wavelengths relevant for classification need to be addressed in further research.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14051154/s1, Table S1: Final dataset as a function of seasonal cut, location, species group, and plant part; Table S2: Hyperparameters used for model training for groups species group (SG) and plant part (PP) for training of MLP and PLS-DA with respect to the dataset variant; Tables S3–S5: RF hyperparameter test 1–3; Table S6: Average species group classification accuracy achieved on the validation dataset with respect to dataset calibration and preprocessing variant for MLP, PLS-DA and RF models; Table S7: Average plant part classification accuracy achieved on the validation dataset with respect to dataset calibration and preprocessing variant for MLP, PLS-DA and RF models.
Author Contributions
Conceptualization: A.B., N.B., R.B. and A.G.; Data curation: R.B., A.K. and A.S.; Formal analysis: R.B.; Funding acquisition: A.B., N.B. and A.G.; Investigation: R.B.; Methodology: N.B., R.B., A.K., V.M. and A.S.; Project administration: N.B., R.B., A.G. and V.M.; Resources: N.B., A.G., E.M.P. and A.S.; Software: R.B.; Supervision: A.G. and E.M.P.; Validation: R.B. and V.M.; Visualization: R.B.; Writing—original draft: R.B.; Writing—review and editing: A.B., N.B., A.G., A.K., V.M., E.M.P. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out within the framework of a research project of the Austrian Competence Center for Feed and Food Quality, Safety and Innovation (FFoQSI). The COMET-K1 competence center FFoQSI is funded by the Austrian federal ministries BMK, BMDW, and the Austrian provinces Lower Austria, Upper Austria, and Vienna within the scope of COMET-Competence Centers for Excellent Technologies. The program COMET is handled by the Austrian Research Promotion Agency FFG (Grant number: 854182).
Data Availability Statement
Restrictions apply to the availability of these data. Data are available from the authors with the permission of the Austrian Competence Center for Feed and Food Quality, Safety and Innovation (FFoQSI).
Acknowledgments
The project was realized with PÖTTINGER Landtechnik GmbH (Grieskirchen, Austria) as a company partner. Many thanks to AREC Raumberg-Gumpenstein and VetFarm Kremesberg for providing their infrastructure and Bernhard Spangl from BOKU Vienna for statistical advice.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ASHA | Async Successive Halving Algorithm |
| D | derivative |
| DC | dark calibrated |
| MLP | multilayer perceptron |
| NIR | near infrared region |
| O | original data |
| PLS-DA | partial least squares discriminant analysis |
| RC | radiometrically calibrated |
| RGB | red, green, blue |
| RF | random forest |
| S | Savitzky–Golay filter |
| SWIR | short wave infrared region |
| UC | uncalibrated |
| VIS | visible spectrum |
| Z | Z-standardization |
References
- Nelson, C.J.; Moore, K.J.; Collins, M. Forages—An Introduction to Grassland Agriculture; Chapter Forages and Grasslands in a Changing World; John Wiley & Sons: Hoboken, NJ, USA, 2017; Volume 1, pp. 3–17. [Google Scholar]
- Buchgraber, K.; Schaumberger, A.; Pötsch, E.M. Grassland Farming in Austria—Status quo and future prospective. In Proceedings of the 16th Symposium of the European Grassland Federation “Grassland Farming and Land Management Systems in Mountainous Regions”, Grassland Science in Europe, Gumpenstein, Austria, 29–31 August 2011; Volume 16, pp. 13–24. [Google Scholar]
- Pötsch, E.M.; Blaschka, A.; Resch, R. Impact of different management systems and location parameters on floristic diversity of mountainous grassland. In Proceedings of the 13th International Occasional Symposium of the European Grassland Federation (EGF): “Integrating Efficient Grassland Farming and Biodiversity”, Grassland Science in Europe, Tartu, Estonia, 29–31 August 2005; Volume 10, pp. 315–318. [Google Scholar]
- Schellberg, J.; da Pontes, L.S. Plant functional traits and nutrient gradients on grassland. In Proceedings of the 16th Symposium of the European Grassland Federation “Grassland Farming and Land Management Systems in Mountainous Regions”, Grassland Science in Europe, Gumpenstein, Austria, 29–31 August 2011; Volume 16, pp. 470–483. [Google Scholar]
- Connolly, J.; Sebastià, M.T.; Kirwan, L.; Finn, J.A.; Llurba, R.; Suter, M.; Collins, R.P.; Porqueddu, C.; Helgadóttir, Á.; Baadshaug, O.H.; et al. Weed suppression greatly increased by plant diversity in intensively managed grasslands: A continental-scale experiment. J. Appl. Ecol. 2018, 55, 852–862. [Google Scholar] [CrossRef] [PubMed]
- Haughey, E.; Suter, M.; Hofer, D.; Hoekstra, N.J.; McElwain, J.C.; Lüscher, A.; Finn, J.A. Higher species richness enhances yield stability in intensively managed grasslands with experimental disturbance. Sci. Rep. 2018, 8, 15047. [Google Scholar] [CrossRef]
- Lüscher, A.; Mueller-Harvey, I.; Soussana, J.F.; Rees, R.M.; Peyraud, J.L. Potential of legume-based grassland–livestock systems in Europe: A review. Grass Forage Sci. 2014, 69, 206–228. [Google Scholar] [CrossRef]
- Niderkorn, V.; Martin, C.; Le Morvan, A.; Rochette, Y.; Awad, M.; Baumont, R. Associative effects between fresh perennial ryegrass and white clover on dynamics of intake and digestion in sheep. Grass Forage Sci. 2017, 72, 691–699. [Google Scholar] [CrossRef]
- Suter, M.; Connolly, J.; Finn, J.A.; Loges, R.; Kirwan, L.; Sebastià, M.T.; Lüscher, A. Nitrogen yield advantage from grass–legume mixtures is robust over a wide range of legume proportions and environmental conditions. Glob. Chang. Biol. 2015, 21, 2424–2438. [Google Scholar] [CrossRef]
- Rasmussen, J.; Søegaard, K.; Pirhofer-Walzl, K.; Eriksen, J. N2-fixation and residual N effect of four legume species and four companion grass species. Eur. J. Agron. 2012, 36, 66–74. [Google Scholar] [CrossRef]
- Jensen, E.S.; Peoples, M.B.; Boddey, R.M.; Gresshoff, P.M.; Hauggaard-Nielsen, H.; Alves, B.J.; Morrison, M.J. Legumes for mitigation of climate change and the provision of feedstock for biofuels and biorefineries: A review. Agron. Sustain. Dev. 2012, 32, 329–364. [Google Scholar] [CrossRef]
- Peratoner, G.; Pötsch, E.M. Methods to describe the botanical composition of vegetation in grassland research. Die Bodenkultur J. Land Manag. Food Environ. 2019, 70, 1–18. [Google Scholar] [CrossRef]
- Wachendorf, M.; Fricke, T.; Möckel, T. Remote sensing as a tool to assess botanical composition, structure, quantity and quality of temperate grasslands. Grass Forage Sci. 2018, 73, 1–14. [Google Scholar] [CrossRef]
- Möckel, T.; Dalmayne, J.; Prentice, H.C.; Eklundh, L.; Purschke, O.; Schmidtlein, S.; Hall, K. Classification of Grassland Successional Stages Using Airborne Hyperspectral Imagery. Remote Sens. 2014, 6, 7732–7761. [Google Scholar] [CrossRef]
- Wijesingha, J.; Astor, T.; Schulze-Bruninghoff, D.; Wengert, M.; Wachendorf, M. Predicting Forage Quality of Grasslands Using UAV-Borne Imaging Spectroscopy. Remote Sens. 2020, 12, 126. [Google Scholar] [CrossRef]
- Fricke, T.; Wachendorf, M. Combining ultrasonic sward height and spectral signatures to assess the biomass of legume-grass swards. Comput. Electron. Agric. 2013, 99, 236–247. [Google Scholar] [CrossRef]
- Grüner, E.; Wachendorf, M.; Astor, T. The potential of UAV-borne spectral and textural information for predicting aboveground biomass and N fixation in legume-grass mixtures. PLoS ONE 2020, 15, e0234703. [Google Scholar] [CrossRef] [PubMed]
- Peciña, M.V.; Bergamo, T.F.; Ward, R.D.; Joyce, C.B.; Sepp, K. A novel UAV-based approach for biomass prediction and grassland structure assessment in coastal meadows. Ecol. Indic. 2021, 122, 107227. [Google Scholar] [CrossRef]
- Schut, A.G.T.; Ketelaars, J.J.M.H. Monitoring grass swards using imaging spectroscopy. Grass Forage Sci. 2003, 58, 276–286. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Dube, T.; Mafongoya, P.L. Spectrometric proximally sensed data for estimating chlorophyll content of grasslands treated with complex fertilizer combinations. J. Appl. Remote Sens. 2020, 14, 024517. [Google Scholar] [CrossRef]
- Conti, L.; Malavasi, M.; Galland, T.; Komárek, J.; Lagner, O.; Carmona, C.P.; Bello, F.; Rocchini, D.; Šímová, P. The relationship between species and spectral diversity in grassland communities is mediated by their vertical complexity. Appl. Veg. Sci. 2021, 24, e12600. [Google Scholar] [CrossRef]
- Möckel, T.; Dalmayne, J.; Schmid, B.C.; Prentice, H.C.; Hall, K. Airborne Hyperspectral Data Predict Fine-Scale Plant Species Diversity in Grazed Dry Grasslands. Remote Sens. 2016, 8, 133. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Klingler, A.; Schaumberger, A.; Vuolo, F.; Kalmár, L.B.; Pötsch, E.M. Comparison of Direct and Indirect Determination of Leaf Area Index in Permanent Grassland. PFG–J. Photogramm. Remote Sens. Geoinf. Sci. 2020, 88, 369–378. [Google Scholar] [CrossRef]
- Adagbasa, E.G.; Adelabu, S.A.; Okello, T.W. Application of deep learning with stratified K-fold for vegetation species discrimation in a protected mountainous region using Sentinel-2 image. Geocarto Int. 2019, 37, 142–162. [Google Scholar] [CrossRef]
- He, Y.; Yang, J.; Guo, X. Green Vegetation Cover Dynamics in a Heterogeneous Grassland: Spectral Unmixing of Landsat Time Series from 1999 to 2014. Remote Sens. 2020, 12, 3826. [Google Scholar] [CrossRef]
- Melville, B.; Lucieer, A.; Aryal, J. Assessing the Impact of Spectral Resolution on Classification of Lowland Native Grassland Communities Based on Field Spectroscopy in Tasmania, Australia. Remote Sens. 2018, 10, 308. [Google Scholar] [CrossRef]
- Pfitzner, K.; Bartolo, R.; Whiteside, T.; Loewensteiner, D.; Esparon, A. Hyperspectral Monitoring of Non-Native Tropical Grasses over Phenological Seasons. Remote Sens. 2021, 13, 738. [Google Scholar] [CrossRef]
- Suzuki, Y.; Okamoto, H.; Takahashi, M.; Kataoka, T.; Shibata, Y. Mapping the spatial distribution of botanical composition and herbage mass in pastures using hyperspectral imaging. Grassl. Sci. 2012, 58, 1–7. [Google Scholar] [CrossRef]
- Yu, H.; Kong, B.; Wang, G.; Sun, H.; Wang, L. Hyperspectral database prediction of ecological characteristics for grass species of alpine grasslands. Rangel. J. 2018, 40, 19–29. [Google Scholar] [CrossRef]
- Bonesmo, H.; Kaspersen, K.; Bakken, A.K. Evaluating an image analysis system for mapping white clover pastures. Acta Agric. Scand. Sect.-Soil Plant Sci. 2004, 54, 76–82. [Google Scholar] [CrossRef]
- Bateman, C.J.; Fourie, J.; Hsiao, J.; Irie, K.; Heslop, A.; Hilditch, A.; Hagedorn, M.; Jessep, B.; Gebbie, S.; Ghamkhar, K. Assessment of Mixed Sward Using Context Sensitive Convolutional Neural Networks. Front. Plant Sci. 2020, 11, 159. [Google Scholar] [CrossRef] [PubMed]
- Skovsen, S.K.; Laursen, M.S.; Kristensen, R.K.; Rasmussen, J.; Dyrmann, M.; Eriksen, J.; Gislum, R.; Jørgensen, R.N.; Karstoft, H. Robust Species Distribution Mapping of Crop Mixtures Using Color Images and Convolutional Neural Networks. Sensors 2020, 21, 175. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Liang, N.; Zuo, Z.; Parsons, D.; Morel, J.; Shi, J.; Wang, Z.; Luo, L.; Zhao, L.; Fang, H.; et al. Estimation of Botanical Composition in Mixed Clover–Grass Fields Using Machine Learning-Based Image Analysis. Front. Plant Sci. 2021, 12, 622429. [Google Scholar] [CrossRef]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7. [Google Scholar] [CrossRef] [PubMed]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 13536971. [Google Scholar] [CrossRef]
- Oldeland, J.; Wesuls, D.; Jürgens, N. RLQ and fourth-corner analysis of plant species traits and spectral indices derived from HyMap and CHRIS-PROBA imagery. Int. J. Remote Sens. 2012, 33, 6459–6479. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 11 October 2021).
- Yu, H.; Samuels, D.C.; yong Zhao, Y.; Guo, Y. Architectures and accuracy of artificial neural network for disease classification from omics data. BMC Genom. 2019, 20, 167. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Al-Sarayreh, M.; Irie, K.; Hackell, D.; Bourdot, G.; Reis, M.M.; Ghamkhar, K. Identification of Weeds Based on Hyperspectral Imaging and Machine Learning. Front. Plant Sci. 2021, 11, 611622. [Google Scholar] [CrossRef] [PubMed]
- von Bueren, S.K.; Burkart, A.; Hueni, A.; Rascher, U.; Tuohy, M.P.; Yule, I.J. Deploying four optical UAV-based sensors over grassland: Challenges and limitations. Biogeosciences 2015, 12, 163–175. [Google Scholar] [CrossRef]
- Mortensen, A.K.; Karstoft, H.; Søegaard, K.; Gislum, R.; Jørgensen, R.N. Preliminary Results of Clover and Grass Coverage and Total Dry Matter Estimation in Clover-Grass Crops Using Image Analysis. J. Imaging 2017, 3, 59. [Google Scholar] [CrossRef]
- Dao, P.D.; He, Y.; Lu, B. Maximizing the quantitative utility of airborne hyperspectral imagery for studying plant physiology: An optimal sensor exposure setting procedure and empirical line method for atmospheric correction. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 140–150. [Google Scholar] [CrossRef]
- Locher, F.; Heuwinkel, H.; Gutser, R.; Schmidhalter, U. Development of Near Infrared Reflectance Spectroscopy Calibrations to Estimate Legume Content of Multispecies Legume-Grass Mixtures. Agron. J. 2005, 97, 11–17. [Google Scholar] [CrossRef][Green Version]
- Demetriades-Shah, T.H.; Steven, M.D.; Clark, J.A. High resolution derivative spectra in remote sensing. Remote Sens. Environ. 1990, 33, 55–64. [Google Scholar] [CrossRef]
- Moore, K.J.; Moser, L.E.; Vogel, K.P.; Waller, S.S.; Johnson, B.E.; Pedersen, J.F. Describing and Quantifying Growth Stages of Perennial Forage Grasses. Agron. J. 1991, 83, 1073–1077. [Google Scholar] [CrossRef]
- Sekachev, B.; Manovich, N.; Zhiltsov, M.; Zhavoronkov, A.; Kalinin, D.; Hoff, B.; TOsmanov; Kruchinin, D.; Zankevich, A.; DmitriySidnev; et al. opencv/cvat: v1.1.0. 2020. Available online: https://zenodo.org/record/4009388#.Yhwz-pYRVPY (accessed on 12 December 2021). [CrossRef]
- Todorov, V. rrcov: Scalable Robust Estimators with High Breakdown Point; R Package Version 1.5–5; 2020. Available online: https://cran.r-project.org/ (accessed on 12 December 2021).
- Müllner, D. fastcluster: Fast Hierarchical, Agglomerative Clustering Routines for R and Python. J. Stat. Softw. 2013, 53, 1–18. [Google Scholar] [CrossRef]
- Borchers, H.W. Pracma: Practical Numerical Math Functions; R Package Version 2.3.3. 2021. Available online: https://cran.r-project.org/ (accessed on 12 December 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Dowle, M.; Srinivasan, A. Data.Table: Extension of ‘Data.Frame’; R Package Version 1.14.0. 2021. Available online: https://cran.r-project.org/ (accessed on 12 December 2021).
- Wickham, H. Dtplyr: Data Table Back-End for ‘Dplyr’, R Package Version 1.1.0. 2021. Available online: https://cran.r-project.org/ (accessed on 12 December 2021).
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- de Mendiburu, F. Agricolae: Statistical Procedures for Agricultural Research; R Package Version 1-3.5. 2021. Available online: https://cran.r-project.org/ (accessed on 12 December 2021).
- Liaw, R.; Liang, E.; Nishihara, R.; Moritz, P.; Gonzalez, J.E.; Stoica, I. Tune: A Research Platform for Distributed Model Selection and Training. arXiv 2018, arXiv:1807.05118. [Google Scholar]
- Moritz, P.; Nishihara, R.; Wang, S.; Tumanov, A.; Liaw, R.; Liang, E.; Elibol, M.; Yang, Z.; Paul, W.; Jordan, M.I.; et al. Ray: A Distributed Framework for Emerging AI Applications. arXiv 2017, arXiv:1712.05889. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; Dasgupta, S., McAllester, D., Eds.; PMLR: Atlanta, GA, USA, 2013; Volume 28, pp. 115–123. [Google Scholar]
- Wright, M.N.; Ziegler, A. Ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- Mevik, B.H.; Wehrens, R. The pls Package: Principal Component and Partial Least Squares Regression in R. J. Stat. Softw. 2007, 18, 1–23. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002; ISBN 0-387-95457-0. [Google Scholar]
- de Castro, A.I.; Jurado-Expósito, M.; Gómez-Casero, M.T.; López-Granados, F. Applying Neural Networks to Hyperspectral and Multispectral Field Data for Discrimination of Cruciferous Weeds in Winter Crops. Sci. World J. 2012, 2012, 630390. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.L.; Bischl, B. Tunability: Importance of Hyperparameters of Machine Learning Algorithms. J. Mach. Learn. Res. 2019, 20, 1–32. [Google Scholar]
- Wessels, L.; Barnard, E. Avoiding false local minima by proper initialization of connections. IEEE Trans. Neural Netw. 1992, 3, 899–905. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and Biochemical Sources of Variability in Canopy Reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Basinger, N.T.; Jennings, K.M.; Hestir, E.L.; Monks, D.W.; Jordan, D.L.; Everman, W.J. Phenology affects differentiation of crop and weed species using hyperspectral remote sensing. Weed Technol. 2020, 34, 897–908. [Google Scholar] [CrossRef]
- Li, M.; Zang, S.; Zhang, B.; Li, S.; Wu, C. A Review of Remote Sensing Image Classification Techniques: The Role of Spatio-contextual Information. Eur. J. Remote Sens. 2014, 47, 389–411. [Google Scholar] [CrossRef]
- Abbasian, H.; Drummond, C.; Japkowicz, N.; Matwin, S. Robustness of Classifiers to Changing Environments. In Advances in Artificial Intelligence; Farzindar, A., Kešelj, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 232–243. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).