Nightlights and Subnational Economic Activity: Estimating Departmental GDP in Paraguay
Abstract
:1. Introduction
2. Materials and Methods
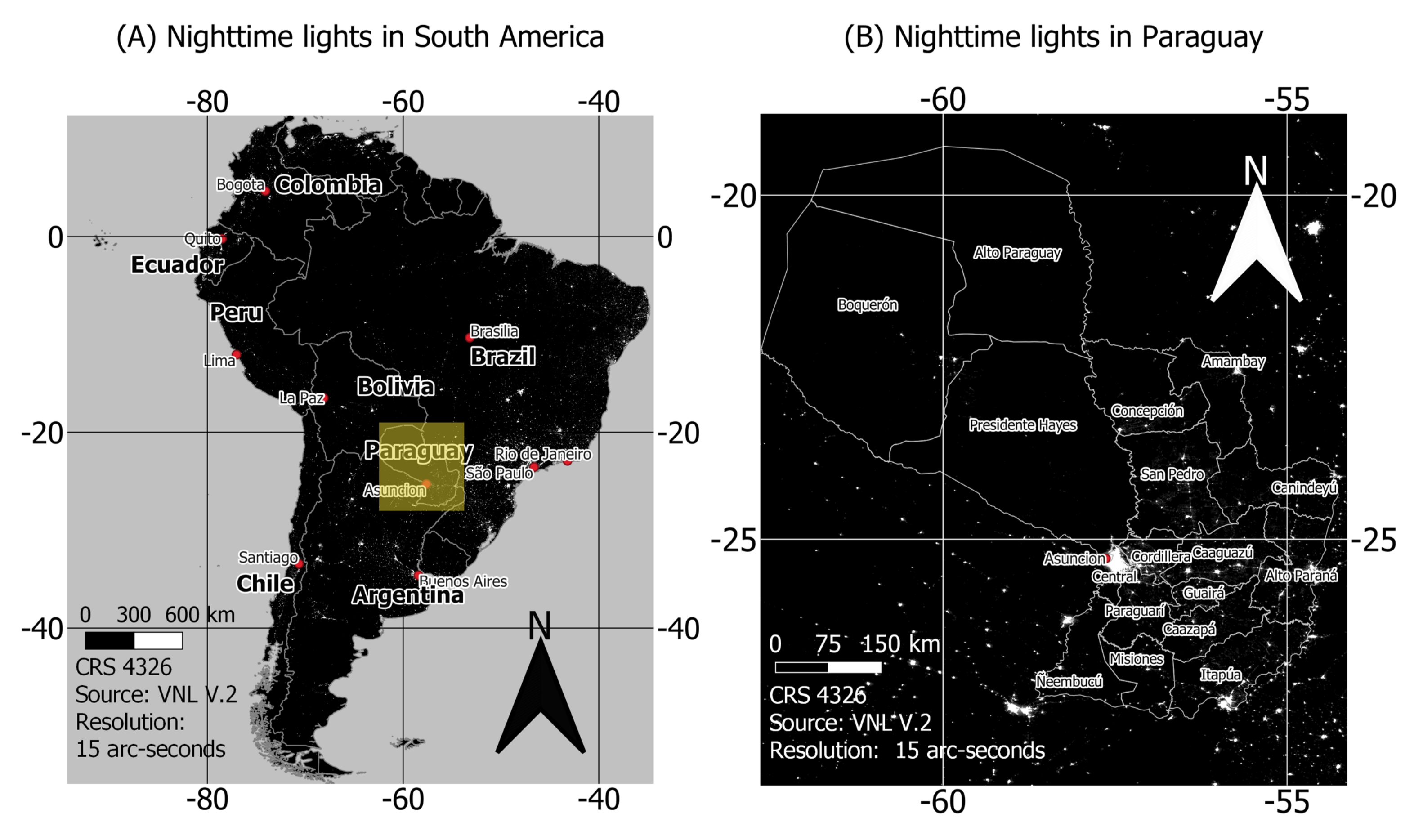
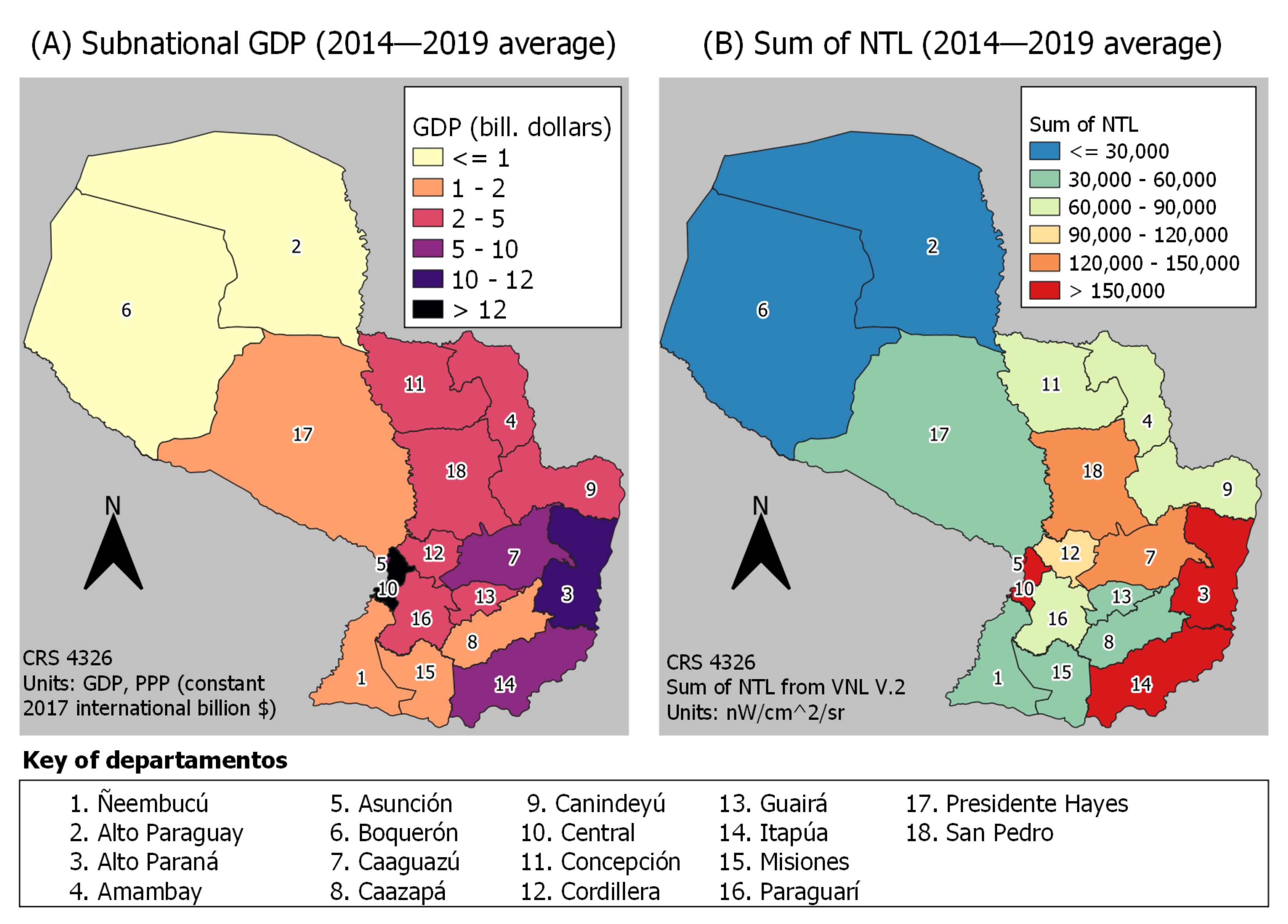
2.1. Study Area
2.2. Data
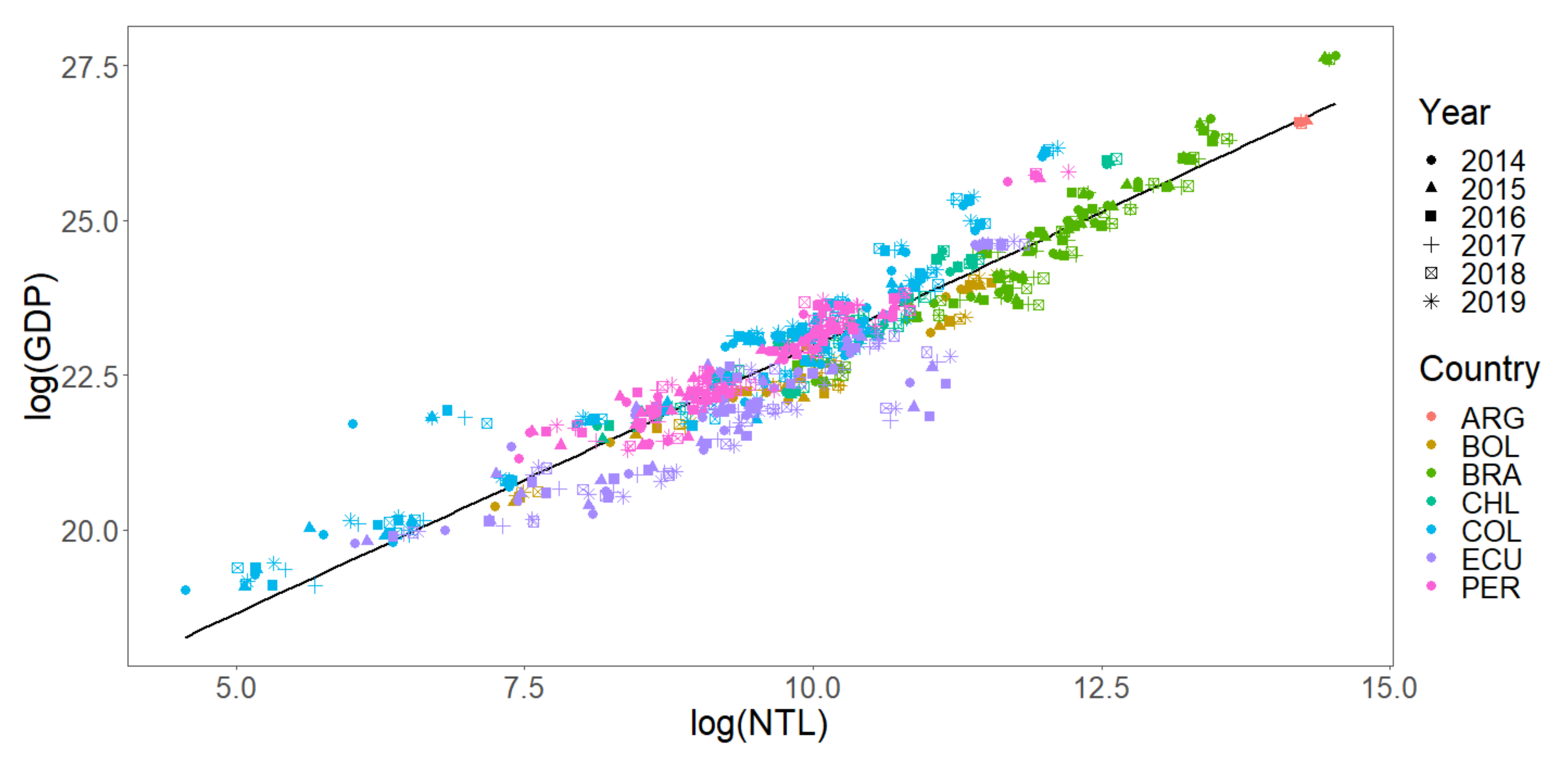
2.3. Empirical Strategy
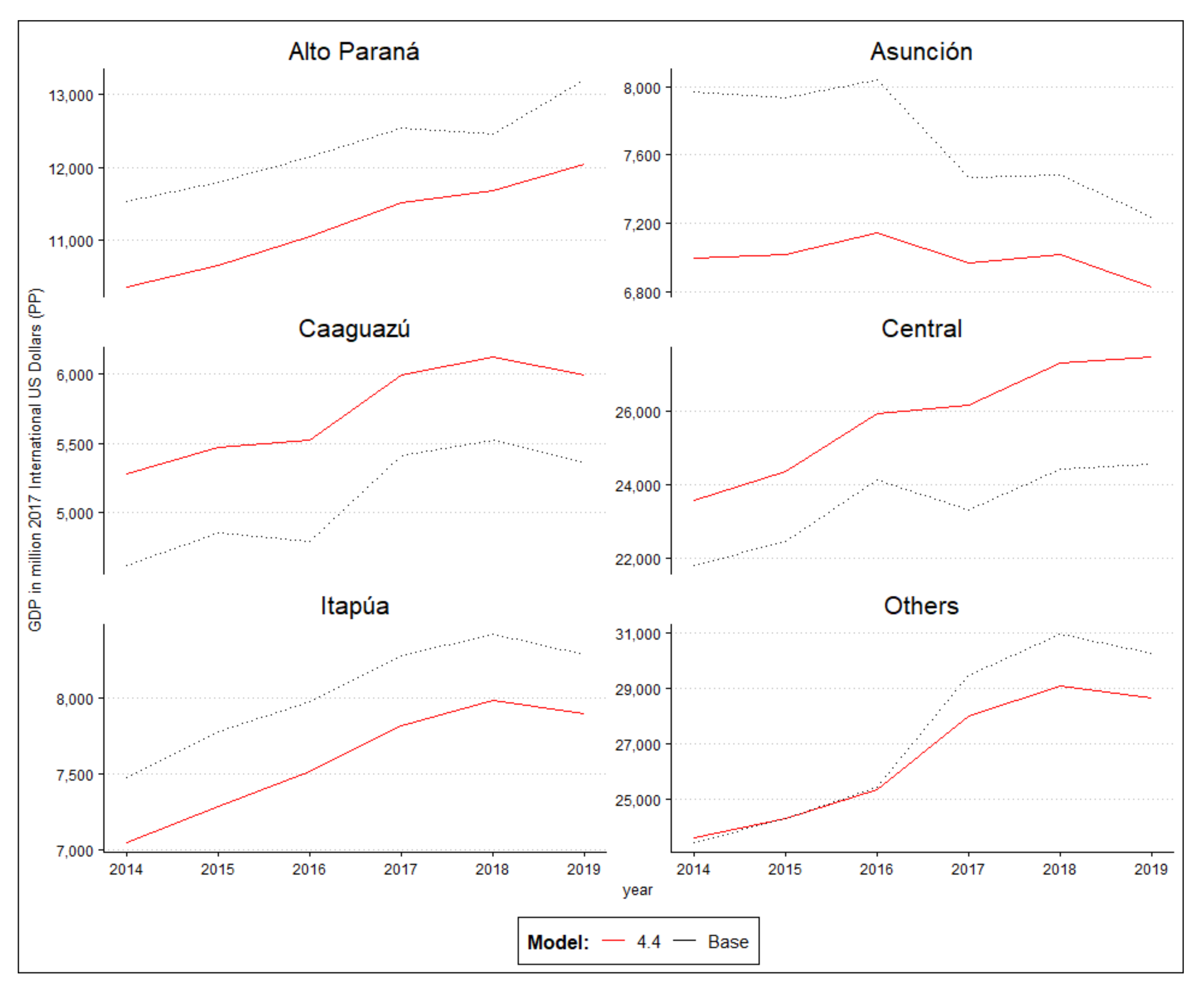
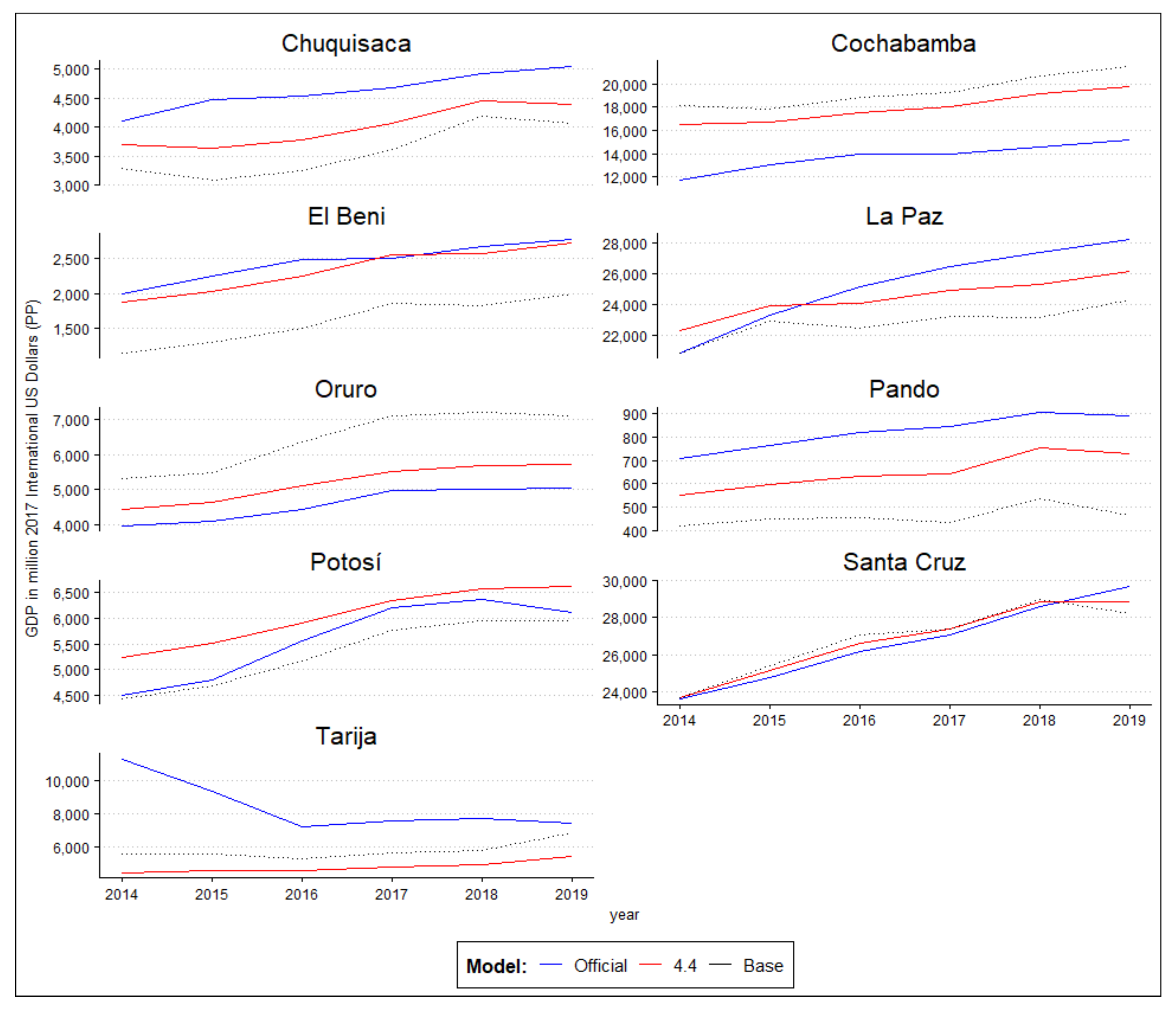
2.4. Out-of-Sample Prediction
3. Results
4. Discussion
Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lenzen, M.; Geschke, A.W.J. Implementing the material footprint to measure progress towards Sustainable Development Goals 8 and 12. Nat. Sustain. 2021. [Google Scholar] [CrossRef]
- Peña-Sánchez, A.R.; Ruiz-Chico, J.; Jiménez-García, M.; López-Sánchez, J.A. Tourism and the SDGs: An Analysis of Economic Growth, Decent Employment, and Gender Equality in the European Union (2009–2018). Sustainability 2020, 12, 5480. [Google Scholar] [CrossRef]
- Liu, S. Interactions between industrial development and environmental protection dimensions of Sustainable Development Goals (SDGs): Evidence from 40 countries with different income levels. Environ.-Socio-Econ. Stud. 2020, 8, 60–66. [Google Scholar] [CrossRef]
- Kynčlová, P.; Upadhyaya, S.; Nice, T. Composite index as a measure on achieving Sustainable Development Goal 9 (SDG-9) industry-related targets: The SDG-9 index. Appl. Energy 2020, 265, 114755. [Google Scholar] [CrossRef]
- Bundervoet, T.; Maiyo, L.; Sanghi, A. Bright Lights, Big Cities: Measuring National and Subnational Economic Growth in Africa from Outer Space, with an Application to Kenya and Rwanda; World Bank Policy Research Working Paper; World Bank: Washington, DC, USA, 2015. [Google Scholar]
- Rangel-Gonzalez, E.; Llamosas-Rosas, I. An Alternative Method to Measure Non-Registered Economic Activity in Mexico Using Satellite Nightlights. 2019. Available online: https://urldefense.proofpoint.com/v2/url?u=https-3A__www.imf.org_-2D_media_Files_Conferences_2019_7th-2Dstatistics-2Dforum_session-2Diii-2Dgonzalez.ashx&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=HZF_zs-aVMZKPZ_P0n0ubz4cB0YKCDtdn1Wbk6NWga0&m=PWwAzqm6DIUKgu9mMAbAUxBcJE_dDR6L3__EsqzSAb4GyLqJ032YT7yMXytIjExc&s=L6CmyrqjtDPX9jtxzWFOfU0aalhAZwGNtbx-WWGZW0g&e= (accessed on 1 July 2021).
- Chen, X.; Nordhaus, W.D. Using luminosity data as a proxy for economic statistics. Proc. Natl. Acad. Sci. USA 2011, 108, 8589–8594. [Google Scholar] [CrossRef] [Green Version]
- Henderson, J.V.; Storeygard, A.; Weil, D.N. Measuring economic growth from outer space. Am. Econ. Rev. 2012, 102, 994–1028. [Google Scholar] [CrossRef] [Green Version]
- Hodler, R.; Raschky, P.A. Regional Favoritism. Q. J. Econ. 2014, 129, 995–1033. [Google Scholar] [CrossRef]
- Bickenbach, F.; Bode, E.; Nunnenkamp, P.; Söder, M. Night lights and regional GDP. Rev. World Econ. 2016, 152, 425–447. [Google Scholar] [CrossRef] [Green Version]
- Gibson, J.; Boe-Gibson, G. Nighttime Lights and County-Level Economic Activity in the United States: 2001 to 2019. Remote Sens. 2021, 13, 2741. [Google Scholar] [CrossRef]
- Chen, X.; Nordhaus, W. A test of the new VIIRS lights data set: Population and economic output in Africa. Remote Sens. 2015, 7, 4937–4947. [Google Scholar] [CrossRef] [Green Version]
- Gibson, J.; Olivia, S.; Boe-Gibson, G. Night lights in economics: Sources and uses. J. Econ. Surv. 2020, 34, 955–980. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Zhizhin, M.; Hsu, F.C. Why VIIRS data are superior to DMSP for mapping nighttime lights. Proc.-Asia-Pac. Adv. Netw. 2013, 35, 62. [Google Scholar] [CrossRef] [Green Version]
- Gibson, J.; Olivia, S.; Boe-Gibson, G.; Li, C. Which night lights data should we use in economics, and where? J. Dev. Econ. 2021, 149, 102602. [Google Scholar] [CrossRef]
- Shi, K.; Yu, B.; Huang, Y.; Hu, Y.; Yin, B.; Chen, Z.; Chen, L.; Wu, J. Evaluating the ability of NPP-VIIRS nighttime light data to estimate the gross domestic product and the electric power consumption of China at multiple scales: A comparison with DMSP-OLS data. Remote Sens. 2014, 6, 1705–1724. [Google Scholar] [CrossRef] [Green Version]
- Gibson, J. Better night lights data, for longer. Oxf. Bull. Econ. Stat. 2021, 83, 770–791. [Google Scholar] [CrossRef]
- Dai, Z.; Hu, Y.; Zhao, G. The suitability of different nighttime light data for GDP estimation at different spatial scales and regional levels. Sustainability 2017, 9, 305. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Nordhaus, W.D. VIIRS nighttime lights in the estimation of cross-sectional and time-series GDP. Remote Sens. 2019, 11, 1057. [Google Scholar] [CrossRef] [Green Version]
- Andreano, M.S.; Benedetti, R.; Piersimoni, F.; Savio, G. Mapping Poverty of Latin American and Caribbean Countries from Heaven Through Night-Light Satellite Images. Soc. Indic. Res. Int. Interdiscip. J.-Qual.-Life Meas. 2021, 156, 533–562. [Google Scholar] [CrossRef]
- Instituto Nacional de Estadística (Bolivia). Producto Interno Bruto Departamental. Available online: https://urldefense.proofpoint.com/v2/url?u=https-3A__www.ine.gob.bo_index.php_estadisticas-2Deconomicas_pib-2Dy-2Dcuentas-2Dnacionales_producto-2Dinterno-2Dbruto-2Ddepartamental_producto-2Dinterno-2Dbruto-2Ddepartamental_-231589484093225-2Db57379da-2Db2f6&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=E4H3pBTBVA1l8W9NNr2Vx6et25n3KeIfyPh82yzXuMk&e= (accessed on 1 March 2021).
- Instituto Brasileiro de Geografia e Estatística. Produto Interno Bruto dos Municípios. Available online: https://urldefense.proofpoint.com/v2/url?u=https-3A__www.ibge.gov.br_estatisticas_economicas_contas-2Dnacionais_9088-2Dproduto-2Dinterno-2Dbruto-2Ddos-2Dmunicipios.html-3F-3D-26t-3Dresultados&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=zEc8uS6Rj2qt6bprOC3BSYWaUSJs7-SlTLGeSmKEAnY&e= (accessed on 1 March 2021).
- Banco Central de Chile. Producto Interno Bruto Regional. Available online: https://urldefense.proofpoint.com/v2/url?u=https-3A__si3.bcentral.cl_estadisticas_Principal1_Excel_CCNN_regional_excel.html&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=MayuP-aGdpug4SaemNx5TxnUPyDqqOjn_OKo2YxT6M8&e= (accessed on 1 March 2021).
- Dirección Nacional de Estadística (Colombia). PIB por Departamento. Available online: https://urldefense.proofpoint.com/v2/url?u=https-3A__www.dane.gov.co_index.php_estadisticas-2Dpor-2Dtema_cuentas-2Dnacionales_cuentas-2Dnacionales-2Ddepartamentales&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=EbP0tikaQ_5u6kTRPpgCuYtvPFTyCbGTo5Ja-773E1s&e= (accessed on 1 March 2021).
- Banco Central del Ecuador. Cuentas Nacionales Regionales. Available online: https://urldefense.proofpoint.com/v2/url?u=https-3A__contenido.bce.fin.ec_documentos_Estadisticas_SectorReal_CuentasProvinciales_Indice.htm&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=iLNaJkSnq6BVMfOdIB58ZP4V-tbZfIImZv5Q0y5tIko&e= (accessed on 1 March 2021).
- Instituto Nacional de Estadística e Informática (Perú). Producto Bruto Interno por Departamentos (Cifras Preliminares). Available online: https://urldefense.proofpoint.com/v2/url?u=https-3A__www.inei.gob.pe_estadisticas_indice-2Dtematico_producto-2Dbruto-2Dinterno-2Dpor-2Ddepartamentos-2D9089_&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=nYm7-FChipHZVrZrbR_iR6ZDcK_NI7qZZnsNceiK4hE&e= (accessed on 1 March 2021).
- Dirección Provincial de Estadística (Buenos Aires, Argentina). Producto Bruto Geografico—Provincia de Buenos Airea-Año 2018 y Serie 2004–2018. Base 2004. Available online: https://urldefense.proofpoint.com/v2/url?u=http-3A__www.estadistica.ec.gba.gov.ar_dpe_index.php_prensa2018_513-2Dpbg-2D2018&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=SS6uLjNrvM00S_AbXbVPr5kVfW5vNgPUwlevn5Stto0&e= (accessed on 1 March 2021).
- Earth Observation Group. Annual VNL V2. Available online: https://urldefense.proofpoint.com/v2/url?u=https-3A__eogdata.mines.edu_products_vnl_&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=4h_UB5Vr0nCzl-srRahNzjnTo1V2i3fp-eY9C1M_21k&e= (accessed on 25 June 2021).
- Elvidge, C.D.; Zhizhin, M.; Ghosh, T.; Hsu, F.C.; Taneja, J. Annual time series of global VIIRS nighttime lights derived from monthly averages: 2012 to 2019. Remote Sens. 2021, 13, 922. [Google Scholar] [CrossRef]
- WorldPop—School of Geography and Environmental Science, University of Southampton; Department of Geography and Geosciences, University of Louisville; Departement de Geographie, Universite de Namur) and Center for International Earth Science Information Network (CIESIN), Columbia University. Global High Resolution Population Denominators Project—Funded by The Bill and Melinda Gates Foundation (OPP1134076). 2018. Available online: https://urldefense.proofpoint.com/v2/url?u=http-3A__www.worldpop.org&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=Npvvoxj00rmBkqe5wcp327U4641JFV1rLztPhojtpLQ&e= (accessed on 25 June 2021).
- Database of Global Administrative Boundaries (GADM) Version 3.6. 2018. Available online: https://urldefense.proofpoint.com/v2/url?u=http-3A__www.gadm.org&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=CLYS64gqYBnjI2ZUN3VbprAA3HVfocnyt_Xn9SqAWbU&e= (accessed on 25 June 2021).
- Lessmann, C.; Seidel, A. Regional inequality, convergence, and its determinants—A view from outer space. Eur. Econ. Rev. 2017, 92, 110–132. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Yao, J. Illuminating economic growth. J. Econ. 2021. [Google Scholar] [CrossRef]
- Martinez, L.R. How Much Should We Trust the Dictator’s GDP Growth Estimates; Becker Friedman Institute for Economics Working Paper 2021-78; University of Chicago: Chicago, IL, USA, 2021. [Google Scholar]
- Haddad, E.; Perobelli, F.; Castro, G.; Araújo, I.; Ramirez-Alvarez, P.E.; Fernandes, R. Tool Kits in Multi-Regional and Multi-Sectoral General Equilibrium Modeling for Paraguay; Technical Report; Núcleo de Economia Regional e Urbana da Universidade de São Paulo (NEREUS): São Paulo, Brazil, 2021. [Google Scholar]
- World Bank. GDP Growth (Annual %)—Paraguay. Available online: https://urldefense.proofpoint.com/v2/url?u=https-3A__data.worldbank.org_indicator_NY.GDP.MKTP.KD.ZG-3Flocations-3DPY_&d=DwIGAw&c=-35OiAkTchMrZOngvJPOeA&r=PIf8F-g-Zjd8VnENokL6gg&m=bzB_ZWonfTu_eRX7j8_K06pySrZt4zSW46DERrsUXrgo6UIANlbF1ziJhBHHW6jf&s=Uz62gYOqjg4_NBxJIM2baYfQmuHDHBW6KxVwu0h6uHQ&e= (accessed on 12 December 2021).
| # | Indicator |
|---|---|
| 1.5.2 | Direct economic loss attributed to disasters in relation to global gross domestic product (GDP) |
| 7.3.1 | Energy intensity measured in terms of primary energy and GDP |
| 8.1.1 | Annual growth rate of real GDP per capita |
| 8.2.1 | Annual growth rate of real GDP per employed person |
| 8.4.1/12.2.1 | Material footprint, material footprint per capita, and material footprint per GDP |
| 8.4.2 | Domestic material consumption, domestic material consumption per capita, and domestic material consumption per GDP |
| 8.9.1 | Tourism direct GDP as a proportion of total GDP and in growth rate |
| 9.2.1 | Manufacturing value added as a proportion of GDP and per capita |
| 9.4.1 | CO2 emission per unit of value added |
| 9.5.1 | Research and development expenditure as a proportion of GDP |
| 10.4.1 | Labor share of GDP |
| 11.5.2 | Direct economic loss in relation to global GDP, damage to critical infrastructure and number of disruptions to basic services, attributed to disasters |
| 12.2.2 | Domestic material consumption, domestic material consumption per capita, and domestic material consumption per GDP |
| 12.c.1 | Amount of fossil fuel subsidies (production and consumption) per unit of GDP |
| 14.7.1 | Sustainable fisheries as a proportion of GDP in small island developing States, least developed countries and all countries |
| 17.1.1 | Total government revenue as a proportion of GDP, by source |
| 17.3.2 | Volume of remittances (in United States dollars) as a proportion of total GDP |
| 17.13.1 | Macroeconomic Dashboard |
| ARG | BOL | BRA | CHL | COL | ECU | PRY | PER | |
|---|---|---|---|---|---|---|---|---|
| Av. GDP | 353.85 | 10.24 | 113.66 | 27.26 | 21.57 | 7.56 | NA | 13.76 |
| [5.03] | [9.27] | [190.09] | [44.69] | [40.87] | [12.82] | NA | [27.46] | |
| Av. log(NTL) | 11.54 | 9.95 | 12.11 | 10.34 | 9.27 | 9.32 | 9.41 | 9.52 |
| [0.86] | [1.27] | [1.06] | [1.04] | [1.84] | [1.31] | [1.08] | [0.94] | |
| Regions | 1 * | 9 | 27 | 16 | 32 | 24 | 18 | 26 |
| (3.1) | (3.2) | (3.3) | (3.4) | (3.5) | |
|---|---|---|---|---|---|
| log(NTL) | *** | *** | *** | *** | *** |
| log(NTL) | *** | ||||
| Observations | 761 | 761 | 761 | 761 | 761 |
| Country Random Effects | N | N | Y | N | Y |
| Admin-1 Random Effects | N | N | N | Y | Y |
| (4.1) | (4.2) | (4.3) | (4.4) | (4.5) | (4.6) | |
|---|---|---|---|---|---|---|
| log(NTL) | *** | *** | *** | *** | *** | *** |
| log(Pop) | *** | *** | *** | *** | *** | *** |
| log(CountryGDP) | *** | *** | *** | |||
| log(CountryArea) | *** | *** | *** | |||
| log(NumberRegions) | * | *** | *** | |||
| Observations | 761 | 761 | 761 | 761 | 761 | 761 |
| Country Random Effects | N | N | N | Y | N | Y |
| Admin-1 Random Effects | N | N | N | N | Y | Y |
| Country | (3.1) | (3.2) | (3.3) | (3.4) | (3.5) | (4.1) | (4.2) | (4.3) | (4.4) | (4.5) | (4.6) | Base |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bolivia | 25.0 | 23.9 | 24.5 | 67.6 | 68.8 | 19.5 | 19.6 | 19.3 | 19.9 | 18.8 | 18.6 | 24.5 |
| Brazil | 72.3 | 24.7 | 71.1 | 149.8 | 148.9 | 48.9 | 52.2 | 53.2 | 51.6 | 59.4 | 58.4 | 51.4 |
| Chile | 60.2 | 43.2 | 54.9 | 140.8 | 142.0 | 28.0 | 28.1 | 27.1 | 26.8 | 30.4 | 30.1 | 37.8 |
| Colombia | 96.8 | 92.5 | 94.4 | 136.0 | 151.9 | 69.0 | 70.3 | 67.5 | 64.8 | 66.7 | 62.3 | 85.9 |
| Ecuador | 84.6 | 80.8 | 78.8 | 138.4 | 140.9 | 43.0 | 42.3 | 37.2 | 36.5 | 42.4 | 42.0 | 72.3 |
| Peru | 95.3 | 81.0 | 90.6 | 183.3 | 183.9 | 52.3 | 55.1 | 46.0 | 46.9 | 51.9 | 49.8 | 70.8 |
| Average | 72.4 | 57.7 | 69.1 | 136.0 | 139.4 | 43.5 | 44.6 | 41.7 | 41.1 | 44.9 | 43.5 | 57.1 |
| Departamento | (3.1) | (3.2) | (3.3) | (3.4) | (3.5) | (4.1) | (4.2) | (4.3) | (4.4) | (4.5) | (4.6) | Base | IIOAS |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alto Pry. | 0.3 | 0.4 | 0.3 | 2.6 | 2.7 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 |
| Alto Paraná | 14.0 | 13.9 | 14.2 | 7.9 | 7.8 | 13.3 | 13.2 | 13.2 | 13.5 | 12.3 | 12.5 | 15.0 | 16.5 |
| Amambay | 3.2 | 3.2 | 3.1 | 5.2 | 5.2 | 2.5 | 2.5 | 2.4 | 2.4 | 2.4 | 2.4 | 2.8 | 1.8 |
| Asunción | 10.1 | 9.9 | 10.2 | 7.2 | 7.2 | 9.0 | 9.1 | 9.0 | 9.1 | 8.4 | 8.5 | 10.4 | 18.6 |
| Boquerón | 1.4 | 1.5 | 1.3 | 4.0 | 4.1 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 1.1 | 2.2 |
| Caaguazú | 6.3 | 6.1 | 6.3 | 6.3 | 6.3 | 7.0 | 7.0 | 7.0 | 6.9 | 7.5 | 7.5 | 6.0 | 5.1 |
| Caazapá | 2.0 | 2.1 | 1.9 | 4.5 | 4.6 | 2.0 | 2.0 | 2.0 | 1.9 | 2.4 | 2.3 | 1.6 | 1.4 |
| Canindeyú | 3.2 | 3.1 | 3.1 | 5.1 | 5.2 | 2.9 | 2.9 | 2.9 | 2.8 | 3.1 | 3.0 | 2.7 | 3.0 |
| Central | 24.2 | 25.3 | 25.2 | 9.3 | 9.1 | 30.0 | 29.6 | 30.3 | 30.6 | 29.4 | 30.2 | 28.4 | 31.3 |
| Concepción | 3.4 | 3.3 | 3.3 | 5.2 | 5.3 | 3.1 | 3.2 | 3.1 | 3.0 | 3.3 | 3.2 | 2.9 | 1.6 |
| Cordillera | 4.5 | 4.4 | 4.4 | 5.7 | 5.7 | 4.1 | 4.1 | 4.1 | 4.0 | 4.2 | 4.1 | 4.1 | 1.7 |
| Guairá | 3.0 | 3.0 | 2.9 | 5.1 | 5.1 | 2.8 | 2.8 | 2.8 | 2.7 | 3.0 | 2.9 | 2.5 | 1.7 |
| Itapúa | 9.6 | 9.4 | 9.6 | 7.1 | 7.0 | 9.1 | 9.1 | 9.1 | 9.2 | 8.8 | 8.9 | 9.7 | 7.0 |
| Misiones | 2.7 | 2.6 | 2.6 | 4.9 | 4.9 | 1.9 | 1.9 | 1.9 | 1.8 | 1.8 | 1.8 | 2.2 | 0.9 |
| Ñeembucú | 1.7 | 1.8 | 1.6 | 4.3 | 4.4 | 1.2 | 1.3 | 1.2 | 1.2 | 1.3 | 1.2 | 1.4 | 1.0 |
| Paraguarí | 3.0 | 2.9 | 2.9 | 5.0 | 5.1 | 3.0 | 3.1 | 3.0 | 2.9 | 3.4 | 3.3 | 2.5 | 1.5 |
| Pte. Hayes | 1.9 | 1.9 | 1.8 | 4.4 | 4.5 | 1.5 | 1.6 | 1.5 | 1.5 | 1.7 | 1.6 | 1.5 | 1.8 |
| San Pedro | 5.4 | 5.2 | 5.3 | 6.0 | 6.0 | 5.5 | 5.5 | 5.5 | 5.4 | 5.8 | 5.7 | 5.0 | 2.4 |
| Deviation * | 3.0 | 2.9 | 2.9 | 6.7 | 6.8 | 2.7 | 2.8 | 2.8 | 2.7 | 3.0 | 2.9 | 2.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McCord, G.C.; Rodriguez-Heredia, M. Nightlights and Subnational Economic Activity: Estimating Departmental GDP in Paraguay. Remote Sens. 2022, 14, 1150. https://doi.org/10.3390/rs14051150
McCord GC, Rodriguez-Heredia M. Nightlights and Subnational Economic Activity: Estimating Departmental GDP in Paraguay. Remote Sensing. 2022; 14(5):1150. https://doi.org/10.3390/rs14051150
Chicago/Turabian StyleMcCord, Gordon Carlos, and Mario Rodriguez-Heredia. 2022. "Nightlights and Subnational Economic Activity: Estimating Departmental GDP in Paraguay" Remote Sensing 14, no. 5: 1150. https://doi.org/10.3390/rs14051150
APA StyleMcCord, G. C., & Rodriguez-Heredia, M. (2022). Nightlights and Subnational Economic Activity: Estimating Departmental GDP in Paraguay. Remote Sensing, 14(5), 1150. https://doi.org/10.3390/rs14051150







