Polarization Estimation with a Single Vector Sensor for Radar Detection
Abstract
:1. Introduction
1.1. Summary of Relevant Literature
- 1.
- Nehorai and Paldi [28,29] first introduced a six-dimensional vector sensor and proposed a direction estimation method based on the vector cross-product, and then deduced mean-square angular error and covariance of vector angular error as performance measures. Subsequently, Reference [30] analyzed parameter estimation of a single incident wave in active/passive mode, and then characterized the best possible accuracy of unbiased estimators using the Cramér–Rao bound. References [31,32,33] analyzed the identifiability, uniqueness, and beamformer in vector sensors, respectively. References [34,35] focused on parameter estimation of partially polarized incident waves, which does not require a priori information about the array system such as sensor positions. References [36,37] estimated the parameters for signals of completely polarized waves and incompletely polarized waves. Reference [38] identified and tracked multiple wideband signals based on Reference [39].
- 2.
- Li and Compton [40] first applied the ESPRIT-based method to a six-dimensional vector sensor, which could achieve angle and polarization parameter estimation. Reference [41] proposed ESPRIT-based method for angle and polarization parameters using crossed dipoles. Based on Reference [41], References [42,43,44] improved the ESPRIT-based method for different situations. Reference [42] proposed an angle-only ESPRIT-based method to simplify computations; Reference [43] changed a uniform linear array to a square array, which can extend the angle estimation to two dimensions; and Reference [44] focused on the coherent signal and combined the ESPRIT algorithm with spatial smoothing techniques using a uniform linear array. Reference [45] proposed a maximum likelihood method for joint DOA and polarization estimation based on manifold separation, and Reference [46] also used maximum likelihood estimation to obtain the angle and polarization parameters of partially polarized waves. Reference [47] compared three estimation methods for polarization parameters with a prior knowledge of direction. Reference [48] proposed an asymptotically statistically efficient method of direction estimation for coherent signals.
- 3.
- Zoltowski and Wong [37] first used the vector cross-product DOA estimator in the ESPRIT-based direction-finding scheme involving multiple vector sensors. References [37,49,50] all analyzed the sparse array to solve the problem of direction ambiguity in parameter estimation. Reference [51] extracted five invariants from the Poynting vector on the basis of Reference [40], thereby simplifying the computation of parameter estimation. Reference [39] decoupled the angle and polarization parameters using a vector sensor in order to reduce the four-dimension spectral search of MUSIC to two dimensions. References [52,53] all used dislocation arrays (i.e., the three dipoles and the three loops were located separately, instead of being collocated in a point-like geometry) to solve the coupling problem of electric field sensors and magnetic field sensors. Reference [54] proposed an optimized root-MUSIC method, which softens the conditions of the previous antenna-array; that is, the number, orientation, or types of antennas could vary from array grid point to array grid point.
1.2. Innovative Points of This Paper
- Compared with References [8,9,11,12,13,14,15,16,17,18,19,20,21,23,24,25], the presented method in this paper only needs the data collected from the range cell under test, and does not resort to secondary data or prior knowledge of the target and interference. Therefore, the presented method can estimate the parameters of interference with variable polarization.
- As for a single vector using a crossed dipole, the received signals contain three signals: jamming interference, target echo, and noise. Due to this, the number of signals is greater than that of the receiving antennas, meaning that the polarization parameters cannot be estimated directly by the ESPRIT-based method [41,42,43,44]. Moreover, References [28,29,30,31,32,33,37,40,41,42,43,49,50,51,52,53,54] all assumed that incoming signals were uncorrelated, and their performance degraded rapidly as the incident signals became highly correlated. However, the presented method can combine the polarization invariant and waveform information to solve the above problem.
- For parameter estimation, we propose the two-dimensional golden selected method (TDGSM) to further optimize estimation with minimum calculation, and to prove that the presented method in this paper is convergent and globally optimal.
1.3. Organizational Framework of This Paper
2. Mathematical Model of a Single Vector Sensor
3. The Polarization Estimation under Synchronization
3.1. Polarization Invariant
3.2. Optimal Polarization of VPA
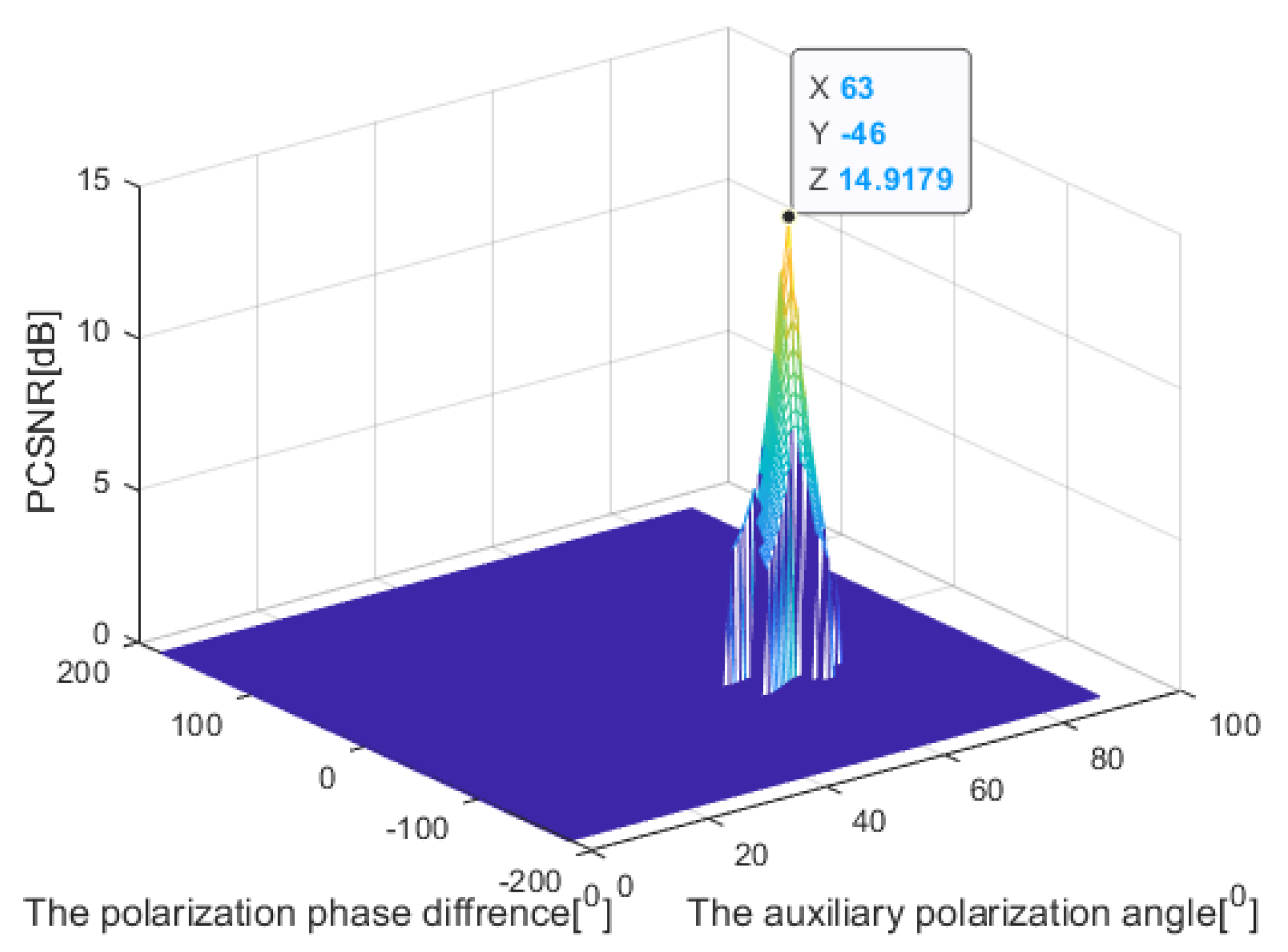
3.3. Two-Dimensional Golden Section Method
- Randomly select a point in the area of D; calculate and .
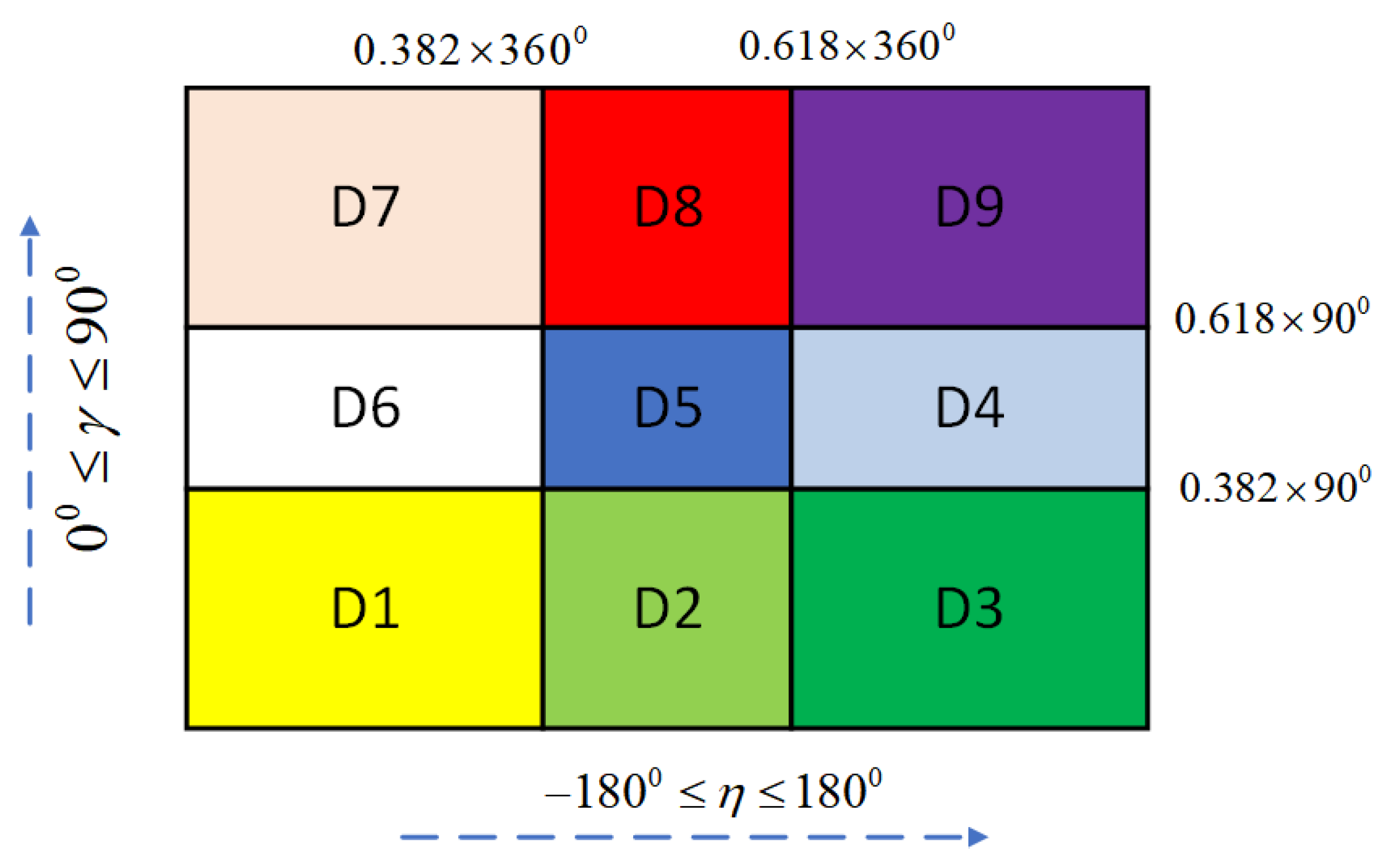
- Let the minimum be and maximum be for the interval, The two golden section points of areLet the minimum be and maximum be for the interval. The two golden section points of areThe area of D is divided into nine areas by , , , and ; i.e., , , as shown in Figure 2. The center of is , the diameter of is , and .
- If where is the required accuracy, stop the calculation and go to Step 6; otherwise, go to Step 4.
- Calculate the PCSNR of nine golden section points. If the maximum of is greater than , i.e., , let and is in the range of , , , go to Step 5; otherwise, go to Step 6.
- Let , return to Step 2.
- The estimated parameter is and the iteration is stopped.
4. Performance Analysis
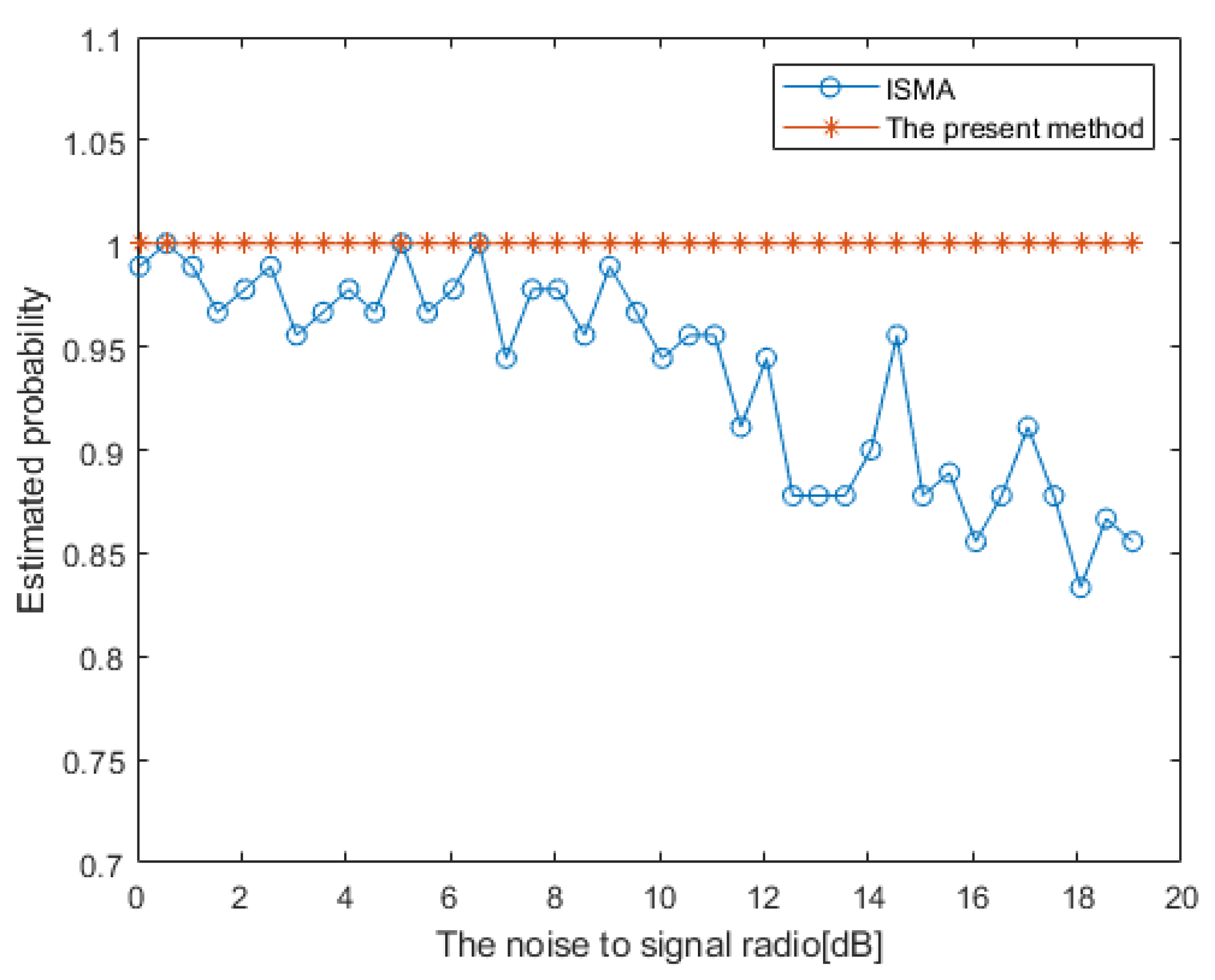
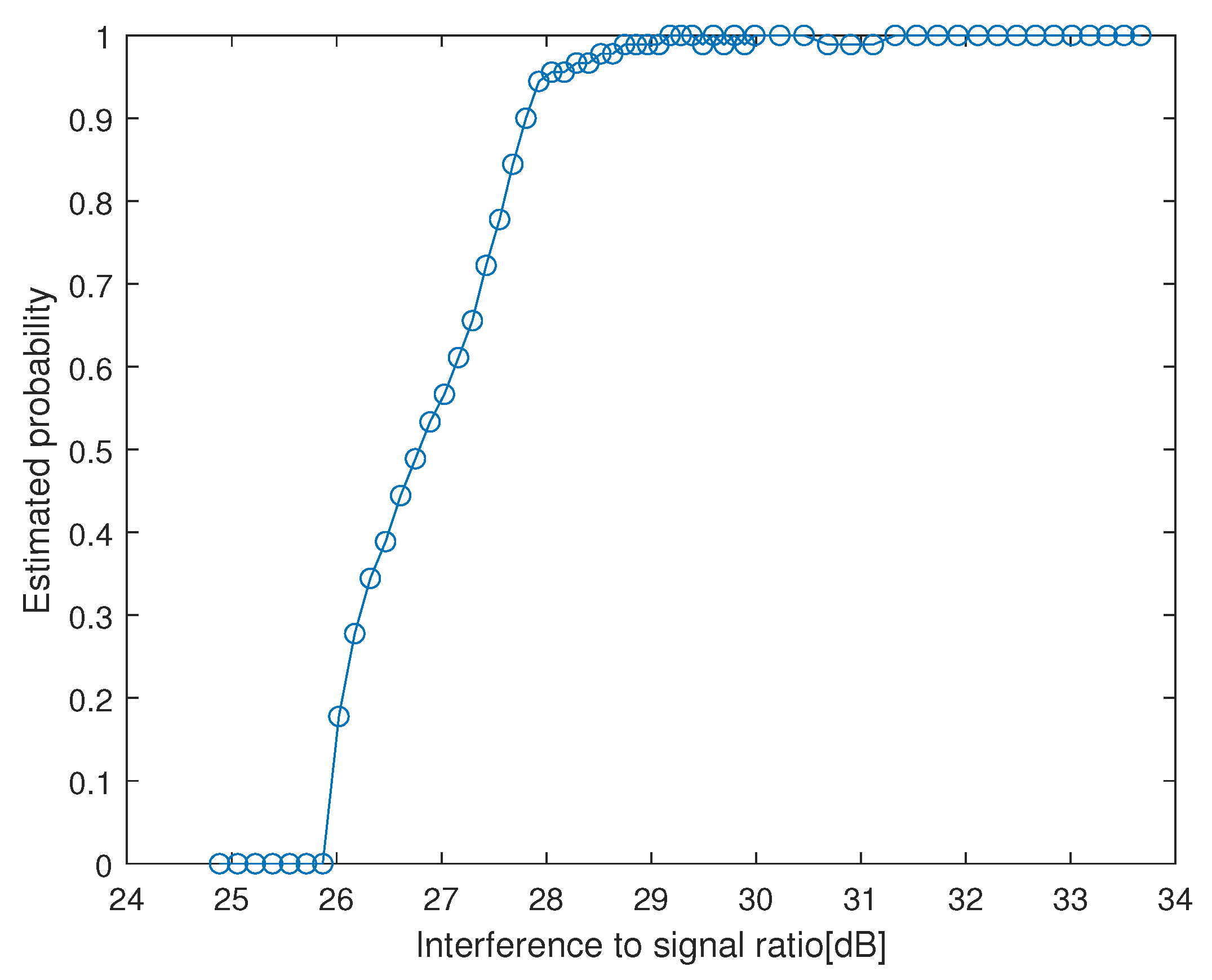
4.1. Robustness Analysis of Different SNRs
4.2. Complexity Analysis
4.3. Applicability Analysis
5. Simulation
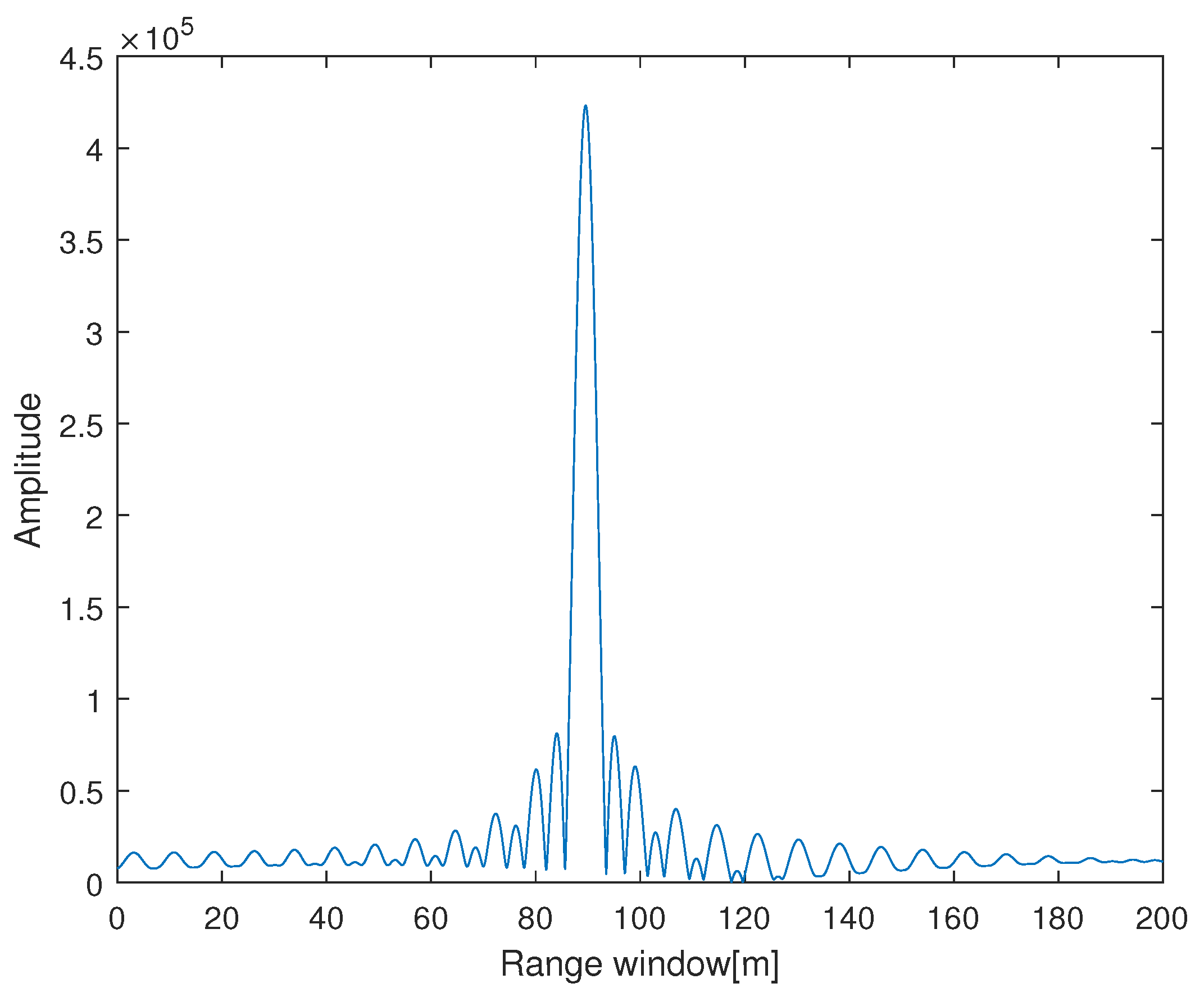
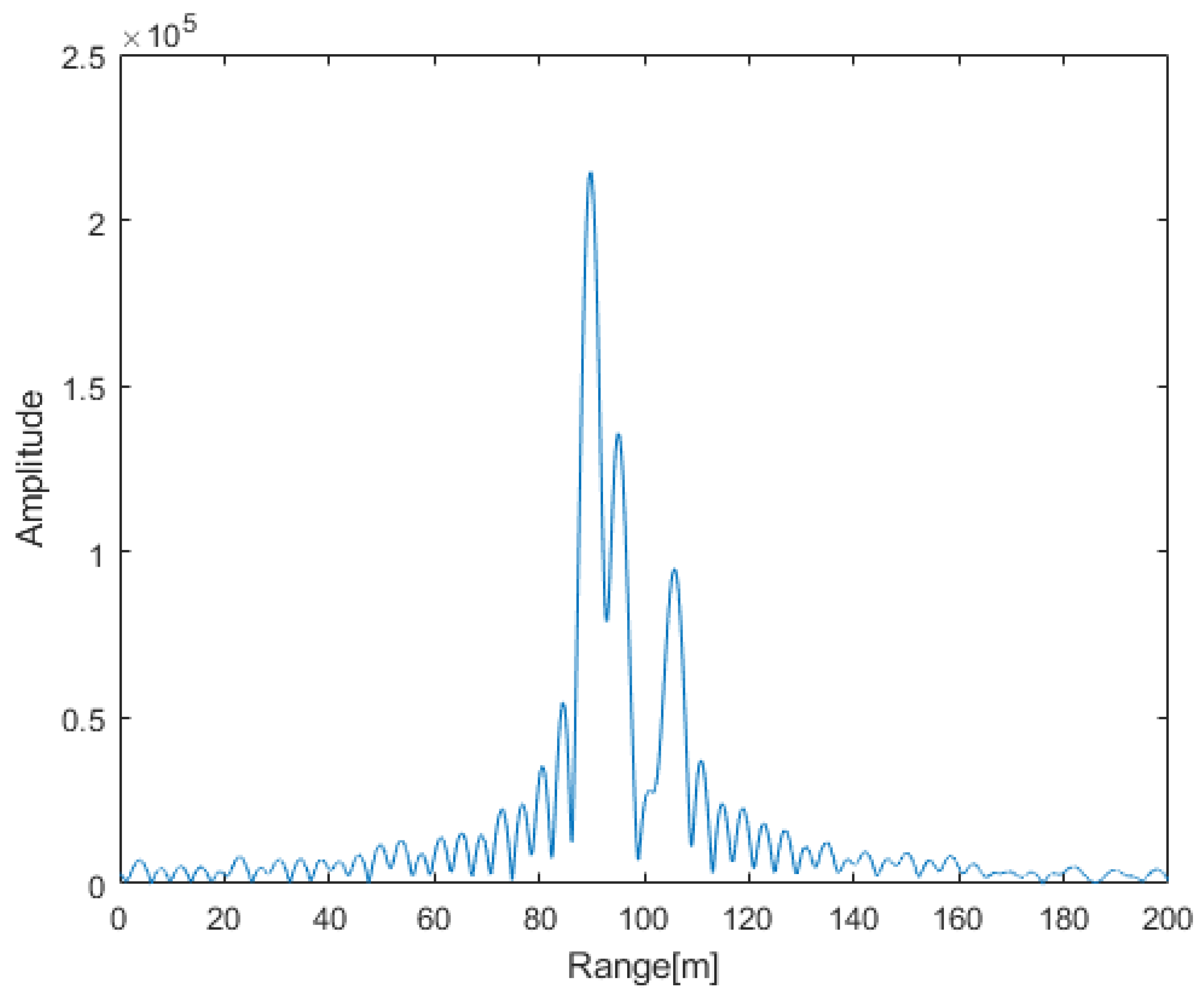
- Radar transmits horizontal polarization and uses a crossed dipole as receiving antenna. Its signal amplitude is , carrier frequency , pulse width , bandwidth , pulse repetition period , and pulse number .
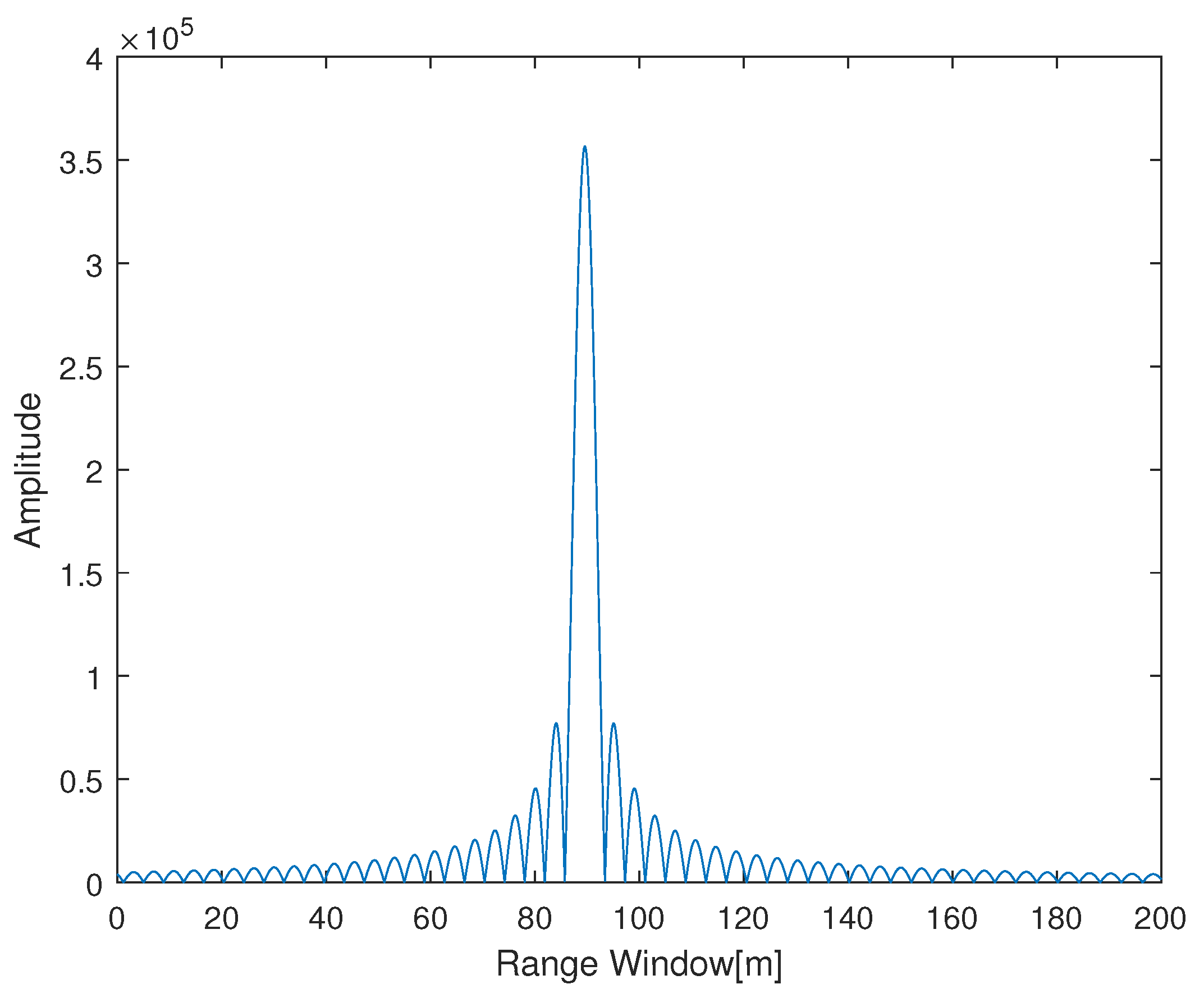
- The distance between the distributed target, the window’s center, and target’s relative RCS are [90 m 2; 95 m 1.2; 105 m, 1]. The speed of light , and the scattering matrix .
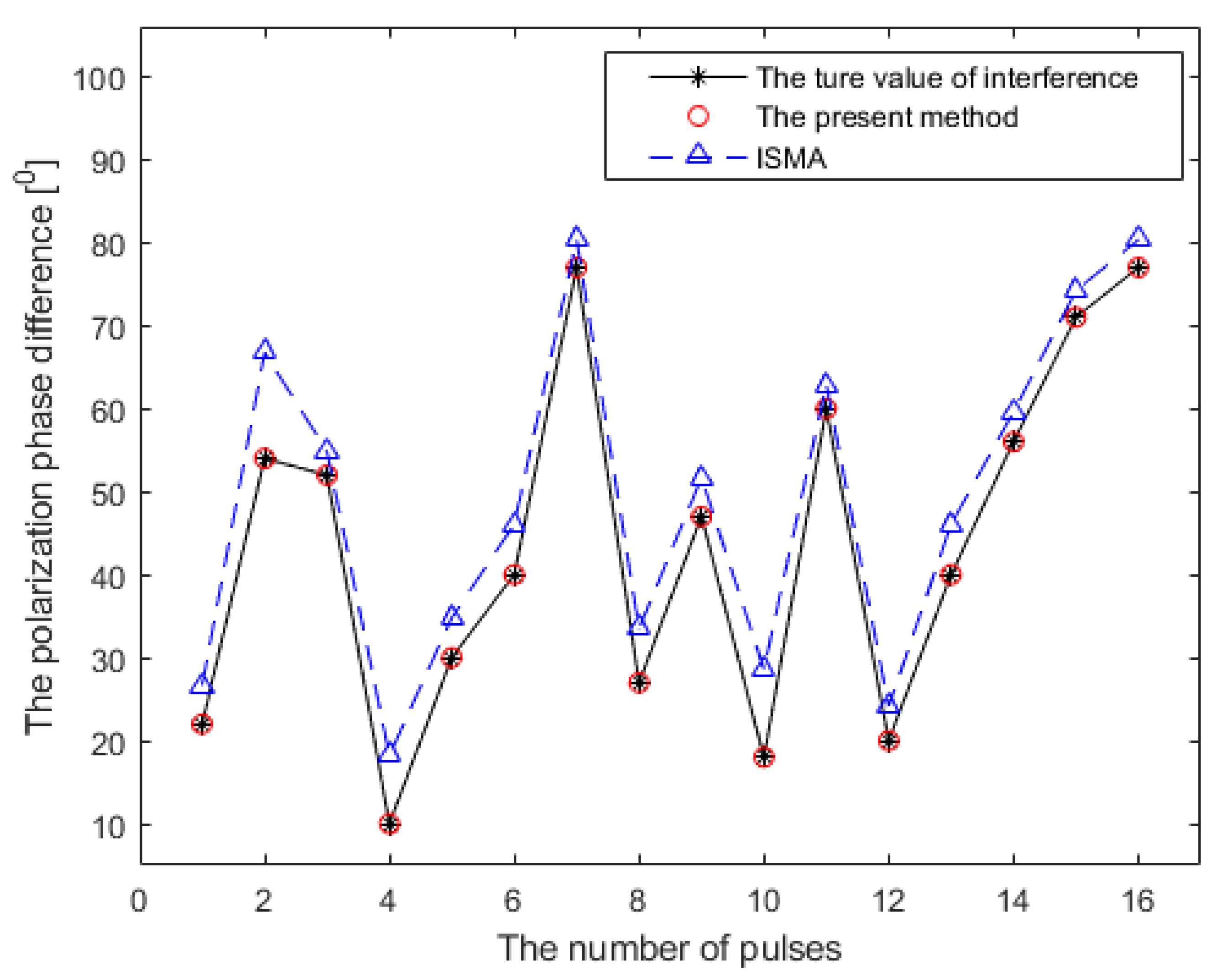
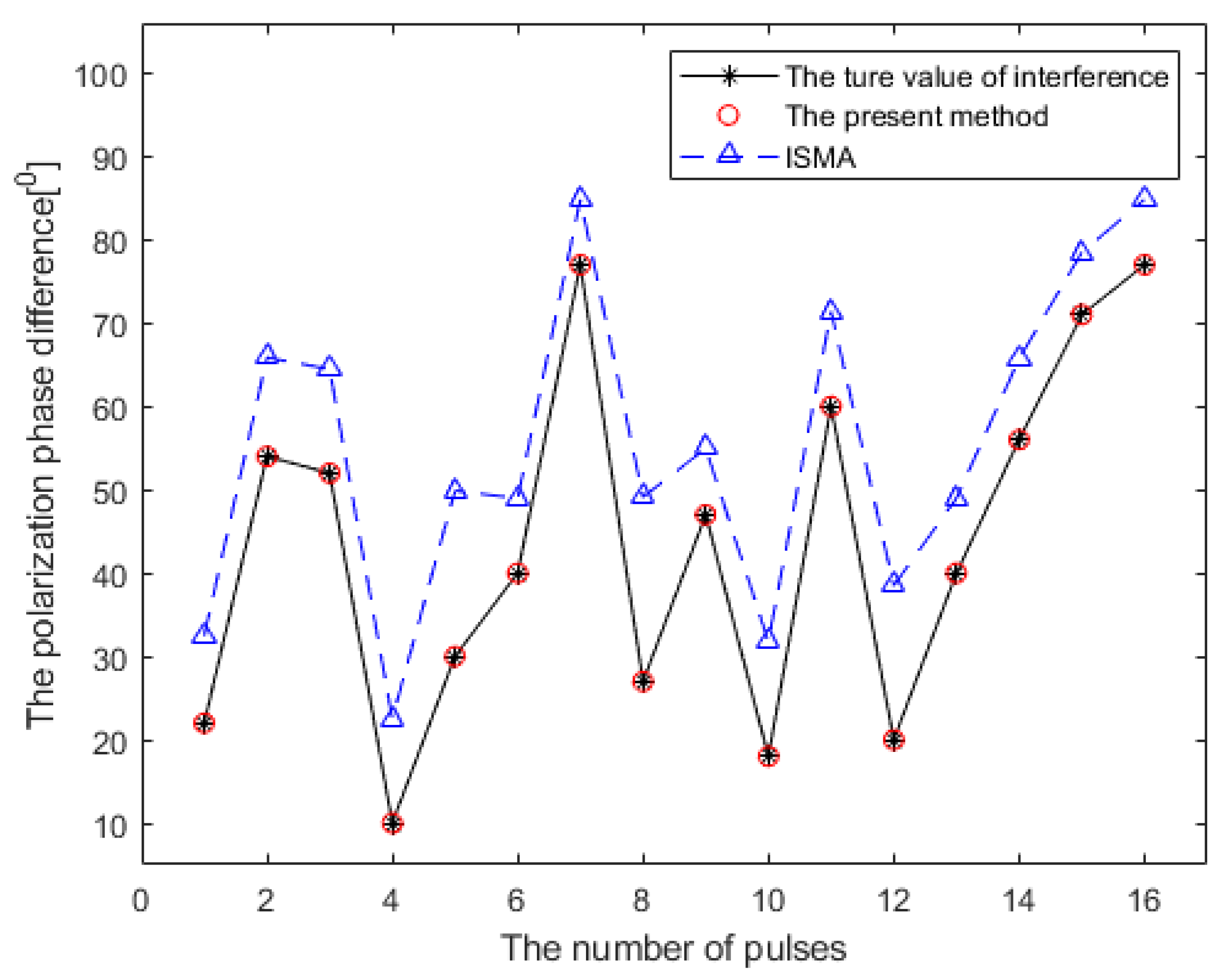
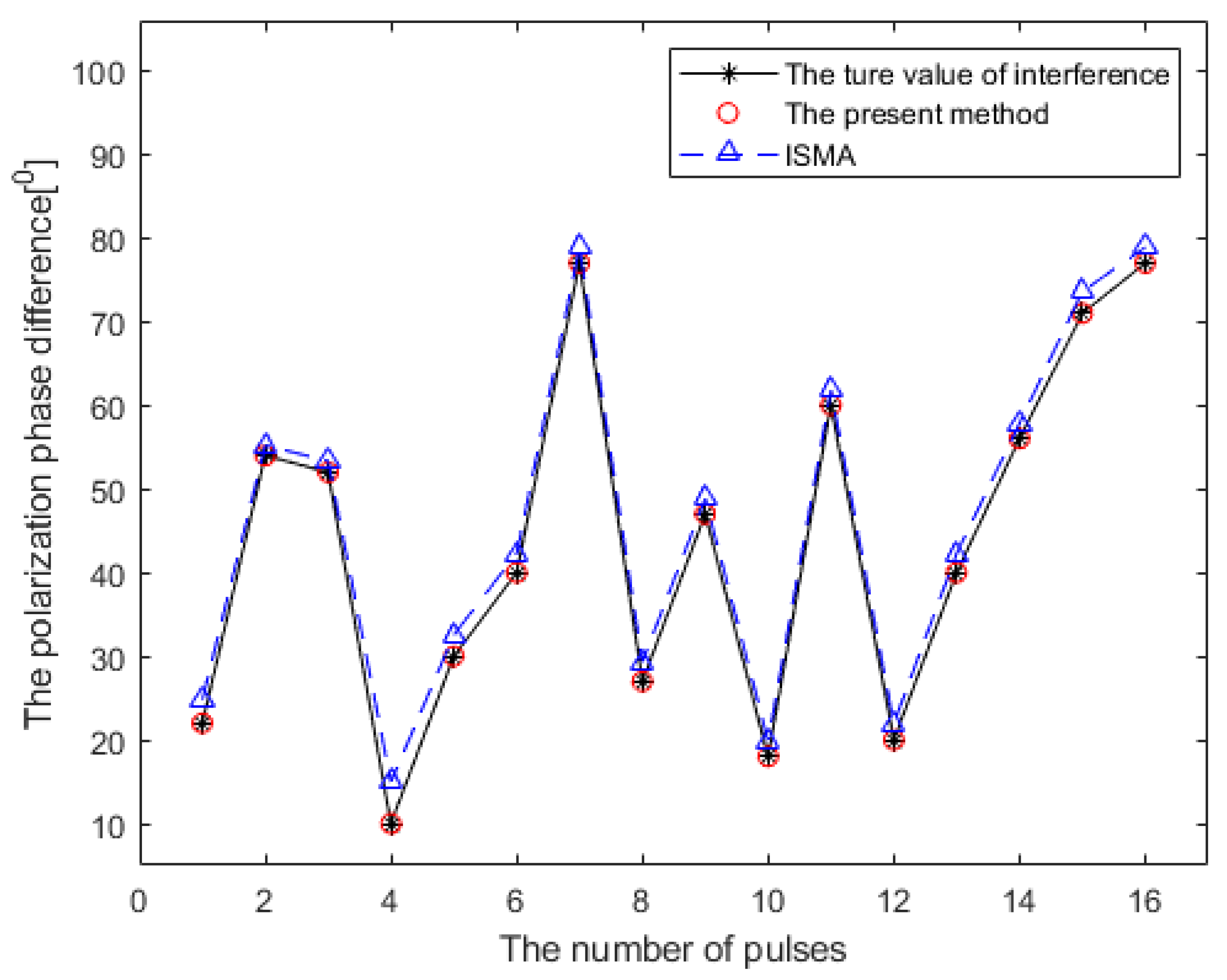
- The jammer’s carrier frequency , ISR = 34 dB. The polarization parameter of the jammer is changing between different pulses. In order to observe the accuracy of estimation in different pulses, we fix the auxiliary polarization angle and randomly select the polarization phase difference in different pulses, as exhibited in Table 1.
- Assume that the noise in the crossed dipole follows the Gaussian distribution and = 0 dB.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, H.L.; Liu, N.; Zhang, L.R. An interference suppression method for multistatic radar based on noise subspace projection. IEEE Sensors J. 2020, 15, 8797–8805. [Google Scholar] [CrossRef]
- Chen, G.; Wang, J.; Zuo, L. Two-stage clutter and interference cancellation method in passive bistatic radar. IET Signal Process. 2020, 6, 342–351. [Google Scholar]
- Ge, M.G.; Cui, G.L.; Yu, X.X. Main lobe jamming suppression via blind source separation sparse signal recovery with subarray configuration. IET Radar Sonar Navig. 2020, 3, 431–438. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Kong, Y.G.; Zhang, X. Vital sign extraction in the presence of radar mutual interference. IEEE Signal Process. Lett. 2020, 27, 1745–1749. [Google Scholar] [CrossRef]
- Sinclair, G. The transmission and reception of elliptically polarized waves. Proc. IRE 1950, 2, 148–151. [Google Scholar] [CrossRef]
- Kennaugh, E.M. Polarization Properties of Radar Reflections. Electronic Thesis, Ohio State University, Columbus, UK, 1952. [Google Scholar]
- Huynen, J.R. Phenomenological theory of radar targets. Ph.D. Thesis, Technical University, Delft, The Netherland, 1970. [Google Scholar]
- Zhe, G.; Deng, H.; Himed, B. Adaptive radar beamforming for interference mitigation in radar-wireless spectrum sharing. IEEE Signal Process. Lett. 2014, 4, 484–488. [Google Scholar]
- Zhe, X.; Chen, B.; Yang, M. Transmitter polarization optimization with polarimetric MIMO radar for mainlobe interference suppression. Digital Signal Process. 2017, 65, 19–26. [Google Scholar]
- Zhang, X.; Cao, D.; Xu, L.L. Joint polarization and frequency diversity for deceptive jamming suppression in MIMO radar. IET Radar Sonar Navig. 2019, 13, 263–271. [Google Scholar] [CrossRef]
- Mao, X.P.; Jun, L.A. Null phase-shift polarization filtering for high-frequency radar. IEEE Trans. Aerosp. Electron. Syst. 2007, 4, 1397–1408. [Google Scholar] [CrossRef]
- Jun, L.A.; Mao, X.P.; Deng, W.B. Oblique projection polarization filtering and its performance in high frequency surface wave radar. In Proceedings of the International Conference on Microwave and Millimeter Wave Technology IEEE, Chengdu, China, 8–11 May 2010; pp. 1618–1621. [Google Scholar]
- Mao, X.P.; Jun, L.A.; Hou, H.J. Oblique projection polarization filtering for interference suppression in high-frequency surface wave radar. IET Radar Sonar Navig. 2012, 2, 71–80. [Google Scholar] [CrossRef]
- Hong, H.; Mao, X.P.; Hu, C. A multi-domain collaborative filter for HFSWR based on oblique projection. In Proceedings of the IEEE National Radar Conference Proceedings, Atlanta, GA, USA, 7 May 2012; pp. 907–912. [Google Scholar]
- Zhe, X.; Chen, B.; Yang, M. Transmitter/receiver polarization optimisation based on oblique projection filtering for mainlobe interference suppression in polarimetric multiple-input–multiple-output radar. IET Radar Sonar Navig. 2018, 1, 137–144. [Google Scholar]
- Shi, L.F. Study with the Suppression of Interference Radar Polarization Information. Ph.D. Thesis, University of National Defense, Changsha, China, 2007. [Google Scholar]
- Chang, Y.L.; Wong, X.S.; Li, Y.Z. Polarization filter realization method for multiple noise FM interference. Aerosp. Electron. Warf. 2010, 3, 39–42. [Google Scholar]
- Ren, B.; Shi, L.F.; Wang, H.J. Investigation on of polarization filtering scheme to suppress GSM interference in radar main beam. J. Electron. Inf. Technol. 2014, 2, 459–464. [Google Scholar]
- Dai, H.X.; Li, Y.Z.; Wang, X.S. Interference cancellation and polarization suppression technology based on monopulse radar. Radar Sci. Technol. 2010, 5, 431–437. [Google Scholar]
- Dai, H.Y.; Huan, Z.; Lei, H. Interference cancellation and polarization suppression technology based on the pattern difference between sum-and-difference beams in mono-pulse radar. In Proceedings of the Radar Conference IEEE, Lille, France, 13 October 2015; pp. 1–6. [Google Scholar]
- Ma, J.Z.; Shi, L.F.; Li, Y.Z. Angle estimation of extended targets in main-lobe interference with polarization filtering. IEEE Trans. Aerosp. Electron. Syst. 2017, 1, 169–189. [Google Scholar] [CrossRef]
- Ma, J.Z.; Shi, L.F.; Xiao, S.P. Mitigation of cross-eye jamming using a dual-polarization array. J. Syst. Eng. Electron. 2018, 3, 491–498. [Google Scholar]
- Li, J.L.; Luo, J.; Chang, Y.L. Virtual polarization receiver based on the spatial polarization characteristics of antenna. Chin. J. Radio Sci. 2009, 3, 389–393. [Google Scholar]
- Dai, H.Y.; Wang, X.S.; Li, Y.Z. Main-lobe jamming suppression method of using spatial polarization characteristics of antennas. IEEE Trans. Aerosp. Electron. Syst. 2012, 3, 2167–2179. [Google Scholar] [CrossRef]
- Tohid, T.; Norouzi, Y.; Rajabi, A. A novel method for interference cancellation using polarization filter. In Proceedings of the IEEE Microwaves, Radar and Remote Sensing Symposium, Kiev, Ukraine, 29–31 August 2017; pp. 233–238. [Google Scholar]
- He, J.; Wang, Y.; Shu, T.; Truong, T.K. Polarization, Angle, and Delay Estimation For Tri-Polarized Systems in Multipath Environments. IEEE Trans. Wirel. Commun. 2022. [Google Scholar] [CrossRef]
- Xie, L.; He, Z.; Tong, J.; Liu, T.; Li, J.; Xi, J. Regularized Covariance Estimation for Polarization Radar Detection in Compound Gaussian Sea Clutter. IEEE Trans. Geosci. Remote Sens. 2022. [Google Scholar] [CrossRef]
- Nehorai, A.; Paldi, E. Superresolution compact array radiolocation technology (SuperCART) project. In Proceedings of the Conference Record of the Twenty-Fifth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 4–6 November 1991; pp. 566–572. [Google Scholar]
- Nehorai, A.; Paldi, E. Vector-sensor array processing for electromagnetic source localization. IEEE Trans. Signal Process. 1994, 2, 376–398. [Google Scholar] [CrossRef]
- Hochwald, B.; Nehorai, A. Polarimetric modeling and parameter estimation with applications to remote sensing. IEEE Trans. Signal Process. 1995, 8, 1923–1935. [Google Scholar] [CrossRef]
- Hochwald, B.; Nehorai, A. Identifiability in array processing models with vector-sensor applications. IEEE Trans. Signal Process. 1996, 1, 83–95. [Google Scholar] [CrossRef]
- Tan, K.C.; Ho, K.C.; Nehorai, A. Uniqueness study of measurements obtainable with arrays of electromagnetic vector sensors. IEEE Trans. Signal Process. 1996, 4, 1036–1039. [Google Scholar]
- Nehorai, A.; Ho, K.C.; Tan, B.T.G. Minimum-noise-variance beamformer with an electromagnetic vector sensor. IEEE Trans. Signal Process. 1999, 3, 601–618. [Google Scholar] [CrossRef]
- Ho, K.C.; Tan, K.C.; Tan, B.T.G. Estimation of directions of-arrival of partially polarized signals with electromagnetic vector sensors. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing Conference Proceedings, Atlanta, CA, USA, 9 May 1996. [Google Scholar]
- Ho, K.C.; Tan, K.C.; Tan, B.T.G. Efficient method for estimating directions-of-arrival of partially polarized signals with electromagnetic vector sensors. IEEE Trans. Signal Process. 1997, 10, 2485–2498. [Google Scholar]
- Ho, K.C.; Tan, K.C.; Nehorai, A. Estimating directions of arrival of completely and incompletely polarized signals with electromagnetic vector sensors. IEEE Trans. Signal Process. 1999, 10, 2845–2852. [Google Scholar] [CrossRef]
- Zoltowski, M.D.; Wong, K.T. Extended-aperture spatial diversity and polarizational diversity using a sparse array of electric dipoles or magnetic loops. In Proceedings of the IEEE 47th Vehicular Technology Conference. Technology in Motion, Phoenix, AZ, USA, 4–7 May 1997. [Google Scholar]
- Ko, C.C.; Zhang, J.; Nehorai, A. Separation and tracking of multiple broadband sources with one electromagnetic vector sensor. IEEE Trans. Aerosp. Electron. Syst. 2002, 2, 1109–1116. [Google Scholar] [CrossRef]
- Wong, K.T.; Zoltowski, M.D. Self-initiating MUSIC-based direction finding and polarization estimation in spatio-polarizational beamspace. IEEE Trans. Antennas Propag. 2000, 8, 1235–1245. [Google Scholar]
- Li, J. Direction and polarization estimation using arrays with small loops and short dipoles. IEEE Trans. Antennas Propag. 1993, 3, 379–387. [Google Scholar] [CrossRef]
- Li, J.; Compton, R.T. Angle and polarization estimation using ESPRIT with a polarization sensitive array. IEEE Trans. Antennas Propag. 1991, 9, 1376–1383. [Google Scholar] [CrossRef]
- Li, J.; Compton, R.T. Angle estimation using a polarization sensitive array. IEEE Trans. Antennas Propag. 1991, 10, 1539–1543. [Google Scholar] [CrossRef]
- Li, J.; Compton, R.T. Two dimensional angle and polarization estimation using the ESPRIT algorithm. IEEE Trans. Antennas Propag. 1992, 5, 550–555. [Google Scholar] [CrossRef]
- Li, J.; Compton, R.T. Angle and polarization estimation in a coherent signal environment. IEEE Trans. Aerosp. Electron. Syst. 1993, 3, 706–716. [Google Scholar] [CrossRef]
- Qiu, S.; Sheng, W.; Ma, X.; Kirubarajan, T. A Maximum Likelihood Method for Joint DOA and Polarization Estimation Based on Manifold Separation. IEEE Trans. Aerosp. Electron. Syst. 2021, 4, 2481–2500. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. Efficient parameter estimation of partially polarized electromagnetic waves. IEEE Trans. Signal Process. 1994, 11, 3114–3125. [Google Scholar] [CrossRef]
- Li, J. On polarization estimation using a crossed-dipole array. IEEE Trans. Signal Process. 1994, 2, 977–980. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Zheng, D. Efficient direction and polarization estimation with a COLD array. IEEE Trans. Antennas Propag. 1996, 4, 539–547. [Google Scholar] [CrossRef]
- Zoltowski, M.D.; Wong, K.T. Closed-form eigenstructure-based direction finding using arbitrary but identical subarrays on a sparse uniform Cartesian array grid. IEEE Trans. Signal Process. 2000, 8, 2205–2210. [Google Scholar] [CrossRef] [Green Version]
- Zoltowski, M.D.; Wong, K.T. ESPRIT-based 2-D direction finding with a sparse uniform array of electromagnetic vector-senors. IEEE Trans. Signal Process. 2000, 8, 2195–2204. [Google Scholar] [CrossRef]
- Wong, K.T.; Zoltowski, M.D. Closed-form direction finding and polarization estimation with arbitrarily spaced electromagnetic vector-sensors at unknown locations. IEEE Trans. Antennas Propag. 2000, 5, 671–681. [Google Scholar] [CrossRef] [Green Version]
- Wong, K.T. Direction finding/polarization estimation–dipole and/or loop triad(s). IEEE Trans. Aerosp. Electron. Syst. 2001, 2, 679–684. [Google Scholar]
- Wong, K.T.; Yuan, X. Vector cross-product direction-finding with an electromagnetic vector-sensor of six orthogonally oriented but spatially noncollocating dipoles/loops. IEEE Trans. Signal Process. 2011, 1, 160–171, Erratum in IEEE Trans. Signal Process. 2014, 4, 1028–1030. [Google Scholar] [CrossRef]
- Wong, K.T.; Li, L.S.; Zoltowski, M.D. Root-MUSIC-based direction-finding and polarization estimation using diversely polarized possibly collocated antennas. IEEE Trans. Wirel. Propag. Lett. 2004, 1, 129–132. [Google Scholar] [CrossRef]
- Comption, R.T. The tripole antenna: An adaptive array with full polarization flexibility. IEEE Trans. Antennas Propag. 1981, 6, 944–952. [Google Scholar] [CrossRef]
- Comption, R.T. The performance of a tripole adaptive array against cross-polarized jamming. IEEE Trans. Antennas Propag. 1983, 4, 682–685. [Google Scholar] [CrossRef]
- Yeung, C.K.A.; Wong, K.T. CRB: Sinusoid-sources estimation using collocated dipoles/loops. IEEE Trans. Aerosp. Electron. Syst. 2009, 1, 94–109. [Google Scholar] [CrossRef]
- Li, Y.Z.; Xiao, S.P.; Wang, X.S. Polarization cancellation method for self-defense suppression interference based on auxiliary antenna. In Radar Polarization Anti-jamming Technology; Li, Y.Z., Ed.; National Defense Industry Press: Beijing, China, 2010; pp. 151–160. [Google Scholar]

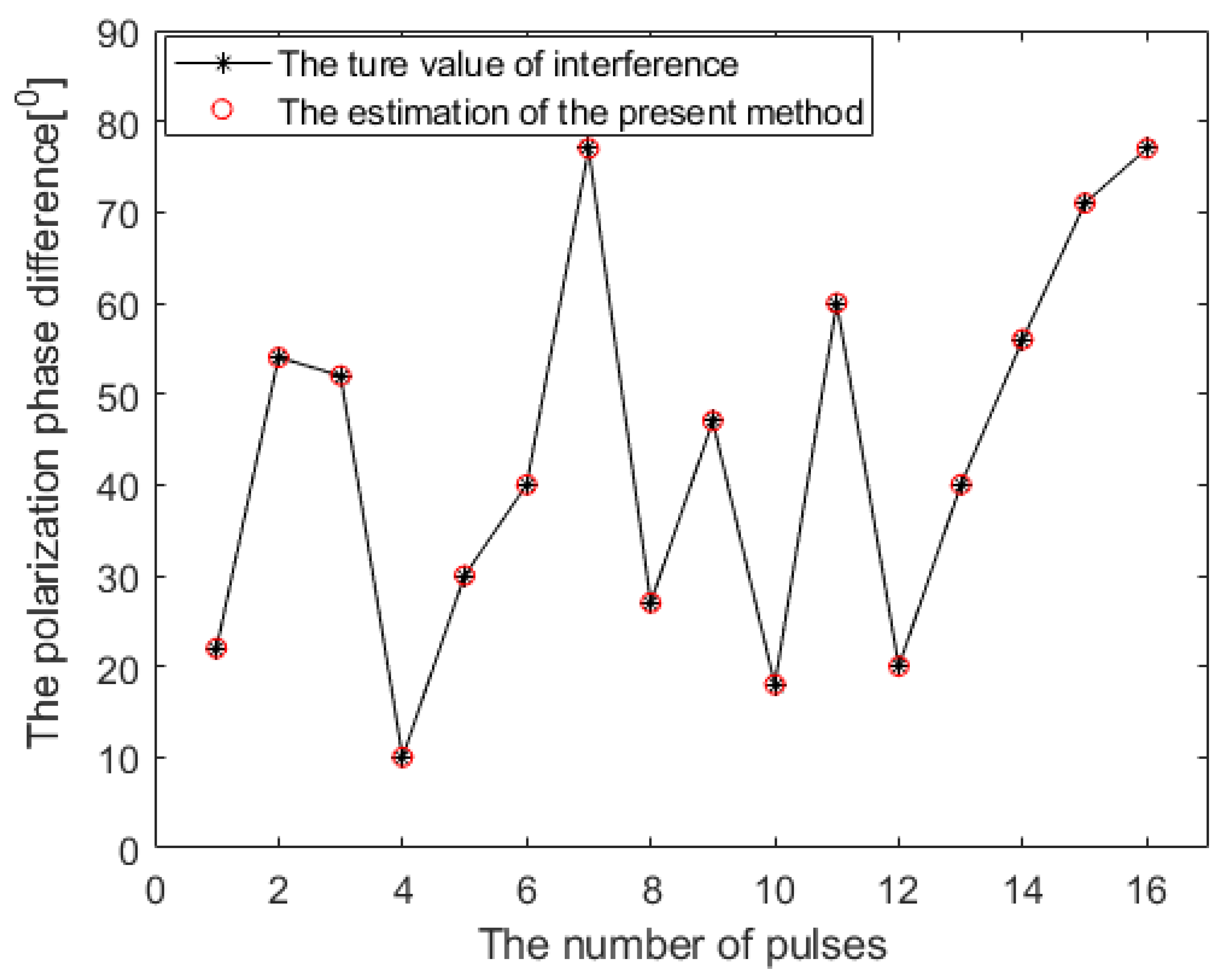

| Num. | Polarization Phase Difference | Num. | Polarization Phase Difference | Num. | Polarization Phase Difference |
|---|---|---|---|---|---|
| 1 | 7 | 13 | |||
| 2 | 8 | 14 | |||
| 3 | 9 | 15 | |||
| 4 | 10 | 16 | |||
| 5 | 11 | ||||
| 6 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Yang, J. Polarization Estimation with a Single Vector Sensor for Radar Detection. Remote Sens. 2022, 14, 1137. https://doi.org/10.3390/rs14051137
He Y, Yang J. Polarization Estimation with a Single Vector Sensor for Radar Detection. Remote Sensing. 2022; 14(5):1137. https://doi.org/10.3390/rs14051137
Chicago/Turabian StyleHe, Yaomin, and Jian Yang. 2022. "Polarization Estimation with a Single Vector Sensor for Radar Detection" Remote Sensing 14, no. 5: 1137. https://doi.org/10.3390/rs14051137
APA StyleHe, Y., & Yang, J. (2022). Polarization Estimation with a Single Vector Sensor for Radar Detection. Remote Sensing, 14(5), 1137. https://doi.org/10.3390/rs14051137







