Numerical Prediction of Duality Principle with Bloch-Floquet Periodic Boundary Condition in Fully Anisotropic FDTD

Abstract

In this paper, in accordance with fully anisotropic electromagnetic materials, the duality principle is successfully validated by the fully anisotropic finite-difference time-domain (FDTD) with Bloch-Floquet periodic boundary condition (BPBC), which in theory is first effectively applied to the verification of time-domain electromagnetic computation. Starting from the conventional duality principle of isotropy, those conditions can be given without any loss term. Without loss of generality, the electromagnetic duality rules involving dielectric and magnetic lossy tensors could be obtained by combining complex extension from original real parameters. In our further research, we introduce the duality principle into the BPBC cases, then execute and validate three different fully anisotropic models by means of the FDTD method under either TE or TM modes. From highly accurate numerical point of view, we apply ourselves to a more effective verification which can forecast the reflection and transmission coefficients and detect the subsurface echoes through the duality principle.

1. Introduction

To master the electromagnetic propagation in free space, we concentrate much on concrete fields and signal process in the final analysis. In electrostatic fields, the actual excitations are electric charge which causes electrostatics and electric current that engenders magnetostatics [1]. Thanks to the hypothesis of displacement current proposed by Maxwell in symmetry relation, it foreshadows that time-varying fields can form the outward radiation which has been validated by Hertz’s experiments afterward. However, it is not the final destination for scientists in theoretical physics. As early as 1931, Dirac prophesied existences about magnetic charge or current by supplementary formula [2], and hence promoted further searching in specific magnetic materials and commonly known duality principle. Since the birth of computer, numerical techniques applied in electromagnetic field, such as FDTD [3] et al., have launched the real-time research and simulated the exploration of the Maxwell’s Equations in the interdisciplinary cooperation, which promotes the industry progress of modern technology and provides the powerful calculating platform for manufacturing new materials. In view of numerical technique, it is quite significant for lacking some condition how to launch the technology expansion of electromagnetic duality principle.

In the early time, the duality principle was employed to solve the field radiation as the reliable symmetry. Harrison in 1971 proposed the annular slot antenna from its duality [4], and then determines those responses from an unsheathed coaxial cable connector mounted flush with the skin of a missile to intense plane-wave pulses. Afterward in 1988, Jaggrad et al. came up with canonical sources and duality in chiral media [5] to solve corresponding radiated problems. The duality transformations were proposed for general bi-isotropic (nonreciprocal chiral) media by Lindell and Viitanen [6] in 1992 for handling the plane-wave reflection. Next, Lindell [7] in 1995 put forward the duality transformation for two-dimensional static problems, and applied to straight TEM transmission-line geometries. In 2013, Jazebi, et al. [8] raised the duality-synthesized circuit for eddy current effects in transformer windings, and created a completely dual transformer model for the calculation in electromagnetic transients. Moreover in 2015, Jazebi and Leon [9] advanced the duality-based transformer model including eddy current effects in the windings, which made the model be capable of accurately representing the leakage inductance, copper losses, as well as skin and proximity effects. Besides, Liang and Wu in 2018 combined the duality principle of characteristic modes with the analysis and design of aperture antennas [10], and construct the relationship of the eigenvalues and the eigencurrents for the aperture and the complementary plate.

On the other hand, it is a vital direction for the duality principle to discuss lumped circuits under the electromagnetic research. In general, capacitors and inductors can respectively store electric and magnetic potential energy, which shows the duality characteristic in the lumped component. In 1992, Yang put forward the mutual capacitance-duality principle evolved from planar network [11], and further obtained the transitional process from admittance to impedance in line with the lumped circuits. Next in 1993, Wolfs proposed a current-sourced DC-DC converter derived via the duality principle from the half-bridge converter which decrease energy consumption when tackling with the lumped device [12], and then advanced the application by duality principle for the nonplanar circuits [13] to seek more new ladder structures with the voltage source. Afterward in 1998, Kaplan and Suissa [14] came up with the treatment of extremely-low- frequency magnetic and electric field sensors via electromagnetic duality, and effectively dealt with those DC sensors under the magnetic and electric fields. Moreover, Bai and Zhang [15] posed the conformation of multilevel current source converter topologies using the duality principle in 2008. Besides in 2015, Samie et al. [16] developed the prognostic models with the duality principles for DC-to-DC converters.

In the recent decade, people gradually realized that the duality principle can be promoted from the view of the Maxwell’s Equations. Starting from 2005, Lindell and Sihvola [17] proposed the transformation method for problems involving perfect electromagnetic conductor (PEMC) structures which made people understand more explorations on the magnetic current structure need proceeding. Gheorghisor and Kahn [18] in 2007 put forward electromagnetic fields in complementary and self-complementary structures, and discovered that at low frequencies, when the only one TEM mode propagates, field solutions for this TEM mode exhibit discontinuous behavior as the aspect ratio approaches one from above and below. In 2014, Prudencio, et al. came up with a geometrical approach to duality transformations for tellegen media [19]. Recently, Kastner in 2020 presented the half-way duality in electromagnetics by an explicit expression for half-curl operator [20], and meanwhile achieved the solution to a reactive surface is inferred from its perfect electric conductor (PEC) half-way duality.

In 2013, Marengo proposed his opinion on the generalized optical theorem in anisotropy based on modified reciprocity theorem plus duality [21]. Recently, we first presented the Bloch-Floquet periodic boundary condition (PBC) with fully anisotropic FDTD [22]. The electromagnetic duality principle brings many new physical properties in engineering technology in the long-term development; therefore, in the electromagnetic propagation of fully anisotropy, it needs to further discuss how to expand the new theory in the light of new technique research.

In this paper, we develop a numerical prediction of duality principle with Bloch-Floquet PBC in three-dimensional (3D) fully anisotropic FDTD, the new contributions of this work are: (a) the verification of duality principle is presented under the specific relationship with fully anisotropy; (b) the duality principles of electric and magnetic loss tensors are derived under the Bloch-Floquet PBC; (c) with the Bloch-Floquet PBC, the cross-boundary calculation is successfully validated by the duality principle, and then we can capture the almost same transmission results after the radiation of the plane waves when exchanging parameters.

The organization in this paper is given as follows. We will respectively illustrate the duality principle of fully anisotropy in Section 2 and the exchange of iterative parameters in the 3D fully anisotropic FDTD in Section 3. Under duality principle, transmission coefficients can be discussed in Section 4 by using a fully anisotropic single- and multi-layered models, and transverse periodic distribution of fully anisotropies to validate our proposal. Finally, we will draw the conclusion in Section 5.

2. Duality Principle for Fully Anisotropy

As is well known, the duality principle belongs to a common physical concept in physics, which can solve engineering or physical problems for improving the efficiency, reducing the problem complexity and leading to the higher solving quality. Besides, it has the wide application for the duality principle to the engineering electromagnetics. Hence, with the further research of the duality principle, people will be able to understand more electromagnetic problems.

Under the condition of linear lossless isotropy, the duality principle in electromagnetism [23] must meet the requirement as below,

$${\mathit{H}}_{dual}=\mathit{E}, {\mathit{E}}_{dual}=-\mathit{H}, {\mu }_{dual}=\epsilon , {\epsilon }_{dual}=\mu ,$$

(1)

For fully anisotropies in our past work [24], Maxwell’s Equations can be defined below

$$\mathit{E}=\chi \nabla \times \mathit{H}$$

(2)

$$\mathit{H}=-\mathit{\upsilon }\nabla \times \mathit{E}$$

(3)

where the vectors E and H are respectively the electric and magnetic fields, and general tensor χ and υ can be respectively given as

$$\chi ={(\mathrm{j}\omega \hspace{0.17em}\tilde{\mathsf{\epsilon }})}^{-1}$$

(4)

$$\mathit{\upsilon }={(\mathrm{j}\omega \hspace{0.17em}\tilde{\mathsf{\mu }})}^{-1}$$

(5)

where angular frequency represents ω = 2π f, and the complex permittivity and permeability tensors $\tilde{\mathsf{\epsilon }}$ and $\tilde{\mathsf{\mu }}$ under the fixed angular frequency can be defined as

$$\tilde{\mathsf{\epsilon }}={\epsilon }_0\left({\mathsf{\epsilon }}_r-\mathrm{j}\frac{{\sigma }_e}{\omega {\epsilon }_0}\right)$$

(6)

$$\tilde{\mathsf{\mu }}={\mu }_0\left({\mathsf{\mu }}_r-\mathrm{j}\frac{{\sigma }_m}{\omega {\mu }_0}\right)$$

(7)

For these two Equations depicted above, the electromagnetic loss tensors σ_e and σ_m belong to the dispersive elements in the complex frequency domain. The complex permittivity and permeability tensors $\tilde{\mathsf{\epsilon }}$ and $\tilde{\mathsf{\mu }}$ have to meet the exchange rule that the real and the imaginary parts execute duality principle at the same time, and then we obtain the dual variables as below

$$\begin{gathered} {\epsilon }_{0,dual}={\mu }_0, {\mu }_{0,dual}={\epsilon }_0,{\mathsf{\epsilon }}_{r,dual}={\mathsf{\mu }}_r, {\mathsf{\mu }}_{r,dual}={\mathsf{\epsilon }}_r,{\sigma }_{e,dual}={\eta }_0^{-2}{\sigma }_m, \\ {\sigma }_{m,dual}={\eta }_0^2{\sigma }_e \end{gathered}$$

(8)

where the vacuum wave impedance ${\eta }_0=\sqrt{\frac{{\mu }_0}{{\epsilon }_0}}=\sqrt{\frac{{\epsilon }_{0,dual}}{{\mu }_{0,dual}}}$ can be denoted as a constant. Here, the Equation (8) with duality principle represents the conversion process for the fully anisotropy in the medium parameters.

3. Duality Principle under Bloch-Floquet Condition

Under the condition of plane waves, our proposal about the Bloch-Floquet PBC mainly concentrates on the characteristic analysis and the research discussion at the transmission process with the periodic electromagnetic materials. Transverse wave vectors k_x and k_y are the fixed constants for the wave vector k = (k_x, k_y, k_z) when the planes xOz and yOz is separately chosen as the Bloch-Floquet periodic boundary, therefore in the air, the longitudinal wave vector k_z must satisfy below

$$k_z=\pm \sqrt{\mathit{k}\cdot \mathit{k}-(k_x^2+k_y^2)}=\pm \sqrt{{\left(\frac{2\pi f}{c_0}\right)}^2-(k_x^2+k_y^2)}$$

(9)

where c₀ represents the light velocity in vacuum and k_z needs to be the real number. Hence, the minimum cut-off frequency f_min can be expressed as

$$f_{\min }=\frac{c_0}{2\pi }\sqrt{k_x^2+k_y^2}$$

(10)

As the truncation planes xOz and yOz with the Bloch-Floquet periodic boundary, it is necessary for the time-domain field components at the periodic boundary x = 0 and y = 0 to satisfy the following BPBCs:

$${\zeta }_t(x=0,y,z,t)={\zeta }_t(x=L_x,y,z,t)\hspace{0.17em}{e}^{\mathrm{j}{k}_x{L}_x}$$

(11)

$${\zeta }_t(x,y=0,z,t)={\zeta }_t(x,y=L_y,z,t)\hspace{0.17em}{e}^{\mathrm{j}{k}_y{L}_y}$$

(12)

where the spatial function ζ_t (x, y, z) represent the time-domain component for arbitrary direction in electric or magnetic fields, L_w (w = x, y) can be denoted as the periodic length of the Bloch-Floquet PBC along the w-direction. Taking truncation subscript j = 0 as an instance, the field components in the periodic alternation are solved in the fully anisotropic FDTD, expressed as below

$${E_{w,x}|}_{i+\frac{1}{2},j_{\max },k}^{n+1}={E_{w,x}|}_{i+\frac{1}{2},0,k}^{n+1}{e}^{-\mathrm{j}{k}_y{T}_y}$$

(13)

$${E_{w,z}|}_{i,j_{\max },k+\frac{1}{2}}^n={E_{w,z}|}_{i,0,k+\frac{1}{2}}^n{e}^{-\mathrm{j}{k}_y{T}_y}$$

(14)

$${H_{w,y}|}_{i+\frac{1}{2},j_{\max },k+\frac{1}{2}}^{n+\frac{1}{2}}={H_{w,y}|}_{i+\frac{1}{2},0,k+\frac{1}{2}}^{n+\frac{1}{2}}{e}^{-\mathrm{j}{k}_y{T}_y}$$

(15)

where those specific FDTD iterations can be shown as

$$\begin{gathered} {E_{w,x}|}_{i+\frac{1}{2},0,k}^{n+1}={[{\mathbf{P}}_E]}_{wx}{E_x|}_{i+\frac{1}{2},0,k}^n-{[{\mathbf{Q}}_E]}_{wx}\Delta z^{-1}({H_y|}_{i+\frac{1}{2},0,k+\frac{1}{2}}^{n+\frac{1}{2}}-{H_y|}_{i+\frac{1}{2},0,k-\frac{1}{2}}^{n+\frac{1}{2}}) \\ +{[{\mathbf{Q}}_E]}_{wx}\Delta y^{-1}({H_z|}_{i+\frac{1}{2},\frac{1}{2},k}^{n+\frac{1}{2}}-{H_z|}_{i+\frac{1}{2},j_{\max }-\frac{1}{2},k}^{n+\frac{1}{2}}{e}^{-\mathbf{j}{k}_y{T}_y}), \end{gathered}$$

(16)

$$\begin{gathered} {E_{w,z}|}_{i,0,k+\frac{1}{2}}^n={[{\mathbf{P}}_E]}_{wz}{E_z|}_{i,0,k+\frac{1}{2}}^n+{[{\mathbf{Q}}_E]}_{wz}\Delta x^{-1}({H_y|}_{i+\frac{1}{2},0,k+\frac{1}{2}}^{n+\frac{1}{2}}-{H_y|}_{i-\frac{1}{2},0,k+\frac{1}{2}}^{n+\frac{1}{2}}) \\ -{[{\mathbf{Q}}_E]}_{wz}\Delta y^{-1}({H_x|}_{i,\frac{1}{2},k+\frac{1}{2}}^{n+\frac{1}{2}}-{H_x|}_{i,j_{\max }-\frac{1}{2},k+\frac{1}{2}}^{n+\frac{1}{2}}{e}^{-\mathrm{j}{k}_y{T}_y}), \end{gathered}$$

(17)

$$\begin{gathered} {H_{w,y}|}_{i+\frac{1}{2},0,k+\frac{1}{2}}^{n+\frac{1}{2}}={[{\mathbf{P}}_H]}_{wy}{H_y|}_{i+\frac{1}{2},0,k+\frac{1}{2}}^{n-\frac{1}{2}}+{[{\mathbf{Q}}_H]}_{wy}\Delta x^{-1}({E_z|}_{i+1,0,k+\frac{1}{2}}^n-{E_z|}_{i,0,k+\frac{1}{2}}^n) \\ -{[{\mathbf{Q}}_H]}_{wy}\Delta z^{-1}({E_x|}_{i+\frac{1}{2},0,k+1}^n-{E_x|}_{i+\frac{1}{2},0,k}^n), \end{gathered}$$

(18)

where iterative tensors from the fully anisotropic FDTD are respectively P_H, Q_H, P_E and Q_E, as shown below

$${\mathbf{P}}_H={(\mathsf{\mu }\Delta t^{-1}+0.5{\mathsf{\sigma }}_m)}^{-1}(\mathsf{\mu }\Delta t^{-1}-0.5{\mathsf{\sigma }}_m)$$

(19)

$${\mathbf{Q}}_H=\mathsf{\mu }\Delta t^{-1}-0.5{\mathsf{\sigma }}_m$$

(20)

$${\mathbf{P}}_E={(\mathsf{\epsilon }\Delta t^{-1}+0.5{\mathsf{\sigma }}_e)}^{-1}(\mathsf{\epsilon }\Delta t^{-1}-0.5{\mathsf{\sigma }}_e)$$

(21)

$${\mathbf{Q}}_E=\mathsf{\epsilon }\Delta t^{-1}-0.5{\mathsf{\sigma }}_e$$

(22)

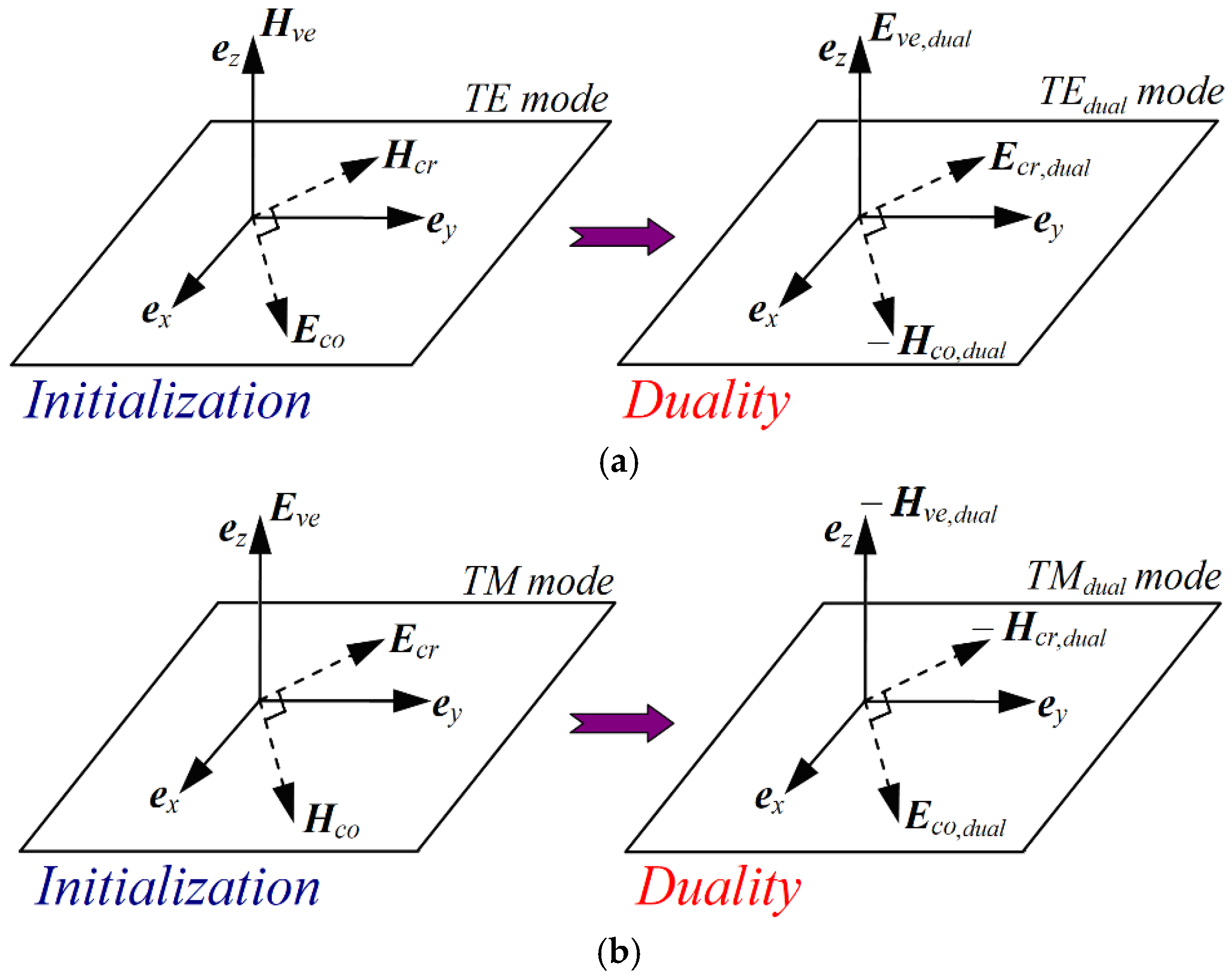
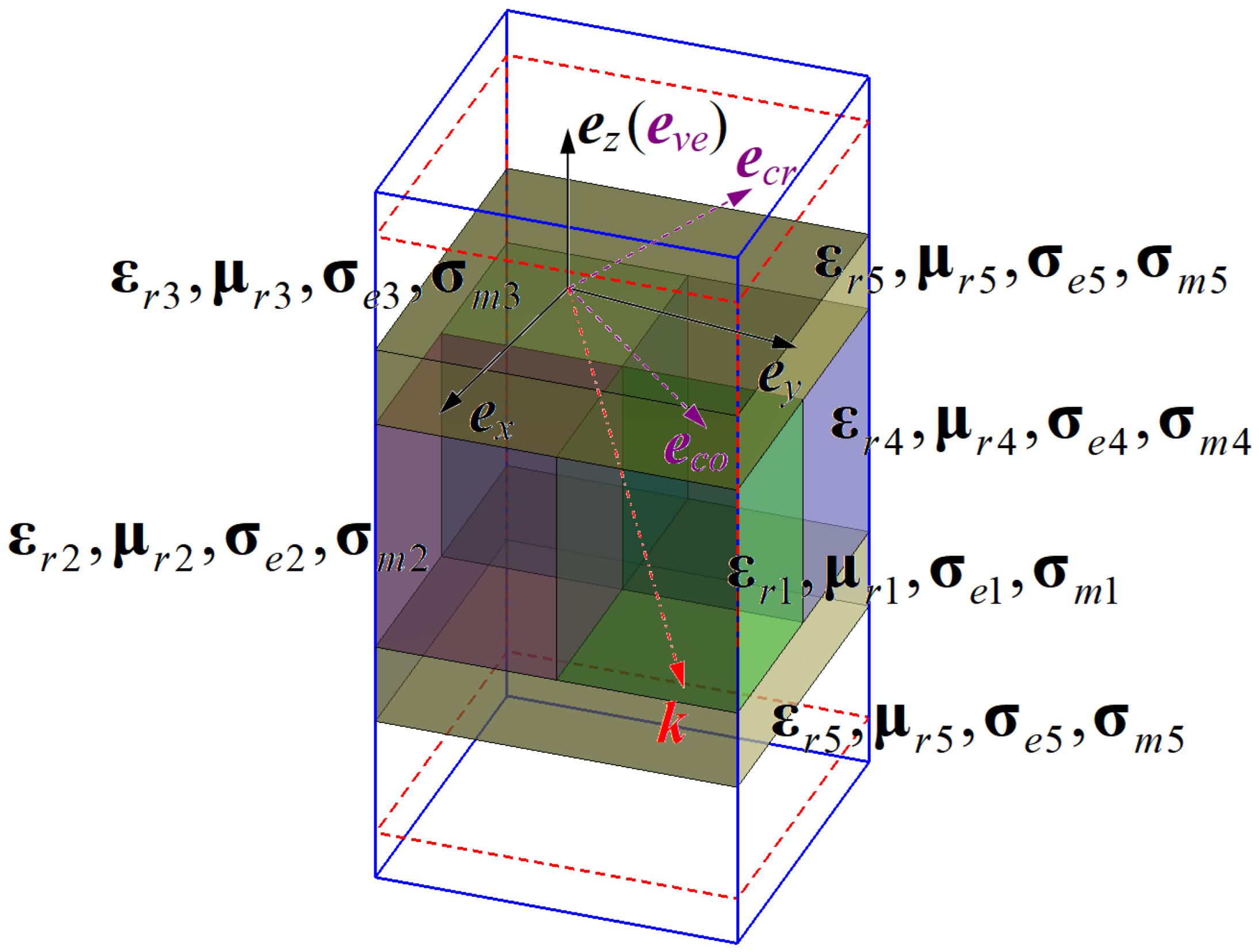
Relying on the duality principle from the Equations (1) and (8), those expressions with the Equations (12)–(21) can be easily obtained at the truncation plane j = 0 in the fully anisotropic FDTD. Besides, with regard to the installation from the plane waves, we usually divide them into TE or TM modes under the condition of oblique incidences. Therefore, the preprocessing under the TE or TM mode can be respectively executed by the duality principle, shown in Figure 1.

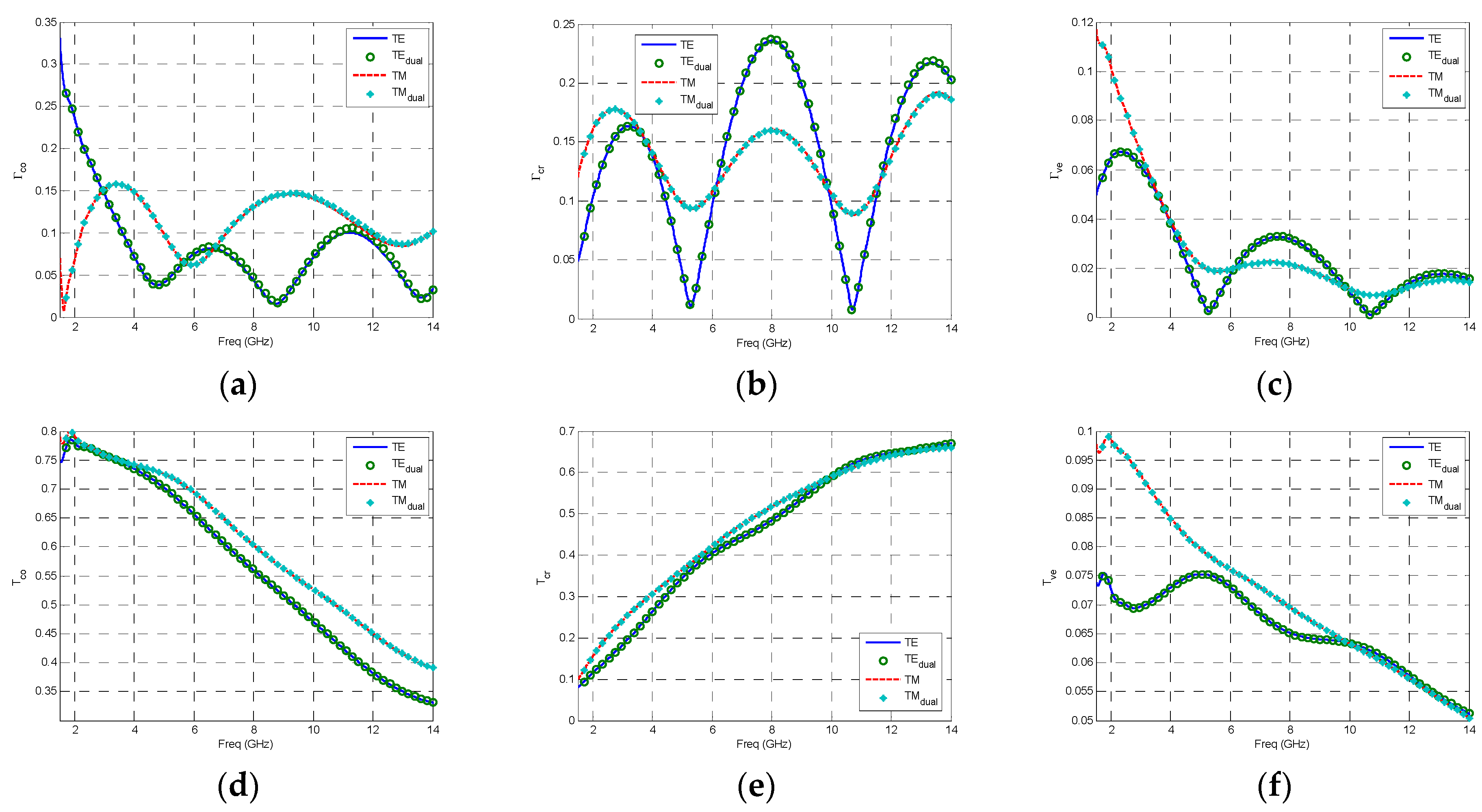
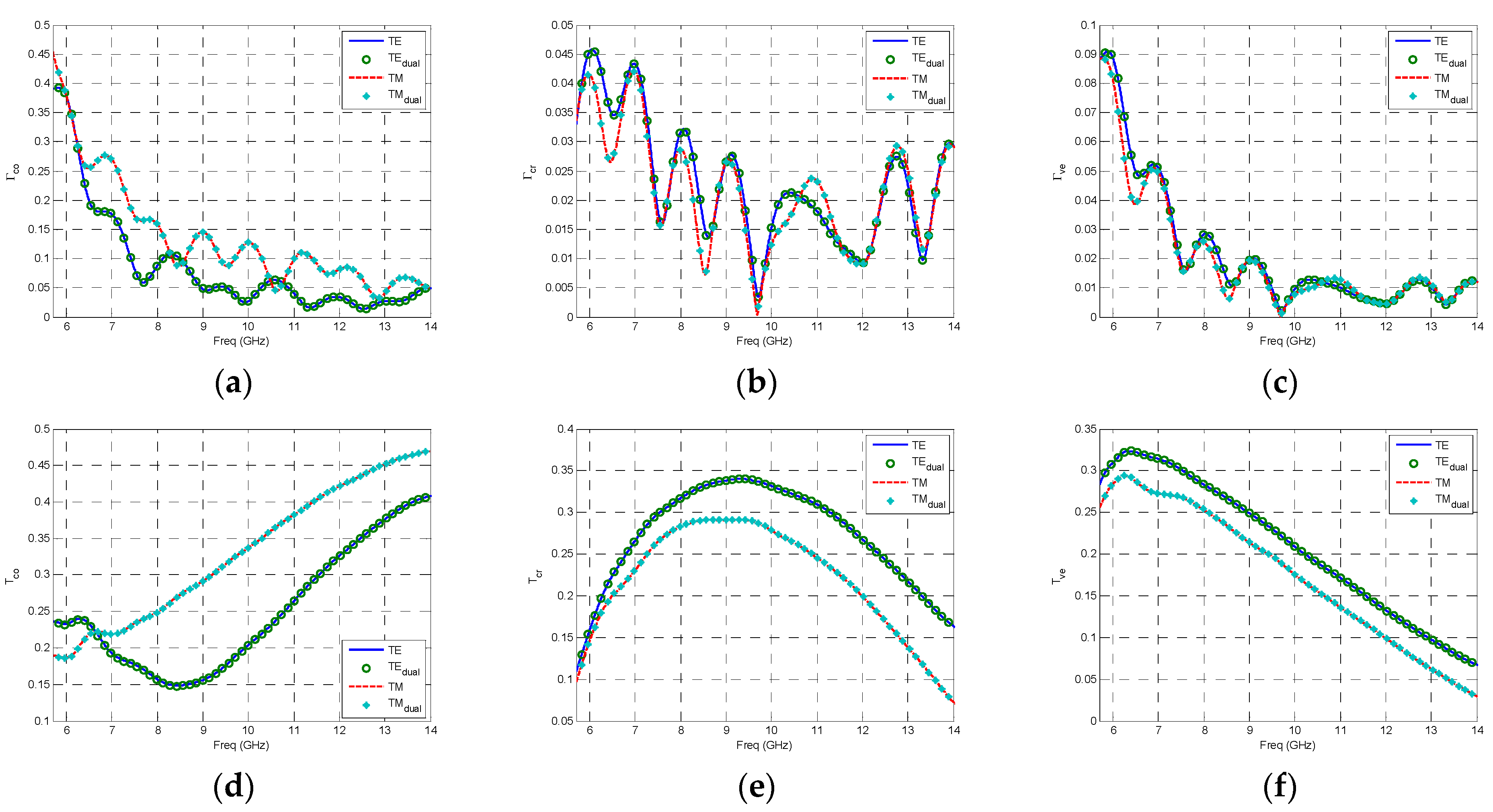
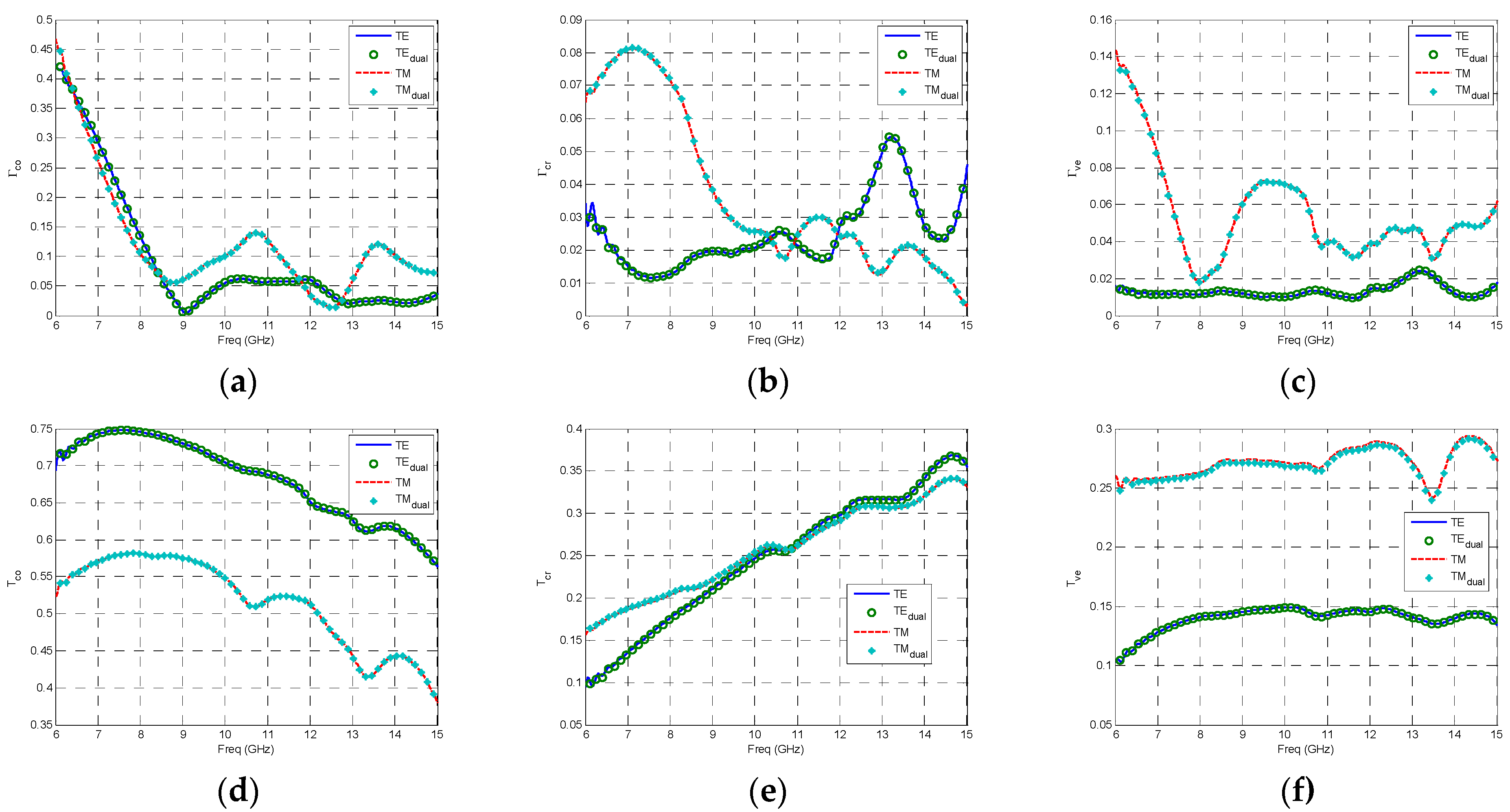
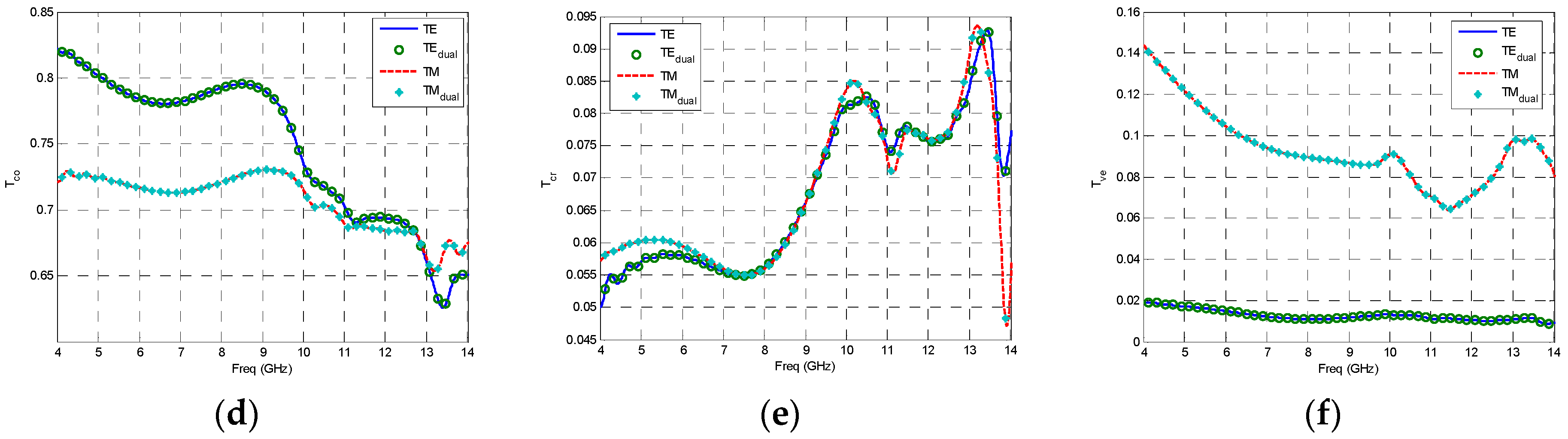
Apparently, via the plane-wave mode processed by the above duality principle, we can take TM mode from TE_dual mode, and meanwhile TE mode can be converted from TM_dual mode. As found in Figure 1, only the transverse polarized field E_co exists in the TE mode while only the transverse polarized field H_co does in the TM mode. Consequently, when the incident plane waves completely penetrate into the periodic materials, the complex reflection and transmission coefficients with the process of duality principle can be defined as

$${\Gamma }_{q,TE}(f)={\frac{E_{ref,q}(f)}{E_{inc}(f)}|}_{TE}={\frac{H_{dual,ref,q}(f)}{H_{dual,inc}(f)}|}_{T{E}_{dual}}$$

(23)

$${\Gamma }_{q,TM}(f)={\frac{H_{ref,q}(f)}{H_{inc}(f)}|}_{TM}={\frac{E_{dual,ref,q}(f)}{E_{dual,inc}(f)}|}_{T{M}_{dual}}$$

(24)

$$T_{q,TE}(f)={\frac{E_{tra,q}(f)}{E_{inc}(f)e^{j{k}_z{d}_{rt}}}|}_{TE}={\frac{H_{dual,tra,q}(f)}{H_{dual,inc}(f)e^{j{k}_z{d}_{rt}}}|}_{T{E}_{dual}}$$

(25)

$$T_{q,TM}(f)={\frac{H_{tra,q}(f)}{H_{inc}(f)e^{j{k}_z{d}_{rt}}}|}_{TM}={\frac{E_{dual,tra,q}(f)}{E_{dual,inc}(f)e^{j{k}_z{d}_{rt}}}|}_{T{M}_{dual}}$$

(26)

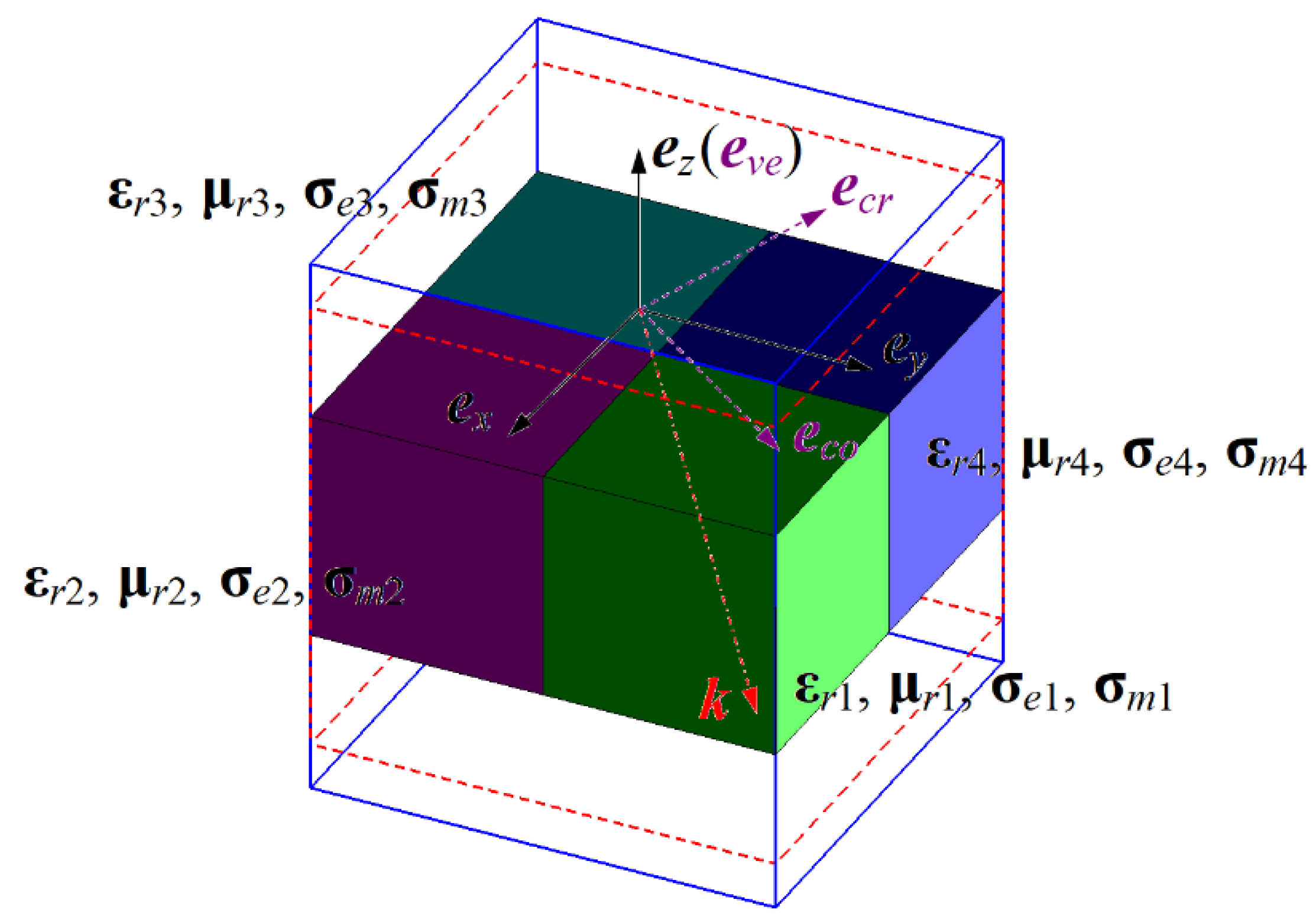
where the symbol q can be respectively expressed as the fields’ direction co, cr and ve which are respectively named as the horizontal co-polarization, the horizontal cross-polarization and the vertical polarization, and we define the variable d_rt as the distance between incident and transmission surface. As is known to all, the interleaving form with the Yee’s grid appears in the 3D model when employing the FDTD method, however, we still utilize the fully anisotropic FDTD method to validate the duality principle by the fully anisotropies under the truncation in line with Bloch-Floquet PBC.

4. Numerical Examples

We apply fully anisotropic FDTD formulations to implementing the proposed electromagnetic duality principle in the fully anisotropies. On the one hand, the fully anisotropic FDTD can validate the general laws of electromagnetic solving method which meets the physical theory; on the other hand, we are necessary to perform the reasonable equivalent substitution for seeking some new physical phenomena in the engineering experiments.

4.1. Monolayer Fully Anisotropy

To effectively validate our proposed duality method with the Equations (1) and (8), we first consider the simplest monolayer problem with fully anisotropies. As seen in Figure 2, the plane wave is employed by propagating from the top to the bottom of the monolayer fully anisotropy, and the Bloch-Floquet PBC is applied at the transverse truncation region in this 3D model. As the air on the top and bottom region, the longitudinal section is truncated by 8-layered PMLs with the parameters κ_max = 7 and α_max = 0.05. The monolayer fully anisotropy is 10 mm × 10 mm × 10 mm in 3D size, its spatial incremental is Δx = Δy = Δz = 0.25 mm in 3D directions. The fixed transverse vectors k_x and k_y are respectively given as 10 rad/m and 20 rad/m. The specific fully anisotropic parameters are respectively

$$\begin{gathered} {\mathsf{\epsilon }}_r=\left[\begin{array}{ccc}4.0& 0.2+\mathrm{j}1.0& 0.1-\mathrm{j}0.8\\ 0.2-\mathrm{j}1.0& 3.0& 0.05+\mathrm{j}0.2\\ 0.1+\mathrm{j}0.8& 0.05-\mathrm{j}0.2& 2.0\end{array}\right], \\ {\mathsf{\sigma }}_e=\left[\begin{array}{ccc}0.03& 0.05& -0.08\\ -0.05& 0.09& 0.02\\ 0.08& -0.02& 0.5\end{array}\right] \end{gathered}$$

$$\begin{gathered} {\mathsf{\mu }}_r=\left[\begin{array}{ccc}2.0& 0.05-\mathrm{j}0.5& 0.1+\mathrm{j}0.6\\ 0.05+\mathrm{j}0.5& 3.0& 0.2-\mathrm{j}0.1\\ 0.1-\mathrm{j}0.6& 0.2+\mathrm{j}0.1& 4.0\end{array}\right], \\ {\mathsf{\sigma }}_m=\left[\begin{array}{ccc}3000& 1300& -200\\ -1300& 9000& -600\\ 200& 600& 1000\end{array}\right] \end{gathered}$$

After running the fully anisotropic FDTD and the Fourier transform methods to capture the data in the frequency domain, the oblique plane-wave incidences with the TE and TM modes can be respectively obtained in frequency range [1.8 GHz, 14 GHz], and their reflection and transmission coefficients Γ_q (q = co, cr, ve) and T_q (q = co, cr, ve) can be also computed under the condition of the duality field, shown in Figure 3. Obviously reflected in Figure 3, the duality-principle-based results have the excellent agreements with those obtained from the initialized fields in the monolayer fully anisotropy. Therefore, once we know the complex permittivity and permeability tensors $\tilde{\mathsf{\epsilon }}$ and $\tilde{\mathsf{\mu }}$ from Equations (6) and (7), we can easily predict the same numerical results by the duality media parameters ${\tilde{\mathsf{\epsilon }}}_{dual}$ and ${\tilde{\mathsf{\mu }}}_{dual}$ when exchanging the TE and TM mode.

4.2. Multi-Layered Fully Anisotropy

As illustrated above, the duality principle with the Equations (1) and (8) has been validated for the simplest monolayer fully anisotropy by the Bloch-Floquet PBC with 3D FDTD method, however, it is not quite enough for the single medium to satisfy requirements of the engineering applications and the physical experiments. Without loss of generality, we already adopt the longitudinal four-layered fully anisotropies as the modeling continuity, shown in Figure 4. All constitutive tensors in Figure 4 are listed in the Appendix A.

As shown in Figure 4, the every layer with the same thickness is 10 mm × 10 mm × 10 mm in size for this 3D multi-layered model. Under the FDTD initialization, its spatial incremental in all directions is Δx = Δy = Δz = 0.2 mm. The fixed transverse vectors k_x and k_y are respectively 50 rad/m and 100 rad/m. The transverse sections are truncated by the Bloch-Floquet PBC, and the longitudinal sections as the air are terminated by 8-layered PMLs with the same conditions above. After executing the fully anisotropic FDTD and the Fourier transform techniques, we can obtain the numerical results respectively from both TE and TM modes in frequency range [5.85 GHz, 14 GHz], and the reflection and transmission coefficients Γ_q (q = co, cr, ve) and T_q (q = co, cr, ve) are also achieved compared with the results from duality field, shown in Figure 5.

As reflected in Figure 5, the reflection curves Γ_co, Γ_cr and Γ_ve can obtain the wonderful numerical agreements after taking the advantage of the duality exchange rules, even though more 3D complicated geometry is built based on multilayer structures. It is further turned out that the duality principle can be applied to the Bloch-Floquet PBC with the fully anisotropic FDTD in the multi-layered cases. It can be clearly seen that the duality rule is not influenced by the grid transformation to lead to the obvious numerical deformity. Hence, the numerical prediction can be effectively worked at the vertical stratification and there is no obvious bias under the fully anisotropic FDTD method.

4.3. Transverse Model Distribution with Multi-Layered Fully Anisotropy

As demonstrated in the Equations (13)–(15), the Yee’s grid distributions are not overlapping for the electric and magnetic fields. That is to say, both electric and magnetic fields have to exchange the temporal iterative sequence and the grid position when processing the duality principle. However, it may be a very difficult problem for the Bloch-Floquet PBC. To further expand the application of duality principle, above four kinds of fully anisotropies are distributed transversely which depicted in Figure 4, therefore, the Bloch-Floquet PBC has to confront the synchronous process through medium alternation with the fully anisotropic FDTD iteration, shown in Figure 6. There is only one-layered anisotropy in this transverse model, but it is actually a multi-layered model because of the air background in the incident and the transmission regions. More importantly in the general space, air is also the simplest and most special anisotropy.

As seen in Figure 6, four transverse-distribution-based media in size are equal to each other with each subdomain 9 mm × 9 mm × 10 mm in size and its spatial incremental Δx = Δy = Δz = 0.15 mm in all directions. The fixed transverse vectors k_x and k_y are 100 rad/m and 50 rad/m, respectively. Their transverse sections are truncated by the Bloch-Floquet PBC, and the longitudinal sections are chosen by 8-layered above PMLs. Through the complete calculation of the 3D FDTD method and the Fourier transform by time-domain data, the frequency-domain results can be restricted at the range of [6.0 GHz, 15 GHz] under the incidence with both TE and TM modes, and then their reflection and transmission coefficients Γ_q (q = co, cr, ve) and T_q (q = co, cr, ve) are also implemented under the duality principle, shown in Figure 7. As a result for the fully anisotropic FDTD, the numerical prediction is available at the Bloch-Floquet boundary even though the sudden change of medium parameters.

To further verify the reliability and generality of our proposed method, we change the longitudinal height of the above 3D transverse model to 6 mm, add a new fully anisotropy in the upper and lower regions respectively, and the specific parameters of Medium 5 are recorded in the Appendix A. The thickness of the two newly added fully anisotropy Medium 5 is 2 mm, as shown in Figure 8.

Through the translucent 3D model, it can be clearly found that the four transversely distributed Medium 1–4 realize the longitudinal electromagnetic crossing for the upper and lower Medium 5. The fixed transverse vectors k_x and k_y can be selected as 12 rad/m and 34 rad/m. Considering frequency range of [4.0 GHsz, 14.0 GHz], we can obtain the reflection and transmission coefficient in the TE and TM modes. For the duality principle, the reflection and transmission coefficient can also be obtained in Figure 9 under their corresponding dual field. Obviously, under the Bloch-Floquet periodic boundary, the vertical and horizontal medium mutations do not affect the dual relationship of fully anisotropy. From this point of view, Equation (8) meets the requirements of numerical prediction.

5. Conclusions

The discussion of anisotropy is rarely published in lots of papers. Fewer people have analyzed and introduced the feasibility and effectiveness of the duality principle on the numerical anisotropy. In this paper, we concentrate on the dual relationship from the traditional isotropic extension to a wider range of anisotropy, and its correctness is verified by numerical algorithm, such as the fully anisotropic FDTD method. The duality principle belongs to a common means for handling the engineering applications and physical experiments, but it is not far enough for everyone to deeply understand and explore more in the numerical research of the fully anisotropy. Our proposed duality principle can not only adapt to the 3D fully anisotropic FDTD method, but also suit the other numerical verifications with the complicated anisotropies. Generally in experiment, the plane wave is either a simple vertical incidence, or known incident angle or electric field direction. However, the specific plane-wave mode, such as the TE or TM modes, is difficult to be calibrated. By employing the 3D FDTD method, we successfully achieve the exchange rule of duality principle to the equivalent electromagnetics on the Bloch-Floquet PBC, and master the plane-wave direction and the specific properties of those fully anisotropies. Meanwhile, the fully anisotropic duality principle can be adopted to determine the transmission characteristics under another mode by the numerical simulation, which can be applied to guiding theory for the unknown topics on the engineering applications or the physical experiments. With the high accuracy by electromagnetic computation and detection of subsurface echoes, we believe that the duality principle, as an important verification means, will be widespread in the more numerical algorithm because of the high symmetry from the Maxwell’s Equations.