Gaussian Process Regression Model for Crop Biophysical Parameter Retrieval from Multi-Polarized C-Band SAR Data
Abstract
:1. Introduction
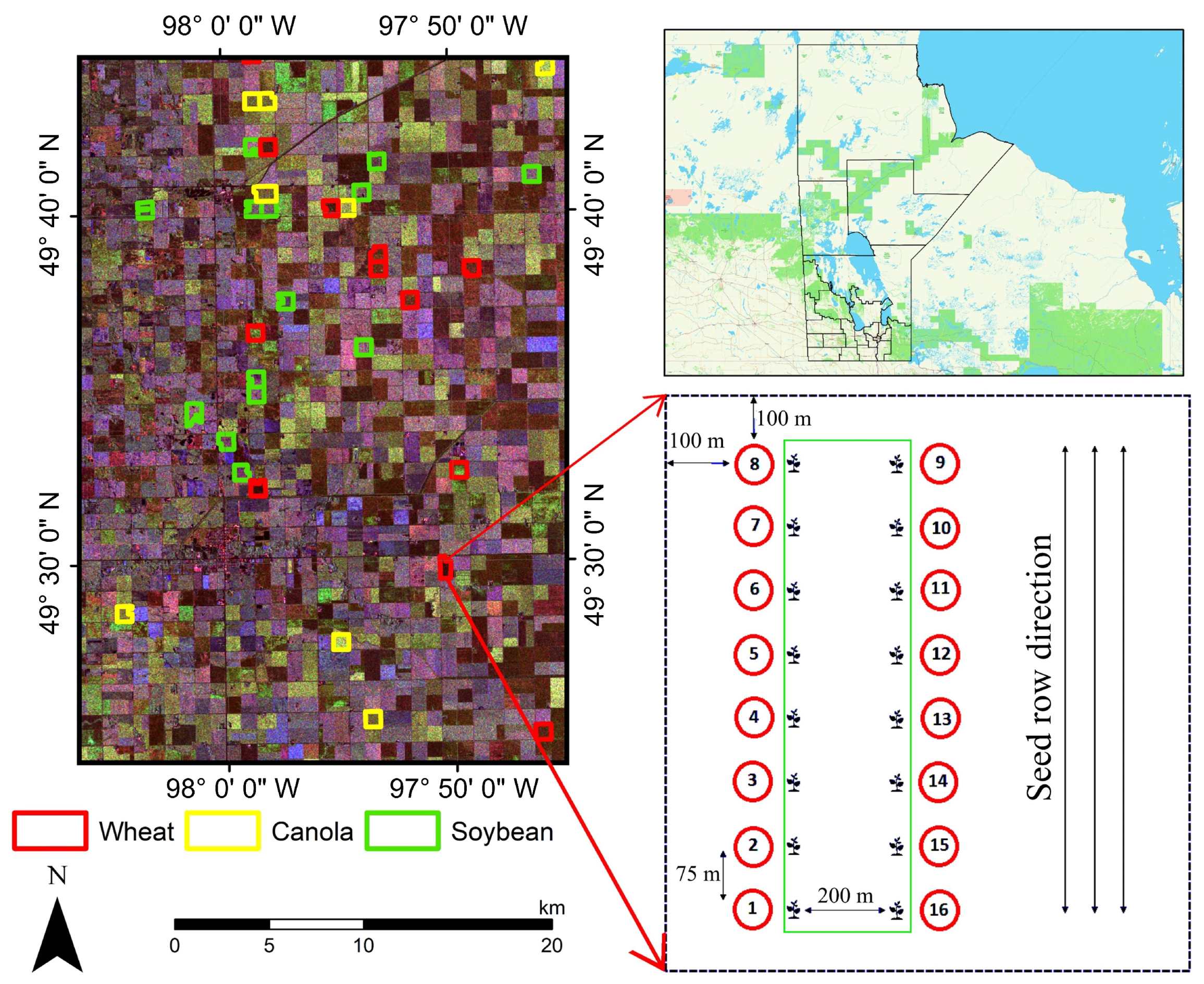
2. Study Area and Dataset
2.1. Sampling Strategy
2.2. SAR Data Processing
3. Methodology
3.1. Gaussian Process Regression
3.1.1. Notations
3.1.2. Kernel Functions
3.1.3. Prediction
3.1.4. Optimization
3.2. Data Preparation
3.2.1. Data Skewness Analysis
3.2.2. Experimental Design
4. Results and Discussions
4.1. Sensitivity Analysis of HH, HV, VV to Crop Development
4.1.1. Wheat
4.1.2. Canola
4.1.3. Soybean
4.2. Correlation Analysis: Backscatter vs. Biophysical Parameters
4.2.1. Wheat
4.2.2. Canola
4.2.3. Soybeans
4.3. Biophysical Parameter Estimation
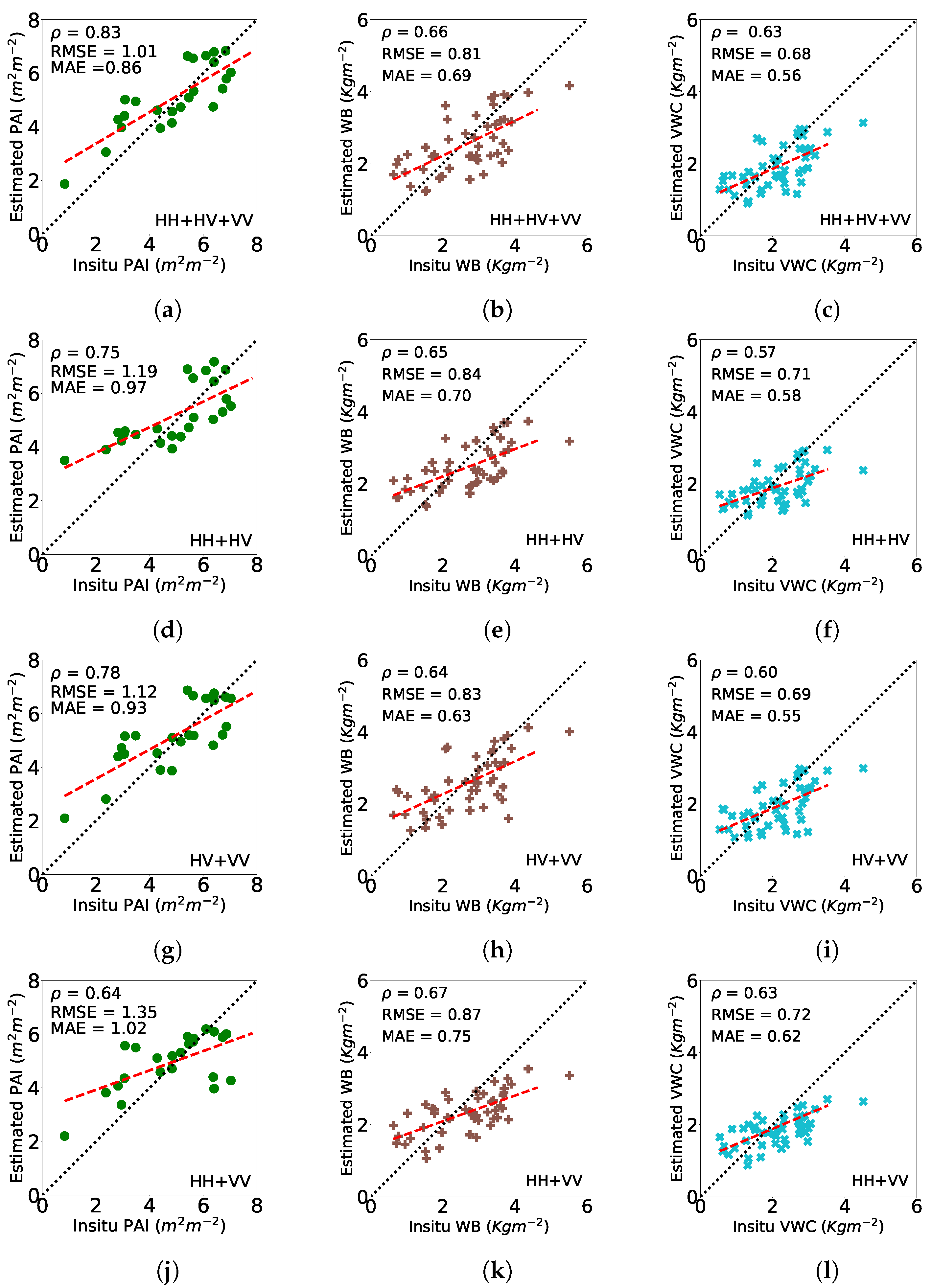
4.3.1. Wheat
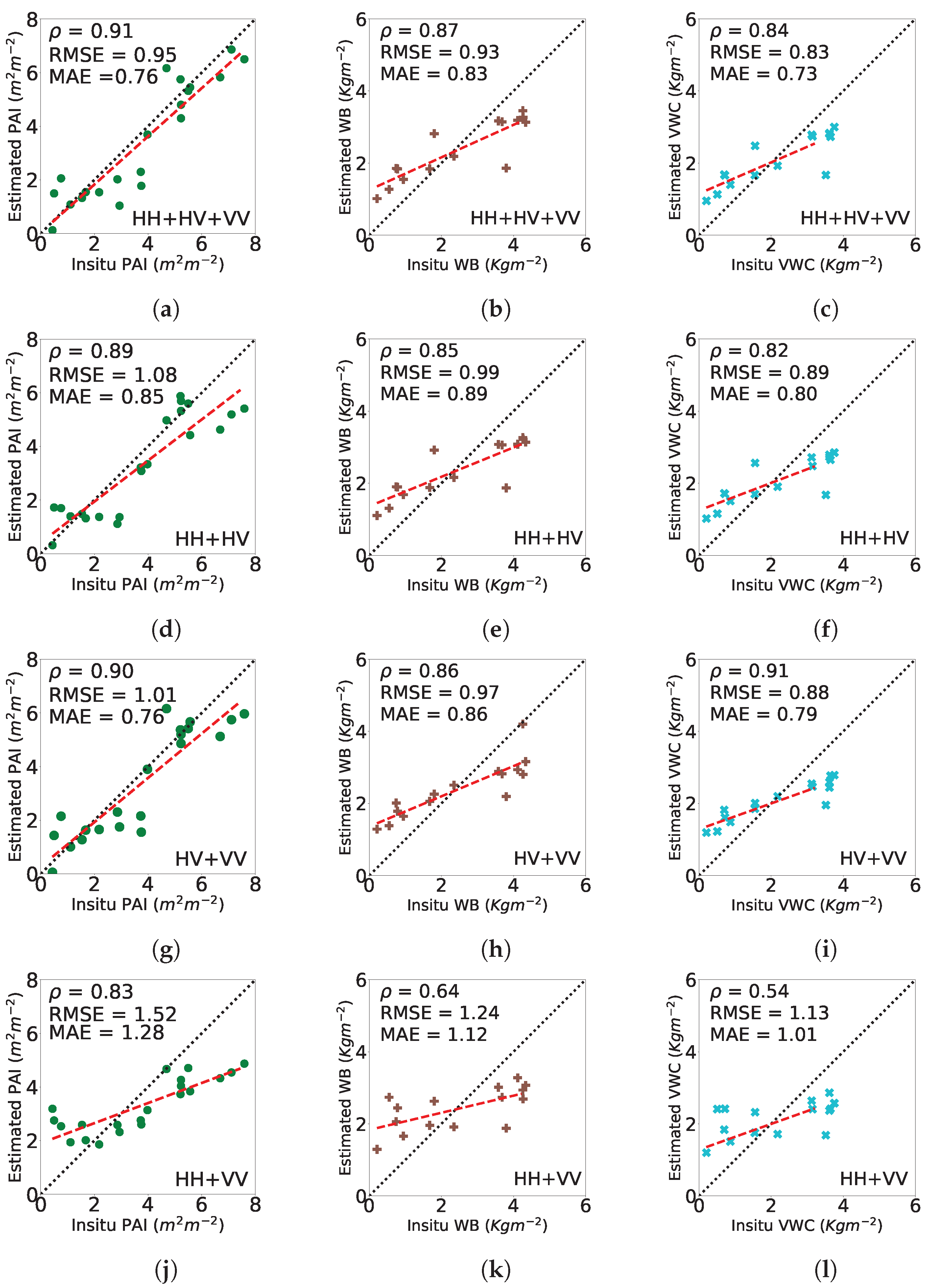
4.3.2. Canola
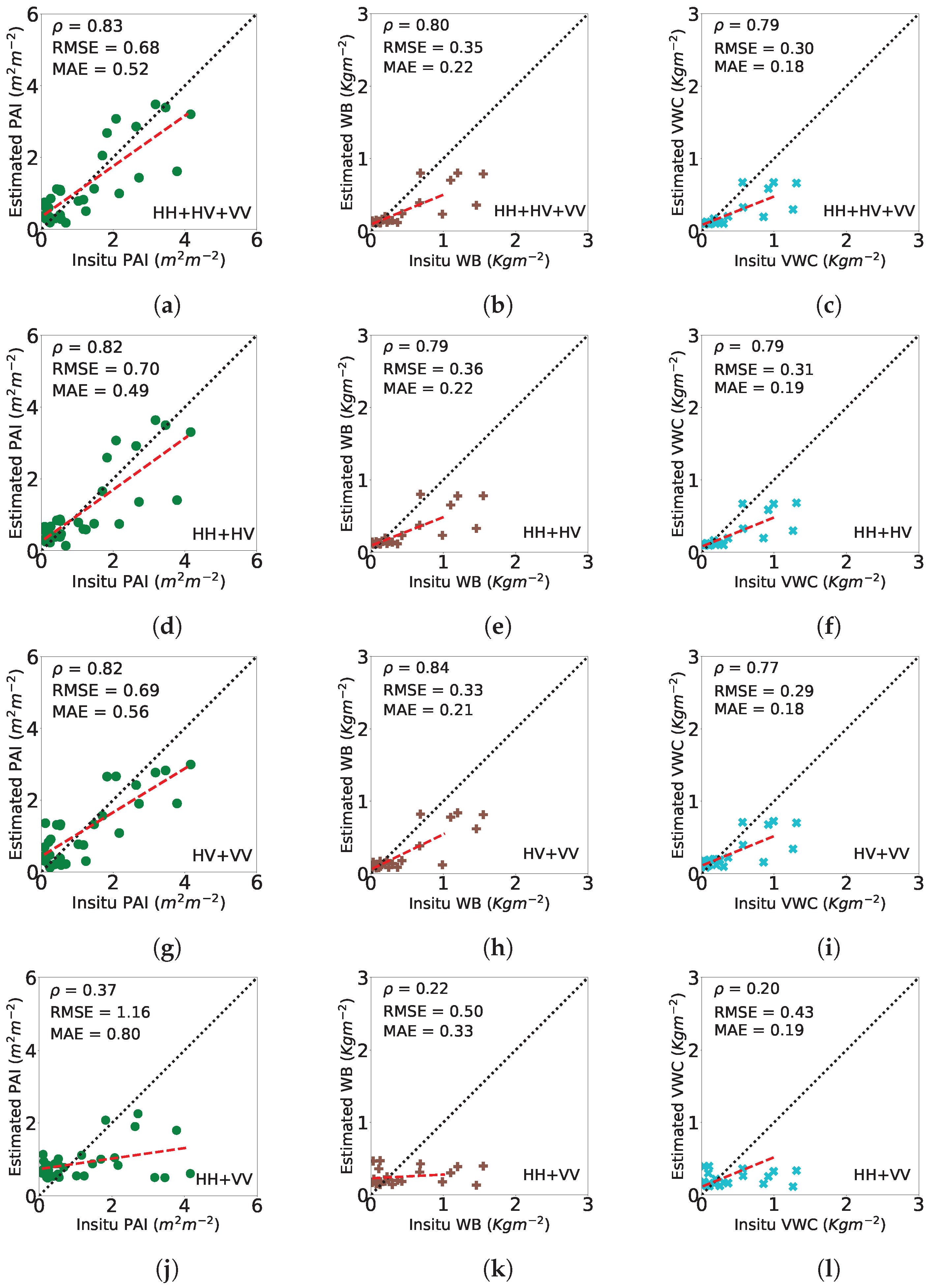
4.3.3. Soybeans
4.4. Limitations and Scope for Future Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 15 June | 23 June | 9 July | 17 July | ||
|---|---|---|---|---|---|
| Wheat | Phenology | Tillering stage | Booting stage | Early flowering stage | Early dough stage |
| PAI | 0.83–5.20 | 2.95–7.70 | 4.37–7.72 | 5.13–8.80 | |
| WB | 0.43–3.45 | 0.78–3.59 | 2.02–5.90 | 1.51–4.26 | |
| VWC | 0.36–2.99 | 0.67–3.01 | 0.97–4.86 | 0.97–3.05 | |
| Canola | Phenology | Leaf development | Inflorescence emergence | Flowering stage | Pod development |
| PAI | 0.39–1.79 | 0.16–6.12 | 1.82–6.35 | 3.64–8.33 | |
| WB | 0.21–1.99 | 0.78–3.79 | 1.80–5.03 | 2.60–4.47 | |
| VWC | 0.20–1.84 | 0.71–3.51 | 1.55–4.35 | 2.24–3.90 | |
| Soybean | Phenology | Leaf development | Fifth trifoliate stage | Pod development | Flowering stage |
| PAI | 0.07–0.94 | 0.01–0.55 | 0.27–5.70 | 0.25–4.18 | |
| WB | 0.02–0.13 | 0.03–0.42 | 0.07–1.45 | 0.13–1.63 | |
| VWC | 0.01–0.11 | 0.03–0.36 | 0.06–1.26 | 0.11–1.33 |
References
- Bettina, B.; Antoine, R.; Anja, K.; Giampiero, G. The Use of Remote Sensing Within the Mars Crop Yield Monitoring System of the European Commission. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 935–940. [Google Scholar]
- Boogaard, H.; Wolf, J.; Supit, I.; Niemeyer, S.; van Ittersum, M.K. A regional implementation of WOFOST for calculating yield gaps of autumn-sown wheat across the European Union. Field Crops Res. 2013, 143, 130–142. [Google Scholar] [CrossRef]
- Kross, A.; Mcnairn, H.; Lapen, D.R.; Sunohara, M.; Champagne, C. Assessment of RapidEye vegetation indices for estimation of leaf area index and biomass in corn and soybean crops. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 235–248. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Xiao, X.; Bajgain, R.; Starks, P.J.; Steiner, J.L.; Doughty, R.B.; Chang, Q. Estimating leaf area index and aboveground biomass of grazing pastures using Sentinel-1, Sentinel-2 and Landsat images. ISPRS J. Photogramm. Remote Sens. 2019, 154, 189–201. [Google Scholar] [CrossRef] [Green Version]
- Jia, M.; Tong, L.; Zhang, Y.; Chen, Y. Rice Biomass Estimation Using Radar Backscattering Data at S-band. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 469–479. [Google Scholar] [CrossRef]
- Huang, Y.; Walker, J.P.; Gao, Y.; Wu, X.; Monerris, A. Estimation of Vegetation Water Content From the Radar Vegetation Index at L-Band. IEEE Trans. Geosci. Remote Sens. 2016, 54, 981–989. [Google Scholar] [CrossRef]
- Bhogapurapu, N.; Dey, S.; Bhattacharya, A.; Mandal, D.; Lopez-Sanchez, J.M.; McNairn, H.; López-Martínez, C.; Rao, Y.S. Dual-polarimetric descriptors from Sentinel-1 GRD SAR data for crop growth assessment. ISPRS J. Photogramm. Remote Sens. 2021, 178, 20–35. [Google Scholar] [CrossRef]
- Mcnairn, H.; Brisco, B. The application of C-band polarimetric SAR for agriculture: A review. Can. J. Remote Sens. 2004, 30, 525–542. [Google Scholar] [CrossRef]
- Ulaby, F.T. Radar response to vegetation. IEEE Trans. Antennas Propag. 1975, 23, 36–45. [Google Scholar] [CrossRef]
- Steele-Dunne, S.C.; Mcnairn, H.; Monsiváis-Huertero, A.; Judge, J.; Liu, P.W.; Papathanassiou, K.P. Radar Remote Sensing of Agricultural Canopies: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2249–2273. [Google Scholar] [CrossRef] [Green Version]
- Cable, J.W.; Kovacs, J.M.; Jiao, X.; Shang, J. Agricultural Monitoring in Northeastern Ontario, Canada, Using Multi-Temporal Polarimetric RADARSAT-2 Data. Remote Sens. 2014, 6, 2343–2371. [Google Scholar] [CrossRef] [Green Version]
- Inoue, Y.; Kurosu, T.; Maeno, H.; Uratsuka, S.; Kozu, T.; Dabrowska-Zielinska, K.; Qi, J. Season-long daily measurements of multifrequency (Ka, Ku, X, C, and L) and full-polarization backscatter signatures over paddy rice field and their relationship with biological variables. Remote Sens. Environ. 2002, 81, 194–204. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E. Relationship between X-band backscattering coefficients from high-resolution satellite SAR and biophysical variables in paddy rice. Remote Sens. Lett. 2013, 4, 288–295. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Wang, C. Capability of C-band backscattering coefficients from high-resolution satellite SAR sensors to assess biophysical variables in paddy rice. Remote Sens. Environ. 2014, 140, 257–266. [Google Scholar] [CrossRef]
- Wiseman, G.; Mcnairn, H.; Homayouni, S.; Shang, J. RADARSAT-2 Polarimetric SAR Response to Crop Biomass for Agricultural Production Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4461–4471. [Google Scholar] [CrossRef]
- Bériaux, E.; Waldner, F.; Collienne, F.; Bogaert, P.; Defourny, P. Maize Leaf Area Index Retrieval from Synthetic Quad Pol SAR Time Series Using the Water Cloud Model. Remote Sens. 2015, 7, 16204–16225. [Google Scholar] [CrossRef] [Green Version]
- Yuzugullu, O.; Marelli, S.P.; Erten, E.; Sudret, B.; Hajnsek, I. Determining Rice Growth Stage with X-Band SAR: A Metamodel Based Inversion. Remote Sens. 2017, 9, 460. [Google Scholar] [CrossRef] [Green Version]
- Pichierri, M.; Hajnsek, I.; Zwieback, S.; Rabus, B.T. On the potential of Polarimetric SAR Interferometry to characterize the biomass, moisture and structure of agricultural crops at L-, C- and X-Bands. Remote Sens. Environ. 2018, 204, 596–616. [Google Scholar] [CrossRef]
- Jiao, X.; Mcnairn, H.; Shang, J.; Pattey, E.; Liu, J.; Champagne, C. The sensitivity of RADARSAT-2 polarimetric SAR data to corn and soybean leaf area index. Can. J. Remote Sens. 2011, 37, 69–81. [Google Scholar] [CrossRef]
- Jiao, X.; McNairn, H.; Shang, J.; Liu, J. The sensitivity of multi-frequency (X, C and L-band) radar backscatter signatures to bio-physical variables (LAI) over corn and soybean fields. In Proceedings of the ISPRS TC VII Symposium—100 Years ISPRS, Vienna, Austria, 5–7 July 2010; Volume 38, pp. 317–321. [Google Scholar]
- Fontanelli, G.; Paloscia, S.; Zribi, M.; Chahbi, A. Sensitivity analysis of X-band SAR to wheat and barley leaf area index in the Merguellil Basin. Remote Sens. Lett. 2013, 4, 1107–1116. [Google Scholar] [CrossRef] [Green Version]
- Ulaby, F.T.; Sarabandi, K.; McDonald, K.; Whitt, M.W.; Dobson, M.C. Michigan microwave canopy scattering model. Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Prévot, L.; Champion, I.; Guyot, G. Estimating surface soil moisture and leaf area index of a wheat canopy using a dual-frequency (C and X bands) scatterometer. Remote Sens. Environ. 1993, 46, 331–339. [Google Scholar] [CrossRef]
- Karam, M.A.; Amar, F.; Fung, A.K.; Mougin, E.; Lopes, A.; Vine, D.M.L.; Beaudoin, A. A microwave polarimetric scattering model for forest canopies based on vector radiative transfer theory. Remote Sens. Environ. 1995, 53, 16–30. [Google Scholar] [CrossRef]
- Roo, R.D.D.; Du, Y.; Ulaby, F.T.; Dobson, M.C. A semi-empirical backscattering model at L-band and C-band for a soybean canopy with soil moisture inversion. IEEE Trans. Geosci. Remote Sens. 2001, 39, 864–872. [Google Scholar] [CrossRef]
- Attema, E.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Graham, A.; Harris, R. Extracting biophysical parameters from remotely sensed radar data: A review of the water cloud model. Prog. Phys. Geogr. 2003, 27, 217–229. [Google Scholar] [CrossRef]
- Hosseini, M.; Mcnairn, H. Using multi-polarization C- and L-band synthetic aperture radar to estimate biomass and soil moisture of wheat fields. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 50–64. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Lopez-Sanchez, J.M.; Bhattacharya, A.; Mcnairn, H.; Rao, Y.S. Crop biophysical parameter retrieval from Sentinel-1 SAR data with a multi-target inversion of Water Cloud Model. Int. J. Remote Sens. 2020, 41, 5503–5524. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Mcnairn, H.; Bhattacharya, A.; Rao, Y.S. Joint estimation of Plant Area Index (PAI) and wet biomass in wheat and soybean from C-band polarimetric SAR data. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 24–34. [Google Scholar] [CrossRef]
- Hosseini, M.; McNairn, H.; Mitchell, S.; Robertson, L.D.; Davidson, A.; Ahmadian, N.; Bhattacharya, A.; Borg, E.; Conrad, C.; Dabrowska-Zielinska, K.; et al. A comparison between support vector machine and water cloud model for estimating crop leaf area index. Remote Sens. 2021, 13, 1348. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.; Moreno, J.F. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. Isprs J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.; Camps-Valls, G.; Moreno, J.F. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods - A comparison. Isprs J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz, J.S.; Alonso, L.; Delegido, J.; Rivera, J.P.; Camps-Valls, G.; Moreno, J.F. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bruzzone, L.; Rojo-álvarez, J.L.; Melgani, F. Robust support vector regression for biophysical variable estimation from remotely sensed images. IEEE Geosci. Remote Sens. Lett. 2006, 3, 339–343. [Google Scholar] [CrossRef]
- Kganyago, M.; Mhangara, P.; Adjorlolo, C. Estimating Crop Biophysical Parameters Using Machine Learning Algorithms and Sentinel-2 Imagery. Remote Sens. 2021, 13, 4314. [Google Scholar] [CrossRef]
- Prins, A.J.; Niekerk, A.V. Crop type mapping using LiDAR, Sentinel-2 and aerial imagery with machine learning algorithms. Geo-Spat. Inf. Sci. 2021, 24, 215–227. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Bhattacharya, A.; Rao, Y.S.; Mcnairn, H. Crop Biophysical Parameters Estimation with a Multi-Target Inversion Scheme using the Sentinel-1 SAR Data. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6611–6614. [Google Scholar]
- Dey, S.; Chaudhuri, U.; Mandal, D.; Bhattacharya, A.; Banerjee, B.; Mcnairn, H. BiophyNet: A Regression Network for Joint Estimation of Plant Area Index and Wet Biomass From SAR Data. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1701–1705. [Google Scholar] [CrossRef]
- Sharifi, A.; Hosseingholizadeh, M. Application of Sentinel-1 Data to Estimate Height and Biomass of Rice Crop in Astaneh-ye Ashrafiyeh, Iran. J. Indian Soc. Remote Sens. 2019, 48, 11–19. [Google Scholar] [CrossRef]
- Bahrami, H.; Homayouni, S.; Safari, A.; Mirzaei, S.; Mahdianpari, M.; Reisi-Gahrouei, O. Deep Learning-Based Estimation of Crop Biophysical Parameters Using Multi-Source and Multi-Temporal Remote Sensing Observations. Agronomy 2021, 11, 1363. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Verrelst, J.; Muñoz-Marí, J.; Laparra, V.; Mateo-Jimenez, F.; Gómez-Dans, J.L. A Survey on Gaussian Processes for Earth-Observation Data Analysis: A Comprehensive Investigation. IEEE Geosci. Remote Sens. Mag. 2016, 4, 58–78. [Google Scholar] [CrossRef] [Green Version]
- Verrelst, J.; Alonso, L.; Caicedo, J.P.R.; Moreno, J.F.; Camps-Valls, G. Gaussian Process Retrieval of Chlorophyll Content From Imaging Spectroscopy Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 867–874. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Moreno, J.F.; Camps-Valls, G. Gaussian Processes uncertainty estimates in experimental Sentinel-2 LAI and leaf chlorophyll content retrieval. Isprs J. Photogramm. Remote Sens. 2013, 86, 157–167. [Google Scholar] [CrossRef]
- Royo, C.; Villegas, D. Field Measurements of Canopy Spectra for Biomass Assessment of Small-Grain Cereals. In Biomass-Detect Prod Usage; IntechOpen: London, UK, 2011; Volume 52. [Google Scholar]
- Mcnairn, H.; Shang, J. A Review of Multitemporal Synthetic Aperture Radar (SAR) for Crop Monitoring. Multitemporal Remote Sens. 2016, 317–340. [Google Scholar] [CrossRef]
- Bhuiyan, H.A.K.M.; Mcnairn, H.; Powers, J.; Friesen, M.; Pacheco, A.; Jackson, T.J.; Cosh, M.H.; Colliander, A.; Berg, A.A.; Rowlandson, T.L.; et al. Assessing SMAP Soil Moisture Scaling and Retrieval in the Carman (Canada) Study Site. Vadose Zone J. 2018, 17, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Mcnairn, H.; Jackson, T.J.; Wiseman, G.; Belair, S.; Berg, A.A.; Bullock, P.; Colliander, A.; Cosh, M.H.; Kim, S.; Magagi, R.; et al. The Soil Moisture Active Passive Validation Experiment 2012 (SMAPVEX12): Prelaunch Calibration and Validation of the SMAP Soil Moisture Algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2784–2801. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Gómez-Chova, L.; Muñoz-Marí, J.; Vila-Francés, J.; Amorós-López, J.; Calpe-Maravilla, J. Retrieval of oceanic chlorophyll concentration with relevance vector machines. Remote Sens. Environ. 2006, 105, 23–33. [Google Scholar] [CrossRef]
- Rasmussen, C.; Williams, C.K.I. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); The MIT Press: Cambridge, UK, 2005. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An Analysis of Transformations. J. R. Stat. Soc. Ser. B-Methodol. 1964, 26, 211–243. [Google Scholar] [CrossRef]
- GPy. GPy: A Gaussian Process Framework in Python. 2012. Available online: http://github.com/SheffieldML/GPy (accessed on 28 October 2021).
- Cortes, C.; Vapnik, V.N. Support-Vector Networks. Mach. Learn. 2004, 20, 273–297. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support Vector Regression; Springer: Berlin, Germany, 2015; pp. 67–80. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2004, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Brown, S.C.M.; Quegan, S.; Morrison, K.; Bennett, J.C.; Cookmartin, G. High-resolution measurements of scattering in wheat canopies-implications for crop parameter retrieval. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1602–1610. [Google Scholar] [CrossRef] [Green Version]
- Jia, M.; Tong, L.; Zhang, Y.; Chen, Y. Multitemporal radar backscattering measurement of wheat fields using multifrequency (L, S, C, and X) and full-polarization. Radio Sci. 2013, 48, 471–481. [Google Scholar] [CrossRef]
- Han, J.; Zhang, Z.; Cao, J. Developing a New Method to Identify Flowering Dynamics of Rapeseed Using Landsat 8 and Sentinel-1/2. Remote Sens. 2021, 13, 105. [Google Scholar] [CrossRef]
- Ratha, D.; Mandal, D.; Kumar, V.; Mcnairn, H.; Bhattacharya, A.; Frery, A.C. A Generalized Volume Scattering Model-Based Vegetation Index From Polarimetric SAR Data. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1791–1795. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Kumar, V.; Ratha, D.; Dey, S.; Bhattacharya, A.; Lopez-Sanchez, J.M.; Mcnairn, H.; Rao, Y.S. Dual polarimetric radar vegetation index for crop growth monitoring using sentinel-1 SAR data. Remote Sens. Environ. 2020, 247, 111954. [Google Scholar] [CrossRef]
- Pacheco, A.; Mcnairn, H.; Li, Y.; Lampropoulos, G.A.; Powers, J. Using RADARSAT-2 and TerraSAR-X satellite data for the identification of canola crop phenology. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XVIII; International Society for Optics and Photonics: Bellingham, DC, USA, 2016; Volume 9998, p. 999802. [Google Scholar]


| Acquisition Date | Day of Year (DOY) | Beam Mode | Incidence Angle Range (Deg.) | In-Situ Measurement Window |
|---|---|---|---|---|
| 15 June 2016 | 167 | FQ7W | 24.98–28.32 | 13 June, 15 June |
| 23 June 2016 | 175 | FQ7W | 24.98–28.32 | 18 June, 20 June, 27 Jun |
| 9 July 2016 | 191 | FQ7W | 24.98–28.32 | 6 July, 11 July, 12 July |
| 17 July 2016 | 199 | FQ7W | 24.98–28.32 | 17 July, 20 July, 21 July |
| Crop | Variables | Initial Skewness | Values | Final Skewness |
|---|---|---|---|---|
| Wheat | HH | 1.293 | −0.013 | |
| HV | 2.437 | −0.569 | ||
| VV | 1.222 | −0.379 | ||
| PAI | −0.270 | 1.120 | − | |
| Canola | HH | 0.898 | −0.122 | |
| HV | 1.995 | 0.200 | ||
| VV | 0.515 | 0.220 | −3. | |
| PAI | 0.246 | 0.519 | − | |
| Soybean | HH | 1.090 | −0.310 | |
| HV | 1.550 | −0.311 | ||
| VV | 0.698 | 0.009 | − | |
| PAI | 0.819 | 0.149 | − |
| Crop | Variables | Initial Skewness | Values | Final Skewness |
|---|---|---|---|---|
| Wheat | HH | 1.108 | 0.027 | − |
| HV | 1.789 | −0.365 | ||
| VV | 1.192 | −0.494 | ||
| WB | 0.150 | 0.754 | − | |
| VWC | 0.311 | 0.693 | − | |
| Canola | HH | 0.675 | 0.179 | − |
| HV | 1.325 | 0.305 | ||
| VV | 0.869 | 0.252 | − | |
| WB | 0.089 | 0.644 | − | |
| VWC | 0.069 | 0.673 | − | |
| Soybean | HH | 0.859 | −0.034 | |
| HV | 1.548 | −0.398 | ||
| VV | 0.909 | 0.004 | − | |
| WB | 1.552 | 0.042 | − | |
| VWC | 1.567 | 0.043 | − |
| PAI | HH | −0.63 | −0.35 | −0.18 | 0.26 | −0.57 |
| HV | −0.12 | −0.73 | −0.39 | 0.49 | 0.05 | |
| VV | −0.59 | −0.68 | −0.29 | 0.12 | −0.69 | |
| WB | HH | −0.08 | −0.69 | −0.26 | −0.16 | −0.51 |
| HV | −0.01 | −0.19 | −0.26 | 0.06 | −0.23 | |
| VV | −0.03 | −0.65 | −0.31 | 0.06 | −0.47 | |
| VWC | HH | −0.09 | −0.67 | −0.20 | −0.07 | −0.47 |
| HV | −0.01 | −0.18 | −0.29 | 0.13 | −0.24 | |
| VV | −0.03 | −0.63 | −0.29 | 0.13 | −0.46 |
| PAI | HH | 0.55 | −0.30 | −0.21 | 0.09 | −0.51 |
| HV | 0.27 | 0.38 | 0.31 | −0.01 | 0.47 | |
| VV | 0.28 | −0.12 | 0.01 | 0.02 | −0.48 | |
| WB | HH | 0.26 | 0.56 | −0.06 | −0.43 | −0.55 |
| HV | 0.43 | 0.51 | −0.20 | −0.64 | 0.13 | |
| VV | −0.04 | 0.41 | −0.55 | −0.10 | −0.58 | |
| VWC | HH | 0.26 | 0.56 | −0.10 | −0.48 | −0.54 |
| HV | 0.41 | 0.52 | −0.24 | −0.66 | 0.12 | |
| VV | −0.03 | 0.40 | −0.57 | −0.14 | −0.57 |
| PAI | HH | −0.09 | 0.09 | 0.26 | 0.03 | 0.39 |
| HV | 0.23 | 0.55 | 0.56 | 0.32 | 0.64 | |
| VV | −0.25 | −0.08 | 0.47 | 0.26 | 0.31 | |
| WB | HH | 0.34 | 0.11 | −0.01 | −0.09 | 0.38 |
| HV | −0.01 | 0.54 | 0.54 | 0.56 | 0.77 | |
| VV | 0.23 | −0.06 | 0.09 | 0.26 | 0.34 | |
| VWC | HH | 0.33 | 0.10 | −0.01 | −0.09 | 0.37 |
| HV | −0.01 | 0.56 | 0.54 | 0.56 | 0.76 | |
| VV | 0.21 | −0.08 | 0.09 | 0.26 | 0.33 |
| Linear Polarization Combinations | p-Value | ||
|---|---|---|---|
| PAI | HH+HV+VV | 0.83 | |
| HH+HV | 0.75 | ||
| HV+VV | 0.78 | ||
| HH+VV | 0.64 | ||
| WB | HH+HV+VV | 0.66 | |
| HH+HV | 0.65 | ||
| HV+VV | 0.64 | ||
| HH+VV | 0.67 | ||
| VWC | HH+HV+VV | 0.63 | |
| HH+HV | 0.57 | ||
| HV+VV | 0.60 | ||
| HH+VV | 0.63 |
| Algorithm | RMSE | MAE | R2 | ||
|---|---|---|---|---|---|
| PAI | GPR | 1.12 | 0.93 | 0.78 | 0.61 |
| SVR | 1.39 | 1.09 | 0.63 | 0.40 | |
| RFR | 1.48 | 1.19 | 0.61 | 0.36 | |
| WB | GPR | 0.83 | 0.63 | 0.64 | 0.41 |
| SVR | 0.92 | 0.76 | 0.54 | 0.30 | |
| RFR | 0.86 | 0.72 | 0.60 | 0.36 | |
| VWC | GPR | 0.69 | 0.55 | 0.60 | 0.37 |
| SVR | 0.74 | 0.60 | 0.49 | 0.25 | |
| RFR | 0.68 | 0.56 | 0.59 | 0.35 |
| Linear Polarization Combinations | p-Value | ||
|---|---|---|---|
| PAI | HH+HV+VV | 0.91 | |
| HH+HV | 0.89 | ||
| HV+VV | 0.90 | ||
| HH+VV | 0.83 | ||
| WB | HH+HV+VV | 0.87 | |
| HH+HV | 0.85 | ||
| HV+VV | 0.86 | ||
| HH+VV | 0.64 | ||
| VWC | HH+HV+VV | 0.84 | |
| HH+HV | 0.82 | ||
| HV+VV | 0.91 | ||
| HH+VV | 0.54 |
| Algorithm | RMSE | MAE | R2 | ||
|---|---|---|---|---|---|
| PAI | GPR | 1.01 | 0.76 | 0.90 | 0.81 |
| SVR | 1.47 | 1.18 | 0.86 | 0.74 | |
| RFR | 1.11 | 0.85 | 0.89 | 0.79 | |
| WB | GPR | 0.97 | 0.86 | 0.86 | 0.75 |
| SVR | 1.17 | 0.99 | 0.73 | 0.53 | |
| RFR | 1.04 | 0.88 | 0.76 | 0.58 | |
| VWC | GPR | 0.88 | 0.79 | 0.91 | 0.83 |
| SVR | 1.04 | 0.90 | 0.71 | 0.52 | |
| RFR | 0.94 | 0.79 | 0.73 | 0.53 |
| Linear Polarization Combinations | p-Value | ||
|---|---|---|---|
| PAI | HH+HV+VV | 0.83 | |
| HH+HV | 0.82 | ||
| HV+VV | 0.82 | ||
| HH+VV | 0.37 | ||
| WB | HH+HV+VV | 0.80 | |
| HH+HV | 0.79 | ||
| HV+VV | 0.84 | ||
| HH+VV | 0.22 | ||
| VWC | HH+HV+VV | 0.79 | |
| HH+HV | 0.79 | ||
| HV+VV | 0.77 | ||
| HH+VV | 0.20 |
| Algorithm | RMSE | MAE | R2 | ||
|---|---|---|---|---|---|
| PAI | GPR | 0.69 | 0.56 | 0.82 | 0.67 |
| SVR | 1.21 | 0.85 | 0.57 | 0.32 | |
| RFR | 1.08 | 0.82 | 0.62 | 0.39 | |
| WB | GPR | 0.33 | 0.21 | 0.84 | 0.70 |
| SVR | 0.35 | 0.22 | 0.78 | 0.60 | |
| RFR | 0.35 | 0.22 | 0.76 | 0.57 | |
| VWC | GPR | 0.29 | 0.18 | 0.77 | 0.59 |
| SVR | 0.31 | 0.19 | 0.77 | 0.59 | |
| RFR | 0.30 | 0.19 | 0.76 | 0.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghosh, S.S.; Dey, S.; Bhogapurapu, N.; Homayouni, S.; Bhattacharya, A.; McNairn, H. Gaussian Process Regression Model for Crop Biophysical Parameter Retrieval from Multi-Polarized C-Band SAR Data. Remote Sens. 2022, 14, 934. https://doi.org/10.3390/rs14040934
Ghosh SS, Dey S, Bhogapurapu N, Homayouni S, Bhattacharya A, McNairn H. Gaussian Process Regression Model for Crop Biophysical Parameter Retrieval from Multi-Polarized C-Band SAR Data. Remote Sensing. 2022; 14(4):934. https://doi.org/10.3390/rs14040934
Chicago/Turabian StyleGhosh, Swarnendu Sekhar, Subhadip Dey, Narayanarao Bhogapurapu, Saeid Homayouni, Avik Bhattacharya, and Heather McNairn. 2022. "Gaussian Process Regression Model for Crop Biophysical Parameter Retrieval from Multi-Polarized C-Band SAR Data" Remote Sensing 14, no. 4: 934. https://doi.org/10.3390/rs14040934
APA StyleGhosh, S. S., Dey, S., Bhogapurapu, N., Homayouni, S., Bhattacharya, A., & McNairn, H. (2022). Gaussian Process Regression Model for Crop Biophysical Parameter Retrieval from Multi-Polarized C-Band SAR Data. Remote Sensing, 14(4), 934. https://doi.org/10.3390/rs14040934








