A Global Conversion Factor Model for Mapping Zenith Total Delay onto Precipitable Water
Abstract
:1. Introduction
2. Method of Establishing the GΠ Model
2.1. Methods of Obtaining the Conversion Factor
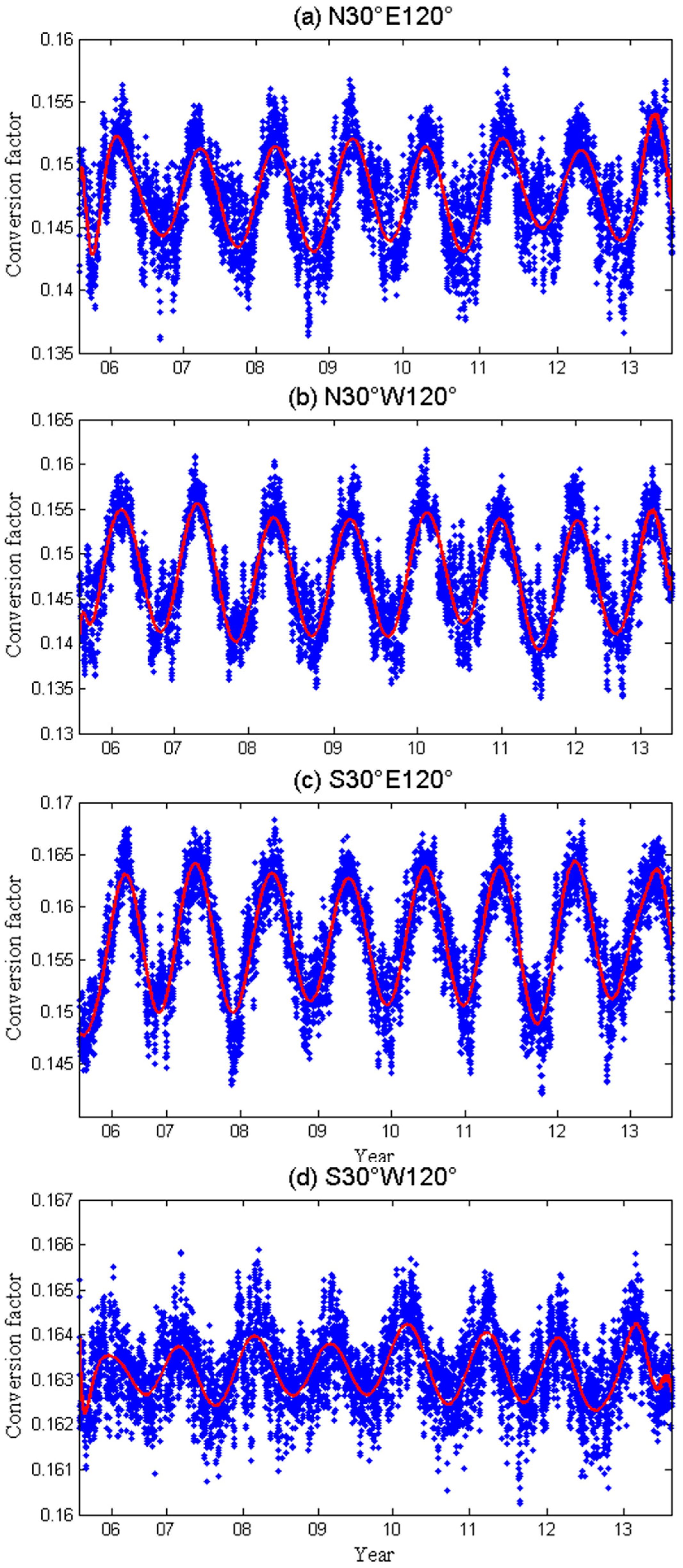
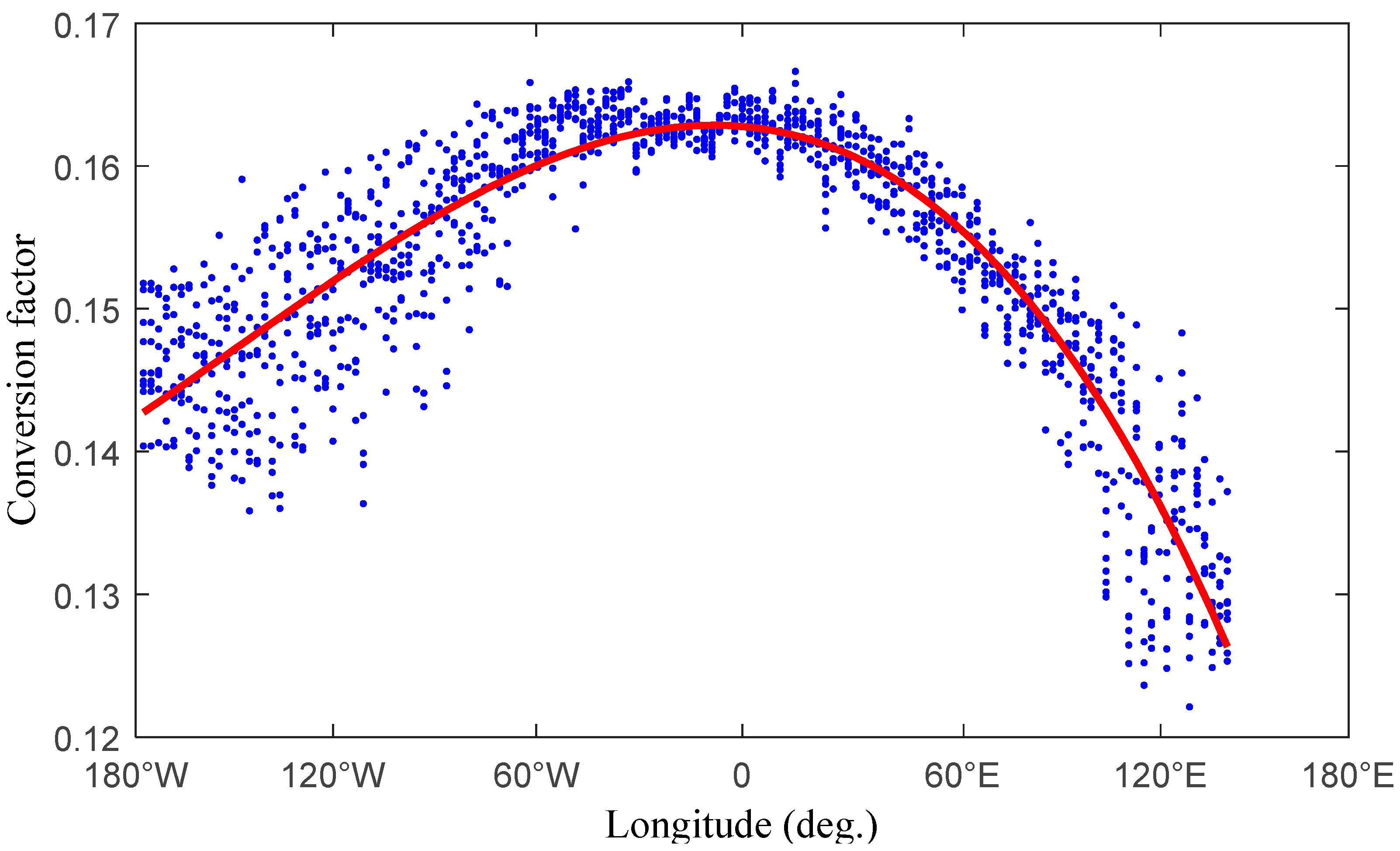
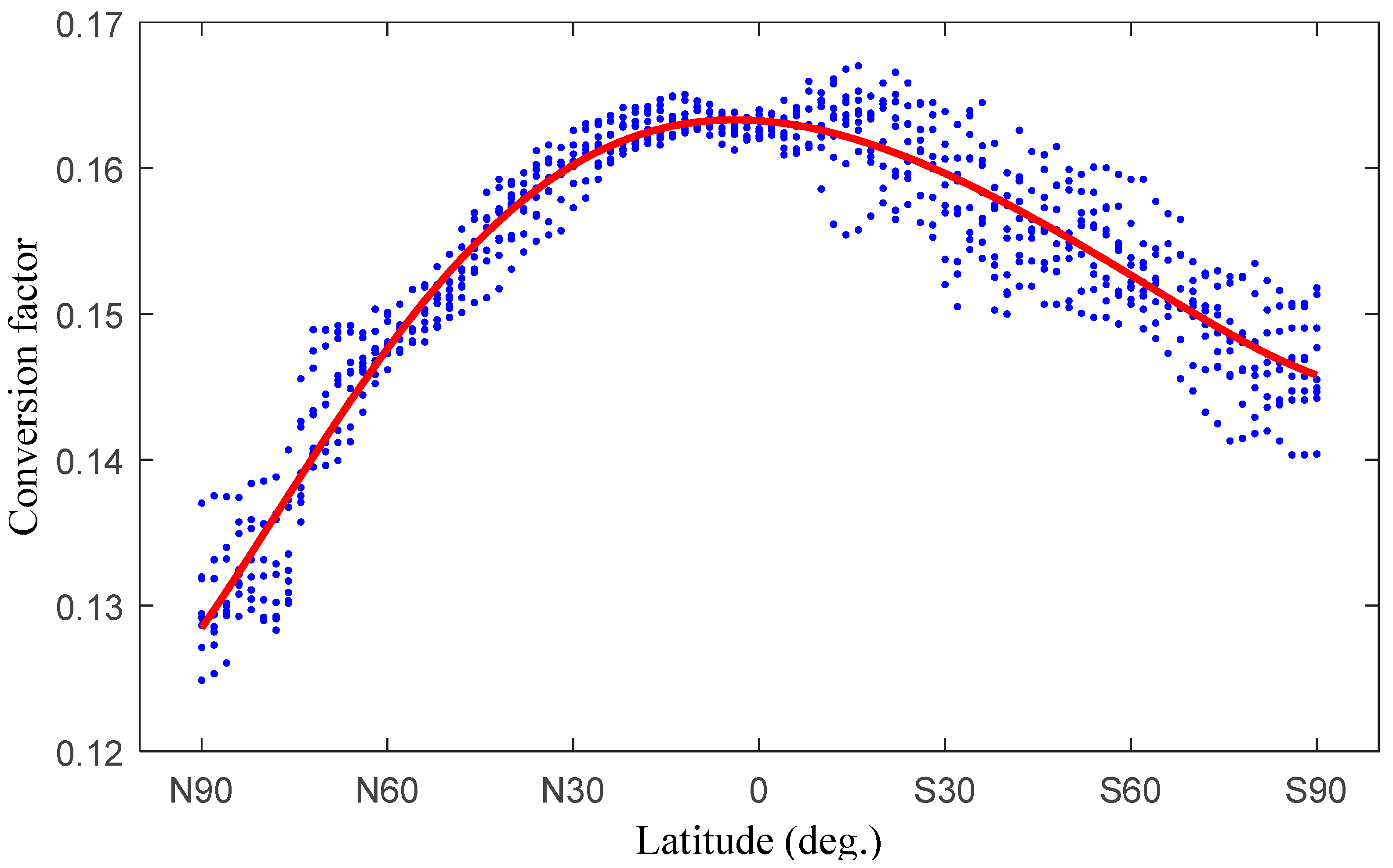
2.2. Analysis of the Conversion Factor
- Relationship between the conversion factor and the annual change.
- 2.
- Relationship between the conversion factor and the semiannual change.
- 3.
- Relationship between the conversion factor and the elevation.
- 4.
- Analysis of the modelling grid division.
2.3. Expression of the Conversion Factor Model
3. Result
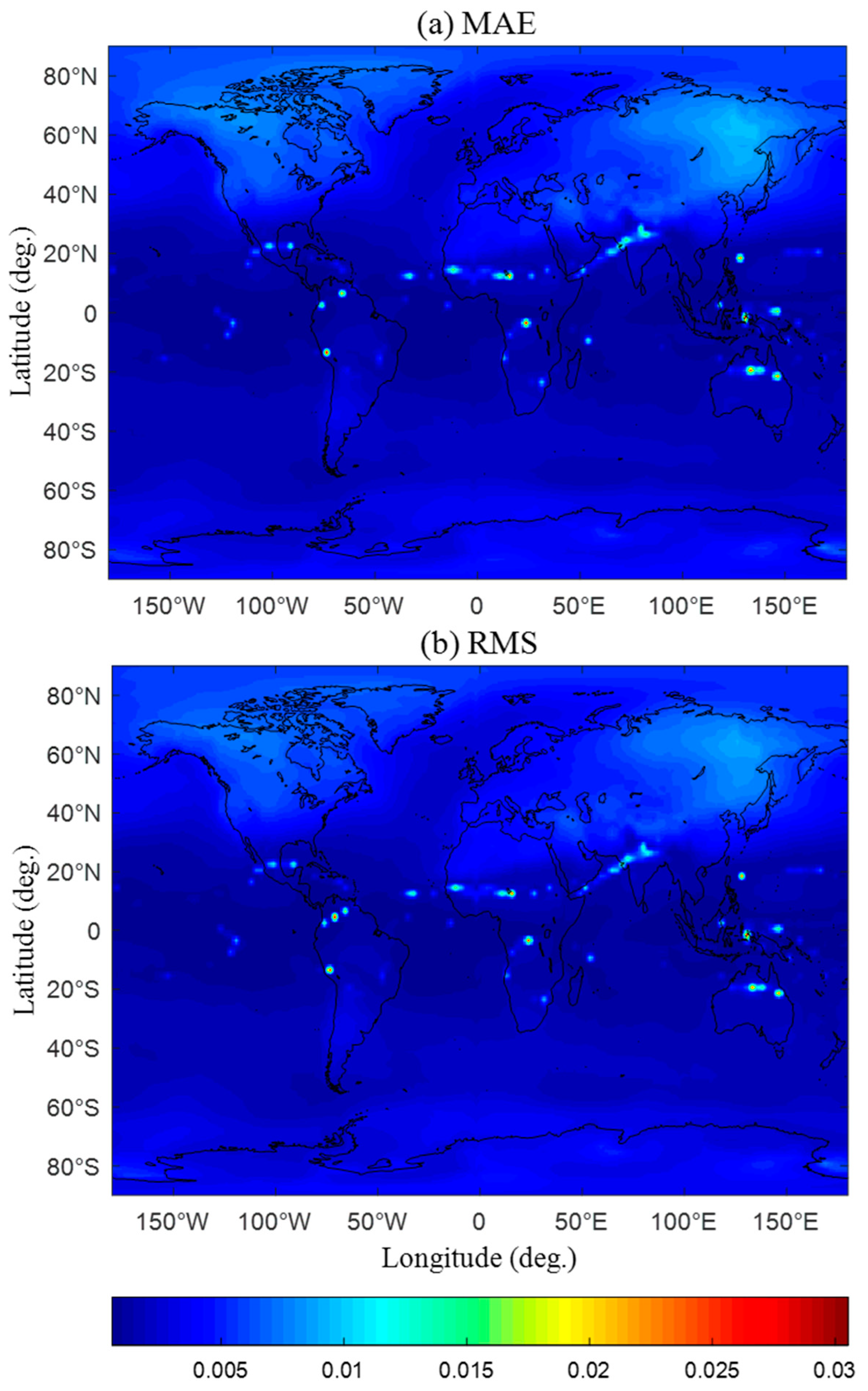
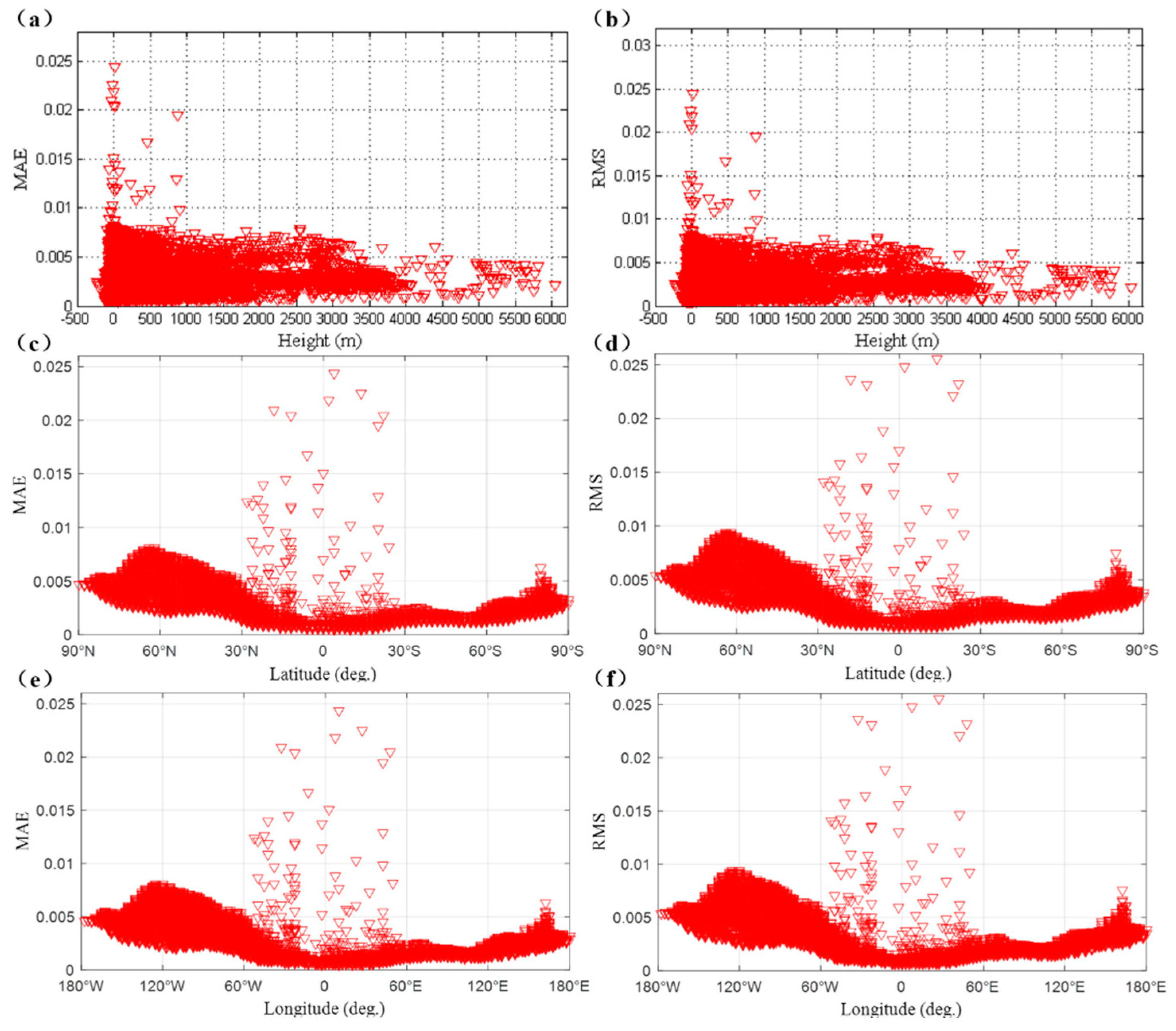
3.1. Internal Accuracy Testing
3.2. External Accuracy Testing
3.3. Case Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, Y.; Shan, L.; Zhao, Q. Establishing a method of short-term rainfall forecasting based on GNSS-derived PWV and its application. Sci. Rep. 2017, 7, 12465. [Google Scholar] [CrossRef] [PubMed]
- Wong, M.S.; Jin, X.; Liu, Z.; Nichol, J.; Chan, P.W. Multi-sensors study of precipitable water vapour over mainland China. Int. J. Climatol. 2015, 35, 3146–3159. [Google Scholar] [CrossRef]
- Yao, Y.B.; Zhang, B.; Yue, S.Q.; Xu, C.Q.; Peng, W.F. Global empirical model for mapping zenith wet delays onto precipitable water. J. Geod. 2013, 87, 439–448. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Duan, J.; Bevis, M.; Fang, P.; Bock, Y.; Chiswell, S.; Businger, S.; Rocken, C.; Solheim, F.; van Hove, T.; Ware, R.; et al. GPS meteorology: Direct estimation of the absolute value of precipitable water. J. Appl. Meteorol. Climatol. 1996, 35, 830–838. [Google Scholar] [CrossRef] [Green Version]
- Flores, A.; Ruffini, G.; Rius, A. 4D tropospheric tomography using GPS slant wet delays. Ann. Geophys. 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Bi, Y.; Mao, J.; Li, C. Preliminary results of 4-D water vapor tomography in the troposphere using GPS. Adv. Atmos. Sci. 2006, 23, 551–560. [Google Scholar] [CrossRef]
- Chen, J. On the error analysis for the remote sensing of atmospheric water vapor by ground based GPS. Acta Geod. Cartogr. Sin. 1998, 27, 113–118. [Google Scholar]
- Rocken, C.; Hove, T.V.; Johnson, J.; Solheim, F.; Ware, R.; Bevis, M.; Chiswell, S.; Businger, S. GPS/STORM—GPS sensing of atmospheric water vapor for meteorology. J. Atmos. Ocean. Technol. 1995, 12, 468–478. [Google Scholar] [CrossRef]
- Rocken, C.; Ware, R.; Van Hove, T.; Solheim, F.; Alber, C.; Johnson, J.; Bevis, M.; Businger, S. Sensing atmospheric water vapor with the Global Positioning System. Geophys. Res. Lett. 1993, 20, 2631–2634. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, M.J.; Lázaro, C.; Nunes, A.L.; Pires, N.; Bastos, L.; Mendes, V.B. GNSS-derived path delay: An approach to compute the wet tropospheric correction for coastal altimetry. IEEE Geosci. Remote Sens. Lett. 2010, 7, 596–600. [Google Scholar] [CrossRef]
- Fernandes, M.J.; Lázaro, C.; Ablain, M.; Pires, N. Improved wet path delays for all ESA and reference altimetric missions. Remote Sens. Environ. 2015, 169, 50–74. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, M.J.; Lázaro, C. GPD+ wet tropospheric corrections for CryoSat-2 and GFO altimetry missions. Remote Sens. 2016, 8, 851. [Google Scholar] [CrossRef] [Green Version]
- Vázquez, B.G.E.; Grejner-Brzezinska, D.A. GPS-PWV estimation and validation with radiosonde data and numerical weather prediction model in Antarctica. GPS Solut. 2013, 17, 29–39. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Z.; Liang, H.; Xu, X.; Wu, P. Precipitable water vapor on the Tibetan Plateau estimated by GPS, water vapor radiometer, radiosonde, and numerical weather prediction analysis and its impact on the radiation budget. J. Geophys. Res. Atmos. 2005, 110, 1–11. [Google Scholar] [CrossRef]
- Tregoning, P.; Herring, T.A. Impact of a priori zenith hydrostatic delay errors on GPS estimates of station heights and zenith total delays. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Mendes, V.B. Modeling the neutral-atmospheric propagation delay in radiometric space techniques. UNB Geod. Geomat. Eng. Tech. Rep. 1999, 199, 10. [Google Scholar]
- Ross, R.J.; Rosenfeld, S. Estimating mean weighted temperature of the atmosphere for Global Positioning System applications. J. Geophys. Res. Atmos. 1997, 102, 21719–21730. [Google Scholar] [CrossRef] [Green Version]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Byun, S.H.; Bar-Sever, Y.E. A new type of troposphere zenith path delay product of the international GNSS service. J. Geod. 2009, 83, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Mendes, V.B.; Prates, G.; Santos, L.; Langley, R.B. An evaluation of the accuracy of models for the determination of the weighted mean temperature of the atmosphere. In Proceedings of the 2000 National Technical Meeting of The Institute of Navigation, Anaheim, CA, USA, 26–28 January 2000; pp. 433–438. [Google Scholar]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products. 2009. Available online: http://igscb.jpl.nasa.gov/igscb/resource/pubs/UsingIGSProductsVer21.pdf (accessed on 22 January 2022).
- Fernandes, M.J.; Pires, N.; Lázaro, C.; Nunes, A.L. Tropospheric delays from GNSS for application in coastal altimetry. Adv. Space Res. 2013, 51, 1352–1368. [Google Scholar] [CrossRef]
- Notarpietro, R.; Cucca, M.; Gabella, M.; Venuti, G.; Perona, G. Tomographic reconstruction of wet and total refractivity fields from GNSS receiver networks. Adv. Space Res. 2011, 47, 898–912. [Google Scholar] [CrossRef]
- Yao, Y.B.; Zhu, S.; Yue, S.Q. A globally applicable, season-specific model for estimating the weighted mean temperature of the atmosphere. J. Geod. 2012, 86, 1125–1135. [Google Scholar] [CrossRef]
- MacDonald, A.E.; Xie, Y.; Ware, R.H. Diagnosis of three-dimensional water vapor using a GPS network. Mon. Weather Rev. 2002, 130, 386–397. [Google Scholar] [CrossRef]
- Zhang, S. Research and Application of Remote Sensing Water Vapor Using Ground Based GPS/Met. Ph.D. Thesis, Wuhan University, Wuhan, China, 2009. [Google Scholar]
- Kouba, J. Implementation and testing of the gridded Vienna Mapping Function 1 (VMF1). J. Geod. 2008, 82, 193–205. [Google Scholar] [CrossRef]
- Jin, S.; Park, J.U.; Cho, J.H.; Park, P.H. Seasonal variability of GPS-derived zenith tropospheric delay (1994–2006) and climate implications. J. Geophys. Res. Atmos. 2007, 112, 1–11. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géod. (1946–1975) 1972, 105, 279–298. [Google Scholar] [CrossRef]






| Model | MAE | RMS | ||||
|---|---|---|---|---|---|---|
| Mean | Max | Min | Mean | Max | Min | |
| GΠ | 0.0026 | 0.026 | 0.0005 | 0.0031 | 0.0317 | 0.0006 |
| Model | MAE | RMS | ||||
|---|---|---|---|---|---|---|
| Mean | Max | Min | Mean | Max | Min | |
| GΠ | 0.0026 | 0.0244 | 0.0005 | 0.0030 | 0.0304 | 0.0006 |
| Height Range (m) | MAE | RMS | ||||
|---|---|---|---|---|---|---|
| Mean (10−3) | Max (10−3) | Min (10−3) | Mean (10−3) | Max (10−3) | Min (10−3) | |
| <500 | 2.5 | 24.4 | 0.5 | 2.9 | 30.4 | 0.6 |
| 500~1000 | 2.9 | 19.5 | 0.6 | 3.4 | 22.1 | 0.7 |
| 1000~2000 | 3 | 7.7 | 0.5 | 3.5 | 8.9 | 0.7 |
| >2000 | 3 | 7.9 | 0.7 | 3.6 | 9.1 | 0.9 |
| Longitude Range | MAE | RMS | ||||
|---|---|---|---|---|---|---|
| Mean (10−3) | Max (10−3) | Min (10−3) | Mean (10−3) | Max (10−3) | Min (10−3) | |
| 0°~30° | 2 | 24.4 | 0.5 | 2.3 | 30.4 | 0.6 |
| 30°~60° | 2.4 | 10.2 | 0.6 | 2.9 | 11.6 | 0.8 |
| 60°~90° | 2.7 | 22.5 | 0.5 | 3.2 | 30.4 | 0.6 |
| 90°~120° | 2.8 | 11.5 | 0.5 | 3.4 | 13 | 0.6 |
| 120°~150° | 2.7 | 21.8 | 0.5 | 3.2 | 24.8 | 0.6 |
| 150°~180° | 2.4 | 6.3 | 0.6 | 2.8 | 7.5 | 0.8 |
| Latitude Range | MAE | RMS | ||||
|---|---|---|---|---|---|---|
| Mean (10−3) | Max (10−3) | Min (10−3) | Mean (10−3) | Max (10−3) | Min (10−3) | |
| 0°~30° | 1.4 | 24.4 | 0.5 | 1.7 | 30.4 | 0.6 |
| 30°~60° | 2.8 | 7.8 | 1.1 | 3.3 | 9.1 | 1.4 |
| 60°~90° | 3.7 | 8.1 | 1.3 | 4.3 | 9.4 | 1.6 |
| Station | HKSC | ANJI | ||||
|---|---|---|---|---|---|---|
| Lat. (°) | Lon. (°) | Height (m) | Lat. (°) | Lon. (°) | Height (m) | |
| Value | 22.32 | 114.13 | 20.15 | 30.37 | 119.41 | 35.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Liu, K.; Zhang, T.; He, L.; Shen, Z.; Xiong, S.; Shi, Y.; Chen, L.; Liao, W. A Global Conversion Factor Model for Mapping Zenith Total Delay onto Precipitable Water. Remote Sens. 2022, 14, 1086. https://doi.org/10.3390/rs14051086
Zhao Q, Liu K, Zhang T, He L, Shen Z, Xiong S, Shi Y, Chen L, Liao W. A Global Conversion Factor Model for Mapping Zenith Total Delay onto Precipitable Water. Remote Sensing. 2022; 14(5):1086. https://doi.org/10.3390/rs14051086
Chicago/Turabian StyleZhao, Qingzhi, Kang Liu, Tengxu Zhang, Lin He, Ziyu Shen, Si Xiong, Yun Shi, Lichuan Chen, and Weiming Liao. 2022. "A Global Conversion Factor Model for Mapping Zenith Total Delay onto Precipitable Water" Remote Sensing 14, no. 5: 1086. https://doi.org/10.3390/rs14051086
APA StyleZhao, Q., Liu, K., Zhang, T., He, L., Shen, Z., Xiong, S., Shi, Y., Chen, L., & Liao, W. (2022). A Global Conversion Factor Model for Mapping Zenith Total Delay onto Precipitable Water. Remote Sensing, 14(5), 1086. https://doi.org/10.3390/rs14051086







