Strain Field Features and Three-Dimensional Crustal Deformations Constrained by Dense GRACE and GPS Measurements in NE Tibet
Abstract
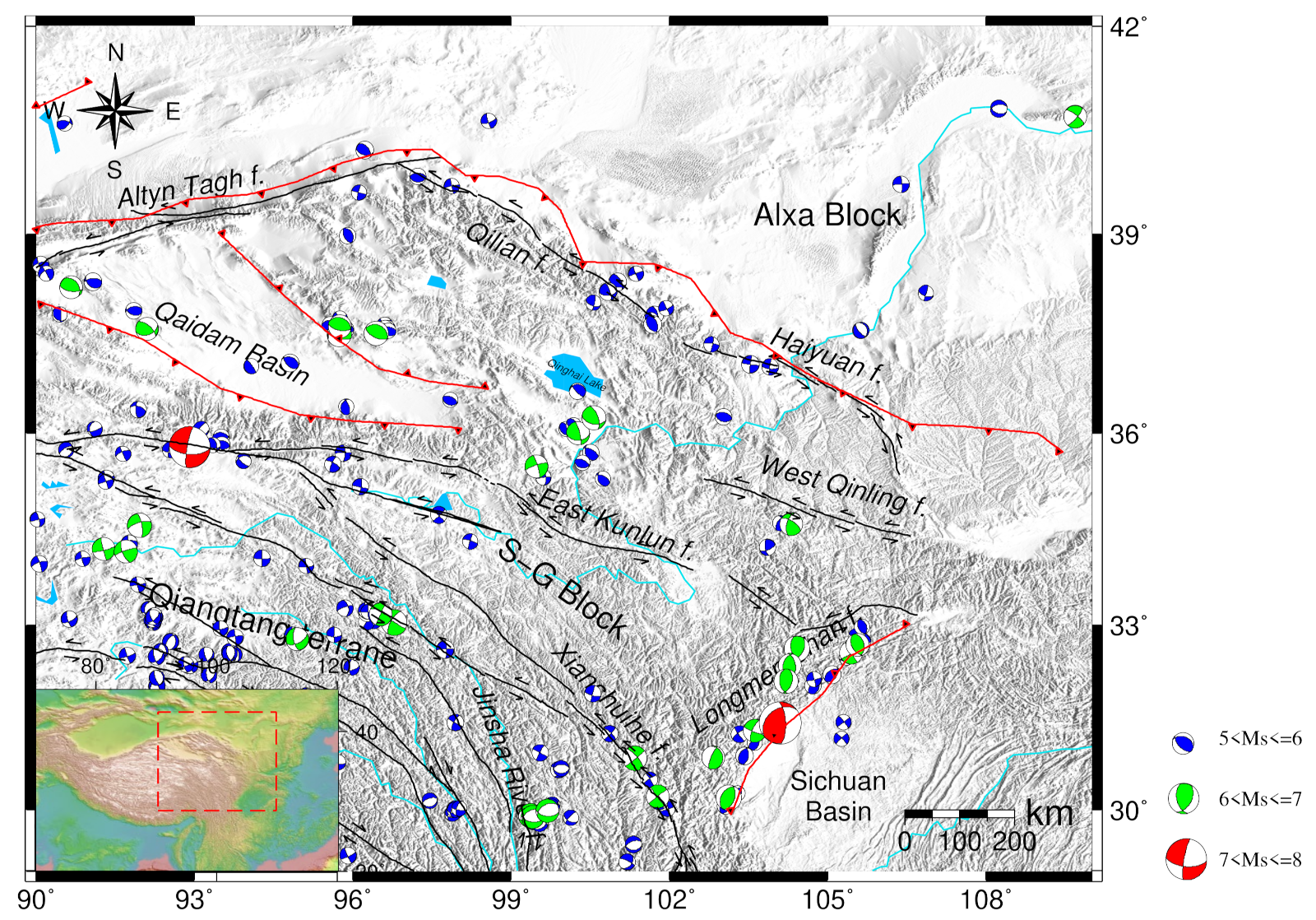
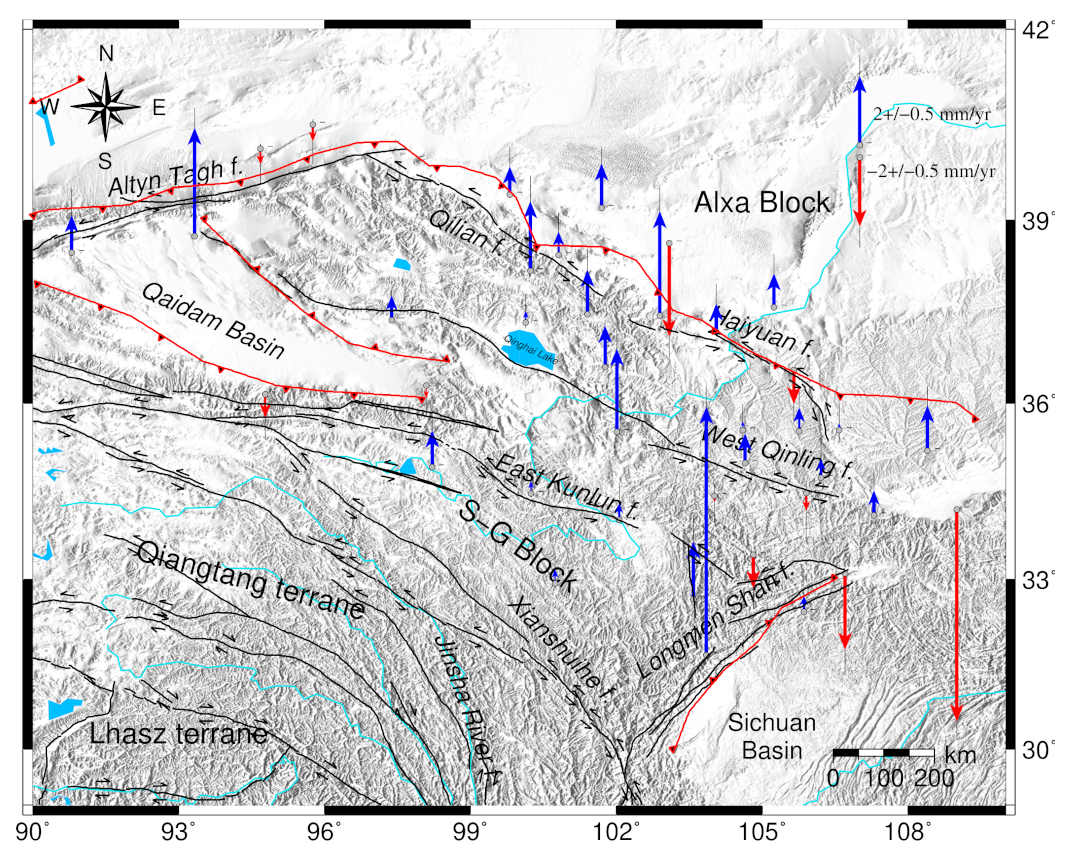
1. Introduction
2. Geodetic Data and Processing Approaches
2.1. GPS Data and Processing
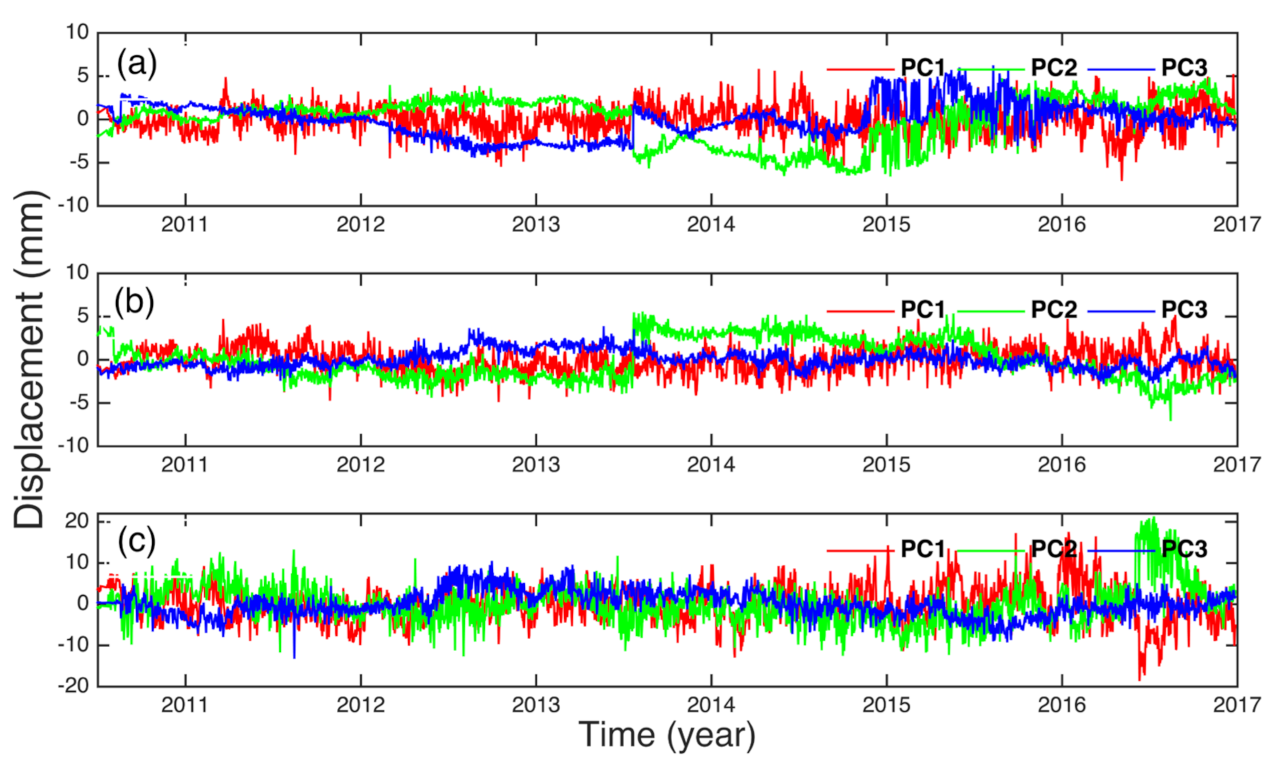
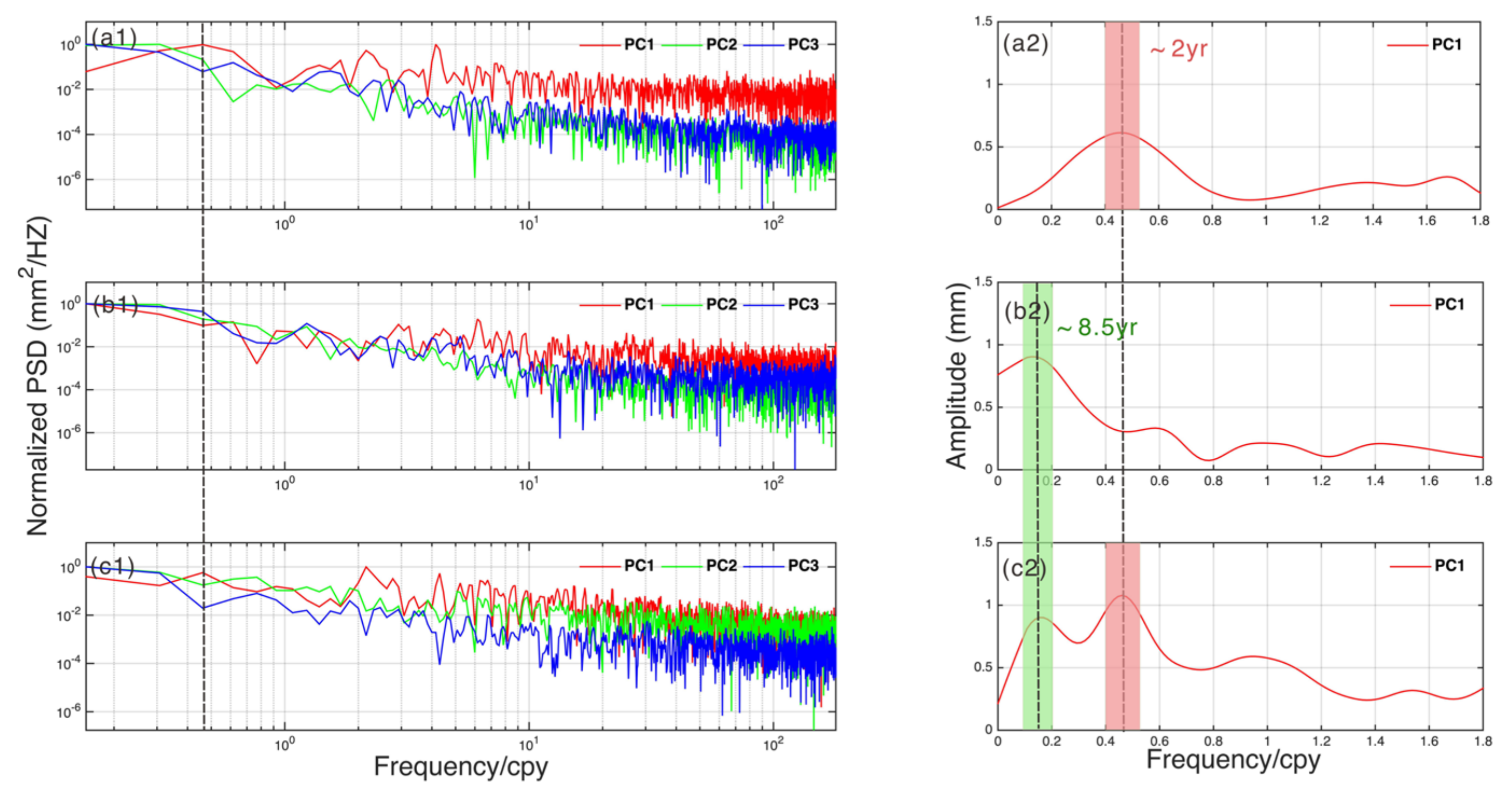
2.2. Common Mode Errors
3. GRACE Data and Processing
4. Results and Discussion
4.1. Influence of CMEs on the Evaluation of GPS Velocities
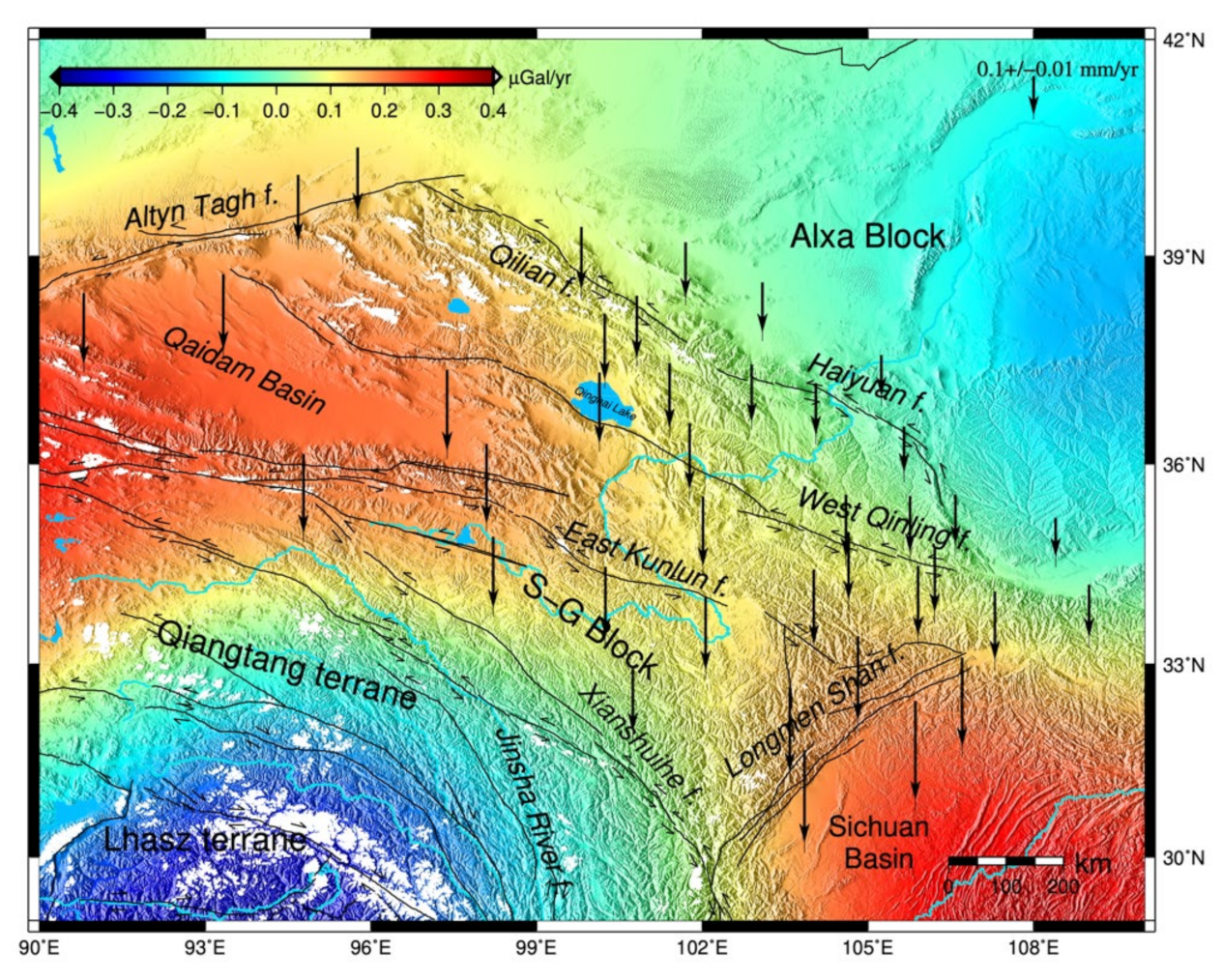
4.2. Analysis of Surface Vertical Seasonal Loading
4.3. Three Dimensional Crustal Deformation Rates
4.4. Dilatation Strain and Maximum Shear Strain Rates of the Plateau
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yin, A.; Harrison, T.M. Geologic Evolution of the Himalayan-Tibetan Orogen. Ann. Rev. Earth Planet. 2003, 28, 211–280. [Google Scholar] [CrossRef]
- Molnar, P.; England, P.; Martinod, J. Mantle Dynamics, Uplift of the Tibetan Plateau, and the Indian Monsoon. Rev. Geophys. 1993, 31, 357–396. [Google Scholar] [CrossRef]
- Tapponnier, P. Oblique Stepwise Rise and Growth of the Tibet Plateau. Science 2001, 294, 1671–1677. [Google Scholar] [CrossRef]
- Zhao, Q.; Wu, W.; Wu, Y. Using Combined GRACE and GPS Data to Investigate the Vertical Crustal Deformation at the Northeastern Margin of the Tibetan Plateau. J. Asian Earth Sci. 2017, 134, 122–129. [Google Scholar] [CrossRef]
- Zhou, M.D.; Zhang, Y.S.; Shi, Y.L.; Zhang, S.X.; Fan, B. Three-Dimensional Crustal Velocity Structure in the Northeastern Margin of the Qinghai-Tibetan Plateau. Prog. Geophys. 2006, 21, 127–134. [Google Scholar]
- Shen, Z.K.; Lü, J.; Wang, M.; Bürgmann, R. Contemporary Crustal Deformation around the Southeast Borderland of the Tibetan Plateau. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Wang, Q. Present-Day Crustal Deformation in China Constrained by Global Positioning System Measurements. Science 2001, 294, 574–577. [Google Scholar] [CrossRef] [PubMed]
- Qu, W.; Gao, Y.; Chen, H.; Liang, S.; Han, Y.; Zhang, Q.; Wang, Q.; Hao, M. Review on Characteristics of Present Crustal Tectonic Movement and Deformation in Qing- Hai-Tibet Plateau, China Using GPS High Precision Monitoring Data. J. Earth Sci. Environ. 2021, 43, 182–204. [Google Scholar]
- Wang, M.; Shen, Z. Present-Day Crustal Deformation of Continental China Derived From GPS and Its Tectonic Implications. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018774. [Google Scholar] [CrossRef]
- Wu, Y.; Zheng, Z.; Nie, J.; Chang, L.; Su, G.; Yin, H.; Liang, H.; Pang, Y.; Chen, C.; Jiang, Z.; et al. High-Precision Vertical Movement and Three-Dimensional Deformation Pattern of the Tibetan Plateau. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023202. Available online: https://agupubs.onlinelibrary.wiley.com/doi/epdf/10.1029/2021JB023202 (accessed on 10 April 2022). [CrossRef]
- van Dam, T.; Wahr, J.; Lavallée, D. A Comparison of Annual Vertical Crustal Displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Fu, Y.; Freymueller, J.T. Seasonal and Long-Term Vertical Deformation in the Nepal Himalaya Constrained by GPS and GRACE Measurements. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Hao, M.; Freymueller, J.T.; Wang, Q.; Cui, D.; Qin, S. Vertical Crustal Movement around the Southeastern Tibetan Plateau Constrained by GPS and GRACE Data. Earth Planet. Sci. Lett. 2016, 437, 1–8. [Google Scholar] [CrossRef]
- Pan, Y.; Shen, W.-B.; Shum, C.K.; Chen, R. Spatially Varying Surface Seasonal Oscillations and 3-D Crustal Deformation of the Tibetan Plateau Derived from GPS and GRACE Data. Earth Planet. Sci. Lett. 2018, 502, 12–22. [Google Scholar] [CrossRef]
- Liang, S.; Gan, W.; Shen, C.; Xiao, G.; Liu, J.; Chen, W.; Ding, X.; Zhou, D. Three-dimensional Velocity Field of Present-day Crustal Motion of the Tibetan Plateau Derived from GPS Measurements. J. Geophys. Res. Solid Earth 2013, 118, 5722–5732. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Zhang, T.; Shen, W.B.; Pan, Y.; Wei, L. Study of Seasonal and Long-Term Vertical Deformation in Nepal Based on GPS and GRACE Observations. Adv. Space Res. 2018, 61, 1005–1016. [Google Scholar] [CrossRef]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS Antenna Phase Center Model Igs08.Atx: Status and Potential Improvements. J. Geod. 2016, 90, 343–364. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. (Eds.) IERS Conventions (2010); IERS Technical Note; No. 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Zhang, K.L.; Liang, S.M.; Gan, W.J. Crustal Strain Rates of Southeastern Tibetan Plateau Derived from GPS Measurements and Implications to Lithospheric Deformation of the Shan-Thai Terrane. Earth Planet. Phys. 2019, 3, 47–54. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by Surface Loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, H.; Wright, T.J.; Lou, Y.; Zhang, R.; Zhang, W.; Shi, C.; Huang, J.; Wei, N. Crustal Deformation in the India-Eurasia Collision Zone From 25 Years of GPS Measurements: Crustal Deformation in Asia From GPS. J. Geophys. Res. Solid Earth 2017, 122, 9290–9312. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A New Release of the International Terrestrial Reference Frame Modeling Nonlinear Station Motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, R.; Ding, H.; Xu, X.; Zheng, G.; Shen, W.; Xiao, Y.; Li, S. Common Mode Component and Its Potential Effect on GPS-Inferred Three-Dimensional Crustal Deformations in the Eastern Tibetan Plateau. Remote Sens. 2019, 11, 1975. [Google Scholar] [CrossRef]
- He, X.; Hua, X.; Yu, K.; Xuan, W.; Lu, T.; Zhang, W.; Chen, X. Accuracy Enhancement of GPS Time Series Using Principal Component Analysis and Block Spatial Filtering. Adv. Space Res. 2015, 55, 1316–1327. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of Apparent Seasonal Variations from GPS-Derived Site Position Time Series. J. Geophys. Res. B Solid Earth 2002, 107, ETG 9-1–ETG 9-16. [Google Scholar] [CrossRef]
- Ray, J.; Altamimi, Z.; Collilieux, X.; Van Dam, T. Anomalous Harmonics in the Spectra of GPS Position Estimates. GPS Solut. 2008, 12, 55–64. [Google Scholar] [CrossRef]
- Van Dam, T.; Collilieux, X.; Wuite, J.; Altamimi, Z.; Ray, J. Nontidal Ocean Loading: Amplitudes and Potential Effects in GPS Height Time Series. J. Geod. 2012, 86, 1043–1057. [Google Scholar] [CrossRef]
- Jiang, W.-P.; Deng, L.; Li, Z.; Zhou, X.; Liu, H. Effects on Noise Properties of GPS Time Series Caused by Higher-Order Ionospheric Corrections. Adv. Space Res. 2014, 53, 1035–1046. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallee, D.; Clarke, P.; Nurutdinov, K. A New Global Mode of Earth Deformation: Seasonal Cycle Detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef]
- Jiang, W.-P.; Li, Z.; Van Dam, T.; Ding, W. Comparative Analysis of Different Environmental Loading Methods and Their Impacts on the GPS Height Time Series. J. Geod. 2013, 87, 687–703. [Google Scholar] [CrossRef]
- Williams, S.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error Analysis of Continuous GPS Time Series. J. Geophys. Res. Solid Earth 2004, 109. preprint. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.; Tiberius, C.C.J.M.; Teunissen, P. Assessment of Noise in GPS Coordinate Time Series: Methodology and Results. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Bian, Y.; Yue, J.; Ferreira, V.G.; Cong, K.; Cai, D. Common Mode Component and Its Potential Effect on GPS-Inferred Crustal Deformations in Greenland. Pure Appl. Geophys. 2021, 178, 1805–1823. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Webb, F.; Prawirodirdjo, L.; Kedar, S.; Jamason, P. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis: SPATIOTEMPORAL FILTERING GPS NETWORK. J. Geophys. Res. 2006, 111, B03405. [Google Scholar] [CrossRef]
- Ming, F.; Yang, Y.; Zeng, A.; Zhao, B. Spatiotemporal Filtering for Regional GPS Network in China Using Independent Component Analysis. J. Geod. 2017, 91, 419–440. [Google Scholar] [CrossRef]
- Dong, D.; Herring, T.A.; King, R.W. Estimating Regional Deformation from a Combination of Space and Terrestrial Geodetic Data. J. Geod. 1998, 72, 200–214. [Google Scholar] [CrossRef]
- Mao, A.; Harrison, C.; Dixon, T. Noise in GPS Coordinate Time Series. J. Geophys. Res. 1999, 104, 2797–2816. [Google Scholar] [CrossRef]
- Zhang, J.; Bock, Y.; Johnson, H.; Fang, P.; Williams, S.; Genrich, J.; Wdowinski, S.; Behr, J. Southern California Permanent GPS Geodetic Array: Error Analysis of Daily Position Estimates and Site Velocities. J. Geophys. Res. Solid Earth 1997, 102, 18035–18055. [Google Scholar] [CrossRef]
- Altamimi, Z.; Collilieux, X.; Métivier, L. ITRF2008: An Improved Solution of the International Terrestrial Reference Frame. J. Geod. 2011, 85, 457–473. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef]
- University of Texas Center For Space Research (UTCSR). Grace Static Field Geopotential Coefficients CSR Release 6.0; UTCSR: Austin, TX, USA, 2018. [Google Scholar] [CrossRef]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Poropat, L.; Thomas, M.; Dahle, C.; Esselborn, S.; Knig, R.; Flechtner, F. A New High-Resolution Model of Non-Tidal Atmosphere and Ocean Mass Variability for de-Aliasing of Satellite Gravity Observations: AOD1B RL06. Geophys. J. Int. 2017, 221, 169–263. [Google Scholar] [CrossRef]
- Save, H.; Tapley, B.; Bettadpur, S. GRACE RL06 Reprocessing and Results from CSR; EGU General Assembly: Vienna, Austria, 2018. [Google Scholar]
- Göttl, F.; Schmidt, M.; Seitz, F. Mass-Related Excitation of Polar Motion: An Assessment of the New RL06 GRACE Gravity Field Models. Earth Planets Space 2018, 70, 195. [Google Scholar] [CrossRef]
- Swenson, S.C.; Chambers, D.P.; Wahr, J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output. J. Geophys. Res. Solid Earth 2008, 113(B8). [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Variations in the Earth’s Oblateness during the Past 28 Years. J. Geophys. Res. Solid Earth 2005, 109. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s Oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time Variability of the Earth’s Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Kusche, J.; Schrama, E. Surface Mass Redistribution Inversion from Global GPS Deformation and Gravity Recovery and Climate Experiment (GRACE) Gravity Data. J. Geophys. Res. Solid Earth 2005, 110, B09409. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Li, J.; Zhang, Z. Reducing Leakage Error in GRACE-Observed Long-Term Ice Mass Change: A Case Study in West Antarctica. J. Geod. 2015, 89, 925–940. [Google Scholar] [CrossRef]
- Serpelloni, E.; Faccenna, C.; Spada, G.; Dong, D.; Williams, S.D.P. Vertical GPS Ground Motion Rates in the Euro-Mediterranean Region: New Evidence of Velocity Gradients at Different Spatial Scales along the Nubia-Eurasia Plate Boundary. J. Geophys. Res. Solid Earth 2013, 118, 6003–6024. [Google Scholar] [CrossRef]
- Belmont, A.D.; Dartt, D.G. Variation with Longitude of the Quasi-Biennial Oscillation. Mon. Weather Rev. 1968, 96, 767–777. [Google Scholar] [CrossRef]
- Ding, H. Attenuation and Excitation of the ∼6 Year Oscillation in the Length-of-Day Variation. Earth Planet. Sci. Lett. 2019, 507, 131–139. [Google Scholar] [CrossRef]
- Ding, H.; Jin, T.; Li, J.; Jiang, W. The Contribution of a Newly Unraveled 64 Years Common Oscillation on the Estimate of Present-Day Global Mean Sea Level Rise. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022147. [Google Scholar] [CrossRef]
- Kuang, X.; Jiao, J.J. Review on Climate Change on the Tibetan Plateau during the Last Half Century. J. Geophys. Res. Atmos. 2016, 121, 3979–4007. [Google Scholar] [CrossRef]
- Guo, D.; Yu, E.; Wang, H. Will the Tibetan Plateau Warming Depend on Elevation in the Future? J. Geophys. Res. Atmos. 2016, 121, 3969–3978. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent Contributions of Glaciers and Ice Caps to Sea Level Rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Kang, S.; Lei, Y. Increased Mass over the Tibetan Plateau: From Lakes or Glaciers? Geophys. Res. Lett. 2013, 40, 2125–2130. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring Lake Level Changes on the Tibetan Plateau Using ICESat Altimetry Data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Xu, Z.X.; Gong, T.L.; Li, J.Y. Decadal Trend of Climate in the Tibetan Plateau-Regional Temperature and Precipitation. Hydrol. Process. 2010, 22, 3056–3065. [Google Scholar] [CrossRef]
- Cardozo, N.; Allmendinger, R.W. SSPX: A Program to Compute Strain from Displacement/Velocity Data. Comput. Geosci. 2009, 35, 1343–1357. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Shen, Z.; He, L.; Shen, W.; Li, W. Strain Field Features and Three-Dimensional Crustal Deformations Constrained by Dense GRACE and GPS Measurements in NE Tibet. Remote Sens. 2022, 14, 2638. https://doi.org/10.3390/rs14112638
Zhang T, Shen Z, He L, Shen W, Li W. Strain Field Features and Three-Dimensional Crustal Deformations Constrained by Dense GRACE and GPS Measurements in NE Tibet. Remote Sensing. 2022; 14(11):2638. https://doi.org/10.3390/rs14112638
Chicago/Turabian StyleZhang, Tengxu, Ziyu Shen, Lin He, Wenbin Shen, and Wei Li. 2022. "Strain Field Features and Three-Dimensional Crustal Deformations Constrained by Dense GRACE and GPS Measurements in NE Tibet" Remote Sensing 14, no. 11: 2638. https://doi.org/10.3390/rs14112638
APA StyleZhang, T., Shen, Z., He, L., Shen, W., & Li, W. (2022). Strain Field Features and Three-Dimensional Crustal Deformations Constrained by Dense GRACE and GPS Measurements in NE Tibet. Remote Sensing, 14(11), 2638. https://doi.org/10.3390/rs14112638








