A Novel Time-Domain Frequency Diverse Array HRWS Imaging Scheme for Spotlight SAR
Abstract
:1. Introduction
2. Methods
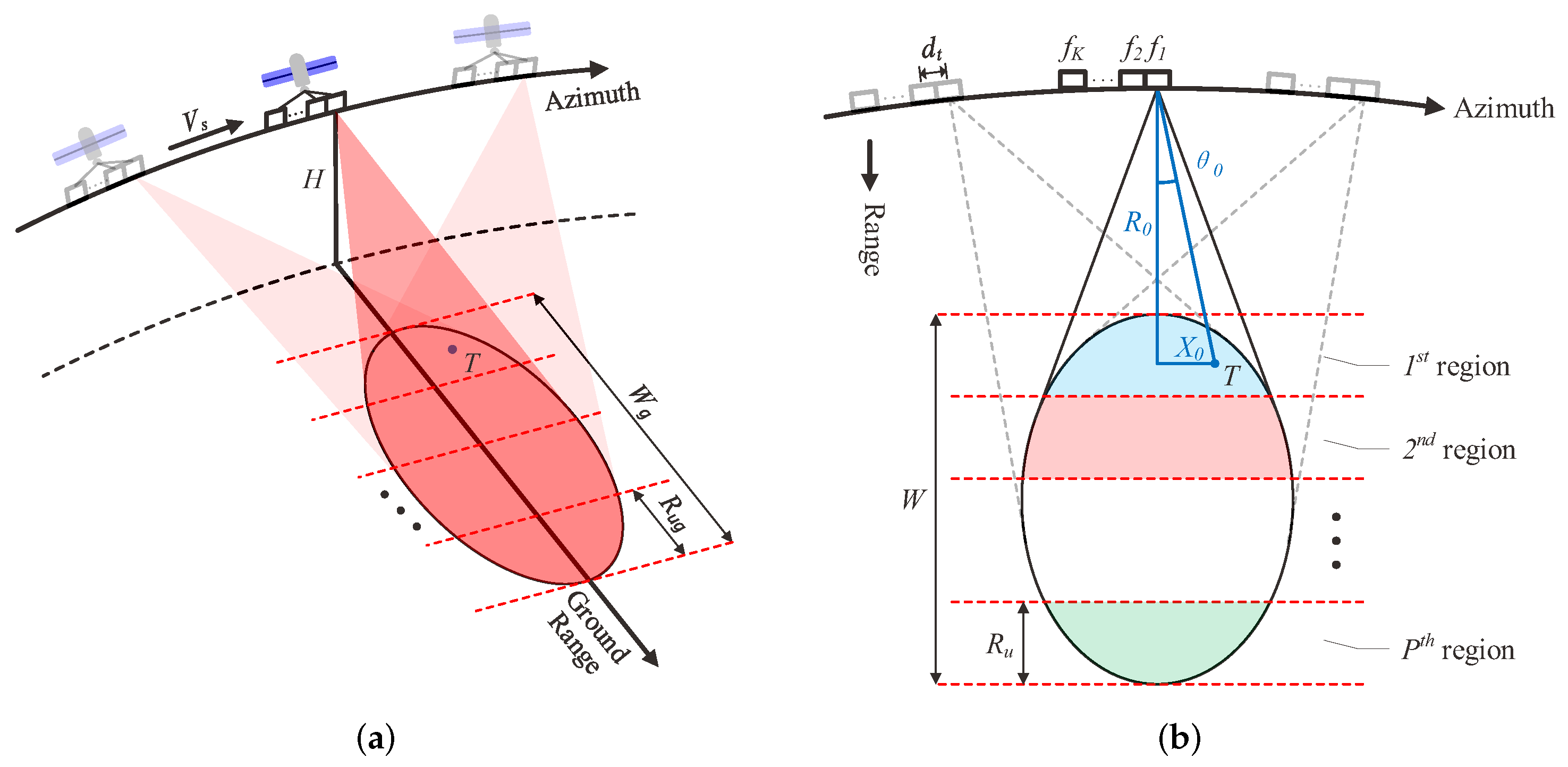
2.1. Geometry and Signal Model
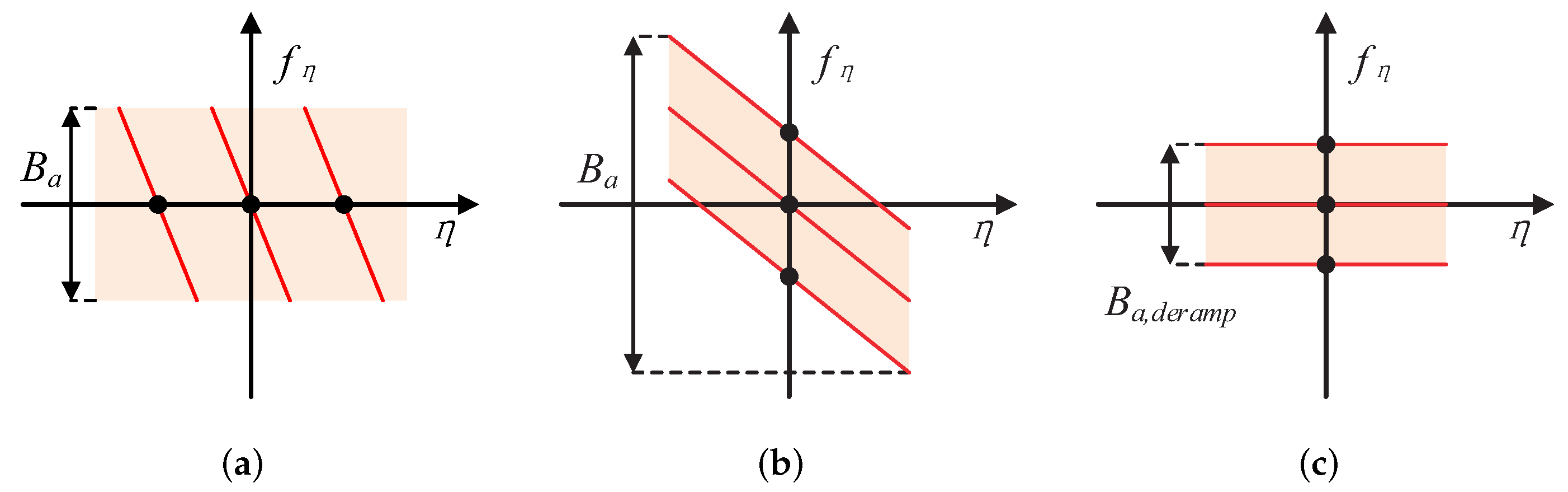
2.2. Range Ambiguity Analysis of Spotlight FDA-SAR Echoes
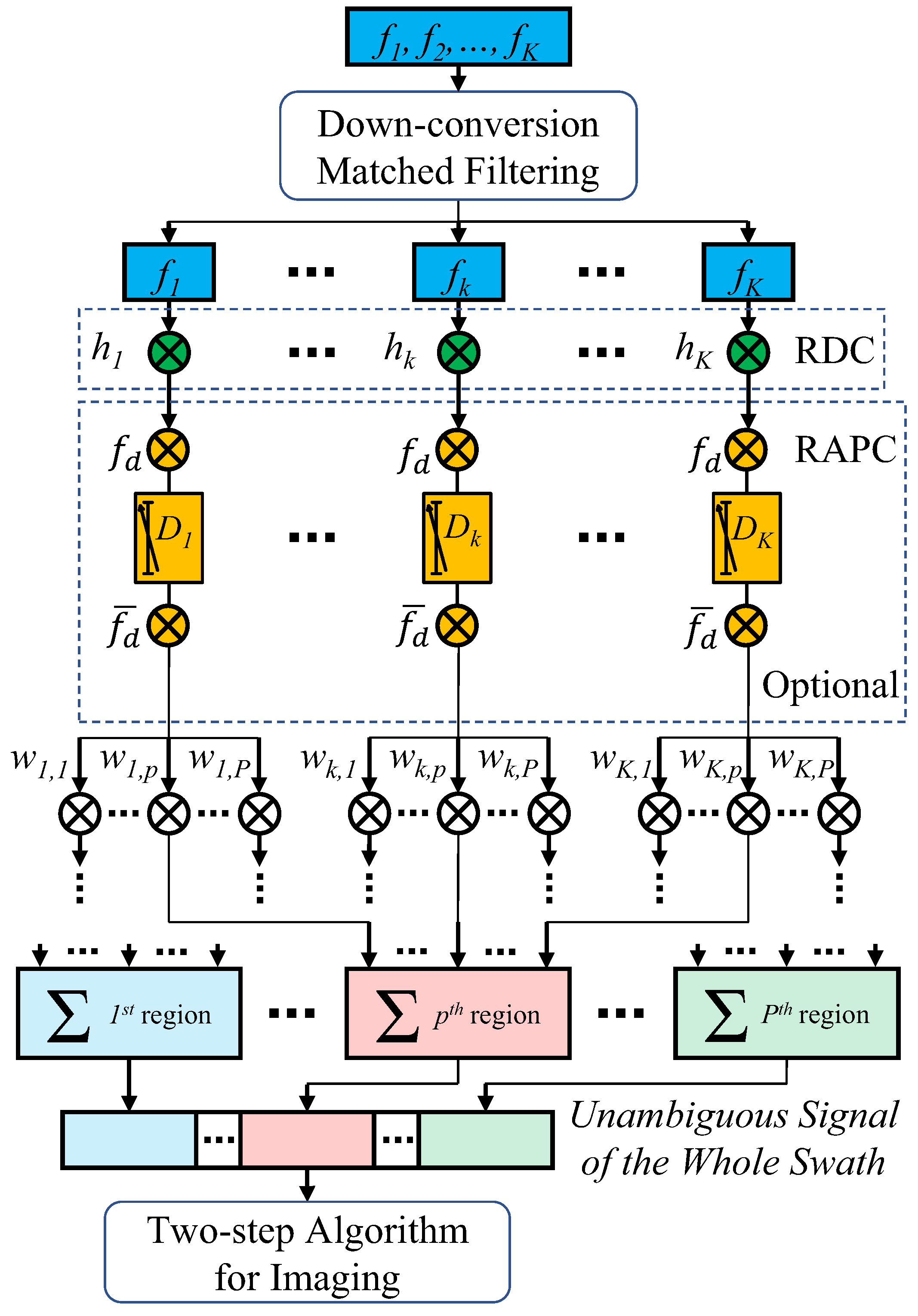
2.3. Range Ambiguity Resolution Approach for Spotlight FDA-SAR
2.3.1. Range Dependence Compensation
2.3.2. Time-Domain Transmission Beamforming
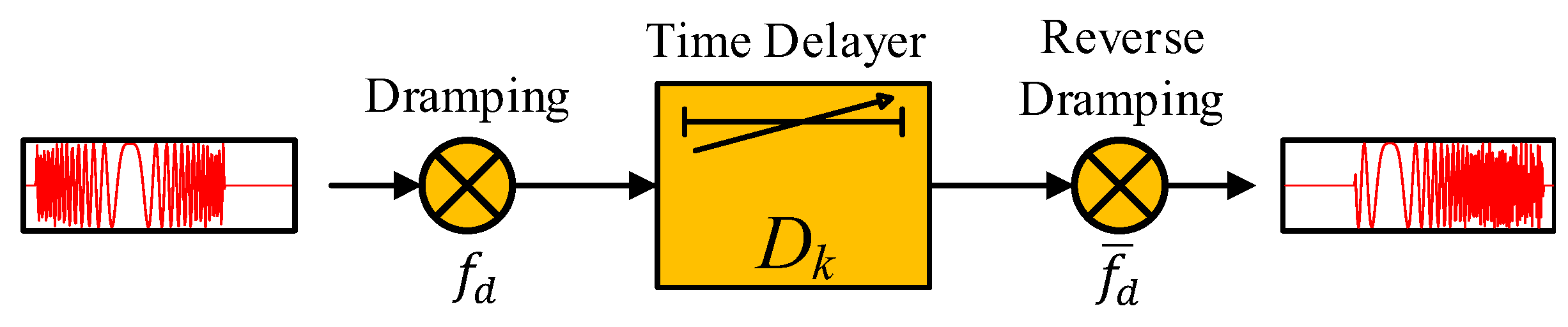
2.4. Residual Angle Phase Compensation
2.5. Performance Analysis
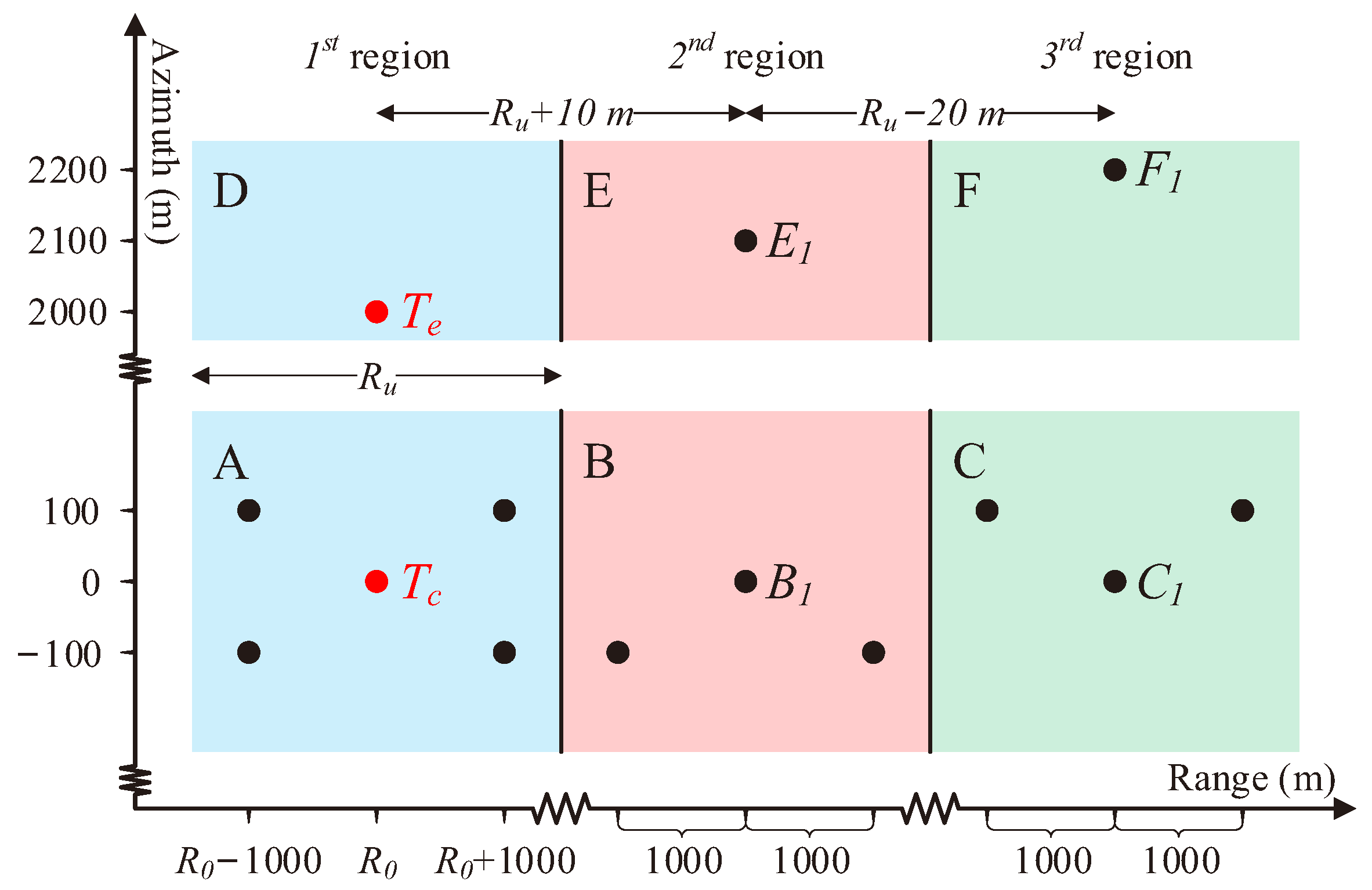
3. Simulation Results
3.1. Simulation Parameters
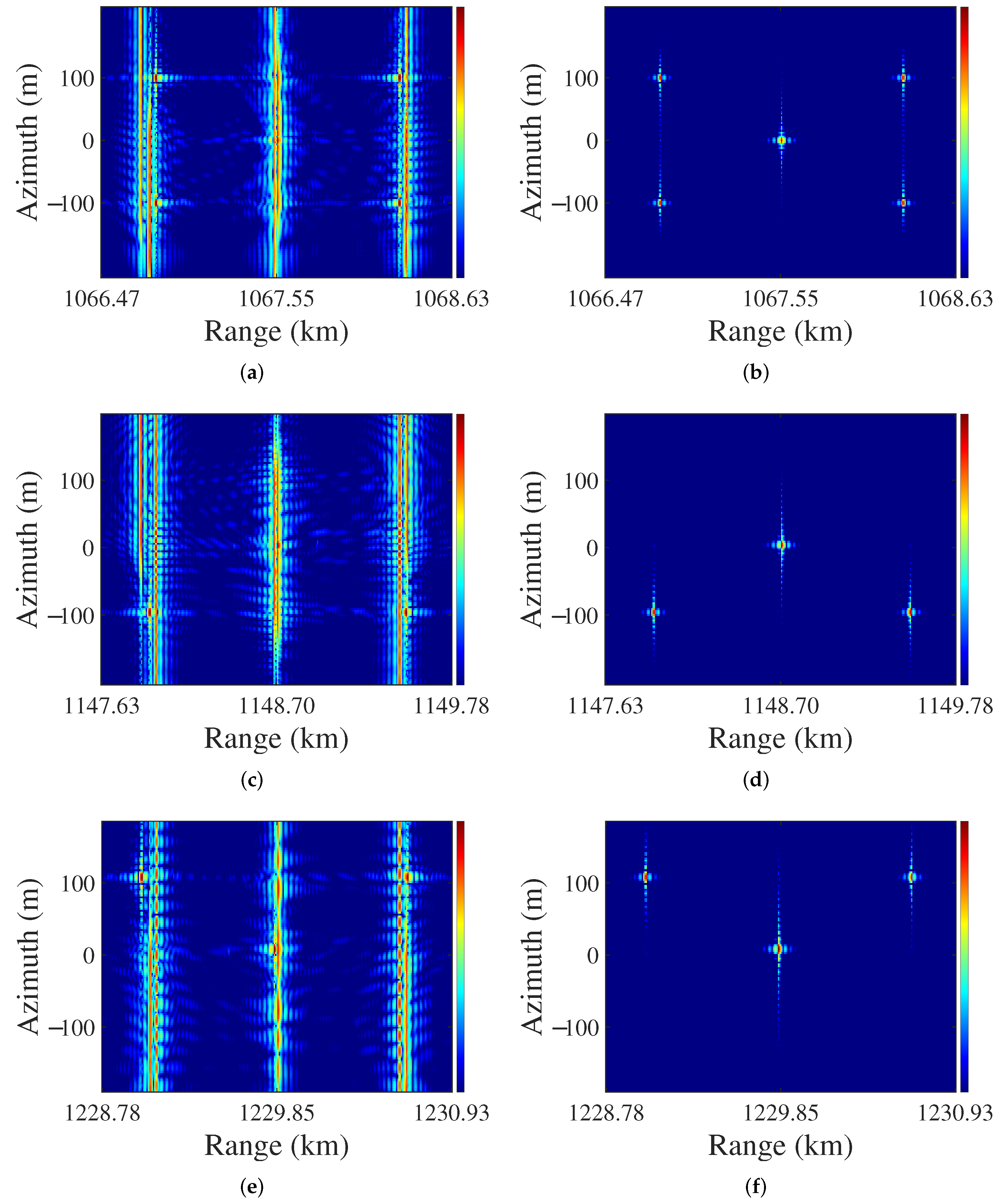
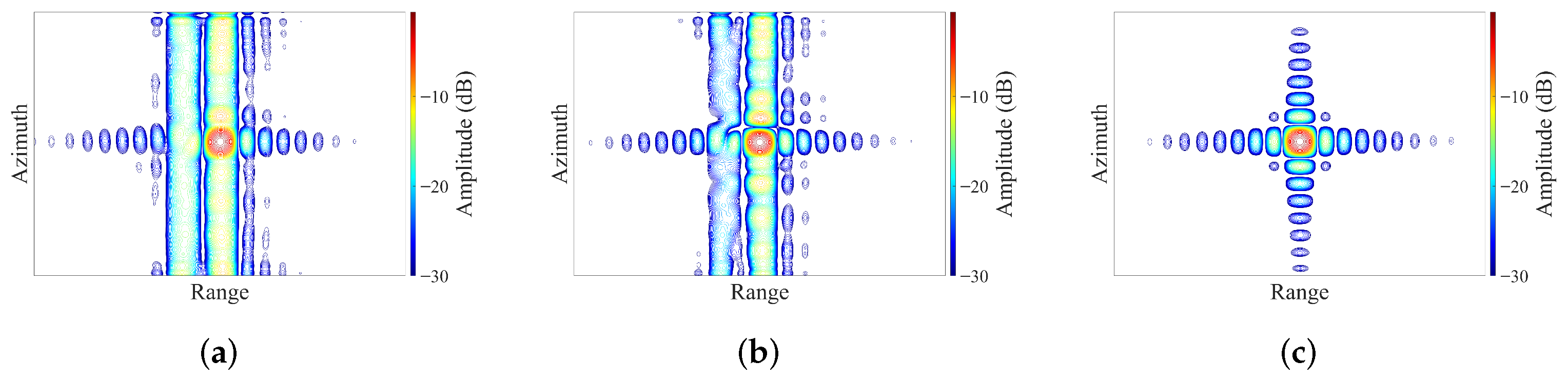
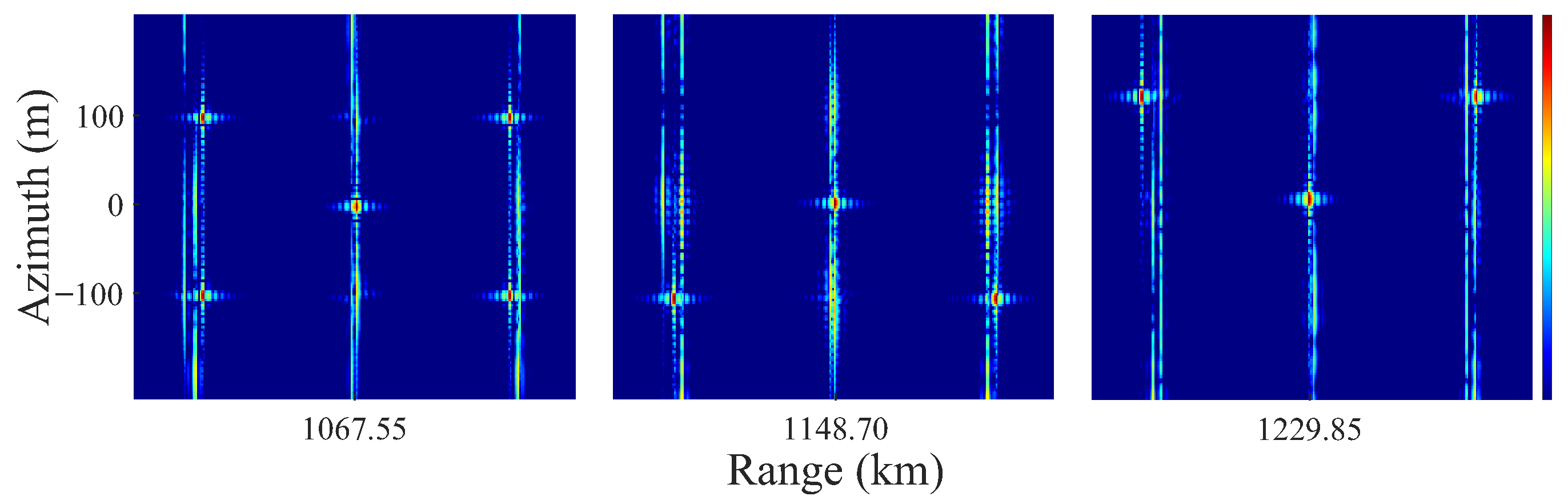
3.2. Central Area Time-Domain Processing
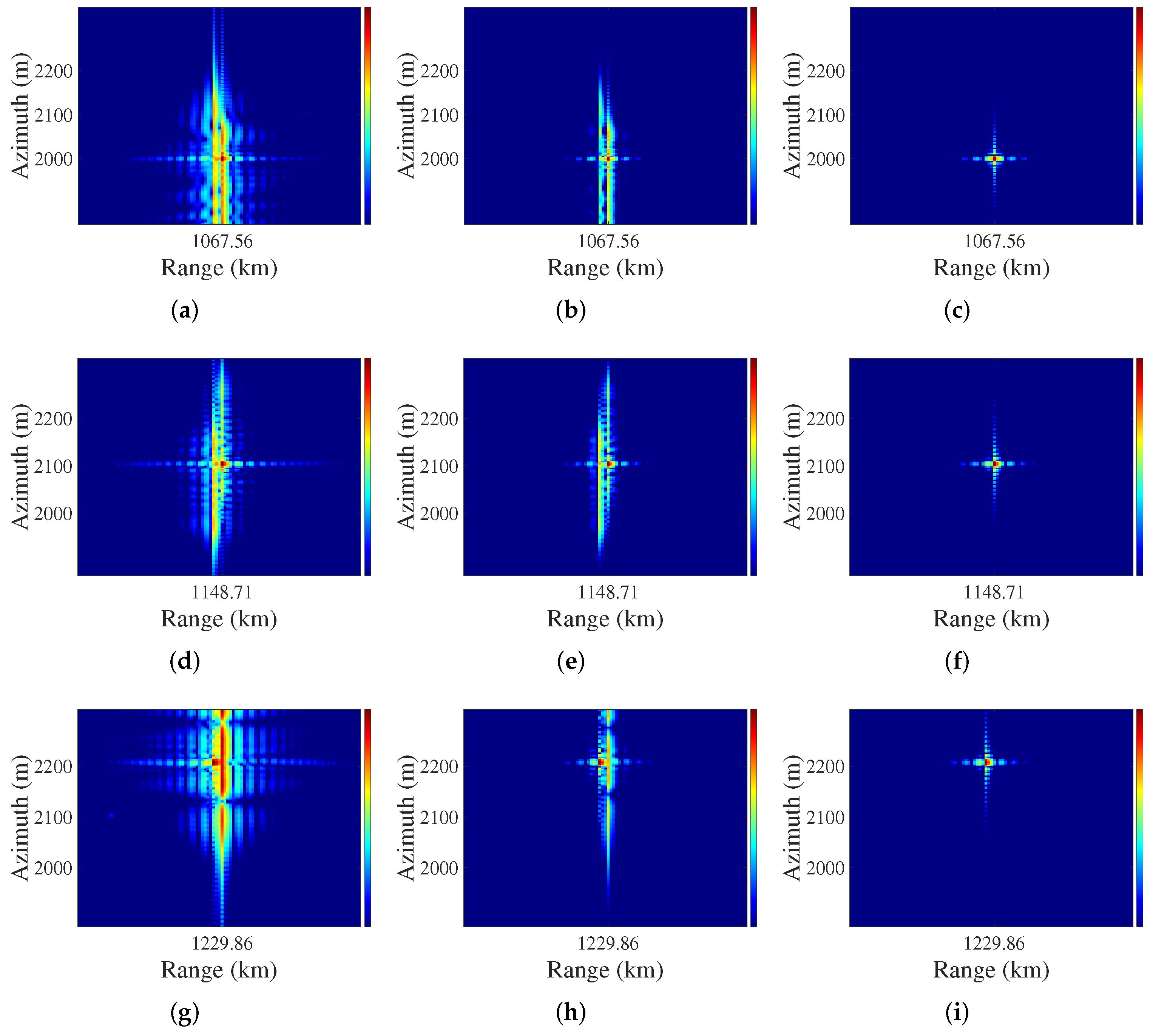
3.3. RAPC
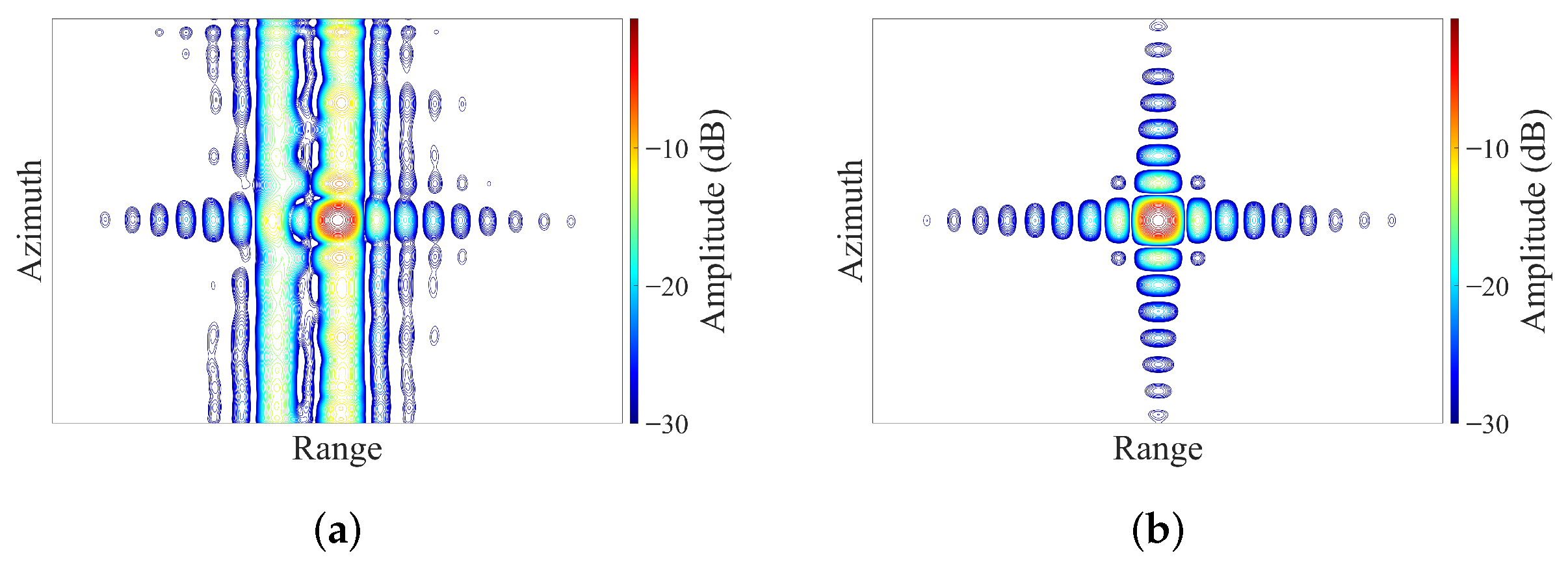
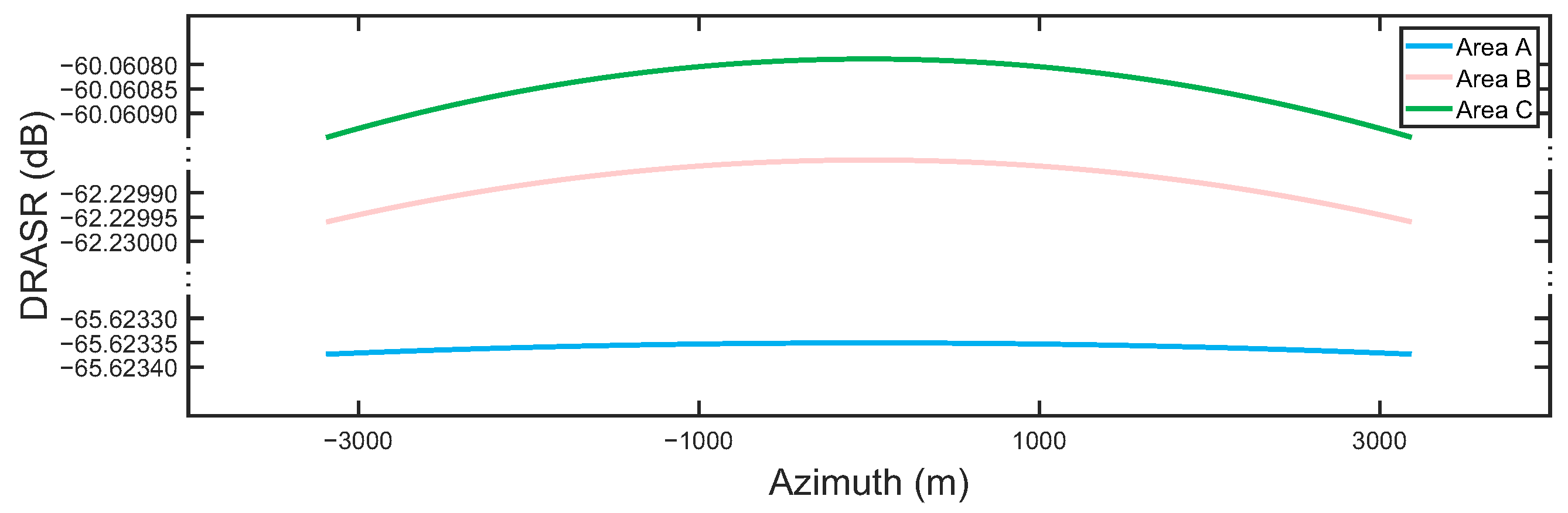
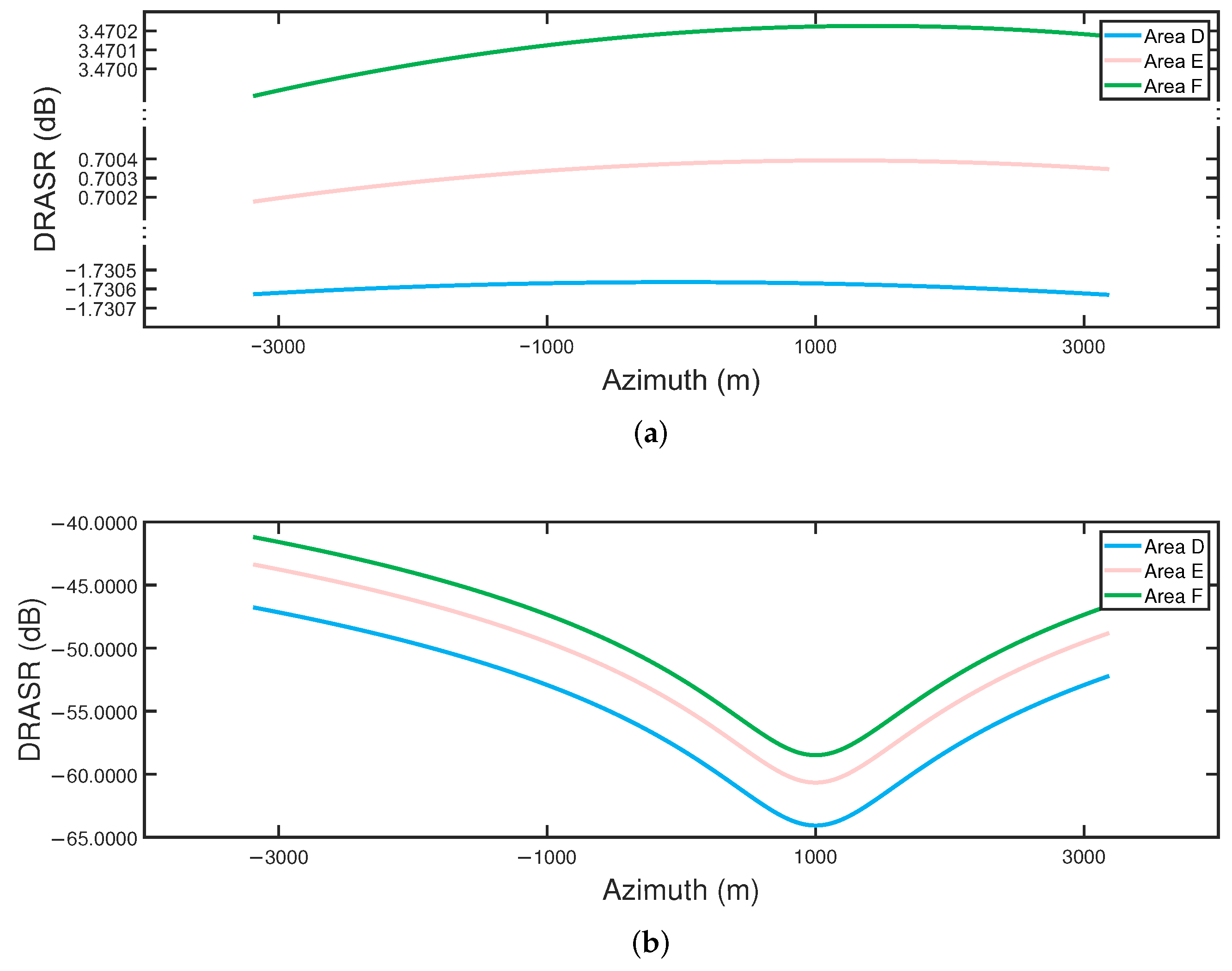
3.4. Performance Analysis
3.5. Conventional Approach
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Mittermayer, J.; Moreira, A.; Loffeld, O. Spotlight SAR data processing using the frequency scaling algorithm. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2198–2214. [Google Scholar] [CrossRef]
- Antonik, P.; Wicks, M.; Griffiths, H.; Baker, C. Frequency diverse array radars. In Proceedings of the 2006 IEEE Conference on Radar, Verona, NY, USA, 24–27 April 2006; pp. 215–217. [Google Scholar] [CrossRef]
- Antonik, P.; Wicks, M.C.; Griffiths, H.D.; Baker, C.J. Range-dependent beamforming using element level waveform diversity. In Proceedings of the 2006 International Waveform Diversity Design Conference, Lihue, HI, USA, 22–27 January 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Secmen, M.; Demir, S.; Hizal, A.; Eker, T. Frequency Diverse Array Antenna with Periodic Time Modulated Pattern in Range and Angle. In Proceedings of the 2007 IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; pp. 427–430. [Google Scholar] [CrossRef]
- Farooq, J.; Temple, M.A.; Saville, M.A. Exploiting frequency diverse array processing to improve SAR image resolution. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, S.; Liao, G. Range Ambiguous Clutter Suppression for Airborne FDA-STAP Radar. IEEE J. Sel. Top. Signal Process. 2015, 9, 1620–1631. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; So, H.C. Space-Time Adaptive Processing with Vertical Frequency Diverse Array for Range-Ambiguous Clutter Suppression. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5352–5364. [Google Scholar] [CrossRef]
- Wang, C.; Xu, J.; Liao, G.; Xu, X.; Zhang, Y. A Range Ambiguity Resolution Approach for High-Resolution and Wide-Swath SAR Imaging Using Frequency Diverse Array. IEEE J. Sel. Top. Signal Process. 2017, 11, 336–346. [Google Scholar] [CrossRef]
- Lin, C.; Huang, P.; Wang, W.; Li, Y.; Xu, J. Unambiguous Signal Reconstruction Approach for SAR Imaging Using Frequency Diverse Array. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1628–1632. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Zhou, Y.; Zhao, Q.; Wang, W. Elevated Frequency Diversity Array: A Novel Approach to High Resolution and Wide Swath Imaging for Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, W.; Chen, Z.; Zhao, Q.; Zhang, H.; Deng, Y.; Wang, R. High-Resolution and Wide-Swath SAR Imaging Mode Using Frequency Diverse Planar Array. IEEE Geosci. Remote Sens. Lett. 2021, 18, 321–325. [Google Scholar] [CrossRef]
- Fornaro, G.; Lanari, R.; Sansosti, E.; Tesauro, M. A two-step spotlight SAR data focusing approach. In Proceedings of the IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No.00CH37120), Honolulu, HI, USA, 24–28 July 2000; Volume 1, pp. 84–86. [Google Scholar] [CrossRef]
- Rommel, T.; Rincon, R.; Younis, M.; Krieger, G.; Moreira, A. Implementation of a MIMO SAR Imaging Mode for NASA’s Next Generation Airborne L-Band SAR. In Proceedings of the EUSAR 2018, 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 4–7 June 2018; pp. 1–5. [Google Scholar]
- Kim, J.H.; Younis, M.; Moreira, A.; Wiesbeck, W. A Novel OFDM Chirp Waveform Scheme for Use of Multiple Transmitters in SAR. IEEE Geosci. Remote Sens. Lett. 2013, 10, 568–572. [Google Scholar] [CrossRef]
- Jin, G.; Deng, Y.; Wang, W.; Wang, R.; Zhang, Y.; Long, Y. Segmented Phase Code Waveforms: A Novel Radar Waveform for Spaceborne MIMO-SAR. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5764–5779. [Google Scholar] [CrossRef]
| Schemes | Mixers | Delayers | FTs/IFTs Operations |
|---|---|---|---|
| Spotlight FDA-SAR without RAPC | 0 | 0 | |
| Spotlight FDA-SAR with RAPC | K | 0 | |
| Strip-map FDA-SAR | 0 |
| Parameters | Values |
|---|---|
| Carrier frequency | 5.4 GHz |
| Platform height | 710 km |
| Platform velocity | 7503 m/s |
| Incident angle | 45° |
| Steering angle | −1° to 1° |
| Number of transmission channels | 6 |
| Antenna size (height × length) | 10 m × 2 m |
| Signal bandwidth | 100 MHz |
| Sampling frequency | 133 MHz |
| Pulse duration | 5 s |
| PRF | 1866 Hz |
| Frequency increment | 622 Hz |
| Azimuth beam width | 0.318° |
| Point | Area | Region | Azimuth | Range | ||||
|---|---|---|---|---|---|---|---|---|
| PSLR/dB | ISLR/dB | IRW | PSLR/dB | ISLR/dB | IRW | |||
| A | 1st region | −13.24 | −10.20 | 0.886 | −13.25 | −10.18 | 0.886 | |
| B | 2nd region | −13.26 | −10.21 | 0.887 | −13.27 | −10.16 | 0.884 | |
| C | 3rd region | −13.28 | −10.15 | 0.885 | −13.27 | −10.16 | 0.886 | |
| D | 1st region | −13.26 | −10.28 | 0.885 | −13.24 | −10.24 | 0.885 | |
| E | 2nd region | −13.24 | −10.33 | 0.886 | −13.26 | −10.25 | 0.886 | |
| F | 3rd region | −13.27 | −10.31 | 0.886 | −13.26 | −10.25 | 0.886 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, Y.; Zhang, Z.; Chen, Z.; Qiu, J.; Ren, M.; Meng, X. A Novel Time-Domain Frequency Diverse Array HRWS Imaging Scheme for Spotlight SAR. Remote Sens. 2022, 14, 1085. https://doi.org/10.3390/rs14051085
Wen Y, Zhang Z, Chen Z, Qiu J, Ren M, Meng X. A Novel Time-Domain Frequency Diverse Array HRWS Imaging Scheme for Spotlight SAR. Remote Sensing. 2022; 14(5):1085. https://doi.org/10.3390/rs14051085
Chicago/Turabian StyleWen, Yuhao, Zhimin Zhang, Zhen Chen, Jinsong Qiu, Mingshan Ren, and Xiangrui Meng. 2022. "A Novel Time-Domain Frequency Diverse Array HRWS Imaging Scheme for Spotlight SAR" Remote Sensing 14, no. 5: 1085. https://doi.org/10.3390/rs14051085
APA StyleWen, Y., Zhang, Z., Chen, Z., Qiu, J., Ren, M., & Meng, X. (2022). A Novel Time-Domain Frequency Diverse Array HRWS Imaging Scheme for Spotlight SAR. Remote Sensing, 14(5), 1085. https://doi.org/10.3390/rs14051085










