Centennial Total Solar Irradiance Variation
Abstract
1. Introduction
2. Materials and Methods
2.1. TSI Composite
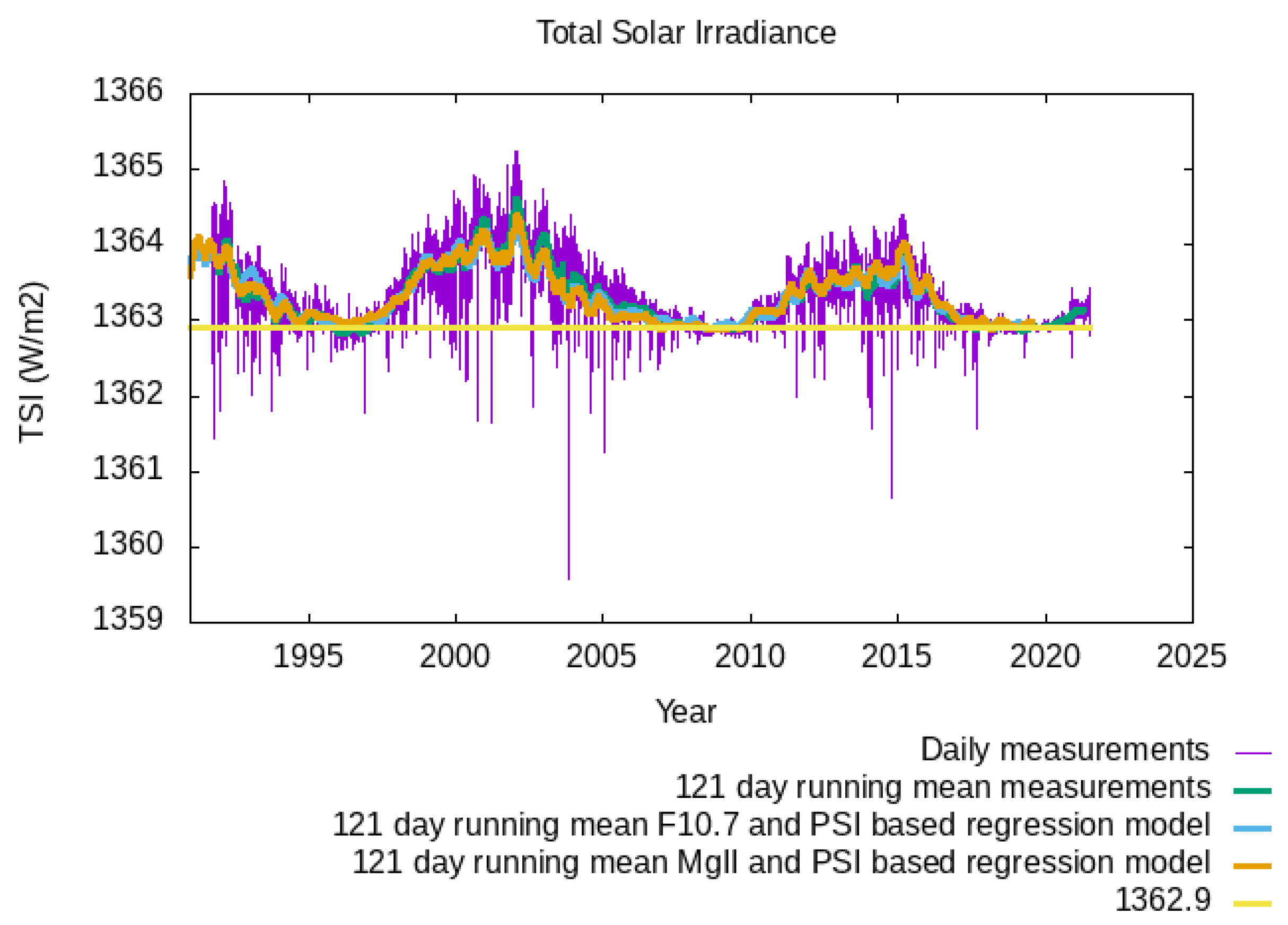
- The are scaled with an instrument adjustment factor , such that the adjusted time series have the same absolute level. The reference absolute level is the one from the Differential Absolute Radiometer (DIARAD) instrument, as part of the Solar Variability and Irradiance Monitor (SOVIM) experiment on the International Space Station (ISS) [24], with application of the new calibration procedure of [25]. The corresponding TSI level at solar minimum, also known as the quiet sun TSI level, is 1362.9 W/m2.
- The adjusted time series are quality-controlled by intercomparison. Parts of individual time series which differ too much from the other time series—for details, see [9]—are removed, and the Total Irradiance Monitor (TIM) on the Solar Radiation and Climate Experiment (SORCE) satellite [26] is corrected for its apparent linear drift compared to the other TSI radiometers. This results in quality-controlled adjusted time series .
- For every day t, the composite is calculated as the mean of the available time series :
2.2. Daily TSI Regression Model
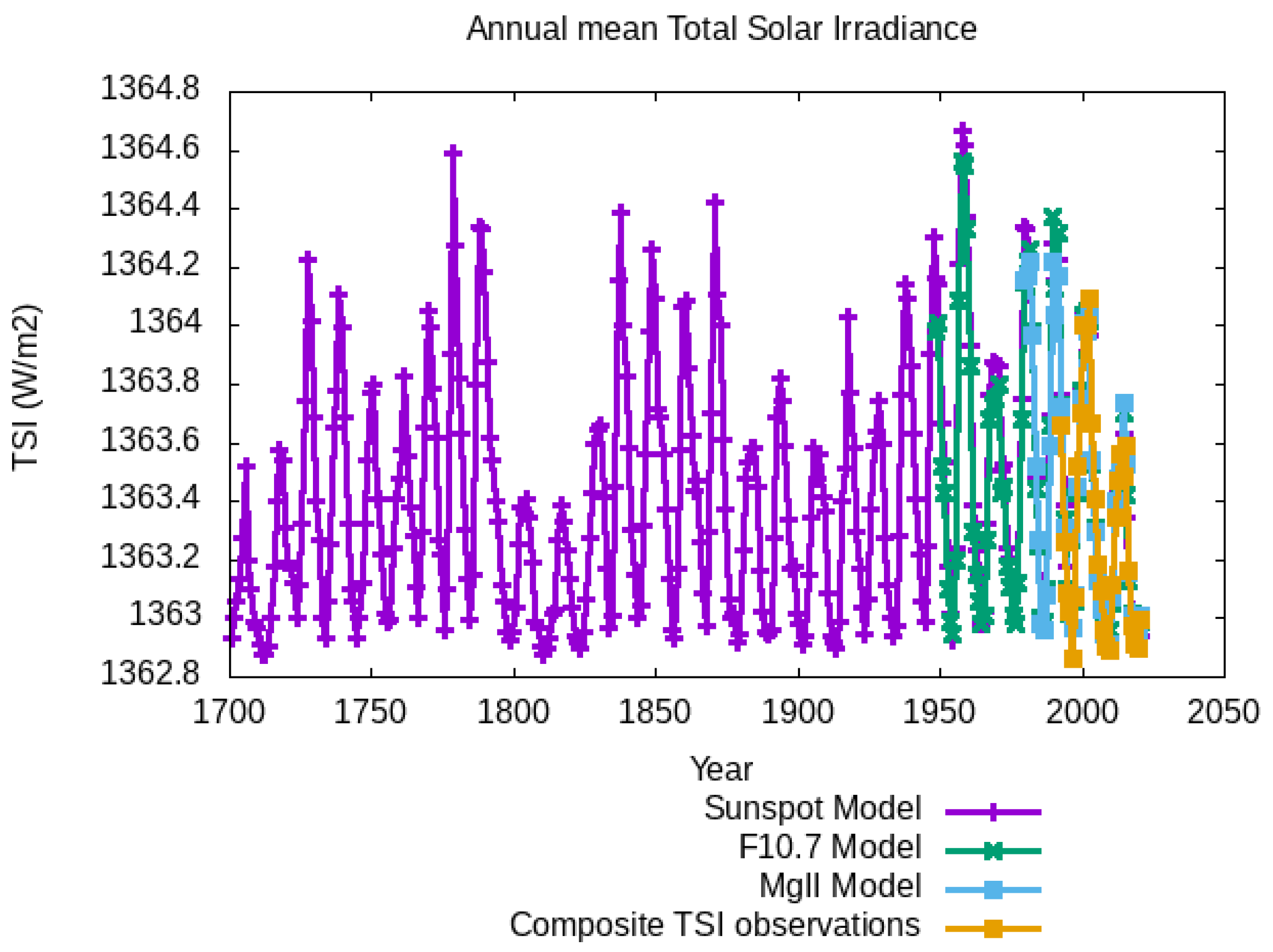
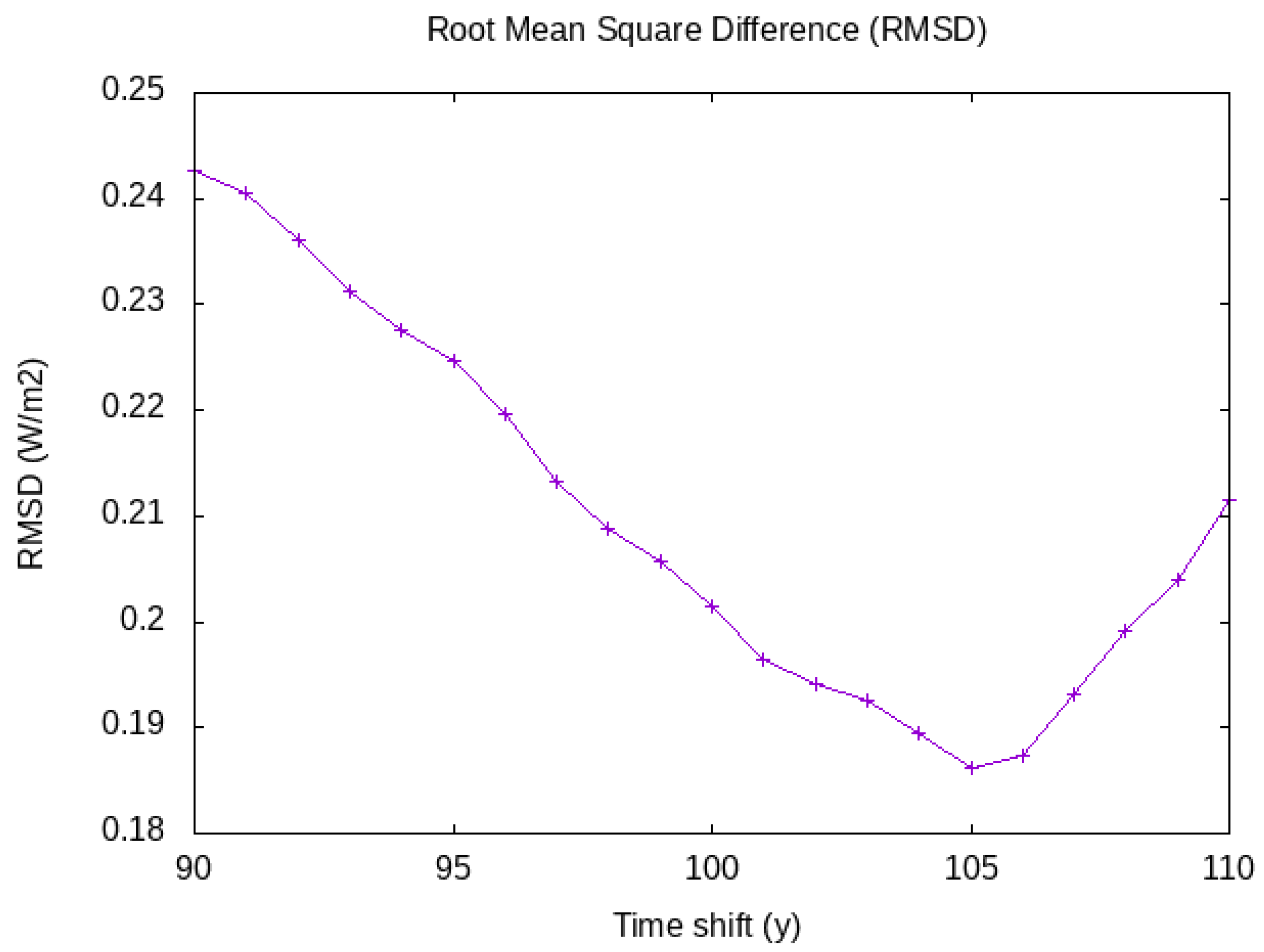
3. Results
- The above-mentioned MgII index, extending from 1979 to 2020;
- The above-mentioned F10.7 radio flux, extending from 1948 to 2020;
- The SILSO SN, extending from 1700 to 2020.
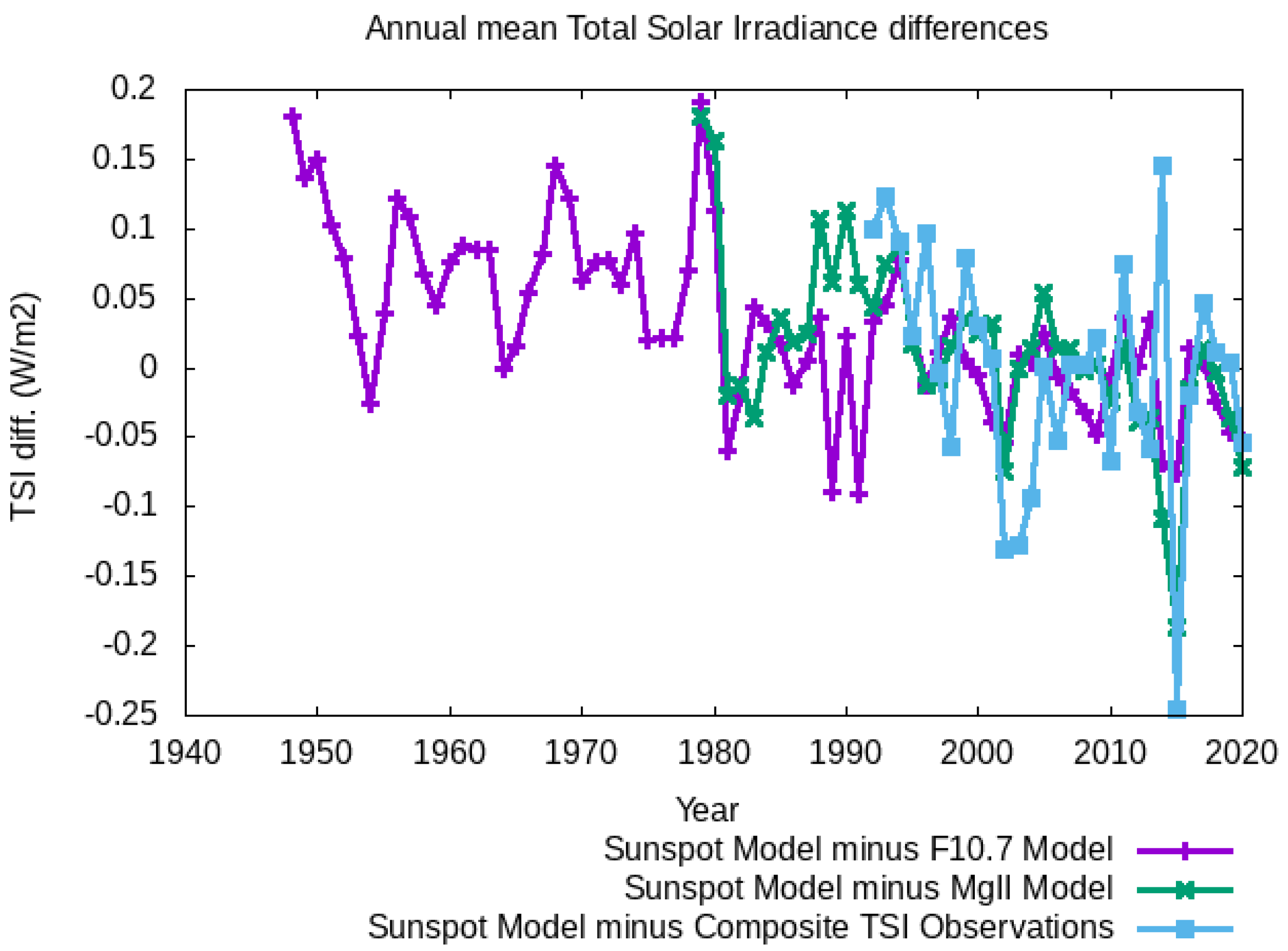
- The purple curve shows the difference between the SN-based model and the F10.7-based model.
- The green curve shows the difference between the SN-based model and the MgII-based model.
- The light blue curve shows the difference between the SN-based model and the composite TSI observations.
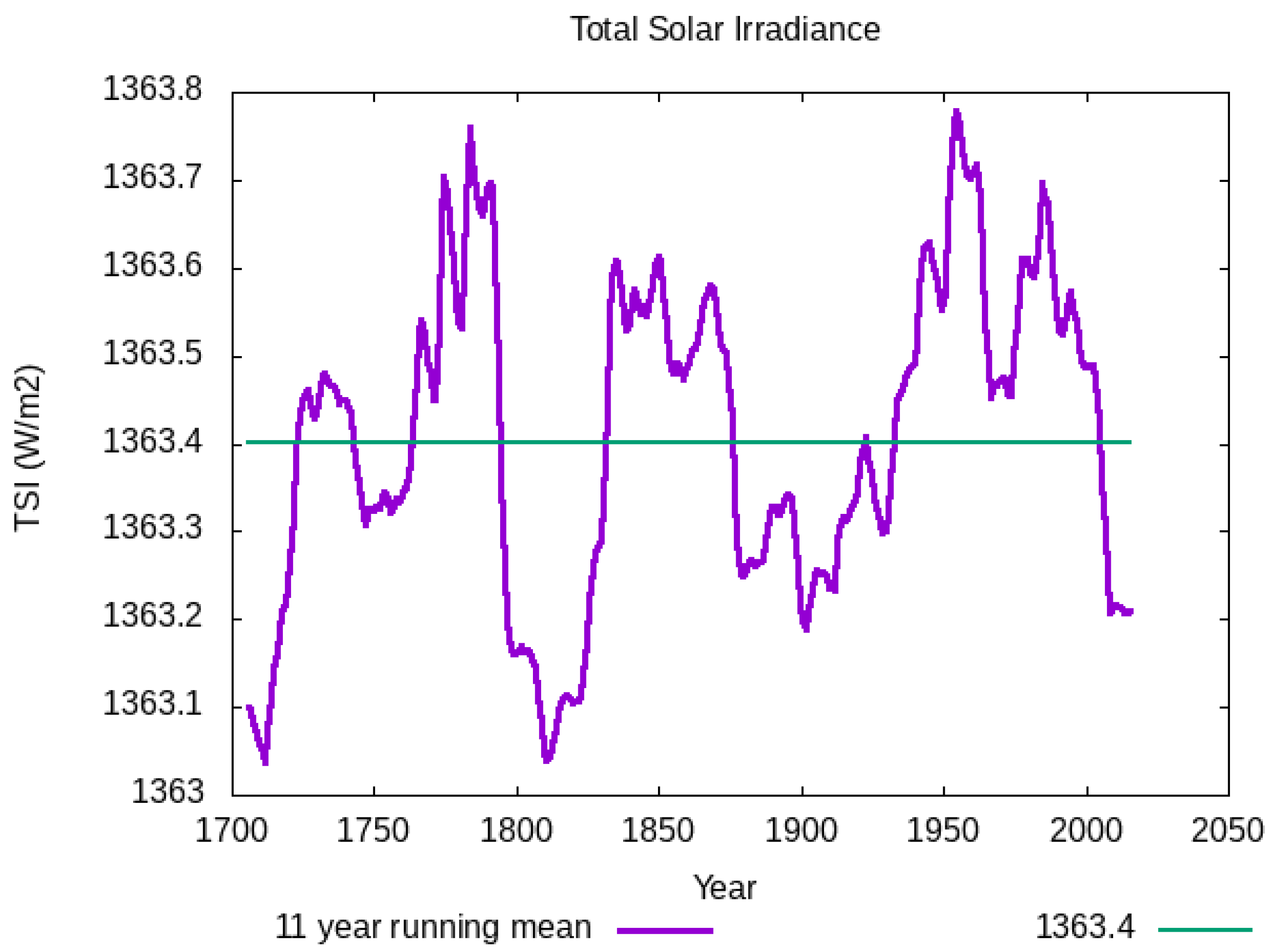
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACRIM | Active Cavity Radiometer Irradiance Monitor |
| DIARAD | Differential Absolute Radiometer |
| ECV | Essential Climate Variable |
| ERB | Earth Radiation Budget |
| ERBS | Earth Radiation Budget Satellite |
| ISS | International Space Station |
| LIA | Little Ice Age |
| PMO | Physikalishes und Meteorologisches Observatorium |
| PREMOS | Precision Monitoring of Solar variability |
| PSI | Photometric Sunspot Index |
| RMSE | Root Mean Square Error |
| SILSO | Sunspot Index and Long-term Solar Observations |
| SN | Sunspot Number |
| SORCE | Solar Radiation and Climate Explorer |
| SOVA | Solar Variability |
| SOVIM | Solar Variability and Irradiance Monitor |
| TCTE | Total Solar Irradiance Calibration Transfer Experiment |
| TIM | Total Irradiance Monitor |
| TSI | Total Solar Irradiance |
| TSIS | Total and spectral Solar Irradiance Sensor |
| VIRGO | Variability of Irradiance and Gravity Oscillations |
References
- Houghton, J.; Townshend, J.; Dawson, K.; Mason, P.; Zillman, J.; Simmons, A. The GCOS at 20 years: The origin, achievement and future development of the Global Climate Observing System. Weather 2012, 67, 227–235. [Google Scholar] [CrossRef]
- Plamondon, J.A. The Mariner Mars 1969 Temperature Control Flux Monitor. Jet Propuls. Lab. Space Program Summary 1969, 37–59, 162–168. [Google Scholar]
- Hickey, J.R.; Alton, B.M.; Kyle, H.L.; Hoyt, D. Total solar irradiance measurements by ERB/Nimbus-7. A review of nine years. Space Sci. Rev. 1988, 48, 321–334. [Google Scholar] [CrossRef]
- Crommelynck, D.; Fichot, A.; Lee, R.B., III; Romero, J. First realisation of the space absolute radiometric reference (SARR) during the ATLAS 2 flight period. Adv. Space Res. 1995, 16, 17–23. [Google Scholar] [CrossRef]
- Dewitte, S.; Crommelynck, D.; Mekaoui, S.; Joukoff, A. Measurement and uncertainty of the long-term total solar irradiance trend. Sol. Phys. 2004, 224, 209–216. [Google Scholar] [CrossRef]
- Willson, R.C.; Mordvinov, A.V. Secular total solar irradiance trend during solar cycles 21–23. Geophys. Res. Lett. 2003, 30, 1199. [Google Scholar] [CrossRef]
- Fröhlich, C. Evidence of a long-term trend in total solar irradiance. Astron. Astrophys. 2009, 501, L27–L30. [Google Scholar] [CrossRef]
- Dudok de Wit, T.; Kopp, G.; Fröhlich, C.; Schöll, M. Methodology to create a new total solar irradiance record: Making a composite out of multiple data records. Geophys. Res. Lett. 2003, 44, 1196–1203. [Google Scholar]
- Dewitte, S.; Nevens, S. The total solar irradiance climate data record. Astrophys. J. 2016, 830, 25. [Google Scholar] [CrossRef]
- Domingo, V.; Ermolli, I.; Fox, P.; Fröhlich, C.; Haberreiter, M.; Krivova, N.; Vögler, A. Solar surface magnetism and irradiance on time scales from days to the 11-year cycle. Space Sci. Rev. 2009, 145, 337–380. [Google Scholar] [CrossRef]
- Livingston, W.; Wallace, L. The Sun’s immutable basal quiet atmosphere. Sol. Phys. 2003, 212, 227–237. [Google Scholar] [CrossRef]
- Eddy, J.A. The maunder minimum. Sciences 1976, 192, 1189–1202. [Google Scholar] [CrossRef]
- Abreu, J.A.; Beer, J.; Steinhilber, F.; Tobias, S.M.; Weiss, N.O. For how long will the current grand maximum of solar activity persist ? Geophys. Res. Lett. 2008, 35, L20109. [Google Scholar] [CrossRef]
- Krivova, N.A.; Vieira, L.E.A.; Solanki, S.K. Reconstruction of solar spectral irradiance since the Maunder minimum. J. Geophys. Res. Space Phys. 2010, 115, A12112. [Google Scholar] [CrossRef]
- Lean, J.; Skumanich, A.; White, O. Estimating the Sun’s radiative output during the Maunder Minimum. Geophys. Res. Lett. 1992, 19, 1591–1594. [Google Scholar] [CrossRef]
- Balmaceda, L.; Krivova, N.A.; Solanki, S.K. Reconstruction of solar irradiance using the Group sunspot number. Adv. Space Res. 2007, 40, 986–989. [Google Scholar] [CrossRef][Green Version]
- Shapiro, A.I.; Schmutz, W.; Rozanov, E.; Schoell, M.; Haberreiter, M.; Shapiro, A.V.; Nyeki, S. A new approach to the long-term reconstruction of the solar irradiance leads to large historical solar forcing. Astron. Astrophys. 2011, 529, A67. [Google Scholar] [CrossRef]
- Schrijver, C.J.; Livingston, W.C.; Woods, T.N.; Mewaldt, R.A. The minimal solar activity in 2008–2009 and its implications for long-term climate modeling. Geophys. Res. Lett. 2011, 38, L06701. [Google Scholar] [CrossRef]
- Lean, J.L. Estimating solar irradiance since 850 CE. Earth Space Sci. 2018, 5, 133–149. [Google Scholar] [CrossRef]
- Clette, F.; Cliver, E.W.; Lefèvre, L.; Svalgaard, L.; Vaquero, J.M.; Leibacher, J.W. Preface to topical issue: Recalibration of the sunspot number. Sol. Phys. 2016, 291, 2479–2486. [Google Scholar] [CrossRef]
- Clette, F.; Lefèvre, L. The new sunspot number: Assembling all corrections. Sol. Phys. 2016, 291, 2629–2651. [Google Scholar] [CrossRef]
- Kuhn, T.S. The Structure of Scientific Revolutions; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]
- Dewitte, S.; Clerbaux, N. Measurement of the Earth radiation budget at the top of the atmosphere—A review. Remote Sens. 2017, 9, 1143. [Google Scholar] [CrossRef]
- Mekaoui, S.; Dewitte, S.; Conscience, C.; Chevalier, A. Total solar irradiance absolute level from DIARAD/SOVIM on the International Space Station. Adv. Space Res. 2010, 45, 1393–1406. [Google Scholar] [CrossRef]
- Dewitte, S.; Janssen, E.; Mekaoui, S. Science results from the Sova-Picard total solar irradiance instrument. AIP Conf. Proc. 2013, 1531, 688–691. [Google Scholar]
- Kopp, G. Science Highlights and Final Updates from 17 Years of Total Solar Irradiance Measurements from the SOlar Radiation and Climate Experiment/Total Irradiance Monitor (SORCE/TIM). Sol. Phys. 2021, 296, 1–16. [Google Scholar] [CrossRef]
- Woods, T.; Cahalan, R.; Denig, W.; Kopp, G.; Pilewskie, P.; Sparn, T. Rapid Coordination Extends Space-Based Sun-Climate Record. Eos Trans. Am. Geophys. Union 2014, 95, 429–430. [Google Scholar] [CrossRef]
- Pilewskie, P.; Kopp, G.; Richard, E.; Coddington, O.; Sparn, T.; Woods, T. TSIS-1 and continuity of the total and spectral solar irradiance climate data record. In EGU General Assembly Conference Abstracts; European Geophyscial Union: Vienna, Austria, 2018; p. 5527. [Google Scholar]
- Lee, R.B., III; Gibson, M.A.; Wilson, R.S.; Thomas, S. Long-term total solar irradiance variability during sunspot cycle 22. J. Geophys. Res. Space Phys. 2014, 100, 1667–1675. [Google Scholar] [CrossRef]
- Willson, R.C. Irradiance observations of SMM, Spacelab 1, UARS, and ATLAS experiments. In International Astronomical Union Colloquiums; Cambridge University Press: Cambridge, MA, USA, 1994; Volume 143, pp. 54–62. [Google Scholar]
- Crommelynck, D.; Dewitte, S. Solar constant temporal and frequency characteristics. Sol. Phys. 1997, 173, 177–191. [Google Scholar] [CrossRef]
- Crommelynck, D.; Domingo, V.; Fichot, A.; Fröhlich, C.; Penelle, B.; Romero, J.; Wehrli, C. Preliminary results from the SOVA experiment on board the European Retrievable Carrier (EURECA). Metrologia 1993, 30, 375. [Google Scholar] [CrossRef]
- Dewitte, S.; Crommelynck, D.; Joukoff, A. Total solar irradiance observations from DIARAD/VIRGO. J. Geophys. Res. Space Phys. 2004, 109, A02102. [Google Scholar] [CrossRef]
- Greg, K.; Lawrence, G. The total irradiance monitor (TIM): Instrument design. Sol. Phys. 2005, 230, 91–109. [Google Scholar]
- Meftah, M.; Dewitte, S.; Irbah, A.; Chevalier, A.; Conscience, C.; Crommelynck, D.; Mekaoui, S. SOVAP/Picard, a spaceborne radiometer to measure the total solar irradiance. Sol. Phys. 2014, 289, 1885–1899. [Google Scholar] [CrossRef]
- Schmutz, W.; Fehlmann, A.; Finsterle, W.; Kopp, G.; Thuillier, G. Total solar irradiance measurements with PREMOS/PICARD. AIP Conf. Proc. 2013, 1531, 624–627. [Google Scholar]
- Hudson, H.S.; Silva, S.; Woodard, M.; Willson, R.C. The effects of sunspots on solar irradiance. Sol. Phys. 1982, 76, 211–219. [Google Scholar] [CrossRef]
- Mandal, S.; Krivova, N.A.; Solanki, S.K.; Sinha, N.; Banerjee, D. Sunspot area catalog revisited: Daily cross-calibrated areas since 1874. Astron. Astrophys. 2020, 640, A78. [Google Scholar] [CrossRef]
- Tapping, K.F. The 10.7 cm solar radio flux (F10. 7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Nicolet, M.; Bossy, L. Solar radio fluxes as indices of solar activity. Planet. Space Sci. 1985, 33, 507–555. [Google Scholar] [CrossRef]
- Snow, M.; Weber, M.; Machol, J.; Viereck, R.; Richard, E. Comparison of Magnesium II core-to-wing ratio observations during solar minimum 23/24. J. Space Weather Space Clim. 2014, 4, A04. [Google Scholar] [CrossRef]
- Lean, J.L.; Rottman, G.J.; Kyle, H.L.; Woods, T.N.; Hickey, J.R.; Puga, L.C. Detection and parameterization of variations in solar mid-and near-ultraviolet radiation (200–400 nm). J. Geophys. Res. Atmos. 1997, 102, 29939–29956. [Google Scholar] [CrossRef]
- de Toma, G.; White, O.R.; Chapman, G.A.; Walton, S.R.; Preminger, D.G.; Cookson, A.M. Solar cycle 23: An anomalous cycle? Astrophys. J. 2004, 609, 1140. [Google Scholar] [CrossRef][Green Version]
- Gleissberg, W. Secularly smoothed data on the minima and maxima of sunspot frequency. Sol. Phys. 1967, 2, 231–233. [Google Scholar] [CrossRef]
- Feynman, J.; Ruzmaikin, A. The Centennial Gleissberg Cycle and its association with extended minima. J. Geophys. Res. Space Phys. 2014, 119, 6027–6041. [Google Scholar] [CrossRef]
- Wang, Y.M.; Lean, J.L. A New Reconstruction of the Sun’s Magnetic Field and Total Irradiance since 1700. Astrophys. J. 2021, 920, 100. [Google Scholar] [CrossRef]
- Myhre, G.; Myhre, C.L.; Forster, P.M.; Shine, K.P. Halfway to doubling of CO2 radiative forcing. Nat. Geosci. 2017, 10, 710–711. [Google Scholar] [CrossRef]
- Mann, M.E. Little ice age. Encycl. Glob. Environ. Chang. 2002, 1, 504–509. [Google Scholar]
- Haustein, K.; Otto, F.E.; Venema, V.; Jacobs, P.; Cowtan, K.; Hausfather, Z.; Schurer, A.P. A limited role for unforced internal variability in twentieth-century warming. J. Clim. 2019, 32, 4893–4917. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Hulot, G.; Gallet, Y.; Roth, R.; Licht, A.; Joos, F.; Khokhlov, A. Evidence for distinct modes of solar activity. Astron. Astrophys. 2014, 562, L10. [Google Scholar] [CrossRef]
- Inceoglu, F.; Simoniello, R.; Knudsen, M.F.; Karoff, C.; Olsen, J.; Turck-Chiéze, S.; Jacobsen, B.H. Grand solar minima and maxima deduced from 10Be and 14C: Magnetic dynamo configuration and polarity reversal. Astron. Astrophys. 2015, 577, A20. [Google Scholar] [CrossRef][Green Version]


| Reference | TSI Increase Since Maunder Minimum |
|---|---|
| [15] | 3.3 W/m2 |
| [16] | 1.3 W/m2 |
| [14] | 1.25 W/m2 |
| [17] | 6 W/m2 |
| [18] | 0.34 W/m2 |
| [19] | 0.93 W/m2 |
| Instrument | Reference | Start | End | ai |
|---|---|---|---|---|
| ACRIM 2 | [30] | 1991 | 2001 | 0.999220 |
| SOVA 1 | [32] | 1992 | 1993 | 0.998723 |
| SOVA 2 | [32] | 1992 | 1993 | 0.99744 |
| DIARAD/VIRGO | [33] | 1997 | 2017 | 0.997873 |
| PMO-6/VIRGO | [33] | 1997 | 2017 | 0.998241 |
| ACRIM 3 | [6] | 2002 | 2013 | 1.001572 |
| TIM/SORCE | [26,34] | 2003 | 2017 | 1.0039663 |
| SOVA-Picard | [25,35] | 2010 | 2013 | 1.001152 |
| PREMOS | [36] | 2010 | 2013 | 1.001719 |
| TIM/TCTE | [27] | 2013 | 2019 | 1.001267 |
| TIM/TSIS 1 | [28] | 2018 | 2021 | 1.001014 |
| Instrument | RMSD (W/m2) |
|---|---|
| ACRIM 2 | 0.16 |
| DIARAD/VIRGO | 0.10 |
| PMO-6/VIRGO | 0.12 |
| TIM/SORCE | 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dewitte, S.; Cornelis, J.; Meftah, M. Centennial Total Solar Irradiance Variation. Remote Sens. 2022, 14, 1072. https://doi.org/10.3390/rs14051072
Dewitte S, Cornelis J, Meftah M. Centennial Total Solar Irradiance Variation. Remote Sensing. 2022; 14(5):1072. https://doi.org/10.3390/rs14051072
Chicago/Turabian StyleDewitte, Steven, Jan Cornelis, and Mustapha Meftah. 2022. "Centennial Total Solar Irradiance Variation" Remote Sensing 14, no. 5: 1072. https://doi.org/10.3390/rs14051072
APA StyleDewitte, S., Cornelis, J., & Meftah, M. (2022). Centennial Total Solar Irradiance Variation. Remote Sensing, 14(5), 1072. https://doi.org/10.3390/rs14051072








