Sentinel-1 Satellite Radar Images: A New Source of Information for Study of River Channel Dynamics on the Lower Vistula River, Poland
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Area
2.2. River Channel Properties
2.3. Data Sources
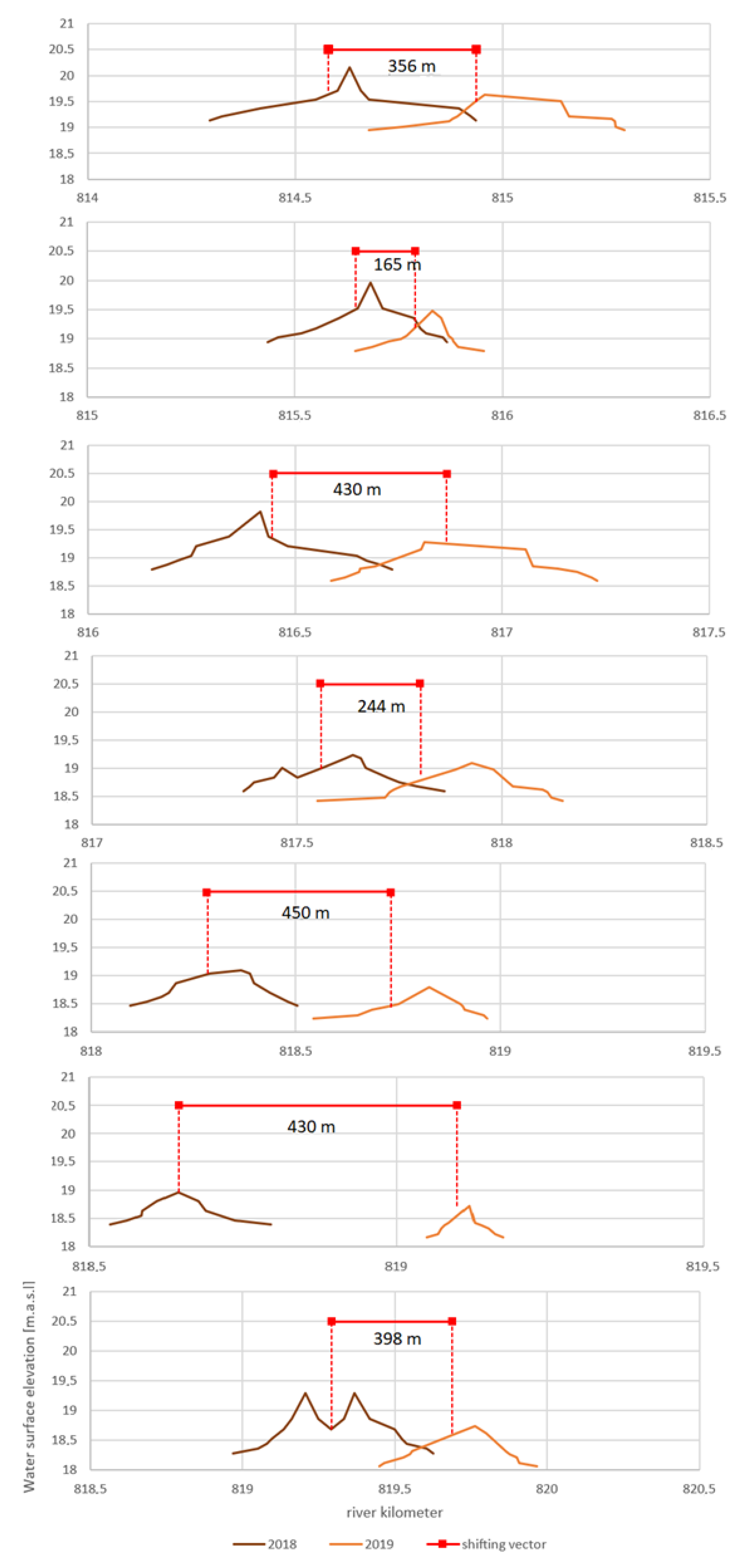
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gomez, B.; Naff, R.L.; Hubbell, D.W. Temporal variations in bedload transport rates associated with the migration of bedforms. Earth Surf. Processes Landf. 1989, 14, 135–156. [Google Scholar] [CrossRef]
- Redolfi, M. Free alternate bars in rivers: Key physical mechanisms and simple formation criterion. Water Resour. Res. 2021, 57, e2021WR030617. [Google Scholar] [CrossRef]
- Łoś, H.; Pawłowski, B. The use of Sentinel-1 imagery in the analysis of river ice phenomena on the Lower Vistula in the 2015–2016 winter season. In Proceedings of the Signal Processing Symposium (SPSympo), Jachranka, Poland, 12–14 September 2017; pp. 1–5. [Google Scholar]
- Majewski, W. The lower vistula and its ice problems. Arch. Hydro Eng. Environ. Mech. 2021, 68, 41–83. [Google Scholar] [CrossRef]
- Arnauda, F.; Schmitt, L.; Johnstone, K.; Rollet, A.J.; Piégaya, H. Engineering impacts on the Upper Rhine channel and floodplain over two centuries. Geomorphology 2019, 330, 13–27. [Google Scholar] [CrossRef]
- Rodrigues, S.; Mosselman, E.; Claude, N.; Wintenberger, C.L.; Juge, P. Alternate bars in a sandy gravel bed river: Generation, migration and interactions with superimposed dunes. Earth Surf. Processes Landf. 2015, 40, 610–628. [Google Scholar] [CrossRef]
- Claude, N.; Rodrigues, S.; Bustillo, V.; Bréhéret, J.G.; Macaire, J.J.; Jugé, P. Estimating bedload transport in a large sand-gravel bed river from direct sampling, dune tracking and empirical formulas. Geomorphology 2012, 179, 40–57. [Google Scholar] [CrossRef]
- Brasington, J.; Langham, J.; Rumsby, B. Methodological sensitivity of morphometric estimates of coarse fluvial sediment transport. Geomorphology 2003, 53, 299–316. [Google Scholar] [CrossRef]
- Lane, S.N.; Westaway, R.M.; Hicks, D.M. Estimation of erosion and deposition volumes in a large, gravel-bed, braided river using synoptic remote sensing. Earth Surf. Processes Landf. 2003, 28, 249–271. [Google Scholar] [CrossRef]
- Coleman, S.E.; Nikora, V.I. Exner equation: A continuum approximation of a discrete granular system. Water Resour. Res. 2009, 45, W09421. [Google Scholar] [CrossRef]
- Yalin, N.S.; Da Silva, A.M.F. Fluvial Processes; IAHR Monograph, IAHR: Delft, The Netherlands, 2001. [Google Scholar]
- Ballio, F.; Nikora, V.; Coleman, S.E. On the definition of solid discharge in hydro-environment research and applications. J. Hydraul. Res. 2014, 52, 173–184. [Google Scholar] [CrossRef]
- Skibiński, J. Rozwój łapaczek rumowiska używanych w Polsce oraz niektóre inne metody pomiarów wleczenia. Gospod. Wodna 1961, 22, 215–220. [Google Scholar]
- Karasiew, I.F.; Szumkow, I.G. Gidrometria; Gidrometeoizdat: Leningrad, Russia, 1985. [Google Scholar]
- Kostaschuk, R.A.; Ilersich, S.A.; Hickin, E.J. (Eds.) River Geomorphology; John Wiley & Sons: Chichester, UK, 1995. [Google Scholar]
- Lisimenka, A.; Kubicki, A. Bedload transport in the Vistula River mouth derived from dune migration rates, southern Baltic Sea. Oceanologia 2019, 61, 384–394. [Google Scholar] [CrossRef]
- Piętka, Z. Zastosowanie Izotopów Promieniotwórczych i Trwałych w Hydrologii i Oceanografii; Biuletyn PIHM: Warszawa, Poland, 1960. [Google Scholar]
- Carling, P.A.; Gölz, E.; Orr, H.G.; Radecki-Pawlik, A. The morphodynamics of fluvial sand dunes in the River Rhine, near Mainz, Germany. I., Sedimentology and morphology. Sedimentology 2000, 47, 227–252. [Google Scholar] [CrossRef]
- Czernik, S. Kilka uwag w sprawie regulacji ujścia Wisły. Gospod. Wodna 1954, 14, 304–309. [Google Scholar]
- Skibiński, J. Próba ustalenia najbardziej właściwego sposobu prowadzenia pomiarów wleczenia na Wiśle w profilu Nadwilanówka. Gospod. Wodna 1962, 22, 425–426. [Google Scholar]
- Goncarov, V.N. Dinamika Ruslovych Potokov; Gidrometeoizdat: Leningrad, Russia, 1962. [Google Scholar]
- Samov, G.I. Recnyje Nanosy; Gidrometeoizdat: Leningrad, Russia, 1959. [Google Scholar]
- Meyer-Peter, E.; Müller, R. Eine Formel zur Berechnung des Geschiebetriebs; Mitteilungen aus der Versuchsastalt für Wasserbau und Erdbau; Schweizerische Bauzeitung: Zürich, Switzerland, 1946; p. 16. [Google Scholar]
- Skibiński, J. Próba ilościowej oceny intensywności transportu rumowiska wleczonego w rzekach środkowej Polski. In Zeszyty Naukowe SGGW-AR w Warszawie; Rozprawy Naukowe: Warszawa, Poland, 1976. [Google Scholar]
- Ahmari, H.; Da Silva, A.M. Regions of bars, meandering and braiding in da Silva and Yalin’s plan. J. Hydraul. Res. 2011, 49, 718–727. [Google Scholar] [CrossRef]
- Ashley, G.M. Classification of large-scale subaqueous bedforms: A new look at an old problem. J. Sedim. Petrol. 1990, 60, 160–172. [Google Scholar]
- Wang, B.; Xu, Y.J. Sediment trapping by emerged channel bars in the lowermost mississippi river during a major flood. Water 2015, 7, 6079–6096. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Li, H.; Wang, Z.; Wang, B.; Xu, Y. Three decadal morphodynamic evolution of a large channel bar in the middle Yangtze River: Influence of natural and anthropogenic interferences. Catena 2021, 199, 105128. [Google Scholar] [CrossRef]
- Cavallo, C.; Nones, M.; Papa, M.N.; Gargiulo, M.; Ruello, G. Monitoring the morphological evolution of a reach of the Italian Po River using multispectral satellite imagery and stage data. Geocarto Int. 2021, 1–23. [Google Scholar] [CrossRef]
- Państwowa Inspekcja Ochrony Środowiska. Atlas Posterunków Wodowskazowych dla Potrzeb Państwowego Monitoringu Środowiska; Biblioteka Monitoringu Środowiska: Warszawa, Poland, 1996. [Google Scholar]
- Habel, M. Effects of flow regulation and river channelization on sandbar bird nesting availability at the Lower Vistula River. Ecol. Quest. 2018, 29, 43–53. [Google Scholar] [CrossRef]
- Babiński, Z. Hydromorphological consequences of regulating the lower Vistula, Poland. Regul. Rivers Res. Manag. 1992, 7, 337–348. [Google Scholar] [CrossRef]
- Grochulski., J. (Ed.) Monografia Dróg Wodnych Śródlądowych w Polsce; Wydawnictwo Komunikacji i Łączności: Warszawa, Poland, 1985. [Google Scholar]
- Ingarden, R. Rzeki i Kanały Żeglowne w Byłych Trzech Zaborach I Znaczenie ich Gospodarcze Dla Polski; Ministerstwo Robót Publicznych: Warszawa, Poland, 1921. [Google Scholar]
- Habel, M. Morfodynamika Dna Doliny Dolnej Wisły Poniżej Zbiornika Włocławskiego. Ph.D. Thesis, IGiPZ PAN Warszawa, Warszawa, Poland, 2011. [Google Scholar]
- Polska Państwowa Służba Hydrograficzna. Materiał Wleczony i Unoszony w Korycie Wisły: Sprawozdanie z Prac Państwowej służby Hydrograficznej Przeprowadzonych w Latach 1923–1939; Prace Państwowego Instytutu Hydrologiczno-Meteorologicznego; Wydawnictwa Komunikacyjne: Warszawa, Poland, 1954; p. 33. [Google Scholar]
- Brański, J.; Kondzielski, A. Uziarnienie rumowiska unoszonego wzdłuż biegu Wisły. Gospod. Wodna 1986, 6, 140–143. [Google Scholar]
- Du Boys, P. Etudes du régime du Rhône et de l’action exercée par les eaux sur un lit à fond de graviers indéfiniment affouillable. Ann. Ponts Chaussées 1879, 5, 141–195. [Google Scholar]
- Sentinel Technical Guides. Available online: sentinel.esa.int/web/sentinel/sentinel-technical-guides (accessed on 16 April 2021).
- The Alaska Satellite Facility. Available online: asf.alaska.edu (accessed on 16 April 2021).
- Sat4Envi. Available online: https://dane.sat4envi.imgw (accessed on 20 September 2021).
- Dane Publiczne IMGW-PIB. Available online: danepubliczne.imgw.pl (accessed on 16 April 2021).
- Magnuszewski, A. Application of satellite sentinel-1 radar images for description of ice phenomena on dębe reservoir. Acta Sci. Pol. Form. Circumiectus 2018, 4, 121–130. [Google Scholar] [CrossRef]
- Science Toolbox Exploitation Platform. Available online: https://step.esa.int/main/download/snap-download/ (accessed on 7 September 2020).
- Kryniecka, K.; Magnuszewski, A. Application of satellite sentinel-2 images to study alternate sandbars movement at Lower Vistula River (Poland). Remote Sens. 2021, 13, 1505. [Google Scholar] [CrossRef]
- Babiński, Z.; Habel, M. Value of bedload movement in alluvial rivers using analysis of sandbar migration. In MARID 2016, Proceedings of the Fifth International Conference on Marine and River Dune Dynamics, Caernarfon, UK, 4–6 April 2016; Van Landeghem, K.J.J., Garlan, T., Baas, J.H., Eds.; Bangor University and SHOM: Bangor, UK, 2016. [Google Scholar]
- Habel, M.; Babiński, Z.; Szatten, D.; Chalov, S.; Rozlah, Z.; Maerker, M. Clastic sediment transport renewal below Włocławek Reservoir. In Geography in the Face of ModernWorld Challenges; Chaberek-Karwacka, G., Malinowska, M., Eds.; University of Gdańsk: Gdańsk, Poland, 2016; pp. 93–114. [Google Scholar]
- Kryniecka, K.; Magnuszewski, A. Use of Sentinel-2 images for the detection of sandbars along the lower Vistula. Form. Circumiectus 2020, 19, 23–33. [Google Scholar] [CrossRef]
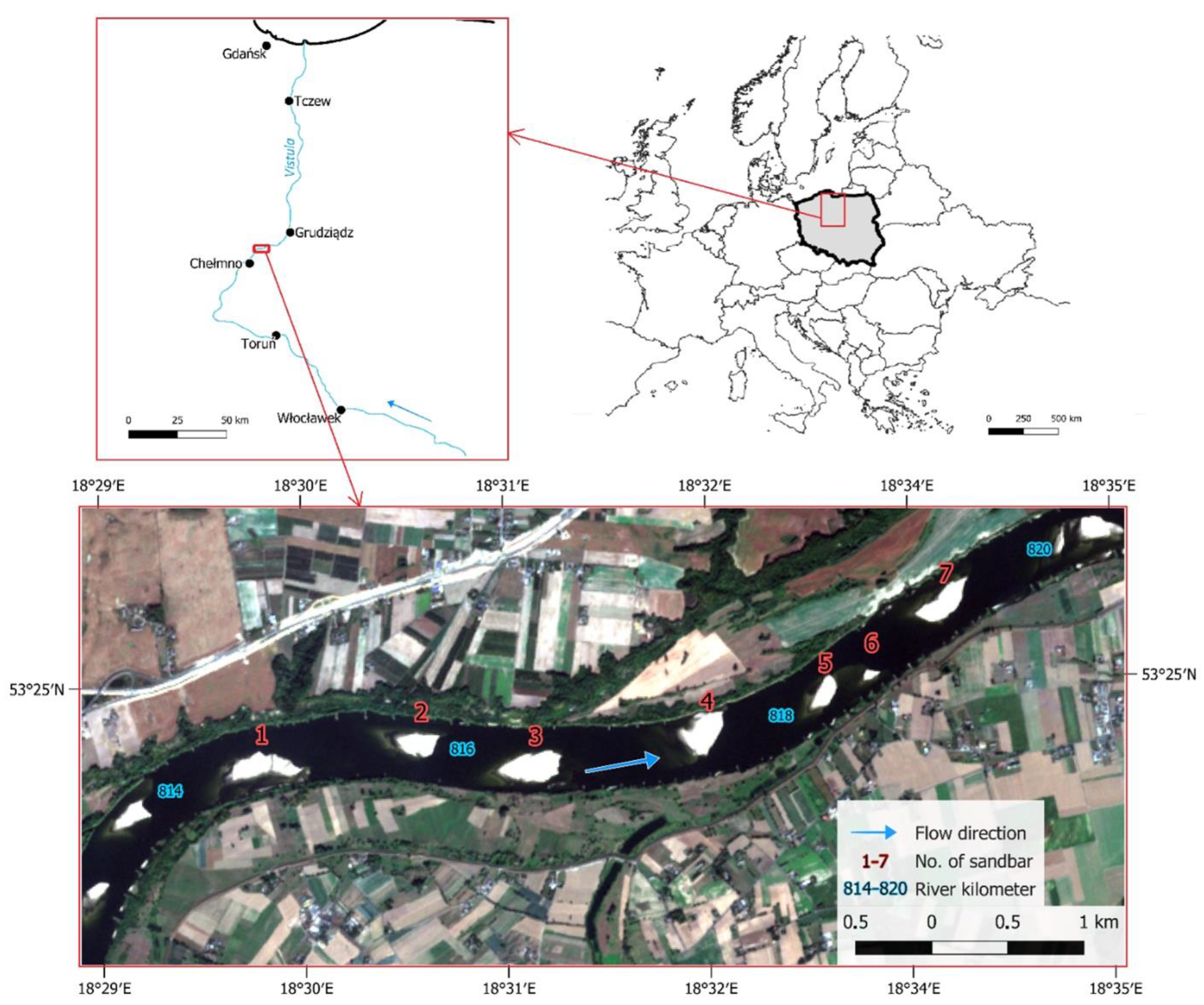

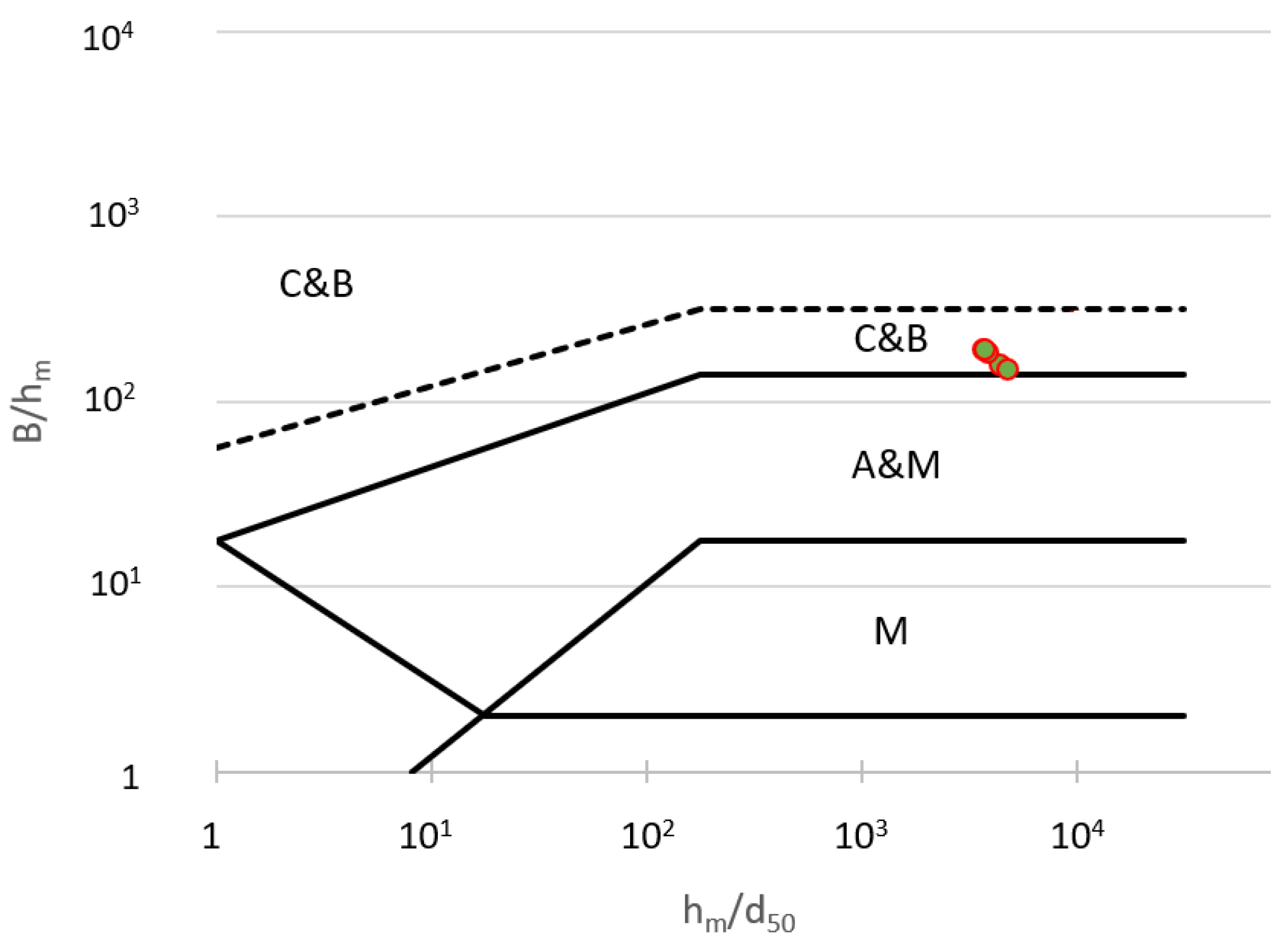
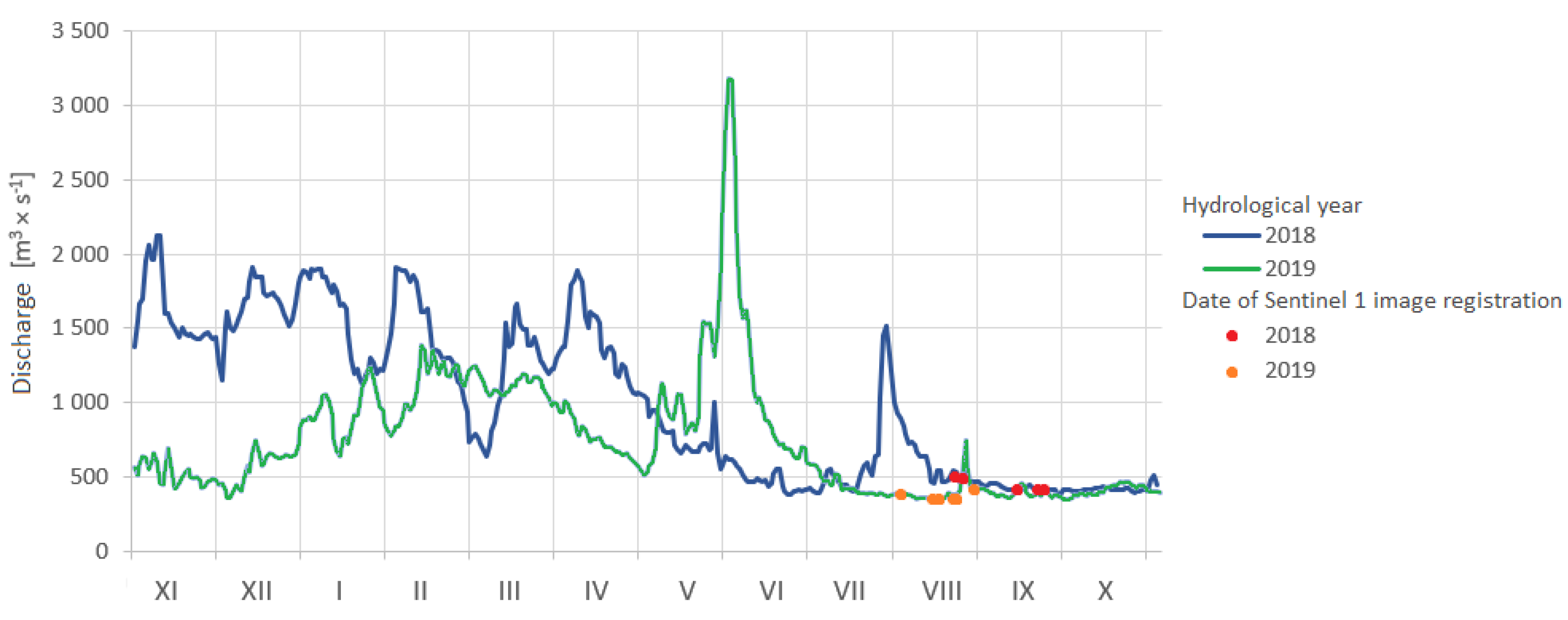



| Lower Vistula River Characteristic Discharges | Discharge at Toruń Gauge Q (m3·s−1) | Discharge at Tczew Gauge Q (m3·s−1) |
|---|---|---|
| Average low flow—MLQ | 359 | 419 |
| Average mean flow—MMQ | 992 | 1080 |
| Average high flow—MHQ | 3740 | 3840 |
| Sentinel-1 Image Sensing Date | River Stage H (cm) | Water Level (m a.s.l.) | Discharge Q (m3·s−1) |
|---|---|---|---|
| 2018 | |||
| 4 August 2018 | 260 | 21.56 | 729 |
| 21 August 2018 | 216 | 21.12 | 535 |
| 22 August 2018 | 199 | 20.95 | 467 |
| 5 September 2018 | 182 | 20.78 | 446 |
| 17 September 2018 | 174 | 20.70 | 422 |
| 26 September 2018 | 158 | 20.54 | 376 |
| 27 September 2018 | 166 | 20.62 | 398 |
| 2019 | |||
| 1 July 2019 | 220 | 21.16 | 571 |
| 1 August 2019 | 168 | 20.64 | 390 |
| 13 August 2019 | 152 | 20.48 | 350 |
| 16 August 2019 | 158 | 20.54 | 363 |
| 22 August 2019 | 208 | 21.04 | 542 |
| 25 August 2019 | 178 | 20.74 | 417 |
| 31 August 2019 | 173 | 20.69 | 403 |
| Sandbar No. | Sandbar Height (m) | Sandbar Length (m) | Sandbar Shift in the Period | ||
|---|---|---|---|---|---|
| 2018 | 2019 | 2018 | 2019 | 26 September 2018–31 August 2019 | |
| 1 | 1.02 | 0.68 | 641 | 617 | 356 |
| 2 | 1.02 | 0.68 | 433 | 310 | 165 |
| 3 | 1.34 | 0.68 | 580 | 642 | 430 |
| 4 | 0.64 | 0.68 | 491 | 599 | 244 |
| 5 | 0.64 | 0.58 | 408 | 424 | 450 |
| 6 | 0.58 | 0.58 | 262 | 124 | 430 |
| 7 | 1.02 | 0.68 | 658 | 518 | 398 |
| average | 0.89 | 0.65 | 496 | 462 | 353 |
| Sandbar No. | Elevation of the Channel Thalweg Runs (m a.s.l.) | Elevation of the Sandbar Top in 2019 (m a.s.l.) | Height of Sediment in Motion hb (m) |
|---|---|---|---|
| 1 | 17.54 | 19.63 | 2.09 |
| 2 | 18.30 | 19.47 | 1.17 |
| 3 | 18.60 | 19.27 | 0.67 |
| 4 | 18.17 | 19.09 | 0.92 |
| 5 | 17.37 | 18.82 | 1.45 |
| 6 | 16.70 | 18.75 | 2.05 |
| 7 | 17.30 | 18.74 | 1.44 |
| average | – | – | 1.40 |
| Sandbar No. | Bedform Steepness Index from Sentinel-1 Measurements h/l | Bedform Steepness Index from Formula (4) h/l = 0.1027 l −0.6149 | ||
|---|---|---|---|---|
| 2018 | 2019 | 2018 | 2019 | |
| 1 | 0.0016 | 0.0011 | 0.0019 | 0.0020 |
| 2 | 0.0024 | 0.0022 | 0.0025 | 0.0030 |
| 3 | 0.0023 | 0.0011 | 0.0021 | 0.0019 |
| 4 | 0.0013 | 0.0011 | 0.0023 | 0.0020 |
| 5 | 0.0016 | 0.0014 | 0.0025 | 0.0025 |
| 6 | 0.0022 | 0.0047 | 0.0033 | 0.0053 |
| 7 | 0.0015 | 0.0013 | 0.0019 | 0.0022 |
| average | 0.0018 | 0.0018 | 0.0024 | 0.0027 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kryniecka, K.; Magnuszewski, A.; Radecki-Pawlik, A. Sentinel-1 Satellite Radar Images: A New Source of Information for Study of River Channel Dynamics on the Lower Vistula River, Poland. Remote Sens. 2022, 14, 1056. https://doi.org/10.3390/rs14051056
Kryniecka K, Magnuszewski A, Radecki-Pawlik A. Sentinel-1 Satellite Radar Images: A New Source of Information for Study of River Channel Dynamics on the Lower Vistula River, Poland. Remote Sensing. 2022; 14(5):1056. https://doi.org/10.3390/rs14051056
Chicago/Turabian StyleKryniecka, Klaudia, Artur Magnuszewski, and Artur Radecki-Pawlik. 2022. "Sentinel-1 Satellite Radar Images: A New Source of Information for Study of River Channel Dynamics on the Lower Vistula River, Poland" Remote Sensing 14, no. 5: 1056. https://doi.org/10.3390/rs14051056
APA StyleKryniecka, K., Magnuszewski, A., & Radecki-Pawlik, A. (2022). Sentinel-1 Satellite Radar Images: A New Source of Information for Study of River Channel Dynamics on the Lower Vistula River, Poland. Remote Sensing, 14(5), 1056. https://doi.org/10.3390/rs14051056







