Abstract
In this paper, we study a geometric dilution of a precision (GDOP)-based localization performance metric for multisite radar adopting a time-of-arrival (TOA)-based localization scheme. In contrast to the existing literature, we consider an actual uncertain measurement situation where the detection probabilities of radar nodes are assumed to be less than unity. The aim is to formulate a general signal-decoupled metric to describe the system localization performance while fully considering detection and estimation operations. Specifically, to match the uncertain measurements, we first establish effectively detected time delay measurements (TDMs) for localization and modify the traditional performance bounds for TDM estimation. Then, by combining the localization performance with the effective detection (ED) via probability, we propose a novel geometric dilution of precision with uncertain measurements (GDOP-UM) metric. The proposed metric can truly characterize the localization performance under the uncertain measurement situation. Finally, the simulation results show that the proposed GDOP-UM can describe the actual localization performance regardless of how the detection performance changes.
1. Introduction
Multisite radar system (MSRS) is a type of radar equipped with multiple distributed transmitters and receivers. Benefiting from different signal propagation paths for measurements, MSRSs can obtain gain in target information [1]. In recent decades, MSRSs have shown considerable advantages over traditional radar systems in various aspects, such as detection [2,3,4,5,6], parameter estimation [7,8], tracking [9,10], and localization [10,11,12,13].
Multiple signal propagation paths allow MSRSs to perform indirect localization [13], such as time-difference-of-arrival (TDOA), direction-of-arrival (DOA), and time-of-arrival (TOA)-based localization schemes [14]. Due to the low cost and convenience of data processing, the TOA-based localization is widely adopted in MSRSs [8].
Benefiting from the development of signal theory, to obtain good low probability of intercept (LPI) performance, modern radars often use complex and even time-varying signals to detect targets. Confronted with increasingly complex electromagnetic environments and mission requirements, the systems require better detection capabilities and higher resource utilization. Therefore, many researchers aim to perform optimization design of the system resources or layout, including geometric optimization [15,16,17], resource scheduling [9,15,18,19], waveform design [20,21], etc.
However, due to rapid changes in the mission environment, the optimization design of the system resources or layout needs to be done quickly or even in real time. Accurate evaluation of the system performance is key for radar system design. For the optimization of the system resources or layout, confronting complex signals and fast implementation requirements, quick and accurate evaluation of the system performance is particularly important.
Coincidentally, geometric dilution of precision (GDOP) provides us with a powerful tool for quickly characterizing the relative accuracy of TOA localization in different positions with a given system layout over a specific geographic area [13,22]. Due to its specific derivation directly from a time delay measurement (TDM) set, the GDOP is signal-decoupled and simple in form. Hence, it can provide a general rapid evaluation of the localization performance while adapting to different signal forms.
The GDOP was originally adopted in Global Positioning System (GPS) applications to demonstrate the dependency of the attainable TOA localization accuracy for an arrangement of satellite positions with respect to the target [23,24]. In recent decades, the concept of GDOP has been introduced to the radar community as a Fisher-information-matrix-related measure [13,22,25,26,27,28,29,30]. In [13,25], researchers applied the GDOP to verify the performance of the algorithm proposed in the papers. In more papers covering the GDOP, researchers fully utilized the advantage of the GDOP, namely the above mentioned concise form and independence from signals, to optimize the system resources or layout.
For example, in [27,28,29,30], the GDOP was used to optimize the positions of radar nodes. In [22], the GDOP was applied to ensure the optimal antenna subset selection scheme. In these aforementioned works, researchers used the GDOP as an off-the-shelf tool, and hence all these GDOP metrics have similar expressions as adopted in GPS. We call these GDOP metrics traditional GDOP (T-GDOP).
However, GPS commonly applies a cooperative localization scheme to obtain the location information of users, and its TDMs are generally obtained deterministically with fixed system errors [23,24]. In most of the works mentioned earlier, TDMs are also assumed to be accurately obtained in advance and entirely credible. Nevertheless, different from GPS, MSRSs commonly apply non-cooperative localization schemes to locate a target. For MSRSs, TDMs are obtained by the early detection and parameter estimation processes, and these processes result in the uncertainty of TDMs [13,25].
Specifically, the acquisition of TDMs is probabilistic, and the acquisition probability and the quality of TDMs closely depend on the signal-to-noise ratio (SNR) of received signals. In particular, due to the range attenuation of radiation, the SNR of received signals may be low. The low SNR further results in poor detection and estimation performance with small probabilities of detection and large estimation errors [13,25,31,32]. Therefore, considering the actual detection and estimation process, the assumption that all TDMs are entirely credible is invalid.
Further, the T-GDOP based on this assumption is no longer applicable [24]. In [9,33,34,35,36,37], several Cramér–Rao lower bounds (CRLBs) considering the uncertainty of measurements are investigated. However, the signal-decoupled performance evaluation metrics considering uncertain measurements need to be further improved.
In this paper, we aim to establish a signal-decoupled metric based on GDOP to describe the TOA localization performance for MSRSs with uncertain measurements. The main contributions of this paper are concluded as follows:
- To adapt the uncertainty of signal detection, considering the fact that the actual detection probability of a target is always less than 1, we establish the first TDM model under uncertain measurements to describe the TOA localization process more accurately. To adapt the uncertainty of TDM estimation in low SNR, we propose a modified performance bound for TDM estimation by introducing the Ziv-Zakai bound (ZZB).
- By considering the effect of detection and estimation on the subsequent TOA localization, we combine the detection and localization performance via the probabilities under different detection results and further propose a novel geometric dilution of precision with uncertain measurements (GDOP-UM) metric for localization performance analysis of actual applications.
- To verify the reasonability and accuracy of the proposed GDOP-UM metric, elaborate simulations are performed and analyzed under a fixed-node-position scenario. Moreover, we perform simulations under an unfixed-node-position scenario for a typical geometric optimization application, namely, optimizing the system localization performance by adjusting the node positions. The simulations also show the accuracy and applicability of the GDOP-UM metric.
The proposed GDOP-UM metric can be widely applicable. Similar ideas may be widely applied to formulate GDOP-like metrics for other time-delay-based or hybrid indirect localization methods, such as the TDOA localization scheme.
The rest of the paper is organized as follows. The system model and uncertain measurements are established in Section 2 and Section 3, respectively. In Section 4, we modify the traditional performance bounds for TDM estimation and further formulate the GDOP-UM metric. Simulations are presented in Section 5, and Section 6 summarizes our conclusions.
2. Mathematical Model
We consider an MSRS equipped with M transmitters and N receivers, and then we include transmit–receive (T-R) channels. Let us denote and as the 2D Cartesian position coordinates of the mth transmitter and the nth receiver, respectively, where and , is the transpose operator, and is the real space. Let denote the position matrix including all the radar nodes. Assume that a target is located at the position , and the estimate of the target position is expressed as . Since the influence of Doppler on localization performance is not considered, herein we do not consider the motion state of the target.
Let denote the theoretical time delay for the th T-R channel, i.e., from the mth transmitter, to the target, to the nth receiver, and then we have
where c is the speed of light, and denotes the bistatic distance corresponding to the th T-R channel.
To an MSRS, the TDMs of all T-R channels are first estimated in the receivers, and the obtained TDMs are sent to the fusion center to perform TOA localization. If TDMs of all T-R channels are available and accurately estimated, then there is a group of TDMs, , for performing TOA localization of the target. For the th T-R channel, the TDM can be represented as
where denotes the bistatic distance measurement corresponding to the th T-R channel. is a zero-mean random Gaussian error with the standard deviation , and is given by [17,31,37,38]
where represents the root-mean-square (RMS) bandwidth of the signal (Herein, we assume the parameters of the signals from all transmitters are the same. is not commonly used in radar signal processing as B. However, the mathematical expression of can be greatly simplified by resorting to . Additional, can be derived from B [31]), defined as [31]
where is the signal spectrum and denotes the modulus of a complex number. Assume the spectrum of the transmitted signals is a rectangular spectrum, and then is given by [31]
where B denotes the signal bandwidth.
In (7), is the SNR of the received signal corresponding to the th T-R channel. For a given deterministic signal, depends on the path loss , and . Specifically, can be calculated as [37]
where and are the transmitting antenna gain and receiving antenna gain, and represent pattern propagation factors for the transmitter-to-target path and for receiver-to-target path, and denotes the bistatic radar cross section (RCS) of the target. k and are the Boltzmann constant and the standard temperature, respectively. , , , and are the transmitted average power, wavelength, integration time, receiver noise figure and system loss factor, respectively.
3. Localization Measurements with Detection Uncertainty
In the previous literature investigating TOA localization and its performance evaluation [13,22,25,26,27,28], for all the T-R channels, it was assumed that the target was effectively detected and that TDMs were accurately estimated with small estimation errors, illustrated as Figure 1. Therefore, for the traditional TOA performance evaluation, TDMs of all the T-R channels, i.e., , are utilized with the early detection uncertainty ignored.
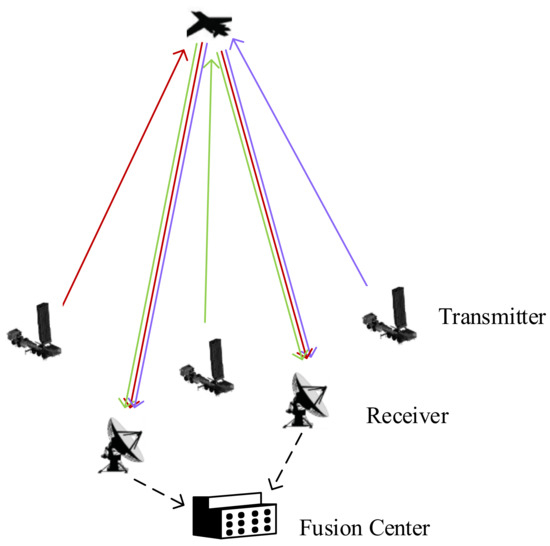
Figure 1.
Sketch of TOA localization via an MSRS.
However, TDMs are normally obtained by utilizing the cross-correlation operation between the target echo and the transmitted signal under a synchronized clock [13,25,32,39]. Hence, the acquisition and performance of TDMs largely depend on SNR [13,25]. Different from the existing research, this paper considers the TOA localization scenario where the TDMs are obtained with detection uncertainty. Specifically, when the SNR of the signal corresponding to one certain channel is extremely low, i.e., the output peak of the matched filter is below the filtered noise level [31], the TDM for this channel is unreliable and even unavailable.
Given that such a TDM is regarded as missing or unobservable, it will not be used in the subsequent TOA localization and corresponding performance evaluation [10]. We notice that the detection performance of the system heavily depends on SNR [31,40] as well. Therefore, by performing independent detection for each T-R channel, we assume that, when the target is effectively detected, the TDM for the corresponding channel is available. Then, as in [33,34,35,36], for the th T-R channel, a binary variable is introduced to indicate whether the target is effectively detected:
where is the detection probability of the target corresponding to the th T-R channel, and can be calculated as [8,31,40]
where is the Marcum Q-function, and is the probability of false alarm.
Then, considering all the T-R channels, a detection sequence with possibilities is established. Let denote the lth possible detection sequence, where , and is defined the same as (11). The occurrence probability of the detection sequence can then be calculated as
where represents the probability function, which is fundamental to the proposed metric. We notice that is related to the detection results of all the T-R channels, namely the detection probability . is dependent on SNR via the Marcum Q-function. Hence, is also affected by SNR.
Then, for the detection result corresponding to , the available TDMs for all the channels can be further reformulated as , where ⊙ is the Hadamard product. The non-zero elements in represent the actually available TDMs. Let denote the number of non-zero elements in , namely the number of available TDMs for all the channels corresponding to . Clearly, can be calculated as , where denotes the 1-norm of a vector.
Different from the assumption of effective detection by all T-R channels in previous literature [13,22,25,26,27,28], available TDMs of three or more T-R channels can ensure the uniqueness and reliability of the TOA localization result [12,31]. Therefore, is necessary for effective TOA localization instead of . depends on the localization scheme and the system requirements. In this paper, we investigate the two-dimensional TOA localization.
Without loss of generality, we assume that there is no available prior information, and three or more T-R channels can then ensure the uniqueness of the TOA localization result. To ensure the uniqueness and reliability of the TOA localization result, we let . We further define the detection with as complete detection (CD), i.e., the target is detected by all the T-R channels and define the detection with as effective detection (ED), i.e., the target is detected by at least three T-R channels. Herein, the performance evaluation for TOA localization is analyzed under ED.
As stated above, we assume that is satisfied under the detection sequence . We extract the non-zero TDMs from , and we establish an effectively detected TDM vector as
To the TDM , where , we assume that the signal is transmitted by the th transmitter and received by the th receiver, where and .
Remark 1.
The detection process is a probabilistic random process. Different from the idealized deterministic localization measurement model adopted in existing researches, the TDM model for TOA localization established herein is more practical and reasonable, with the actual early detection process fully considered.
4. GDOP with Uncertain Measurements for MSRSs
Once the effectively detected TDM vectors s are established, the TOA localization can be performed with s and the corresponding radar positions. Then, we can further evaluate the localization performance in terms of the GDOP-like metric.
For the detection sequence , the theoretical time delay for the TDM can be calculated as [13]
By derivation, we obtain
Considering all the effectively detected TDMs of all T-R channels, we can reformulate (16) in the matrix form as below:
with
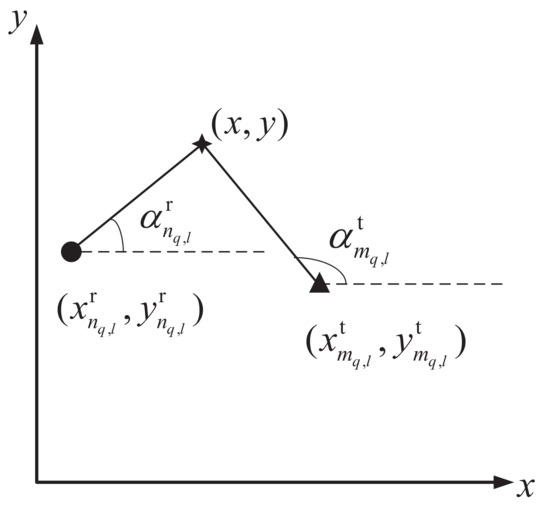
Figure 2.
Geometric relationship between the radar nodes and the target.
According to the generalized inverse, (17) can be further rewritten as
Proposition 1.
Given the detection sequence , the corresponding localization error covariance matrix can be expressed as
where
Note that denotes the expectation operator, represents the diagonal matrix, and is the standard deviation of error for the TDM .
Proof.
Recall (20) and let , and then . Therefore, the localization error covariance matrix can be further given by
with defined in (23). □
For the T-GDOP, similar as (7), is usually set based on the derivation of the CRLB with certain measurements [22,25,37] (In some other papers, is simply set as a constant [26,28]). Clearly, such a cannot match the actual TOA localization with uncertain measurements.
The ZZB is an estimator bound that matches a priori bound (APB) at low SNR and the CRLB at high SNR, and thus it can provide a more complete and reasonable description of the estimation error of TDMs [31,41]. To adapt to the uncertainty of TDM estimation in low SNR, the ZZB is introduced to modify the performance bounds for the TDM estimation. Specifically, for uncertain measurements is modified as [31,41]
where is the complementary error function and is the upper incomplete gamma function:
In (25), and are the applicable APB and CRLB, given by
where T is the data recording duration and is set as the duration of the matched filter output, and is the pulse width.
In Figure 3, a specific example about ZZB is given with CRLB as the benchmark. We found that, in the case of high SNR (SNR≥17dB), the ZZB (corresponding to uncertain measurements) and the CRLB (corresponding to certain measurements) are equal. When SNR is lower, the CRLB increases to a high level as SNR decreases. In contrast, as SNR decreases to a certain level, the ZZB approaches the APB. In fact, in actual applications, the estimation errors of TDMs in low SNR can be limited to a range of possible time delays by utilizing some a priori knowledge [31]. Moreover, compared with actual measurements, the ZZB is verified to be more accurate for measuring the accuracy of TDMs [13,31].
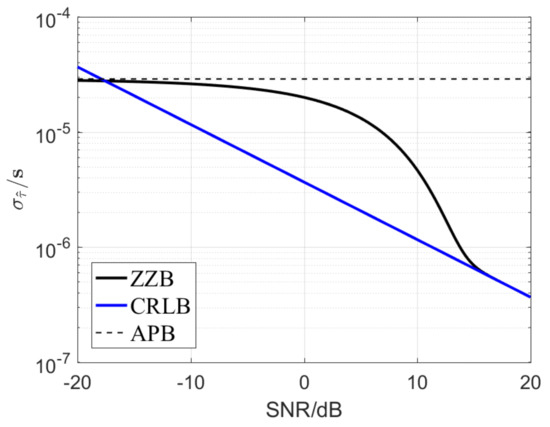
Figure 3.
versus SNR for various bounds (the signal parameters are shown in Table 1).

Table 1.
Performance parameters of the radar nodes.
Then, considering the probabilistic uncertainty of detection sequences occurrence, the GDOP-UM metric is further given in the following Proposition 2.
Proposition 2.
Considering all the effective detection sequences (i.e., ) and their corresponding probabilities, GDOP-UM can be formulated as
where is the GDOP-like value corresponding to the detection sequence , formulated as [27,28]
where denotes the trace of a matrix.
Proof.
Herein, the GDOP-UM is formulated as the weighted sum of the GDOP-like values corresponding to appropriate detection sequences, weighted by the corresponding possibilities. Considering the necessity of ED for TOA localization, we have
It should be noted that, the probabilities of some ineffective detection sequences (i.e., ) may be extremely high. To eliminate the influence of probabilities of ineffective detection sequences on the integrated GDOP-UM, the detection sequence probabilities as the weighted values are normalized. Specifically, is calculated as
We notice that, the integrated GDOP-UM is directly dependent on the detection and TDM estimation performance of T-R channels, which depend on the SNR. For a given deterministic signal, the SNR depends on the path loss . Hence, the GDOP-UM is fundamentally dependent on the path loss.
Remark 2.
It can be seen from (32) that, similar to the T-GDOP, the proposed GDOP-UM only depends on the relative angular relationship and the relative distances between the target and radar nodes. Since the GDOP-UM is related to the system detection performance, it is more sensitive to the relative distances than the T-GDOP.
Remark 3.
We notice that, when the probability of CD is 1, i.e., when the probability of the detection sequence being an -dimensional vector made from ones is 1; if the performance descriptions of TDM estimation are the same, the proposed GDOP-UM is then equivalent to the T-GDOP. Hence, the T-GDOP can be regarded as a particular case of the GDOP-UM under CD with high SNR, and clearly the proposed GDOP-UM is more generalized.
We also compare the computational complexity of the GDOP-UM and the T-GDOP. One addition, subtraction, multiplication and division is defined as a flop, and the computational complexities of vector operations are calculated with the vector dimensions considered. Then, we give the computational complexity analysis for both algorithms in Table 2.

Table 2.
Computational complexity analysis for the GDOP-UM and the T-GDOP.
We note that, to the GDOP-UM, the last term of the cumulative sum of computational complexity (namely when ) is then equivalent to the overall computational load of the T-GDOP. Therefore, the computational complexity of the GDOP-UM is larger than that of the T-GDOP. However, since the GDOP-UM performs an accurate evaluation of localization performance under all possible detection results, such a larger computational load is inevitable and acceptable. The specific realization process of the GDOP-UM metric is given as Algorithm 1.
| Algorithm 1 Realization of the GDOP-UM Metric. |
|
Initialize the radar positions and the target position ; Initialize the summation of with as ; Initialize the value of GDOP-UM as ; for do if then Calculate the occurrence probability of the detection sequence , , according to (13); ; else Break; end if end for for do if then Calculate the GDOP-like value corresponding to the detection sequence according to (23), (24), (25) and (33); Calculate the normalized probability of the detection sequence , , according to (35); ; else Break; end if end for Output as the final value of the GDOP-UM. |
5. Numerical Results
In this section, we perform elaborate numerical simulations to verify the accuracy and applicability of the proposed GDOP-UM. We separately consider two situations where the positions of radar nodes are fixed and the node positions are to be optimized. For all the simulations, we consider a scenario including a radar mission area (RMA) and a radar placement area (RPA). The RMA is a rectangle region of , and the RPA is a rectangle region of . These two areas are not overlapping. A target randomly appears in the RMA. Referring to [31,32,37], without loss of generality, typical performance parameters of the radar nodes for all the simulations are selected and given in Table 1.
5.1. Fixed Node Positions
In this subsection, we select several representative radar node placement schemes, and analyze the corresponding system localization performance by simulation results.
5.1.1. Linearly Placed Away from the RMA
For this simulation, the radar nodes are placed linearly and away from the RMA with a long baseline. We notice that, neither the T-GDOP nor the derived GDOP-like metrics reflect absolute physical accuracy, and they only show the distribution of localization accuracy in a given area.
Hence, it is difficult to directly compare GDOP-like metrics with some metrics reflecting absolute physical accuracy (such as CRLB, etc.), and different GDOP-like metrics cannot be directly compared by numerical values. Hence, we study the GDOP-UM with the most commonly used T-GDOP introduced in [13,22,25,27,28] as the benchmark, and analyze the trend differences of the localization performance characterization shown by the two metrics. The simulation results of the corresponding localization and detection performance are shown as Figure 4.
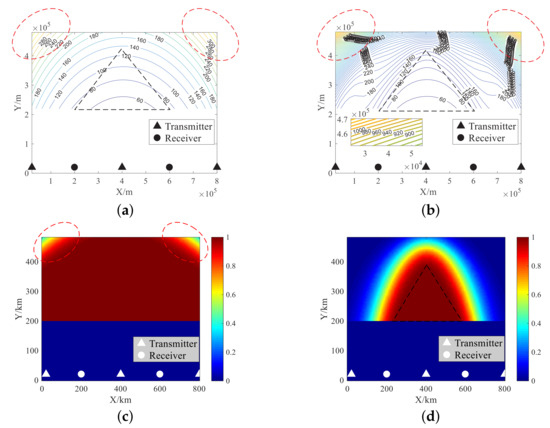
Figure 4.
Simulation results of the system localization and detection performance. In the following simulations, the contour lines with respect to localization represent the values of GDOP-like components measured in meters, and the values shown in the grids regarding detection represent the probabilities of detection. The regions where and are, respectively, the RPA and the RMA. (a) The T-GDOP. (b) The GDOP-UM. (c) The probability of ED. (d) The probability of CD.
Figure 4d shows the probability of CD. We note that, for the small area that is approximately surrounded by a black triangle located in the middle of the RMA, the probability of CD is 1, i.e., the target appearing in this area will be effectively detected by all T-R channels (As we stated before, the detection probability of radar nodes is always less than 1. Therefore, the probability of CD here is 1 because of the truncation error of the computer system. The actual probability of CD is infinitely close to 1). However, for the much wider area outside the black triangle in the RMA, the probability of CD is much less than 1 and even equals 0. This indicates that the system may not necessarily or even completely fail to achieve CD of the target. Then, the T-GDOP based on the absolute CD assumption is clearly no longer applicable.
Additionally, we give the results of the probability of ED in Figure 4c. As we mentioned before, ED is the prerequisite and guarantee for effective TOA localization. We notice that, in the areas circled by two red ellipses in Figure 4c, the probability of ED is less than 1. This indicates that the system has poor detection performance in these areas, and it is even difficult to obtain enough effective TDMs to support TOA localization.
Hence, theoretically, in these two areas, sharp deterioration of the localization performance is inevitable [31]. However, we find that, the T-GDOP values shown in Figure 4a keep increasing smoothly even in the poor-detection areas circled by the two red ellipses, which means that the localization performance deteriorates smoothly as well in these areas. Therefore, such simulation results also show that the T-GDOP cannot accurately describe the actual system localization performance, especially in the low-SNR situation.
Figure 4b is the simulation result of the GDOP-UM. As we explained before, the GDOP-UM is derived based on ED. We found that, in the entire RMA, the values of the GDOP-UM increase in exactly the same trend as the performance deterioration of ED. We also noticed that, in the area surrounded by the black triangle in the RMA, the probability of CD is 1, and the performance descriptions of TDM estimation based on the CRLB and the ZZB are almost the same in this high-SNR area (shown as Figure 3 with an SNR of not less than 14 dB). Comparing Figure 4a,b, as analyzed before, the GDOP-UM is nearly equivalent to the T-GDOP. Different from the T-GDOP, in the poor-detection areas circled by the two red ellipses, the values of the GDOP-UM increase sharply.
This indicates that the sharp deterioration of the localization performance in poor-detection areas can also be described accurately by the GDOP-UM. All of these results conform to the theoretical analysis and our expectations and validate the accuracy of the proposed GDOP-UM.
Then, focusing on the GDOP-UM and recalling the Formula (32), the GDOP-UM can be regarded as a weighted sum of several GDOP-like components s under appropriate detection sequences, weighted by the corresponding probabilities. We enumerate s under several detection sequences with higher probabilities at a representative location km in Table 3. For comparison, the detection sequence corresponding to CD, i.e., , is also selected.

Table 3.
Values of the occurrence probabilities and s under certain detection sequences at the location km.
Theoretically, with the location km, if TDMs from the nodes on the right of the RPA (e.g., the second receiver and the third transmitter) are used, then a long propagation path will result in an extremely low SNR of the signal and further lead to poor performance in detection and localization.
We find from Table 3 that the s are much larger when the TDMs of the second receiver or the third transmitter are used than when the TDMs of these nodes are not used. In particular, when the TDMs of the second receiver and the third transmitter are both used, e.g., when the detection sequence is , the localization and detection performance are both quite poor with at m and the detection probability at . The proposed GDOP-UM is formulated by comprehensively considering all effective detection sequences.
Hence, under the detection sequence will increase the value of the integrated GDOP-UM to show the impact of some low-quality TDMs on the localization results. Since the occurrence probability of the detection sequence is much lower than the other listed sequences in Table 3, the final value of the GDOP-UM, m, is more biased towards s under the other listed sequences. The above simulations also show the accuracy of the GDOP-UM in describing the TOA localization performance. We also give simulation results of the detection and localization performance for two specific representative detection sequences in Figure 5 to more intuitively corroborate the above analysis.
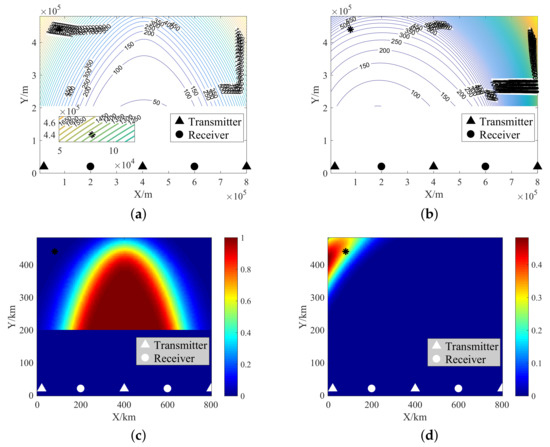
Figure 5.
Simulation results of s for the GDOP-UM and detection performance under certain detection sequences (the location of the black “*” point is km). (a) under . (b) under . (c) Detection performance under . (d) Detection performance under .
We notice that, although the data fusion of different radar nodes is not our focus, how to select proper data for TOA localization is worth discussing. In conclusion, the above simulation results show that, in the high-SNR area, the T-GDOP is nearly equivalent with the GDOP-UM, and both metrics can truly characterize the localization performance distribution. However, in the low-SNR area, the T-GDOP fails to characterize the localization performance distribution accurately. In contrast, the localization performance of all considered detection results, the GDOP-UM still shows its accuracy.
5.1.2. Linearly Placed near the RMA
For this simulation, the radar nodes are placed linearly and near the RMA with a long baseline. We analyze the system localization performance via the GDOP-UM with the T-GDOP as the benchmark. The simulation results of the corresponding localization and detection performance are shown as Figure 6. We find from Figure 6c that, when the nodes are placed near the RMA, the probability of CD in most areas of the RMA (located in the middle) is 1.
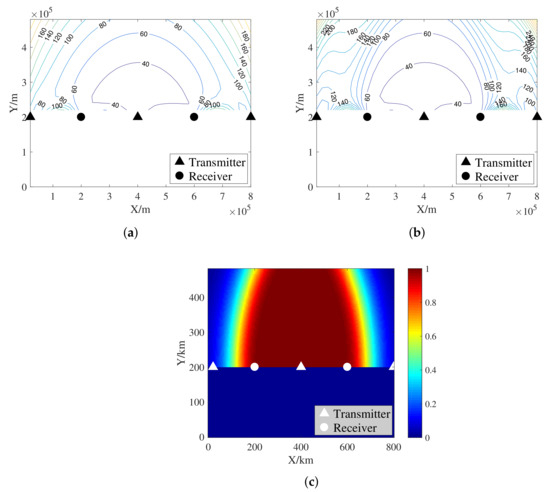
Figure 6.
Simulation results of the system localization and detection performance. (a) The T-GDOP. (b) The GDOP-UM. (c) The probability of CD.
Similar to the situation when the nodes are linearly placed far away from the RMA, we find from Figure 6a,b that the GDOP-UM is nearly equivalent to the T-GDOP in these areas. This phenomenon proves once again that the T-GDOP can be regarded as a particular case of the GDOP-UM under CD with high SNR. Compared with the T-GDOP, the GDOP-UM can more clearly show its precise characteristics in low-SNR scenarios. Based on the above discussion, for more meaningful conclusions, we select some representative node placement schemes with typical low-SNR scenarios to study the GDOP-UM in the next subsection.
5.1.3. Some Other Node Placement Schemes
We also compare the localization performance in terms of the GDOP-UM for different node placement schemes. Four representative node placement schemes are considered, and the simulation results are shown in Figure 7. We found that different node placement schemes present different characteristics in terms of the localization performance. When nodes are placed in line with a short baseline as shown in Figure 7a, in the area that is located near the extension of the baseline and close to the RPA, the system localization performance deteriorates sharply and is even worse than that in the far zone of the RMA.
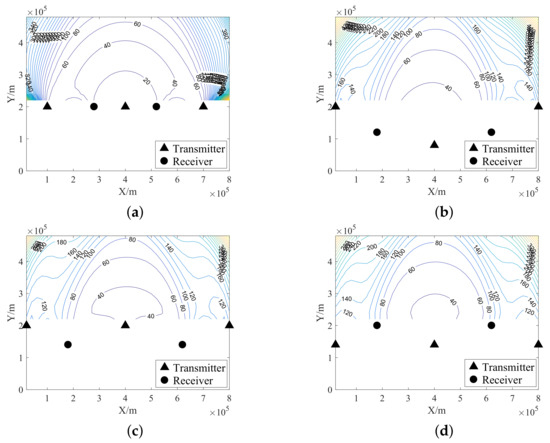
Figure 7.
Other node placement schemes and the corresponding GDOP-UM. (a) Placement in line with a short baseline. (b) Placement in an arc. (c) Placement in different regions for transmitters and receivers (transmitters are close to the RMA). (d) Placement in different regions for transmitters and receivers (receivers are close to the RMA).
This phenomenon is due to the utilization of TDMs with low SNRs of some T-R channels and, more importantly, because of the short equivalent system baseline. We also notice that, when nodes are placed in an arc or placed in different regions for transmitters and receivers, as shown in Figure 7b–d, respectively, the growth trend of the system localization performance is similar. To the placement scheme in an arc as shown in Figure 7b, since the transmitter in the middle of the RPA is far away from the RMA and since this leads to a long signal propagation path, the system localization performance is relatively poor. The localization performance for the other two placement schemes is essentially the same.
We found that when the transmitters are placed far from the RMA as shown in Figure 7d, compared to the placement scheme as shown in Figure 7c, the electromagnetic energy density in the RMA is significantly reduced while maintaining similar localization performance. Hence, better LPI performance can be obtained [42]. How to ascertain a node placement scheme to obtain optimal localization performance with good LPI performance is also an important and meaningful issue to be studied; however, this is not the focus of this paper.
In conclusion, the above simulation results proved that different node placement schemes may lead to different localization performance. No matter what node deployment scheme the radar system adopts, the corresponding localization performance can be finely characterized with the GDOP-UM.
5.2. Unfixed Node Positions
We found from the above simulation that different node placement schemes may lead to different system localization performance. Additionally, as we mentioned before, geometric optimization is a typical application of the GDOP-like metrics. Therefore, in this subsection, we study the optimal node placement scheme with respect to localization performance via the proposed GDOP-UM metric. We choose the same optimization model as [16,43] and ignore the distance constraint between the radar nodes.
Both the T-GDOP and the GDOP-UM are considered, and the maximum value of the GDOP-like metrics in the RMA is used as the objective function. A particle swarm optimization (PSO) algorithm is applied to solve the non-convex optimization problem, with the swarm size at 200 and the maximum number of iterations at 200. The other common parameters of the PSO algorithm are consistent with [16,43].
Figure 8 shows the simulation results of the probability of CD for the node placement optimization result, with the T-GDOP as the optimization metric. As we mentioned before, due to the neglect of measurement uncertainty, the T-GDOP metric mainly depends on the relative angles between the target and the radar nodes but is not sensitive to relative distances. Hence, we see from Figure 8 that the receivers are placed far away from the RMA to obtain proper relative angles.
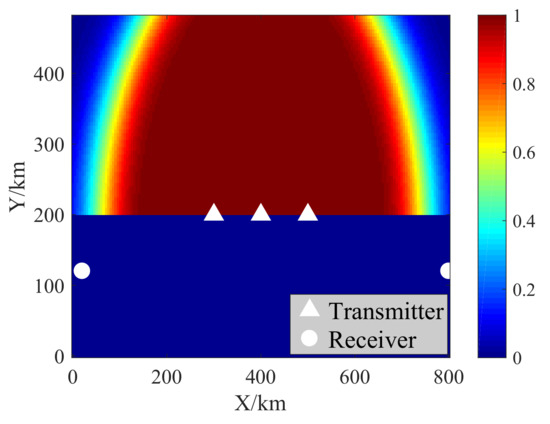
Figure 8.
Probability of CD for the node placement optimization result with the T-GDOP as the optimization metric.
We also notice that, as mentioned earlier, absolute CD is a necessary assumption for the T-GDOP derivation. However, for such a node placement scheme, a vast area with the CD probability of less than 1 exists in the RMA. In other words, with the T-GDOP as the metric, the optimization result cannot ensure the necessary assumption for the T-GDOP derivation. Therefore, as we discussed in Section 5.1, the T-GDOP is not suitable as the optimization metric.
We also give the simulation results of localization performance in terms of the GDOP-UM as Figure 9, and the node placement schemes are optimized with the T-GDOP and the GDOP-UM as the optimization metrics, respectively. As we mentioned before, the GDOP-UM is more sensitive to the relative distances between the radar nodes and the target. We find from Figure 9b that, using the optimization result with the GDOP-UM as the metric, most radar nodes are well separated in the border of the RMA and the RPA. Such a configuration can ensure a higher SNR of the received signal and reduce the influence of uncertain measurements on localization.
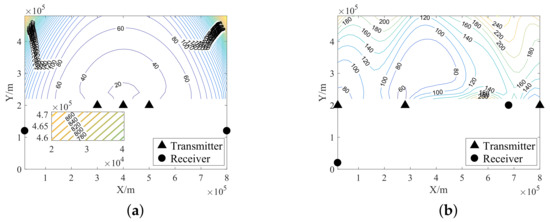
Figure 9.
Comparison of optimization results of localization performance shown by the GDOP-UM. (a) Optimized with the T-GDOP as the optimization metric. (b) Optimized with the GDOP-UM as the optimization metric.
We mentioned before that, when all radar nodes are collinear, the localization performance in some areas near the extension of the baseline will deteriorate sharply (similar to the situation shown in Figure 7a). To avoid such a situation and provide a long equivalent system baseline length, one receiver is deployed away from the RMA.
For the node placement scheme optimized with the T-GDOP used as the optimization metric as shown in Figure 9a, the localization performance in the near zone of the RMA is better due to appropriate relative angles and short signal propagation paths. However, for the far zone of the RMA, the SNR of the received signal is low because of long signal paths. Therefore, the localization performance deteriorates sharply with the decrease of the probability of CD, and the maximum value of the GDOP-UM is m.
In contrast, for the placement scheme optimized with the GDOP-UM as the optimization metric, the localization performance is well distributed in the RMA, with the maximum value of the GDOP-UM at m. In conclusion, the above simulation results show that, compared with the T-GDOP, the GDOP-UM is more accurate and more suitable to be an optimization metric, and it can lead to an optimization solution with higher quality. Therefore, the GDOP-UM provides us with a powerful tool for optimizing the resources or layout of multi-sensor systems.
6. Conclusions
In this paper, given the uncertainty of the pre-processing for the TOA localization, a signal-decoupled localization performance evaluation metric considering uncertain measurements was studied. We first proposed an effectively detected TDM model and a modified performance bound for TDM estimation to match the uncertain measurements. Then, by comprehensively considering all the detection results for effective localization and the corresponding localization performance, we proposed a novel GDOP-UM metric.
This metric can truly describe the system localization performance no matter how the detection performance changes. We performed numerical simulations for two representative application scenarios. The simulation results show that the T-GDOP can be regarded as a particular case of the GDOP-UM. The T-GDOP is nearly equivalent to the GDOP-UM under a fully high-SNR situation but is not available for low-SNR cases. The proposed GDOP-UM can also truly describe the localization performance under a low-SNR situation. Additionally, simulation results for a typical node placement optimization application further verify the accuracy and applicability of the proposed GDOP-UM.
Author Contributions
Conceptualization, Y.W., T.Z., W.Y.; methodology, Y.W., L.K.; validation, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W., T.Z., W.Y.; visualization, Y.W.; project administration, W.Y., L.K.; funding acquisition, W.Y., L.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grants 61771110, U19B2017 and 61871103, in part by Fundamental Research Funds of Central Universities under Grant ZYGX2020ZB029, in part by Chang Jiang Scholars Program, and in part by the 111 Project No. B17008.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MSRS | Multisite radar system |
| TOA | Time-of-arrival |
| CRLB | Cramér–Rao lower bound |
| GDOP | Geometric dilution of precision |
| TDM | Time delay measurement |
| SNR | Signal-to-noise ratio |
| T-GDOP | Traditional GDOP |
| ZZB | Ziv–Zakai bound |
| GDOP-UM | GDOP with uncertain measurements |
| CD | Complete detection |
| ED | Effective detection |
| APB | A priori bound |
| RMA | Radar mission area |
| RPA | Radar placement area |
| m | Index of transmitter |
| n | Index of receiver |
| l | Index of detection sequence |
| The lth possible detection sequence | |
| Number of available TDMs for all T-R channels | |
| Effectively detected TDM vector | |
| Localization error covariance matrix | |
| Standard deviation of error for the TDM | |
| The GDOP-like value corresponding to | |
| GDOP-UM metric |
References
- Chernyak, V.S. Fundamentals of Multisite Radar Systems: Multistatic Radars and Multistatic Radar Systems; Gordon and Breach: New York, NY, USA, 1998. [Google Scholar]
- Yoon, Y.; Kim, Y. An efficient genetic algorithm for maximum coverage deployment in wireless sensor networks. IEEE Trans. Cybern. 2013, 43, 1473–1483. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.S.; Cimini, L.J.; Chizhik, D.; Valenzuela, R.A. Spatial diversity in radars–Models and detection performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Shi, C.; Qiu, W.; Wang, F.; Salous, S.; Zhou, J. Power control scheme for spectral coexisting multistatic radar and massive MIMO communication systems under uncertainties: A robust Stackelberg game model. Signal Process. 2019, 94, 146–155. [Google Scholar] [CrossRef]
- Friedlander, B. On the relationship between MIMO and SIMO radars. IEEE Trans. Signal Process. 2009, 57, 394–398. [Google Scholar] [CrossRef]
- D’Addio, E.; Farina, A. Overview of detection theory on multistatic radars. IET Proc.—Commun. Radar Signal Process. 1986, 133, 613–623. [Google Scholar] [CrossRef]
- Tajer, A.; Jajamovich, G.H.; Wang, X.; Moustakides, G.V. Optimal joint target detection and parameter estimation by MIMO radar. IEEE J. Sel. Top. Signal Process. 2010, 4, 127–145. [Google Scholar] [CrossRef] [Green Version]
- Skolnik, M.I. Radar Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Yan, J.; Liu, H.; Bao, Z. Power allocation scheme for target tracking in clutter with multiple radar system. Signal Process. 2018, 144, 453–458. [Google Scholar] [CrossRef]
- Gorji, A.A.; Tharmarasa, R.; Kirubarajan, T. Widely separated MIMO versus multistatic radars for target localization and tracking. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2179–2194. [Google Scholar] [CrossRef]
- Bekkerman, I.; Tabrikian, J. Target detection and localization using MIMO radars and sonars. IEEE Trans. Signal Process. 2006, 54, 3873–3883. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Doğançay, K. Optimal geometry analysis for multistatic TOA localization. IEEE Trans. Signal Process. 2016, 64, 4180–4193. [Google Scholar] [CrossRef]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target localization accuracy gain in MIMO radar-based systems. IEEE Trans. Inf. Theory 2010, 56, 2783–2803. [Google Scholar] [CrossRef] [Green Version]
- Khan, U.F.; Lazaridis, P.I.; Mohamed, H.; Albarracín, R.; Zaharis, Z.D.; Atkinson, R.C.; Tachtatzis, C.; Glover, I.A. An efficient algorithm for partial discharge localization in high-voltage systems using received signal strength. Sensors 2018, 18, 4000. [Google Scholar] [CrossRef] [Green Version]
- Radmard, M.; Chitgarha, M.M.; Majd, M.N.; Nayebi, M.M. Antenna placement and power allocation optimization in MIMO detection. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1468–1478. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, S.; Zhou, T.; Li, N. Geometric optimization of distributed MIMO radar systems with spatial distance constraints. IEEE Access 2020, 8, 199227–199241. [Google Scholar] [CrossRef]
- Wang, Y.; Yi, W.; Kong, L. Antenna placement for distributed MIMO radar with different missions in different subareas. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 7–14 May 2021; pp. 1–6. [Google Scholar]
- Yi, W.; Yuan, Y.; Hoseinnezhad, R.; Kong, L. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems. IEEE Trans. Signal Process. 2020, 68, 1602–1617. [Google Scholar] [CrossRef]
- Yuan, Y.; Yi, W.; Hoseinnezhad, R.; Varshney, P.K. Robust power allocation for resource-aware multi-target tracking with colocated MIMO radars. IEEE Trans. Signal Process. 2020, 69, 443–458. [Google Scholar] [CrossRef]
- Zhou, T.; Yi, W.; Kong, L. Non-Cooperative passive direct localization based on waveform estimation. Remote Sens. 2021, 13, 264. [Google Scholar] [CrossRef]
- Zheng, H.; Jiu, H.; Li, H.; Liu, H. Joint design of the transmit beampattern and angular waveform for colocated MIMO radar under a constant modulus constraint. Remote Sens. 2021, 13, 3392. [Google Scholar] [CrossRef]
- Sun, B.; Chen, H.; Yang, D.; Li, X. Antenna selection and placement analysis of MIMO radar networks for target localization. Int. J. Distrib. Sens. Netw. 2014, 10, 769404. [Google Scholar] [CrossRef]
- Yarlagadda, R.; Ali, I.; Al-Dhahir, N.; Hershey, J. GPS GDOP metric. IEE Proc.-Radar Sonar Navig. 2000, 147, 259–264. [Google Scholar] [CrossRef]
- Langley, R.B. Dilution of precision. GPS World 1999, 10, 52–59. [Google Scholar]
- Dianat, M.; Taban, M.R.; Dianat, J.; Sedighi, V. Target localization using least squares estimation for MIMO radars with widely separated antennas. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2730–2741. [Google Scholar] [CrossRef]
- Yin, C.; Xu, S.; Wang, D. Location accuracy of multistatic radars (TR/sup n/) based on ranging information. In Proceedings of the International Radar Conference, Beijing, China, 8–10 October 1996; pp. 34–38. [Google Scholar]
- Lackpour, A.; Proska, K. GOMERS: Genetic optimization of a multistatic extended radar system. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Yang, Y.; Yi, W.; Zhang, T.; Cui, G.; Kong, L.; Yang, X. Antenna placement of multistatic radar system with detection and localization performance. In Proceedings of the 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; pp. 620–625. [Google Scholar]
- Kilani, M.; Gagnon, G.; Gagnon, F. Multistatic radar placement optimization for cooperative radar-communication systems. IEEE Commun. Lett. 2018, 22, 1576–1579. [Google Scholar] [CrossRef]
- Liang, J.; Huan, M.; Deng, M.; Bao, M.; Wang, G. Optimal transmitter and receiver placement for localizing 2D interested-region target with constrained sensor regions. Signal Process. 2021, 183, 108032. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Richards, M.A.; Scheer, J.A.; Holm, W.A. Principles of Modern Radar: Basic Principles; Scitech: New York, NY, USA, 2010. [Google Scholar]
- Farina, A.; Ristic, B.; Timmoneri, L. Cramer-Rao bound for nonlinear filtering with Pd< 1 and its application to target tracking. IEEE Trans. Signal Process. 2002, 50, 1916–1924. [Google Scholar]
- Hernandez, M.; Ristic, B.; Farina, A.; Timmoneri, L. A comparison of two Crame/spl acute/r-Rao bounds for nonlinear filtering with P/sub d/<1. IEEE Trans. Signal Process. 2004, 52, 2361–2370. [Google Scholar]
- Anastasio, V.; Colone, F.; Lallo, A.; Farina, A.; Gumiero, F.; Lombardo, P. Optimization of multistatic passive radar geometry based on CRLB with uncertain observations. In Proceedings of the 7th European Radar Conference, Paris, France, 30 September–1 October 2010; pp. 340–343. [Google Scholar]
- Anastasio, V.; Farina, A.; Colone, F.; Lombardo, P. Cramér-Rao lower bound with pd< 1 for target localisation accuracy in multistatic passive radar. IET Radar Sonar Navig. 2014, 8, 767–775. [Google Scholar]
- Niu, C.; Zhang, Y.; Guo, J. Pareto optimal layout of multistatic radar. Signal Process. 2018, 142, 152–156. [Google Scholar] [CrossRef]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target localisation techniques and tools for multiple-input multiple-output radar. IET Radar Sonar Navig. 2009, 3, 314–327. [Google Scholar] [CrossRef]
- Li, J.; Wu, R. An efficient algorithm for time delay estimation. IEEE Trans. Signal Process. 1998, 46, 2231–2235. [Google Scholar] [CrossRef]
- Cui, G.; DeMaio, A.; Piezzo, M. Performance prediction of the incoherent radar detector for correlated generalized Swerling-chi fluctuating targets. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 356–368. [Google Scholar] [CrossRef]
- Bell, K.L.; Steinberg, Y.; Ephraim, Y.; Trees, H.L.V. Extended Ziv–Zakai lower bound for vector parameter estimation. IEEE Trans. Inf. Theory 1997, 43, 624–637. [Google Scholar] [CrossRef]
- Shi, C.; Wang, F.; Salous, S.; Zhou, J. Joint transmitter selection and resource management strategy based on low probability of intercept optimization for distributed radar networks. Radio Sci. 2018, 53, 1108–1134. [Google Scholar] [CrossRef]
- Wang, Y.; Yi, W.; Yang, S.; Mallick, M.; Kong, L. Antenna placement algorithm for distributed MIMO radar with distance constrains. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).