Estimating the Pre-Historical Volcanic Eruption in the Hantangang River Volcanic Field: Experimental and Simulation Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. 3D Model Preparation
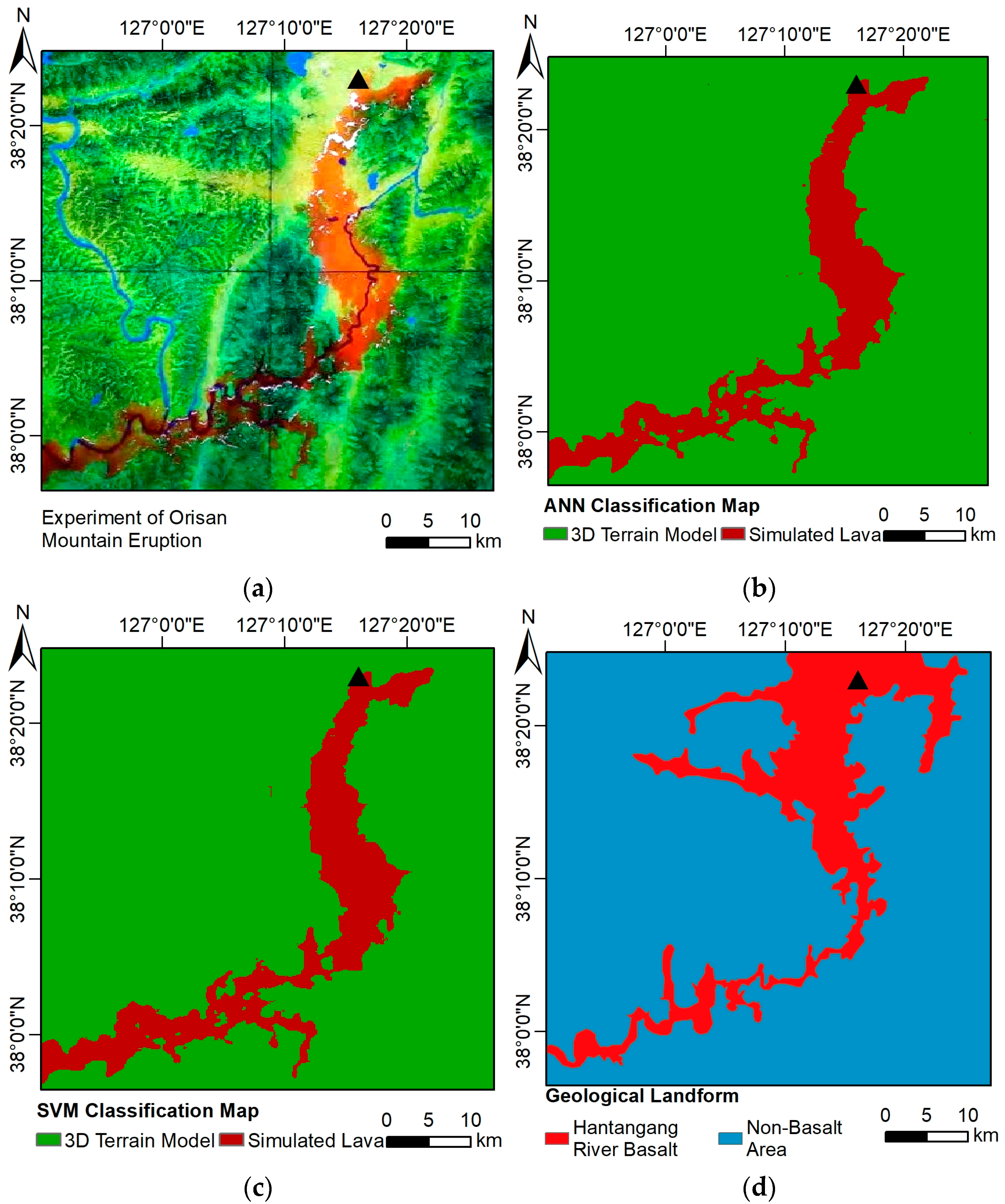
2.3. Experimental Preparation
2.4. Artificial Neural Network
2.5. Support Vector Machine
2.6. Q-LavHA Simulation
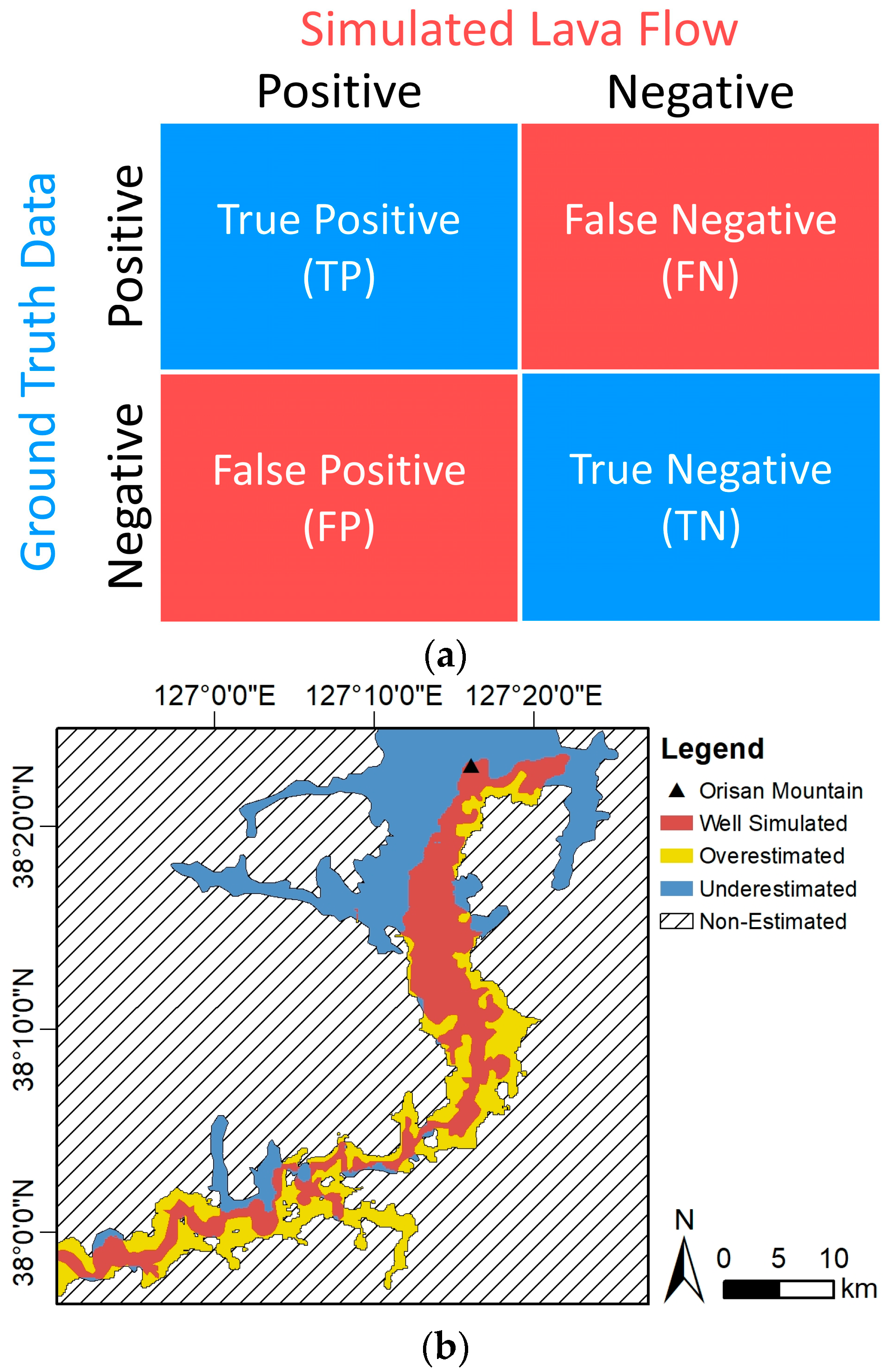
2.7. Accuracy Assessment
3. Results
3.1. Experimental Results
3.2. Classification Results
3.3. Q-LavHA Simulation Results
4. Discussion
4.1. Experimental Accuracy
4.2. Effusion Rate Analysis of Q-LavHA
4.3. Multiple Vent Eruption
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Self, S. The effects and consequences of very large explosive volcanic eruptions. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 2073–2097. [Google Scholar] [CrossRef] [PubMed]
- Newhall, C.G.; Self, S. The volcanic explosivity index (VEI): An estimate of explosive magnitude for historical volcanism. J. Geophys. Res. 1982, 87, 1231–1238. [Google Scholar] [CrossRef]
- Pyle, D.M. Sizes of Volcanic Eruptions, 2nd ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2015; ISBN 9780123859389. [Google Scholar]
- Mason, B.G.; Pyle, D.M.; Oppenheimer, C. The size and frequency of the largest explosive eruptions on Earth. Bull. Volcanol. 2004, 66, 735–748. [Google Scholar] [CrossRef]
- Scandone, R.; Bartolini, S.; Martí, J. A scale for ranking volcanoes by risk. Bull. Volcanol. 2016, 78, 2. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Dehn, J.; Calvari, S. Lava effusion rate definition and measurement: A review. Bull. Volcanol. 2007, 70, 1. [Google Scholar] [CrossRef]
- Thordarson, T.; Self, S. Atmospheric and environmental effects of the 1783-1784 Laki eruption: A review and reassessment. J. Geophys. Res. Atmos. 2003, 108, AAC-7. [Google Scholar] [CrossRef] [Green Version]
- Keszthelyi, L.; Self, S. Some physical requirements for the emplacement of long basaltic lava flows. J. Geophys. Res. Solid Earth 1998, 103, 27447–27464. [Google Scholar] [CrossRef] [Green Version]
- Miyamoto, H.; Sasaki, S. Numerical simulations of flood basalt lava flows: Roles of parameters on lava flow morphologies. J. Geophys. Res. Solid Earth 1998, 103, 27489–27502. [Google Scholar] [CrossRef] [Green Version]
- Weon, J.K. A study on the Quaternary volcanism in the Korean Peninsula–in the Choogaryong Rift Valley. J. Geol. Soc. Korea 1983, 19, 159–168. [Google Scholar]
- Won, C.K.; Kim, Y.K.; Lee, M.W. The study on the geochemistry of Choogaryong alkali basalt. J. Geol. Soc. Korea 1990, 26, 70–81. [Google Scholar]
- Lee, D.S.; Ryu, K.J.; Kim, K.H. Geotectonic interpretation of Choogaryong Rift Valley, Korea. J. Geol. Soc. Korea 1983, 19, 19–38. [Google Scholar]
- Ryu, S.; Oka, M.; Yagi, K.; Sakuyama, T.; Itaya, T. K-Ar ages of the Quaternary basalts in the Jeongok area, the central part of Korean Peninsula. Geosci. J. 2011, 15, 1–8. [Google Scholar] [CrossRef]
- Kil, Y.; Ahn, K.S.; Woo, K.S.; Lee, K.C.; Jwa, Y.-J.; Jung, W.; Sohn, Y.K. Geoheritage Values of the Quaternary Hantangang River Volcanic Field in the Central Korean Peninsula. Geoheritage 2019, 11, 765–782. [Google Scholar] [CrossRef]
- Woo, K.S.; Sohn, Y.K.; Kil, Y.; Jwa, Y.J.; Ju, S.O. The aspiring Hantangang Global Geopark in Korea: Justification to be endorsed by UNESCO Global Geopark. In Proceedings of the EGU General Assembly, Vienna, Austria, 8–13 April 2018; Volume 20, p. 2935. [Google Scholar]
- Hasiuk, F. Making things geological: 3-D printing in the geosciences. GSA Today 2014, 24, 28–29. [Google Scholar] [CrossRef] [Green Version]
- Bishwal, R.M. Scope of 3-D Printing in Mining and Geology: An Overview. J. Geol. Soc. India 2019, 93, 482–486. [Google Scholar] [CrossRef]
- Kyriakopoulos, C. 3D printing: A remedy to common misconceptions about earthquakes. Seismol. Res. Lett. 2019, 90, 1689–1691. [Google Scholar] [CrossRef]
- Zhang, G.; Gong, J.; Li, Y.; Sun, J.; Xu, B.; Zhang, D.; Zhou, J.; Guo, L.; Shen, S.; Yin, B. An efficient flood dynamic visualization approach based on 3D printing and augmented reality. Int. J. Digit. Earth 2020, 13, 1302–1320. [Google Scholar] [CrossRef]
- Liang, T.; Knappett, J.A.; Bengough, A.G.; Ke, Y.X. Small-scale modelling of plant root systems using 3D printing, with applications to investigate the role of vegetation on earthquake-induced landslides. Landslides 2017, 14, 1747–1765. [Google Scholar] [CrossRef] [Green Version]
- Horowitz, S.S.; Schultz, P.H. Printing space: Using 3D printing of digital terrain models in geosciences education and research. J. Geosci. Educ. 2014, 62, 138–145. [Google Scholar] [CrossRef]
- Wabiński, J.; Mościcka, A. Natural heritage reconstruction using full-color 3D Printing: A case study of the valley of five Polish ponds. Sustainability 2019, 11, 5907. [Google Scholar] [CrossRef] [Green Version]
- Kumari, R.; Kr, S. Machine Learning: A Review on Binary Classification. Int. J. Comput. Appl. 2017, 160, 11–15. [Google Scholar] [CrossRef]
- Kotsiantis, S.B. Supervised Machine Learning: A Review of Classification Techniques. Informatica 2007, 31, 249–269. [Google Scholar]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support Vector Machine Versus Random Forest for Remote Sensing Image Classification: A Meta-Analysis and Systematic Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Mohanty, K.K.; Majumdar, T.J. An artificial neural network (ANN) based software package for classification of remotely sensed data. Comput. Geosci. 1996, 22, 81–87. [Google Scholar] [CrossRef]
- Jeatrakul, P.; Wong, K.W. Comparing the performance of different neural networks for binary classification problems. In Proceedings of the 2009 Eighth International Symposium on Natural Language Processing, Bangkok, Thailand, 20–22 October 2009; pp. 111–115. [Google Scholar] [CrossRef] [Green Version]
- Faris, H.; Aljarah, I.; Mirjalili, S. Training feedforward neural networks using multi-verse optimizer for binary classification problems. Appl. Intell. 2016, 45, 322–332. [Google Scholar] [CrossRef]
- Roßbach, P. Neural Networks vs. Random Forests—Does it always have to be Deep Learning. Ger. Frankf. Sch. Financ. Manag. 2018. Available online: https://blog.frankfurt-school.de/wp-content/uploads/2018/10/Neural-Networks-vs-Random-Forests.pdf (accessed on 1 February 2022).
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Trees vs Neurons: Comparison between random forest and ANN for high-resolution prediction of building energy consumption. Energy Build. 2017, 147, 77–89. [Google Scholar] [CrossRef]
- Boateng, E.Y.; Otoo, J.; Abaye, D.A. Basic Tenets of Classification Algorithms K-Nearest-Neighbor, Support Vector Machine, Random Forest and Neural Network: A Review. J. Data Anal. Inf. Process. 2020, 08, 341–357. [Google Scholar] [CrossRef]
- Kadavi, P.R.; Lee, C.-W. Land cover classification analysis of volcanic island in Aleutian Arc using an artificial neural network (ANN) and a support vector machine (SVM) from Landsat imagery. Geosci. J. 2018, 22, 653–665. [Google Scholar] [CrossRef]
- Syifa, M.; Park, S.J.; Lee, C.W. Detection of the Pine Wilt Disease Tree Candidates for Drone Remote Sensing Using Artificial Intelligence Techniques. Engineering 2020, 6, 919–926. [Google Scholar] [CrossRef]
- Nur, A.S.; Park, S.; Lee, K.J.; Moon, J.; Lee, C.W. Mapping of post-wildfire burned area using KOMPSAT-3A and sentinel-2 imagery: The case of Sokcho wildfire, Korea. Korean J. Remote Sens. 2020, 36, 1551–1565. [Google Scholar] [CrossRef]
- Syifa, M.; Kadavi, P.R.; Lee, C.W.; Pradhan, B. Landsat images and artificial intelligence techniques used to map volcanic ashfall and pyroclastic material following the eruption of Mount Agung, Indonesia. Arab. J. Geosci. 2020, 13, 133. [Google Scholar] [CrossRef]
- Syifa, M.; Kadavi, P.; Lee, C.-W. An Artificial Intelligence Application for Post-Earthquake Damage Mapping in Palu, Central Sulawesi, Indonesia. Sensors 2019, 19, 542. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kadavi, P.R.; Lee, W.J.; Lee, C.W. Analysis of the pyroclastic flow deposits of Mount Sinabung and Merapi using Landsat imagery and the artificial neural networks approach. Appl. Sci. 2017, 7, 935. [Google Scholar] [CrossRef] [Green Version]
- Syifa, M.; Panahi, M.; Lee, C.W. Mapping of post-wildfire burned area using a hybrid algorithm and satellite data: The case of the camp fire wildfire in California, USA. Remote Sens. 2020, 12, 623. [Google Scholar] [CrossRef] [Green Version]
- Mossoux, S.; Saey, M.; Bartolini, S.; Poppe, S.; Canters, F.; Kervyn, M. Q-LAVHA: A flexible GIS plugin to simulate lava flows. Comput. Geosci. 2016, 97, 98–109. [Google Scholar] [CrossRef]
- Becerril, L.; Larrea, P.; Salinas, S.; Mossoux, S.; Ferrés, D.; Widom, E.; Siebe, C.; Martí, J. The historical case of Paricutin volcano (Michoacán, México): Challenges of simulating lava flows on a gentle slope during a long-lasting eruption. Nat. Hazards 2021, 107, 809–829. [Google Scholar] [CrossRef]
- Prieto-Torrell, C.; Rodriguez-Gonzalez, A.; Aulinas, M.; Fernandez-Turiel, J.L.; Cabrera, M.C.; Criado, C.; Perez-Torrado, F.J. Modelling and simulation of a lava flow affecting a shore platform: A case study of Montaña de Aguarijo eruption, El Hierro (Canary Islands, Spain). J. Maps 2021, 17, 502–511. [Google Scholar] [CrossRef]
- Dille, A.; Poppe, S.; Mossoux, S.; Soulé, H.; Kervyn, M. Modeling Lahars on a Poorly Eroded Basaltic Shield: Karthala Volcano, Grande Comore Island. Front. Earth Sci. 2020, 8, 1–17. [Google Scholar] [CrossRef]
- Oswald, C.; Rinner, C.; Robinson, A. Applications of 3D printing in physical geography education and urban visualization. Cartographica 2019, 54, 278–287. [Google Scholar] [CrossRef]
- Rodriguez-Gonzalez, A.; Aulinas, M.; Mossoux, S.; Perez-Torrado, F.J.; Fernandez-Turiel, J.L.; Cabrera, M.; Prieto-Torrell, C. Comparison of real and simulated lava flows in the Holocene volcanism of Gran Canaria (Canary Islands, Spain) with Q-LavHA: Contribution to volcanic hazard management. Nat. Hazards 2021, 107, 1785–1819. [Google Scholar] [CrossRef]
- Lee, Y.S.; Min, K.D.; Hwang, J.H. The Geodynamic Evolution of the Chugaryeong Fault Valley in a View Point of Paleomagnetism. Econ. Environ. Geol. 2001, 34, 555–571. [Google Scholar]
- Kee, W.S.; Lim, S.B.; Kim, H.C.; Kim, B.C.; Hwang, S.K.; Song, K.Y.; Kim, Y.H. Geological Report of the Yeoncheon Sheet (1:50,000); Korea Institute of Geoscience and Mineral Resources (KIGAM): Daejeon, Korea, 2008. [Google Scholar]
- Shin, S.; Cheon, Y.; Choi, J.H.; Cheong, D.; Choi, S.Y.; Lim, H.S.; Bae, H.; Lee, H.K. Late Pleistocene sedimentary environment and reverse faulting along the Chugaryung Fault in the central Korean Peninsula: A case study on the Cheorwon Basin. Geosci. J. 2020, 24, 615–623. [Google Scholar] [CrossRef]
- Choi, S.-J.; Chwae, U.-C.; Lee, H.-K.; Song, Y.-G.; Kang, I.-M. Review on the Chugaryeong Fault. Econ. Environ. Geol. 2012, 45, 441–446. [Google Scholar] [CrossRef] [Green Version]
- Nagaoka, S.; Danhara, T.; Itaya, T.; Sakuyama, T.; Watanabe, M.; Bae, K.; Matsufuji, K. Stratigraphy and age of Quaternary basaltic lavas and reconstruction of paleogeography in Chongokni, Korea. In Loess-Paleosol and Paleolithic Chronology in East Asia; Matsufuji, K., Ed.; Yuzankaku: Tokyo, Japan, 2008; pp. 87–102. [Google Scholar]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef] [Green Version]
- Purinton, B.; Bookhagen, B. Validation of digital elevation models (DEMs) and comparison of geomorphic metrics on the southern Central Andean Plateau. Earth Surf. Dyn. 2017, 5, 211–237. [Google Scholar] [CrossRef] [Green Version]
- Van Zyl, J.J. The shuttle radar topography mission (SRTM): A breakthrough in remote sensing of topography. Acta Astronaut. 2001, 48, 559–565. [Google Scholar] [CrossRef]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Smith, B.; Sandwell, D. Accuracy and resolution of shuttle radar topography mission data. Geophys. Res. Lett. 2003, 30, 3–6. [Google Scholar] [CrossRef] [Green Version]
- Alganci, U.; Besol, B.; Sertel, E. Accuracy assessment of different digital surface models. ISPRS Int. J. Geo-Inf. 2018, 7, 114. [Google Scholar] [CrossRef] [Green Version]
- Stoter, J.; Post, M.; Van Altena, V.; Nijhuis, R.; Bruns, B. Fully automated generalization of a 1:50k map from 1:10k data. Cartogr. Geogr. Inf. Sci. 2014, 41, 1–13. [Google Scholar] [CrossRef]
- Hasiuk, F.; Harding, C. Touchable topography: 3D printing elevation data and structural models to overcome the issue of scale. Geol. Today 2016, 32, 16–20. [Google Scholar] [CrossRef]
- Hasiuk, F.J.; Harding, C.; Renner, A.R.; Winer, E. TouchTerrain: A simple web-tool for creating 3D-printable topographic models. Comput. Geosci. 2017, 109, 25–31. [Google Scholar] [CrossRef]
- Han, S.-H.; Kim, K.W.; Kim, S.; Youn, Y.C. Artificial Neural Network: Understanding the Basic Concepts without Mathematics. Dement. Neurocognitive Disord. 2018, 17, 83. [Google Scholar] [CrossRef] [PubMed]
- Pham, B.T.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Prasad, P.; Loveson, V.J.; Kotha, M.; Yadav, R. Application of machine learning techniques in groundwater potential mapping along the west coast of India. GIScience Remote Sens. 2020, 57, 735–752. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, B.; Wang, L.; Wang, N. A self-trained semisupervised SVM approach to the remote sensing land cover classification. Comput. Geosci. 2013, 59, 98–107. [Google Scholar] [CrossRef]
- Soman, K.; Sathiya, A.; Suganthi, N. Classification of stress of automobile drivers using Radial Basis Function Kernel Support Vector Machine. In Proceedings of the International Conference on Information Communication and Embedded Systems (ICICES2014), Chennai, India, 27–28 February 2015. [Google Scholar] [CrossRef]
- Felpeto, A.; Araña, V.; Ortiz, R.; Astiz, M.; García, A. Assessment and modelling of lava flow hazard on Lanzarote (Canary Islands). Nat. Hazards 2001, 23, 247–257. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Rowland, S.K. FLOWGO: A kinematic thermo-rheological model for lava flowing in a channel. Bull. Volcanol. 2001, 63, 20–44. [Google Scholar] [CrossRef]
- Favalli, M.; Mazzarini, F.; Pareschi, M.T.; Boschi, E. Topographie control on lava flow paths at Mount Etna, Italy: Implications for hazard assessment. J. Geophys. Res. Earth Surf. 2009, 114, 1–13. [Google Scholar] [CrossRef]
- Kereszturi, G.; Cappello, A.; Ganci, G.; Procter, J.; Németh, K.; Del Negro, C.; Cronin, S.J. Numerical simulation of basaltic lava flows in the auckland volcanic field, New Zealand—implication for volcanic hazard assessment. Bull. Volcanol. 2014, 76, 879. [Google Scholar] [CrossRef]
- Dragoni, M. A dynamical model of lava flows cooling by radiation. Bull. Volcanol. 1989, 51, 88–95. [Google Scholar] [CrossRef]
- Lesher, C.E.; Spera, F.J. Thermodynamic and Transport Properties of Silicate Melts and Magma, 2nd ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2015; ISBN 9780123859389. [Google Scholar]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Saito, T.; Rehmsmeier, M. The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef] [Green Version]
- Beauxis-aussalet, E.; Hardman, L. Visualization of Confusion Matrix for Non-Expert Users. In IEEE Conference on Visual Analytics Science and Technology (VAST)-Poster Proceedings; 2014; Available online: https://ir.cwi.nl/ (accessed on 22 December 2021).
- Ohsaki, M.; Wang, P.; Matsuda, K.; Katagiri, S.; Watanabe, H.; Ralescu, A. Confusion-matrix-based kernel logistic regression for imbalanced data classification. IEEE Trans. Knowl. Data Eng. 2017, 29, 1806–1819. [Google Scholar] [CrossRef]
- Rahmati, O.; Moghaddam, D.D.; Moosavi, V.; Kalantari, Z.; Samadi, M.; Lee, S.; Bui, D.T. An automated Python language-based tool for creating absence samples in groundwater potential mapping. Remote Sens. 2019, 11, 1375. [Google Scholar] [CrossRef] [Green Version]
- Pham, B.T.; Shirzadi, A.; Shahabi, H.; Omidvar, E.; Singh, S.K.; Sahana, M.; Asl, D.T.; Bin Ahmad, B.; Quoc, N.K.; Lee, S. Landslide susceptibility assessment by novel hybrid machine learning algorithms. Sustainability 2019, 11, 4386. [Google Scholar] [CrossRef] [Green Version]
- Hakim, W.L.; Rezaie, F.; Nur, A.S.; Panahi, M.; Khosravi, K.; Lee, C.-W.; Lee, S. Convolutional neural network (CNN) with metaheuristic optimization algorithms for landslide susceptibility mapping in Icheon, South Korea. J. Environ. Manag. 2022, 305, 114367. [Google Scholar] [CrossRef] [PubMed]
- Fadhillah, M.F.; Lee, S.; Lee, C.; Park, Y.-C. Application of Support Vector Regression and Metaheuristic Optimization Algorithms for Groundwater Potential Mapping in Gangneung-si, South Korea. Remote Sens. 2021, 13, 1196. [Google Scholar] [CrossRef]
- Hakim, W.L.; Nur, A.S.; Rezaie, F.; Panahi, M.; Lee, C.-W.; Lee, S. Convolutional neural network and long short-term memory algorithms for groundwater potential mapping in Anseong, South Korea. J. Hydrol. Reg. Stud. 2022, 39, 100990. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Lyons, M.B.; Keith, D.A.; Phinn, S.R.; Mason, T.J.; Elith, J. A comparison of resampling methods for remote sensing classification and accuracy assessment. Remote Sens. Environ. 2018, 208, 145–153. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random forest wetland classification using ALOS-2 L-band, RADARSAT-2 C-band, and TerraSAR-X imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
- Ren, J. ANN vs. SVM: Which one performs better in classification of MCCs in mammogram imaging. Knowl.-Based Syst. 2012, 26, 144–153. [Google Scholar] [CrossRef] [Green Version]
- Chang, K.T.; Tsai, B.W. The effect of dem resolution on slope and aspect mapping. Cartogr. Geogr. Inf. Syst. 1991, 18, 69–77. [Google Scholar] [CrossRef]



| Input Parameters | Symbol | Unit | Values | Sources | |
|---|---|---|---|---|---|
| Velocity Constant | Gravity | g | 9.81 | Constant for Earth | |
| Viscosity and Yield Strength | a | a | 0.04 | [72] | |
| b | b | 0.01 | [72] | ||
| c | c | 0.08 | [72] | ||
| Thermal Parameters | Eruption temperature | °C | 1200 | [73] | |
| Crust temperature | °C | 600 | [46] | ||
| Offset | °C | 150 | [46] | ||
| Thermal conductivity constant | d | - | −0.16 | [41] | |
| Crystal Parameters | Rate of crystallization | - | 0.004 | [46] | |
| Latent heat of crystallization | [73] | ||||
| Inverse of maximum crystal concentration | R | - | 1.51 | [69] | |
| Conductivity Parameters | Lava thermal conductivity | 0.6 | [73] | ||
| Temperature at the base of the basalt crust | °C | 700 | [69] | ||
| Thickness of the basalt crust | % | 19 | [69] | ||
| Convection Parameters | Wind speed | U | 5 | [69] | |
| - | 0.0036 | [69] | |||
| Air temperature | °C | 25 | [69] | ||
| Air density | 0.4412 | Constant for Earth | |||
| Air specific heat capacity | 1009 | Constant for Earth | |||
| Radiation Parameters | Stephan–Boltzmann constant | Constant for Earth | |||
| Emissivity of basalt | - | 0.95 | Constant for Earth | ||
| Evaluation Criteria | Orisan Mountain | 680 m Peak |
|---|---|---|
| Overall Accuracy | 84.43% | 82.11% |
| Error Rate | 15.57% | 17.89% |
| True Positive Rate | 16.82% | 5.68% |
| False Positive Rate | 0.16% | 0.47% |
| False Negative Rate | 83.18% | 94.32% |
| True Negative Rate | 99.84% | 99.53% |
| Classification Class | ANN | SVM | ||||||
|---|---|---|---|---|---|---|---|---|
| Producer’s Accuracy (%) | User’s Accuracy (%) | Overall Accuracy | Kappa Coefficient | Producer’s Accuracy (%) | User’s Accuracy (%) | Overall Accuracy (%) | Kappa Coefficient | |
| Simulated Lava | 96.36 | 99.78 | 99.63 | 0.97 | 96.85 | 99.89 | 99.69 | 0.98 |
| 3D Terrain Model | 99.98 | 99.62 | 99.99 | 99.67 | ||||
| Evaluation Criteria | ANN | SVM |
|---|---|---|
| Overall Accuracy | 84.28% | 85.04% |
| Error Rate | 15.72% | 14.96% |
| True Positive Rate | 17.55% | 42.80% |
| False Positive Rate | 11.93% | 6.79% |
| False Negative Rate | 82.45% | 57.20% |
| True Negative Rate | 88.07% | 93.21% |
| Eruptive Vent Coordinates | Slope (Degree) | Aspect |
|---|---|---|
| 127.267215°, 38.390937° | 1.06° | 206.29 (South) |
| 127.262726°, 38.264870° | 23.02° | 208.07 (Southwest) |
| 127.182083°, 38.069179° | 30.75° | 232.97 (Southwest) |
| 127.088953°, 38.061274° | 22.68° | 203.50 (Southwest) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hakim, W.L.; Ramayanti, S.; Park, S.; Ko, B.; Cheong, D.-K.; Lee, C.-W. Estimating the Pre-Historical Volcanic Eruption in the Hantangang River Volcanic Field: Experimental and Simulation Study. Remote Sens. 2022, 14, 894. https://doi.org/10.3390/rs14040894
Hakim WL, Ramayanti S, Park S, Ko B, Cheong D-K, Lee C-W. Estimating the Pre-Historical Volcanic Eruption in the Hantangang River Volcanic Field: Experimental and Simulation Study. Remote Sensing. 2022; 14(4):894. https://doi.org/10.3390/rs14040894
Chicago/Turabian StyleHakim, Wahyu Luqmanul, Suci Ramayanti, Sungjae Park, Bokyun Ko, Dae-Kyo Cheong, and Chang-Wook Lee. 2022. "Estimating the Pre-Historical Volcanic Eruption in the Hantangang River Volcanic Field: Experimental and Simulation Study" Remote Sensing 14, no. 4: 894. https://doi.org/10.3390/rs14040894
APA StyleHakim, W. L., Ramayanti, S., Park, S., Ko, B., Cheong, D.-K., & Lee, C.-W. (2022). Estimating the Pre-Historical Volcanic Eruption in the Hantangang River Volcanic Field: Experimental and Simulation Study. Remote Sensing, 14(4), 894. https://doi.org/10.3390/rs14040894









