VO-LVV—A Novel Urban Regional Living Vegetation Volume Quantitative Estimation Model Based on the Voxel Measurement Method and an Octree Data Structure

Abstract

Currently, three-dimensional (3D) point clouds are widely used in the field of remote sensing and mapping, including the measurement of living vegetation volume (LVV) in cities. However, the existing quantitative methods for LVV measurement are mainly based on single tree modeling or on the calculation of single tree species’ growth parameters, which cannot be applied to the many tree species and complex forest layer structures present in urban regions, and thus are unsuitable for broad application. LVV measurement is based primarily on vegetation point cloud data, which can be obtained through many methods and often lack some information, thus posing problems in the use of traditional LVV measurement methods. To address the above problems, this paper proposes a novel LVV estimation model, which combines the voxel measurement method with an organizing point cloud based on an octree structure (we called it VO-LVV), to estimate the LVV of typical vegetation and landforms in cities. The point cloud data of single plants and multiple plants were obtained through preprocessing to verify the improvement in the calculation efficiency and accuracy of the proposed method. The results indicated that the VO-LVV estimation method, compared with the traditional method, enabled substantial efficiency improvement and higher calculation accuracy. Furthermore, the new method can be simultaneously applied to scenarios of single plants and multiple plants, and can be used for the calculation of LVV in areas with various vegetation types in cities.

1. Introduction

As a major part of urban ecosystems, vegetation has important ecological functions in maintaining carbon and oxygen balance, purifying water bodies, regulating climate, and conserving water sources [1,2]. Early studies of urban vegetation systems often used two-dimensional (2D) greening indicators, such as the green space rate, green coverage rate, and per capita public green area [3,4]. Various 2D greening indicators have been used and have played important roles in the promotion of greening construction in a certain period of time [5,6,7]. However, these indicators only roughly express the distribution and development level of vegetation space. In other words, expressing the true ecological functions and environmental benefits of regional vegetation in a precise manner remains difficult [8].

For this reason, researchers proposed a three-dimensional (3D) greening indicator, living vegetation volume (LVV, also called 3D green quantity) [9], which is defined as the portion occupied by fresh stems and leaves of vegetation. Since the concept was proposed, the development and applications of the LVV have attracted increasing attention and have become major areas of research interest in this field. The LVV directly reflects the basis for vegetation productivity, including vegetation yield, the environment, and economic benefits [10,11]. Furthermore, the LVV can accurately indicate whether the arrangement of vegetation is scientific and can be used to evaluate the ecological benefits of the vegetation system. It has become an important green quantity index used in countries worldwide to strengthen research [12,13]. However, in the estimation of urban regional LVV, the vegetation in cities has diverse species, various spatial structures, and complex overlap. Furthermore, the vegetation is often buried between buildings, thus making information extraction difficult. Therefore, traditional methods such as remote sensing technology and hyperspectral technology cannot meet the requirements of LVV measurement in cities [14,15].

Early urban regional LVV measurements were based primarily on field vegetation quadrat morphology measurement [12,15,16,17], and on remote sensing object morphology and spectral information retrieval [18,19,20,21]. The former methods include plane greening indicators, simulated 3D greening indicators, estimation of LVV by tridimensional volume, and plane quantity estimation by 2D greening indicators [12,15,17]. The accuracy of these methods depends on the results of field sampling surveys and belongs to the semi-automatic mode. The latter methods depend on the corresponding hyperspectral images obtained through remote sensing. They first draw inferences regarding the vegetation area, vegetation types, and several tree measurement factors from the images, and they then calculate the entire LVV for a specific area [18,19,20,21]. Although the methods somewhat reduce the workload of manual collection and interpretation, they only provide information regarding the horizontal distribution of vegetation, but cannot accurately extract its vertical structure.

With the development of 3D point cloud modeling, researchers have extensively explored applications in LVV measurement. Commonly used methods include the vegetation height measurement method [22] and the wrapped surface approach [23]. For instance, the authors of [24] used light detection and ranging (LiDAR) to obtain individual wood structure parameters (tree height, diameter at breast height, crown width, and canopy closure), then established a regional biomass measurement model and validated it through comparison with field-measured vegetation samples. According to LiDAR point cloud data and high-resolution remote sensing image data, the authors of [25] used the separation zone method to identify the distribution areas of different types of vegetation. The data were then segmented on the scale of the vegetation layer. After the edge feature points were extracted, the redundant data points were removed, and irregular triangulations were constructed to effectively calculate the LVV in this area. Notably, the voxel measurement method is a relatively effective and efficient method for accurate volume estimation [26], and it has also been used to measure morphological parameters. For example, the authors of [27] used voxel measurement methods to automatically identify individual trees from the mobile laser scanning (MLS) data. After the individual vegetation voxel grid was extended, the derived morphological parameters, including the tree height and crown diameter of street trees on a road, were efficiently estimated. The authors of [28] researched the role of the voxel measurement method in the construction of 3D models, combined with a binary space partitioning tree and grid division of these two voxel models, thus providing an efficient digital city 3D model organization method. Unfortunately, this method has not been used in LVV measurement.

In summary, the existing LVV measurement methods are based mainly on single tree modeling or single tree species’ growth parameter calculations; therefore, they cannot be applied to the areas with many tree species and complex vegetation structures, and are unsuitable for large-scale application. Furthermore, vegetation often undergoes continuous changes due to factors such as growth and pruning. Updating the regional LVV rapidly is difficult through traditional manual measurement or current point cloud measurement methods. Additionally, the existing methods do not solve the problem of missing point clouds in the original data. To address these deficiencies, this study constructed the VO-LVV model, an LVV model based on point cloud data, which is suitable for urban scenes. Specifically, we used an octree structure to organize the point cloud. We built a voxel measurement model to estimate the LVV value. Experiments confirmed that our novel model has a faster calculation speed and higher measurement accuracy than the traditional model, and this will contribute to the large-scale application of LVV measurement in urban regions.

The main research included the following: (1) To establish a measurement method suitable for multiple types of vegetation in urban regions, we designed and implemented the VO-LVV (LVV calculation combines the voxel measurement method with an organizing point cloud based on an octree structure) measurement model based on a vegetation point cloud organization from the octree structure. (2) In view of the lack of information in the vegetation point cloud data obtained through different methods, multiple index parameters were included in the theoretical analysis to adjust the model and make the estimation results better fit the true values. (3) A typical vegetation distribution area was selected as the experimental site, and the same time phase point data for the experimental area were collected through three data acquisition methods.

The remainder of this paper is organized as follows: Section 2 introduces the principle and design of our proposed LVV estimation model based on an octree. Section 3 focuses on the implementation of the VO-LVV estimation method based on the C++ programing environment. Section 4 introduces validation experiments comparing our method with the traditional method to process the point cloud datasets with different sources. Finally, Section 5 draws conclusions and discusses future research directions.

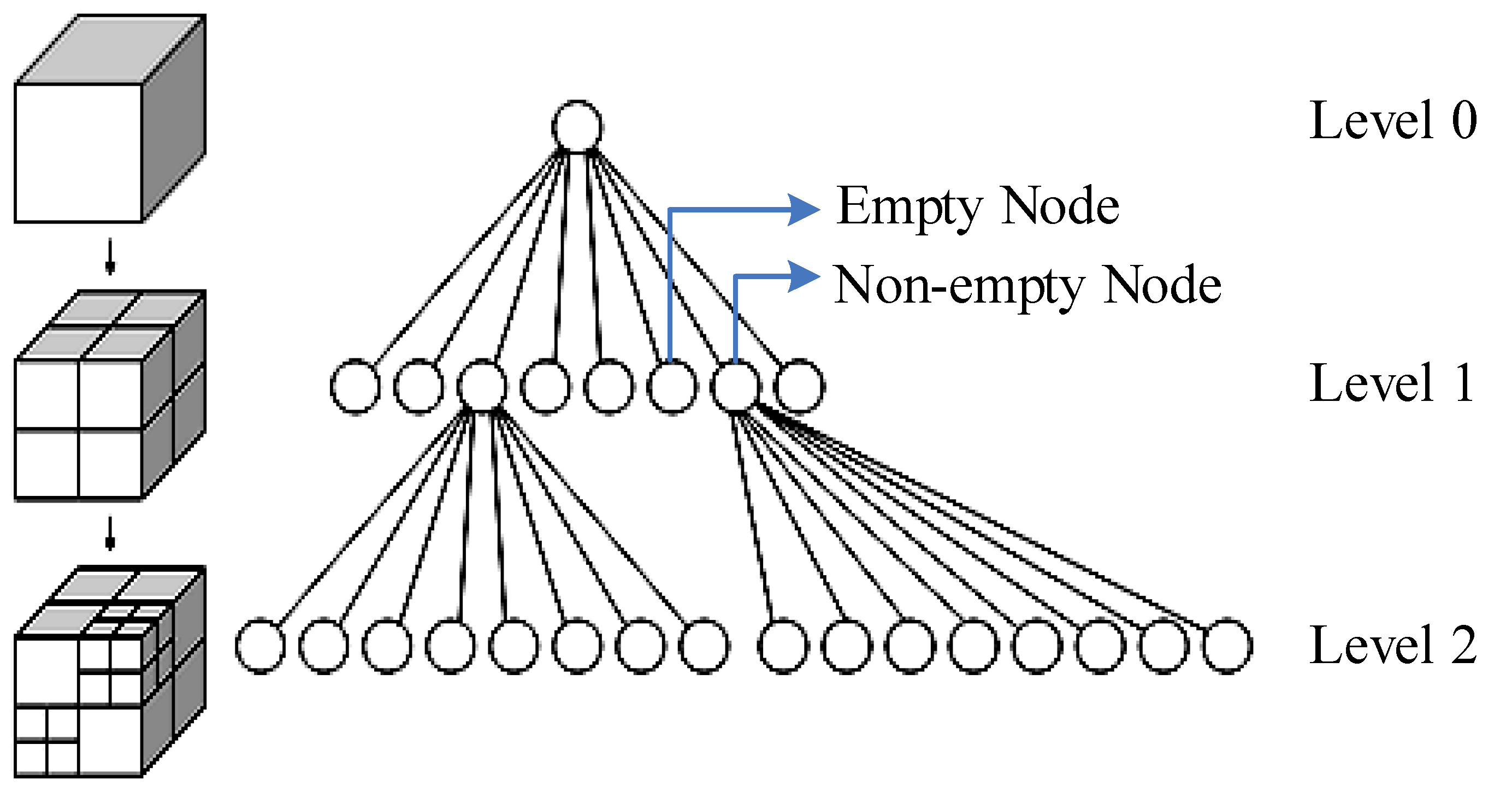
2. Principle and Design of a Novel LVV Estimation Model Based on a Voxel Method and an Octree

The voxel estimation method has a fairly high calculation speed and good calculation accuracy, owing to the organization of the point cloud data [29]. However, this method has several application limitations. According to [26,30], in the calculation of LVV for a single plant, the procedure of accumulation is by traversing each individual element grid in the coordinate space. However, with the increase of voxel resolution, this will greatly increase the calculation time. Using an octree to organize the point cloud is an ideal scheme, because the octree enables very efficient point cloud searching. An octree is a spatial, segmented, hierarchical data structure whose nodes are recursively decomposed into eight sub-nodes until the minimum resolution is reached [31,32], as illustrated in Figure 1.

As shown in Figure 1, for vegetation point cloud data, first, a large bounding box surrounding the entire point cloud is generated according to the distribution range of the dataset in the three coordinate directions of X, Y, and Z, and the root node of level 0 of the octree is obtained. Second, the point cloud density in each non-empty node is judged according to the set target density threshold. If the density is less than the threshold requirement, the node is recursively divided along three coordinate axes. In each iteration, the cuboid space represented by the current node is equally divided into eight congruent small cuboids to obtain the corresponding child nodes, until the number of points in each non-empty child node meets the density threshold. Then, the cyclic iteration is stopped, and the tree meshing structure is obtained.

Let t represent the target density threshold of the octree algorithm, n represent the number of non-empty sub-nodes obtained by dividing the vegetation point cloud by the octree based on this threshold, and hm represent the maximum level of the tree structure obtained by octree division. Let the set of voxel centers (M) associated with the vegetation point cloud be represented by Equation (1):

$$M=\left\{m_i\right|\left(x_i,y_i,z_i\right),1\le i\le \left|M\right|\}$$

(1)

The point cloud density contained in the voxel centered on m_i must meet the threshold, that is, Equation (2):

$$\frac{\left|m_i\right|}{V_i}\ge t$$

(2)

where $V_i$ indicates the volume of the corresponding voxel when the octree level is i, and a detailed calculation formula is provided below. Furthermore, the global number set corresponding to all non-empty child nodes is obtained through the octree multi-level tree structure, which is represented by Equation (3):

$$B=\left\{b_i\right|1\le i\le n\}$$

(3)

In Equation (3), B, the global index number, corresponds to the non-empty node, and $1\le b_i\le \left|M\right|$. Similarly, the corresponding relationship between node level and node number is obtained from the octree multi-level index structure, and the node level calculation function (H) is further obtained, as shown in Equation (4):

$$H\left(b_i\right)=h_i \left(h_i\in \left[0,h_m\right]\right)$$

(4)

Assume that the root node corresponds to level 0, and the edge length set of the root node along the three coordinate axes is $L_0=\left(l_0^x,l_0^y,l_0^z\right)$. Since each division is an octave, which is equivalent to a bisection along a single dimension, the edge length of a single non-empty child node of level i along the 3D direction can be obtained as shown in Equation (5):

$$\left(l_i^x,l_i^y,l_i^z\right)=\frac{\left(l_0^x,l_0^y,l_0^z\right)}{2^i}$$

(5)

Furthermore, the volume, Vi, of a single non-empty node in the corresponding level i is obtained, as shown in Equation (6):

$$V_i=l_i^x\times l_i^y\times l_i^z$$

(6)

All non-empty sub-nodes are accumulated according to different levels to obtain the total estimated volume of LVV (V), as shown in Equation (7):

$$V={{\displaystyle \sum }}_{i=1}^n{V}_{H\left(b_i\right)}$$

(7)

Equation (7) describes the LVV of vegetation in an ideal situation. However, owing to the lack of information with the point cloud acquisition method, the calculation results must be magnified, and the specific value of the magnification depends on the differences in the vegetation data acquisition method and crown shape. Therefore, a better-fitting regional total LVV based on the octree is obtained after the adaptive parameter optimization of the theoretical model quantity value, as shown in Equation (8):

$$V={{\displaystyle \sum }}_{i=1}^n{V}_{H\left(b_i\right)}\times c(Q)\times c(P)$$

(8)

where $c(Q)$ is the morphological completion parameter. The specific method for calculation of this parameter is described later for a specific case. $c(P)$ is the information completion parameter. For $c(P)$, owing to the lack of information in the 3D point cloud data, parameter fitting of the calculation results was also necessary in the algorithms in this study. In the vegetation point cloud data, for data collected by airborne LiDAR or UAV airborne oblique photogrammetry approaches, only the upper half of the vegetation canopy information can be obtained (unlike the MLS LiDAR instrument, which can penetrate vegetation, the middle of the model built in this way is hollow) and can be considered to be approximately half of the complete canopy model, i.e.,$c(P)=2$. For MLS LiDAR data, the information on the back of the tree crown can be considered to be missing; that is, the amount of data obtained is only 0.75 times the original data, and $c(P)=4/3$. Furthermore, the parameter can also be more accurately measured and calculated by fitting specific examples to obtain more accurate values. Through parameter fitting, the LVV measured by this method is effectively optimized.

Thus, according to the above theoretical principles and rules, we extracted a novel LVV calculation method based on the voxel measurement method and an octree data structure, which we call the VO-LVV estimation model. On the basis of the above principles, the calculation process was designed as illustrated in Figure 2.

As shown in Figure 2, the entire process of the VO-LVV model is as follows:

(1)

The 3D bounding box of the vegetation point cloud data is constructed, which will be used as the partition space of the voxel model and octree.

(2)

According to the set voxel resolution, the voxel model is constructed; on this basis, the octree index is established for each vegetation point cloud.

(3)

The voxel density at each node is calculated and compared with the set threshold.

(4)

When the density is lower than this threshold, it is necessary to search the leaf node of the point and infer with the voxel of smaller scale until the voxel of the smallest scale is accessed.

(5)

When the density is higher than a certain threshold, the voxel is considered to be completely covered by the vegetation point cloud. At that time, the voxel volume is calculated and accumulated into the results according to the voxel level.

(6)

According to the observed original data, depending on the data collection method and vegetation type, parameter fitting is performed, and the corrected LVV calculation value is finally obtained.

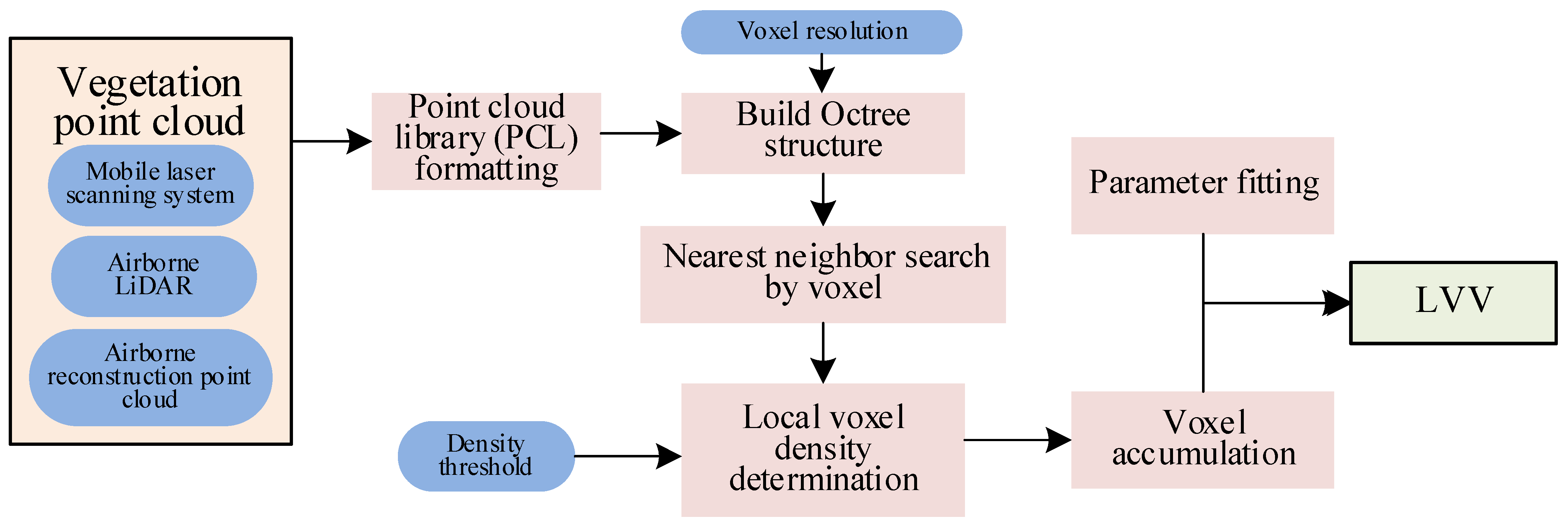
3. Implementation of the VO-LVV Estimation Model

The VO-LVV estimation model was developed in the C++ compilation environment and integrated with the point cloud library (PCL), thus facilitating point cloud data processing. The research was based on LiDAR point cloud data, collected with a laser scanning instrument, and dense point cloud data, constructed from 3D modeling with UAV remote sensing images. After commercial software extraction of the vegetation information in the environment, a quantitative analysis of LVV for a single plant or regional vegetation was obtained. Specifically, this method was required to achieve the following:

(1)

Obtain the XYZ space coordinate information for all point clouds.

(2)

Construct an octree organizational structure for the point cloud collection.

(3)

Use the voxel nearest neighbor method to establish a fast search method for point clouds in voxel space.

(4)

Establish a method for measuring the volume of voxels at different levels.

Take LAS, an ordinary format point cloud, as the input. According to the above requirements, to enable LiDAR point cloud data to be processed in the PCL library, the mycloud point cloud class is constructed as the LAS data processing object. The structure of this type of object is shown in Figure 3.

In the mycloud class, the PointXYZ format in the PCL point cloud library is used to store the LAS format point cloud. When the point cloud class is initialized, liblas::Reader is used to directly read the point cloud XYZ coordinate value. The procedure can be described with the pseudocode in Appendix A.

After the PointCloud format of LAS data is obtained, the octreepointcloudsearch class is initialized to establish an octree according to the preset voxel resolution parameters, and instantiate the hierarchical information and density measurement function at the branch nodes of the octree point cloud based on this class. By traversing the octree, the voxel nearest neighbor search method is used to calculate the point cloud density in the disassembled element, and the voxels reaching a certain density are accumulated. The procedure of VO-LVV can be described with the pseudocode in Appendix B.

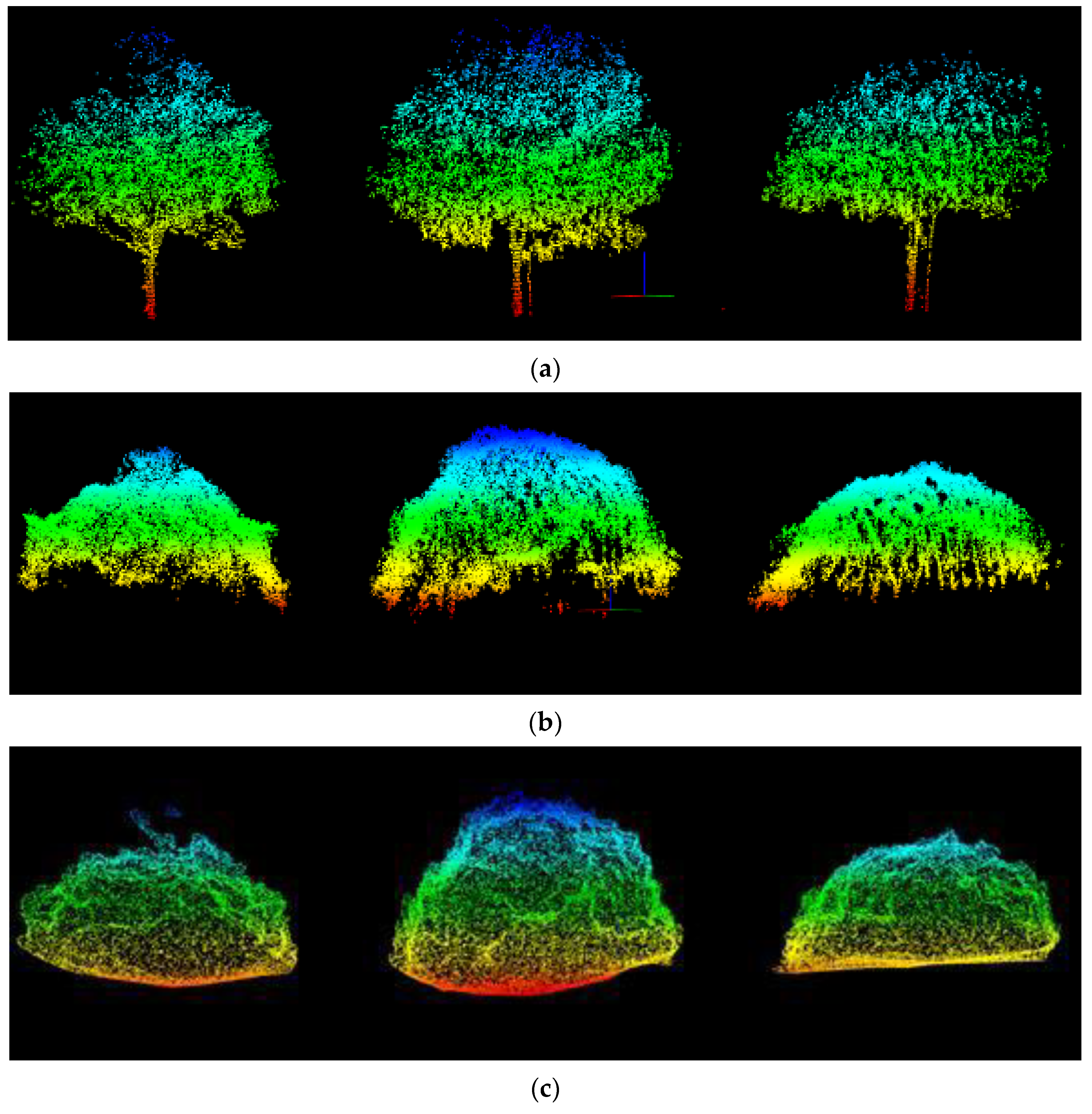
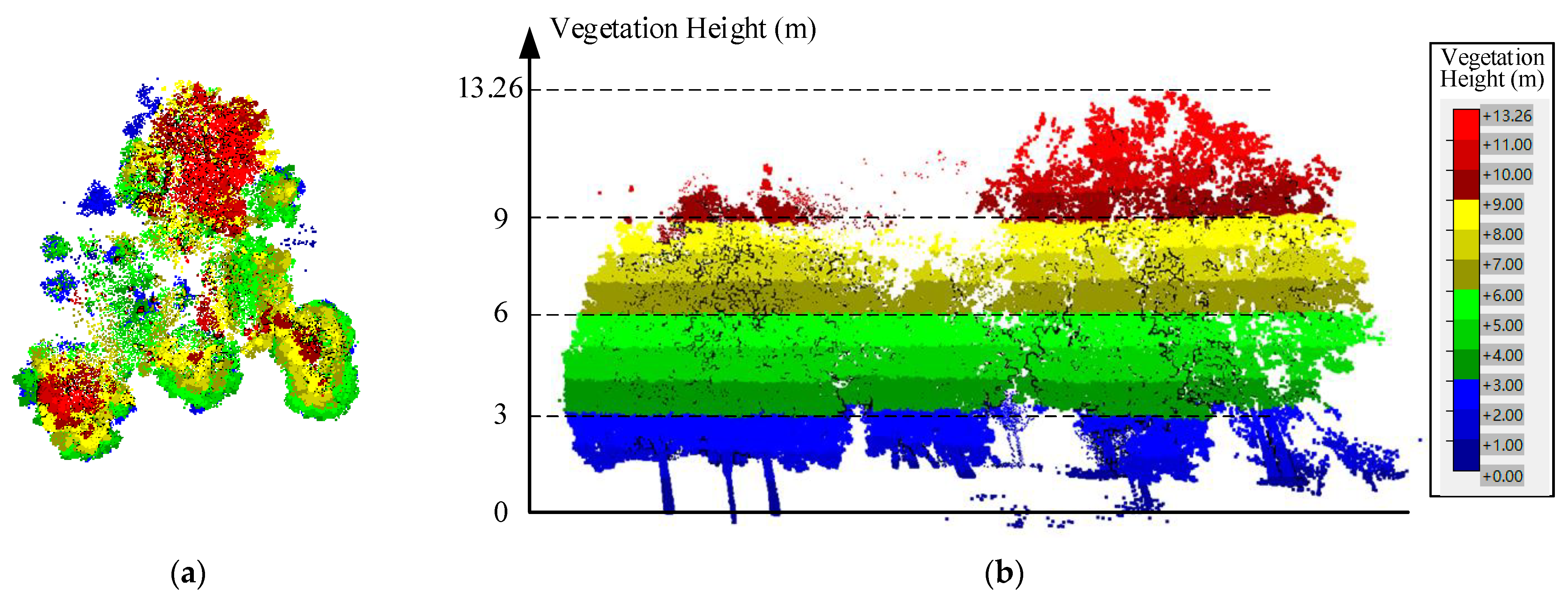
4. Experimental Verification of the VO-LVV Estimation Model

The VO-LVV estimation method in this study uses 3D point cloud data on vegetation to construct an octree search space; therefore, different point cloud data sources have differences in point cloud quality and parameters, and thus substantially influence the performance of the method. To build a generally applicable method, testing on different datasets and analysis of the sources of error were necessary.

In this study, we selected an experimental area (the longitude and latitude is: 103.933113°, 30.761321°) at the University of Electronic Science and Technology of China (UESTC) for data collection, and used three methods—the MLS system, UAV airborne LiDAR, and UAV airborne oblique photogrammetry—to obtain the corresponding point cloud dataset in the same time phase. The detailed parameters’ information of the MLS system and UAV airborne LiDAR are listed in

Table 1. Measurement parameters of the MLS system and UAV airborne LiDAR equipment.

Type	iScan-S-Z (MLS)	Zenmuse L1 (Airborne LiDAR)
Limit measurement distance	119 m	450 m
Laser emission frequency	1.01 × 107 p/s	2.4 × 106 p/s (single echo), 4.8 × 106 p/s (multiple echo)
Ranging accuracy	0.9 mm (at 50 m)	3 cm (at 100 m)
Angular resolution	0.0088°	0.01°
System accuracy	5 cm (at 100 m)	10 cm (at 50 m)

. For UAV airborne oblique photogrammetry equipment, we used the DJI M300 UAV (https://www.dji.com/cn, accessed on 3 January 2022) and the Zenmuse P1 camera (https://www.dji.com/cn/zenmuse-p1, accessed on 3 January 2022).

We then used MicroStation for the point cloud classification process to coarsely extract the multi-vegetation point clouds from the original data. Since the trees in these data are properly spaced from each other, and the canopies of adjacent plants do not overlap, the point cloud data of multiple plants could be segmented by using the fence tool. The point cloud data obtained from the above three methods were classified to obtain rows of plants in the same place. The quality information of those point cloud datasets is shown in

Table 2. Quality comparison of three types of point cloud data collected at the same site and in the same time phase.

Point Cloud Source	Data Format	Point Cloud Quantity	Point Cloud Density, Resolution	Data Details
MLS	.las	23,762	8000 points/m3, 5 cm	Missing part of the crown dorsal information
UAV Airborne LiDAR	.las	50,398	8000 points/m3, 5 cm	Missing the trunk and crown bottom
UAV Airborne oblique photogrammetry	.las	58,7005	1,000,000 points/m3, 1 cm	Missing the trunk and crown bottom

.

Of note, on the basis of the quality of the above three types of data and our previous calculation experience, the two key parameters in this method—the voxel resolution and the density threshold—were adjusted. The voxel resolution (that is, the minimum voxel size) divided by the octree $l_m^x=l_m^y=l_m^z=0.2 \mathrm{m}$, and the density threshold $t=1000 \mathrm{points}/{\mathrm{m}}^3$.

With the point cloud processing software, the visualization effects of the point clouds acquired by the three methods are shown in Figure 4. From top to bottom, the vegetation point clouds acquired by MLS (Figure 4a), UAV airborne LiDAR (Figure 4b), and 3D reconstruction with the UAV airborne oblique photogrammetry technique (Figure 4c) are shown. Owing to the different angles of data acquisition, some information is missing in the raw data acquired through the different methods: the MLS LiDAR data has a cavity in the canopy on the side with its back to the acquisition equipment, whereas the point cloud in the airborne LiDAR and 3D reconstruction with UAV airborne oblique photogrammetry images has a more severe absence of information at the bottom of the canopy.

First, the preprocessed single tree LAS point cloud data were imported into the calculation program used in this study for analysis. Two traditional LVV measurement methods were selected for comparison. The first was the commonly used measurement method based on a triangular mesh, i.e., the aforementioned wrapped surface approach [26], which constructs a triangular mesh on the point cloud on the crown surface to form a closed envelope, then uses the generated polyhedron as the fitting model for calculation. The second was the formula measurement method [17], which according to the observed crown shape, fits the most approximate regular geometry, which is input into the diameter-height correlation equation on the basis of the measured crown width, crown height, and tree measurement factors. The LVV value calculated with the formula method can be approximated as the true value of LVV. In this experiment, the vegetation canopy in the verified area was ellipsoidal, and the calculation formula of LVV is shown in Equation (9):

$$V=\frac{\pi d^{2}h}{6}$$

(9)

where $d$ is crown width and $h$ is crown height. For our approach, because the equation simulates a plant as a regular round shape on the cross-section of each layer, but the cross-section of each layer of an actually measured plant is usually elliptical, when Equation (8) is used to estimate the total LVV, this method must be corrected by the shape completion parameter $c(Q)$. The calculation method of $c(Q)$ is as shown in Equation (10):

$$C(Q)=\frac{\Vert \overrightarrow{a}\Vert }{\Vert \overrightarrow{b}\Vert }$$

(10)

where $\overrightarrow{a}$ is the maximum crown diameter vector measured at the maximum cross-section of the vegetation point cloud, and $\overrightarrow{b}$ is the crown diameter vector perpendicular to $\overrightarrow{a}$ on the cross-section. A comparison of calculation results of the same vegetation in the verification area under the same time phase is shown in

Table 3. Comparison of different LVV measurement methods (for a single tree *).

Calculation Method	Measurement Data	Calculated LVV (m3)	Calculation Time (s)
Wrapped surface approach	MLS	16.1555	0.308
	Airborne LiDAR	13.1832	1.673
	3D reconstruction point cloud	18.8464	7.660
VO-LVV method (voxel resolution: 0.2 m, density threshold: 1000/m3)	MLS	11.3601	0.007
	Airborne LiDAR	10.2427	0.024
	3D reconstruction point cloud	20.6150	0.075
True value (based diameter-height correlation equation)	Crown width	4.355 m	/
	Crown height	2.592 m
	LVV in theory	25.7401 m3

* Note: This single tree is the middle one in Figure 4, and other single trees can be calculated in the same way.

.

From Table 3, it can be found that:

(1)

Through the testing of vegetation point cloud samples, as compared with the wrapped surface approach, our LVV measurement method used in this study enabled faster calculation, and the acceleration ratio generally reached approximately 44:1–102:1, thus indicating good calculation efficiency.

(2)

For point cloud data from three different sources, when the same calculation method is used, e.g., the wrapped surface approach or the VO-LVV measurement method, the corresponding LVV results can be calculated. However, comparison of the proximity of the results to the true value of LVV indicated that the colocation results from the point cloud data based on 3D reconstruction with the UAV airborne oblique photogrammetry technique were better than those obtained through the other methods (MLS or UAV airborne LiDAR). Therefore, the point cloud data with higher point density appear to improve the LVV calculation accuracy. Meanwhile, the mean value (16.0617) of the first method for the three data sources is closer to the true value (25.7401) than that of the second method (14.0726).

(3)

For the most suitable point cloud data source for LVV estimation, i.e., the point cloud data from 3D reconstruction, the absolute value of the measurement error rate (difference between measured value and true value/true value) was 19.9%, thus indicating better measurement accuracy than the 26.8% absolute value of the traditional wrapped surface approach.

To verify the calculations of this method in complex scenarios, we tested the method on a sample of multiple plants (three plants in one row). Similar to the single tree experiment, the wrapped surface approach and formula method were used to measure each single plant separately, then accumulate and compare the total green value. Unlike the other methods, our method calculated these vegetation point clouds as a whole. A comparison of calculation results obtained from the multiple plants experiment is shown in

Table 4. Comparison of different LVV calculation methods (for multiple plants).

Calculation Method	Measurement Data	Calculated LVV (m3)	Calculation Time (s)
Wrapped surface approach	MLS	58.1347	2.291
	Airborne LiDAR	39.9395	6.199
	3D reconstruction point cloud	67.7621	26.942
VO-LVV method (voxel resolution: 0.2 m, density threshold: 1000/m3)	MLS	39.2171	0.016
	Airborne LiDAR	39.1926	0.063
	3D reconstruction point cloud	68.3091	0.117
True value (based on diameter-height correlation equation)	LVV in theory	79.8619	/

.

From Table 4, it can be found that:

(1)

The VO-LVV estimation method can maintain a linear relationship with a single plant in calculations involving multiple plants. Therefore, this method is suitable for simultaneous calculation scenarios of single trees and multiple plants. In contrast, the wrapped surface approach and formula measurement method can perform calculations for only single trees, and their calculation efficiencies are quite low.

(2)

Similar to the second item in the above analysis from Table 3.

(3)

The VO-LVV estimation method still maintained a good acceleration ratio, as compared with that of the wrapped surface approach, reaching approximately 98:1–230:1.

(4)

For the most suitable point cloud data source for LVV estimation, i.e., the point cloud data from 3D reconstruction, the absolute error rate of the VO-LVV method was 14.5%, whereas the absolute error rate of the wrapped surface approach was 15.2%.

Finally, for the complex vegetation coverage scenes, this study also carried out the corresponding experiment, as shown in Figure 5. The vegetation in this experimental area is dense and overlapped with each other, and there are also great differences in vegetation types. Following the same aforementioned operations, three different types of datasets in this region are acquired through three different methods. By classifying and extracting the three types of datasets, the quality information of these point cloud datasets is shown in

Table 5. Quality comparison of three point cloud datasets collected from the same complex vegetation coverage scene.

Point Cloud Source	Data Format	Point Cloud Quantity	Point Cloud Density, Resolution	Data Details
MLS	.las	301,462	8000 points/m3, 5 cm	Missing part of the crown dorsal information
Airborne LiDAR	.las	723,622	8000 points/m3, 5 cm	Missing the trunk and crown bottom
UAV Airborne oblique photogrammetry	.las	7,137,059	1,000,000 points/m3, 1 cm	Missing the trunk and crown bottom

.

From Table 5, to this complex vegetation scene, only our proposed method can be adopted to calculate the LVV values of three types of point cloud data. The calculated LVV values are 761.9390, 1056.9209, and 1331.9026 m³, respectively. Although it is impossible to obtain the true value through actual measurement in this case, the measured value of our method conforms to the quantitative relationship with the data of the scene’s area size and the vegetation crown height. According to the field investigation and statistics, there are nine plants with a similar crown shape and size and an amount of low vegetation in this area. Take one of the plants, and the measured LVV is about 121.9107 m³. Based on this, it can be estimated that the true value of LVV in this area is about 1219.107–1341.0177 m³. Therefore, it can be generally considered that the method in this paper is effective for the calculation of regional LVV. It can also be considered that this method is effective for the LVV measurement in the complex scenes.

5. Discussion and Conclusions

The existing quantitative methods for LVV measurement are mainly based on single tree modeling or on the calculation of single tree species’ growth parameters, which cannot be applied to the many tree species and complex forest layer structures present in urban regions, and thus are unsuitable for broad application. To address the above problems, this paper proposes a novel LVV estimation model, VO-LVV, which combines the voxel measurement method with an organizing point cloud based on an octree structure, to estimate the LVV of typical vegetation and landforms in cities. The experiential results indicated that our method can be applied to point cloud data obtained through different methods, and this approach provides great advantages in calculation speed, accuracy, and the scope of the algorithm’s application:

• The VO-LVV estimation method, compared with a traditional method, i.e., the wrapped surface approach, enabled substantial efficiency improvement and higher calculation accuracy. For the most suitable point cloud data source (i.e., the point cloud data from 3D reconstruction) for LVV estimation, the maximum calculation acceleration ratio reached 230X, and the best absolute error acceleration rate of the VO-LVV method was 6.9%.
• Furthermore, the new method can be simultaneously applied to scenarios of single plants and multiple plants, and can be used for the calculation of LVV in areas with various vegetation types in cities.
• However, this method also has some limitations in the following aspects:
• In this method, the voxel resolution and density threshold strongly influence the LVV calculation results. Due to the lack of theoretical analysis on voxel scale division in this algorithm, it is unable to process data with low point density.
• This method uses parameter fitting to optimize the lack of information in the original point cloud data, and it does not analyze the spatial distribution of point cloud data; therefore, errors may be present in the estimation results.

Follow-up studies should start by investigating the above problems and should continue to refine the algorithm to improve the measurement accuracy, with a focus on the following aspects:

• The number of verification data will be increased to verify the adaptability of the algorithm in different canopy structures.
• For low point density in the original point cloud data, the commonly used point cloud up-sampling algorithm [33] could be introduced.
• For the lack of information due to the point cloud acquisition method, point cloud completion technology based on deep learning [34] could be used to complete the canopy data and improve the calculation accuracy.
• Among different types of vegetation in cities, the lushness of branches and leaves greatly varies. Other measurement methods for specific tree species could be introduced and combined with the results of this study to yield an adaptive LVV high-precision calculation scheme. Through in-depth improvement of the method reported herein, a rapid estimation model of urban regional LVV could be established, which would enable urban greening measurements to be quickly obtained and analyzed.