Semantic Segmentation of Metoceanic Processes Using SAR Observations and Deep Learning

Abstract

Through the Synthetic Aperture Radar (SAR) embarked on the satellites Sentinel-1A and Sentinel-1B of the Copernicus program, a large quantity of observations is routinely acquired over the oceans. A wide range of features from both oceanic (e.g., biological slicks, icebergs, etc.) and meteorologic origin (e.g., rain cells, wind streaks, etc.) are distinguishable on these acquisitions. This paper studies the semantic segmentation of ten metoceanic processes either in the context of a large quantity of image-level groundtruths (i.e., weakly-supervised framework) or of scarce pixel-level groundtruths (i.e., fully-supervised framework). Our main result is that a fully-supervised model outperforms any tested weakly-supervised algorithm. Adding more segmentation examples in the training set would further increase the precision of the predictions. Trained on 20 × 20 km imagettes acquired from the WV acquisition mode of the Sentinel-1 mission, the model is shown to generalize, under some assumptions, to wide-swath SAR data, which further extents its application domain to coastal areas.

1. Introduction

Since neural-networks-based algorithms have become the state-of-the-art framework for a wide range of image processing problems in the 2010s, the use of deep learning approaches has been extended to many kinds of remote sensing data, including for instance infrared imagery [1], land applications of SAR [2] and SAR-optical fusion [3]. By contrast, the segmentation of oceanic processes from SAR images has been little addressed. Synthetic Aperture Radar (SAR) imagery relies on physical basis very different from optics. Operating in the microwave band, SAR images result from a complex physical imaging process compared with optical imaging, which results in high resolution images (typically few meters resolution). Over the oceans, the SAR imagery is sensitive to the surface roughness which can be impacted by the wind, the waves, the presence of ships or icebergs, a surface viscosity difference caused by oil or biological slicks, the precipitations or by sea ice in polar regions [4]. Contrary to optical images, SAR can be acquired in almost all conditions, especially over cloudy regions and at night. For these reasons, SAR images can be processed into a wide variety of geophysical products such as wind maps, wave spectra, surface currents, and its full potential still remains unexploited, especially in terms of scientific and operational services [5]. Among the instruments in flight, the C-band Sentinel-1 constellation operated by the European Space Agency (ESA) is one of the main real-time providers of SAR images and products. The segmentation of oceanic processes from SAR has already been addressed, but on specific cases such as oil spills [6], ships (though as a detection problem as they appear as ponctual bright areas) [7] or sea-ice [8]. These studies found out that the Convolutional Neural Networks (CNN) [9,10] architecture is the most adapted. Especially, ref. [6] found that they achieve better results than other usual segmentation methods such as logistic regression or k-Means. The present study aims to extend these previous works and more specifically to assess whether deep learning approaches may address the joint semantic segmentation of a wide range of metocean processes in SAR oceanic images.

Deep learning for semantic segmentation tasks mainly relies on the fully-supervised framework, that requires the manual segmentation of hundreds up to thousands of images to build a representative training dataset. For SAR imaging over the ocean, the difficulty to access ground-truthed data sets may partly explain the small amount of studies on this topic. First, this task is quite complex and should be carefully performed by domain experts. On the SAR observations, the signature of the geophysical phenomena is complex and requires specific knowledges of both SAR imaging and of their impact on the sea-surface roughness. Second, this is a time-consuming task. The Common Object in COntext data set [11], also known as COCO, stated that drawing segmentations required 800 s per object, while the categorization task at image-level requires only 30. A second hardship was the high variance in the annotation, especially when multiple annotators were involved in the data set creation. This problem was also raised by [12] in the context of sea ice charts.

Fortunately, the first annotated SAR images data set for classification was released by [13]. It consists in a collection of more than 37,000 $20\times 20\mathrm{km}$ SAR imagettes for 10 categories of geophysical phenomena: Atmospheric Fronts, Biological Slicks, Icebergs, Low Wind Area, Micro-convective Cells, Oceanic Fronts, Pure Ocean Waves, Rain Cells, Sea Ice and Wind Streaks. It was later supplemented by another 10,000 images. In [14], deep learning models trained from this dataset led to promising results with an excellent classification performance [15]. However, this effort could not generalize to imagettes with at least two phenomena, and, as a categorization task, is inherently limited in resolution. Still, even image-level annotation integrates implicit information on the represented features, based on the annotator knowledge, and building up on this valuable effort would be of great interest to train semantic segmentation models [16,17]. This is referred as weak supervision. Most of the works studying weak supervision are based on photographs and make assumptions to leverage the segmentation, typically on image contrast and homogeneity [18], on boundary pixels [19] or on the object compacity [20]. Another possibility is to turn classifiers into segmenters [21,22].

The general objective of this study is to evaluate whether deep learning models and strategies may address the semantic segmentation of SAR oceanic images in terms of metocean processes. Specifically, we aim to assess the relevance for this task of both fully-supervised and weakly-supervised schemes. The proposed approach combines a selection of state-of-the-art deep learning frameworks, the creation of a reference ground-truthed dataset of annotated SAR oceanic images and the design of a benchmarking setting, based on a reference ground-truthed dataset.

In this study, the SAR observations used as groundtruth will first be presented in Section 2. Then, the different algorithms able to obtain the segmentation will be presented in Section 3. The segmentation of metocean phenomena is addressed through both the weakly supervised framework, using the 37 k image-level (one label per image) annotations of the TenGeoP-SARwv dataset, and a fully supervised of 1 k manual annotated groundtruth (2D annotations).

2. Data

The image-level dataset is built from the TenGeoP-SARwv dataset described in [13]. It contains more than 37 k Sentinel-1 Wave Mode (WM) acquisitions categorized at image-level for ten metocean processes. Wave Mode observations are acquired on an area of approximately 20 km by 20 km. Though initially at a resolution of 5 m per pixel, the images are downsampled to 50 m per pixel to reduce the speckle and for computational reasons. The resolution can be further decreased down to 100 m.px⁻¹ without impeding the accuracy of the categorization as shown in the

Table 1. Accuracy of the categorization task depending on the resolution.

Resolution	Accuracy (Validation)	Accuracy (Test)
50 m.px−1	99%	77%
100 m.px−1	98%	75%
200 m.px−1	93%	66%
340 m.px−1	88%	59%

. However, it decreases the resolution of the weakly supervised segmentation, as they commonly use a categorizer as a backbone of the segmentation. The scenes are observed under two incidence angles of 23.8° and 36.8° in co-polarization polarization. It has to be noted that the distribution of the classes in the TenGeoP-SARwv dataset varies with the incidence angle. For example, 93% of the Pure Ocean Waves observations were obtained at an incidence angle of 23.8° where 92% of the Micro Convective Cells correspond to observations at 36.8°. Though these two classes are the extreme cases, it indicates that the SAR signature of the phenomena can be more visible at particular incidence angles.

Interferometric Wide Swath images (IW) are used for testing purpose only. In contrary to WM, they cover large areas of hundred or thousand of kilometers high and a few hundred of kilometers wide. The incidence angle varies between 32.9° and 43.1°. Also, if the WM observations are acquired with a minimum coastal distance of hundreds kilometers, IW product are obtained in coastal area. In this study, IW samples are preprocessed to match the aspect of the WM images described before. The main preprocessing is the computation of the normalized radar cross section and a de-trending to remove the effect of the variable incidence [23].

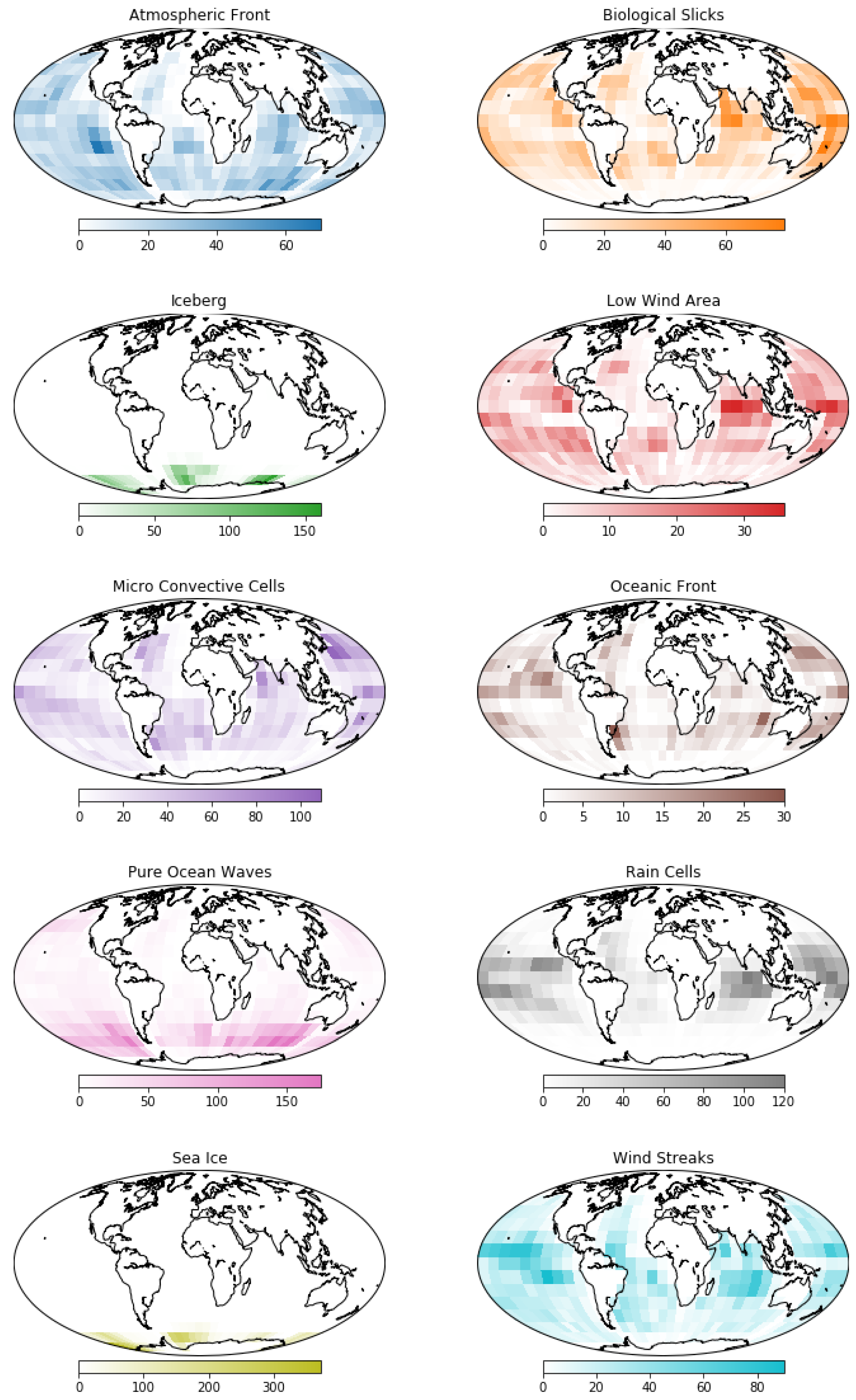
The ten metoceanic processes studied are Atmospheric Fronts (AF), Biological Slicks (BS), Icebergs (IB), Low Wind Areas (LWA), Micro-convective Cells (MCC), Oceanic Fronts (OF), Pure Ocean Waves (POW), Rain Cells (RC), Sea Ice (SI) and Wind Streaks (WS). The Figure 1 indicates the number of observation of these phenomena, over the globe, as determined from the categorization labels from the TenGeoP-SARwv dataset.

For the fully suppervised method only, 100 manually annotated samples per class of TenGeoP-SARwv’s are provided for the training set, and 10 per class for the validation set. All algorithms are evaluated on an independant test set of 10 samples per class. These groundtruths were produced at the pixel-level by manually indicating the area covered by each phenomena appearing in the observations. To account for the fuzziness of the boundary of some phenomena and the difficulty to accurately delimit them, the segmentations are at a resolution of 400 m.px⁻¹. The SAR observation is downscaled to 100 m.px⁻¹ following the results in the Table 1 as using a resolution of 50 m.px⁻¹ would increase the time and memory consumption with a marginal performance increase. The segmentation dataset is available on kaggle. To artificially increase the data, rotation of $\pm \frac{\pi }{2}$ and symmetries (both vertical and horizontal) are used. The quantity of input is thus multiplied by 8. This data augmentation implicitly assumes that, on the scale of one observation, the variation of the incidence angle has negligible effect against the meteorological state.

3. Methodology

Five families of algorithm are tested. The first one is trained using the 1000 manual segmentations under the fully supervised framework. The last four rely on the categorization dataset, using the 37 k pairs of SAR observation/classification to learn a pseudo-segmentation in a weakly-supervised framework. Specifically:

A

uses the small dataset of pixel-level segmentation in a fully supervised framework;

B

calls a categorizer multiple times while masking a small part of the input;

C

uses the constant model size property to run a categorizer on small portions of the image and get partial categorizations;

D

exploits the conservation of spatial information using the Class Activation Maps;

E

considers the image-level annotation as a heavily noised pixel-level segmentation and set constraints on spatial information propagation in the model.

The scripts used to train the categorizers and the segmenters are available on GitHub.

3.1. Fully Supervised Segmentation

All the weakly-supervised methods use the full TenGeoP-SARwv dataset and its more than 37 k image-level annotations. However, some previous work stated that supervised learning was successful in SAR imagery for segmentation. Ref. [6] found that the convolutional neural networks achieve better results than other usual segmentation methods such as logistic regression or k-Means to segment pollution on acquisitions from Sentinel-1 and Envisat. Ref. [8] shows that the regression of the sea ice concentration, seen as a segmentation problem with classes representing the concentration intervals, can be solved with a model’s architecture similar to U-Net [9]. Ref. [24] used Residual Networks [10] to regress the wind direction on tiles of 5 km by 5 km extracted from interferometric wide swath products from Sentinel-1.

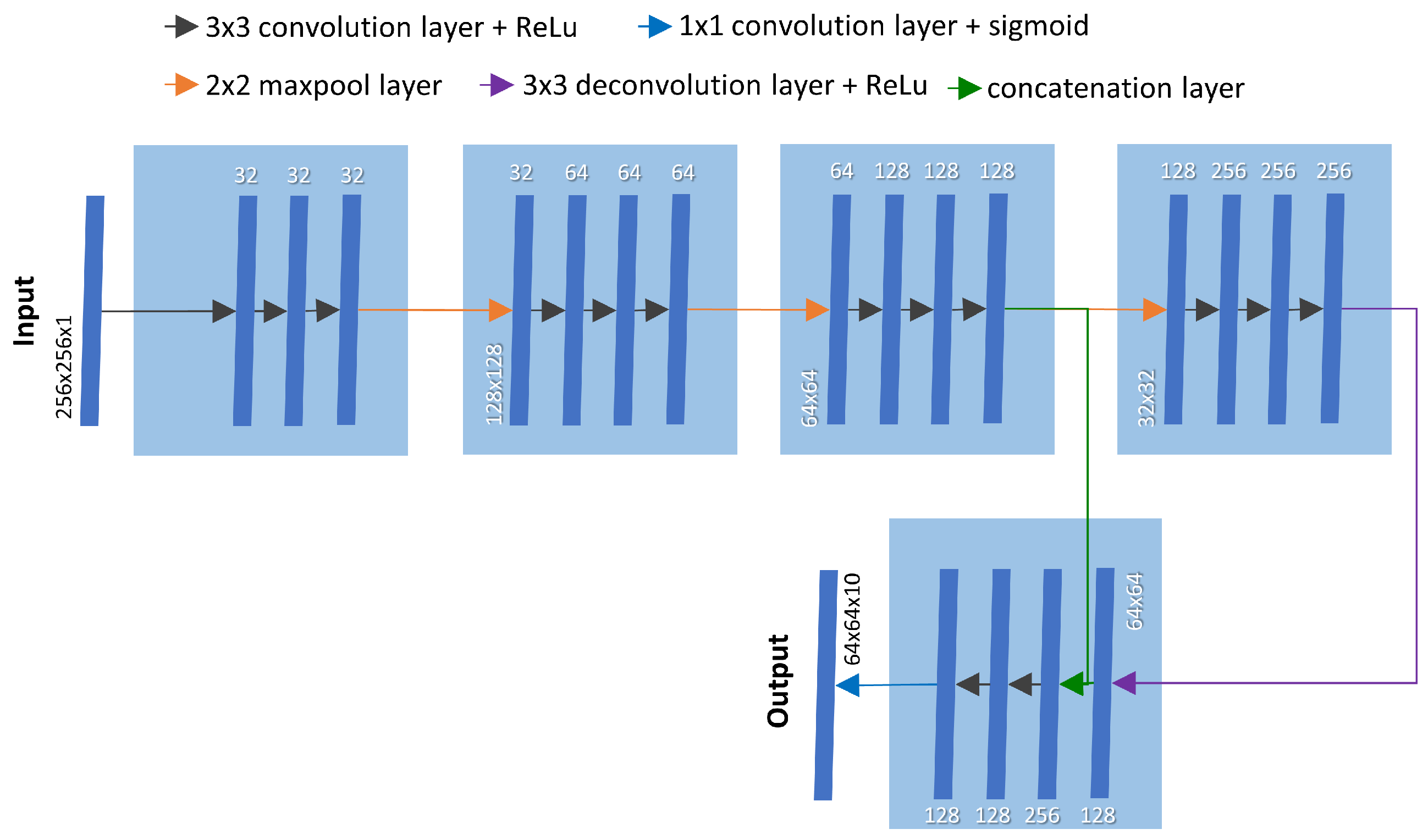
This method relies on the manually pixel-level annotated dataset containing one thousand wave mode in the training set. The segmentation model follows the UNet architecture [9] with a four-story model but a cut-off of the decoder to get a output of 64 × 64 pixels. The architecture is depicted in Figure 2. The model is trained under the Weighted Binary Crossentropy function defined as:

$$WBC{E}_c(y_c,{\tilde{y}}_c)=-\frac{K_{c}C}{\sum K}·\left[\frac{\sum y_c}{{64}^2}{y}_{c}log\left({\tilde{y}}_c\right)+(1-\frac{\sum y_c}{{64}^2})(1-y_c)log(1-{\tilde{y}}_c)\right]$$

(1)

This loss is quite different as the one described in [25] as it uses the vector K which is the inverse of the pixel-wise a priori probability of each phenomena to appear (computed on the training set). C stands for the number of classes and is needed to conserve the same learning rate. $y_c$ and ${\tilde{y}}_c$ are respectively the groundtruth and the predicted segmentation for the class c.

$$K=(34.5,11.8,250.0,14.1,8.2,71.4,2.3,50.0,9.1,8.3)$$

(2)

3.2. Masking the Input (MASK)

This method, as suggested by [22], assumes that the class-output of a categorizer will be affected negatively if a part of the researched object is hidden. Usually, this is done by moving a square mask over the input. With X the input, the masked input $X_{c,a,b}^{\prime }$, where a and b denote the position of the mask, and c its size, is defined by:

$$X_{c,a,b}^{\prime }(x,y)=\left\{\begin{array}{cc}X(x,y)\hfill & \mathrm{if}|x-a|>\frac{c}{2}\mathrm{and}|y-b|>\frac{c}{2}\hfill \\ \\ v\hfill & \mathrm{else},\hfill \end{array}\right.$$

(3)

with v is the value taken by the input when the mask is over it. As one of the TenGeoP-SARwv’s class, namely the Low Wind Area class, can be recognized by an overall low intensity, setting $v=0$ could lead to an increase of the categorization score for this class. Incidentally, it introduces high spatial frequencies that could, a priori, be seen as either an Atmospheric Front or an Oceanic Front. Setting v at the mean value of the image could mitigate this behaviour.

Once the edited inputs are generated, the pseudo-probability of the phenomena i to be depicted on the input X is denoted as $\mathcal{M}{\left(X\right)}_i$, with $\mathcal{M}$ a model trained on the categorization problem. The pseudo-segmentation is defined by:

$${\displaystyle Y(x,y)=\frac{1}{\#A_c\left(x\right)·\#B_c\left(y\right)}\sum _{\begin{array}{c}a\in A_c\left(x\right)\\ b\in B_c\left(y\right)\end{array}}max(0,\mathcal{M}\left(X\right)(x,y)-\mathcal{M}\left(X_{c,a,b}^{\prime }\right)(x,y))}$$

(4)

$$A_c\left(x\right)=\left\{a\in \mathbf{N},|x-a|<\frac{c}{2}\right\}$$

(5)

$$B_c\left(y\right)=\left\{b\in \mathbf{N},|y-b|<\frac{c}{2}\right\}$$

(6)

However, this computation has a complexity of $O(h·w)O\left(\mathcal{M}\right)$. To decrease it and be able to run it in an acceptable time, we use a stride s and compute $Y^{\prime }(x,y)$ only when both indices are multiples of s. Thus, the complexity is reduced to $O\left(\frac{h·w}{s^2}\right)O\left(\mathcal{M}\right)$.

In the experiments, $c=75$ px (3.75 km) and $s=25$ for a 512 × 512 px-wide input. The resolution of the pseudo-segmentation is thus of 16 × 16 px and required to run the categorizer on 256 + 1 images of shape $(512,512)$.

3.3. Partial Categorization (PART)

Using partial categorization to build a pseudo-segmentation relies on the opposite paradigm. Following [21], the categorizer runs on multiple locations and only take a small part of the input at a time.

Some categorizers (such as InceptionV3 [26]) have a number of weights independent of the input size. Indeed, they do not include fully connected layers before a global pooling. Therefore the number of weights is only defined by (1) the number and the shape of the convolution kernels and (2) the number of classes, and of neurons of the fully connected classes. This property enables a categorizer trained for a shape $S_1$ to categorize inputs of shape $S_2$.

A minimal shape can be defined by the architecture of the network. In the case of InceptionV3, the last activation map shrink to a single pixel for an input shape of $(75,75)$. In other words, an InceptionV3 trained on $(512,512)$-input can provide categorization down to inputs of shape $(75,75)$ (given that the resolution does not change). Therefore, it is possible to divide several tiles and obtain the categorization for each of them. The pseudo-segmentation is therefore defined by:

$$Y(x,y)=\mathcal{M}\left(X\left[x-\frac{S_2}{2}:x+\frac{S_2}{2},y-\frac{S_2}{2}:y+\frac{S_2}{2}\right]\right)$$

(7)

Fully-convolutional categorizers also possess the property of translation invariance: if the effect of the borders are considered as marginal, the output of the last convolutional layer, the activation map, will be equivariant with the input. However, as a spatial global average is computed after these convolutional layers, localized information will be lost and the equivariance will become an invariance. In the context of searching the position of a phenomenon, it means that running the categorizer on every possible location is unnecessary: the result on an image after a translation of a few pixels will not change.

In the experiments, the tile shape $S_2$ is either of 129 × 129 or 75 × 75, and the stride of $\frac{S_2}{3}$. As with the previous algorithm, a categorizer has to be run on dozens or hundreds of inputs (depending of the resolution) but these inputs are several times smaller than the full observation.

3.4. Class Activation Maps (CAM)

Even without doing assumption on the scale, shape or intensity of the SAR signatures of the metocean processes, it is possible to obtain a pseudo-segmentation. By essence, a convolutionnal network keeps the localization properties of the input image through its layers. The stride of the convolutions, the size of the kernel and the poolings build a filter system that recognizes shapes [27] and textures [28] and returns activation maps, i.e., the presence of the features recognized by the filters. However, a categorizer has to finally fuse the information of these activation map to obtain an image-level answer. This is usually done using global pooling [29] or dense layers [10,30,31]. The localization information is thus conserved until the last convolutional layer, whose outputs are called Class Activation Maps (or CAM). After that point, localization information is discarded by the use of either dense (also called fully connected) layers or by a global polling. It has been shown that it was possible to use CAM, before the destruction of structural information, to obtain the segmentation of the objects [32]. To get CAM from a categorizer, the global average pooling is removed from the network. Then, the output of the last convolution layer -of shape $(w,h,f)$- is multiplied by the weights of the dense layer -of shape $(f,n)$- to produce a $(w,h,n)$ output, where w and h are respectively the width and height of activation maps, f the number of filters and n the number of classes. The biases are applied if available.

In SAR domain, CAM has been used for segmentation of crop areas under weak supervision on image-level labels [33]. To this end, a categorizer from U-Net architecture [9] is build by adding a global pooling layer after the U-Net module and a dense layer to translate the 32 canals of the output into a single value (the binary classification of the input). This classifier is called U-CAM and achieve a categorization accuracy of around 98%. However, this study was done with low-resolution pictures (50 × 50 pixels, with 200 k samples at a resolution of 30 m.px⁻¹) with only two classes. In contrast, the TenGeoP-SARwv dataset contains images of 512 × 512 pixels, categorized in ten classes. Since the categorization task is more complex, the attempts to train a U-Net classifier did not reach satisfactory result (best accuracies at 40%).

However, since the shape of TenGeoP-SARwv’s images is higher than InceptionV3’s minimal shape, it is possible to use this architecture to build CAM. Similarly to the U-CAM network, this model ends with a global average pooling layer followed by a dense layer. Thus, it is feasable to use the activation map of the ante-penultimate layer to obtain segmentation of the metocean process. As it does not include unpooling layer, the activation maps have a lower space resolution than the input. For an input of shape $(512,512)$, the activation maps have a size of $(14,14)$, representing a spatial resolution of approximately 1.8 km.px⁻¹, whereas U-CAM could keep the same resolution as the input.

This algorithm remind those described in the previous section as it is based on the output of a convolutional layer previously to a pooling phase. However, the spatial propagation of information through the convolution is not clipped to the width of a tile. It can be computed that it is equal to $\frac{1255}{64}\approx 19.6$ pixels in the final activation map (superior to its own width on inputs of 512 × 512).

3.5. Image-Level Classes as Noisy Pixel-Level Segmentation (IM2PX)

Neural networks have been proved to be able to train under very noisy datasets [34]. As such, the image-level labels used in the weak-supervision can be interpreted as segmentations with heavy spatial noise. Under this paradigm, the $(1,10)$ label vector is converted into an image of shape $(h,w,10)$, the value of the vector being used for each pixel. Then, an image-to-image model is given the task to solve the segmentation problem.

Assuming that (1) the segmentation model respect constraints on the spatial information propagation (the value of an output pixel is defined by the value of the input pixels in a constrained neighbourhood), it is possible to infer implicit information on the position of the phenomena. In layman’s term, if a pixel is located far from the features of a class, the segmenter (whose work is to do a pixel-level categorization) won’t be able to assign this class to the pixel, as no pixels of the neighbourhood should (2) give information about it. Thus, if (3) the network has been trained without overfitting, the only pixels with a significative value for the categorization will be those under the neighbourhood of a phenomenon.

Condition (1) can be ensured by studying the model architecture. The spatial propagation of a classic autoencoder is $\rho =\frac{k}{2}(2^n(n+4)-2)$ with n the number of max pooling layer and k the number of successive convolutional layer (of kernel size 3) at each stage. This can be demonstrated by remarking that at the first layer of the stage i of the spatial propagation is ${\rho }_i=2({\rho }_{i-1}+\frac{k}{2})$, and that ${\rho }_0=n\frac{k}{2}+k$ (this is the spatial propagation of the encoding network). To prevent $\rho$ from rising, and for simplicity’s sake, an encoder model was used with $n=3$ and $k=3$. Condition (2) depends on the comprehension of the phenomena. It is not impossible that long-range correlation could provide information on the main phenomena on the picture, but they are considered small enough to be marginal.

4. Results

4.1. Quantitative Results on the Wave-Mode Test Set

Quantitative results are obtained by computing the Dice index (also known as F1-score) over a test set of manually annotated segmentations. The Dice index is defined as:

$$D(x_i,y_i)=\frac{1}{\#S}\sum _{e\in S}\frac{2·x_{e,i}·y_{e,i}}{x_{e,i}+y_{e,i}}$$

(8)

In this equation, S is the set of all the pixels, $x_{e,i}$ is the predicted segmentation of the label i at the pixel e and $y_{e,i}$ the corresponding groundtruth. The Dice index gives values between 0 and 1, the latter being obtained on perfect agreement between the groundtruth and the prediction. Another (equivalent) formulation of the Dice index is as the harmonic mean of the precision and recall, which increase when respectively the false positive and false negative decrease. As such, the Dice index would always be equal to 0 in case of non-detection whereas the range of a mean square error or a crossentropy would depend on the surface covered by the phenomena.

These groundtruths are independent of the datasets used either in the weakly-supervised framework or in the fully supervised one. SAR observations, used as inputs of this test set, originate from a supplementary dataset to TenGeoP-SARwv and contains 100 manual segmentations (with 10 observations from each class).

According to the

Table 2. Dice index for each algorithm and phenomena computed over the test set. A Dice equal to 1 means perfect overlap between the truth and the prediction. Values are given as mean and standard deviation over 10 trainings to account for the random initialization and order of the groundtruths used in the epochs.

Method	AF	BS	IC	LWA	MCC	OF	POW	RC	SI	WS	Mean
A–Fully supervised	29.5% [4.4%]	24.7% [8.4%]	13.5% [2.1%]	69.5% [4.5%]	30.8% [7.4%]	33.7% [6.2%]	47.9% [6.5%]	31.1% [3.5%]	63.3% [11%]	61.1% [7.5%]	40.5% [6.1%]
B–MASK ($v=\mu$)	9.6% [2.1%]	16.1% [2.9%]	4.9% [0.9%]	15.2% [2.8%]	20.6% [3.7%]	18.9% [1.5%]	9.6% [2%]	13.1% [2.3%]	17.2% [4%]	27.2% [8.8%]	15.2% [3.1%]
B–MASK ($v=0$)	10.4% [1.1%]	17.2% [1.6%]	1.2% [0.5%]	5.9% [1.7%]	3.28% [5%]	1.3% [1.2%]	14.8% [2%]	8.2% [1.6%]	19% [8.2%]	51.7% [11.1%]	17.4% [3.4%]
C–PART ($c=75$, $s=25$)	6.9% [1.3%]	29% [1.2%]	2% [0%]	39.2% [9.8%]	23.2% [3.4%]	6.7% [0.9%]	40% [4.9%]	19% [6.2%]	73.3% [4%]	66.9% [5.1%]	30.6% [3.7%]
C–PART ($c=129$, $s=43$)	14.6% [1.7%]	28.9% [0.9%]	2% [0.2%]	63.2% [2.6%]	34.2% [6%]	11.8% [1.5%]	19.2% [4.4%]	23.5% [0.6%]	77.5% [3.5%]	70% [4.8%]	34.5% [2.6%]
D–CAM	16.6% [3.4%]	14.8% [3.4%]	2.2% [0.3%]	47.6% [5.8%]	12% [3.2%]	20.4% [3.2%]	7.3% [1%]	17.9% [2.5%]	40% [9.4%]	14.2% [8%]	19.3% [4%]
E–IM2PX	12.1% [1.9%]	26.9% [1.8%]	1.9% [0.5%]	69.6% [1.5%]	26.5% [5.2%]	10.9% [1.1%]	17.5% [1.5%]	18.8% [3.7%]	69.8% [12.5%]	27.7% [5.6%]	28.2% [3.5%]

, the supervised framework outperforms all the other methods. Compared with the other methods, it gives especially good results for the Rain Cells, the Atmospheric Fronts, the Oceanic Fronts, the Pure Ocean Waves and the Icebergs, with a Dice index of respectively 31.1%, 29.5%, 33.7%, 47.9% and 13.5% for four classes. Incidentally, it has the lowest inference time, requiring only to run a U-Net model a single time.

However, other methods have their merits on specific phenomena. In particular, partial categorizations are powerful to segment Wind Streaks and Sea Ice. Though not obtaining higher performances than the fully-supervised framework, they produces good results on Pure Ocean Waves with a 75 px-wide tile (40%). The Low Wind Area and Micro Convective Cells requiring enough contextual information to be discriminated, 129 px-wide tile is more adapted to phese phenomena, obtaining a Dice index of respectively 63.2% and 34.2%, the latter being the best segmentation over all methodologies.

The noisy segmentation paradigm is competitive on Sea Ice. However, this particular class was defined, in the TenGeoP-SARwv dataset by the presence of sea ice over the whole observation, with no open water area. With this definition, the categorization annotation is effectively the same as the segmentation. This paradigm also obtains the best result for the segmentation of Low Wind Area but, given the standard deviation, should be considered equivalent to the fully-supervised framework.

Mask-based methods and Class Activation Maps, on the other hand, are inefficient on most classes. If we exclude the supervised framework, CAM perform well on Oceanic Front and Atmospheric Fronts whereas the Masking method outperformed the other unsupervised methods on Icebergs.

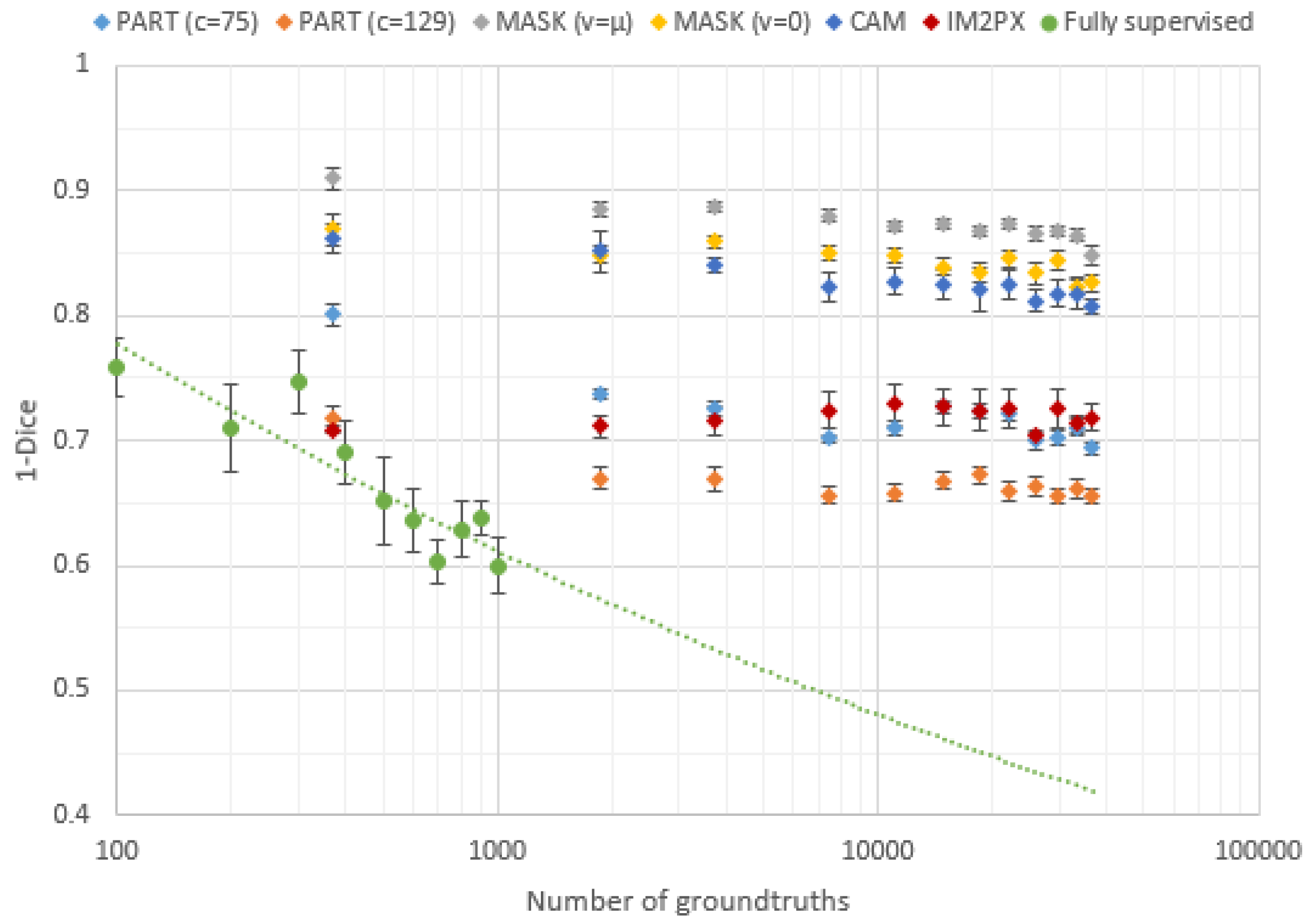
As the quality of the groundtruth in the fully supervised framework is higher, it is possible to obtain better results with much less annotations if they are at pixel-level, as depicted in Figure 3. Assuming the performance follows a power law [35], the fully supervised framework could provide even better results. On the other hand, all the weakly supervised algorithms are converging to much higher loss values. An increase of the groundtruth quantity would not lead to enhanced performances.

4.2. Visual Inspection of Wave-Mode Results

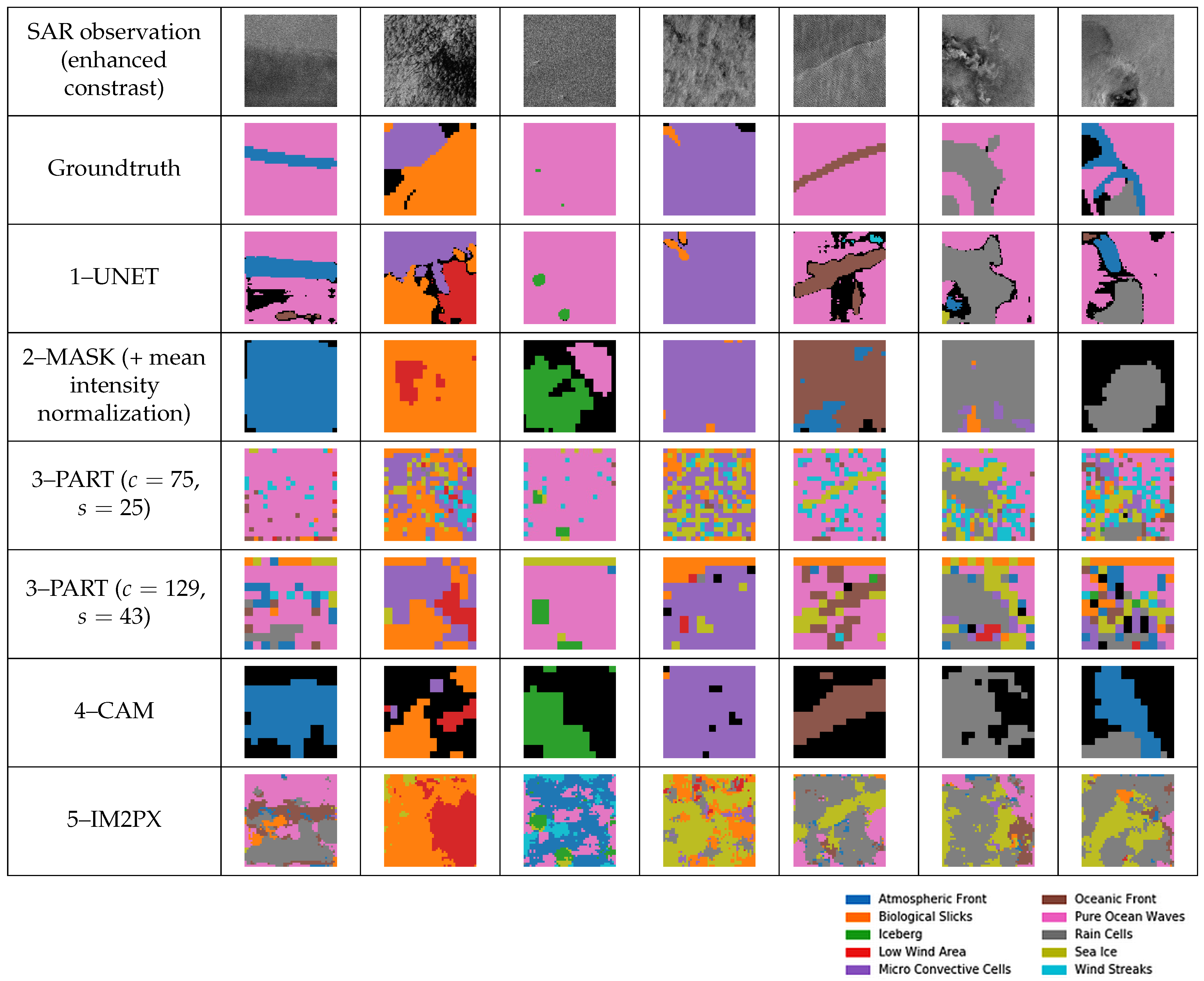
The visual inspection of the segmented wave mode images are given in Figure 4. It confirms that the most promising method is the fully supervised trained U-Net model. The segmentations are sharp enough to have a reliable accuracy on Icebergs, Oceanic and Atmospheric Fronts while retaining the ability to segment global phenomena such as Pure Ocean Waves and Micro Convective Cells. These observations are coherent with the Dice index values.

On the contrary, the partial categorization methods suffer from high noise since the area covered by the tiles are often too small to contain enough context. As visible in the Figure 4, some tiles, scattered over the image, are estimated as Wind Streaks. It also generates confusion between the Oceanic Fronts (and the boundaries of the Rain Cells) and ice leads (and thus the overestimation of the Sea Ice class).

The noisy segmentation paradigm, as per the results compiled in Table 2, was supposed to give good results on the segmentation of Sea Ice, though the result are not especially good on the other phenomena (with the exception of Low Wind Area). However, the aforementioned examples show that this method leads to repeated overestimation of the Sea Ice class, which mitigate the relevance of this method.

The algorithms relying on the Class Activation Maps show capabilities to segment some phenomena, but are impacted by the high spatial propagation of data, as previously discussed. This lead to an overestimation of local phenomena (Icebergs, Atmospheric Fronts, Oceanic Fronts). CAM are also enduring difficulties when multiple phenomena are present, as the more prominent monopolize the activation. This explains the large black areas, which are portions of the observations where the predictions are below a threshold.

5. Discussion and Perspectives

All previous results rely on TenGeoP-SARwv dataset and same mode segmentation groundtruth, generated from the Sentinel-1 Wave Mode which is a 20 × 20 km acquisition mode. However, SAR observations can cover a much larger area whenever acquired in IW Mode, 250 km wide. They cover a wider incidence angle range, from 29 to 46 degrees (w.r.t 23 and 36 for WV) and are acquired over coastal regions. Though they differ from the Wave Mode images, Interferometric Wide Swath can be preprocessed in a similar way in terms of pixel size reduction and incidence angle dependent normalization.

Even though the occurrence of observable classes highly depends on the incidence angle [13], this information is not used in the segmentation process. The possibility to extend the developed methodology to a wider range of incidence angles thus appears realistic.

To this end, Wide Swath observations are divided in tiles of 20 km by 20 km. These mosaics are constructed by ensuring an overlap between each tile. With a construction stride equal to the half of the tile width, a pixel on the border of a tile will be contained in the central part of the next one. Taking advantage of the equivariant property of the fully convolutionnal networks such as U-Net, reconstruction of the mosaic with the central part of predicted tile provide continuity over the whole Wide Swath observation. The segmentation of areas of several hundred kilometers wide can be computed in a few seconds (depending of the available GPU) with the supervised method. However, weakly supervised algorithms relying on multiple categorization for one tile cannot be realistically used for such applications.

At first sight, Figure 5, with a model trained under the fully supervised framework, shows promising results for the segmentation of Wide Swaths, with most metocean processes being well detected. The Rain Cells appearing in the south of the Tuscan Archipelago (in the yellow rectangle) are correctly returned despite their small scale. An Atmospheric Front can be observed at the south-east of Corsica (in the green rectangle). This front delimit two areas of different wind speed and continue in the south-west of the island. The area in the south, with more intense wind, contains Wind Streaks which are nicely highlighted. Ships are also appearing in several places of the observation and are returned as Iceberg as they have a similar signature. This behaviour reflect a contextual difference between the wide swaths acquisition (which are taken in coastal areas) and the wave modes -on which was trained the network- where the probability to have a ship is lower.

Other geographical differences include the orographic waves depicted in the east of Sardigna. They are induced by the western winds and the upwind topography. These orographic waves appear as large scale wind disturbances perpendicular to the wind flow. Such coastal interactions are absent of the TenGeoP-SARwv dataset. Given their similar aspect, they are mis-classified as successive atmospheric fronts. Their classification as a separate new phenomenom would probably require their investigation at a larger scale than 20 × 20 km to identify several wave patterns and the coast vicinity. It can also be noted that, in this area, orographic waves are co-occurring with Wind Streaks. This raises concerns about the implicit segmentation assumption that, at pixel-level, metocean processes are mutually exclusive.

The influence of the coast is also visible in the Gulf of Genoa. There, a different regime with strong North-Eastern offshore winds is influenced by the rapidly changing topography. It leads to a strong turbulent flow and some wind discontinuities aligned with the flow. It is segmented as Rain Cells though the visual inspection does not highlight precipitations.

Overall, even though the classes may not be adapted to all the phenomena met over these coastal regions, the algorithms behaves well in its ability to find the closest one among the possible choices. Introducing new classes, adding several scales of predictions can probably leviate the identified issues.

6. Conclusions

Fully supervised and weakly supervised segmentation are two paradigms under which it is possible to obtain segmentation of metocean processes. Fully supervised segmentation needs pixel-level annotations that are more time consuming to produce than image-level annotation used in weakly supervised frameworks. However, our experiments show that the data quantity required to outperform weakly supervised techniques can be reduced to a few dozens per class. More data leads to even better results. The extrapolation of our results suggests that building a fully groundtruthed dataset of dozen thousands segmented images may result in a significant gain in the segmentation performance.

The metocean phenomena studied in this work are open water processes contained in the TenGeoP-SARwv dataset. They are thus restricted to the ten classes described and suffer from several limitations mainly linked to the representativity of the data. First, as this dataset was created for categorization, the diversity of the phenomena are not as high as they could be in reality. In fact, the Sea Ice class mostly contains images wholly covered by ice, for which the categorization information is effectively equivalent to the segmentation. Not only the diversity could increase with the introduction of the sea/ice boudnary, but this class could also be divided in multiple subclasses [4] depending on the development stage or ice concentration. In the same way, Rain Cells typically occur with three components: a front, a down-burst area corresponding to the descending wind, and a smaller splash area generated by the precipitation. A more detailed analysis of this phenomena could be given by additional sources, for example weather radars.

The representativity of the ocean situation can be impeded by the instrument itself. The area covered by Wave Mode being limited to 20 km by 20 km, some phenomena, such as Wind Streaks with long wavelength are difficult to acquire. A multi-scale approach using IW groundtruths is believed to be beneficial to the semantic segmentation. The extension of the segmentation to coastal areas will also require the integration of new classes such a orographic waves, offshore winds, sea/land breezes or internal waves that do not appear on the Wave Mode acquisitions.

The categorization task assume that a wavemode can belong to only one class. The segmentation decrease this constraint by considering multiple areas assigned to different classes inside one image. Still, an assumption that the phenomena are mutually exclusive at the pixel level is made. If this supposition holds on the standardized TenGeoP-SARwv dataset, it becomes difficult to maintains it on Wide Swath observations as orographic waves or internal waves can be superimposed with Wind Streaks. A multi-label estimation (as opposed with “categorization”) would need a more precise delimitation of each phenomenon.