GPM DPR Retrievals: Algorithm, Evaluation, and Validation

Abstract

The primary goal of the dual-frequency precipitation radar (DPR) aboard the Global Precipitation Measurement (GPM) Core Observatory satellite is to infer precipitation rate and raindrop/particle size distributions (DSD/PSD). The focus of this paper is threefold: (1) to describe the DPR retrieval algorithm that uses an adjustable relationship between rain rate (R) and the mass-weighted diameter (D_m) or an R-D_m relationship in solving for R and D_m simultaneously; (2) to evaluate the DPR algorithm based on the physical simulations that employ measured DSD/PSD to understand the mechanism and error characteristics of the retrieval method; (3) to review ground validation studies for DPR products as well as to analyze the strengths and weaknesses of ground radar and rain gauge/disdrometer validations. Overall, the DPR Version 6 algorithm provides reasonably accurate estimates of R and D_m in rain. Non-uniformity in the rain profile, however, tends to degrade the accuracy of the R and D_m estimates to some extent as the range-independent assumption of the adjustable parameter (ε) of the R-D_m relation is not able to fully account for natural variation of DSD in the vertical profile. The DPR snow rate is underestimated as compared with the independent dual-frequency ratio (DFR) technique. This is possibly the result of the constraint associated with the path integral attenuation (PIA)/differential PIA (δPIA) used in the DPR algorithm to find the best ε and range-independent ε assumption. A range-variable ε model, proposed in the DPR Version 7 algorithm, is expected to improve rain and snow retrieval.

1. Introduction

The dual-frequency precipitation radar (DPR) operating at Ku-band (13.6 GHz) and Ka-band (35.5 GHz), aboard the Global Precipitation Measurement (GPM) Core Observatory satellite is an advanced successor to the highly successful Tropical Rainfall Measuring Mission (TRMM) Precipitation Radar (PR) that operated at a single frequency of Ku-band (13.8 GHz) [1,2,3]. The GPM, similar to the TRMM, is a joint mission of the National Aeronautics and Space Administration (NASA) and the Japan Aerospace Exploration Agency (JAXA). Launched in February 2014, the GPM core satellite orbits the earth about 16 times a day in a non-sun-synchronous orbit with an inclination angle of 65°. Compared to the TRMM PR, DPR has the capability of obtaining the rain drop size distribution (DSD) with improved detection of light rain and precipitating snow, achieved by adding Ka-band radar. The Ka-band radar operates in two modes: (1) a higher range resolution, lower sensitivity mode (KaMS) in the inner swath (125 km) and (2) a lower resolution, higher sensitivity mode (KaHS) that, before May 2018, operated in an interleaved mode in the inner swath. In May 2018, the high sensitivity beams of the interleaved mode were redirected to the outer swath, since then the Ku-band and Ka-band beams have been approximately matched over the full 245 km swath.

The range resolution of DPR Ku-band precipitation radar (KuPR) and KaMS is 0.25 km (1.67 µs pulse duration) but the measurements are oversampled at a range interval of 0.125 km. Alternatively, the KaHS has a 0.5 km range resolution (3.33 µs pulse duration) and a range sampling of 0.25 km. The KuPR conducts a cross-track scan consisting of 49 incidence angles ranging from −17° to +17° relative to nadir and resulting in a swath of 245 km on the ground. The KaMS consists of 25 angle bins in the inner swath with the central beam at nadir, giving a cross-track coverage angle of ±8.5° with a 125 km swath. On 21 May 2018, the KaHS underwent a change in the scan pattern that allows the KaHS beams to match those of the Ku-band in the outer swath (from ±8.5° to ±17°). As a result, matched Ku- and Ka-band measurements are achieved for the full swath. The footprint of DPR on the surface is about 5 km in diameter and the minimum detectable radar reflectivities are 15.46, 19.18, and 13.71 dBZ for the KuPR, KaMS, and KaHS, respectively [4].

DPR level-1 standard products provide information on noise powers, beam directions and geolocation, and surface type (land, ocean, inland water, and coast) for each footprint. Using the level-1 outputs, the DPR level-2 algorithm produces estimates of the 3D precipitation rates and parameters of the hydrometeor size distributions, storm type classification, as well as path attenuations and attenuation-corrected radar reflectivities. The algorithm consists of three products that correspond to the frequency channels being used for the retrieval. The Ku-only (KuPR) algorithms rely solely on the Ku-band measurements and produce data on the precipitating hydrometeors over the full swath while the Ka-only measurements (KaMS and KaHS) provide estimates over the inner swath before 21 May 2018 and over the full swath after 21 May 2018. The dual-frequency (DF) algorithm incorporates the Ku- and Ka-band measurements to maximize the retrieval capability. The DF product is available only for the inner swath before the change in the KaHS scan pattern and for the full swath since then. It should be noted that a database, such as the DSD on the global grid, generated by the DF algorithm and updated monthly, is applied to the single-frequency (SF) algorithms to advance the SF retrieval accuracy, and subsequently, to improve the consistency between the SF and DF estimates.

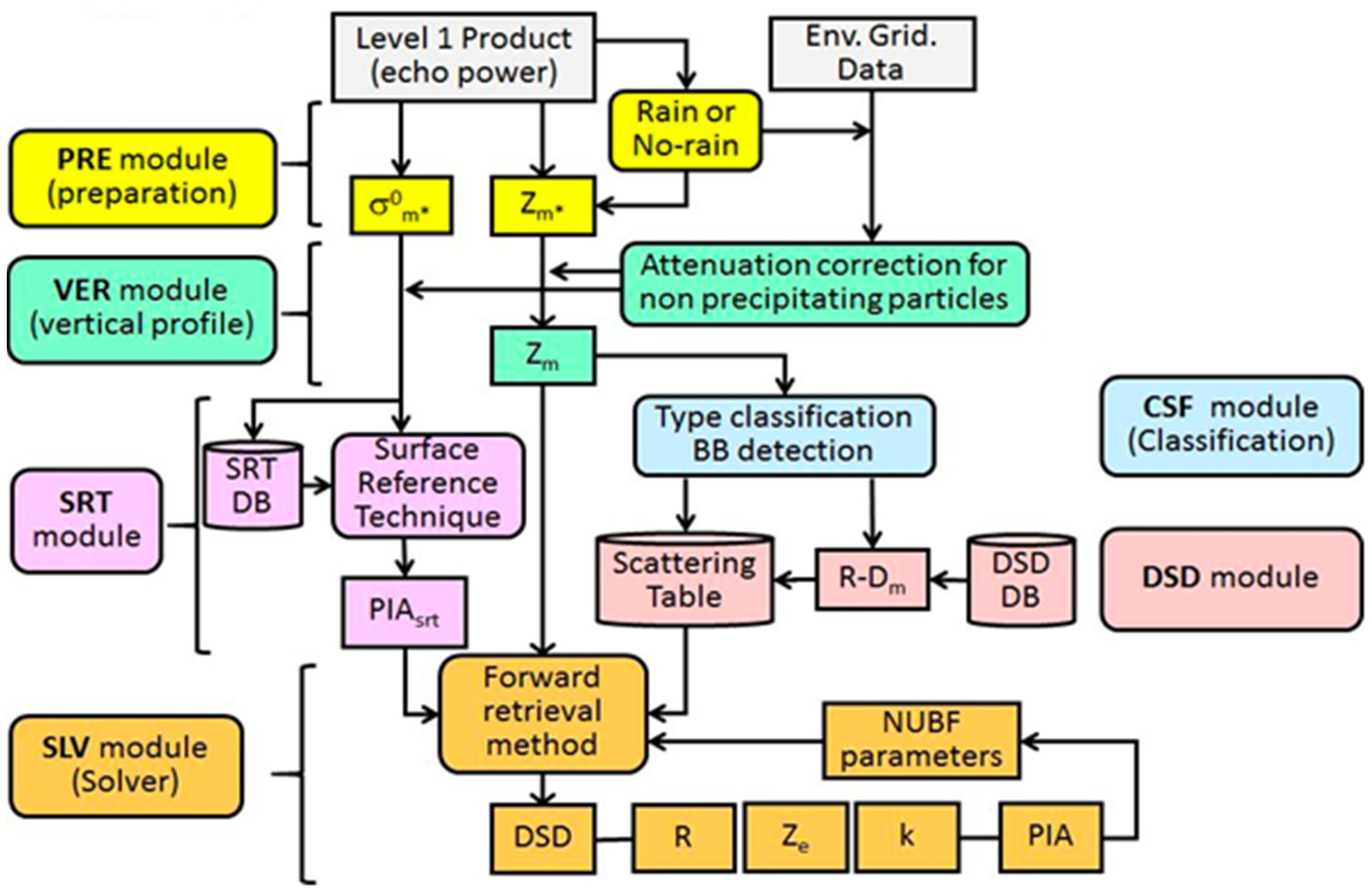
The architecture of the DPR level-2 algorithm has been detailed in [5]. It primarily consists of six modules, which are the preparation (PRE) module, vertical profile (VER) module, classification (CSF) module, DSD module, surface reference technique (SRT) module, and solver (SLV) module. The schematic diagram in Figure 1 illustrates the algorithm flowchart documented in [5], which is generic and valid for both SF and DF algorithms, although the details within the individual modules might differ depending on whether SF or DF data are processed. The similarities and differences of the SF and DF algorithms are discussed in subsequent sections.

The primary tasks of the PRE module are to classify rain/no-rain pixels, convert the received power into measured radar reflectivities, and derive the surface normalized cross section (NRCS or ${\sigma }_m^0$). The module also includes the flags for snow- or ice-covered pixels or fields of view indicating areas covered by surface snow or sea ice, the surface range bin detected from the surface power, and the surface clutter-free bottom that represents the last range bin of the down-looking radar in which the signal is uncontaminated by the surface clutter. A routine, built on the statistical relationship between the NRCS and sidelobe power obtained in the absence of rain [6,7], is implemented to mitigate the sidelobe effects of radar antenna. The main functions of the VER module are to provide vertical profiles of environmental parameters such as pressure, temperature, water vapor, and cloud liquid water by ingesting the ancillary environmental data provided by the Japan Meteorological Agency (JMA) Global Analysis (GANAL) product. From these data, the attenuations resulting from the nonprecipitating particles, such as water vapor, molecular oxygen, and cloud liquid water, are used to correct the measured reflectivities for these atmospheric components [8].

The CSF module is designed to classify precipitation into one of several categories such as stratiform and convective precipitation, as well as precipitation that is neither stratiform nor convective. Because the release of latent heat during the formation of precipitation is strongly related to rain type [9] and also because the hydrometeor melting model depends on precipitation type, this classification is important not only for the DPR algorithm but also for applications to atmospheric circulation and weather prediction models. In addition to the rain classification, the CSF module provides information on the bright-band characteristics such as the bright-band top, peak, and bottom ranges. The flags associated with the heavy ice precipitation, the anvil cloud, the surface snow, and the graupel and hail are also provided [10,11,12,13,14].

The role of the DSD module is to provide the particle size distribution models that are employed in the algorithm for different phase hydrometeors, including rain, mixed-phased, and frozen particles. Mass densities, dielectric constants, and fall velocities of the particles are also specified in the module. For the DPR algorithm, the rain drop size distribution is assumed to follow the gamma distribution with a fixed shape factor (μ) of three. The mixed-phase and frozen particle size distributions are prescribed in liquid space, in which the liquid equivalent (or melted) diameters are used to express the frozen/mixed-phase PSD. The conversion of frozen/mixed-phase PSD to the rain space is made by maintaining the same mass flux between the frozen/mixed-phase (P) and liquid phase (R). Mathematically, it is expressed by the equation: N_p(D)V_p(D) = N_R(D)V_R(D), where D is the liquid equivalent diameter. N_p(D)/N_R(D) and V_p(D)/V_R(D) are the frozen or mixed-phase particle/raindrop size distribution and fall velocity, respectively. The DPR algorithm relies on an adjustable R-D_m relationship in solving radar equations to constrain the DSD estimates. The adjustment parameter ε in the R-D_m relation follows the log-normal distribution and is determined by a series of constraint equations [15,16,17]. The means and standard deviations of ε obtained from the DF algorithm are averaged monthly in 5-by-5-degree (longitude and latitude) grid boxes, and then, stored in the DSD database used primarily as a constraint in the SF algorithms.

The primary purpose of the SRT module is to estimate path integrated attenuation (PIA) using the surface returns. This assumes that differences of measurements of the normalized radar cross section of the surface (NRCS) between the rain and rain-free areas are attributed to the PIA. Because of the variability in the NRCS measurements caused by changes in wind speed and direction over the ocean as well as rapidly changing surface condition over the land, the accuracy of the PIA estimates depends on the variance of the rain-free NRCS. The reliability factor, defined as the ratio of PIA to the standard deviation of the NRCS in a rain-free area, indicates the goodness of the estimates. To build the reference data of no-rain NRCS, two approaches are taken. One is to average rain-free NRCS in the proximity of the rain area; this reference database is then applied to the rain area to estimate the PIA. The second method is to obtain the reference NRCS in the area during times when rain is absent. This reference database is applied to the same area to estimate the PIA in the presence of rain. Because of the way the reference data are created, the first approach is called the spatial reference method, while the second approach is called the temporal reference [18,19]. For the Ku- and Ka-band dual-frequency measurements, the difference of NRCS between the Ku- and Ka-band can serve as additional reference. Considering that the rain-free NRCS can be averaged before or after the rain pixels (where the PIA is estimated) along the satellite track and also considering that, over ocean, an additional reference estimate can be generated from a quadratic fit of the NRCS over the angle bins over the cross-track swath, which, as in the case of the along-track reference, can be conducted before and after the rain pixels, the SRT module arrives at four PIA spatial reference estimates. Over land, the cross-track estimates are unreliable; therefore, only the along-track reference data are used. Adding the temporal reference gives five reference data points over ocean and three data reference points over land. These estimates are combined into an effective PIA estimate by weighting the individual estimates by a factor that is inversely proportional to the variance of the reference estimate.

Exactly the same considerations apply to the differential estimates that are formed from the difference between the NRCS at the two frequencies. An advantage of the differential approach is that the variance of the rain-free reference estimate is typically smaller than the single-frequency counterpart because of the high correlations between the rain-free NRCS at the two frequencies. This lower variance translates into more accurate estimates of differential path attenuation and plays an important role in constraining solutions to the radar equations.

One other approach to improve the accuracy of path attenuation estimates, especially when only the Ku-band data are used, is to combine the SRT with the Hitschfeld–Bordan (HB) method [20]. The methods are complementary in the sense that HB works well for light rain rates and the SRT works well for heavier rain rates. As in the SRT, the weighting factors of the SRT and HB are taken to be inversely proportional to variance of each method.

The solver module aims to retrieve the DSD, precipitation rate, and other physical parameters by solving the radar equations recursively along range profiles using measured reflectivity profiles and information provided by other modules such as rain types and PIA. Since the DPR algorithm makes use of the adjustable R-D_m relation, the core of the algorithm is to find the ε that minimizes a predefined cost function. In Section 2, the basic principles of the retrieval method, as described in [16,17], are reviewed. In Section 3, an assessment is presented of the accuracy of the DPR rain-retrieval algorithm, as described in [17]. New findings related to an evaluation of the DPR snow retrieval are also included in Section 3. A review of the strengths and weaknesses of some of the many ground validation studies is given in Section 4 followed by the summary in Section 5.

2. DPR Algorithm

The GPM DPR algorithm takes on an approach similar to that of the TRMM PR retrieval. In the TRMM PR retrieval, the coefficient of the k-Z relation (where k is specific attenuation and Z is radar reflectivity factor) is modified by a multiplicative factor, ε. This ε is adjusted so that the path attenuation, as derived from the HB equation, matches that obtained from an independent PIA constraint such as the SRT described above [21,22]. Instead of an explicit use of the k-Z relation, the DPR method makes use of the R-D_m relation and modifies it by a similar kind of adjustment parameter as defined in the k-Z relation [16]. The general form of the R-D_m relation, as transformed from the k-Z relation, can be expressed in the following form:

$$\mathrm{R}={\mathsf{\epsilon }}^{\mathsf{\tau }}{\mathrm{aD}}_{\mathrm{m}}^{\mathrm{b}}$$

(1)

where a, b, and τ are constants. For the Version 6 algorithm, these values are 0.401, 6.131, and 4.649 for stratiform rain and 1.370, 5.420, and 4.258 for convective rain, respectively. These are equivalent to the k-Z relation, $\mathrm{k}={\mathsf{\epsilon }\mathsf{\alpha }\mathrm{Z}}^{\mathsf{\beta }}$, where α = 0.000282 and β = 0.7923 for stratiform rain and α = 0.000411 and β = 0.7713 for convective rain at Ku-band, obtained from the DSD measurements in Tropics [23]. Note that in Version 7, the coefficients of (1) are set to the case of stratiform rain. One of the reasons for employing the R-D_m relation rather than the k-Z relation is to establish a constraint equation that is independent of frequency and can be applied to the Ku- and Ka-band measurements to preserve uniformity of the retrieval methods across different frequencies. It should be noted that in Version 6 of the algorithm, a single adjustment is made to the R-D_m relation, i.e., a single range-independent ε is used for each profile.

The assumed gamma DSD, N(D) (m⁻³ mm⁻¹), is expressed by:

$$\mathrm{N}\left(\mathrm{D}\right)={\mathrm{N}}_{\mathrm{w}}\mathrm{f}\left(\mathsf{\mu }\right){\left(\frac{\mathrm{D}}{{\mathrm{D}}_{\mathrm{m}}}\right)}^{\mathsf{\mu }}\exp \left(-\mathsf{\Lambda }\mathrm{D}\right)$$

(2)

$$\mathrm{f}\left(\mathsf{\mu }\right)=\frac{6{(4+\mathsf{\mu })}^{\mathsf{\mu }+1}}{4^4\mathsf{\Gamma }\left(\mathsf{\mu }+4\right)}$$

(3)

$$\mathsf{\Lambda }=\left(4+\mathsf{\mu }\right)/{\mathrm{D}}_{\mathrm{m}}$$

(4)

$${\mathrm{D}}_{\mathrm{m}}=\frac{{{\displaystyle \int }}_0^{\infty }\mathrm{N}\left(\mathrm{D}\right){\mathrm{D}}^4\mathrm{dD}}{{{\displaystyle \int }}_0^{\infty }\mathrm{N}\left(\mathrm{D}\right){\mathrm{D}}^3\mathrm{dD}}$$

(5)

$${\mathrm{N}}_{\mathrm{w}}=\frac{4^4}{{\mathsf{\pi }\mathsf{\rho }}_{\mathrm{w}}}\left(\frac{\mathrm{LWC}}{{\mathrm{D}}_{\mathrm{m}}^4}\right)$$

(6)

where N_w (m⁻³ mm⁻¹) is the normalized intercept, μ is the shape parameter, ρ_w is the water density equal to 1 g cm⁻³, and LWC is the liquid water content (g m⁻³). Γ is the gamma function. From (2)–(6), R is expressed as:

$$\mathrm{R}={\mathrm{N}}_{\mathrm{w}}{\mathrm{I}}_{\mathrm{R}}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu }\right)$$

(7)

$${\mathrm{I}}_{\mathrm{R}}=6\mathsf{\pi }\times {10}^{-4}{{\displaystyle \int }}_0^{\infty }\mathrm{f}\left(\mathsf{\mu }\right)\left(\frac{\mathrm{D}}{{\mathrm{D}}_{\mathrm{m}}}\right)\exp \left(-\mathsf{\Lambda }\mathrm{D}\right){\mathrm{D}}^3\mathrm{V}\left(\mathrm{D}\right)\mathrm{dD}$$

(8)

where I_R (mm² m³ h⁻¹) is the N_w-normalized rain rate, and V(D) (m s⁻¹) is raindrop fall velocity as a function of D. Equating (1), (7) and (8) yields:

$${\mathrm{N}}_{\mathrm{w}}=\frac{{\mathsf{\epsilon }}^{\mathsf{\tau }}{\mathrm{aD}}_{\mathrm{m}}^{\mathrm{b}}}{{\mathrm{I}}_{\mathrm{R}}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu }\right)}$$

(9)

From (2)–(6), the radar reflectivity factor, Z_λ in dBZ, at a wavelength λ (mm) is written as:

$${\mathrm{Z}}_{\mathsf{\lambda }}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu }\right)=10{\log }_{10}\left({\mathrm{N}}_{\mathrm{w}}\right)+{\mathrm{I}}_{\mathrm{b}}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu },\mathsf{\lambda }\right)$$

(10)

$${\mathrm{I}}_{\mathrm{b}}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu },\mathsf{\lambda }\right)=10{\log }_{10}\left(\frac{{\mathsf{\lambda }}^4}{{\mathsf{\pi }}^5{\left|{\mathrm{K}}_{\mathrm{w}}\right|}^2}{{\displaystyle \int }}_0^{\infty }\mathrm{f}\left(\mathsf{\mu }\right)\left(\frac{\mathrm{D}}{{\mathrm{D}}_{\mathrm{m}}}\right)\exp \left(-\mathsf{\Lambda }\mathrm{D}\right){\mathsf{\sigma }}_{\mathrm{b}}\left(\mathrm{D},\mathsf{\lambda }\right)\mathrm{dD}\right)$$

(11)

where I_b is the N_w-normalized radar reflectivity in log₁₀(mm⁷) and σ_b(D,λ) is the radar backscattering cross section in mm². The dielectric factor K_w is related to the complex refractive index of water. |K_w|² is taken to be 0.9255 and 0.8989 for Ku- and Ka-band, respectively [5]. Substituting (9) into (10), we obtain:

$${\mathrm{Z}}_{\mathsf{\lambda }}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu }\right)=10{\log }_{10}({\mathsf{\epsilon }}^{\mathsf{\tau }}\mathrm{a})+10{\mathrm{blog}}_{10}\left({\mathrm{D}}_{\mathrm{m}}\right)-10{\log }_{10}\left({\mathrm{I}}_{\mathrm{R}}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu }\right)\right)+{\mathrm{I}}_{\mathrm{b}}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu },\mathsf{\lambda }\right)$$

(12)

A fixed μ of 3 is assumed for the DPR algorithm [16,17,24,25]. Recalling that a and b are storm-type dependent constants, thus, Equation (12) provides a relationship between Z_Ku/Z_Ka and D_m, i.e., Z_Ku/Z_Ka-D_m relation with ε as a parameter. It is shown that Z_Ku/Z_Ka is uniquely related to D_m for a given ε [17]. Once ε is known, D_m can be solved from (12), and then, N_w is obtained from D_m and either Z_Ku or Z_Ka from (10). With N_w and D_m, the specific attenuations at both Ku and Ka bands, k_λ in dB/km (λ = Ku or Ka), are computed by:

$${\mathrm{k}}_{\mathsf{\lambda }}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu }\right)={\mathrm{N}}_{\mathrm{w}}{\mathrm{I}}_{\mathrm{e}}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu },\mathsf{\lambda }\right)$$

(13)

$${\mathrm{I}}_{\mathrm{e}}\left({\mathrm{D}}_{\mathrm{m}},\mathsf{\mu },\mathsf{\lambda }\right)=4.343\times {10}^{-3}{{\displaystyle \int }}_0^{\infty }\mathrm{f}\left(\mathsf{\mu }\right)\left(\frac{\mathrm{D}}{{\mathrm{D}}_{\mathrm{m}}}\right)\exp \left(-\mathsf{\Lambda }\mathrm{D}\right){\mathsf{\sigma }}_{\mathrm{e}}\left(\mathrm{D},\mathsf{\lambda }\right)\mathrm{dD}$$

(14)

where I_e is the N_w-normalized specific attenuation in mm³ km, and σ_e(D,λ) is the extinction cross section in mm². A recursive forward procedure is applied for the DPR algorithm that starts at storm top and proceeds downward gate-by-gate along the profile from storm top towards the surface until reaching the lowest gate unaffected by the surface clutter.

The equations above constitute the basic DPR algorithm, which is valid for both SF and DF methods. The equations expressed for radar reflectivity factor and specific attenuation are generic and apply to hydrometeors with different phases such as rain, mixed phase, and snow particles. The liquid-equivalent quantities such as particle diameter and mass-weighted diameter, as well as precipitation rate are used across different hydrometeor phase states. A spherical shape is assumed for the scattering computations of snow, mixed phase, and rain particles. A simple scattering model that assumes constant mass density throughout all the particle sizes (independent of particle size) is adopted to compute snow scattering characteristics [5,16]. An effective mixing formula is used in obtaining the dielectric constant of melting snow. A no-breakup and no-coalescence melting layer model is applied to obtain the water fraction of individual melting particles [26].

Once the final R-D_m relationship or ε is determined, the DSD and R can be derived from the Ku-/Ka-band measured reflectivities with the forward recursive procedure. A proper ε leads to better accuracy in the retrieval, therefore, finding the best ε is crucial from the perspective of the DPR algorithm. To determine ε, an optimization method is employed, which has been comprehensively described by [5,16,17]. The procedure is described as follows: Beginning with a series of ε (for example, K values) and letting them be equally spaced in log₁₀(ε_k) (k = 1, 2, …, K), each ε_k corresponds to unique R-D_m and Z_λ-D_m relations as expressed in (1) and (12), respectively, and then, the DSD and R profiles are obtained for each ε_k. D_m is first derived from attenuation-corrected Z_λ using the Z_λ-D_m relation that corresponds to ε_k; N_w follows from D_m and Z_Ku. This gate-by-gate retrieval process continues until reaching the final gate which, in practice, is the gate nearest the surface that is uncorrupted by surface clutter. From the estimated DSD profile, the apparent and attenuation-corrected Ku-/Ka-band reflectivity profile and associated PIA and δPIA can be computed. This procedure is repeated for the K values of ε. The final ε, denoted by ε_f, is chosen as that which minimizes the cost function p, which is the sum of p₁, p₂, and p₃ for the DF algorithm given by the following equations:

$$\mathrm{p}\left({\mathsf{\epsilon }}_{\mathrm{f}}\right)=\min \left({\mathrm{p}}_1\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)+{\mathrm{p}}_2\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)+{\mathrm{p}}_3\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)\right)$$

(15)

$${\mathrm{p}}_1\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)=\frac{{({\log }_{10}{\mathsf{\epsilon }}_{\mathrm{k}})}^2}{{\mathsf{\sigma }}_1^2}$$

(16)

$${\mathrm{p}}_2\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)=\frac{{(\mathsf{\delta }\mathrm{PIA}\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)-{\mathsf{\delta }\mathrm{PIA}}_{\mathrm{SRT}})}^2}{{\mathsf{\sigma }}_2^2}$$

(17)

$${\mathrm{p}}_3\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)=\frac{1}{{\mathsf{\sigma }}_3^2}{\displaystyle \sum }_{\mathrm{n}=1}^{\mathrm{N}}{({\mathrm{Z}}_{\mathrm{m},\mathrm{n},\mathrm{est}}^{\left(\mathrm{Ka}\right)}\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)-{\mathrm{Z}}_{\mathrm{m},\mathrm{n},\mathrm{obs}}^{\left(\mathrm{Ka}\right)})}^2$$

(18)

where N is the total number of range gates in the column. δPIA(ε_k) is the simulated differential PIA when ε in (1) is replaced by ε_k. δPIA_SRT is the differential PIA estimated by the surface reference technique (SRT) [19]. ${\mathrm{Z}}_{\mathrm{m},\mathrm{n},\mathrm{est}}^{\left(\mathrm{Ka}\right)}\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)$ and ${\mathrm{Z}}_{\mathrm{m},\mathrm{n},\mathrm{obs}}^{\left(\mathrm{Ka}\right)}$ are the simulated apparent and measured Ka-band radar reflectivities in dBZ at the nth range bin, respectively. σ₁, σ₂, and σ₃ are considered to be the weighting factors. σ₁ is chosen to be the standard deviation of the distribution of log₁₀(ε) equal to 0.146 for stratiform and 0.113 for convective, obtained from the measured DSD data. σ₂ is the standard deviation of δPIA estimated by the SRT, while σ₃ is determined by running simulation tests that yield the best overall retrieval accuracy. It should be noted that the DF is applied only for the range bins in which both the Ku- and Ka-band measured reflectivities exceed their minimum detectable thresholds. The Ku-band serves as the primary frequency whose reflectivities lead to the estimates of D_m, as in (12). The Ka-band reflectivity profile, however, plays a role in the selection of ε as indicated in (18). It is important to point out that the DSDs, derived from the DF for a given ε, are always the solutions of the Ku-band radar equations. They are, however, not necessarily the solutions of the Ka-band radar equations, as the Ka-band equations are not the governing equations for the retrieval, and enter into the results only as one of the three constraint equations that determine ε. There is an advantage of choosing δPIA over PIA in (17) because of the fact that the error standard deviation of δPIA is usually much smaller than that of the PIA estimated by the SRT, as a result of the strong correlation of the normalized surface cross section (σ⁰) between Ku- and Ka-band [18]. The final solutions of the DSD and R profiles are those that correspond to ε_f.

The cost function p for the SF algorithm is similar to the DF but comprises only two constraint equations p₁ and p₂ as given below:

$$\mathrm{p}\left({\mathsf{\epsilon }}_{\mathrm{f}}\right)=\min \left({\mathrm{p}}_1\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)+{\mathrm{p}}_2\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)\right)$$

(19)

$${\mathrm{p}}_1\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)=\frac{{({\log }_{10}{\mathsf{\epsilon }}_{\mathrm{k}}-{\mathsf{\mu }}_{\mathsf{\epsilon }})}^2}{{\mathsf{\sigma }}_1^2}$$

(20)

$${\mathrm{p}}_2\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)=\frac{{(\mathrm{PIA}\left({\mathsf{\epsilon }}_{\mathrm{k}}\right)-{\mathrm{PIA}}_{\mathrm{SRT}})}^2}{{\mathsf{\sigma }}_2^2}$$

(21)

The final ε or ε_f is chosen by minimizing the sum of p₁ and p₂, which is similar to the DF method. The function p₁ in (20) is similar to that in (16) but it includes the mean value (μ_ε) of ${\log }_{10}\mathsf{\epsilon }$ provided by the DSD database. Instead of the δPIA in (17), the single-wavelength PIA is used in (21). Because the DF has one additional constraint resulting from the 2nd frequency and a more stringent constraint in the form of the δPIA, it provides better accuracy even though the SF and DF approaches are described by the same set of equations given by (1)–(14). The inclusion of μ_ε in (20) is intended to improve the consistency between the SF and DF retrievals as μ_ε is derived from the DF and averaged each month over a 5-by-5-degree latitude/longitude grid.

3. Evaluation of DPR Algorithms

To assess performance of the GPM DPR algorithms and to gain insight into ways to improve the retrievals, a physical evaluation of the methods is required. To achieve this, measured DSD/PSD data acquired from a variety of storm systems during several NASA field campaigns are employed to construct hydrometeor profiles. The measured DSD/PSD spectra are used to compute parameters of the radar and hydrometeors, which include true and measured radar reflectivities, rain attenuation, precipitation rate, and characteristic parameters of DSD. These hydrometeor parameters are taken as true values, while the simulated measured reflectivities serve as inputs to the retrieval algorithms. Thus, the degree to which the radar estimates based on the DSD/PSD-simulated reflectivities agree with the true values directly derived from the DSD/PSD enables a quantification of the retrieval accuracy.

3.1. Rain Estimates

DPR rain and DSD estimates have been comprehensively assessed through DSD-based simulation studies [17] that focused primarily on examination of the methodology and roles of various constraints in the determination of ε_f, aimed at addressing several critical issues that included: (1) How does the non-uniformity of rain profile affect the retrieval accuracy?; (2) How sensitive are the DPR estimates to the initial R-D_m relations?/(3) What roles do the individual constraints play in the retrieval solutions and how do they respond to column-averaged rain rate? (4) How is the retrieval accuracy affected by the δPIA error? In these studies, the DSD profiles were constructed by aligning one-minute time-series DSD spectra to the range gates, consecutively, from top to bottom of the column. The generated profiles, typically non-uniform, were found to statistically resemble realistic profiles in the sense that the spatial correlations of the profiles were in reasonable agreement with those found from the studies reported by Adirosi et al. [27]. The surface model characterizing PIA and δPIA uncertainties was assumed to follow an unbiased Gaussian distribution with standard deviations similar to the DPR observation over the ocean. To better understand the general performance of DPR for rain estimation, below, we summarize several important results based on the studies conducted by Liao et al. [17].

Overall, the DPR DF algorithm performs reasonably well from the storm top to the bottom yielding nearly unbiased estimates of averaged D_m when they are applied to the rain profiles comprising the time-series DSDs. Biases and error variances of the estimated D_m are found to be generally well below 0.5 mm over the entire range of D_m. The rain rate estimates show strong correlations with their true values despite slight underestimations for light rain. Comparisons of the retrievals between the uniform and non-uniform profiles indicate that the assumption of single ε along the rain column gives rise to an increase in error in the estimation of D_m as the degree of non-uniformity increases. This increase in error is even more significant in the estimation of R. Because of the ε adjustment factor, the SF and DF estimates, particularly the DF estimates, are not highly sensitive to the initial choice of the R-D_m relation, and therefore, the retrievals eventually converge to nearly the same solution irrespective of the initial relationship. Moreover, because of the relatively strong constraint imposed by the DF algorithm as compared with the SF in the determination of ε_f, the retrievals of D_m and R from the DF are less dependent on the R-D_m relations than the SF algorithm. To illustrate how the SF and DF algorithms respond to the different R-D_m relations, we show an example of the comparisons between the estimated D_m and N_w as well as R and their respective true values from one DSD profile. In addition to the R-D_m relations adopted by the DPR or (1), two R-D_m relations are included. One is the R-D_m relation that is derived by using the DSD measurement data taken from a large number of the Parsivel disdrometers during several NASA-sponsored field campaigns such as the Iowa Flood Studies (IFloodS) field experiment from 1 May to 15 June 2013, the Integrated Precipitation Validation Experiment (IPHEx) from 1 May to 15 June 2014, and the observations at the NASA Wallops Flight Facility in Wallops Island, Virginia from 2013 to 2014. There are about a total of 170,000 1-min DSD spectra, resulting in an R-D_m regression equation as $\mathrm{R}=0.469{\mathsf{\epsilon }}^{2.403}{\mathrm{D}}_{\mathrm{m}}^{3.002}$. Another is the fitting equation obtained from the gamma DSD model, which is described below.

The fall velocity of rain can be approximately expressed by a power law, such as one, $\mathrm{V}\left(\mathrm{D}\right)=3.78{\mathrm{D}}^{0.67}$, documented by Atlas and Ulbrich [28], from which R in (7) can be rewritten as:

$$\mathrm{R}=1.67\times {10}^{-4}{\mathrm{N}}_{\mathrm{w}}\frac{\mathsf{\Gamma }\left(\mathsf{\mu }+4.67\right)}{{\left(\mathsf{\mu }+4\right)}^{0.67}\mathsf{\Gamma }\left(\mathsf{\mu }+4\right)}{\mathrm{D}}_{\mathrm{m}}^{4.67}$$

(22)

An analysis of the above equation reveals that R changes slowly with μ. This is illustrated by following examples that give (22) at a few μ values: $\mathrm{R}=1.63\times {10}^{-4}{\mathrm{N}}_{\mathrm{w}}{\mathrm{D}}_{\mathrm{m}}^{4.67}$ at μ = 0, $\mathrm{R}=1.64\times {10}^{-4}{\mathrm{N}}_{\mathrm{w}}{\mathrm{D}}_{\mathrm{m}}^{4.67}$ at μ = 3, and $\mathrm{R}=1.65\times {10}^{-4}{\mathrm{N}}_{\mathrm{w}}{\mathrm{D}}_{\mathrm{m}}^{4.67}$ at μ = 6. Thus, a power-law regression is applied to obtain the fitting equation of R/N_w and D_m from the data generated by the gamma DSD from a range of μ. A study by Liao et al. [28] reported that the R-D_m fitting equation, derived from the gamma DSD data, could be given by:

$$\mathrm{R}={\mathrm{aN}}_{\mathrm{w}}{\mathrm{D}}_{\mathrm{m}}^{\mathrm{b}}$$

(23)

where $\mathrm{a}=1.588\times {10}^{-4}$, $\mathrm{b}=4.706$. It should be noted that the coefficients a and b of (11) are obtained based on the fall velocity that follows Lhermitte’s equation [29] rather than that given by Atlas and Ulbrich [28]. These two fall velocity equations are very similar, however, with (23), a modification of the R-D_m approach is a procedure to adjust N_w. As is the case with ε for the DPR algorithm, a constant N_w is assumed in the column.

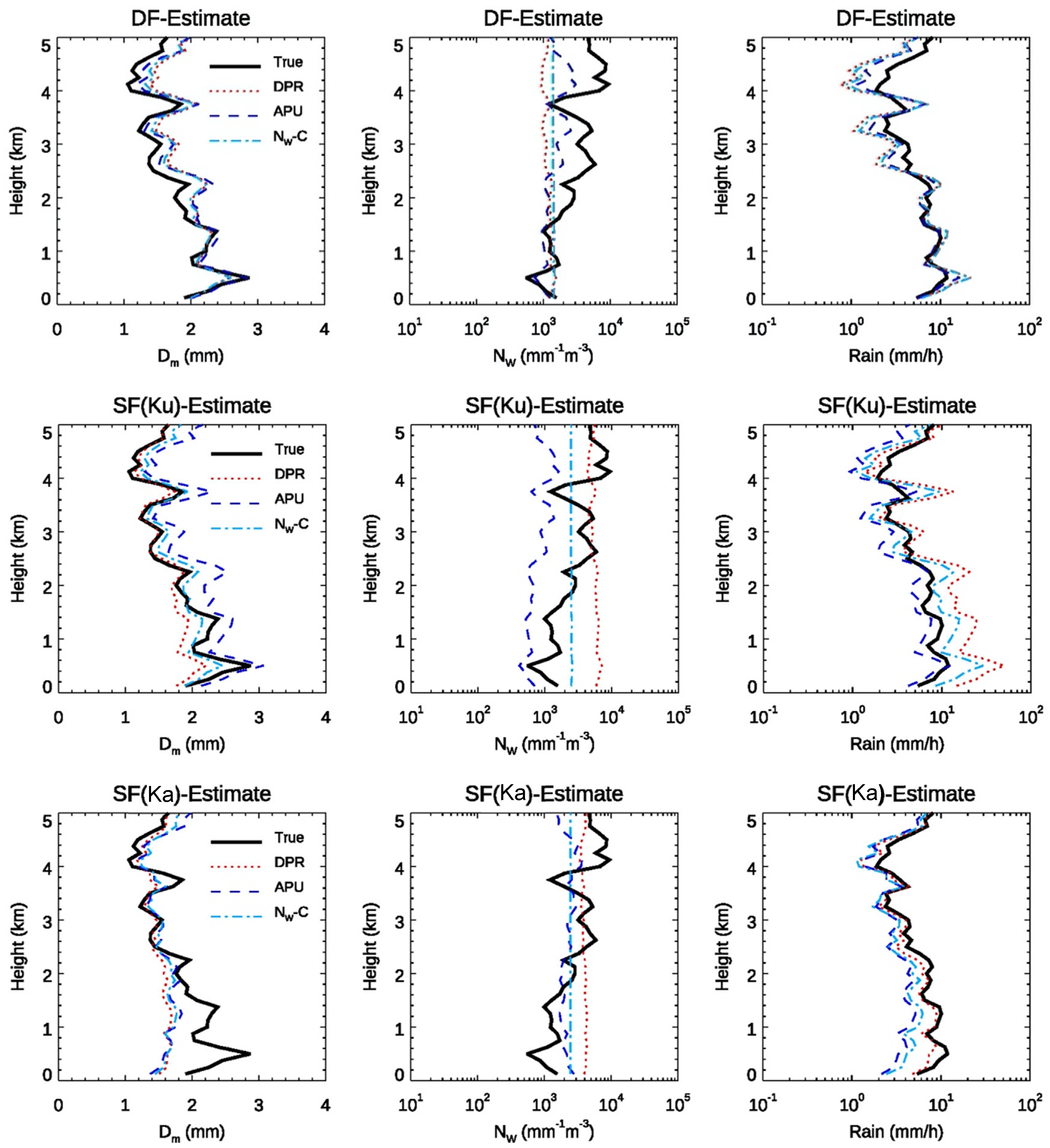
Shown in Figure 2 is an example of the estimates of D_m (left column), N_w (middle column), and R (right column) from the DF (top row) and SF Ku- (middle row) and Ka-band (bottom row) algorithms with respect to three R-D_m relations. It is worth noting that although these results are shown only for one profile, they resemble common features appearing in most of the data. The thick solid black lines represent the true values (denoted by “True”), directly computed from the DSD spectra. The R-D_m relations involved in comparisons include nominal DPR relation (red dotted curves, denoted by “DPR”), the DSD data regression (blue dashed lines, denoted by “APU”), and the fitting equation obtained from the gamma DSD model (light blue dash-dotted lines, denoted by N_w-C). On the one hand, it is apparent that D_m and R from the DF (top row) are nearly invariant with respect to the initial R-D_m assumption and correlated well with their true values. The SF results, on the other hand, deviate to some extent from these three R-D_m relations with the SF Ku-band appearing more variable than its counterpart (Ka-band). It is evident that none of the N_w results from these R-D_m relations capture natural variation of the N_w profile. Instead, they look more like mean values of the true profile, exhibiting much less variation in the column resulting from vertically unchanged ε or N_w assumption. As expected, the results of N_w from the N_w-C are constant along the column, as N_w is a constant adjustable factor and invariant in the column. The D_m and R estimates for the DF are effectively independent of the initial R-D_m relationship. For the SF, the D_m and R estimates are only weakly dependent on the initial R-D_m relationship. These features, in practice, are a significant benefit for the retrieval considering the large variability of the R-D_m relationship [30].

The constraints expressed in (15)–(21) for the DF and SF algorithms play a crucial role in finding the best adjustment factor. However, the relative strength of each individual constraint, p₁, p₂, and p₃, to the solutions depends on rain intensity; p₁ imposes a constraint that is relatively independent of the rain rate whereas p₂ and p₃ impose a weak constraint for light rain and stronger constraint for heavy rain. This behavior implies that the combination of the individual constraints constitutes a stronger constraint for heavy rain than for light rain with the strength level being in between for moderate rain. In addition, the accuracy of the PIA and δPIA is also key in searching for the correct ε, which is also true for μ_e in the SF algorithm.

As described previously, the SF and DF algorithms share the same methodology in estimating DSD and R; however, the difference lies in the constraints that are used to find the best ε [16]. Having modeled the PIA and δPIA with use of statistical properties found in the DPR long-term observation [19], the D_m and R estimated by the SF Ku- and Ka-band as well as DF algorithms indicate that the DF consistently provides more accurate estimates than either of the Ku- and Ka-band SF retrievals. For relatively large D_m, the estimates of D_m from the SF not only show a higher degree of uncertainty but also larger biases than the DF. The Ka-band rain retrieval exhibits good accuracy for moderate-to-heavy rains at the storm top where attenuation is insignificant. It deteriorates rapidly as the retrieval moves toward the surface because of accumulated errors caused by inaccurate attenuation correction. The fact that the DF provides better estimates of D_m and R than the SF consistently throughout the column comes as no surprise as the DF provides additional and more accurate constraints on the solutions.

3.2. Snow Estimates

As described previously, the DPR algorithm uses the same R-D_m relation for both the rain and snow retrievals. The adjustment factor ε in the R-D_m relation is determined by two/three constraint equations for the SF/DF algorithms. Among these constraints, the PIA/δPIA play an important role in choosing the best ε or ε_f. As the attenuation from dry snow is negligibly small at both Ku- and Ka-band, the PIA is almost entirely caused by rain and mixed-phase hydrometeors. The ε_f, to the extent that its selection is determined in part by the attenuation constraint, is chosen on the basis of the rain and mixed phase attenuation rather than that of snow. To physically evaluate the DPR performance in retrieving snow, an independent approach is required. For this reason, the standard dual-frequency technique is applied to compare its estimates with the DPR snow product. In subsequent sections, our discussion focuses on the snow scattering table, the dual-frequency technique, and assessment of the DPR snow estimates.

3.2.1. Scattering Table of Snow Particles

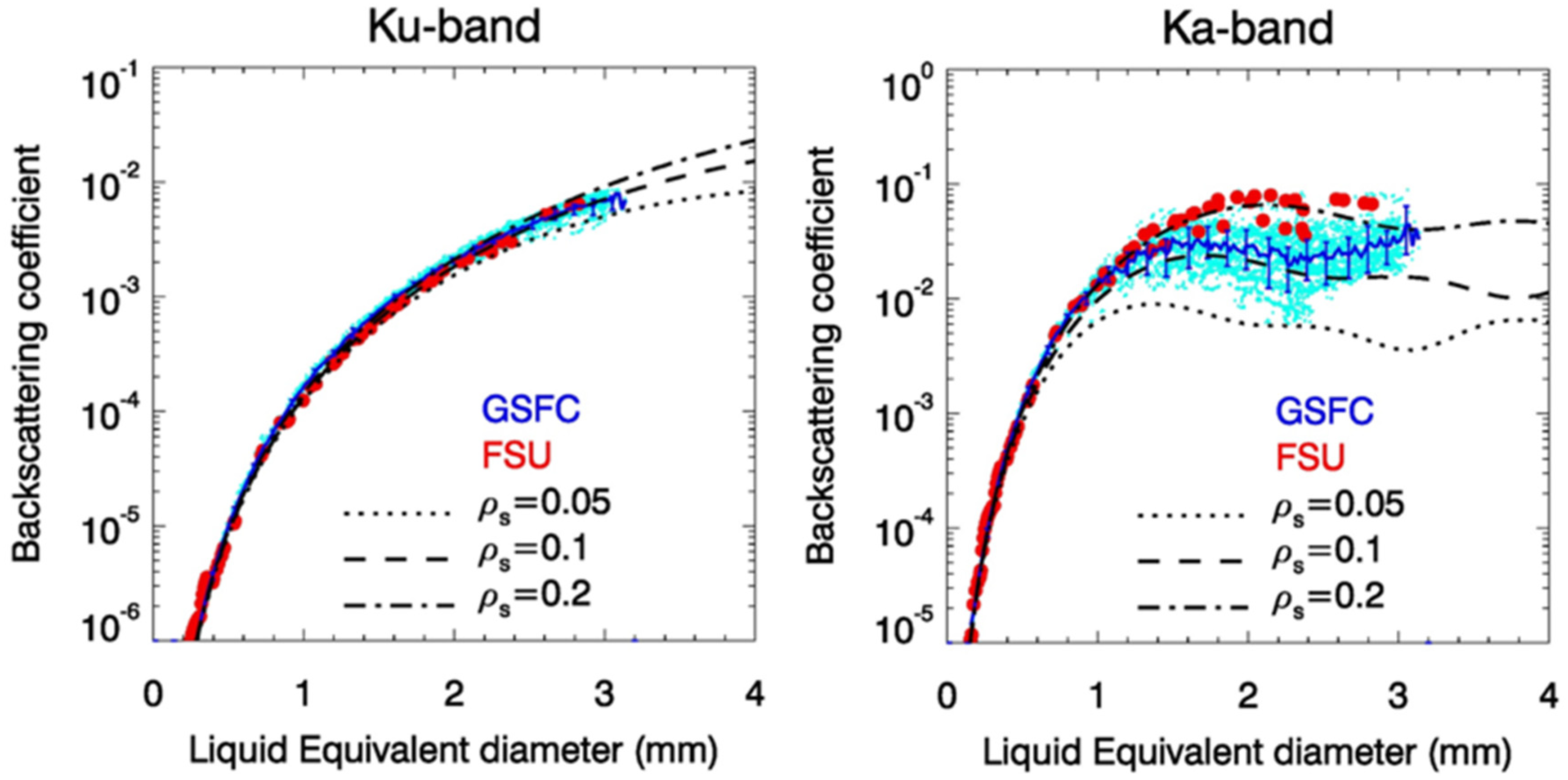
Because of the complexity and variability in the shape and structure of snowflakes, accurately characterizing the electric scattering properties is challenging. This is particularly true for radars that operate at frequencies beyond the Rayleigh scattering regime, such as at Ka-band and above. Instead of characterizing the fluctuations of the electric fields to account for changes in shapes and structures of snowflakes, the DPR relies on a simple spherical scattering model that approximately represents the mean electric fields of snow particles with various shapes when their masses are preserved. In Figure 3 an example of comparisons of the backscattering coefficients is illustrated, defined as the backscattering cross section normalized by liquid-equivalent spherical cross section, at Ku-band (left) and Ka-band (right) between the GSFC [31] and FSU [32,33] scattering database and a randomly oriented spheroidal scattering model. The results from the spheroidal model are computed from particles with an aspect ratio of 0.6. A constant mass density is assumed across all particle sizes with values of 0.05, 0.1, and 0.2 g/cm³ [34]. The scattering parameters are computed by using the T-matrix method [35]. As anticipated, little variation is found at Ku-band among different types of particles if their masses are preserved. This is because the scattering from these particles is approximately in the Rayleigh regime where the scattering properties depend primarily on particle mass rather than the detailed structure and shape. In contrast, the scattering results at Ka-band show large variations especially at diameters greater than 1 mm. This happens because the scattering from relatively electrically large particles enters the non-Rayleigh (or Mie) regime where the shapes and particle structure matter. Because of the significant increase in computing power and memory required and because of convergence issues for large particles, the largest liquid-equivalent diameters of the scattering data from both the GSFC and FSU databases are presently limited to around 3 mm. Although this particle size range covers many snow events, it may lead to truncation errors in estimates for heavy snowstorms in which particle sizes often exceed the database limits. In contrast, scattering computations from the spheroidal or spherical model using the T-matrix method or Mie solution are very efficient and applicable to nearly all particle sizes found in nature. It can be seen from Figure 3 that the FSU database follows well the spheroidal particle results with a density of 0.2 g/cm³. For the GSFC data, high variability in the backscattering results is found at Ka-band. Despite this, most of the results are bounded between curves representing particle densities of 0.1 and 0.2 g/cm³. Although the results shown in Figure 3 are from spheroids, the spherical model that the DPR adopts provides very similar scattering properties to those generated from the spheroidal model. A snow density of 0.1 g/cm³ is assumed for the DPR in obtaining the backscattering and extinction cross sections.

3.2.2. Standard Dual-Frequency Method

The standard dual-frequency technique has long been studied for snow retrieval [36,37,38,39,40,41,42,43,44]. This technique is based on the dual-frequency ratio (DFR), hereinafter referred to as the DFR method. Since the DFR is independent of the particle number concentration and depends solely on D_m for a given shape factor of the gamma PSD (μ), it provides a potential means to solve for the parameters of the PSD. An important advantage of the DFR method for snow retrieval is that the relationship between D_m and DFR is monotonic, and therefore, Dm can be uniquely inferred from DFR for a given scattering model. Consequently, the snow retrieval can be done at each range gate without the influence of the measurements at other range gates along the column. This contrasts with the operational DPR algorithm that relies on the PIA/δPIA and ε that are related to the attenuation and the dependence of the retrieval on rain properties along the column.

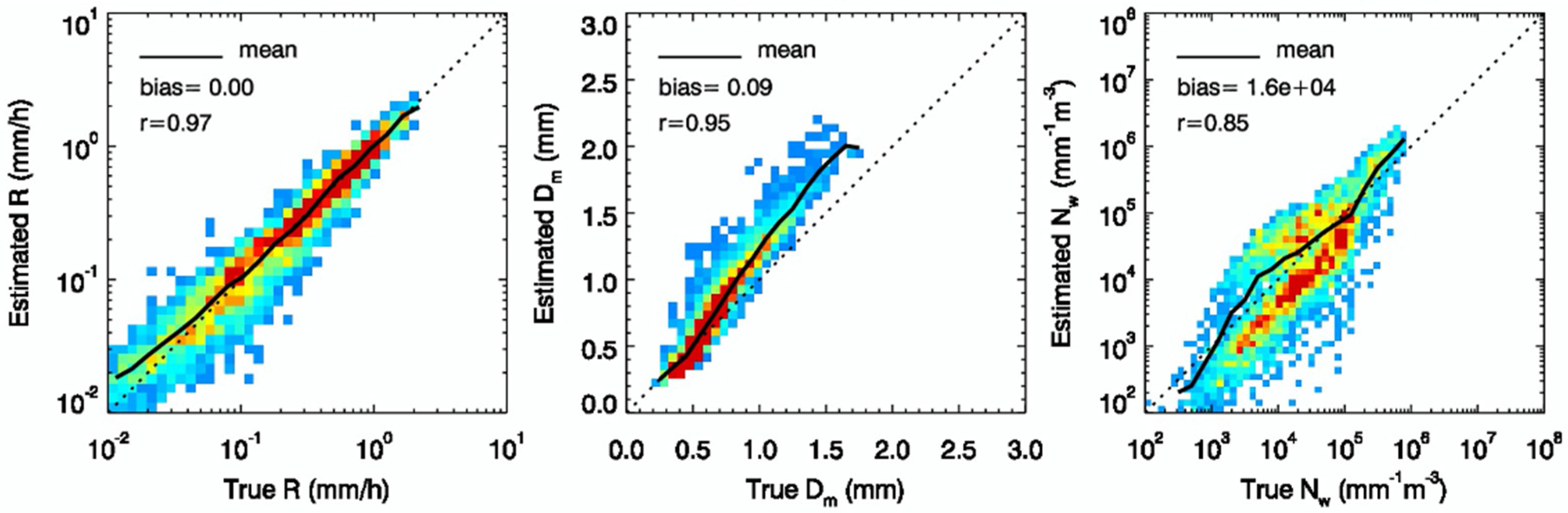
A recent study made by Liao et al. [42] indicated that the DFR could provide good estimates of the PSD and liquid equivalent snowfall rate. As shown in Figure 4, the snow parameters retrieved from the DFR are compared with the same quantities derived from the measured PSD spectra or truth. The color represents the value of two-dimensional probability density function (PDF) of the estimates (ordinate) and truth (abscissa) with the color scale provided in the bottom. The snow parameters involved in the comparisons include R (left), D_m (middle), and N_w (right). In this example, the scattering table is taken from a randomly oriented spheroidal particle model with a fixed density of 0.1 g/cm³, which is used both to simulate the radar reflectivities (inputs to the algorithm) and to infer the snow parameters. A μ = 3 gamma PSD model is assumed for the retrieval. The black solid curves represent means of the estimates in the bin sizes of the true values. The biases of the estimates as well as correlation coefficients (r) are given in each graph. For reference, the one-to-one relation is given by the black dotted line. It is not difficult to conclude that the snow parameters inferred by the DFR technique provide fairly accurate snow estimates. Very high correlations are found between the estimates and their truth. This is particularly true for the cases of R and D_m, in which their correlations are greater than 0.95. Generally, R is slightly overestimated at very light snow rates, but the bias remains relatively low as indicated by the bin-averaged means of the bias (black solid lines). The bias tends to decrease as R increases. The opposite trend is found for D_m, where the bias in D_m increases with an increase in D_m. However, the overall biases of both R and D_m are relatively small. N_w, unsurprisingly, shows large variability and biases. It is important to note that the results shown in Figure 4 do not account for the error caused by the uncertainties in the scattering table, since the same scattering table is used for generating the measured reflectivities and for the retrieval. Additional retrieval errors occur when the scattering table used for simulating the reflectivities differs from that for the retrieval [42].

3.2.3. Comparison of the DFR Retrieval with the DPR Product

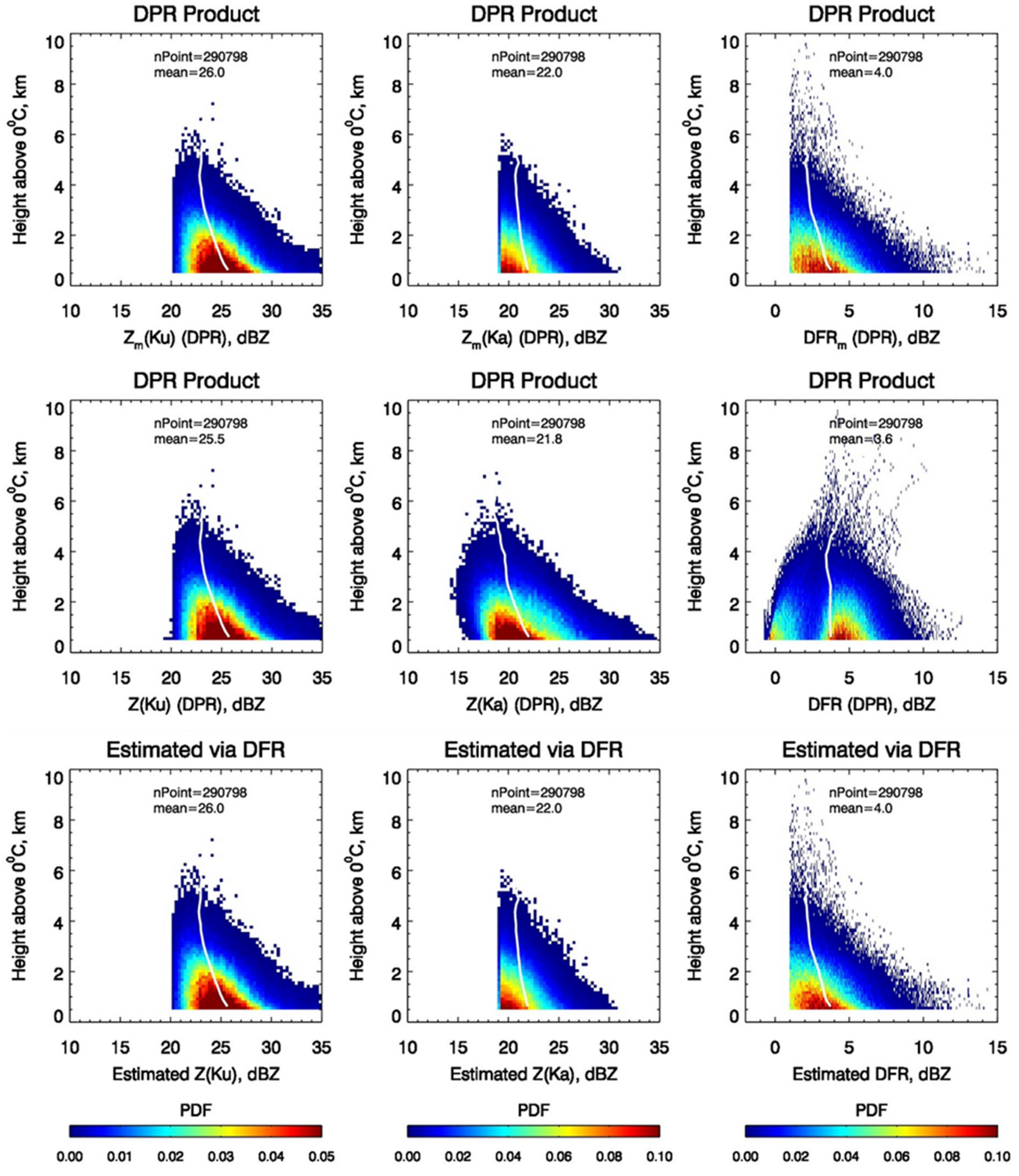
To compare the GPM DPR snow estimates, we take the DPR Version 6 dual-frequency one-day measurements (product, 2A.GPM.DPR) on 1 January 2020, which consist of data files from 16 orbits. The snow data are selected from stratiform storms at heights of 0.5 km or more above the freezing level so as to exclude liquid and mix-phased hydrometeors. Figure 5 displays the PDFs of the Ku- band (left column) and Ka-band (right column) reflectivities as well as DFR (right column) as a function of the height above 0 °C freezing level. The measured reflectivities and DFR from the DPR product are given in the top row, while the attenuation-corrected reflectivities and DFR obtained from the DPR algorithm and the DFR technique are given in the middle and bottom rows, respectively. The solid white lines represent the mean profiles. The total number of data points and their overall means are denoted by ”nPoint” and ”mean”, respectively. In the estimation of PSD using the DFR method, the forward recursion procedure is performed, starting from the storm top and moving downward gate-by-gate until reaching the last range gate (0.5 km above 0 °C level). The attenuations accumulated from previous range gates, which are in general very small for dry snow, are computed from the derived PSD, and then, are used to compensate the measured reflectivities for the attenuation. To conform with the DPR measurements, the thresholds consistent with the minimum detectable reflectivities of 15.46 and 19.18 dBZ at Ku- and Ka-band, respectively [4], are adopted for filtering the data. In other words, only the DPR data with measured reflectivities exceeding these thresholds are selected. It is anticipated that the attenuation-corrected reflectivities should be very close to their measured reflectivities owing to the fact that snow attenuations are small. This is the case for the DFR-based results, as the estimated Ku- and Ka-band reflectivities (bottom row) closely resemble the measured reflectivities (top row). This is not the case, however, for the DPR product since the Ka-band attenuation-corrected reflectivities deviate significantly from the measured reflectivities despite the fact that the Ku-band measured and corrected reflectivities look nearly identical. Moreover, many of the Ka-band corrected reflectivity data fall below the measured reflectivities. The approximate equality of the DPR Ku-band measured and corrected reflectivities can be understood from the fact that the Ku-band radar equation serves as a governing equation, and therefore, the DPR-derived PSDs are able to reproduce the Ku-band measurements. Unlike the Ku-band, the Ka-band measurements are used only as one of the constraints in the retrieval procedure and, as a consequence, the derived PSDs are not constrained to reproduce the Ka-band measured and corrected reflectivities. The implication of large departures of the corrected Ka-band reflectivities (simulated from the derived PSDs) from the actual measured reflectivities is that there are deficiencies in the snow retrieval with the current operational algorithm. The constant ε assumed throughout the column is likely the culprit as the determination of ε is heavily affected by rain and melting snow rather than by the snow alone because of the use of the PIA/δPIA constraint.

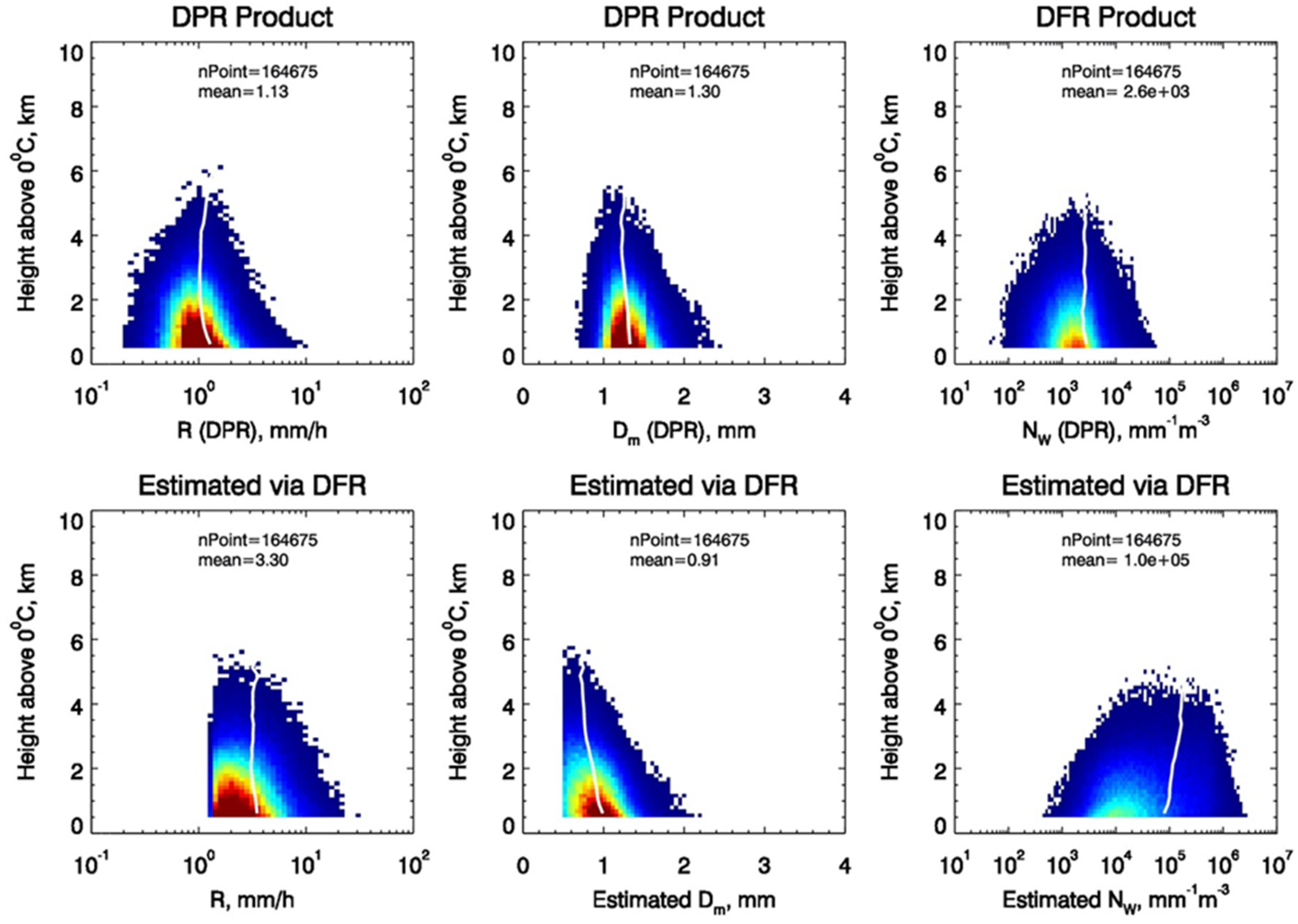
Figure 6 shows the PDFs of R (left column), D_m (middle column), and N_w (right column) acquired from the DPR standard product (top row) and the DFR approach (bottom row) along the height above freezing level. The DPR product and DFR estimates are compared and clearly indicate that obvious discrepancies exist between the two estimates: R from the DPR product are consistently lower than those from the DFR method, while D_m/N_w from the DPR product tend to be larger/smaller than those derived from the DFR approach. These discrepancies are also shown by the vertical mean profiles (white solid lines). 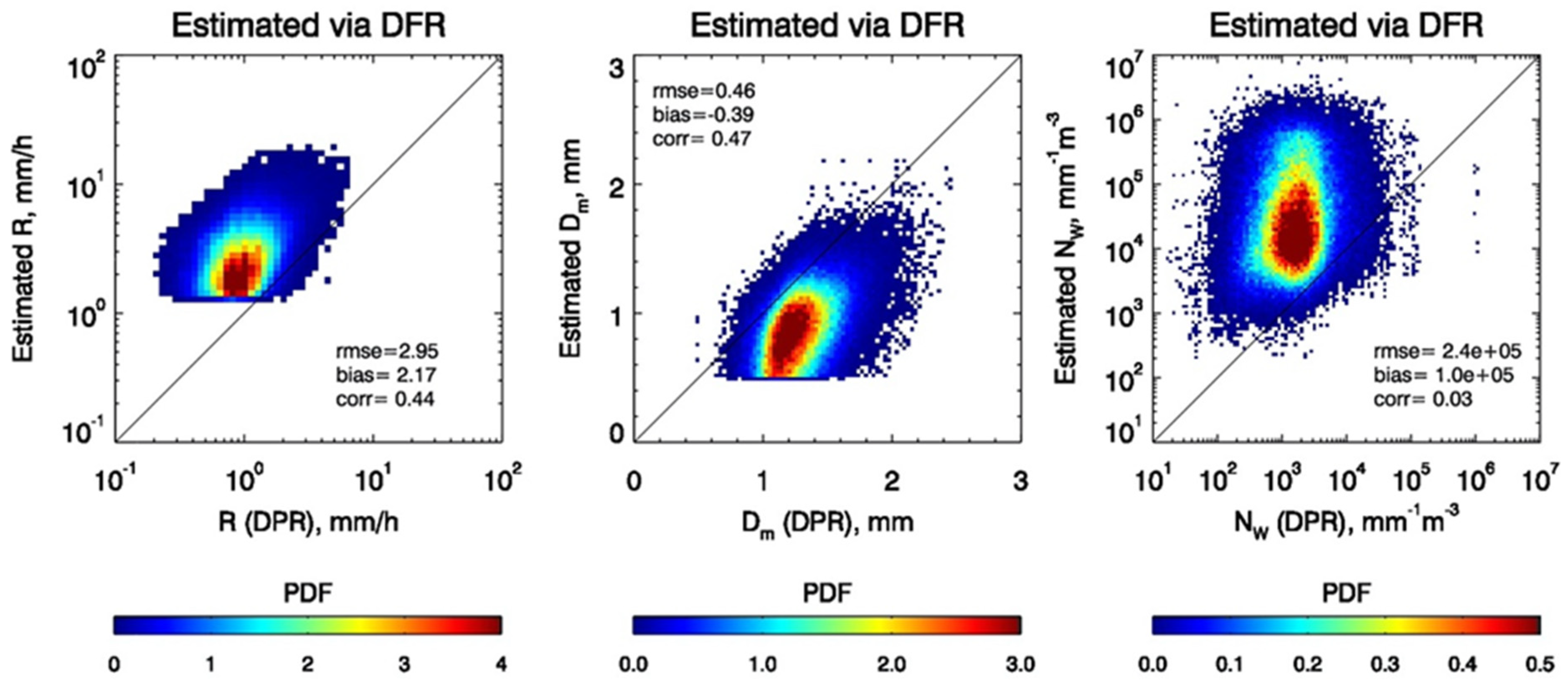As shown in Figure 7, the DFR estimates (ordinate) are directly compared with the DPR product (abscissa); the rms differences (rmse) and biases of the DFR estimates relative to the DPR product as well as their correlation coefficient “corr” are also provided in Figure 7. Clearly, the estimates of R from the DFR method are notably larger than those from the DPR product. This is also true for N_w. However, the estimates of D_m from the DFR are smaller than those of the DPR results. Moderate correlations exist between the DPR product and DFR estimates in R and D_m, but almost no correlation is present between the N_w data derived from the DFR method and the operational result. Furthermore, most of the N_w results from the DPR product are confined to a narrow range of values, while the estimated N_w spans a relatively large dynamic range.

The underestimation of R in snow from the DPR algorithm has been reported in several studies that compared the DPR estimates with other satellite snow products [45,46,47] and the Multi-Radar Multi-Sensor (MRMS) ground radar composite product over the continental United States [48]. As described earlier, the DPR algorithm depends heavily on the constraint of the PIA/δPIA in finding the best ε. The PIA/δPIA, however, is determined primarily by rain and mixed-phase hydrometeors as snow contributes only a negligibly small attenuation. Thus, the assumption of a range-independent ε leads to the selection of ε favorable to rain in the DPR algorithm. A combination of the PIA/δPIA constraint and the ε constant assumption in the column likely results in significant deviations of the attenuation-corrected reflectivities at Ka-band in the snow region and consequently causes the uncertainties in the DPR snow retrieval.

4. Ground Validation

Ground validation is an important component for evaluating and improving the performance of the DPR algorithm. NASA has developed a GPM Ground Validation (GV) program with an emphasis on physical validation of precipitation products from the GPM core satellite by deploying multiple field campaigns and using an array of precipitation instruments, including disdrometers and polarimetric radars [49]. The GPM Validation Network (VN), which is under the GPM GV program, is dedicated to an assessment of the satellite-based measurements and precipitation estimates. The VN includes over 100 S-band Weather Surveillance Radar-1988 Doppler (WSR-88D) radars from the U.S. Next Generation Weather Radar (NEXRAD) network. These radars have been upgraded to enable full polarimetric measurements and are carefully selected from the NEXRAD sites to maximize GR reference data quality. Despite some intrinsic uncertainties of the DPR versus GR comparisons caused by different viewing geometries and operating frequencies as well as possible time offsets, comparisons of the unattenuated radar reflectivities from the GRs to the attenuation-corrected radar reflectivities from the DPR algorithms offer a direct check on the attenuation-correction procedure used in the algorithms for precipitation rate and DSD/PSD retrievals. Biswas and Chandrasekar [50] compared the DPR Version 5 reflectivities at both Ku- and Ka-band with the GRs over 250 GPM satellite overpasses in which significant precipitation is present at 5 NEXRAD sites and found that the matched DPR and GR reflectivities were in good agreement with correlation up to 0.9 at Ku-band and 0.85 at Ka-band. The study also revealed that the DPR-GR correlation from stratiform rain was better than that from convective rain and that the DPR Ku-band reflectivities were positively biased while the DPR Ka-band reflectivities were negatively biased as compared with the GRs. These differences should be expected, however, considering uncertainties involved in the DPR-GV comparisons.

Several studies have been conducted to compare the DPR precipitation estimates with the GR-derived and rain gauge/disdrometer-based rain products. Early work included evaluation of the DPR Version 4 and Version 5 products against four MeteoSwiss polarimetric C-band radar precipitation products for the first two years of the GPM DPR’s operation [51,52]. It was found that the DPR consistently underestimated precipitation across the radar network; relative bias reached −51% in complex terrain in the winter, mainly caused by the presence of snow where the DPR reflectivites were close to the noise level. This comparison study concluded that the DPR performed far better in summer than in winter, in rain than in snow, and in flatter terrain than in complex terrain. Underestimation in rainfall rate from the DPR was also reported in a study by Watters et al. [53] who compared the DPR Version 5 product with those from the radar composite product of the Meteorological Office Radarnet 4 system of Great Britain and Ireland (GBI). A three-year precipitation product from the German national meteorological service (DWD) comprising 17 C-band radars over Germany was compared with the DPR Version 5 product by carefully collocating two datasets. The DPR and GR rain rates were well correlated with a correlation coefficient of 0.61 and the root mean square error was 1.83 mm h⁻¹.

A recent study was carried out to assess the DPR-based DSD estimates by utilizing the GPM VN estimates [54]. The VN DSD was derived from a combination of the differential reflectivity and horizontally polarized reflectivity based on a regression analysis that involved scattering simulations and a large and diverse measured DSD database collected by 2DVDs through the GPM GV effort [55]. Having accurately matched the DPR and GR datasets in space and conducted automated and manual quality control for each GR, the DPR Version 6 DSD product was compared to the VN estimates. It was found that the estimated Dm from the DPR was positively biased by only 0.2 mm across all the precipitation types. However, the DPR tended to overestimate D_m by 0.5–0.6 mm in convective precipitation, which in turn, lead to underestimation of N_w by a factor of two. This resulted in a significant bias to the DPR retrieval of R for DSDs with large Dm. Possible reasons for the discrepancies of the DSD estimates between the DPR and VN products in the convective case are the presence of multiple scattering and non-uniform beam filling at Ka-band, both of which are difficult to correct. Inaccurate attenuation correction may also be a factor. In addition to these factors, the temporal difference between the geometrically matched datasets likely gave rise to uncertainties associated with fast evolving weather systems such as convective precipitation.

The GR has also been used for validation of snow products. Le and Chandrasekar [56] evaluated the surface snowfall flag embedded in the DPR product by taking advantage of the polarimetric GR data that provide hydrometeor phase state. The GR-derived snowfall estimates were subject to large uncertainties associated with the assumptions made for the mass-size conversion, PSD, and fall velocity arising from the fact that a single-frequency radar reflectivity was used. Mroz et al. [48] compared the DPR snowfall rate with those from the MRMS radar snow product over the continental United States during the period from November 2014 to September 2020. A single R-Z relation was used by the MRMS to convert measured reflectivities to snow rate across the entire radar network. Although the snow reference provided by the MRMS is useful to check and understand statistical properties of the DPR estimates, the challenge remains to pinpoint the flaws of the DPR underlying physics and model assumptions in view of complexities in the snow shape and structure.

Estimates of rain rate from dense gauge networks were compared with the DPR Ku-band rain product in Tan et al. [57] and Lasser et al. [58]. Unlike most GRs, highly dense gauge networks allow for spatial and temporal matching between the DPR footprint and the gauges. Despite this, uncertainties caused by marked differences of measurement samples between two instruments, namely point (gauge) versus volume averaged (DPR) measurements, cannot be avoided. Gauge measurements are made at the surface at a single location, while the closest-to-surface DPR rain measurements that are unaffected by surface clutter usually occur at altitudes from a few hundred meters to a couple kilometers above surface, depending on the incident angle and surface topography. Dense gauge networks are able to account for the variation of rain within the DPR footprint to some extent by averaging as many gauges as possible within the DPR footprint; however, they are unable to account for vertical variation of rain within the range gate. As such, non-uniformity of rain contributes to ambiguities in the comparisons between the DPR and gauge measurements.

A few studies have been conducted to compare the DPR rain and DSD estimates to ground-based disdrometer measurements. Disdrometers, similar to rain gauges, provide point measurements but have a clear advantage over gauges as they can measure DSD spectra that provide the DSD parameters. However, disdrometers are not deployed as frequently as rain gauges in operational weather monitoring networks, therefore, their observations are available in relatively few locations, although they are frequently deployed in a variety of ground validation field campaigns and routinely used for collection of data for research purpose. A DPR-disdrometer comparison study over Gadanki, India reported that in an early version of the DPR product, large uncertainties were noted for rainfall rate over 8 mm/h [59]. D’Adderio et al. [60] found that the probability distribution of DPR (Version 4) retrieved D_m was in good agreement with disdrometer measurements over the Mediterranean region, however, uncertainties in N_w occurred. Similar results were found by Sun et al. [61] who compared 18 Parsivel disdrometer observations with the DPR over the Yangtze-Huai River in central China during the period 2016–2018. A study by Wu et al [62] based on an analysis of the comparisons of 5-year data between the Parsivel disdrometer and DPR data indicated that the DPR performed better in winter than in summer. Adirosi et al. [63] attempted to mitigate uncertainties arising from sampling differences by comparing point measurements at ground acquired from a disdrometer with volume measurements aloft obtained by the DPR. Seven different disdrometer observations across Italy during the period from 2014 to 2020 were compared with the DPR SF and DF rain products. It was found that the DF estimates were not obviously superior to the SF estimates. The DPR-HS data seemed to have the best agreement with the disdrometer among other DPR products.

Ground validation work represents an important component in understanding and evaluating the DPR precipitation estimates. It is not surprising that not all these results have been consistent. Part of the reason appears to be a consequence of the differences in the meteorological regimes where the studies were conducted because of regional and seasonal variations in precipitation characteristics. The large variability in the discrepancies between DPR and ground-based estimates among validation studies can likely be attributed to the random errors resulting from sample mismatches and limitations associated with the spaceborne and ground instruments. For example, GR retrieval is affected by poor resolution at far ranges, while DPR is subject to errors in properly quantifying orographic precipitation because of surface clutter. Rain gauge/disdrometer measurements provide continuous measurements in time at a single location, whereas DPR measurements are nearly instantaneous while providing continuous measurements in space but with a large amount of spatial averaging. The space-time matching issue for DPR-GR comparisons is easier because of similar sampling volumes, although different viewing geometries and temporal offsets introduce errors. Because of intrinsic uncertainties involved in spaceborne and ground measurements, validation is built upon statistical comparisons so as to offset some random errors. Due to the complexity of the DPR algorithm that involves model assumptions and constraints used for the retrieval, identification of specific deficiencies is not always easy to achieve.

5. Remarks and Future Work

With the addition of Ka-band measurements, the GPM DPR has demonstrated improved precipitation measurement and estimation as compared with its predecessor, i.e., the TRMM PR, by better constraining DSD/PSD parameters in solving radar equations. DPR has a broad range of applications in precipitation estimation, classification of storm type, as well as detection of precipitating hydrometeor phase state and storm structure. Its standard product has been widely used in a variety of studies, such as in numerical weather forecast models and hydrological models for flood prediction and climate studies. Validation of the DPR product and evaluation of the retrieval accuracy are an important step in understanding the performance of the algorithm and providing insight into improvement of the algorithm. In this study, the basic structure and methodology of the DPR algorithm are first reviewed, and then, its accuracy is evaluated for rain and snow retrievals. The DSD/PSD data are employed for simulating radar measurements, and the estimates from the simulated reflectivities are compared with their true values that are directly derived from the measured DSD/PSD. The degree of agreement between the estimates and truth constitutes a way to quantify retrieval accuracy.

To achieve robustness in the DPR algorithm and also to improve consistency of the retrieval results between the SF and DF algorithms, the DPR SF and DF algorithms make use of a power-law R-D_m relationship with an adjustable factor ε [16]. Constant ε, in the current version of the DPR algorithm (Version 6), is assumed in the column and determined by an optimal approach that minimizes the cost function, defined for the case of the DF algorithm as the sum of three weighted constraint equations that are related to the ε distribution, the independent estimate of δPIA, and the Ka-band reflectivity profile. Instead of δPIA, the SF algorithm uses PIA as one of two constraint equations. Another constraint equation in the SF algorithms is the ε distribution.

As shown by Liao et al. [17], the DF algorithm provides reasonably accurate estimates of rainfall rate and D_m in rain. Absolute biases of the bin-averaged D_m are generally small across the full range of rain rates and these values are generally well below 0.5 mm (error within +/−0.5 mm in the D_m estimate is one of the DPR science requirements documented in [3]). A slight underestimation of rainfall rate is found for the case of light rain, but strong correlation is found between the estimates and truth. Non-uniformity in the rain profile tends to degrade the accuracy of the R and D_m estimates to some extent, as the range-independent assumption of ε is not able to fully account for natural variation of DSD in the vertical profile. Since the R-D_m relation plays a key role in the algorithm, sensitivity of the retrieved R and DSD parameters to the initial R-D_m relation is tested. It is found that the retrieval results are not highly sensitive to the R-D_m relations that are taken from different DSD dataset and gamma DSD models. This is largely because an adjustable parameter in the R-D_m relation is used. As a result of stronger constraints imposed on the DF equations, relative to those of the SF, the estimates in R and DSD from the DF are less affected by the choice of the R-D_m relation than those from the SF. It is important to note that, although R and DSD estimates are not sensitive to the R-D_m relation, the values of the final ε depend on the choice of the R-D_m relation. As mentioned before, the mean value of ${\log }_{10}\epsilon$ or μ_ε, obtained from the DF, is used to represent the mean of the ε distribution for the SF in (9b). Dependence of the final ε of the DF eventually leads to SF estimates of R and DSD. It is useful to note that the example shown in Figure 3 for the SF algorithm, where μ_ε is set to zero, does not use the ε derived from the DF, because our purpose is to evaluate the impact caused by the R-D_m relation alone. Under this assumption, the SF estimates are found to be insensitive to the R-D_m relation. However, if the ε derived from the DF is used in (9b), the estimates from the SF become dependent on the R-D_m selection.

The DPR adopts the same approach used for both rain and snow retrievals. In the Version 6 algorithm, the same ε is assumed along the vertical profile, irrespective of precipitating hydrometeor phase. To evaluate the DPR snow product, an independent approach is required. To see if the DFR technique is reliable for snow estimates, an evaluation is made through a simulation study that is based on the measured PSD data. The DFR method is found to be capable of producing fairly accurate snow parameters, and therefore, serves as an independent approach to assess the DPR snow product.

With the same model assumptions made for the DPR algorithm, the DFR technique is applied for the one-day DPR measurements that comprise 16 orbit data files. To extract snow measurements, the data are selected from stratiform storms and correspond to measurements at heights greater than 0.5 km above freezing level. It is expected that the measured and attenuation-corrected snow reflectivities would be very close, based on the fact that the attenuation of dry snow is negligibly small at both Ku- and Ka-band. However, the attenuation-corrected reflectivities at Ka-band from the DPR DF product deviate significantly from the measured values in the snow region, implying a possible deficiency in the snow estimates. This deficiency does not occur in the DFR results. Comparisons of the DFR-estimated snow parameters with the DPR DF product reveal that the equivalent snowfall rate from the DPR product is significantly lower than that from the DFR estimates, while the D_m from the DPR DF is larger than the DFR’s. Moderate correlations between the DPR product and DFR estimates in R and D_m are found but almost no correlation in N_w between the estimates and the product is noticed. These findings are consistent with several studies that have compared DPR snow estimates with other satellite instruments and ground observations. The underestimation of DPR snow rate is possibly the result of the constraint associated with the PIA/δPIA used in finding the best ε and range-independent ε assumption.

Ground validation plays a key role in evaluating and improving the DPR algorithm. Significant effort has been made to validate the GPM precipitation products acquired from active and passive sensors. The GPM VN includes over 100 WSR-88D radars that enable validation of DPR reflectivity, rainfall rate, and DSD estimates. The DPR validation has been extended to dense gauge networks and disdrometer measurements. The strengths and weaknesses of the ground radar and rain gauge/disdrometer validations from a variety of studies have been reviewed in this paper. Ground instruments offer direct and accurate measurements of the radar reflectivities and hydrometeor properties and are undoubtedly useful in validating DPR measurements and estimates. However, because of marked differences in viewing geometries and resolutions between the satellite and ground observations, unavoidable uncertainties associated with mismatched samples in space and time occur. To some degree, statistical comparisons can mitigate the random errors. Nevertheless, because of the difficulty in perfectly matching the space-ground sample volumes and the limitations of the instruments themselves, the ground radar and rain gauge/disdrometer measurements alone are not enough to fully assess the performance of individual components involved in the DPR algorithm. This is compounded by the complexity of the DPR algorithm that relies on the retrieval methods, model assumptions, and radar calibration. An evaluation of the algorithm based on physical simulations is also required to understand the mechanism and error characteristics of the retrieval method.

In the current DPR (Version 6) algorithm the assumption of a range-invariant ε is made. This assumption puts restrictions on the rain retrieval and in some cases leads to retrievals that do not capture the natural variations in the DSD along the column. The assumption of a range-independent ε also leads to significant underestimation of the snowfall rate. In version 7, a two-scale model of ε will be introduced which will allow more range variability in this parameter. This is an important step toward not only improving rain but also snow retrievals.