Cotton Classification Method at the County Scale Based on Multi-Features and Random Forest Feature Selection Algorithm and Classifier
Abstract
:1. Introduction
2. Materials
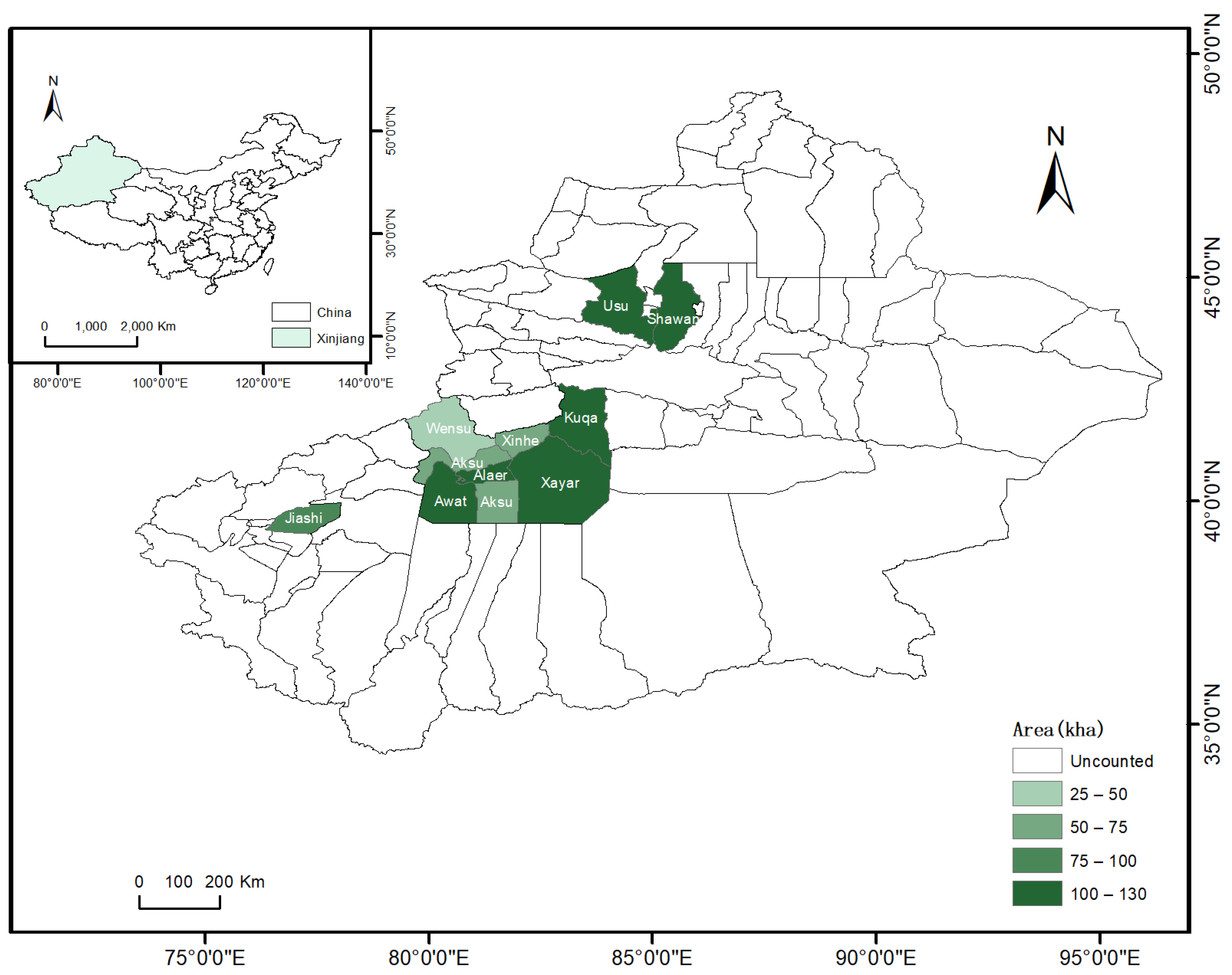
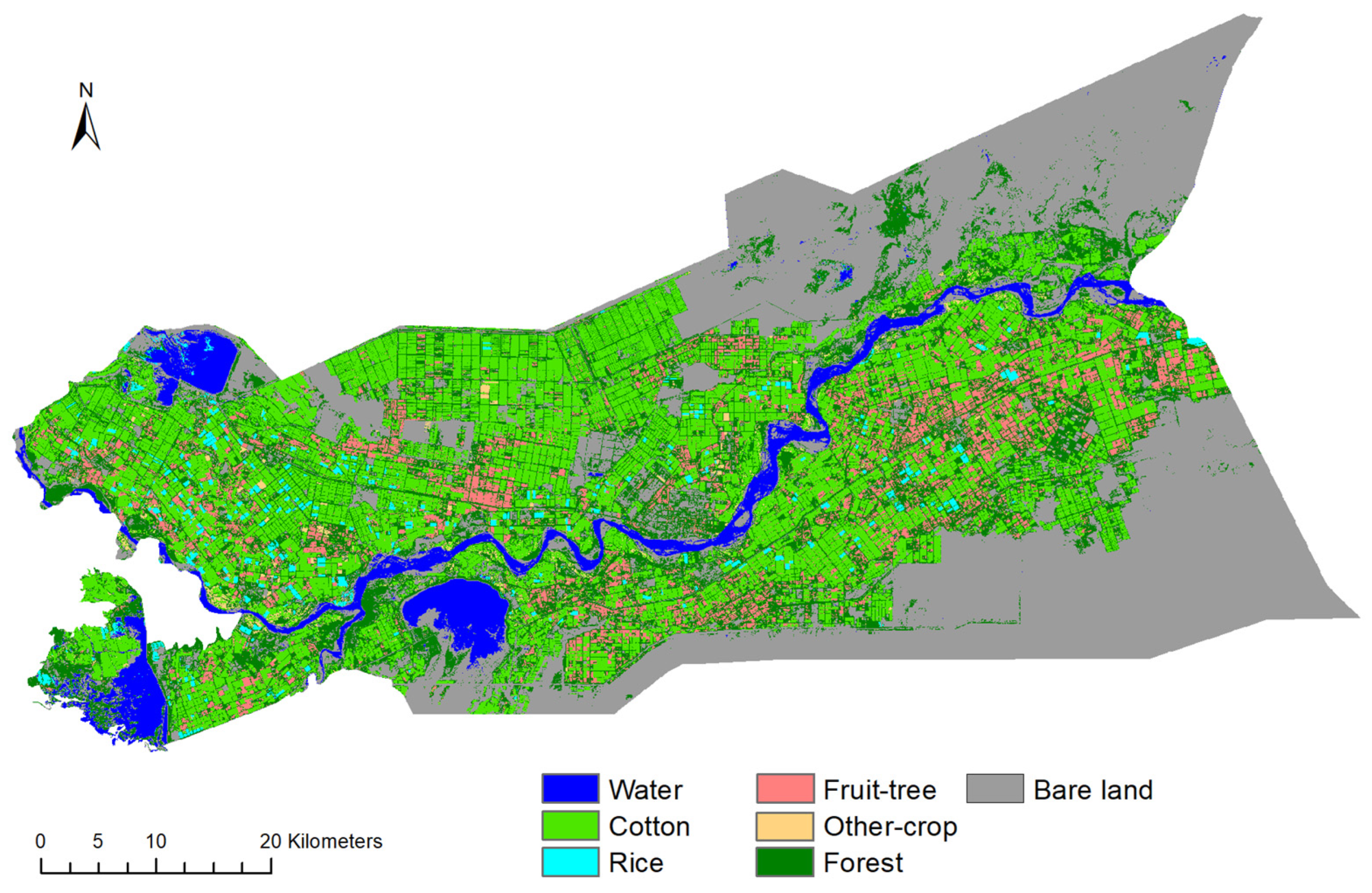
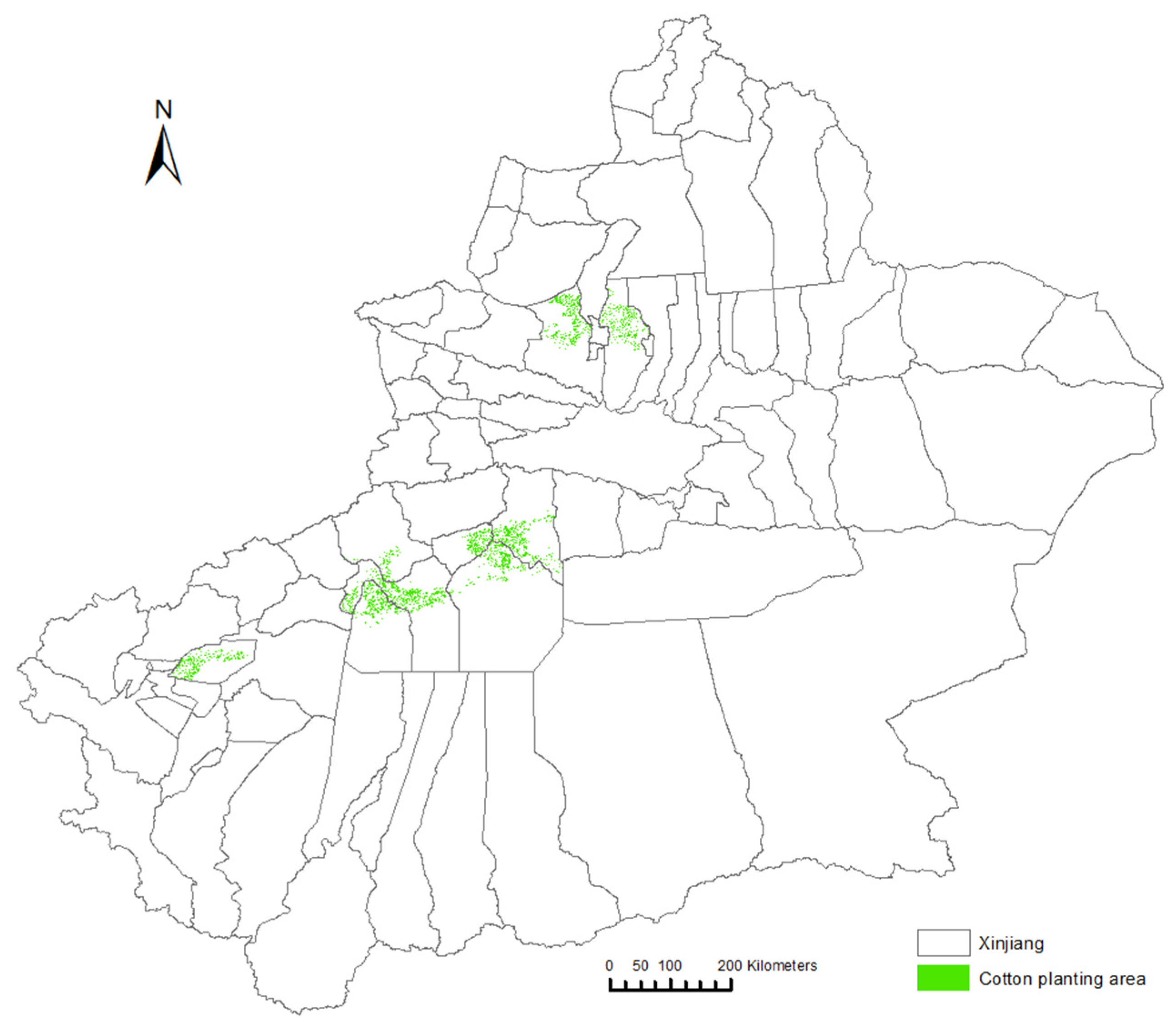
2.1. Study Region
2.2. Data and Preprocessing
2.2.1. Remote Sensing Image Data
2.2.2. Ground Sample Data
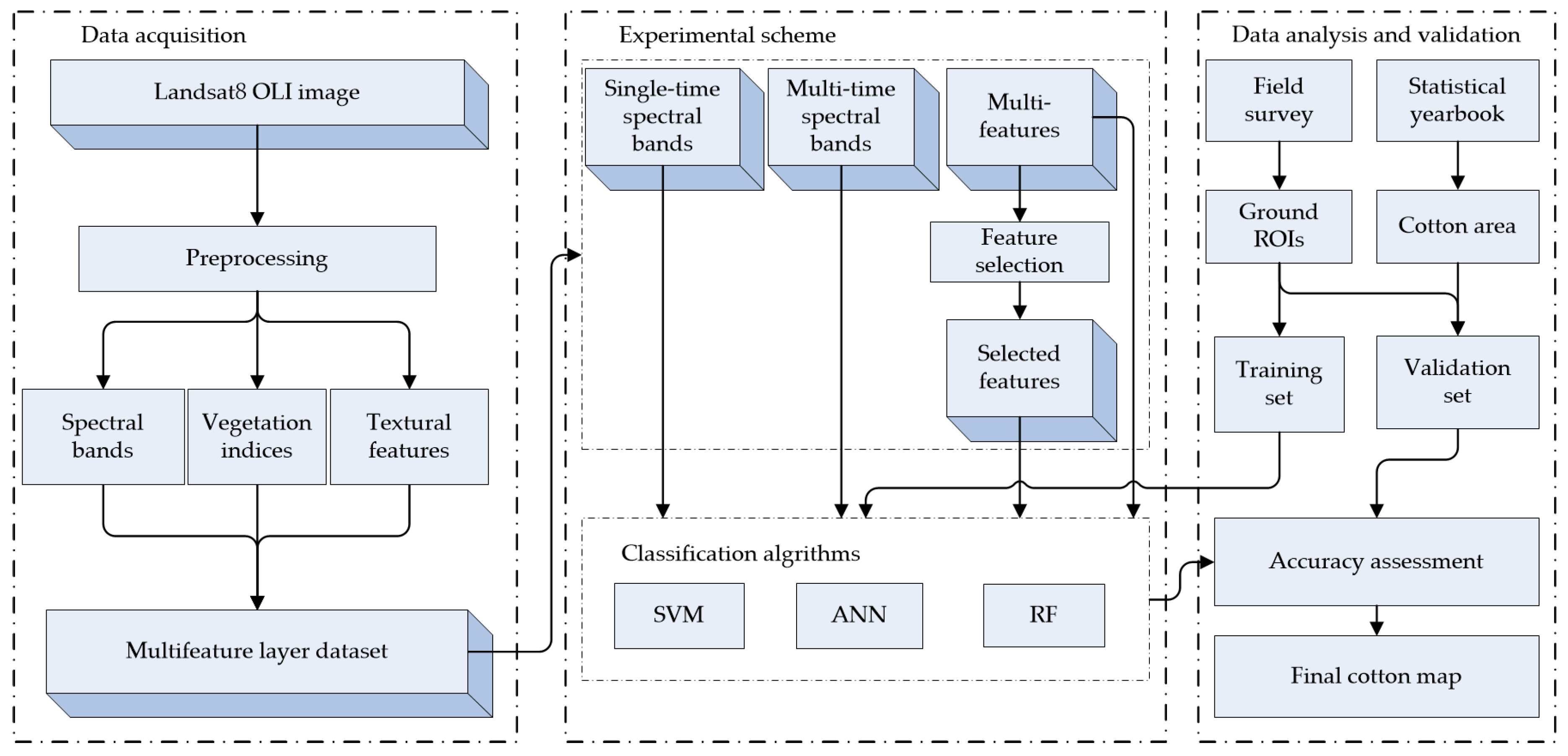
3. Methods
3.1. Feature Extraction
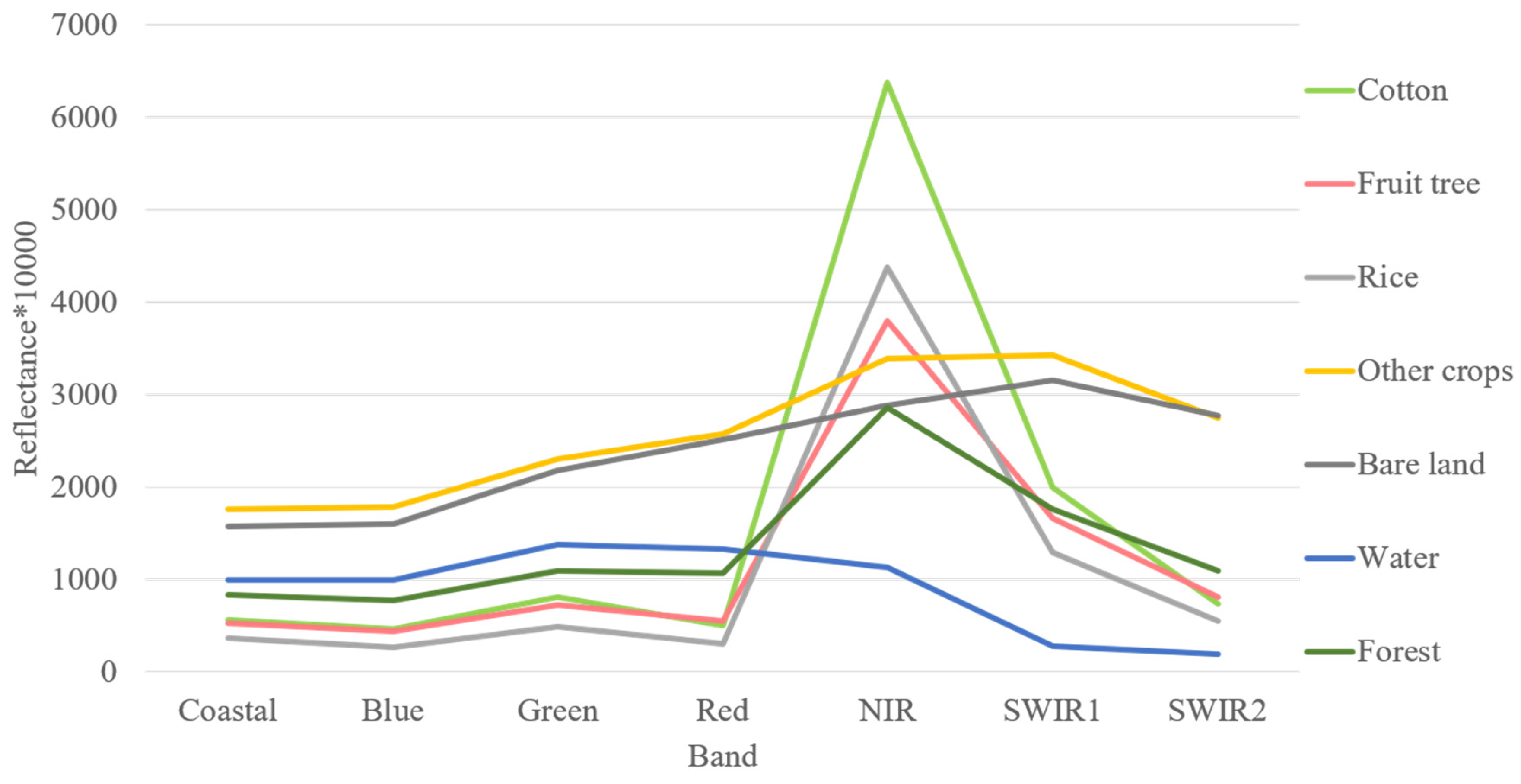
3.1.1. Spectral Bands
3.1.2. Vegetation Indices
3.1.3. Texture Features
3.2. Classification Based on Random Forests
3.2.1. RF Description
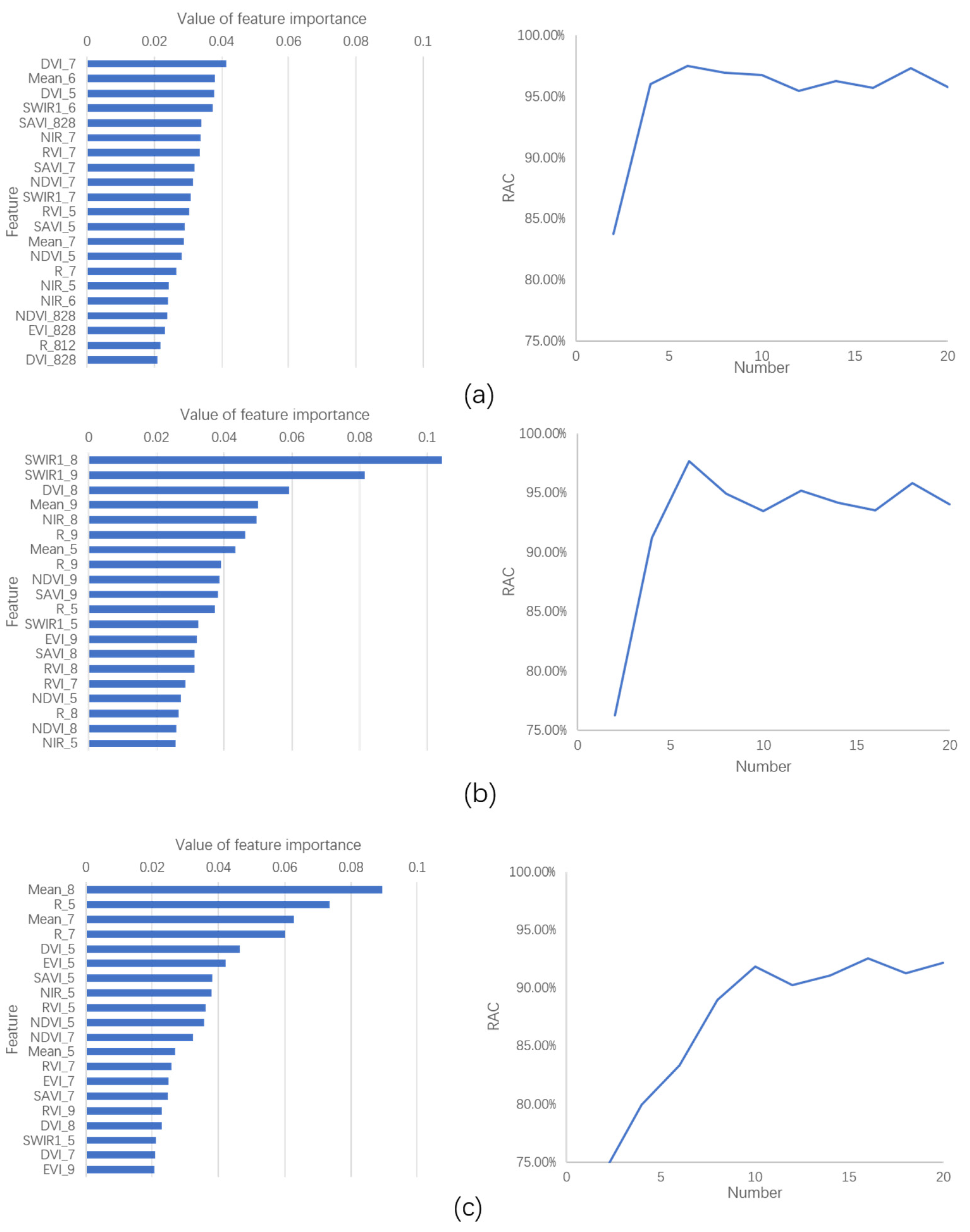
3.2.2. Feature Selection Based on Random Forest (RF)
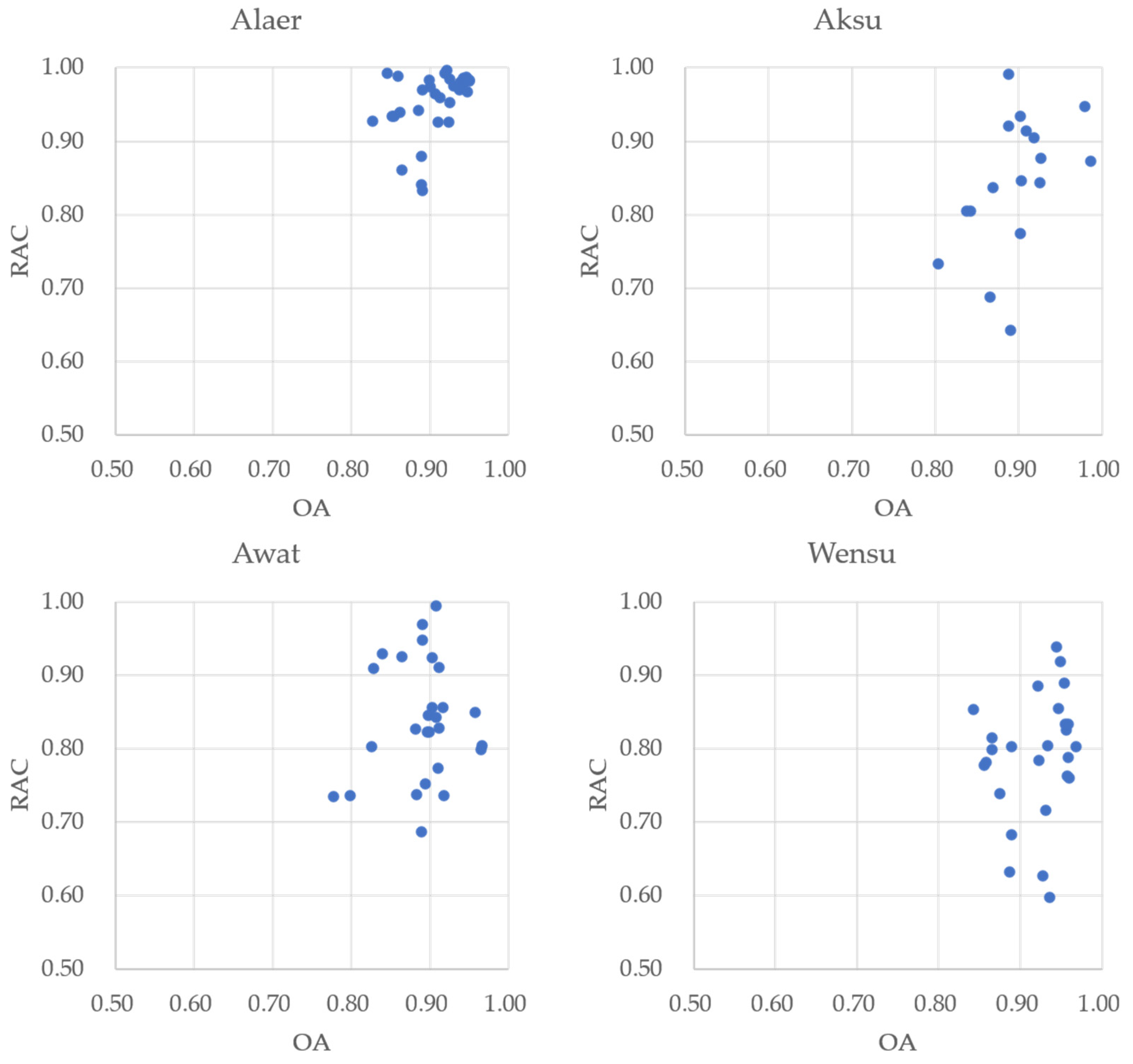
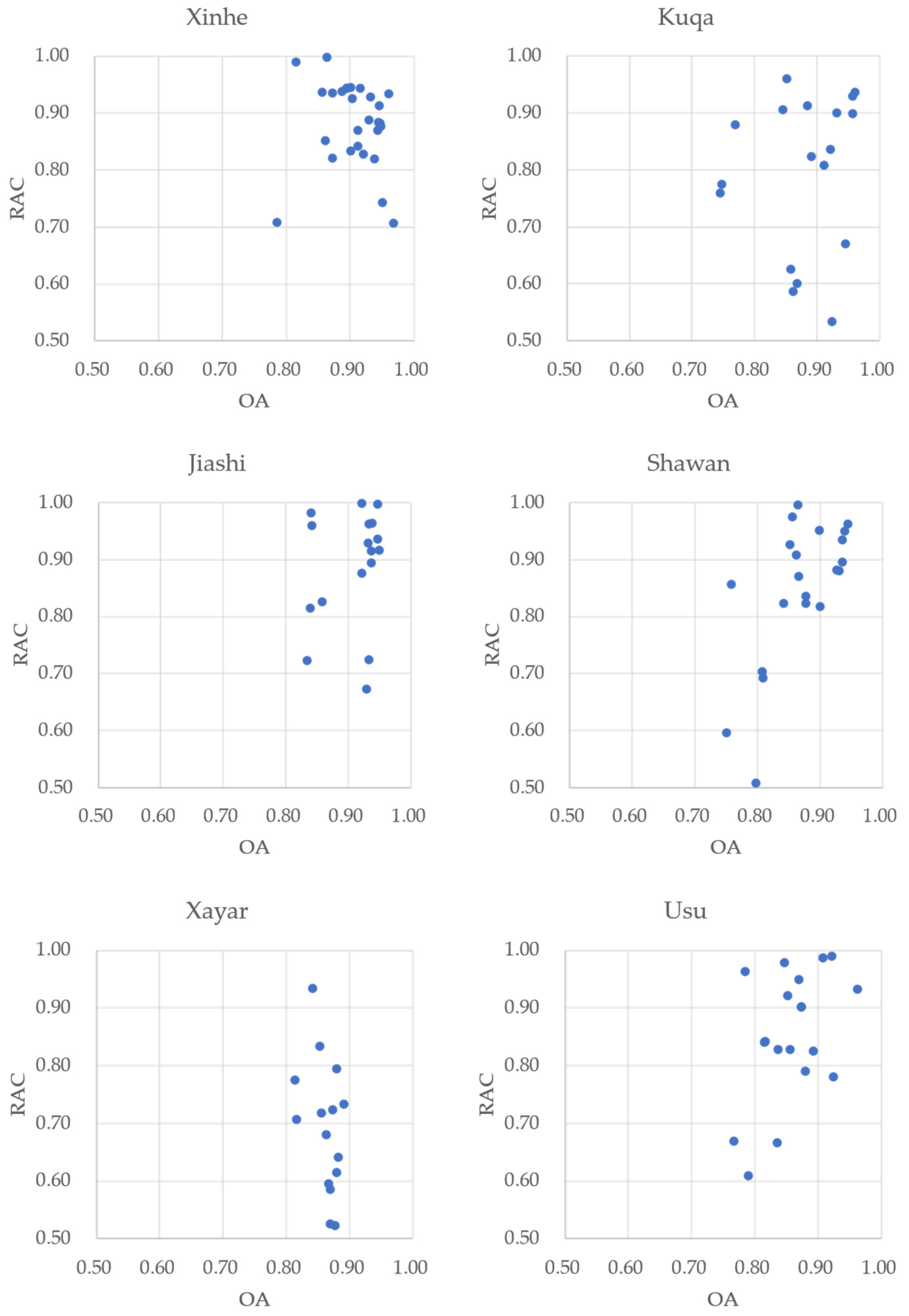
3.3. Accuracy Evaluation
3.4. Experiments
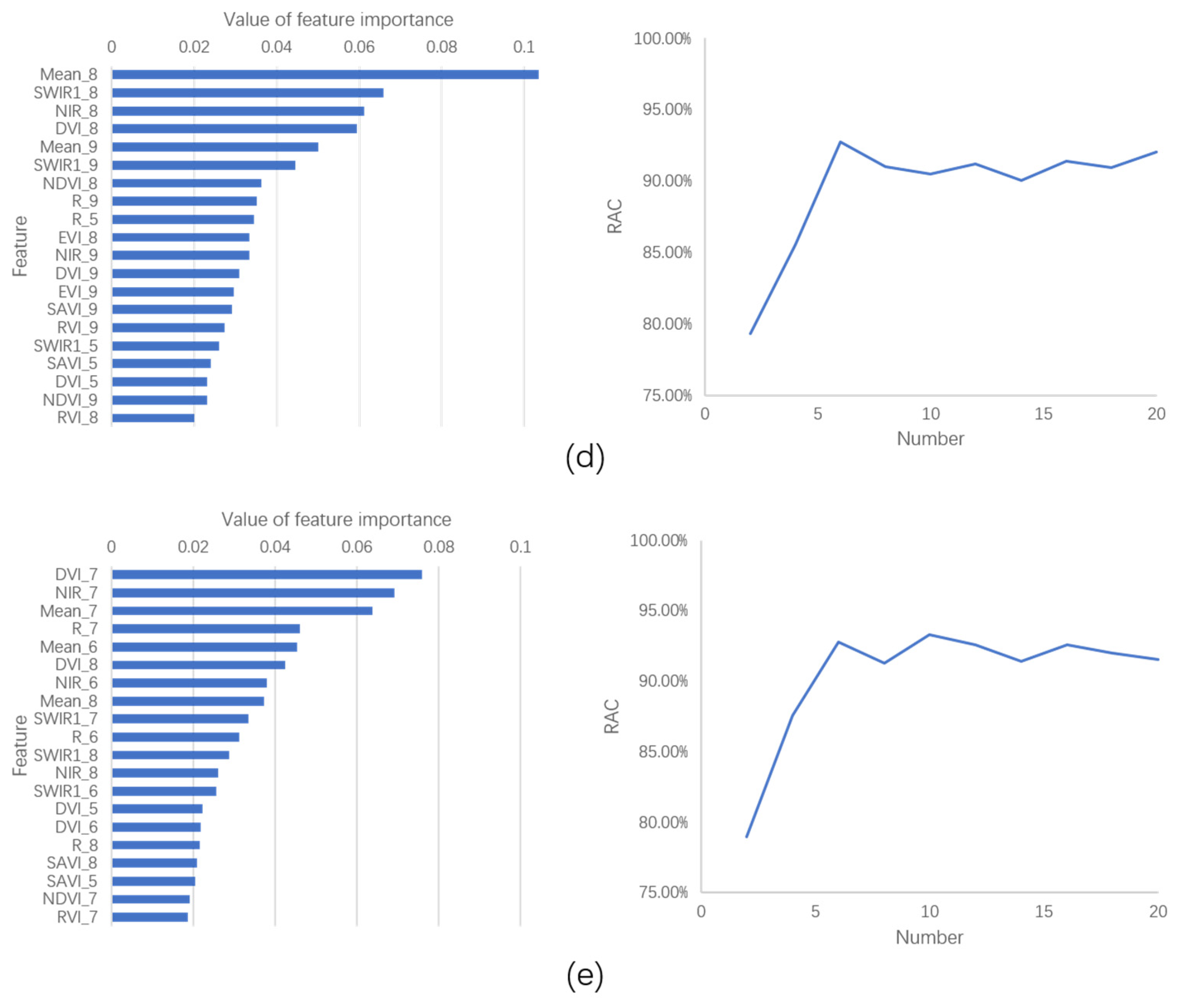
- In terms of feature selection, the RF model was used first to learn the training samples, and the obtained model was used to rank the importance of all features in the learning database. Then, a certain number of features were selected for classification in a stepwise manner. The RAC of the classification results was used as an evaluation index to determine the number of feature bands to be selected.
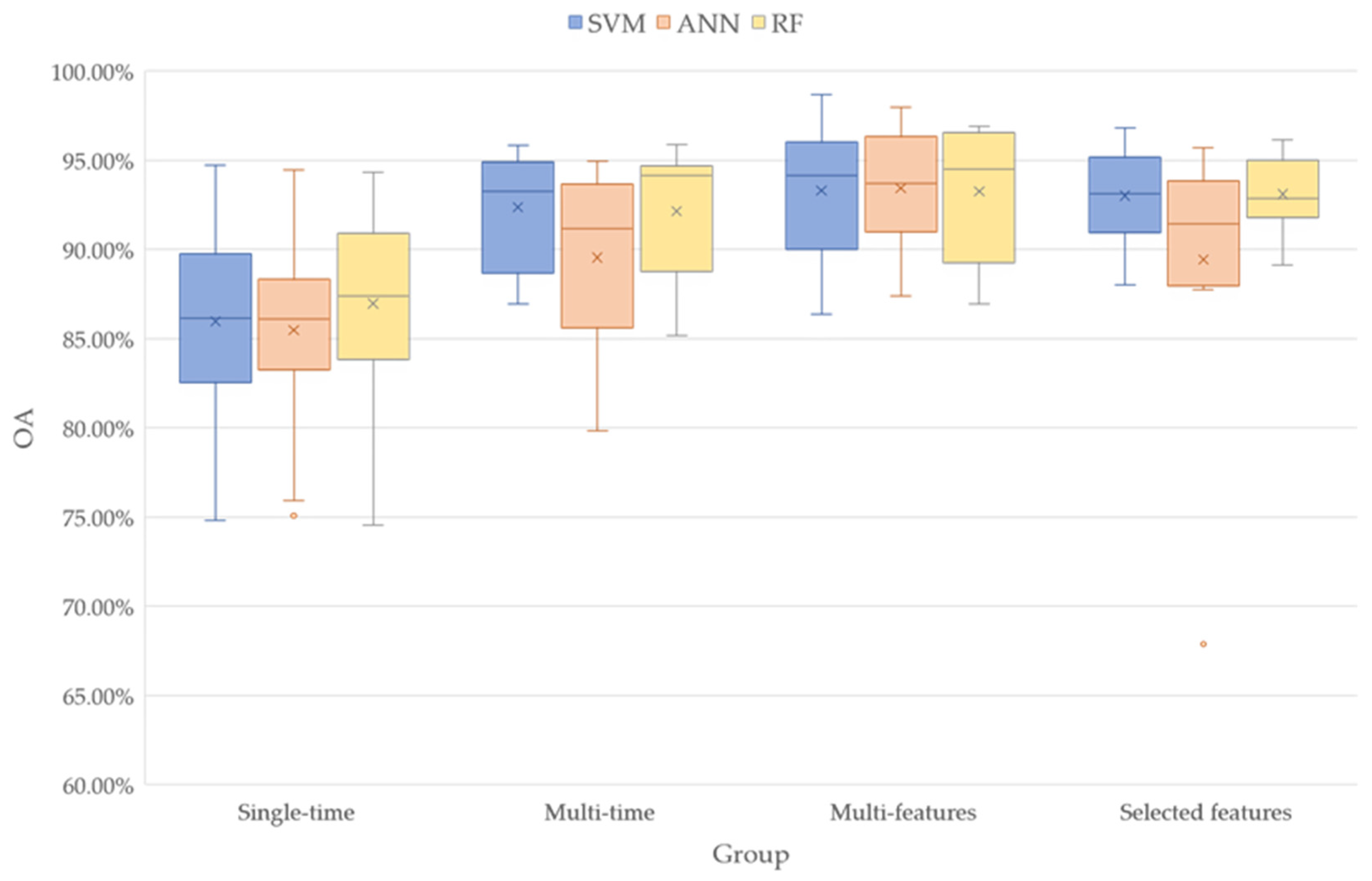
- The classification experiment was divided into three groups according to the different bands of the added images: (1) classification based on single-phase spectral images; (2) classification based on multi-phase spectral images; (3) classification based on the learning feature library of multi-time spectral images, vegetation index, and texture features; and (4) classification based on multi-feature images after feature selection on the learning database.
4. Results and Discussion
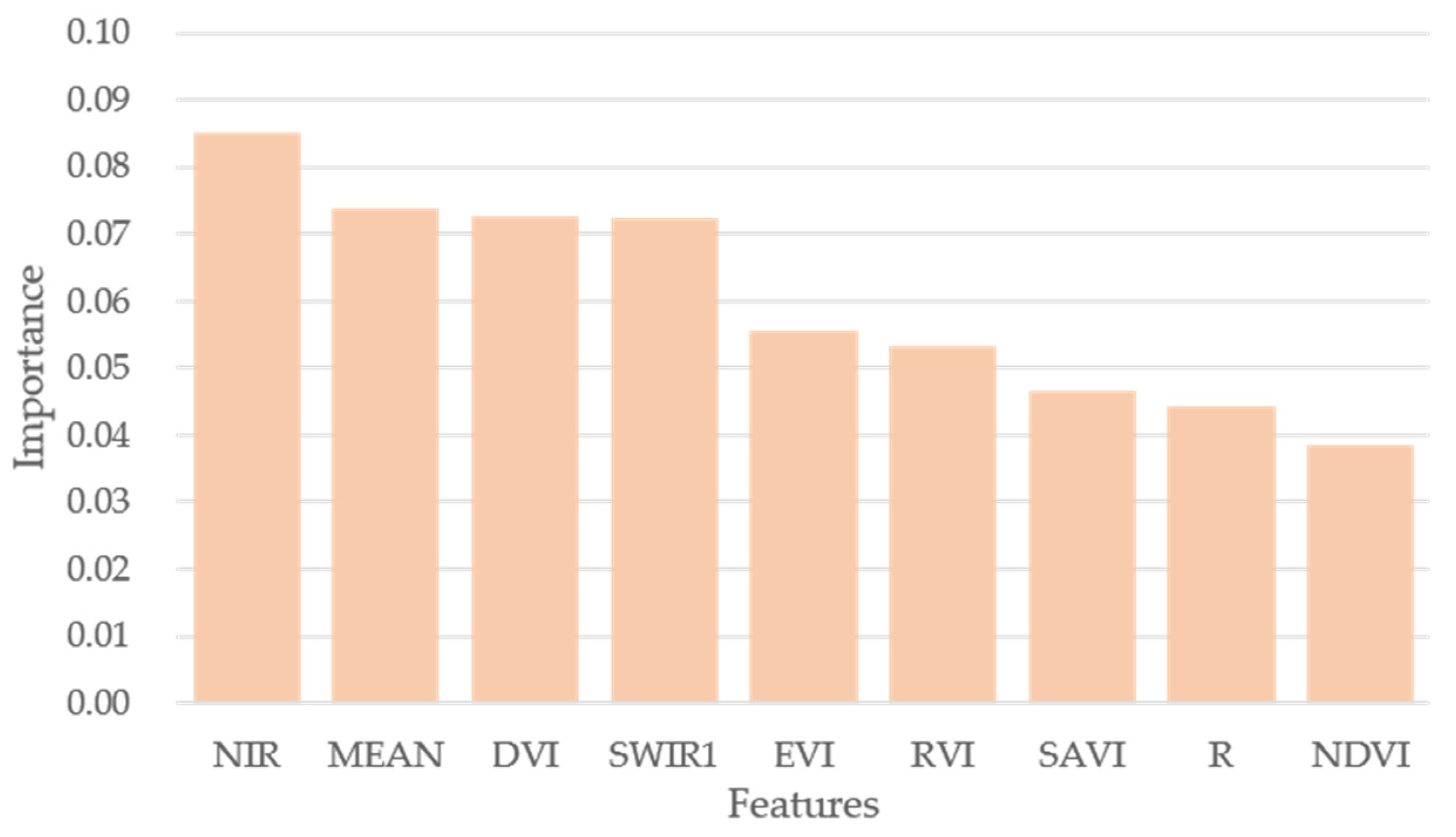
4.1. Feature Selection Based on Random Forest Algorithm
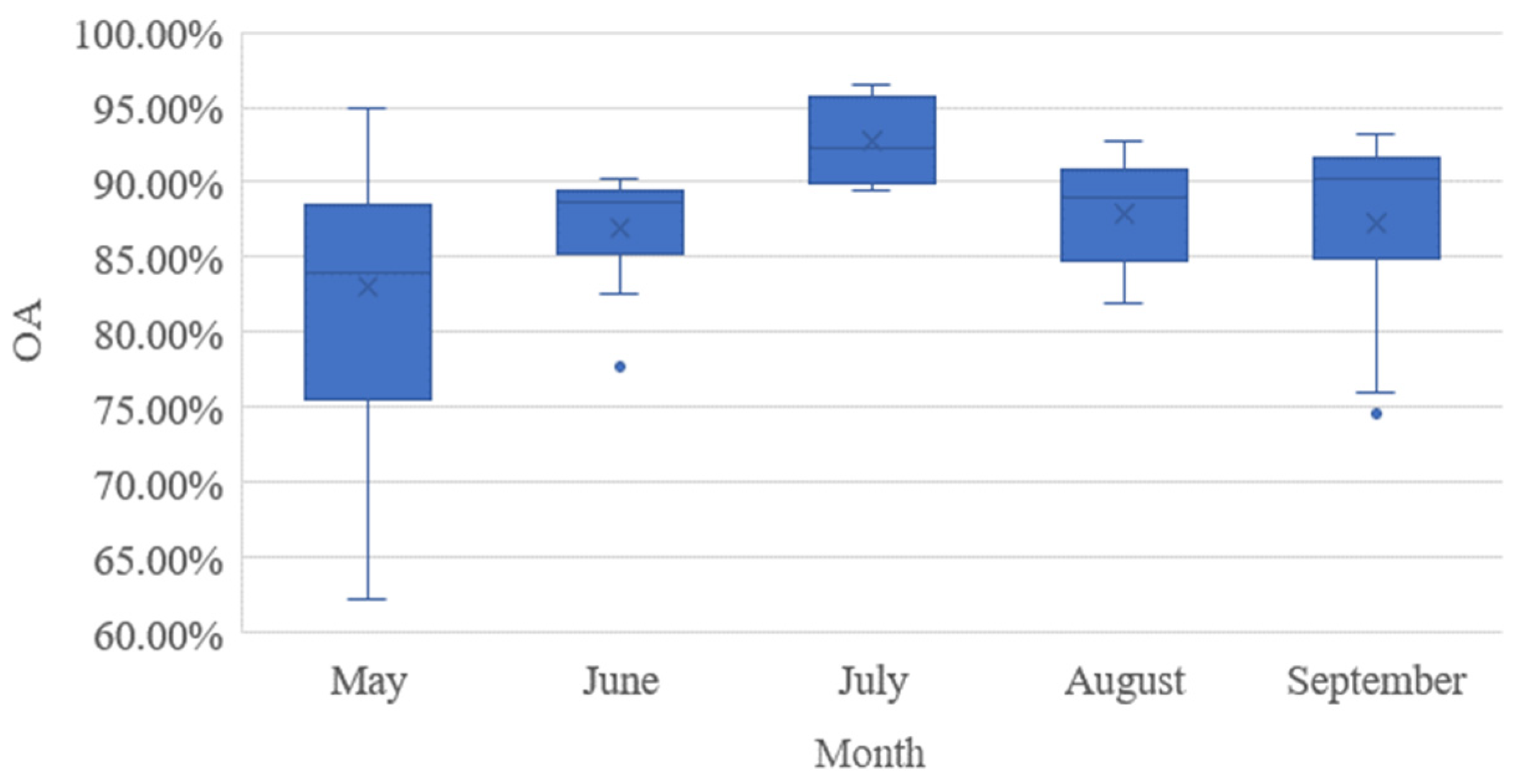
4.2. Optimal Classification Time
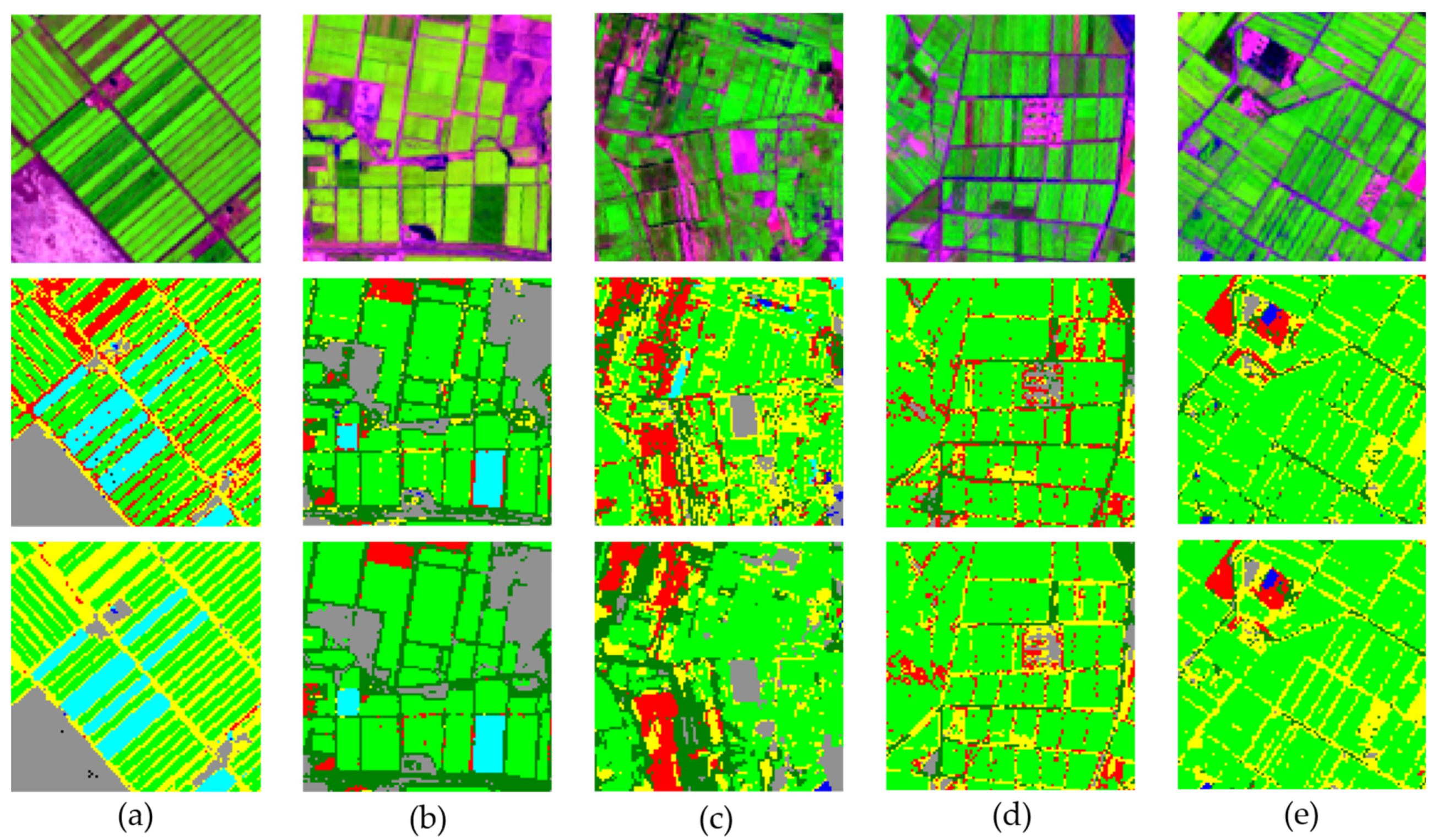
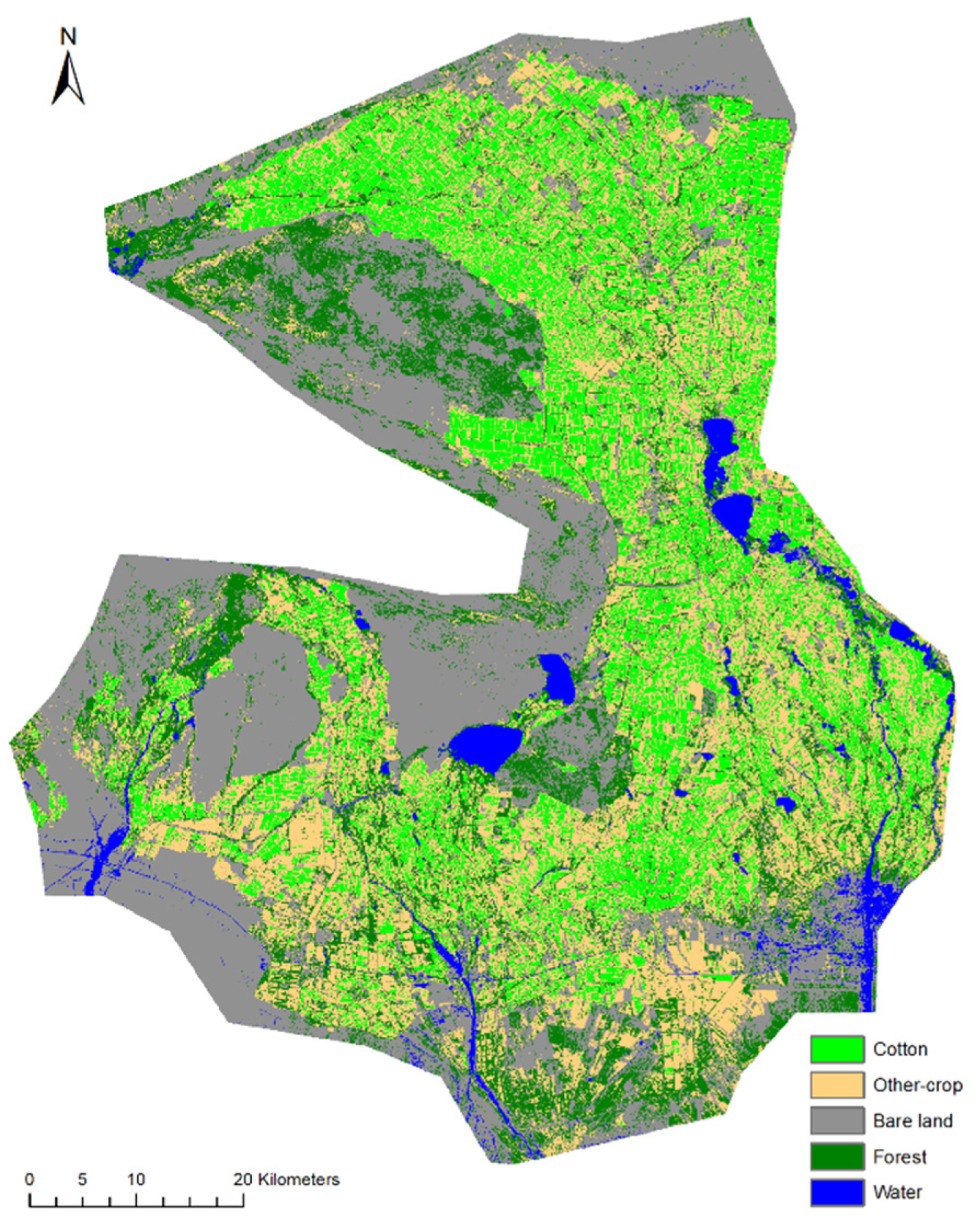
4.3. Classification Results
4.4. Regional Applicability
4.5. Implications and Improvements
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shengyong, M.; Zhicai, Y. China Statistical Yearbook; China Statistics Press: Beijing, China, 2018; ISBN 978-7-5037-8587-0. [Google Scholar]
- Wang, X.; Huang, J.; Feng, Q.; Yin, D. Winter Wheat Yield Prediction at County Level and Uncertainty Analysis in Main Wheat-Producing Regions of China with Deep Learning Approaches. Remote Sens. 2020, 12, 1744. [Google Scholar] [CrossRef]
- Zhuo, W.; Huang, J.; Li, L.; Zhang, X.; Ma, H.; Gao, X.; Huang, H.; Xu, B.; Xiao, X. Assimilating Soil Moisture Retrieved from Sentinel-1 and Sentinel-2 Data into WOFOST Model to Improve Winter Wheat Yield Estimation. Remote Sens. 2019, 11, 1618. [Google Scholar] [CrossRef] [Green Version]
- Zhuo, W.; Fang, S.; Gao, X.; Wang, L.; Wu, D.; Fu, S.; Wu, Q.; Huang, J. Crop yield prediction using MODIS LAI, TIGGE weather forecasts and WOFOST model: A case study for winter wheat in Hebei, China during 2009–2013. Int. J. Appl. Earth Obs. 2022, 106, 102668. [Google Scholar] [CrossRef]
- Zhuo, W.; Huang, J.; Gao, X.; Ma, H.; Huang, H.; Su, W.; Meng, J.; Li, Y.; Chen, H.; Yin, D. Prediction of Winter Wheat Maturity Dates through Assimilating Remotely Sensed Leaf Area Index into Crop Growth Model. Remote Sens. 2020, 12, 2896. [Google Scholar] [CrossRef]
- Waldner, F.; Canto, G.S.; Defourny, P. Automated annual cropland mapping using knowledge-based temporal features. ISPRS J. Photogramm. Remote Sens. 2015, 110, 1–13. [Google Scholar] [CrossRef]
- Chakhar, A.; Ortega-Terol, D.; Hernández-López, D.; Ballesteros, R.; Ortega, J.F.; Moreno, M.A. Assessing the Accuracy of Multiple Classification Algorithms for Crop Classification Using Landsat-8 and Sentinel-2 Data. Remote Sens. 2020, 12, 1735. [Google Scholar] [CrossRef]
- Reddy, C.S.; Jha, C.S.; Diwakar, P.G.; Dadhwal, V.K. Nationwide classification of forest types of India using remote sensing and GIS. Environ. Monit. Assess. 2015, 187, 777. [Google Scholar] [CrossRef]
- Dusseux, P.; Vertes, F.; Corpetti, T.; Corgne, S.; Hubert-Moy, L. Agricultural practices in grasslands detected by spatial remote sensing. Environ. Monit. Assess. 2014, 186, 8249–8265. [Google Scholar] [CrossRef] [PubMed]
- Martins, V.S.; Novo, E.M.; Lyapustin, A.; Aragão, L.E.; Freitas, S.R.; Barbosa, C.C.F. Seasonal and interannual assessment of cloud cover and atmospheric constituents across the Amazon (2000–2015): Insights for remote sensing and climate analysis. ISPRS J. Photogramm. Remote Sens. 2018, 145, 309–327. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Meng, P.; Chen, J. Study on clues for gold prospecting in the Maizijing-Shulonggou area, Ningxia Hui autonomous region, China, using ALI, ASTER and WorldView-2 imagery. J. Vis. Commun. Image Represent. 2019, 60, 192–205. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, D.; Moran, E.; Batistella, M.; Dutra, L.V.; Sanches, I.D.; da Silva, R.F.B.; Huang, J.; Luiz, A.J.B.; de Oliveira, M.A.F. Mapping croplands, cropping patterns, and crop types using MODIS time-series data. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 133–147. [Google Scholar] [CrossRef]
- Conrad, C.; Rahmann, M.; Machwitz, M.; Stulina, G.; Paeth, H.; Dech, S. Satellite based calculation of spatially distributed crop water requirements for cotton and wheat cultivation in Fergana Valley, Uzbekistan. Glob. Planet. Chang. 2013, 110, 88–98. [Google Scholar] [CrossRef]
- Conrad, C.; Fritsch, S.; Zeidler, J.; Rücker, G.; Dech, S. Per-Field Irrigated Crop Classification in Arid Central Asia Using SPOT and ASTER Data. Remote Sens. 2010, 2, 1035–1056. [Google Scholar] [CrossRef] [Green Version]
- Hao, P.-Y.; Tang, H.-J.; Chen, Z.-X.; Meng, Q.-Y.; Kang, Y.-P. Early-season crop type mapping using 30-m reference time series. J. Integr. Agric. 2020, 19, 1897–1911. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, S.; Li, W.; Zhang, C. Parcel-level mapping of crops in a smallholder agricultural area: A case of central China using single-temporal VHSR imagery. Comput. Electron. Agric. 2020, 175, 105581. [Google Scholar] [CrossRef]
- Bagan, H.; Li, H.; Yang, Y.; Takeuchi, W.; Yamagata, Y. Sensitivity of the subspace method for land cover classification. Egypt. J. Remote Sens. Space Sci. 2018, 21, 383–389. [Google Scholar] [CrossRef]
- Lambert, M.-J.; Traoré, P.C.S.; Blaes, X.; Baret, P.; Defourny, P. Estimating smallholder crops production at village level from Sentinel-2 time series in Mali’s cotton belt. Remote Sens. Environ. 2018, 216, 647–657. [Google Scholar] [CrossRef]
- Lane, C.R.; Liu, H.; Autrey, B.C.; Anenkhonov, O.A.; Chepinoga, V.V.; Wu, Q. Improved Wetland Classification Using Eight-Band High Resolution Satellite Imagery and a Hybrid Approach. Remote Sens. 2014, 6, 12187–12216. [Google Scholar] [CrossRef] [Green Version]
- Gómez, C.; White, J.C.; Wulder, M.A. Optical remotely sensed time series data for land cover classification: A review. ISPRS J. Photogramm. Remote Sens. 2016, 116, 55–72. [Google Scholar] [CrossRef] [Green Version]
- Palacios-Orueta, A.; Huesca, M.; Whiting, M.L.; Litago, J.; Khanna, S.; Garcia, M.; Ustin, S.L. Derivation of phenological metrics by function fitting to time-series of Spectral Shape Indexes AS1 and AS2: Mapping cotton phenological stages using MODIS time series. Remote Sens. Environ. 2012, 126, 148–159. [Google Scholar] [CrossRef]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.; Su, W.; Zhang, X.; Zhu, D.; Wu, W. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef] [Green Version]
- Xun, L.; Zhang, J.; Cao, D.; Wang, J.; Zhang, S.; Yao, F. Mapping cotton cultivated area combining remote sensing with a fused representation-based classification algorithm. Comput. Electron. Agric. 2021, 181, 105940. [Google Scholar] [CrossRef]
- Domenikiotis, C.; Spiliotopoulos, M.; Tsiros, E.; Dalezios, N.R. Early cotton yield assessment by the use of the NOAA/AVHRR derived Vegetation Condition Index (VCI) in Greece. Int. J. Remote Sens. 2004, 25, 2807–2819. [Google Scholar] [CrossRef]
- Sun, C.; Bian, Y.; Zhou, T.; Pan, J. Using of Multi-Source and Multi-Temporal Remote Sensing Data Improves Crop-Type Mapping in the Subtropical Agriculture Region. Sensors 2019, 19, 2401. [Google Scholar] [CrossRef] [Green Version]
- Dong, J.; Fu, Y.; Wang, J.; Tian, H.; Fu, S.; Niu, Z.; Han, W.; Zheng, Y.; Huang, J.; Yuan, W. Early-season mapping of winter wheat in China based on Landsat and Sentinel images. Earth Syst. Sci. Data 2020, 12, 3081–3095. [Google Scholar] [CrossRef]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal Convolutional Neural Network for the Classification of Satellite Image Time Series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Hassan-Esfahani, L.; Torres-Rua, A.; Jensen, A.; McKee, M. Assessment of Surface Soil Moisture Using High-Resolution Multi-Spectral Imagery and Artificial Neural Networks. Remote Sens. 2015, 7, 2627–2646. [Google Scholar] [CrossRef] [Green Version]
- Berhane, T.M.; Lane, C.R.; Wu, Q.; Autrey, B.C.; Anenkhonov, O.A.; Chepinoga, V.V.; Liu, H. Decision-Tree, Rule-Based, and Random Forest Classification of High-Resolution Multispectral Imagery for Wetland Mapping and Inventory. Remote Sens. 2018, 10, 580. [Google Scholar] [CrossRef] [Green Version]
- Hubert-Moy, L.; Thibault, J.; Fabre, E.; Rozo, C.; Arvor, D.; Corpetti, T.; Rapinel, S. Mapping Grassland Frequency Using Decadal MODIS 250 m Time-Series: Towards a National Inventory of Semi-Natural Grasslands. Remote Sens. 2019, 11, 3041. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Thenkabail, P.S.; Tilton, J.C.; Gumma, M.K.; Teluguntla, P.; Oliphant, A.; Congalton, R.G.; Yadav, K.; Gorelick, N. Nominal 30-m cropland extent map of continental Africa by integrating pixel-based and object-based algorithms using Sentinel-2 and Landsat-8 data on Google Earth Engine. Remote Sens. 2017, 9, 1065. [Google Scholar] [CrossRef] [Green Version]
- Bazi, Y.; Melgani, F. Convolutional SVM Networks for Object Detection in UAV Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3107–3118. [Google Scholar] [CrossRef]
- Zhu, Z.; Luo, Y.; Wei, H.; Li, Y.; Qi, G.; Mazur, N.; Li, Y.; Li, P. Atmospheric Light Estimation Based Remote Sensing Image Dehazing. Remote Sens. 2021, 13, 2432. [Google Scholar] [CrossRef]
- Ji, S.; Zhang, C.; Xu, A.; Shi, Y.; Duan, Y. 3D Convolutional Neural Networks for Crop Classification with Multi-Temporal Remote Sensing Images. Remote Sens. 2018, 10, 75. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Raczko, E.; Zagajewski, B. Comparison of support vector machine, random forest and neural network classifiers for tree species classification on airborne hyperspectral APEX images. Eur. J. Remote Sens. 2017, 50, 144–154. [Google Scholar] [CrossRef] [Green Version]
- Thanh Noi, P.; Kappas, M. Comparison of Random Forest, k-Nearest Neighbor, and Support Vector Machine Classifiers for Land Cover Classification Using Sentinel-2 Imagery. Sensors 2017, 18, 18. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Al-Shammari, D.; Fuentes, I.; Whelan, B.M.; Filippi, P.; Bishop, T.F.A. Mapping of Cotton Fields Within-Season Using Phenology-Based Metrics Derived from a Time Series of Landsat Imagery. Remote Sens. 2020, 12, 3038. [Google Scholar] [CrossRef]
- Lebourgeois, V.; Dupuy, S.; Vintrou, É.; Ameline, M.; Butler, S.; Bégué, A. A Combined Random Forest and OBIA Classification Scheme for Mapping Smallholder Agriculture at Different Nomenclature Levels Using Multisource Data (Simulated Sentinel-2 Time Series, VHRS and DEM). Remote Sens. 2017, 9, 259. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Chen, S.; Useya, J.; Mugiyo, H. Decision-level fusion of Sentinel-1 SAR and Landsat 8 OLI texture features for crop discrimination and classification: Case of Masvingo, Zimbabwe. Heliyon 2020, 6, e05358. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.M.; He, G.J.; Peng, Y.; Long, T.F. Spectral-spatial multi-feature classification of remote sensing big data based on a random forest classifier for land cover mapping. Clust. Comput. 2017, 20, 2311–2321. [Google Scholar] [CrossRef]
- She, X.; Fu, K.; Wang, J.; Qi, W.; Li, X.; Fu, S. Identification of Cotton Using Random Forest Based on Wide-Band Imaging Spectrometer Data of Tiangong-2. Lect. Notes Electr. Eng. 2019, 5417, 264–276. [Google Scholar] [CrossRef]
- You, N.; Dong, J.; Huang, J.; Du, G.; Zhang, G.; He, Y.; Yang, T.; Di, Y.; Xiao, X. The 10-m crop type maps in Northeast China during 2017–2019. Sci. Data 2021, 8, 41. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Wan, Y.; Ye, Z.; Lai, X. Remote sensing image classification based on the optimal support vector machine and modified binary coded ant colony optimization algorithm. Inf. Sci. 2017, 402, 50–68. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, R.; Wang, S.; Wang, F. Feature Selection Method Based on High-Resolution Remote Sensing Images and the Effect of Sensitive Features on Classification Accuracy. Sensors 2018, 18, 2013. [Google Scholar] [CrossRef] [Green Version]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Cao, X.; Wei, C.; Han, J.; Jiao, L. Hyperspectral Band Selection Using Improved Classification Map. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2147–2151. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Pan, Z.; Wang, H.; Huang, P.; Sun, J.; Qin, F.; Liu, Z. An Improved Multi-temporal and Multi-feature Tea Plantation Identification Method Using Sentinel-2 Imagery. Sensors 2019, 19, 2087. [Google Scholar] [CrossRef] [Green Version]
- Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of Sentinel-2 Red-Edge Bands for Empirical Estimation of Green LAI and Chlorophyll Content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, Y.; Zhu, Z.; Guo, W.; Sun, Y.; Yang, X.; Kovalskyy, V. Continuous Monitoring of Cotton Stem Water Potential using Sentinel-2 Imagery. Remote Sens. 2020, 12, 1176. [Google Scholar] [CrossRef] [Green Version]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Cui, J.; Wang, W.; Lin, C. A Study for Texture Feature Extraction of High-Resolution Satellite Images Based on a Direction Measure and Gray Level Co-Occurrence Matrix Fusion Algorithm. Sensors 2017, 17, 1474. [Google Scholar] [CrossRef] [Green Version]
- Hall-Beyer, M. GLCM Texture: A Tutorial. 2017, 2. Available online: https://www.researchgate.net/publication/315776784?channel=doi&linkId=58e3e0b10f7e9bbe9c94cc90&showFulltext=true (accessed on 1 December 2021).
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Du, P.; Samat, A.; Waske, B.; Liu, S.; Li, Z. Random Forest and Rotation Forest for fully polarized SAR image classification using polarimetric and spatial features. ISPRS J. Photogramm. Remote Sens. 2015, 105, 38–53. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature Selection: A Data Perspective. ACM Comput. Surv. 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Cánovas-García, F.; Alonso-Sarría, F. Optimal Combination of Classification Algorithms and Feature Ranking Methods for Object-Based Classification of Submeter Resolution Z/I-Imaging DMC Imagery. Remote Sens. 2015, 7, 4651–4677. [Google Scholar] [CrossRef] [Green Version]
- Guan, H.; Li, J.; Chapman, M.; Deng, F.; Ji, Z.; Yang, X. Integration of orthoimagery and lidar data for object-based urban thematic mapping using random forests. Int. J. Remote Sens. 2013, 34, 5166–5186. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]

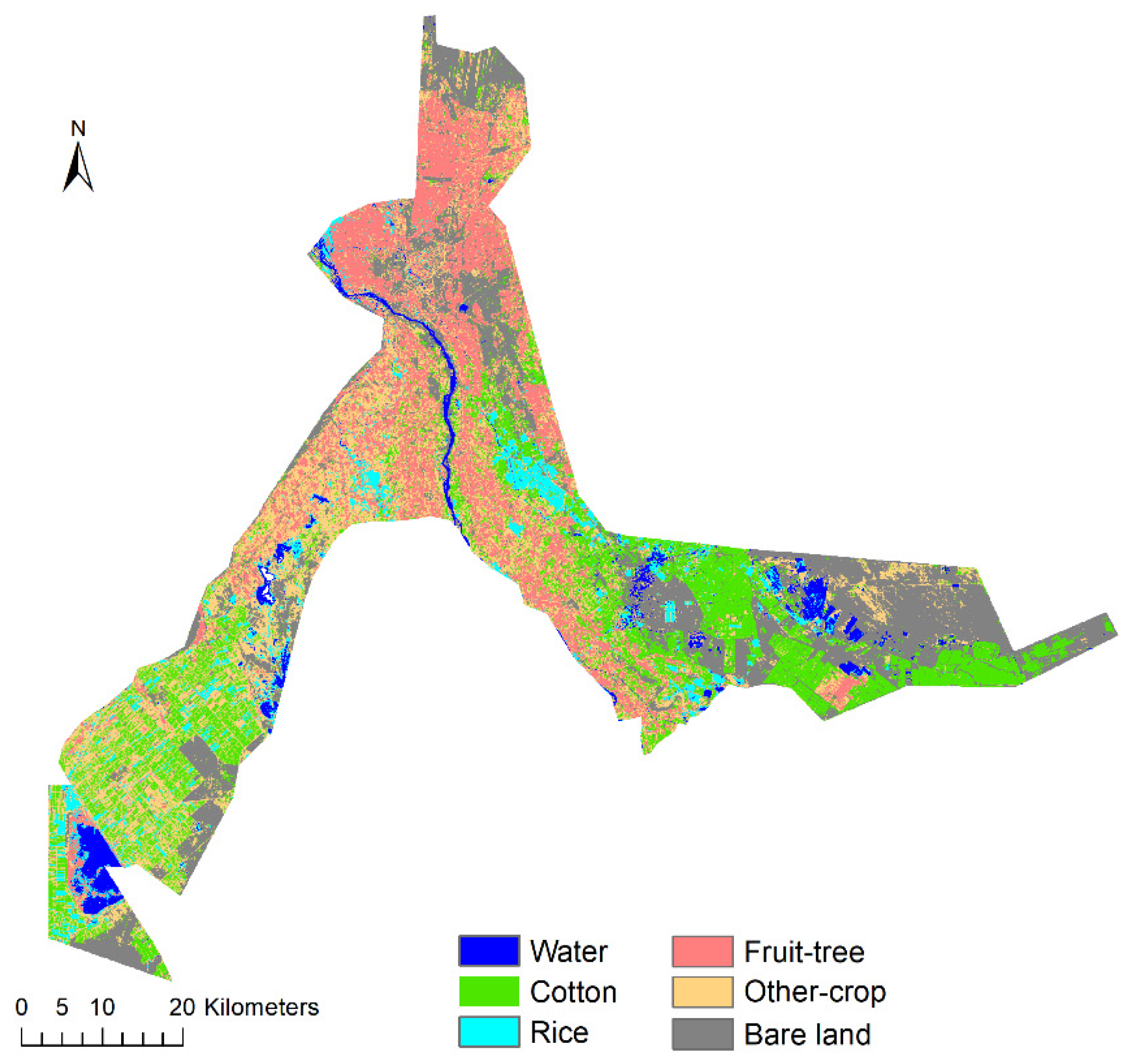
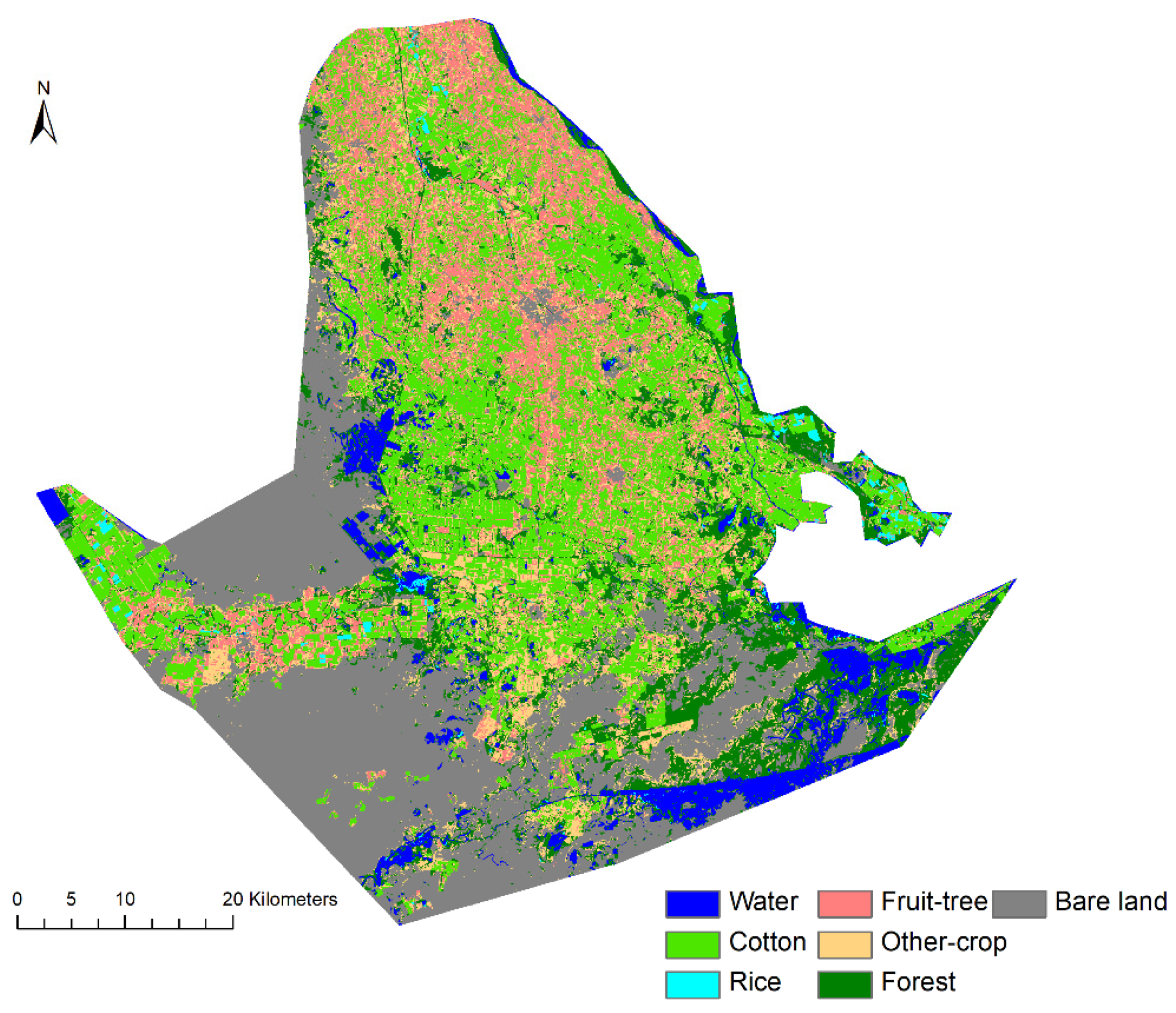
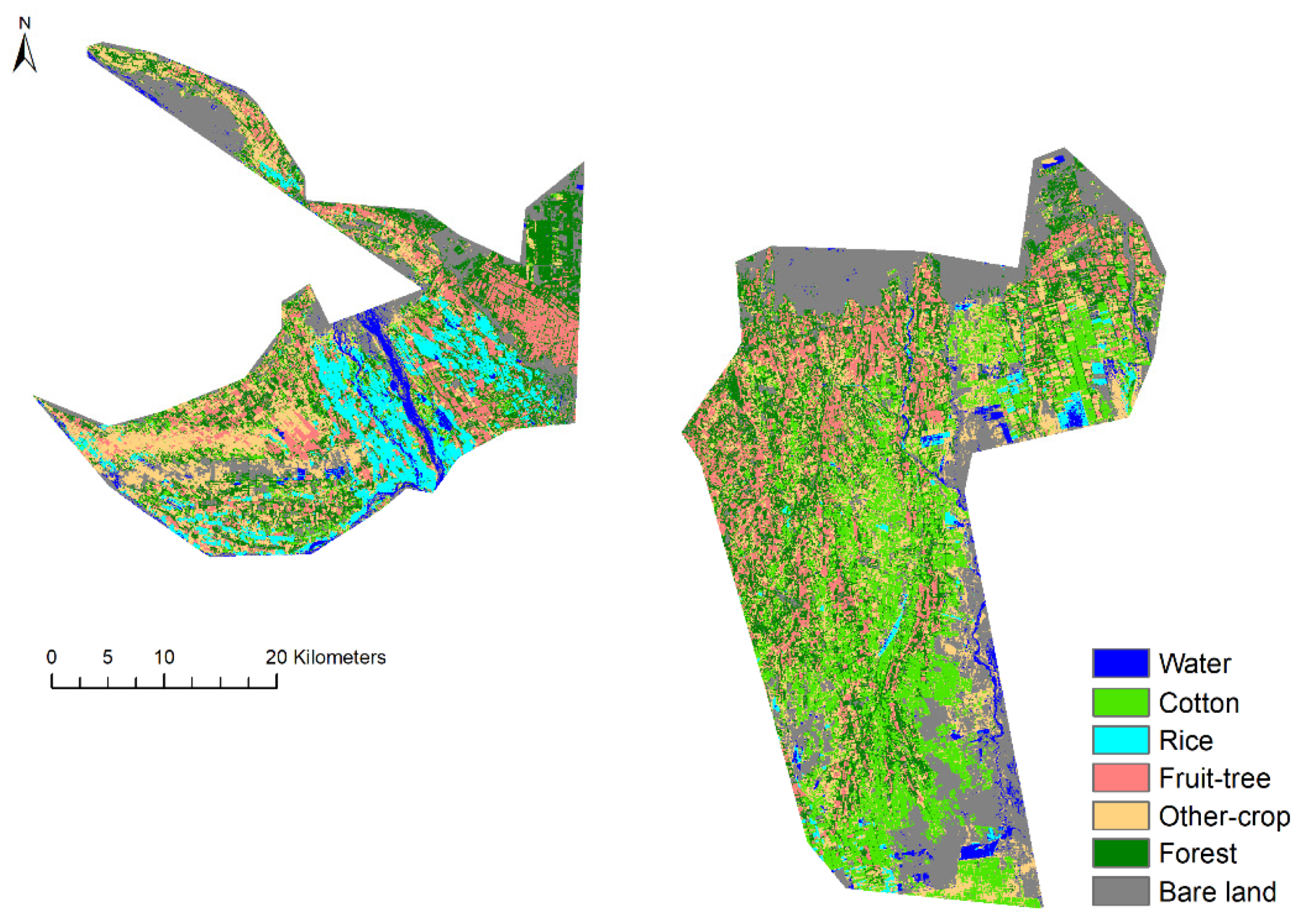
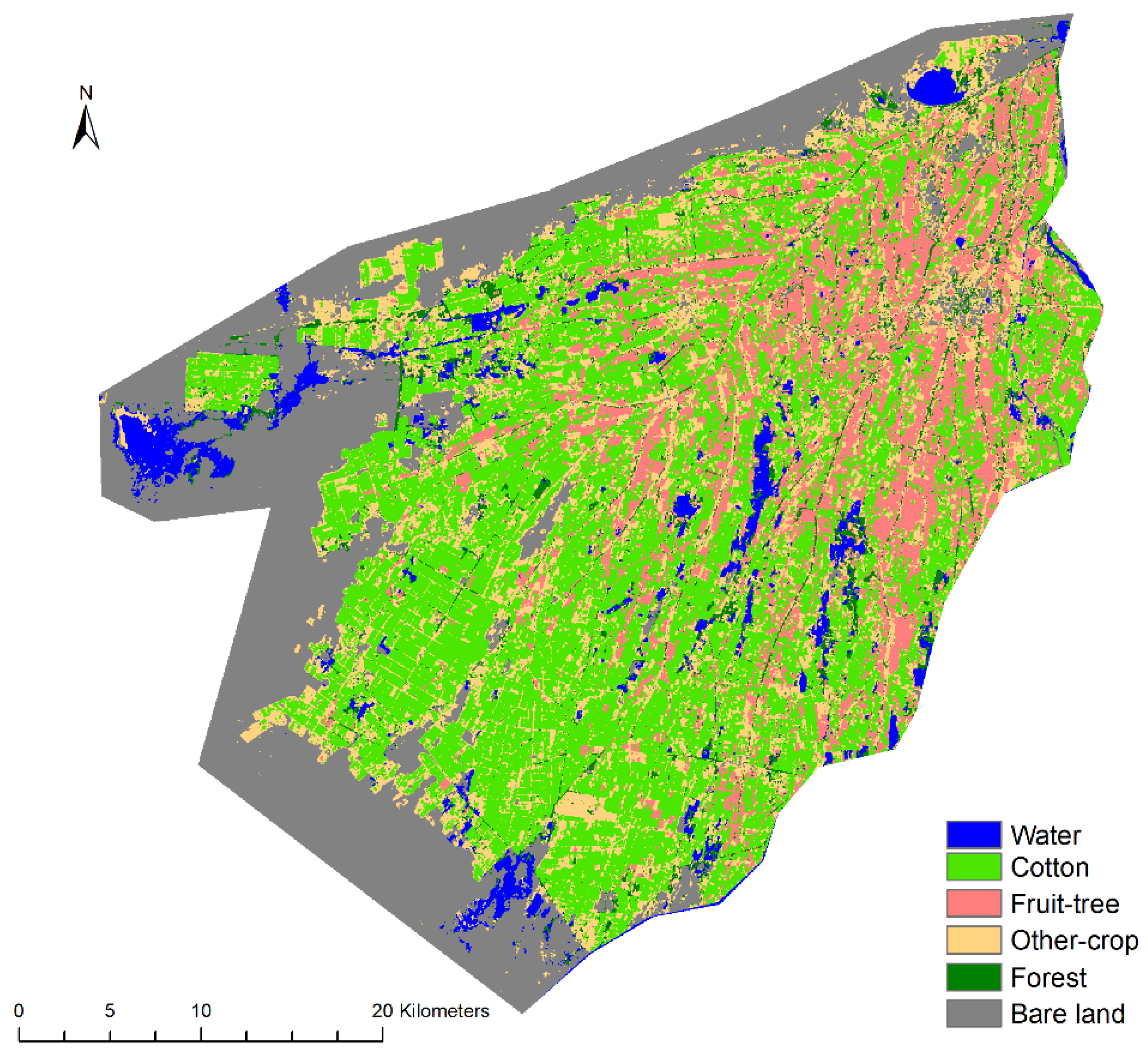
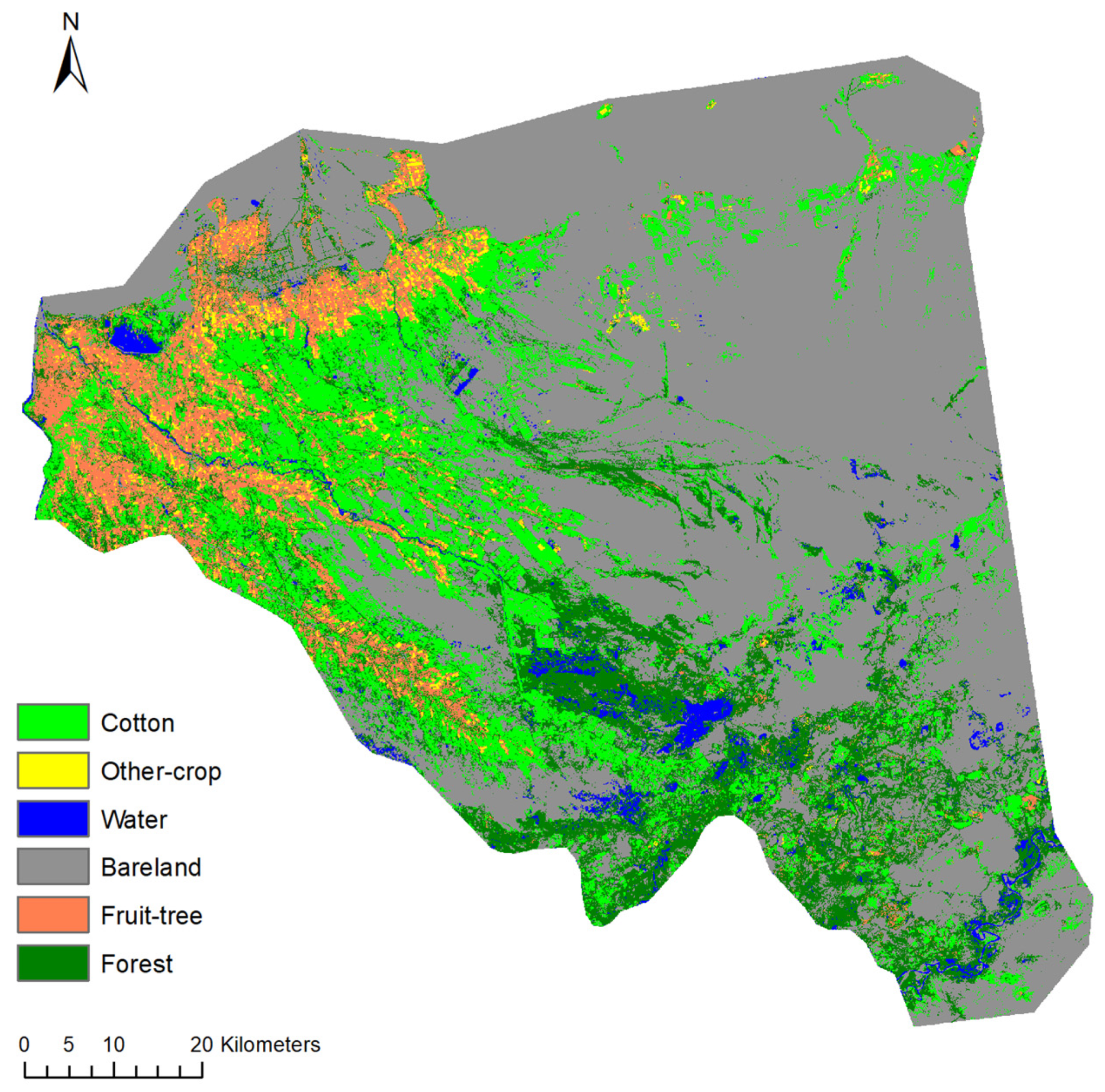
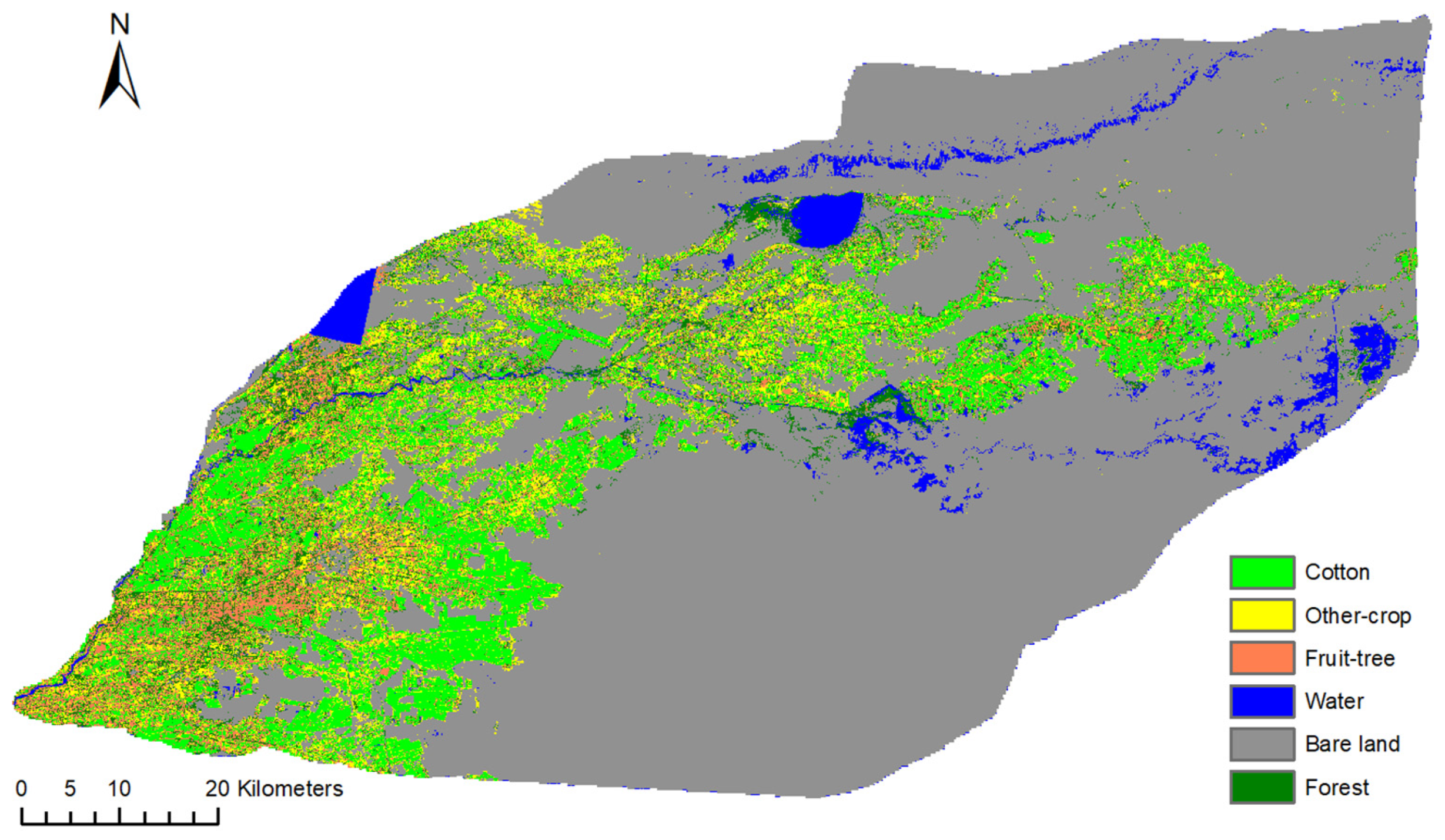
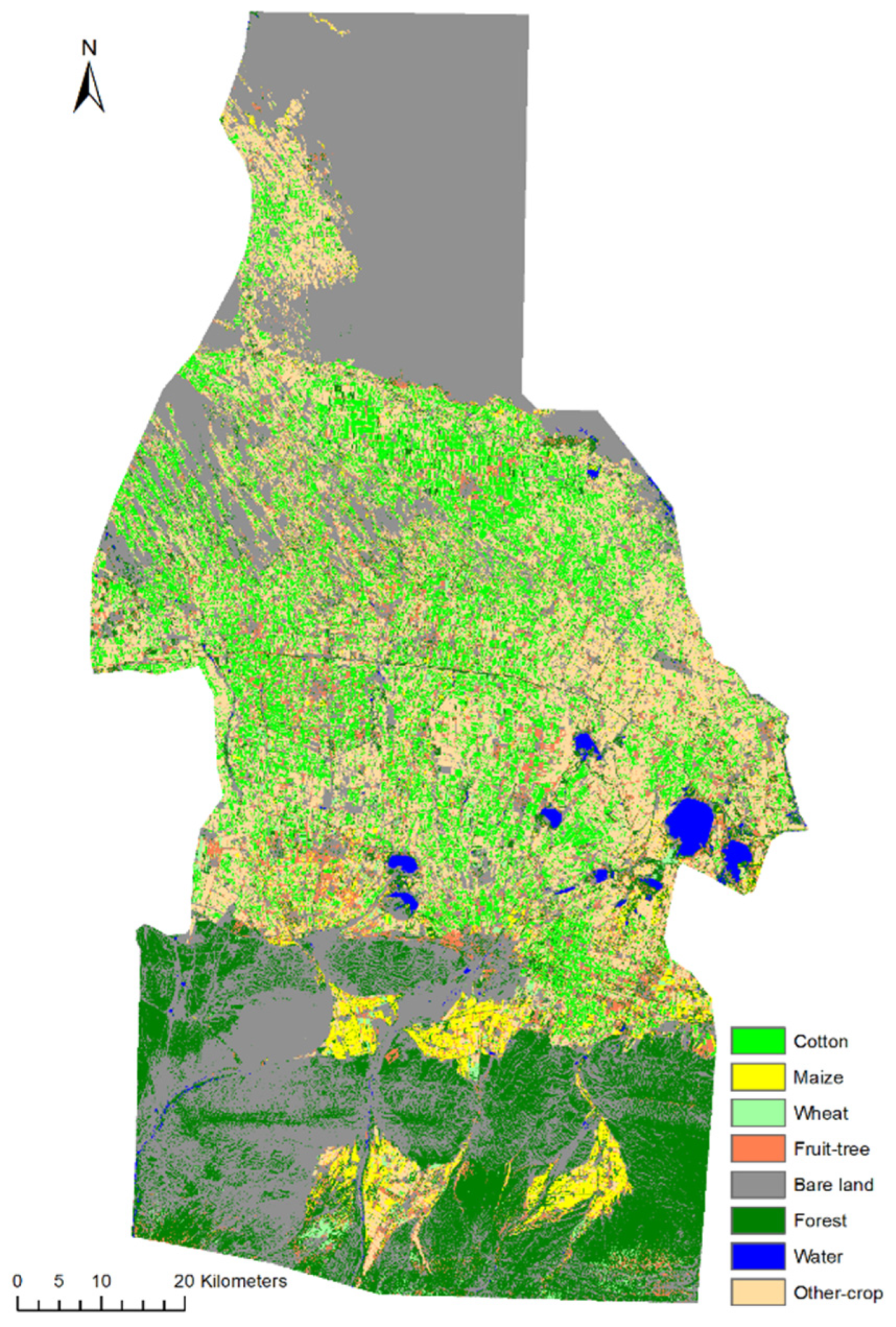
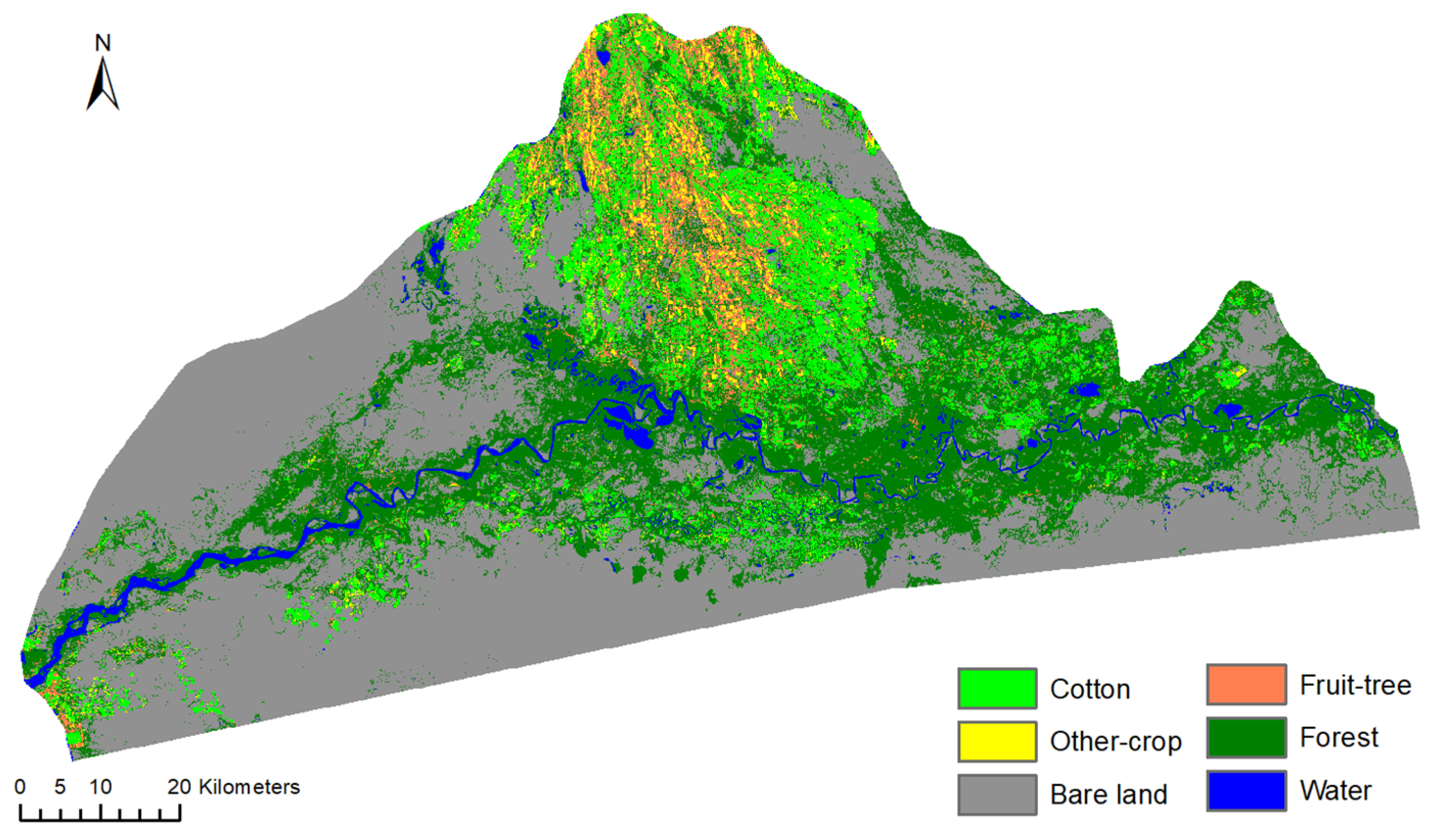
| Author | Study Area | Smallest Unit | Classifier | Satellite |
|---|---|---|---|---|
| Chen, Y.L. et al., 2018 [12] | Brazil | Pixels | DT | MODIS (250 m) |
| Conrad, C. et al., 2013 [13] | Uzbekistan | Objects | DT | SPOT5(2.5–5 m)/ASTER (15–30m) |
| Conrad, C. et al., 2010 [14] | Uzbekistan | Objects | RF | RapidEye (6.5m)/Landsat5 (30 m) |
| Hao, P.Y. et al., 2020 [15] | China | Pixels | NN | Landsat-7/8 (30m)/Sentinel-2 (30 m) |
| Zhang, P. et al., 2018 [16] | China | Objects | RF/SVM | WorldView-2 (0.5 m) |
| Bagan, H. et al., 2018 [17] | China | Pixels | NN | Landsat-5 (30 m) |
| Lambert, M.J. et al., 2020 [18] | Mali | Pixels | RF | Sentinel-2 (30 m) |
| Cotton | Wheat | Rice | Maize | |
|---|---|---|---|---|
| Alaer | 100.66 | - | 4.82 | 3.23 |
| Aksu | 64.99 | 10.23 | 1.75 | 3.61 |
| Awat | 101.64 | 12.20 | - | 3.59 |
| Wensu | 39.91 | 18.84 | 8.45 | 6.39 |
| Xinhe | 67.95 | 11.34 | - | 3.27 |
| Kuqa | 119.55 | 29.25 | - | 5.71 |
| Jiashi | 87.4 | 25.8 | - | 22.77 |
| Shawan | 112.05 | 9.85 | - | 18.60 |
| Xayar | 125.26 | 19.00 | - | 3.25 |
| Usu | 110.74 | 8.87 | 0.54 | 15.13 |
| Vegetation Index | Formula | Description |
|---|---|---|
| DVI | DVI is the difference in reflectivity of the two channels. It is sensitive to vegetation. | |
| RVI | RVI is the ratio of reflectance of two bands. It is suitable for areas with high vegetation coverage. | |
| NDVI | The range of NDVI is −1~1. It is suitable for dynamic monitoring of early and middle growth stages of vegetation | |
| SAVI | L represents the degree of vegetation coverage, and the range is 0~1. L = 0.5 | |
| EVI | EVI enhances the vegetation signal by adding blue bands to correct soil background and aerosol scattering effects. In this study, L is set to 1.5, C1 is set to 6, C2 is set to 7.5. |
| Feature Name | Formulation |
|---|---|
| GLCM Mean | or |
| GLCM Variance | or |
| Homogeneity | |
| Contrast | |
| Dissimilarity | |
| Entropy | |
| Second Moment | |
| Correlation |
| Group | Classifier | OA | Kappa | UA | PA | RAC | |
|---|---|---|---|---|---|---|---|
| Alaer | Single-time | RF | 92.48% | 0.9102 | 98.30% | 99.63% | 95.22% |
| Multi-time | RF | 95.05% | 0.9409 | 99.74% | 99.63% | 98.28% | |
| Multi-features | RF | 95.01% | 0.9403 | 99.71% | 99.93% | 98.25% | |
| Selected features | RF | 94.82% | 0.9381 | 99.08% | 98.83% | 96.77% | |
| Aksu | Single-time | RF | 86.89% | 0.8388 | 75.83% | 95.83% | 83.70% |
| Multi-time | RF | 91.82% | 0.9003 | 85.44% | 96.93% | 90.43% | |
| Multi-features | SVM | 98.65% | 0.9832 | 97.91% | 98.14% | 87.29% | |
| Selected features | RF | 92.66% | 0.9102 | 84.58% | 96.35% | 87.63% | |
| Awat | Single-time | RF | 91.74% | 0.8999 | 97.33% | 95.83% | 73.63% |
| Multi-time | RF | 89.44% | 0.8735 | 99.78% | 95.16% | 75.22% | |
| Multi-features | RF | 96.67% | 0.9596 | 99.73% | 95.16% | 80.33% | |
| Selected features | SVM | 91.21% | 0.8932 | 94.34% | 99.69% | 82.82% | |
| Wensu | Single-time | ANN | 94.45% | 0.9318 | 97.19% | 99.81% | 93.91% |
| Multi-time | RF | 95.89% | 0.9495 | 94.79% | 100.00% | 83.30% | |
| Multi-features | SVM | 95.84% | 0.9491 | 95.30% | 100.00% | 78.78% | |
| Selected features | SVM | 96.79% | 0.9606 | 95.21% | 100.00% | 80.19% | |
| Xinhe | Single-time | RF | 94.32% | 0.9257 | 94.74% | 98.39% | 86.92% |
| Multi-time | RF | 94.41% | 0.9299 | 94.73% | 99.46% | 88.36% | |
| Multi-features | RF | 96.88% | 0.9593 | 94.55% | 94.72% | 70.66% | |
| Selected features | RF | 96.13% | 0.9495 | 94.63% | 97.76% | 93.32% | |
| Kuqa | Single-time | SVM | 91.08% | 0.8861 | 89.70% | 98.91% | 80.82% |
| Multi-time | SVM | 95.64% | 0.9443 | 74.27% | 99.56% | 89.84% | |
| Multi-features | RF | 96.05% | 0.9496 | 80.49% | 100.00% | 93.68% | |
| Selected features | RF | 92.47% | 0.9022 | 68.78% | 94.76% | 83.59% | |
| Jiashi | Single-time | RF | 93.66% | 0.9149 | 82.95% | 98.78% | 89.40% |
| Multi-time | SVM | 94.66% | 0.9285 | 82.49% | 100.00% | 93.59% | |
| Multi-features | SVM | 93.14% | 0.9082 | 78.99% | 99.85% | 92.85% | |
| Selected features | RF | 94.62% | 0.9279 | 82.18% | 100.00% | 99.76% | |
| Shawan | Single-time | RF | 89.93% | 86.84% | 100.00% | 99.60% | 95.19% |
| Multi-time | RF | 94.46% | 92.92% | 100.00% | 99.90% | 96.17% | |
| Multi-features | RF | 94.01% | 92.31% | 100.00% | 99.93% | 94.93% | |
| Selected features | RF | 93.03% | 91.02% | 100.00% | 98.00% | 88.03% | |
| Xayar | Single-time | SVM | 86.36% | 0.8209 | 92.72% | 99.29% | 67.96% |
| Multi-time | SVM | 86.96% | 0.8304 | 100.00% | 98.35% | 58.53% | |
| Multi-features | RF | 88.25% | 0.847 | 100.00% | 95.27% | 64.06% | |
| Selected features | RF | 89.10% | 0.8321 | 100.00% | 93.85% | 73.37% | |
| Usu | Single-time | ANN | 97.58% | 0.9637 | 99.33% | 96.45% | 90.16% |
| Multi-time | ANN | 96.77% | 0.9546 | 99.26% | 98.34% | - | |
| Multi-features | SVM | 90.77% | 0.8708 | 100.00% | 78.78% | 98.62% | |
| Selected features | SVM | 96.20% | 0.9466 | 98.34% | 98.34% | 93.18% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, H.; Fan, Z.; Wang, C.; Zhang, N.; Wang, T.; Chen, R.; Bai, T. Cotton Classification Method at the County Scale Based on Multi-Features and Random Forest Feature Selection Algorithm and Classifier. Remote Sens. 2022, 14, 829. https://doi.org/10.3390/rs14040829
Fei H, Fan Z, Wang C, Zhang N, Wang T, Chen R, Bai T. Cotton Classification Method at the County Scale Based on Multi-Features and Random Forest Feature Selection Algorithm and Classifier. Remote Sensing. 2022; 14(4):829. https://doi.org/10.3390/rs14040829
Chicago/Turabian StyleFei, Hao, Zehua Fan, Chengkun Wang, Nannan Zhang, Tao Wang, Rengu Chen, and Tiecheng Bai. 2022. "Cotton Classification Method at the County Scale Based on Multi-Features and Random Forest Feature Selection Algorithm and Classifier" Remote Sensing 14, no. 4: 829. https://doi.org/10.3390/rs14040829
APA StyleFei, H., Fan, Z., Wang, C., Zhang, N., Wang, T., Chen, R., & Bai, T. (2022). Cotton Classification Method at the County Scale Based on Multi-Features and Random Forest Feature Selection Algorithm and Classifier. Remote Sensing, 14(4), 829. https://doi.org/10.3390/rs14040829







