A Comparative Study of Convolutional Neural Networks and Conventional Machine Learning Models for Lithological Mapping Using Remote Sensing Data
Abstract
:1. Introduction
2. Geological Setting
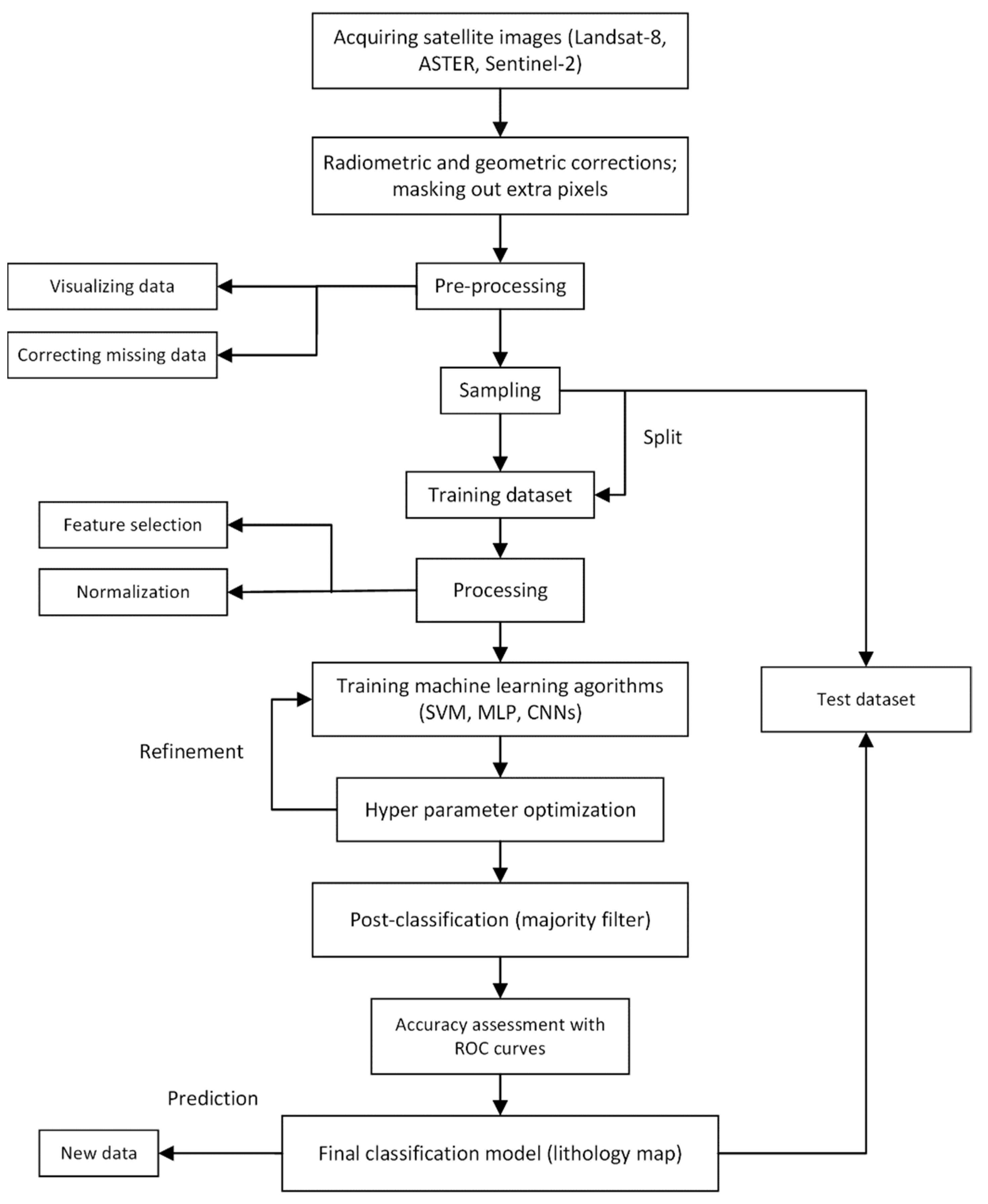
3. Materials and Methods
3.1. Remote-Sensing Data and Ground Truth
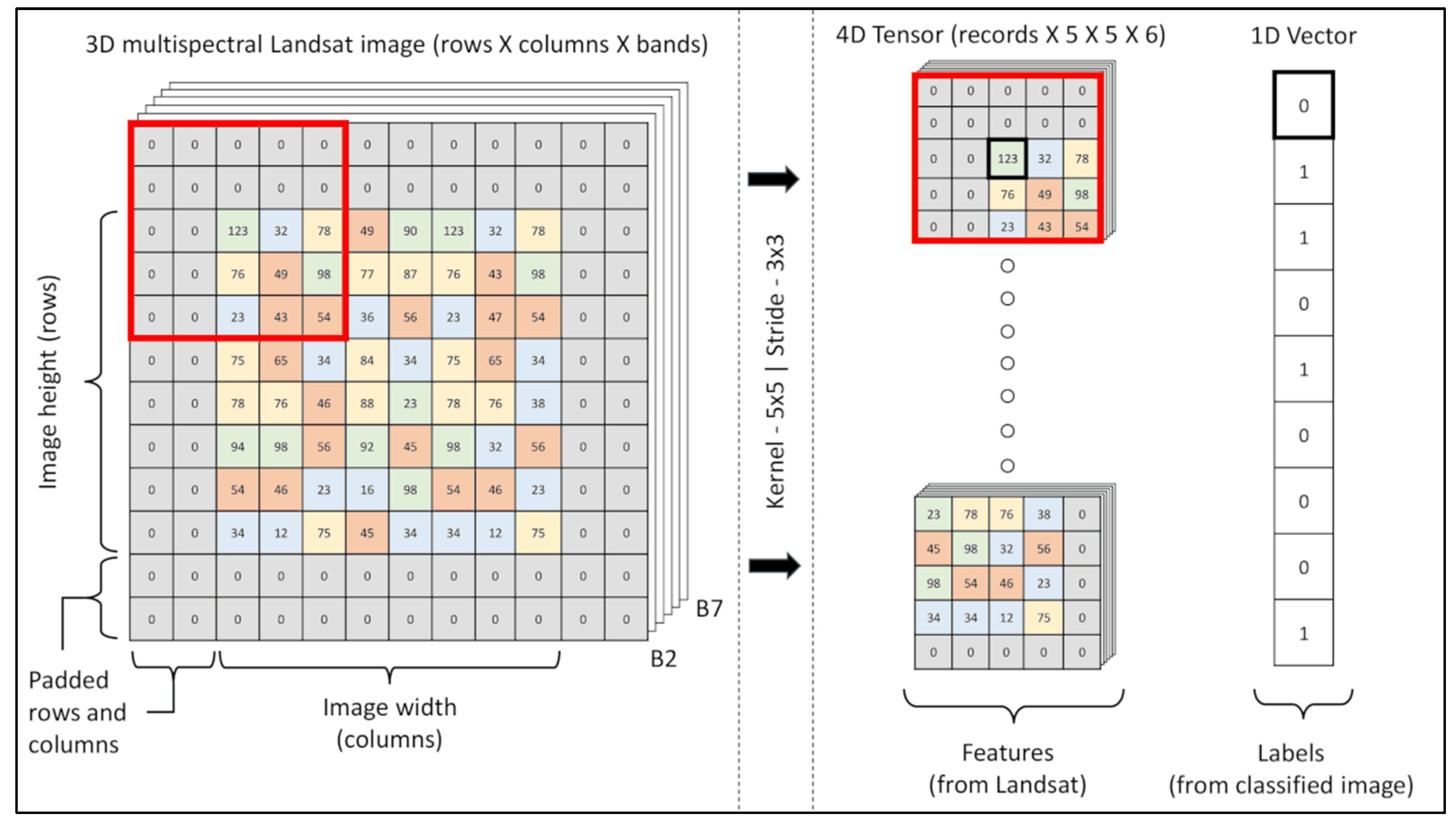
3.2. Preprocessing
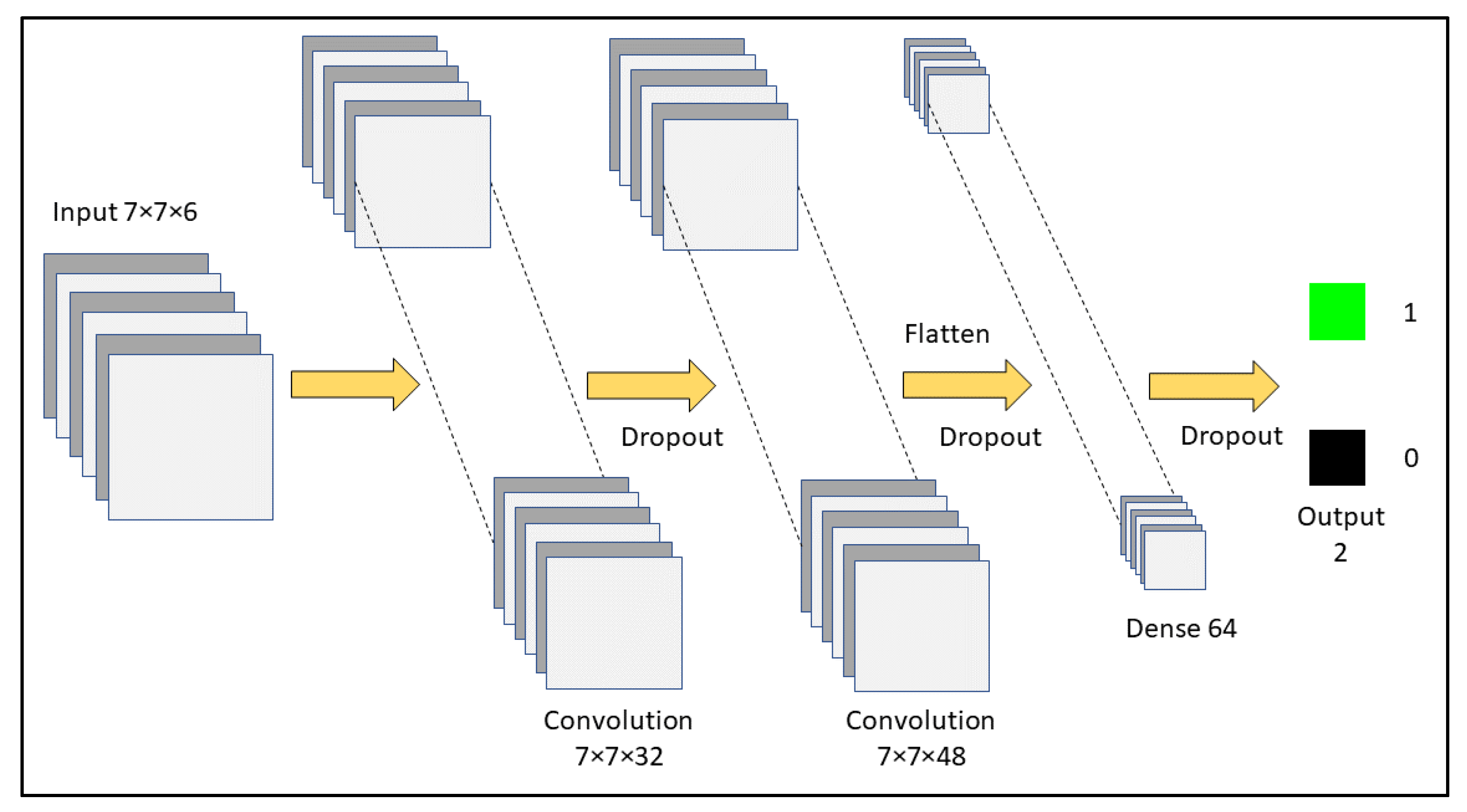
3.3. Machine Learning Methods
3.4. Framework and Experimental Setup
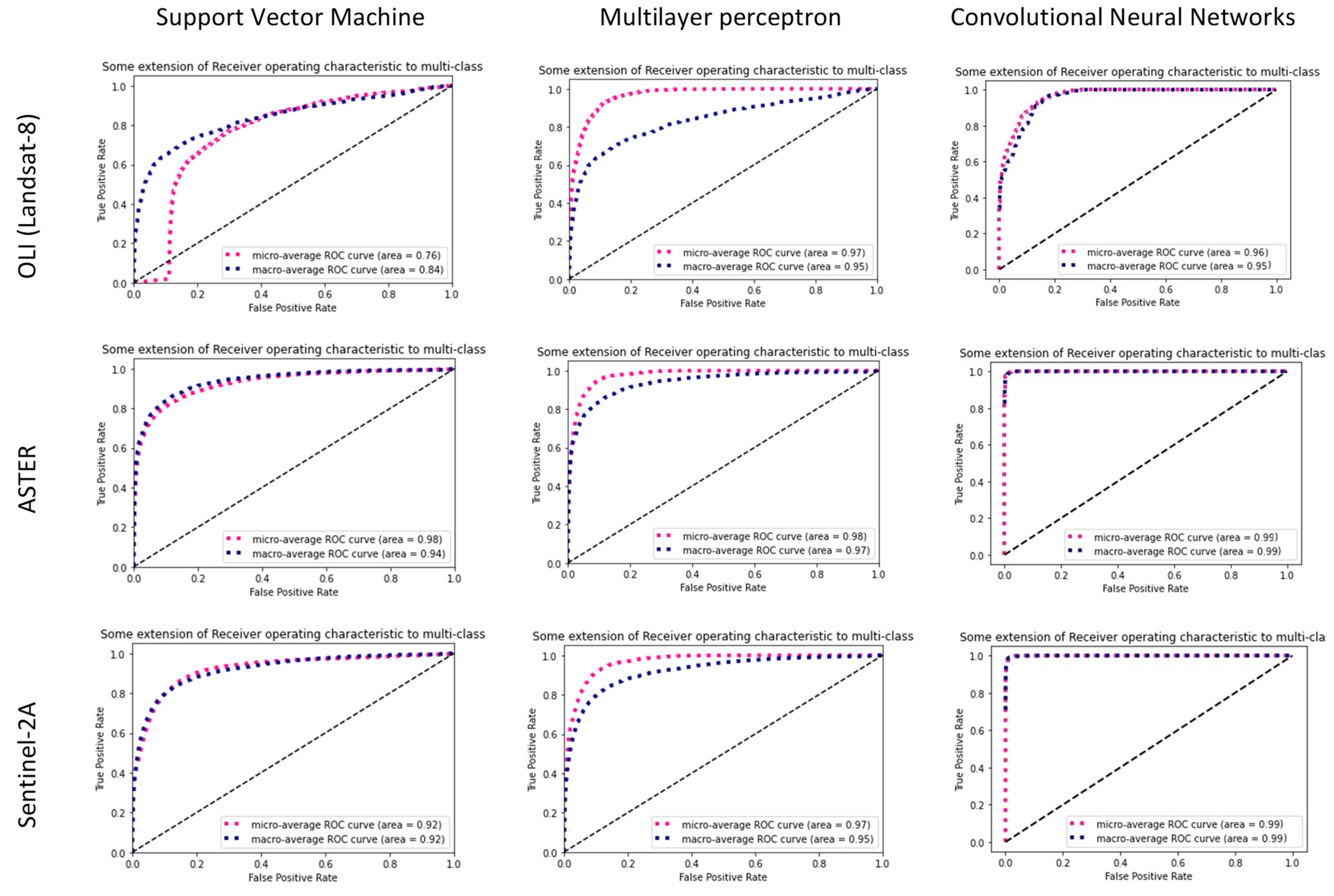
3.5. Receiver Operating Characteristics
4. Results
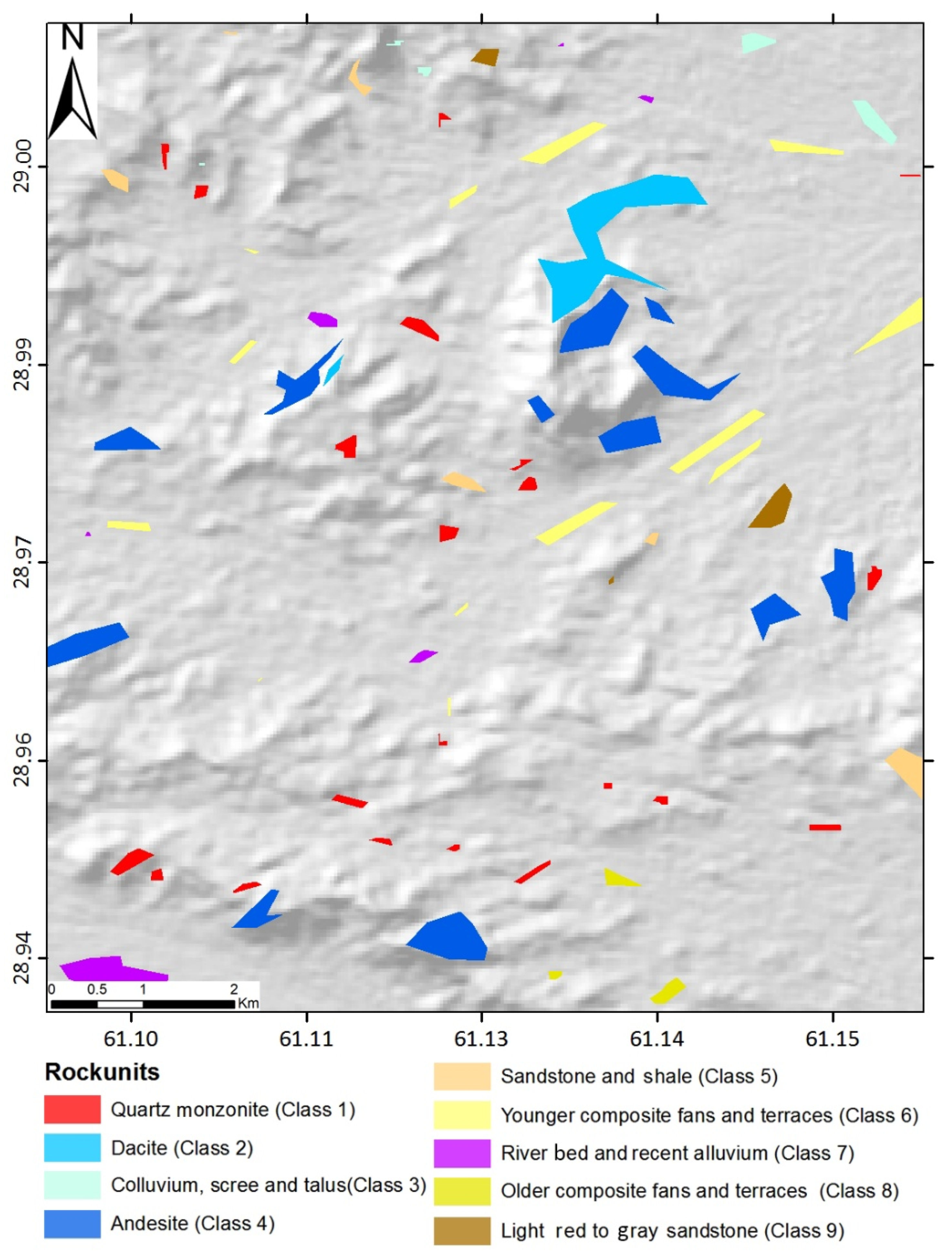
4.1. Classified Lithological Maps
4.2. Accuracy Assessment and Validation
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Satellite/Sensor | Subsystem | Band Number | Spectral Range (Micrometers) | Ground Resolution (m) | Swath Width (Km) | Year of Launch |
|---|---|---|---|---|---|---|
| Landsat 8 | OLI | Band 1 Coastal Aerosol | 0.43–0.45 | 30 | 185 | 2013 |
| Band 2 Blue | 0.45–0.51 | 30 | ||||
| Band 3 Green | 0.53–0.59 | 30 | ||||
| Band 4 Red | 0.64–0.67 | 30 | ||||
| Band 5 Near Infrared (NIR) | 0.85–0.88 | 30 | ||||
| Band 6 SWIR 1 | 1.57–1.65 | 30 | ||||
| Band 7 SWIR 2 | 2.11–2.29 | 30 | ||||
| Band 8 Panchromatic | 0.50–0.68 | 15 | ||||
| Band 9 Cirrus | 1.36–1.38 | 30 | ||||
| TIR | Band 10 Thermal Infrared (TIRS 1) | 10.60–11.19 | 100 | |||
| Band 11 Thermal Infrared (TIRS 2) | 11.50–12.51 | 100 | ||||
| ASTER | VNIR | Band 1 | 0.520–0.600 | 15 | 60 | 1999 |
| Band 2 | 0.630–0.690 | 15 | ||||
| Band 3 | 0.780–0.860 | 15 | ||||
| SWIR | Band 4 | 1.600–1.700 | 30 | |||
| Band 5 | 2.145–2.185 | 30 | ||||
| Band 6 | 2.185–2.225 | 30 | ||||
| Band 7 | 2.235–2.285 | 30 | ||||
| Band 8 | 2.295–2.365 | 30 | ||||
| Band 9 | 2.360–2.430 | 30 | ||||
| TIR | Band 10 | 8.125–8.475 | 90 | |||
| Band 11 | 8.475–8.825 | 90 | ||||
| Band 12 | 8.925–9.275 | |||||
| Band 13 | 10.250–10.950 | |||||
| Band 14 | 10.950–11.650 | |||||
| Sentinel-2 | Band 1 Coastal Aerosol | 0.433–0.453 | 60 | 290 | 2015 | |
| Band 2 Blue | 0.458–0.523 | 10 | ||||
| Band 3 Green | 0.543–0.578 | 10 | ||||
| Band 4 Red | 0.650–0.680 | 10 | ||||
| Band 5 Red Edge 1 | 0.698–0.713 | 20 | ||||
| Band 6 Red Edge 2 | 0.733–0.748 | 20 | ||||
| Band 7 Red Edge 3 | 0.773–0.793 | 20 | ||||
| Band 8 NIR | 0.785–0.900 | 10 | ||||
| Band 8A Narrow NIR | 0.855–0.875 | 20 | ||||
| Band 9 Water-Vapor | 0.935–0.955 | 60 | ||||
| Band 10 SWIR/Cirrus | 1.360–1.390 | 60 | ||||
| Band 11 SWIR 1 | 1.565–1.655 | 20 | ||||
| Band 12 SWIR 2 | 2.100–2.280 | 20 | ||||

References
- Othman, A.; Gloaguen, R. Improving lithological mapping by SVM classification of spectral and morphological features: The discovery of a new chromite body in the Mawat ophiolite complex (Kurdistan, NE Iraq). Remote Sens. 2014, 6, 6867–6896. [Google Scholar] [CrossRef] [Green Version]
- Qing, F.; Zhao, Y.; Meng, X.; Su, X.; Qi, T.; Yue, D. Application of machine learning to debris flow susceptibility mapping along the China–Pakistan Karakoram highway. Remote Sens. 2020, 12, 2933. [Google Scholar] [CrossRef]
- Torabi, A.; Berg, S.S. Scaling of fault attributes: A review. Mar. Pet. Geol. 2011, 28, 1444–1460. [Google Scholar] [CrossRef]
- Ding, W.-C.; Li, T.-D.; Chen, X.-H.; Chen, J.-P.; Xu, S.-L.; Zhang, Y.-P.; Li, B.; Yang, Q. Intra-continental deformation and tectonic evolution of the West Junggar Orogenic Belt, Central Asia: Evidence from remote sensing and structural geological analyses. Geosci. Front. 2020, 11, 651–663. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, J.; Jiang, D.; Zhuang, D.; Mansaray, L.R.; Zhang, B. Targeting mineral resources with remote sensing and field data in the Xiemisitai area, West Junggar, Xinjiang, China. Remote Sens. 2013, 5, 3156–3171. [Google Scholar] [CrossRef] [Green Version]
- Radford, D.D.G.; Cracknell, M.J.; Roach, M.J.; Cumming, G. V Geological mapping in Western Tasmania using radar and random forests. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3075–3087. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Müller, R.D.; Chandra, R. A review of machine learning in processing remote sensing data for mineral exploration. Remote Sens. Environ. 2022, 268, 112750. [Google Scholar] [CrossRef]
- Brimhall, G.H.; Dilles, J.H.; Proffett, J.M. The Role of Geologic Mapping in Mineral Exploration. Wealth Creat. Miner. Ind. Integr. Sci. Business Educ. 2005, 12, 221–241. [Google Scholar]
- Rowan, L.C.; Schmidt, R.G.; Mars, J.C. Distribution of hydrothermally altered rocks in the Reko Diq, Pakistan mineralized area based on spectral analysis of ASTER data. Remote Sens. Environ. 2006, 104, 74–87. [Google Scholar] [CrossRef]
- Latifovic, R.; Pouliot, D.; Campbell, J. Assessment of convolution neural networks for surficial geology mapping in the South Rae geological region, Northwest Territories, Canada. Remote Sens. 2018, 10, 307. [Google Scholar] [CrossRef] [Green Version]
- Asadzadeh, S.; de Souza Filho, C.R. A review on spectral processing methods for geological remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 69–90. [Google Scholar] [CrossRef]
- Rezaei, A.; Hassani, H.; Moarefvand, P.; Golmohammadi, A. Lithological mapping in Sangan region in Northeast Iran using ASTER satellite data and image processing methods. Geol. Ecol. Landsc. 2020, 4, 59–70. [Google Scholar] [CrossRef] [Green Version]
- Lazecký, M.; Spaans, K.; González, P.J.; Maghsoudi, Y.; Morishita, Y.; Albino, F.; Elliott, J.; Greenall, N.; Hatton, E.; Hooper, A.; et al. LiCSAR: An automatic InSAR tool for measuring and monitoring tectonic and volcanic activity. Remote Sens. 2020, 12, 2430. [Google Scholar] [CrossRef]
- Beiranvand Pour, A.; Hashim, M. ASTER, ALI and Hyperion sensors data for lithological mapping and ore minerals exploration. Springerplus 2014, 3, 130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shirmard, H.; Farahbakhsh, E.; Beiranvand Pour, A.; Muslim, A.M.; Müller, R.D.; Chandra, R. Integration of selective dimensionality reduction techniques for mineral exploration using ASTER satellite data. Remote Sens. 2020, 12, 1261. [Google Scholar] [CrossRef] [Green Version]
- van der Meer, F.D.; van der Werff, H.M.A.; van Ruitenbeek, F.J.A.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; van der Meijde, M.; Carranza, E.J.M.; de Smeth, J.B.; Woldai, T. Multi- and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Kuhn, S.; Cracknell, M.J.; Reading, A.M. Lithologic mapping using Random Forests applied to geophysical and remote-sensing data: A demonstration study from the Eastern Goldfields of Australia. Geophysics 2018, 83, B183–B193. [Google Scholar] [CrossRef]
- Farahbakhsh, E.; Chandra, R.; Olierook, H.; Scalzo, R.; Clark, C.; Reddy, S.; Müller, D. Computer vision-based framework for extracting tectonic lineaments from optical remote sensing data. Int. J. Remote Sens. 2020, 41, 1760–1787. [Google Scholar] [CrossRef]
- Sun, T.; Chen, F.; Zhong, L.; Liu, W.; Wang, Y. GIS-based mineral prospectivity mapping using machine learning methods: A case study from Tongling ore district, eastern China. Ore Geol. Rev. 2019, 109, 26–49. [Google Scholar] [CrossRef]
- Cracknell, M.J.; Reading, A.M. Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef] [Green Version]
- Kanevski, M. Machine Learning for Spatial Environmental Data; EPFL Press: New York, NY, USA, 2009. [Google Scholar]
- Ye, B.; Tian, S.; Ge, J.; Sun, Y. Assessment of WorldView-3 data for lithological mapping. Remote Sens. 2017, 9, 1132. [Google Scholar] [CrossRef]
- Farahbakhsh, E.; Shirmard, H.; Bahroudi, A.; Eslamkish, T. Fusing ASTER and QuickBird-2 satellite data for detailed investigation of porphyry copper deposits using PCA; Case study of Naysian deposit, Iran. J. Indian Soc. Remote Sens. 2016, 44, 525–537. [Google Scholar] [CrossRef]
- Beiranvand Pour, A.; Hashim, M.; Hong, J.K.; Park, Y. Lithological and alteration mineral mapping in poorly exposed lithologies using Landsat-8 and ASTER satellite data: North-eastern Graham Land, Antarctic Peninsula. Ore Geol. Rev. 2019, 108, 112–133. [Google Scholar] [CrossRef]
- Sekandari, M.; Masoumi, I.; Beiranvand Pour, A.; Muslim, A.M.; Rahmani, O.; Hashim, M.; Zoheir, B.; Pradhan, B.; Misra, A.; Aminpour, S.M. Application of Landsat-8, Sentinel-2, ASTER and WorldView-3 spectral imagery for exploration of carbonate-hosted Pb-Zn deposits in the Central Iranian Terrane (CIT). Remote Sens. 2020, 12, 1239. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Porwal, A.; Holden, E.-J.; Dentith, M.C. Towards automatic lithological classification from remote sensing data using support vector machines. Comput. Geosci. 2012, 45, 229–239. [Google Scholar] [CrossRef]
- Bressan, T.S.; Kehl de Souza, M.; Girelli, T.J.; Junior, F.C. Evaluation of machine learning methods for lithology classification using geophysical data. Comput. Geosci. 2020, 139, 104475. [Google Scholar] [CrossRef]
- Bachri, I.; Hakdaoui, M.; Raji, M.; Teodoro, A.C.; Benbouziane, A. Machine learning algorithms for automatic lithological mapping using remote sensing data: A case study from Souk Arbaa Sahel, Sidi Ifni Inlier, Western Anti-Atlas, Morocco. ISPRS Int. J. Geo-Inf. 2019, 8, 248. [Google Scholar] [CrossRef] [Green Version]
- Atangana Otele, C.G.; Onabid, M.A.; Assembe, P.S.; Nkenlifack, M. Updated lithological map in the Forest zone of the Centre, South and East regions of Cameroon using multilayer perceptron neural network and Landsat images. J. Geosci. Environ. Prot. 2021, 9, 120–134. [Google Scholar] [CrossRef]
- Venkatesh, Y.V.; Kumar Raja, S. On the classification of multispectral satellite images using the multilayer perceptron. Pattern Recognit. 2003, 36, 2161–2175. [Google Scholar] [CrossRef]
- Sergi, R.; Solaiman, B.; Mouchot, M.-C.; Pasquariello, G.; Pósa, P. Landsat-TM image classification using principal components analysis and neural networks. In Proceedings of the International Geoscience and Remote Sensing Symposium: Quantitative Remote Sensing for Science and Applications, Firenze, Italy, 10–14 July 1995; Volume 3, pp. 1927–1929. [Google Scholar]
- Neupane, B.; Horanont, T.; Aryal, J. Deep learning-based semantic segmentation of urban features in satellite images: A review and meta-analysis. Remote Sens. 2021, 13, 808. [Google Scholar] [CrossRef]
- He, Z.; Liu, H.; Wang, Y.; Hu, J. Generative adversarial networks-based semi-supervised learning for hyperspectral image classification. Remote Sens. 2017, 9, 1042. [Google Scholar] [CrossRef] [Green Version]
- Sang, X.; Xue, L.; Ran, X.; Li, X.; Liu, J.; Liu, Z. Intelligent high-resolution geological mapping based on SLIC-CNN. ISPRS Int. J. Geo-Inf. 2020, 9, 99. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-Y.; Lin, Y.-H.; Kung, C.-C.; Chung, M.-H.; Yen, I.-H. Design and implementation of cloud analytics-assisted smart power meters considering advanced artificial intelligence as edge analytics in demand-side management for smart homes. Sensors 2019, 19, 2047. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Georgiou, T.; Liu, Y.; Chen, W.; Lew, M. A survey of traditional and deep learning-based feature descriptors for high dimensional data in computer vision. Int. J. Multimed. Inf. Retr. 2020, 9, 135–170. [Google Scholar] [CrossRef] [Green Version]
- Shambhu, S.; Koundal, D.; Das, P.; Sharma, C. Binary classification of COVID-19 CT images using CNN: COVID diagnosis using CT. Int. J. E-Health Med. Commun. 2022, 13, 1–13. [Google Scholar] [CrossRef]
- Yang, M.; Liu, Y.; You, Z. The Euclidean embedding learning based on convolutional neural network for stereo matching. Neurocomputing 2017, 267, 195–200. [Google Scholar] [CrossRef]
- Jing, L.; Zhao, M.; Li, P.; Xu, X. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Saliu, O.; Curilla, D.; Lennon, M.; Chung, A. Lessons learned: Deep learning for mineral exploration. In Proceedings of the First EAGE Conference on Machine Learning in Americas, Online, 22–24 September 2020. [Google Scholar]
- Mei, S.; Geng, Y.; Hou, J.; Du, Q. Learning hyperspectral images from RGB images via a coarse-to-fine CNN. Sci. China Inf. Sci. 2022, 65, 152102. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.W.M.; van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [Green Version]
- Parsolang Engineering Consultant Company. Map Report: Deh Reza Exploration Area, Sistan and Baluchestan Province; Parsolang Engineering Consultant Company: Tehran, Iran, 2021. [Google Scholar]
- Groves, D.I.; Santosh, M.; Zhang, L. A scale-integrated exploration model for orogenic gold deposits based on a mineral system approach. Geosci. Front. 2020, 11, 719–738. [Google Scholar] [CrossRef]
- Vaughn, I. Landsat 8 (L8) Data Users Handbook; US Geological Survey: Sioux Falls, SD, USA, 2019.
- Abrams, M.; Hook, S.; Ramachandran, B. ASTER User Handbook; Jet Propulsion Laboratory: Pasadena, CA, USA, 2002.
- SUHET. Sentinel-2 User Handbook; European Space Agency: Paris, France, 2015. [Google Scholar]
- Grosse, R.; Johnson, M.K.; Adelson, E.H.; Freeman, W.T. Ground truth dataset and baseline evaluations for intrinsic image algorithms. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2335–2342. [Google Scholar]
- Krig, S. Ground Truth Data, Content, Metrics, and Analysis. In Computer Vision Metrics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 283–311. [Google Scholar]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Gewali, U.B.; Monteiro, S.T.; Saber, E. Machine learning based hyperspectral image analysis: A survey. arXiv 2018, arXiv:1802.08701. [Google Scholar]
- Liu, P.; Choo, K.-K.R.; Wang, L.; Huang, F. SVM or deep learning? A comparative study on remote sensing image classification. Soft Comput. 2017, 21, 7053–7065. [Google Scholar] [CrossRef]
- Maepa, F.; Smith, R.S.; Tessema, A. Support vector machine and artificial neural network modelling of orogenic gold prospectivity mapping in the Swayze greenstone belt, Ontario, Canada. Ore Geol. Rev. 2021, 130, 103968. [Google Scholar] [CrossRef]
- Abedi, M.; Norouzi, G.-H.; Bahroudi, A. Support vector machine for multi-classification of mineral prospectivity areas. Comput. Geosci. 2012, 46, 272–283. [Google Scholar] [CrossRef]
- Pal, M.; Rasmussen, T.; Porwal, A. Optimized lithological mapping from multispectral and hyperspectral remote sensing images using fused multi-classifiers. Remote Sens. 2020, 12, 177. [Google Scholar] [CrossRef] [Green Version]
- Abdolmaleki, M.; Rasmussen, T.M.; Pal, M.K. Exploration of IOCG mineralizations using integration of space-borne remote sensing data with airborne geophysical data. ISPRSn Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B3-2, 9–16. [Google Scholar] [CrossRef]
- Cardoso-Fernandes, J.; Teodoro, A.C.; Lima, A.; Roda-Robles, E. Semi-Automatization of Support Vector Machines to Map Lithium (Li) Bearing Pegmatites. Remote Sens. 2020, 12, 2319. [Google Scholar] [CrossRef]
- Lek, S.; Guégan, J.F. Artificial neural networks as a tool in ecological modelling, an introduction. Ecol. Modell. 1999, 120, 65–73. [Google Scholar] [CrossRef]
- Wang, G.; Yan, C.; Zhang, S.; Song, Y. Probabilistic neural networks and fractal method applied to mineral potential mapping in Luanchuan region, Henan Province, China. In Proceedings of the Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; pp. 1003–1007. [Google Scholar]
- Subasi, A.; Erçelebi, E. Classification of EEG signals using neural network and logistic regression. Comput. Methods Programs Biomed. 2005, 78, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Li, X.; Yuan, F.; Jowitt, S.M.; Zhang, M.; Zhou, J.; Zhou, T.; Li, X.; Ge, C.; Wu, B. Convolutional neural network and transfer learning based mineral prospectivity modeling for geochemical exploration of Au mineralization within the Guandian–Zhangbaling area, Anhui Province, China. Appl. Geochem. 2020, 122, 104747. [Google Scholar] [CrossRef]
- Xin, M.; Wang, Y. Research on image classification model based on deep convolution neural network. EURASIP J. Image Video Process. 2019, 2019, 40. [Google Scholar] [CrossRef] [Green Version]
- Shuo, H.; Kang, H. Deep CNN for Classification of Image Contents. In Proceedings of the 2021 3rd International Conference on Image Processing and Machine Vision (IPMV), Hong Kong, China, 22–24 May 2021; ACM: New York, NY, USA, 2021; pp. 60–65. [Google Scholar]
- Newman, E.; Kilmer, M.; Horesh, L. Image classification using local tensor singular value decompositions. In Proceedings of the IEEE 7th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Curaçao, The Netherlands, 10–13 December 2017; pp. 1–5. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Kantakumar, L.N.; Neelamsetti, P. Multi-temporal land use classification using hybrid approach. Egypt. J. Remote Sens. Space Sci. 2015, 18, 289–295. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.V.; Antony, G.M. A review of methods and applications of the ROC curve in clinical trials. Drug Inf. J. 2010, 44, 659–671. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kumar, C.; Shetty, A.; Raval, S.; Sharma, R.; Ray, P.K.C. Lithological Discrimination and Mapping using ASTER SWIR Data in the Udaipur area of Rajasthan, India. Procedia Earth Planet. Sci. 2015, 11, 180–188. [Google Scholar] [CrossRef] [Green Version]
- Zanaty, E.A. Support Vector Machines (SVMs) versus Multilayer Perception (MLP) in data classification. Egypt. Inform. J. 2012, 13, 177–183. [Google Scholar] [CrossRef]
- Chandra, R.; Jain, K.; Deo, R.V.; Cripps, S. Langevin-gradient parallel tempering for Bayesian neural learning. Neurocomputing 2019, 359, 315–326. [Google Scholar] [CrossRef] [Green Version]
- Zou, K.H.; O’Malley, A.J.; Mauri, L. Receiver-operating characteristic analysis for evaluating diagnostic tests and predictive models. Circulation 2007, 115, 654–657. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| Landsat 8 OLI | ASTER | Sentinel-2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lithology Type | Class Number | SVM | MLP | CNN | SVM | MLP | CNN | SVM | MLP | CNN |
| Quartz monzonite | 1 | 0.98 | 0.98 | 1 | 0.97 | 0.99 | 1 | 0.88 | 0.98 | 0.99 |
| Dacite | 2 | 0.99 | 0.99 | 0.99 | 0.88 | 0.99 | 1 | 0.89 | 0.99 | 0.99 |
| Colluvium scree and talus | 3 | 0.97 | 0.97 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| Andesite | 4 | 0.91 | 0.91 | 0.99 | 0.90 | 0.95 | 0.99 | 0.80 | 0.91 | 0.97 |
| Sandstone and shale | 5 | 0.97 | 0.97 | 0.99 | 0.89 | 0.97 | 1 | 0.94 | 0.96 | 0.98 |
| Younger composite alluvial fans and terraces | 6 | 0.92 | 0.92 | 0.99 | 0.94 | 0.94 | 0.99 | 0.95 | 0.94 | 0.99 |
| River bed and recent alluvium | 7 | 0.95 | 0.95 | 0.99 | 0.96 | 0.99 | 1 | 0.92 | 0.92 | 0.99 |
| Older composite alluvial fans and terraces | 8 | 0.90 | 0.90 | 1 | 0.95 | 0.90 | 0.99 | 0.95 | 0.91 | 0.99 |
| Light red to gray sandstone | 9 | 0.95 | 0.95 | 0.99 | 0.97 | 0.98 | 1 | 0.96 | 0.94 | 0.99 |
| Au (ppb) | Mn (ppm) | Pb (ppm) | Zn (ppm) | |
|---|---|---|---|---|
| Sample D | 374 | 136 | 9810 | 267 |
| Sample E | 291 | 72,300 | 4505 | 5092 |
| Sample F | 5 | 2830 | 376 | 875 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shirmard, H.; Farahbakhsh, E.; Heidari, E.; Beiranvand Pour, A.; Pradhan, B.; Müller, D.; Chandra, R. A Comparative Study of Convolutional Neural Networks and Conventional Machine Learning Models for Lithological Mapping Using Remote Sensing Data. Remote Sens. 2022, 14, 819. https://doi.org/10.3390/rs14040819
Shirmard H, Farahbakhsh E, Heidari E, Beiranvand Pour A, Pradhan B, Müller D, Chandra R. A Comparative Study of Convolutional Neural Networks and Conventional Machine Learning Models for Lithological Mapping Using Remote Sensing Data. Remote Sensing. 2022; 14(4):819. https://doi.org/10.3390/rs14040819
Chicago/Turabian StyleShirmard, Hojat, Ehsan Farahbakhsh, Elnaz Heidari, Amin Beiranvand Pour, Biswajeet Pradhan, Dietmar Müller, and Rohitash Chandra. 2022. "A Comparative Study of Convolutional Neural Networks and Conventional Machine Learning Models for Lithological Mapping Using Remote Sensing Data" Remote Sensing 14, no. 4: 819. https://doi.org/10.3390/rs14040819
APA StyleShirmard, H., Farahbakhsh, E., Heidari, E., Beiranvand Pour, A., Pradhan, B., Müller, D., & Chandra, R. (2022). A Comparative Study of Convolutional Neural Networks and Conventional Machine Learning Models for Lithological Mapping Using Remote Sensing Data. Remote Sensing, 14(4), 819. https://doi.org/10.3390/rs14040819










