Abstract
Over the past few years, deep learning algorithms have held immense promise for better multi-spectral (MS) optical remote sensing image (RSI) analysis. Most of the proposed models, based on convolutional neural network (CNN) and fully convolutional network (FCN), have been applied successfully on computer vision images (CVIs). However, there is still a lack of exploration of spectra correlation in MS RSIs. In this study, a deep neural network with a spectrum separable module (DSSM) is proposed for semantic segmentation, which enables the utilization of MS characteristics of RSIs. The experimental results obtained on Zurich and Potsdam datasets prove that the spectrum-separable module (SSM) extracts more informative spectral features, and the proposed approach improves the segmentation accuracy without increasing GPU consumption.
1. Introduction
With the rapid development of remote sensing (RS) technology, multi-spectral (MS) images are able to provide increasingly complicated and effective information. As one of the most significant steps in the interpretation of RSIs, segmentation is a comprehensive research topic that includes computer vision (CV), neural networks and RS fields. Segmentation tasks in RS generally focus on extracting a specific category, e.g., water, buildings or cars, or multiple categories all together [1,2]. Today, segmentation for RSIs plays a significant role in disaster prevention and control, land-use planning, urban sprawl detection, etc. [3,4,5,6].
As deep learning (DL) technology has grown rapidly in recent years, CNN [7]- and FCN [8]-based methods have performed competitively in computer vision image (CVI) segmentation tasks [9,10,11,12,13], and have outperformed traditional methods in RSI segmentation [14,15,16,17,18,19]. The major differences between remote sensing images (RSIs) and CVIs are:
- 1.
- As compared with CVIs, RSIs have two major feature dimensions: spatial features and spectral features.
- 2.
- In the spatial dimension, CVIs generally have a lower resolution and a lower variety of objects. Correspondingly, the resolution in RSIs is generally hundreds of times higher than CVIs. Moreover, RSIs have a more complicated spatial distribution, more diverse object textures, and boundary patterns, and extremely unbalanced object categories.
- 3.
- In the spectral dimension, CVIs consist of red, green, and blue spectra (RGB), which indicate unitary spectrum characteristics. However, aside from visible spectra, such as RGB, RSIs contain certain invisible spectra, such as near infrared (NIR), which make it possible to record a wide variety of object spectrum characteristics.
In recent years, many CNN- and FCN-based RSI segmentation methods have focused on spatial features by improving the effectiveness of object textures and boundary patterns and reducing the impact of unbalanced object categories in order to promote segmentation performance. For example, [14] fused semantic and spatial information and alleviated the boundary blur by introducing a channel-weighted multi-scale feature module and boundary attention module into ResNet [20]. On the basis of the infrastructure of SegNet [11], with the help of an attention mechanism, Ref. [15] proposed a lightweight end-to-end network to automatically enhance the spatial and channel features. The authors of [16] designed a multi-scale context aggregation network with adaptive spatial pooling, reduced the spatial information loss during the process of convolution and pooling process, and promoted the semantic representation capability of feature maps. Moreover, Ref. [17] added a 1 × 1 convolution and full connection (FC) layer into the atrous spatial pyramid pooling (ASPP) module, which improved the capacity of fusing multi-scale features in Deeplab. In addition, Ref. [21] proposed balanced cross entropy (BCE) loss to optimize the training of the segmentation network.
These methods, however, lose sight of the spectral features between RSIs and CVIs. As regards CVIs, spectra represent simple color characteristics, so it is reasonable that these spectra share equivalent weights in the convolution units. Correspondingly, the spectrum is extremely significant and complicated for RSIs. For example, there are various spectrum-sensitive objects in RSIs, such as water and trees; therefore, it is important to extract the correlation between spectra. Considering this factor, certain traditional RSI segmentation algorithms leverage the divergence of objects on a specific spectrum or a combination of several spectra. For instance, NDVI [22] and NDWI [23] are two typical object extraction approaches based on spectrum characteristics, and the local spectral histogram method [18,24] calculates a spectral histogram of each spectrum and obtains the qualitative discrimination results using the synthesis stage.
Recently, researchers have taken into account spectral features in CNN-based methods. One-dimensional (1D), two-dimensional (2D), and three-dimensional (3D) CNN-based methods are proposed to model spectral features [25,26,27]. 1D CNN-based methods exploit the spectral features by convolving spectrum-dimension vectors for each pixel, which sacrifice the spatial representation capability [28]. 2D CNN-based methods extract spectral features in a two-stage manner. Firstly, low-dimensional representations of the spectra are obtained using dimensionality reduction methods. Then, general CNNs are leveraged to explore the spatial features [29,30,31]. Obviously, spectral and spatial features are utilized in a dissociated manner in 2D CNN-based methods. The convolution kernels in 3D CNN-based methods are cubic rather than flat, which can be used to easily extract and fuse the spectral and spatial features [32,33]. On the one hand, only local and low-level spectral features can be explored in this way. On the other, the order of spectra can limit the feature extraction capability of 3D kernels. In summary, when tackling RSI segmentation with DL-based methods, we expect to achieve the high-dimension, abstract, and robust feature representation wherein spectral and spatial features are effectively integrated, which is crucial for subsequent classification.
As discussed above, it is worth exploring the integration of traditional methods and DL-based methods of modeling spectra. Therefore, we proposed a deep neural network with a spectrum separable module (DSSM) to explore the possibility of enhancing the capability of extracting spectral features and to improve the segmentation accuracy in MS RSIs. The source codes are available at https://github.com/RuiTan/DSSM (accessed on 18 January 2022). The main contributions of our work are as follows:
- 1.
- A model was designed to realize the self-learning fusion mechanism of MS features through a depth-separable convolution and attention mechanism, which takes dissimilar contributions of different spectra and features into account and reduces the misclassification errors.
- 2.
- On the basis of the above model, an end-to-end MS image segmentation framework called DSSM was proposed to improve the segmentation ability of all surface elements in an experimental dataset and to improve the comprehensive segmentation accuracy.
- 3.
- A series of experiments were conducted to verify the effectiveness and superiority of our proposed method. The experimental results provide a new baseline for further research.
The rest of this article is organized as follows: Section 2 illustrates related work. In Section 3, the proposed method is described in detail. The effectiveness is analyzed and compared with various state-of-the-art (SOTA) methods using the Zurich [34] and Potsdam [35] datasets in Section 4. Finally, Section 5 presents the conclusion.
2. Related Work
In this section, we firstly review the development of image segmentation approaches in the CV field, including the design of the infrastructure, the principle of various SOTA methods, and fine-tuning in terms of specific scenarios. Then, the image segmentation methods in the RS field are reviewed and compared with the proposed algorithms.
Image segmentation, which aims to automatically assign a category to each pixel, is an active research topic in the field of CV and RS. In the CV field, traditional solutions utilize the knowledge of digital image processing tools, topology and mathematics to segment images, which makes it difficult to adequately leverage the color, spatiality, shape, texture, and boundary features [36,37]. To efficiently integrate these diverse features, certain methods based on CNNs provide a new strategy with which to analyze and interpret images [38]. However, the convolution operation, which is the most significant component of CNNs, is an irreversible feature extraction process, and, thus, it is hard to obtain the pixel-level classification results [36]. To solve this problem, with the encoder–decoder architecture, FCN imposes an upsampling and skip-connection module to retrieve the feature map in its original size [8]. Consequently, FCN has become the benchmark in the image segmentation task, and, thus, correlative algorithms are discussed in the following.
Compared with FCN, UNet has a more graceful architecture and a more complicated skip-connection module, which is able to efficiently fuse multi-scale features [9]. On the basis of UNet, UNet++ optimizes the skip-connection module with a pruned, deep supervised subnetwork [10]. PSPNet fuses the multi-scale features through the pyramid pooling module and combines the structural information using CRF [39], which improves the segmentation performance [12]. On the basis of the pyramid pooling module, combined with dilated convolution, Google proposes an ASPP module, which extracts and fuses multi-scale features more effectively [13,40,41,42].
In addition to the optimization of network structure, researchers also improved the convolution units. As regards enhancing the feature extraction capability, the attention mechanism was introduced to tackle the image processing task and to learn the significant correlation of multi-channel feature maps [43,44]. Inspired by this idea, we optimized the feature extraction module to reassign the weight of the feature maps for each spectrum. Furthermore, to decrease the convolution operation parameters, XCeption proposed depth-wise separable convolution (DS-CNN), which reduces the dimension of 3D feature maps and accelerates the speed of training models [45]. On this basis, we conducted the spectrum separable module (SSM) to decouple the spectral information, which makes it possible to reassign the weight of spectral feature maps.
Most of the methods mentioned above obtained SOTA results on various image data sets. However, as mentioned before, considering the characteristics and differences between RSIs and CVIs, fine-tuning and embedding of RS expertise are still needed in RSI segmentation tasks [25,26,46]. Various researchers have made innovations and optimized the framework or structure, obtaining good results on certain RS datasets. More specifically, inspired by atrous convolution, an FCN-based method without downsampling is proposed to obtain and fuse features of different scales [47]. The holistically nested edge detection method, based on SegNet (HNED-SegNet), realizes RSI segmentation through an end-to-end edge detection scheme [48]. Thereafter, Pan proposed a dense pyramid network to enhance the low information flow between dimensional features by independently processing the digital surface model of the image using grouped convolution and connecting an effective data fusion method [49]. ScasNet, which adopted a coarse-to-fine refinement strategy, consists of a pre-trained encoder, various self-cascading convolution units, and a decoder component. It uses a pre-trained encoder to obtain more effective low-dimensional features, utilizes residual correction for multi-scale feature fusion, and obtained SOTA results on multiple challenging benchmark data sets [2]. Various researchers improved the loss function used in network training for the uneven distribution of ground objects of RSIs, such as focal loss [50] and balanced or weighted cross-entropy loss [21,51].
Furthermore, other researchers focus on fusing spectral and spatial features. More specifically, spectral features of each pixel are exploited by 1D CNN, which contains five layers, i.e., an input layer, a 1D convolutional layer, a max-pooling layer, a fully connected layer, and an output layer [28]. In [29,31,52,53], diversiform strategies are utilized to explore the effective representation of hyperspectral data in a lower dimension, including principal components analysis (PCA), 1D CNN, local discriminant embedding (LDE) and fractional order darwinian particle swarm optimization (FODPSO). A lightweight framework, with bag-of-features learning, that integrates 2D and 3D CNNs is proposed to learn the joint spatial-spectral features in [54]. In [55], a mini-graph convolutional network (miniGCN) is integrated with a CNN to extract fused spectral and spatial features in an efficient approach. In contrast, in our work, we focus on exploring the abstract correlation among spectra rather than finding a specific representation, and we model the spectral information in a global manner rather than in a local manner as a 3D CNN does.
In summary, beginning with the idea of decoupling spectral features, we built a spectral separable convolution module, and leveraged the attention mechanism to select effective features in a self-learning manner. Extensive experiments demonstrated that our module effectively improved the baseline segmentation accuracy, and the overall performance achieved SOTA results.
3. Methodology
In this section, we describe the proposed network structure in detail. First, we explain how the proposed spectral feature extraction strategy module explores the links between channels in MS images. Secondly, the detailed network structure of the DSSM is illustrated herein. Finally, the loss function formulation is elaborated.
3.1. Spectrum Separable Module
In this section, we describe the structure and principle of the SSM in detail, focusing on how SSM can improve the representation of spectral features.
In the sixth paragraph in Section 2, we discussed the shortcomings of CNNs in processing RSIs, because the inherent channel correlation inherent to CNNs ignores the different influence capabilities between spectra. Therefore, inspired by the depth-separable concept of DS-CNN, we proposed the spectrum separable module, as shown in Figure 1.
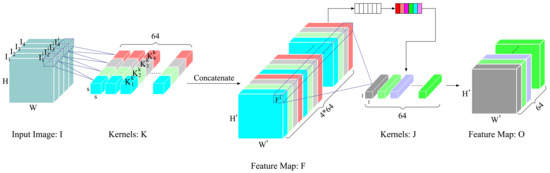
Figure 1.
Overview of the proposed SSM. The network structure of the SSM is composed of spectrum-wise convolution, depth-wise attention and point-wise convolution.
The network structure of the SSM can be divided into three steps: spectrum-wise convolution, depth-wise attention and point-wise convolution.
3.1.1. Spectrum-Wise Convolution
In the spectrum-wise convolution step, refers to the input image. represents the i-th convolutional block on the j-th spectrum where and , and where n is the number of convolutional blocks. Then, for each convolutional block, we adopt four groups of kernels with 64 kernels in each group. denotes the k-th kernel in the j-th group where . Moreover, feature map F can be obtained by concatenating all the convolutional results and is defined to conduct the concatenation operation upon dimension x. Therefore, the i-th value in can be indicated as:
Different from DS-CNNs, we removed the constraint on the number of output feature graphs. We isolated each spectrum, treated them as separate images, and then carried out the convolution operation. Since the input has only one channel, there is no redundant channel correlation. Here, we set the number of convolution kernels per channel to 64 for comparison with the baseline. By separating the spectrum, we convert one input into four inputs. Moreover, for each input, the network can learn the feature type required by each input through backpropagation, which is a capability that CNNs and DS-CNNs do not have. This approach allows us to obtain the feature maps for each spectrum, and fuse them together using a concatenation operation to produce the final feature maps.
Since the concatenation operation is conducted for feature fusion, the spectrum-based feature maps are equally dealt with in the following processes, which can cause a loss of accuracy. For example, the nearshore water may have a different color from the ordinary water in the RGB image due to the shallow depth. However, the corresponding pixel values for the same nearshore water in NIR may not be very different from ordinary water. To achieve better segmentation accuracy, a trade-off should be made to capture both the texture features in RGB and the near-infrared features in NIR for the water area. We expected the proposed network to learn the features based on certain points of focus, and thus an attention mechanism was utilized in the proposed model.
3.1.2. Depth-Wise Attention
In the first step, we obtained feature map F, which contains a number of channels representing multiple types of features. By applying the attention mechanism on F, we enhanced the important features and weakened the unimportant ones. In brief, we gave each channel the ability to self-learn its weights.
In order to obtain the global feature of a channel, the global average pooling method (GAP) was adopted to integrate the global information and obtain the compressed feature graph . This process is represented as , and then G can be calculated by:
Since we want to obtain the weights of a complete channel, GAP is used to integrate the channel’s internal information. Note that GAP is a relatively simple, but effective, pooling method to integrate global information. In addition to this, for example, maximum pooling and random pooling both cause more or less pixel point loss inside the channel, so we chose GAP.
Thereafter, two FC layers were adopted to integrate the multi-channel information, followed by the sigmoid function as the active function with which to generate the weight map S that can be applied to the original feature map. is used to denote this operation, and S can be calculated by:
It is necessary to use the FC to integrate the channel information here, because each channel value of G is the result of a GAP based entirely on a single channel. If it is directly applied to F, the process of obtaining the following T is completely without backpropagation and training, which makes it impossible to learn the law of channel enhancement and attenuation through all channel information.
Finally, the obtained weight map was multiplied directly by the channel corresponding to the original feature map, which is represented by , with which we obtain the weighted feature map T. At this point, the feature map has acquired the ability to express the strength and weaknesses of multiple features. T can be expressed as:
3.1.3. Point-Wise Convolution
We applied the attention mechanism to a series of features corresponding to each spectrum, and the convolution kernel of to integrate the channel correlations. On the one hand, this enabled it to learn nonlinear relationships between channels, and on the other hand, it allows it to configure subsequent input dimensions by specifying the number of convolution kernels.
In Equation (5), refers to the kernels we adopted here, and the final feature map can be obtained by:
3.1.4. Computational Cost
To compare the computational cost between standard convolutional layers and DSSM when the input and output has the same shape, we used the following assumptions:
- 1.
- Both the standard convolutional layer and DSSM take as input a image I as input and produce a feature map F, where is the spatial width and height of a square input image, M is the number of spectra in the input image, and N is the number of channels in the output feature map.
- 2.
- The padding type is the same, which means the spatial size of output feature map should be the same as that of the input image.
- 3.
- During the execution process of the model, the GPU consumption is mainly determined by the model size under the same conditions. In turn, the model size is proportional to the number of parameters. Therefore, in this section, the number of parameters of the module is used to evaluate the computational cost.
Thereafter, in the standard convolutional layer, N convolution kernels of size J are needed to obtain the feature map, where is the spatial length of the convolution kernel, and M is the number of the input image spectrum, and N is the number of output channels as defined previously. Thus, the standard convolution layer has the the computational cost of:
where the cost is greatly influenced by the shape of the input and output. As we all know, the coupling between each spectrum leads to the inevitable equality in the standard convolution.
To solve this problem, SSM was proposed to break the coupling and adopt a 1×1 convolution to integrate the mixed feature map. Here, we need M kernel groups in SSM, then in each group, convolution kernels K of size are designed to obtain specific feature map group for each spectrum. Therefore, the computational cost of the first SSM step is:
These groups are concatenated together, rather than added, to obtain a mixed feature map. Then, N kernels of size are adopted to apply a linear combination of the mixed feature map to obtain the final feature map. Considering the cost of the above step together, SSM has the total cost of:
Therefore, we calculate the following ratio by comparing SSM with the standard convolution:
It is noteworthy that when we set then the cost is the same as that in DS-CNN. Moreover, when is set to be the same as N, we maintain the dimension of the feature map. Now, we solely need to focus on the component of , which is equal to in our implementation, where N and are both 64. Hence, the computational cost was only 1.56% more than standard convolutions, but a much improved spectral feature extraction capability was successfully achieved.
3.2. Network Structure
In order to solve the semantic segmentation problems of MS images, we developed an end-to-end network framework based on Deeplab. The structure of the framework is shown in Figure 2.

Figure 2.
Network Structure.
The DSSM is composed of the following steps:
Step 1: Derive a feature map with spectral information
The MS image is used as the model input and can be processed using the SSM, which results in a feature map with a strong expression ability for spectral information.
Step 2: Feature extraction using XCeption
The feature map is transferred into XCeption for low-dimensional feature extraction.
Step 3: Multi-scale feature extraction using ASPP
The extracted feature map is input into the ASPP module to extract the multi-scale feature, and the result is concatenated to obtain the high-dimensional feature.
Step 4: Upsampling and concatenating
The high-dimensional feature is firstly upsampled and then concatenated with the low-dimensional feature. Finally, a simple convolution and upsampling operation is adopted to return the size of the feature to the input size.
3.3. Loss Function
In our proposed framework, the overall loss function can be indicated as:
3.3.1. Balanced Sparse Softmax Cross Entropy
In image segmentation, there is usually a large deviation in the proportion of pixels of different categories. To cope with the biased sampling class, we defined a balanced sparse softmax cross-entropy-based tradeoff strategy.
Assuming that there are S classes of surface object in our dataset, we adopt to denote the true label, and which means i is the object category. Moreover, each is a binary map that only contains 1 and 0, which represents if the current pixel belongs to the i-th category or not. Similarly, is adopted to refer to the prediction map, where . The difference is that the value of a specific pixel in is the probability of the pixel belonging to i-th category. Following a simple balanced strategy, and balanced sparse softmax cross entropy can be defined as:
where denotes the norm of matrix A and can be defined as:
3.3.2. Dice Coefficient
The dice coefficient is also a commonly used loss function applied in image segmentation tasks [21], which can be defined as:
4. Experiment
We designed and conducted three groups of experiments with the following three objectives:
- 1.
- In order to verify the effectiveness of the proposed DSSM in an MS information fusion, firstly, we compared the segmentation performance of the baseline framework based on RGB, NIR, and RGB-NIR inputs to verify whether RGB-NIR contains more valuable information and improves the performance. Secondly, we compared the proposed DSSM with the baseline framework based on the same set of RGB-NIR inputs to evaluate its effectiveness.
- 2.
- In order to further verify the validity of the proposed SSM, features from different levels were visualized and compared to demonstrate that more abstract and effective features can be extracted from the SSM.
- 3.
- In order to verify the overall performance of the proposed framework, comparison experiments were carried out to compare with other SOTA methods.
4.1. Dataset
4.1.1. Data Introduction
In image segmentation tasks, supervised learn-based frameworks generally require large amounts of data with high quality labels, which are often difficult to obtain. Fortunately, Michele released his self-labeled Zurich dataset in 2015, which includes 20 high-resolution photos of Zurich, Switzerland with a 0.62-m GSD obtained from a QuickBird satellite in August 200. Surface objects in this dataset are classified into eight different categories: road, building, tree, grass, bare soil, water, railway, and swimming pool, and each object is annotated by a specific color. In order to reflect the real-world distribution, the number of pixels in various samples is unbalanced, as shown in Figure 3. In addition, since it was marked manually, these labels are not completely consistent with the real-world objects, and there are some errors or missing labels. The data set contains the original image and the corresponding labels. The original image is an MS image containing four channels of NIR and RGB, with a 16-bit depth. The 16-bit depth image contains a lot of colors and subtle differences among those colors that humans cannot recognize, but that neural networks can easily pick up.
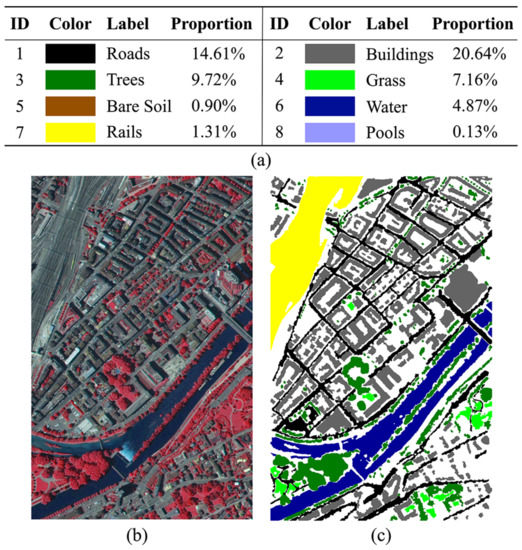
Figure 3.
Example from the Zurich dataset. Class legend with colors and related labels (a); note that a white background is not considered to be a separate class. Original image (RGB) (b) and its ground truth (c).
Another dataset we adopted is the Potsdam dataset provided by ISPRS as shown in Figure 4, which contain 38 images of Potsdam, Germany.
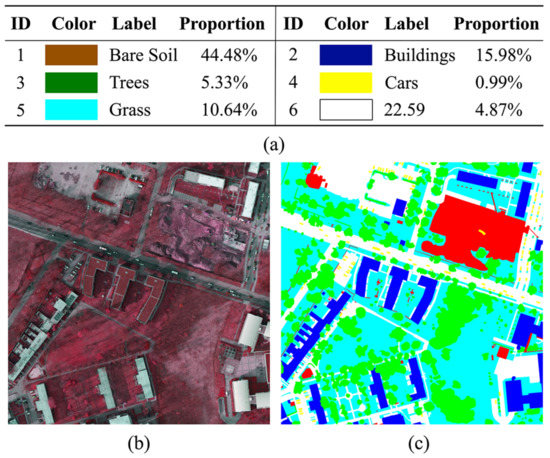
Figure 4.
Example from the Potsdam dataset. Class legend with colors and related labels (a). Original image (RGB) (b) and its ground truth (c).
4.1.2. Sampling Strategy
For the Zurich dataset, as the resolution of the source photos ranges from 650 × 650 to 1700 × 1700, random sampling was conducted to take into account the impact of resource constraints, training efficiency, training effects, and other factors. The 20 photos were randomly sampled to produce 20,000 slices, 256 × 256 in size, preserving the maximum amount of detail and edge information in the original photos. Then, 80% of these participated in training and validation, and the remaining 20% served as test sets.
4.1.3. Data Augmentation
In order to improve the expression ability of the data and the generalization ability of the model, we applied a variety of data enhancement methods to the data, including rotation, flipping, slicing, Gaussian filtering, bilateral filtering, gamma transformation, and so on. In fact, the random slice method mentioned above, which increases the number of samples, was also used for data augmentation.
4.2. Evaluation Methods
In order to evaluate the effectiveness of the proposed framework, we adopted intersection over union () as an evaluation indicator for a single category of ground objects. defines the similarity between the predicted area and the ground reality area of the objects in this set of images. The calculation formula is as follows:
where , , and represent the counts of true positive, false positive, and false negative, respectively, and i refers to the category number. The result of the count is generally obtained by the confusion matrix between the predicted value and the ground reality.
Moreover, FW IoU was used to evaluate the overall segmentation performance, which can be calculated as:
where refers to the percentage of pixels of the i-th ground object. When calculating the average , also took into account the occurrence probability of ground objects, thus making the evaluation of the segmentation result more accurate.
4.3. Experimental Environments
The proposed architecture is implemented using the Tensorflow library. The hardware device is a Ubuntu server equipped with four GeForce RTX 2080 Ti GPUs (each has 12 GB of memory), one Intel i9-9960X CPU and 64 GB of RAM. The detailed hardware configuration and software requirements are shown in Table 1.

Table 1.
Hardware configuration and software requirements in our implementation.
4.4. Comparison of Various Processing Strategies
In the introduction to SSM, we stated that the SSM actually provides a strategy for fusing different spectra from the input image. The purpose of this section of the experiment was to verify the effectiveness of the fusion strategy in the SSM. This group of experiments were conducted on the Zurich and Potsdam datasets.
Before we proposed the SSM, we put forward a hypothesis that different spectra would show different values on different ground objects. On the basis of this assumption, we treated each spectrum of the input image as an independent single spectral image. We convolved them separately, and then we established the nonlinear relationship among the feature maps generated by all the spectra through convolution. This enabled the network to learn which features needed to be learned for each spectrum independently. In order to assess whether more valuable information is contained in RGB-NIR and the effectiveness of the SSM, we designed several processing strategies for comparison, which are as follows:
- 1.
- We fed three spectra of red, green, and blue into the baseline (baseline with RGB).
- 2.
- We fed the NIR into the baseline (baseline with NIR).
- 3.
- We fed four spectra into baseline (baseline with RGB-NIR).
- 4.
- We fed all four spectra into the proposed framework (DSSM with RGB-NIR).
In this group of experiments, the Deeplabv3+ network, which is fine-tuned in terms of cost function and the number of convolutional layers, was adopted as the baseline with which to compare the DSSM.
Figure 5 shows the segmentation results of the baseline with RGB, the baseline with NIR, the baseline with RGB-NIR, and the DSSM with RGB-NIR. Figure 5a,b are the original images and their ground truths. Figure 5c–e refer to the baseline with RGB, the baseline with NIR and the baseline with RGB-NIR, respectively. Figure 5f represents the DSSM with RGB-NIR inputs.
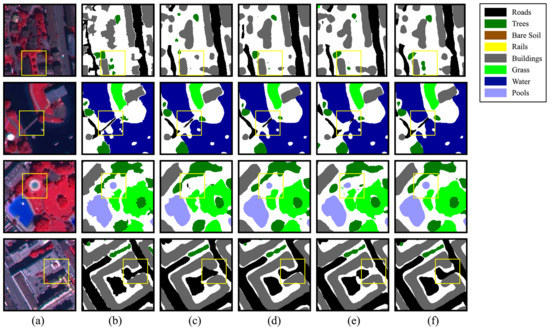
Figure 5.
Comparison of various processing strategies in the Zurich dataset. (a) Original image. (b) Ground truth. (c) Baseline with RGB. (d) Baseline with NIR. (e) Baseline with RGB-NIR. (f) DSSM with RGB-NIR.
As a result of the large receptive field of the original image, the contrast effect of the whole image is not obvious. Therefore, various small image blocks with a size of were cut from the original image. These image blocks were selected from certain parts with extreme differences in segmentation results in typical ground objects.
Firstly, we compared the segmentation differences of different inputs on small isolated trees, as shown in the yellow box in the first line of Figure 5, where three small isolated trees are shown. The baseline with RGB and the baseline with NIR strategies lost the ability to identify small trees, and they roughly identified the area as the background. The RGB-NIR strategy identified a tree, but its outline is quite different from the ground truth. The DSSM with the RGB-NIR strategy identified three complete trees. Although the boundary between the first tree and the second tree is connected, the outline of the two trees can be seen, and the shape of the identified trees is closer to the ground truth than that of the other three strategies.
In the yellow box in the second line of Figure 5, we selected small roads, which are bridges marked as roads. Curiously, the two strategies, RGB and NIR, were able to coarsely divide the bridge. However, when they were mixed, i.e., when the RGB-NIR strategy was used, the recognition ability actually reduced. Their simultaneous use may inhibit the other’s recognition ability. Of course, the RGB-NIR with DSSM strategy also correctly divided the bridge.
In the yellow box in the third line of Figure 5, there is a small and shallow swimming pool. The RGB strategy completely lost the ability to recognize this object, and even identified the shore of the swimming pool as a road. The baseline with NIR, the baseline with RGB-NIR and the DSSM with RGB-NIR were all able to identify the swimming pool, but the predicted contour of the DSSM RGB-NIR was closest to the ground truth.
In the yellow box in the fourth row of Figure 5, there is a road with a shaded area. Both the baseline with NIR and the baseline with RGB-NIR accurately identified the road with a shaded area, while the baseline with RGB and the baseline with RGB-NIR consider that to be the background.
In a previous analysis, we compared four classes in which obvious differences can be observed with the human eye. Since each image block was only in size, the visual effects in most areas using different processing strategies were similar. In Table 2, IoU and FW IoU of different strategies on each ground object are quantitatively given. It can be clearly seen from Table 2 that the fusion strategy of the DSSM proposed by us greatly improved the segmentation effect of each type of ground object. Firstly, the baseline with RGB-NIR performed better than the baseline with RGB and the baseline with NIR by 1.18% in terms of FW IoU using the Zurich dataset. However, as compared with the first three strategies, the DSSM with RGB-NIR consistently outperformed them, registering increased FW IoUs of approximately 3.47%. Furthermore, the confusion matrix for the prediction is shown in Figure 6. The wrong classification frequently occurred for the background; this does not represent an inter-object mistake but a difficulty in distinguishing between background and non-background objects.

Table 2.
The quantitative results of different processing strategies using the Zurich dataset.
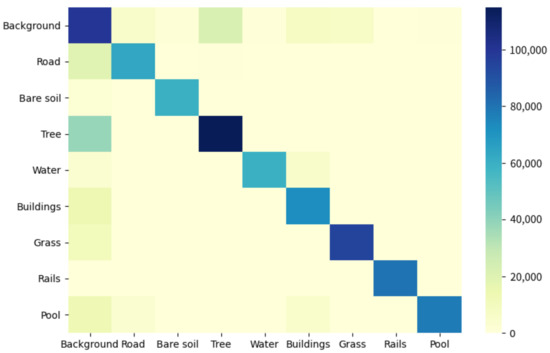
Figure 6.
Confusion matrix for the prediction using the Zurich dataset.
To further verify the efficiency of the DSSM, we also conducted other experiments using the Potsdam dataset. Figure 7 and Table 3 show the effects of the four strategies using the Potsdam dataset. The DSSM with RGB-NIR continued to demonstrate a better segmentation capability than the other three strategies, which increased by 1.92% in terms of FW IoU.
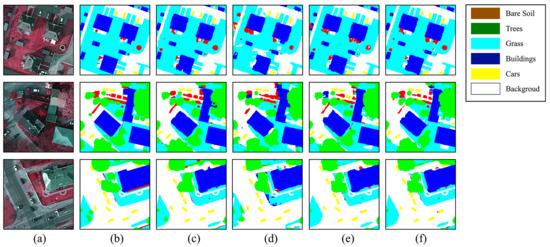
Figure 7.
Comparison of various processing strategies in the Potsdam dataset. (a) Original image. (b) Ground Truth. (c) Baseline with RGB. (d) Baseline with NIR. (e) Baseline with RGB-NIR. (f) DSSM with RGB-NIR.

Table 3.
The quantitative results of different processing strategies using the Potsdam dataset.
In addition to comparing the segmentation accuracy of different strategies, we also compared the consumption cost of each strategy. As can be seen from Table 4, for the first three schemes, we maintained the same size and number of convolution kernels in the baseline. At this point, the number of spectra of the input image only affects the thickness of the convolution kernel, and we already know from the previous analysis that the thickness of the convolution kernel in the CNN does not affect the parameters of the model; thus, their consumption cost remained the same. As compared with the aforementioned three strategies, the consumption cost of the DSSM with RGB-NIR increased by about 20%. Considering that this strategy provides a great improvement in segmentation accuracy, we believe that the increase in consumption is acceptable.

Table 4.
Consumption cost of different processing strategies using the Zurich dataset.
In conclusion, the fusion strategy in our proposed SSM is more effective than that in those strategies that use the pure CNN to obtain the image feature, and it provides an acceptable consumption cost. Another interesting fact is that using the RGB-NIR strategy is sometimes less effective than directly using the NIR strategy, which can be seen in both the qualitative and quantitative results. In the next section, we discuss why the SSM improves the segmentation accuracy in more detail.
4.5. Comparison of Features Extracted from Different Levels
In this group of experiments, we assessed the validity of the SSM from another perspective. Different levels of features extracted from the baseline and DSSM were visualized and contrasted. This group of experiments was conducted using the Zurich dataset.
Figure 8 shows the low-level features extracted from the baseline and DSSM, respectively. Figure 8a,b are the original images and their ground truth. Figure 8c shows the low-level features extracted in the baseline where spectra are convolved in a weight-sharing manner. Figure 8d–g represent the low-level features explored in DSSM in a spectrum-separable way. Concentrating on the yellow boxes in Figure 8d–g, different features are revealed in different spectra. In other words, diversiform characteristics under different spectra can be captured by the SSM. However, as shown in Figure 8c, differentiation among objects becomes less distinct due to the weight-sharing strategy.

Figure 8.
Comparison of spectral features extracted from the baseline and proposed method using the Zurich dataset. (a) Original image. (b) Ground truth. (c) Low-level features in the baseline. (d) Low-level features of the red band in DSSM. (e) Low-level features of the green band in DSSM. (f) Low-level features of the blue band in DSSM. (g) Low-level features of the NIR band in DSSM.
In Figure 9, we visualize different level of features. Figure 9a,b are the original images and their ground truth. Figure 9c,d show the low-level features. They are extracted by one convolutional layer in the baseline and the SSM, respectively, in the proposed method. Obviously, as shown in the yellow boxes, fused low-level features in the DSSM provide a sharper and more legible pattern and information. Figure 9e,f illustrate the high-level features obtained from the ASPP in the baseline and DSSM, respectively. The higher the level is, the more abstract and unrecognizable the pattern will be. As shown in Figure 9e,f, although the features are abstract and hard to recognize, high-level features in the DSSM contain more complicated manifestations.

Figure 9.
Comparison of spectral features extracted from the baseline and proposed method using the Zurich dataset. (a) Original image. (b) Ground truth. (c) Low-level features in the baseline. (d) Fused low-level features in DSSM. (e) High-level features from ASPP in the baseline. (f) High-level features from ASPP in DSSM.
4.6. Comparison of Other Popular Segmentation Methods
In order to verify the overall performance of the DSSM, we compared the DSSM with UNet++, DeeplabV3+, HNED-SegNet, ScasNet, and miniGCN using the Zurich and Potsdam datasets. As discussed in Section 2, UNet++ and DeeplabV3+ are CV-field methods and HNED-SegNet, ScasNet, and miniGCN are RS-field methods. In order to obtain more effective results, only the network structure was customized in the experiment using each method.
As shown in Table 5, the DSSM outperformed the other methods in most surface elements, and provided a satisfying improvement of 5.78% for trees in terms of IoU. Vegetation areas, such as trees, have a similar pattern as other surface elements in a single spectrum. Through establishing the correlations among spectra, we improved the segmentation efficiency of these areas. However, as a result of the extremely irregular shapes and the inaccurate labels of trees, the IoU remained lower than the FW IoU. Moreover, the segmentation accuracy improved by 2.99% for water and pools for the same reason. Other surface elements improved by 1.53% overall when background and rails were excluded.

Table 5.
The quantitative results of popular methods using the Zurich dataset.
Furthermore, the IoU of the DSSM for rails was 1% lower than that of UNet++, because the multi-level skip-connection structure of UNet++ is more effective on these narrow and slender surface elements. Overall, the FW IoU is increased by 2.19%, which demonstrates that the segmentation accuracy of the DSSM in terms of segmenting MS RSIs is generally better than that of other SOTA methods.
The quantitative results using the Potsdam dataset are shown in Table 6, which are similar to those using the Zurich dataset. It is worth noting that our method still has a lot of room for improvement in the results of the buildings. Overall, the FW IoU is increased by 0.19% compared with the best method, which is HNED-SegNet.

Table 6.
The quantitative results of popular methods using the Potsdam dataset.
We also compared the execution time with other methods as shown in Table 7. We define the unit of execution time as the time it takes for the model to predict each batch. Model and data loading times have been excluded from the results. In the actual prediction, each batch contains 64 images of 256 × 256 size. UNet++ takes the shortest time, thanks to its streamlined network structure. Our method takes about 10.85 ms, which is 1.54 ms slower than UNet++. The extra time consumption of the proposed method is acceptable when taking its performance improvement into account.

Table 7.
The comparison of prediction time for a batch of popular methods.
5. Conclusions
In this paper, we propose a deep-learning based, end-to-end network structure DSSM for the semantic segmentation of MS optical RSIs. The framework is mainly composed of an SSM module and a deep neural network.
The SSM is based on a DS-CNN and optimizes the spectral feature extraction strategy. First, features are independently extracted through spectrum-wise convolution, and then the importance of each feature is studied using a depth-wise attention module. Finally, a nonlinear relationship between features is established through point-wise convolution to generate the final feature map. These extracted features not only contain spatial information, but also have a stronger ability to express spectral correlation. We applied the SSM as a prefeature extraction module in deep neural network. The experimental results show that the DSSM has a better segmentation capability than other SOTA methods, and provides an improvement of 2.19% in terms of FW IoU. Moreover, our proposed SSM can be easily grafted onto other deep-learning-based networks.
In future work, we will focus on transforming the processing techniques proposed in the SSM into hyper-spectral RSIs, reducing the complexity of the network and consumption cost, and applying the strategy to other RS tasks, such as change detection.
Author Contributions
Conceptualization, H.Z. and R.T.; methodology, Q.L.; software, L.H.; validation, B.D.; formal analysis, H.F.; investigation, Z.W.; resources, B.D.; data curation, L.H.; writing—original draft preparation, R.T.; writing—review and editing, B.D. and H.Z.; visualization, L.H.; supervision, Q.L.; project administration, H.Z.; funding acquisition, H.F., H.Z. and S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by the National Key R&D Program of China (No. 2018YFB0505001), the National Natural Science Foundation of China (No. 61702374), the Natural Science Foundation of Shanghai (No.21ZR1465100).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Li, E.; Femiani, J.; Xu, S.; Zhang, X.; Wonka, P. Robust rooftop extraction from visible band images using higher order CRF. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4483–4495. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, B.; Wang, L.; Bai, J.; Xiang, S.; Pan, C. Semantic labeling in very high resolution images via a self-cascaded convolutional neural network. ISPRS J. Photogramm. Remote Sens. 2018, 145, 78–95. [Google Scholar] [CrossRef] [Green Version]
- Matikainen, L.; Karila, K. Segment-based land cover mapping of a suburban area—Comparison of high-resolution remotely sensed datasets using classification trees and test field points. Remote Sens. 2011, 3, 1777–1804. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Seto, K.C. Mapping urbanization dynamics at regional and global scales using multi-temporal DMSP/OLS nighttime light data. Remote Sens. Environ. 2011, 115, 2320–2329. [Google Scholar] [CrossRef]
- Lu, X.; Yuan, Y.; Zheng, X. Joint dictionary learning for multispectral change detection. IEEE Trans. Cybern. 2016, 47, 884–897. [Google Scholar] [CrossRef]
- Goldblatt, R.; Stuhlmacher, M.F.; Tellman, B.; Clinton, N.; Hanson, G.; Georgescu, M.; Wang, C.; Serrano-Candela, F.; Khandelwal, A.K.; Cheng, W.H.; et al. Using Landsat and nighttime lights for supervised pixel-based image classification of urban land cover. Remote Sens. Environ. 2018, 205, 253–275. [Google Scholar] [CrossRef]
- O’Shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 39, 640–651. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: Cham, Switzerland, 2018; pp. 3–11. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Sun, X.; Shi, A.; Huang, H.; Mayer, H. BAS Net: Boundary-Aware Semi-Supervised Semantic Segmentation Network for Very High Resolution Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5398–5413. [Google Scholar] [CrossRef]
- Li, H.; Qiu, K.; Chen, L.; Mei, X.; Hong, L.; Tao, C. SCAttNet: Semantic segmentation network with spatial and channel attention mechanism for high-resolution remote sensing images. IEEE Geosci. Remote Sens. Lett. 2020, 18, 905–909. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, S.; Ding, L.; Bruzzone, L. Multi-scale context aggregation for semantic segmentation of remote sensing images. Remote Sens. 2020, 12, 701. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Li, C.; Wei, W.; Jing, W.; Woźniak, M.; Blažauskas, T.; Damaševičius, R. Fully convolutional neural network with augmented atrous spatial pyramid pool and fully connected fusion path for high resolution remote sensing image segmentation. Appl. Sci. 2019, 9, 1816. [Google Scholar] [CrossRef] [Green Version]
- Radoux, J.; Bourdouxhe, A.; Coos, W.; Dufrêne, M.; Defourny, P. Improving ecotope segmentation by combining topographic and spectral data. Remote Sens. 2019, 11, 354. [Google Scholar] [CrossRef] [Green Version]
- Kemker, R.; Salvaggio, C.; Kanan, C. Algorithms for semantic segmentation of multispectral remote sensing imagery using deep learning. ISPRS J. Photogramm. Remote Sens. 2018, 145, 60–77. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Peng, D.; Zhang, Y.; Guan, H. End-to-end change detection for high resolution satellite images using improved unet++. Remote Sens. 2019, 11, 1382. [Google Scholar] [CrossRef] [Green Version]
- Goward, S.N.; Markham, B.; Dye, D.G.; Dulaney, W.; Yang, J. Normalized difference vegetation index measurements from the Advanced Very High Resolution Radiometer. Remote Sens. Environ. 1991, 35, 257–277. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D. A spectral histogram model for texton modeling and texture discrimination. Vis. Res. 2002, 42, 2617–2634. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef] [Green Version]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Santara, A.; Mani, K.; Hatwar, P.; Singh, A.; Garg, A.; Padia, K.; Mitra, P. BASS net: Band-adaptive spectral-spatial feature learning neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5293–5301. [Google Scholar] [CrossRef] [Green Version]
- Ghamisi, P.; Chen, Y.; Zhu, X.X. A self-improving convolution neural network for the classification of hyperspectral data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1537–1541. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Volpi, M.; Ferrari, V. Semantic segmentation of urban scenes by learning local class interactions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Benitez, S.; Breitkopf, U. The ISPRS benchmark on urban object classification and 3D building reconstruction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-3, 293–298. [Google Scholar] [CrossRef] [Green Version]
- Minaee, S.; Boykov, Y.Y.; Porikli, F.; Plaza, A.J.; Kehtarnavaz, N.; Terzopoulos, D. Image segmentation using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef]
- Sultana, F.; Sufian, A.; Dutta, P. Evolution of image segmentation using deep convolutional neural network: A survey. Knowl.-Based Syst. 2020, 201, 106062. [Google Scholar] [CrossRef]
- Wu, J. Introduction to Convolutional Neural Networks; National Key Lab for Novel Software Technology, Nanjing University: Nanjing, China, 2017; Volume 5, p. 495. [Google Scholar]
- Zheng, S.; Jayasumana, S.; Romera-Paredes, B.; Vineet, V.; Su, Z.; Du, D.; Huang, C.; Torr, P.H. Conditional random fields as recurrent neural networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1529–1537. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic image segmentation with deep convolutional nets and fully connected crfs. arXiv 2014, arXiv:1412.7062. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Cheng, G.; Yang, C.; Yao, X.; Guo, L.; Han, J. When deep learning meets metric learning: Remote sensing image scene classification via learning discriminative CNNs. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2811–2821. [Google Scholar] [CrossRef]
- Sherrah, J. Fully convolutional networks for dense semantic labelling of high-resolution aerial imagery. arXiv 2016, arXiv:1606.02585. [Google Scholar]
- Marmanis, D.; Schindler, K.; Wegner, J.D.; Galliani, S.; Datcu, M.; Stilla, U. Classification with an edge: Improving semantic image segmentation with boundary detection. ISPRS J. Photogramm. Remote Sens. 2018, 135, 158–172. [Google Scholar] [CrossRef] [Green Version]
- Pan, X.; Gao, L.; Zhang, B.; Yang, F.; Liao, W. High-resolution aerial imagery semantic labeling with dense pyramid network. Sensors 2018, 18, 3774. [Google Scholar] [CrossRef] [Green Version]
- Nemoto, K.; Hamaguchi, R.; Imaizumi, T.; Hikosaka, S. Classification of rare building change using cnn with multi-class focal loss. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4663–4666. [Google Scholar]
- Gao, X.; Sun, X.; Zhang, Y.; Yan, M.; Xu, G.; Sun, H.; Jiao, J.; Fu, K. An end-to-end neural network for road extraction from remote sensing imagery by multiple feature pyramid network. IEEE Access 2018, 6, 39401–39414. [Google Scholar] [CrossRef]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep learning classification of land cover and crop types using remote sensing data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 778–782. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Roy, S.K.; Chatterjee, S.; Bhattacharyya, S.; Chaudhuri, B.B.; Platoš, J. Lightweight spectral–spatial squeeze-and-excitation residual bag-of-features learning for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5277–5290. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5966–5978. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).