Exploring the Spatiotemporal Coverage of Terrestrial Snow Mass Using a Suite of Satellite Constellation Configurations
Abstract
:1. Introduction
1.1. Limitations of Existing Spaceborne Snow Products
1.2. Limitations of Remote Sensing Snow Techniques
1.3. Snow Mass Mission Trade-Offs
2. Methodology
2.1. Simulation of Sensor Viewing Extent
2.2. Orbital Configuration and Sensor Type
2.2.1. Passive Microwave Radiometer
2.2.2. Synthetic Aparture RADAR
2.2.3. LiDAR Altimetry
2.2.4. Orbital Parameters
2.2.5. Constellations
- (a)
- sensors of PMW radiometer, two C-band SARs, Narrow LiDAR;
- (b)
- sensors of PMW radiometer, Ku-band SAR, narrow LiDAR;
- (c)
- sensor IDs PMW radiometer, Ku-band SAR, wide LiDAR; and
- (d)
- sensor IDs PMW radiometer, Ku-band SAR, two C-band SARs, wide LiDAR, narrow LiDAR.
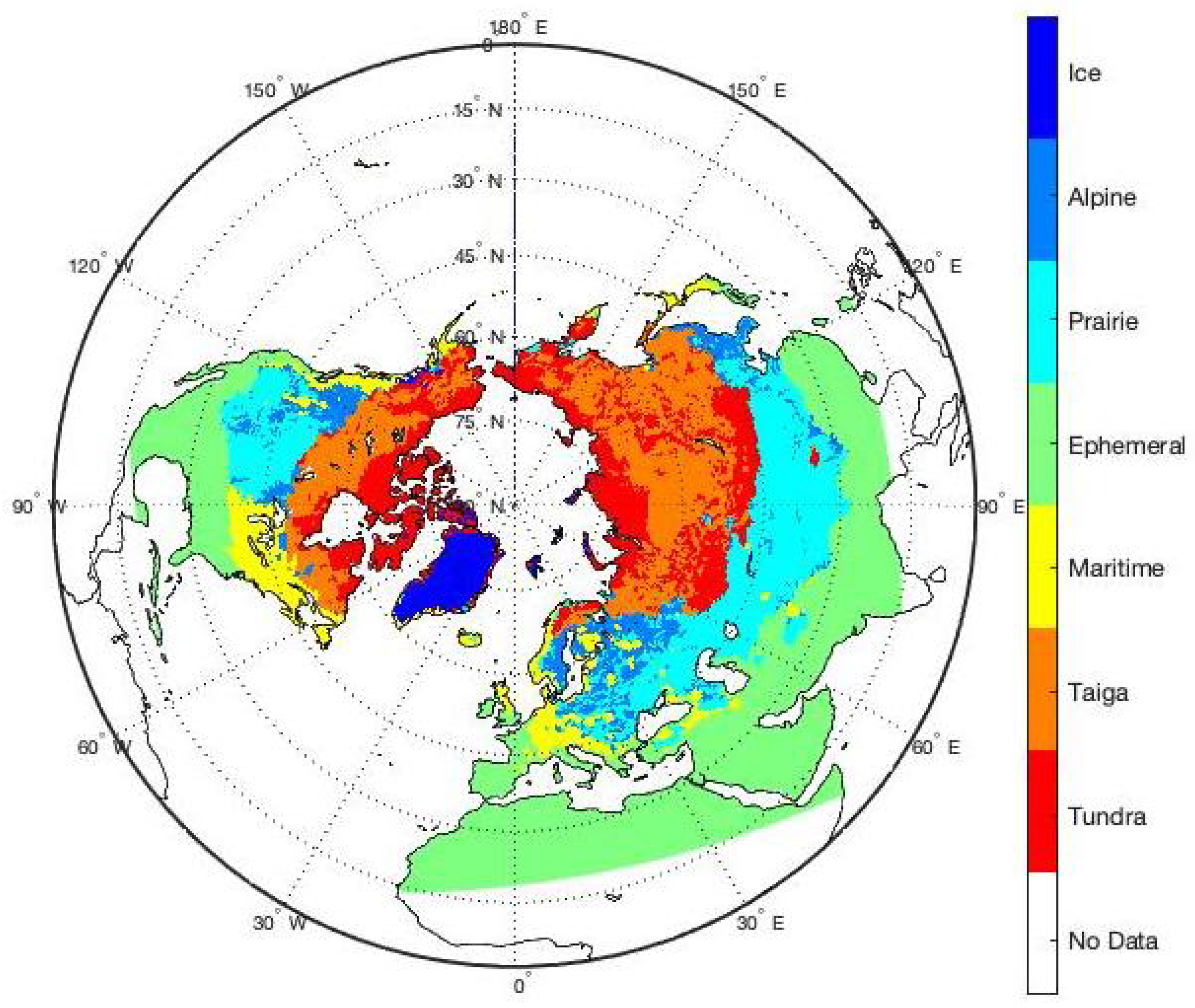
2.3. Dynamic Snow Mask
2.4. Dynamic Cloud Mask
2.5. Evaluation Metrics
2.5.1. Viewed Snow Coverage Percent
2.5.2. Viewing of Snow Classification Coverage Percentage
2.5.3. Temporal Repeat Interval
3. Results
3.1. Sensor Simulation of Viewing Extent
3.2. Dynamic Snow Mask Estimation
3.3. Evaluation of Single Sensor
3.3.1. Viewed Snow Coverage Percentage Analysis
3.3.2. Repeat Interval Analysis
3.4. Evaluation of Constellations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Foster, J.; Tedesco, S.N.M.; Riggs, G.; Hall, D.; Eylander, J. A global snowmelt product using visible, passive microwave and scatterometer satellite data. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. Commission VIII WG 2008, 8, B8. [Google Scholar]
- Kundzewicz, Z.W.; Mata, L.; Arnell, N.W.; Döll, P.; Jimenez, B.; Miller, K.; Oki, T.; Şen, Z.; Shiklomanov, I. The implications of projected climate change for freshwater resources and their management. Hydrol. Sci. J. 2008, 53, 3–10. [Google Scholar] [CrossRef]
- Sturm, M.; Goldstein, M.A.; Parr, C. Water and life from snow: A trillion dollar science question. Water Resour. Res. 2017, 53, 3534–3544. [Google Scholar] [CrossRef]
- Pavelsky, T.M.; Sobolowsk, S.; Kapnick, S.B.; Barnes, J.B. Changes in orographic precipitation patterns caused by a shift from snow to rain. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Thackeray, C.W.; Fletcher, C.G. Snow albedo feedback: Current knowledge, importance, outstanding issues and future directions. Prog. Phys. Geogr. 2016, 40, 392–408. [Google Scholar] [CrossRef]
- Wipf, S.; Stoeckli, V.; Bebi, P. Winter climate change in alpine tundra: Plant responses to changes in snow depth and snowmelt timing. Clim. Chang. 2009, 94, 105–121. [Google Scholar] [CrossRef] [Green Version]
- Coppola, E.; Raffaele, F.; Giorgi, F. Impact of climate change on snow melt driven runoff timing over the Alpine region. Clim. Dyn. 2018, 51, 1259–1273. [Google Scholar] [CrossRef]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes in snowmelt runoff timing in western North America under a “business as usual” climate change scenario. Clim. Chang. 2004, 62, 217–232. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Conrad, C. Snow-cover variability in central Asia between 2000 and 2011 derived from improved MODIS daily snow-cover products. Int. J. Remote. Sens. 2013, 34, 3879–3902. [Google Scholar] [CrossRef]
- Tedesco, M.; Narvekar, P.S. Assessment of the NASA AMSR-E SWE product. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2010, 3, 141–159. [Google Scholar] [CrossRef]
- Wehner, M.F.; Arnold, J.R.; Knutson, T.; Kunkel, K.E.; LeGrande, A.N. Droughts, floods, and wildfires. Clim. Sci. Spec. Rep. Fourth Natl. Clim. Assess. 2017, I, 231–256. [Google Scholar]
- Clifford, D. Global estimates of snow water equivalent from passive microwave instruments: History, challenges and future developments. Int. J. Remote. Sens. 2010, 31, 3707–3726. [Google Scholar] [CrossRef]
- Brown, R.; Tapsoba, D.; Derksen, C. Evaluation of snow water equivalent datasets over the Saint-Maurice river basin region of southern Québec. Hydrol. Process. 2018, 32, 2748–2764. [Google Scholar] [CrossRef] [Green Version]
- Larue, F.; Royer, A.; De Sève, D.; Langlois, A.; Roy, A.; Brucker, L. Validation of GlobSnow-2 snow water equivalent over Eastern Canada. Remote. Sens. Environ. 2017, 194, 264–277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashcroft, P.; Wentz, F.J. AMSR Level 2A Algorithm; Rep. 121599B-1; Remote Sensing System: Santa Rosa, CA, USA, 2000. [Google Scholar]
- Chang, A.; Foster, J.L.; Hall, D.K. Nimbus-7 SMMR derived global snow cover parameters. Ann. Glaciol. 1987, 9, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Frei, A.; Tedesco, M.; Lee, S.; Foster, J.; Hall, D.K.; Kelly, R.; Robinson, D.A. A review of global satellite-derived snow products. Adv. Space Res. 2012, 50, 1007–1029. [Google Scholar] [CrossRef] [Green Version]
- Takala, M.; Ikonen, J.; Luojus, K.; Lemmetyinen, J.; Metsämäki, S.; Cohen, J.; Arslan, A.N.; Pulliainen, J. New snow water equivalent processing system with improved resolution over Europe and its applications in hydrology. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2016, 10, 428–436. [Google Scholar] [CrossRef]
- Pulliainen, J.; Luojus, K.; Derksen, C.; Mudryk, L.; Lemmetyinen, J.; Salminen, M.; Ikonen, J.; Takala, M.; Cohen, J.; Smolander, T.; et al. Patterns and trends of Northern Hemisphere snow mass from 1980 to 2018. Nature 2020, 581, 294–298. [Google Scholar] [CrossRef]
- Derksen, C.; Lemmetyinen, J.; King, J.; Belair, S.; Garnaud, C.; Lapointe, M.; Crevier, Y.; Burbidge, G.; Siqueira, P. A Dual-Frequency Ku-Band RADAR Mission Concept for Seasonal Snow. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5742–5744. [Google Scholar]
- Mortimer, C.; Mudryk, L.; Derksen, C.; Luojus, K.; Brown, R.; Kelly, R.; Tedesco, M. Evaluation of long-term Northern Hemisphere snow water equivalent products. Cryosphere 2020, 14, 1579–1594. [Google Scholar] [CrossRef]
- Vuyovich, C.M.; Jacobs, J.M.; Daly, S.F. Comparison of passive microwave and modeled estimates of total watershed SWE in the continental United States. Water Resour. Res. 2014, 50, 9088–9102. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; DiGirolamo, N.E.; Bayr, K.J. MODIS snow-cover products. Remote. Sens. Environ. 2002, 83, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Conde, V.; Nico, G.; Catalao, J.; Kontu, A.; Gritsevich, M. Wide-area mapping of snow water equivalent by Sentinel-1&2 data. In Proceedings of the19th EGU General Assembly, Vienna, Austria, 3–8 May 2020; EGU General Assembly Conference Abstracts. p. 9580. [Google Scholar]
- Macelloni, G.; Brogioni, M.; Montomoli, F.; Lemmetyinen, J.; Pulliainen, J.; Rott, H.; Voglmeier, K.; Hajnsek, I.; Scheiber, R.; Rommen, B. On the synergic use of Sentinel-1 and CoreH2O SAR data for the retrieval of snow water equivalent on land and glaciers. In Proceedings of the Living Planet Symposium, Edenburgh, UK, 9–13 September 2013. [Google Scholar]
- Tsai, Y.L.S.; Dietz, A.; Oppelt, N.; Kuenzer, C. Remote Sensing of Snow Cover Using Spaceborne SAR: A Review. Remote. Sens. 2019, 11, 1456. [Google Scholar] [CrossRef] [Green Version]
- Storvold, R.; Malnes, E.; Larsen, Y.; Høgda, K.A.; Hamran, S.E.; Müller, K.; Langley, K.A. SAR remote sensing of snow parameters in Norwegian areas-Current status and future perspective. In Proceedings of the PIERS 2006 Cambridge—Progress in Electromagnetics Research Symposium, Proceedings, Cambridge, MA, USA, 26–29 March 2006; pp. 182–186. [Google Scholar] [CrossRef] [Green Version]
- Lievens, H.; Demuzere, M.; Marshall, H.P.; Reichle, R.H.; Brucker, L.; Brangers, I.; de Rosnay, P.; Dumont, M.; Girotto, M.; Immerzeel, W.W.; et al. Snow depth variability in the Northern Hemisphere mountains observed from space. Nat. Commun. 2019, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.; Gatebe, C.; Hall, D.; Newlin, J.; Misakonis, A.; Elder, K.; Marshall, H.P.; Hiemstra, C.; Brucker, L.; De Marco, E.; et al. NASA’s SnowEx campaign: Observing seasonal snow in a forested environment. In Proceedings of the2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1388–1390. [Google Scholar]
- Derksen, C.; King, J.; Belair, S.; Garnaud, C.; Vionnet, V.; Fortin, V.; Lemmetyinen, J.; Crevier, Y.; Plourde, P.; Lawrence, B.; et al. Development of the Terrestrial Snow Mass Mission. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 614–617. [Google Scholar]
- Drobot, S.D.; Barber, D.G. Towards development of a snow water equivalence (SWE) algorithm using microwave radiometry over snow covered first-year sea ice. Photogramm. Eng. Remote. Sens. 1998, 64, 415–423. [Google Scholar]
- Foster, J.L.; Sun, C.; Walker, J.P.; Kelly, R.; Chang, A.; Dong, J.; Powell, H. Quantifying the uncertainty in passive microwave snow water equivalent observations. Remote. Sens. Environ. 2005, 94, 187–203. [Google Scholar] [CrossRef]
- Li, D.; Durand, M.; Margulis, S.A. Potential for hydrologic characterization of deep mountain snowpack via passive microwave remote sensing in the Kern River basin, Sierra Nevada, USA. Remote. Sens. Environ. 2012, 125, 34–48. [Google Scholar] [CrossRef]
- Tong, J.; Dery, S.J.; Jackson, P.L.; Derksen, C. Testing snow water equivalent retrieval algorithms for passive microwave remote sensing in an alpine watershed of Western Canada. Can. J. Remote. Sens. 2010, 36, S74–S86. [Google Scholar] [CrossRef]
- Saberi, N.; Kelly, R.; Flemming, M.; Li, Q. Review of snow water equivalent retrieval methods using spaceborne passive microwave radiometry. Int. J. Remote. Sens. 2020, 41, 996–1018. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.P.; Koskinen, J.; Bojkov, B. Estimating northern hemisphere snow water equivalent for climate research through assimilation of space-borne radiometer data and ground-based measurements. Remote. Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Kim, E.; Forman, B.A.; Wang, L.; Lemoigne-Stewart, J.; Nag, S.; Kumar, S.; Vuyovich, C.; Blair, B.; Hofton, M. Space-Time Coverage Scenarios for A Global Snow Satellite Constellation. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5614–5616. [Google Scholar]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote. Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.; Markus, T.; Hancock, D.; Morison, J.; Palm, S.; Farrell, S.; Ivanoff, A. ATLAS/ICESat-2 L3A Sea Ice Freeboard, Version 3 ed; National Snow and Ice Data Center: Boulder, CO, USA, 2020; Volume 10, p. 5067. [Google Scholar]
- Liang, S. Comprehensive Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Sayer, A.; Hsu, N.; Bettenhausen, C. Implications of MODIS bow-tie distortion on aerosol optical depth retrievals, and techniques for mitigation. Atmos. Meas. Tech. 2015, 8, 5277–5288. [Google Scholar] [CrossRef] [Green Version]
- Bormann, K.J.; Westra, S.; Evans, J.P.; McCabe, M.F. Spatial and temporal variability in seasonal snow density. J. Hydrol. 2013, 484, 63–73. [Google Scholar] [CrossRef]
- Sturm, M.; Benson, C. Scales of spatial heterogeneity for perennial and seasonal snow layers. Ann. Glaciol. 2004, 38, 253–260. [Google Scholar] [CrossRef] [Green Version]
- Nag, S.; Hughes, S.P.; Le Moigne, J. Streamlining the design tradespace for Earth imaging constellations. In Proceedings of the AIAA SPACE 2016, Long Beach, CA, USA, 13–16 September 2016; p. 5561. [Google Scholar]
- Oki, T.; Imaoka, K.; Kachi, M. AMSR instruments on GCOM-W1/2: Concepts and applications. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1363–1366. [Google Scholar]
- Attema, E.; Bargellini, P.; Edwards, P.; Levrini, G.; Lokas, S.; Moeller, L.; Rosich-Tell, B.; Secchi, P.; Torres, R.; Davidson, M.; et al. Sentinel-1—The RADAR mission for GMES operational land and sea services. ESA Bull. 2007, 131, 10–17. [Google Scholar]
- Abdalati, W.; Zwally, H.J.; Bindschadler, R.; Csatho, B.; Farrell, S.L.; Fricker, H.A.; Harding, D.; Kwok, R.; Lefsky, M.; Markus, T.; et al. The ICESat-2 laser altimetry mission. Proc. IEEE 2010, 98, 735–751. [Google Scholar] [CrossRef]
- Brunt, K.M.; Neumann, T.A.; Walsh, K.M.; Markus, T. Determination of local slope on the Greenland Ice Sheet using a multibeam photon-counting LiDAR in preparation for the ICESat-2 Mission. IEEE Geosci. Remote. Sens. Lett. 2013, 11, 935–939. [Google Scholar] [CrossRef] [Green Version]
- Qi, W.; Dubayah, R.O. Combining TanDEM-X InSAR and simulated GEDI LiDAR observations for forest structure mapping. Remote. Sens. Environ. 2016, 187, 253–266. [Google Scholar] [CrossRef]
- Helfrich, S.R.; McNamara, D.; Ramsay, B.H.; Baldwin, T.; Kasheta, T. Enhancements to, and forthcoming developments in the Interactive Multisensor Snow and Ice Mapping System (IMS). Hydrol. Process. Int. J. 2007, 21, 1576–1586. [Google Scholar] [CrossRef]
- Robinson, D.A.; Frei, A. Seasonal variability of Northern Hemisphere snow extent using visible satellite data. Prof. Geogr. 2000, 52, 307–315. [Google Scholar] [CrossRef]
- Foster, J.; Hall, D.; Kelly, R.; Chiu, L. Seasonal snow extent and snow mass in South America using SMMR and SSM/I passive microwave data (1979–2006). Remote. Sens. Environ. 2009, 113, 291–305. [Google Scholar] [CrossRef] [Green Version]
- Vermote, E.; Kotchenova, S.; Ray, J. MODIS surface reflectance user’s guide. In MODIS Land Surface Reflectance Science Computing Facility, Version; National Aeronautics and Space Administration: Washington, DC, USA, 2011; Volume 1. [Google Scholar]
- Lau, N.C.; Crane, M.W. Comparing satellite and surface observations of cloud patterns in synoptic-scale circulation systems. Mon. Weather. Rev. 1997, 125, 3172–3189. [Google Scholar] [CrossRef]
- Sturm, M.; Taras, B.; Liston, G.E.; Derksen, C.; Jonas, T.; Lea, J. Estimating snow water equivalent using snow depth data and climate classes. J. Hydrometeorol. 2010, 11, 1380–1394. [Google Scholar] [CrossRef]
- Jiuliang, L.; Zhen, L. Temporal series analysis of snow water equivalent of satellite passive microwave data in northern seasonal snow classes (1978–2010). In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 3606–3609. [Google Scholar]
- Kwon, Y.; Yoon, Y.; Forman, B.A.; Kumar, S.; Wang, L. Synthetic Study of Spaceborne LiDAR Snow Depth Retrieval Assimilation within the NASA Land Information System. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2018. [Google Scholar]





| ID | Sensor Type | Orbit Altitude [km] | Inclination Angle [°] | Swath Width [km] | Prototype (Status) |
|---|---|---|---|---|---|
| 1 | PMW Radiometer | 510 | 97 | 1450 | AMSR2 (Existing) |
| 2 | Ku-band SAR | 705 | 98 | 500 | TSMM (Hypothetical) |
| 3 | C-band SAR | 705 | 98 | 250 | Sentinel-1 A/B (Existing) |
| 4 | Wide LiDAR | 481 | 92 | 20 | ICESat-2 (Hypothetical) |
| 5 | Narrow LiDAR | 481 | 92 | 6 | ICESat-2 (Existing) |
| 6 | Low-inclination LiDAR | 415 | 51.6 | 6.5 | GEDI (Existing) |
| Constellation ID | Sensor Marks | Sensor Mixture |
|---|---|---|
| C1 | ✠★★\ | PMW & two C-band SARs & narrow LiDAR |
| C2 | ✠✮\ | PMW & Ku-band SAR & narrow LiDAR |
| C3 | ✠✮  | PMW & Ku-band SAR & wide LiDAR |
| C4 | ✠★★✮\  | PMW & two C-band SARs & Ku-band SAR & |
| narrow LiDAR & wide LiDAR |
 = wide LiDAR.
= wide LiDAR.| Tundra | Taiga | Maritime | Ephemeral | Prairie | Alpine | |
|---|---|---|---|---|---|---|
| Radiometer | 1 | 0 | 0 | 1 | 1 | 0 |
| SAR | 1 | 0 | 1 | 1 | 1 | 1 |
| LiDAR (cloud-free) | 1 | 1 | 1 | 1 | 1 | 1 |
| LiDAR (cloud-covered) | 0 | 0 | 0 | 0 | 0 | 0 |
| Snow Class | |||||||
|---|---|---|---|---|---|---|---|
| Sensor ID | Tundra | Taiga | Maritime | Ephemeral | Prairie | Alpine | |
| 1-day | PMW | 98.8 | 0.00 | 0.00 | 67.1 | 77.0 | 0.00 |
| Ku-band SAR | 55.2 | 0.00 | 34.5 | 22.1 | 25.2 | 33.5 | |
| C-band SAR | 29.3 | 0.00 | 17.5 | 10.2 | 12.5 | 17.9 | |
| Wide LiDAR | 1.88 | 1.83 | 0.795 | 0.802 | 0.768 | 1.61 | |
| Narrow LiDAR | 0.686 | 0.374 | 0.316 | 0.344 | 0.346 | 0.447 | |
| Low-inclination LiDAR | 0.0901 | 0.105 | 0.211 | 0.522 | 0.158 | 0.163 | |
| 3-day | PMW | 100 | 0.00 | 0.00 | 93.7 | 95.8 | 0.00 |
| Ku-band SAR | 93.8 | 0.00 | 80.5 | 58.5 | 63.7 | 75.8 | |
| C-band SAR | 68.6 | 0.00 | 47.4 | 30.6 | 35.7 | 46.1 | |
| Wide LiDAR | 5.20 | 3.71 | 2.08 | 2.44 | 2.07 | 2.73 | |
| Narrow LiDAR | 1.92 | 1.14 | 0.832 | 1.04 | 0.911 | 0.913 | |
| Low-inclination LiDAR | 0.269 | 0.303 | 0.597 | 1.17 | 1.23 | 0.519 | |
| 30-day | PMW | 100 | 0.00 | 0.00 | 98.2 | 97.8 | 0.00 |
| Ku-band SAR | 97.7 | 0.00 | 96.0 | 93.3 | 90.3 | 94.3 | |
| C-band SAR | 94.9 | 0.00 | 91.5 | 87.7 | 82.2 | 88.9 | |
| Wide LiDAR | 18.3 | 13.8 | 8.84 | 11.4 | 9.22 | 9.70 | |
| Narrow LiDAR | 10.6 | 7.80 | 5.18 | 7.00 | 5.32 | 5.18 | |
| Low-inclination LiDAR | 2.00 | 2.12 | 3.60 | 8.20 | 7.30 | 3.01 | |
| Integration Period | Efficacy | ||||
|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| 1-day | 9.8 | 20 | 29 | 39 | 49 |
| 3-day | 9.9 | 20 | 30 | 40 | 50 |
| 30-day | 10 | 20 | 30 | 40 | 50 |
| Snow Class | ||||||
|---|---|---|---|---|---|---|
| Sensor ID | Tundra | Taiga | Maritime | Ephemeral | Prairie | Alpine |
| PMW | 1.03 | - | - | 1.54 | 1.31 | - |
| Ku-band SAR | 2.12 | - | 3.40 | 4.61 | 3.92 | 3.07 |
| C-band SAR | 4.15 | - | 6.76 | 9.11 | 7.77 | 6.08 |
| Wide LiDAR | 64.1 | 61.3 | 179 | 75.1 | 93.1 | 85.0 |
| Narrow LiDAR | 172 | 159 | 450 | 172 | 221 | 210 |
| Low-inclination LiDAR | 390 | 400 | 332 | 136 | 138 | 292 |
| Snow Class | |||||||
|---|---|---|---|---|---|---|---|
| Constellation ID | Tundra | Taiga | Maritime | Ephemeral | Prairie | Alpine | |
| 1-day | (a) | 97.8 | 0.710 | 34.5 | 77.1 | 90.9 | 25.6 |
| (b) | 98.8 | 0.710 | 29.0 | 72.7 | 91.4 | 32.1 | |
| (c) | 98.7 | 1.83 | 29.6 | 72.9 | 91.4 | 33.8 | |
| (d) | 98.7 | 2.54 | 47.6 | 78.3 | 93.4 | 42.0 | |
| 3-day | (a) | 100 | 2.00 | 68.9 | 98.0 | 99.0 | 67.4 |
| (b) | 100 | 2.00 | 74.2 | 98.0 | 99.2 | 81.4 | |
| (c) | 100 | 5.19 | 74.7 | 98.1 | 99.2 | 81.8 | |
| (d) | 100 | 7.14 | 87.3 | 98.4 | 99.3 | 87.0 | |
| 30-day | (a) | 100 | 19.7 | 95.9 | 98.9 | 99.0 | 98.4 |
| (b) | 100 | 19.7 | 96.8 | 98.8 | 99.1 | 99.0 | |
| (c) | 100 | 44.5 | 96.9 | 98.9 | 99.1 | 99.0 | |
| (d) | 100 | 49.2 | 97.8 | 99.2 | 99.2 | 99.2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Forman, B.A.; Kim, E. Exploring the Spatiotemporal Coverage of Terrestrial Snow Mass Using a Suite of Satellite Constellation Configurations. Remote Sens. 2022, 14, 633. https://doi.org/10.3390/rs14030633
Wang L, Forman BA, Kim E. Exploring the Spatiotemporal Coverage of Terrestrial Snow Mass Using a Suite of Satellite Constellation Configurations. Remote Sensing. 2022; 14(3):633. https://doi.org/10.3390/rs14030633
Chicago/Turabian StyleWang, Lizhao, Barton A. Forman, and Edward Kim. 2022. "Exploring the Spatiotemporal Coverage of Terrestrial Snow Mass Using a Suite of Satellite Constellation Configurations" Remote Sensing 14, no. 3: 633. https://doi.org/10.3390/rs14030633
APA StyleWang, L., Forman, B. A., & Kim, E. (2022). Exploring the Spatiotemporal Coverage of Terrestrial Snow Mass Using a Suite of Satellite Constellation Configurations. Remote Sensing, 14(3), 633. https://doi.org/10.3390/rs14030633








