Coarse-to-Fine Image Registration for Multi-Temporal High Resolution Remote Sensing Based on a Low-Rank Constraint
Abstract
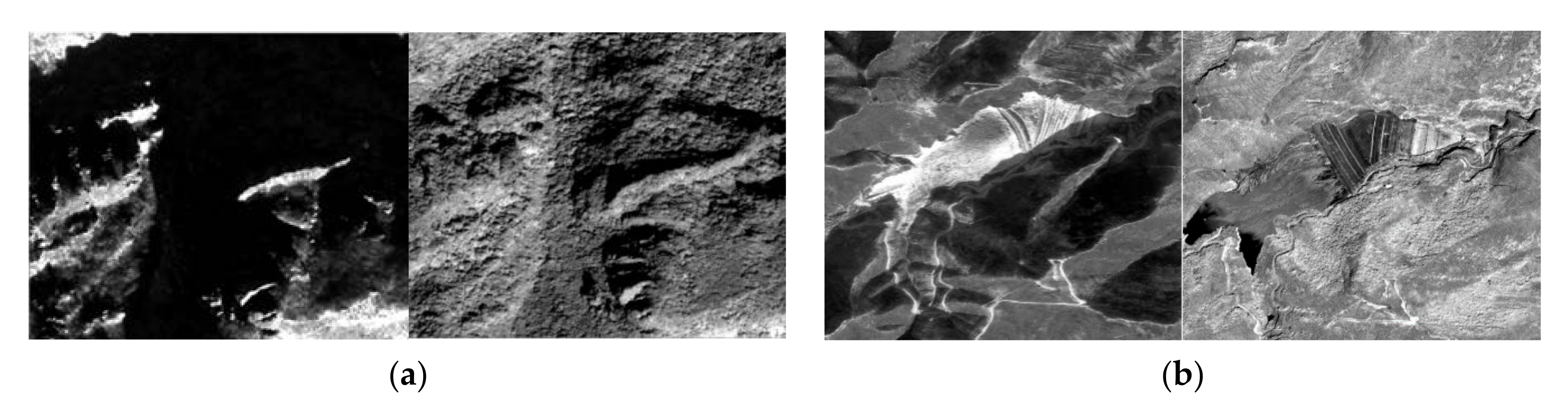
:1. Introduction
- (1)
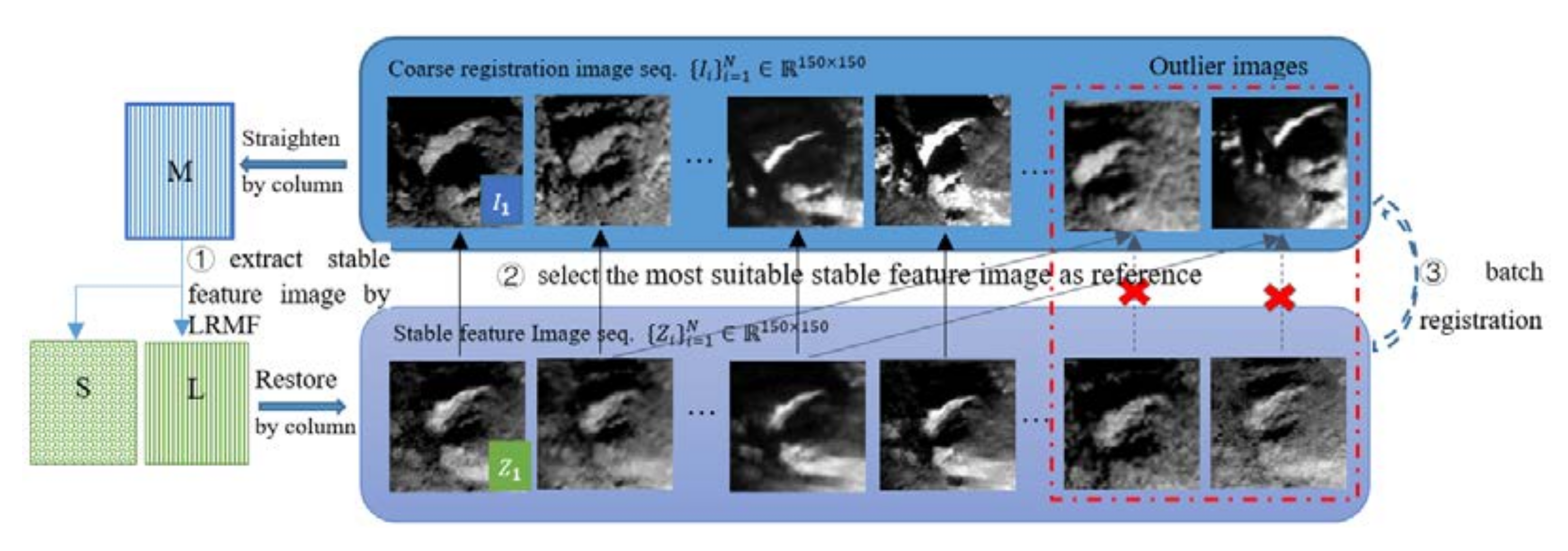
- Inspired by the excellent image denoising and restoration ability of the low-rank decomposition algorithm, we design a low-rank constraint-based batch reference (LRC-BRE) method to restore the stable features holding highly spatial co-occurrence in the image sequence, and construct a corresponding batch reference, in which each original image has a respective reference.
- (2)
- To match the original image and the reference image, the regional mutual information is considered to filter the match outliers, named as a match outlier filtering (MOF). Additionally, a dual-weighted block fitting (DWBF) is developed based on the feature inverse distance weight and feature regional similarity weight. The above two operators are integrated to form the block feature matching and local linear transformation (BFM-LLT) registration processing, which has good robustness and alignment accuracy for the coarse registration of multi-temporal remote sensing images with medium and low texture differences and for the registration of original images and stable feature images restored by LRC-BRE.
- (3)
- A new comprehensive coarse-to-fine registration (CCFR) framework integrated by LRC-BRE and BFM-LLT is proposed for HMR-LC images. By taking the recovered stable feature image as the reference baseline image, the proposed framework transforms the direct registration of large difference HMR-LC image pairs into the indirect registration of small and medium difference image pairs, and realizes the applicability of the mainstream image registration methods.
- (4)
- On GF-2 and GF-1 satellite remote sensing image datasets with low-stability land-cover and complex terrain, the experimental results show that the comprehensive registration framework CCFR is more effective than the latest registration algorithm in visual quality and quantitative evaluation, owing to the combining of LRC-BRE with good batch reference and BFM-LLT with improved alignment effect.
2. Methods
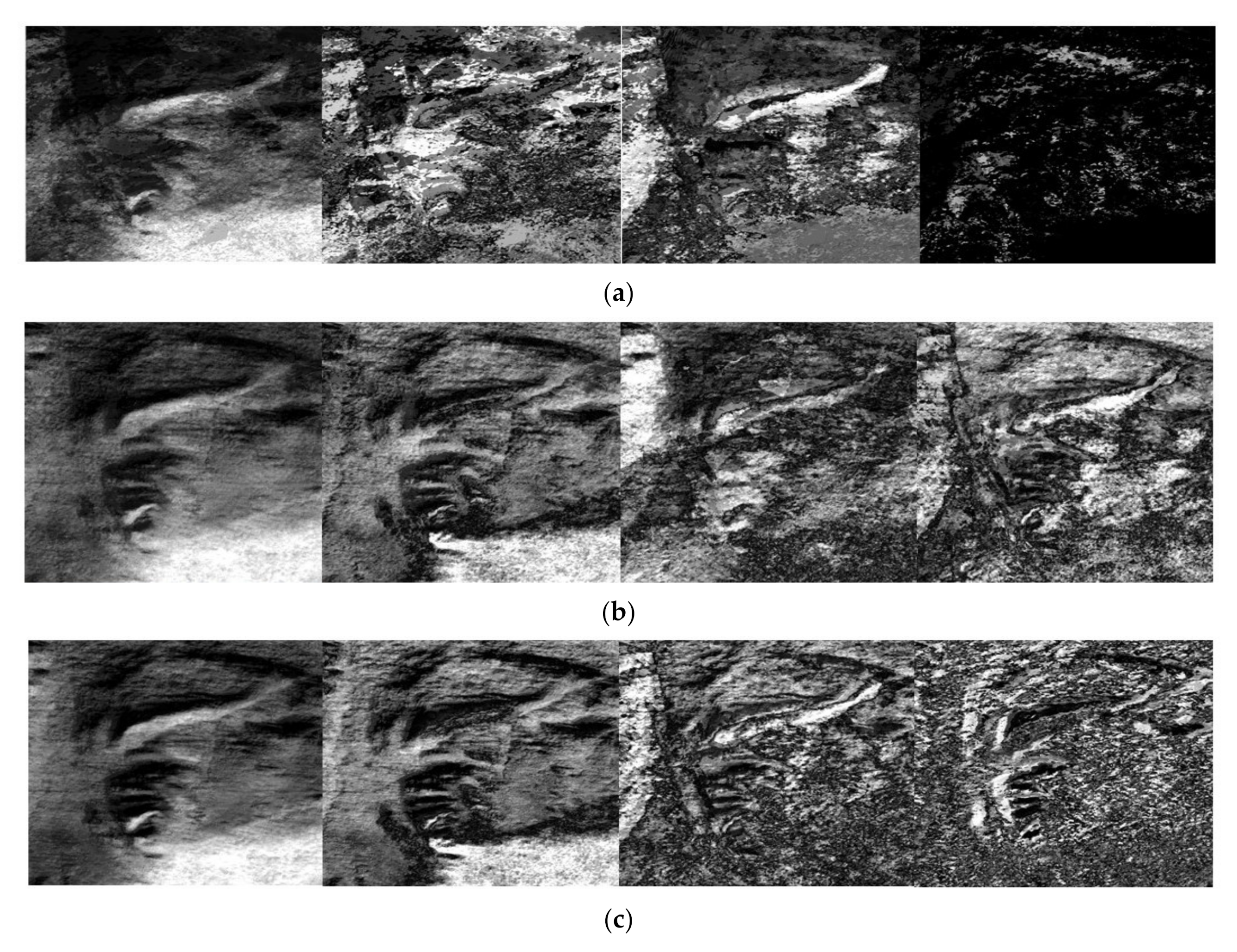
2.1. LRC-BRE: A Low-Rank Constraint-Based Batch Reference Extraction
2.2. BFM-LLT: Block Feature Matching and Local Linear Transformation
2.2.1. Match Outlier Filtering (MOF)
2.2.2. Dual-Weighted Block Fitting (DWBF)
2.3. Algorithm of CCFR
| Algorithm 1: CCFR |
| Input: images set |
| Step 1: is aligned by geocoding, cropped and interpolated (optional) to obtain a group of image sequences G with the same size and the same resolution: |
| Step 2: The lowest outlier image from image sequence G is calculated by: |
| Step 3: With as the reference image, based on the BFM-LLT method, the image pairs are coarsely registered in turn to obtain a new image sequence , and the matching results are recorded in the matrix set : |
| BFM-LLT () |
| where , represents the block region in row j and column k of the image , and represents the feature matching result of the block region in row j and column k of the image . When the number of matching inner points in the region is insufficient, there is true. |
| Step 4: Generate a stable feature image block sequence for each block sequence: where and respectively represent the block stable feature image and block sparse matrix re-stored corresponding to , and ϵ is a penalty factor. |
| Step 5: For each , its globally most suitable stable feature image is synthesized by: |
| where is the most appropriate block stable feature image for . The Best () is given in Formula (1). |
| Step 6: Block feature matching and local linear transformation are carried out on the image pair in turn to obtain the accurately registered image sequence: |
| BFM-LLT () |
| output: |
3. Results and Evaluations
3.1. Experimental Data and Related Algorithms
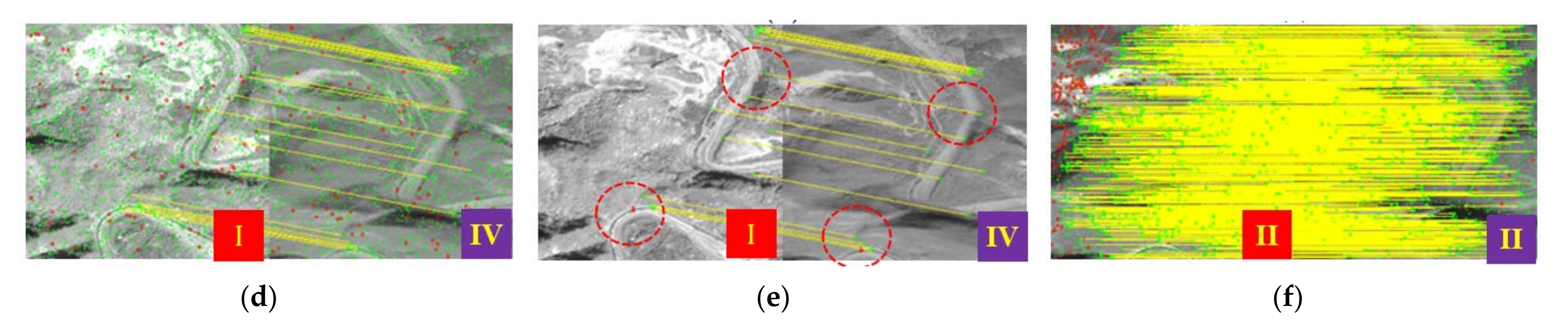
3.2. Visual Quality
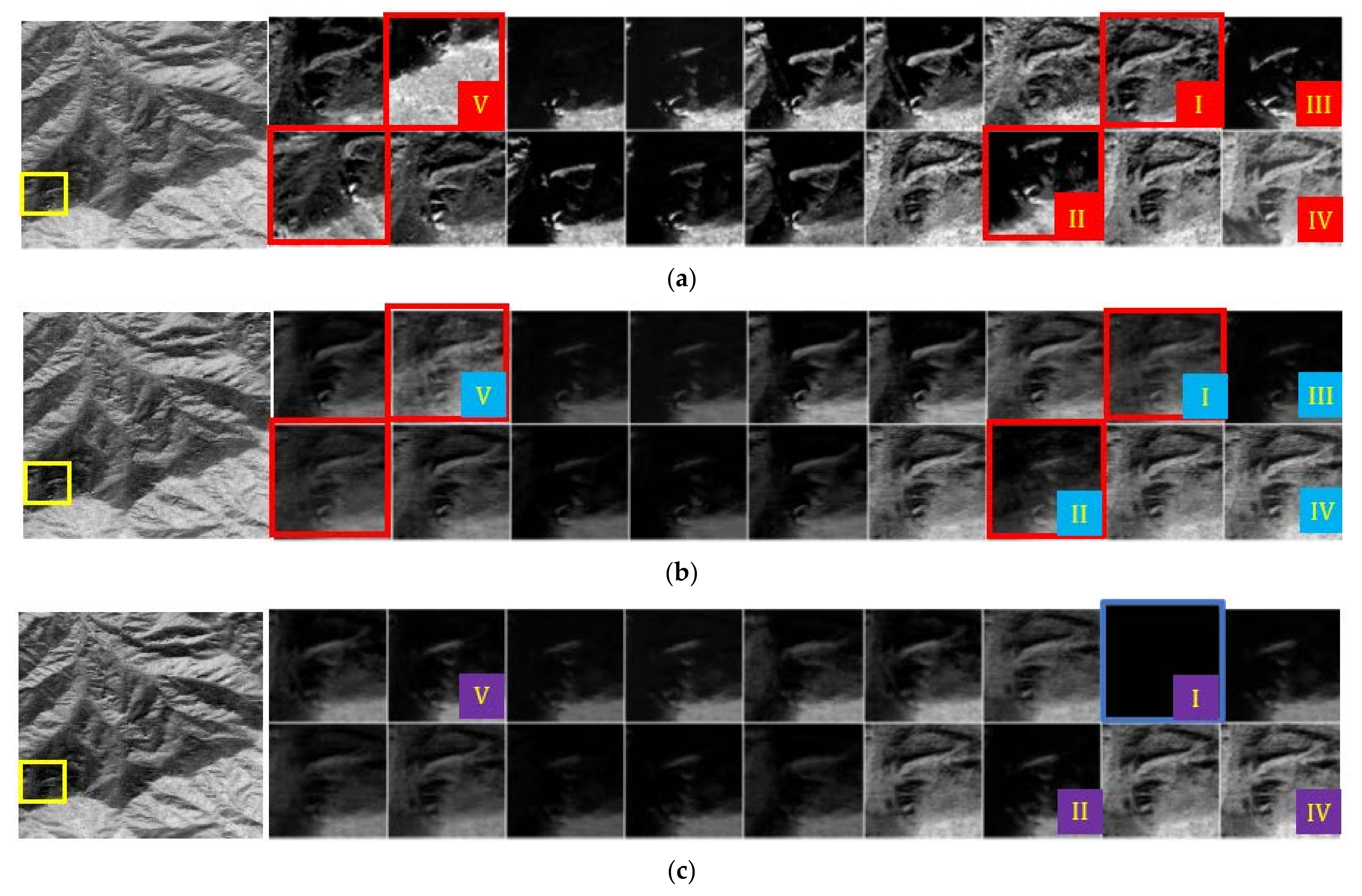
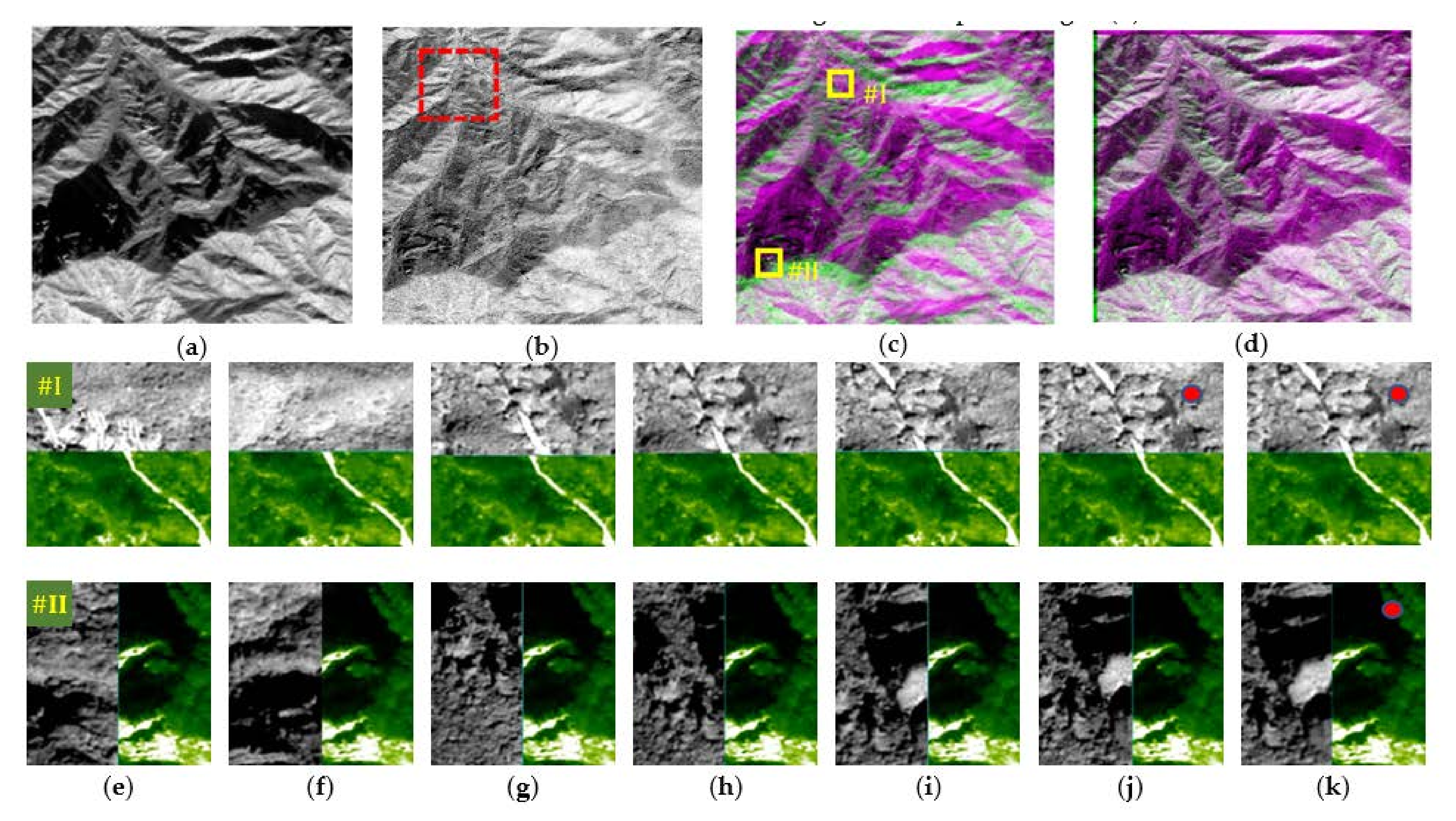
3.2.1. Ecological Reserve
3.2.2. Mine Production Area
3.2.3. Mine Environmental Treatment Area
3.3. Evaluation of Registration Results
4. Discussion
4.1. Quantitative Comparison of Feature Matching Results
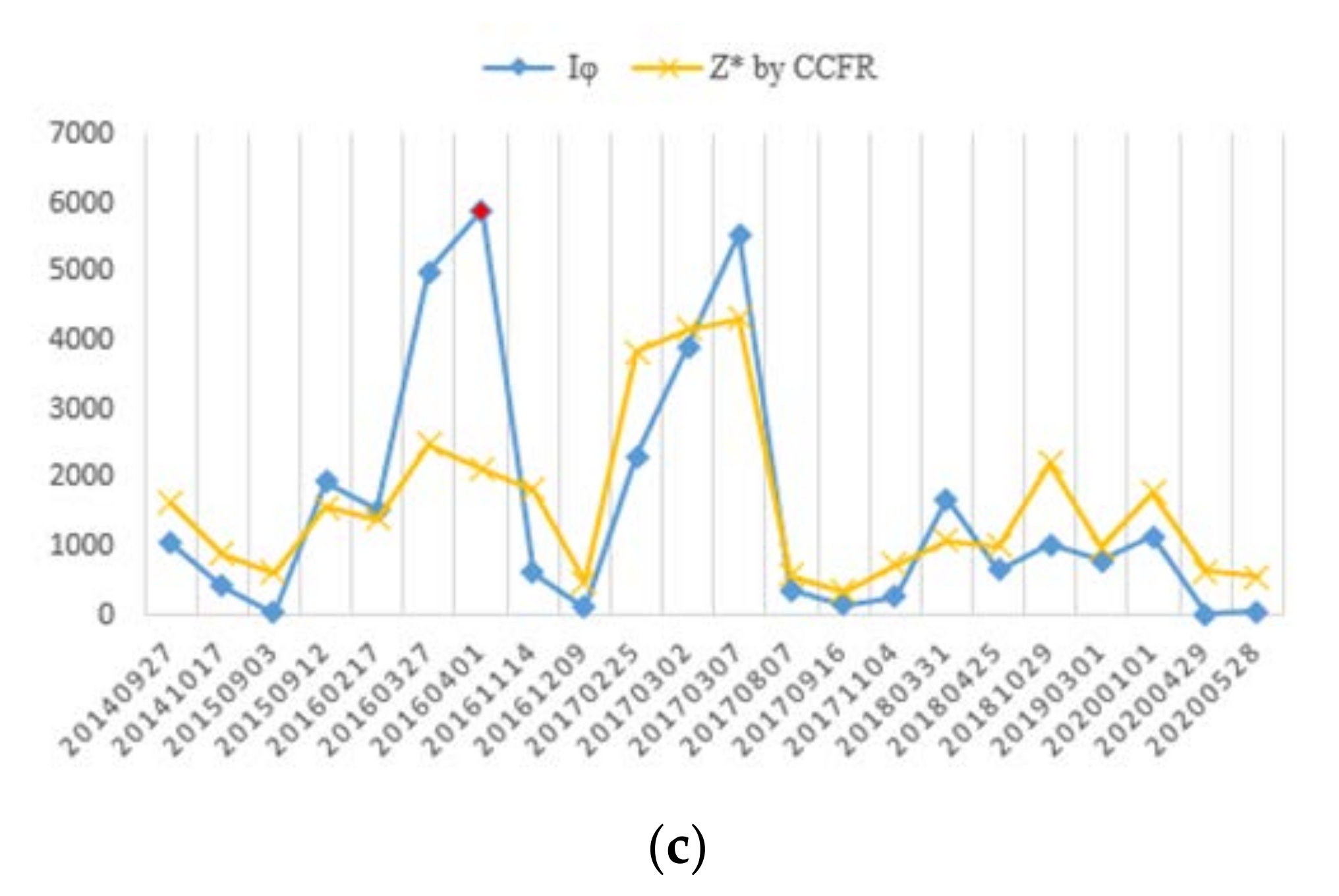
4.2. Correlation Factors of Restored Stable Feature Image Quality
4.3. Registration with Different Optical Satellite Images
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shen, H.; Meng, X.; Zhang, L. An Integrated Framework for the Spatio–Temporal–Spectral Fusion of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7135–7148. [Google Scholar] [CrossRef]
- Zhou, Y.; Rangarajan, A.; Gader, P.D. An Integrated Approach to Registration and Fusion of Hyperspectral and Multispectral Images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3020–3033. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, L.-J.; Ma, G.-C.; Jia, H.-J.; Jin, X. Emergency monitoring of high-level landslide disasters in Jinsha River using domestic remote sensing satellites. J. Remote Sens. 2019, 23, 252–261. [Google Scholar]
- Song, F.; Yang, Z.; Gao, X.; Dan, T.; Yang, Y.; Zhao, W.; Yu, R. Multi-Scale Feature Based Land Cover Change Detection in Mountainous Terrain Using Multi-Temporal and Multi-Sensor Remote Sensing Images. IEEE Access 2018, 6, 77494–77508. [Google Scholar] [CrossRef]
- Bordone Molini, A.; Valsesia, D.; Fracastoro, G.; Magli, E. DeepSUM: Deep Neural Network for Super-Resolution of Unregistered Multitemporal Images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3644–3656. [Google Scholar] [CrossRef] [Green Version]
- Guan, X.-B.; Shen, H.-F.; Gan, W.-X.; Zhang, L.-P. Estimation and spatiotemporal analysis of winter NPP in Wuhan based on Landsat TM/ETM+ Images. Remote Sens. Technol. Appl. 2015, 30, 884–890. [Google Scholar]
- Ye, Y. Fast and Robust Registration of Multimodal Remote Sensing Images via Dense Orientated Gradient Feature. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W7, 1009–1015. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Wen, Z.; Wu, Y.; Jiao, L.; Gong, M.; Zheng, Y.; Liu, L. Remote Sensing Image Registration with Modified SIFT and Enhanced Feature Matching. IEEE Geosci. Remote Sens. Lett. 2017, 14, 3–7. [Google Scholar] [CrossRef]
- Chang, H.-H.; Wu, G.-L.; Chiang, M.-H. Remote Sensing Image Registration Based on Modified SIFT and Feature Slope Grouping. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1363–1367. [Google Scholar] [CrossRef]
- Chen, S.; Zhong, S.; Xue, B.; Li, X.; Zhao, L.; Chang, C.-I. Iterative Scale-Invariant Feature Transform for Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3244–3265. [Google Scholar] [CrossRef]
- Chen, S.; Li, X.; Zhao, L.; Yang, H. Medium-Low Resolution Multisource Remote Sensing Image Registration Based on SIFT and Robust Regional Mutual Information. Int. J. Remote Sens. 2018, 39, 3215–3242. [Google Scholar] [CrossRef]
- Feng, R.; Du, Q.; Li, X.; Shen, H. Robust Registration for Remote Sensing Images by Combining and Localizing Feature- and Area-Based Methods. ISPRS Journal of Photogrammetry and Remote Sensing. 2019, 151, 15–26. [Google Scholar] [CrossRef]
- Feng, R.; Du, Q.; Luo, H.; Shen, H.; Li, X.; Liu, B. A Registration Algorithm Based on Optical Flow Modification for Multi-temporal Remote Sensing Images Covering the Complex-terrain Region. J. Remote Sens. 2021, 25, 630. [Google Scholar] [CrossRef]
- Feng, R.; Du, Q.; Shen, H.; Li, X. Region-by-Region Registration Combining Feature-Based and Optical Flow Methods for Remote Sensing Images. Remote Sens. 2021, 13, 1475. [Google Scholar] [CrossRef]
- Schubert, A.; Small, D.; Jehle, M.; Meier, E. COSMO-Skymed, TerraSAR-X, and RADARSAT-2 Geolocation Accuracy after Compensation for Earth-System Effects. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Aguilar, M.A.; del Mar Saldana, M.; Aguilar, F.J. Assessing Geometric Accuracy of the Orthorectification Process from Geoeye-1 and Worldview-2 Panchromatic Images. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 427–435. [Google Scholar] [CrossRef]
- Chen, L.-C.; Li, S.-H.; Chen, J.-J.; Rau, J.-Y. Method of Ortho-Rectification for High-Resolution Remote Sensing Image, October 9, 2008. Available online: https://www.patentsencyclopedia.com/app/20080247669 (accessed on 25 October 2021).
- Hasan, R.H. Evaluation of the Accuracy of Digital Elevation Model Produced from Different Open Source Data. J. Eng. 2019, 25, 100–112. [Google Scholar] [CrossRef] [Green Version]
- Nag, S. Image Registration Techniques: A Survey. engrXiv 2017. [Google Scholar] [CrossRef] [Green Version]
- Zitová, B.; Flusser, J. Image Registration Methods: A Survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef] [Green Version]
- Martinez, A.; Garcia-Consuegra, J.; Abad, F. A Correlation-Symbolic Approach to Automatic Remotely Sensed Image Rectification. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium, IGARSS’99 (Cat. No.99CH36293), Hamburg, Germany, 28 June–2 July 1999. [Google Scholar]
- Hel-Or, Y.; Hel-Or, H.; David, E. Fast Template Matching in Non-Linear Tone-Mapped Images. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Chen, H.-M.; Varshney, P.K.; Arora, M.K. Performance of Mutual Information Similarity Measure for Registration of Multitemporal Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2445–2454. [Google Scholar] [CrossRef]
- Kern, J.P.; Pattichis, M.S. Robust Multispectral Image Registration Using Mutual-Information Models. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1494–1505. [Google Scholar] [CrossRef]
- Zhao, L.-Y.; Lü, B.-Y.; Li, X.-R.; Chen, S.-H. Multi-source remote sensing image registration based on scale-invariant feature transform and optimization of regional mutual information. Acta Physica Sinica. 2015, 64, 124204. [Google Scholar] [CrossRef]
- Ravanbakhsh, M.; Fraser, C.S. A Comparative Study of DEM Registration Approaches. J. Spat. Sci. 2013, 58, 79–89. [Google Scholar] [CrossRef]
- Murphy, J.M.; Le Moigne, J.; Harding, D.J. Automatic Image Registration of Multimodal Remotely Sensed Data with Global Shearlet Features. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1685–1704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. SURF: Speeded Up Robust Features. In Computer Vision—ECCV 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Morel, J.-M.; Yu, G. ASIFT: A New Framework for Fully Affine Invariant Image Comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Ke, Y.; Sukthankar, R. PCA-SIFT: A More Distinctive Representation for Local Image Descriptors. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004. CVPR 2004, Washington, DC, USA, 27 June–2 July 2004. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An Efficient Alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary Robust Invariant Scalable Keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Rosten, E.; Porter, R.; Drummond, T. Faster and Better: A Machine Learning Approach to Corner Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 105–119. [Google Scholar] [CrossRef] [Green Version]
- Ye, Y.; Shan, J.; Bruzzone, L.; Shen, L. Robust Registration of Multimodal Remote Sensing Images Based on Structural Similarity. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2941–2958. [Google Scholar] [CrossRef]
- Sedaghat, A.; Ebadi, H. Remote Sensing Image Matching Based on Adaptive Binning SIFT Descriptor. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5283–5293. [Google Scholar] [CrossRef]
- Brox, T.; Bruhn, A.; Papenberg, N.; Weickert, J. High Accuracy Optical Flow Estimation Based on a Theory for Warping. In Lecture Notes in Computer Science; Springer Berlin Heidelberg: Berlin, Heidelberg, 2004; pp. 25–36. [Google Scholar]
- Ren, Z.; Li, J.; Liu, S.; Zeng, B. Meshflow Video Denoising. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017. [Google Scholar]
- Liu, L.; Chen, F.; Liu, J.-B. Optical Flow and Feature Constrains Algorithm for Remote Sensing Image Registration. Comput. Eng. Des. 2014, 35, 3127–3131. [Google Scholar]
- Xu, F.; Yu, H.; Wang, J.; Yang, W. Accurate Registration of Multitemporal UAV Images Based on Detection of Major Changes. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018. [Google Scholar]
- Brigot, G.; Colin-Koeniguer, E.; Plyer, A.; Janez, F. Adaptation and Evaluation of an Optical Flow Method Applied to Coregistration of Forest Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2923–2939. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Ganesh, A.; Wright, J.; Xu, W.; Ma, Y. RASL: Robust Alignment by Sparse and Low-Rank Decomposition for Linearly Correlated Images. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2233–2246. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Shen, B.; Ling, H. Online Robust Image Alignment via Iterative Convex Optimization. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Candes, E.; Li, X.; Ma, Y.; Wright, J. Robust Principal Component Analysis?: Recovering Low-Rank Matrices from Sparse Errors. In Proceedings of the 2010 IEEE Sensor Array and Multichannel Signal Processing Workshop, Jerusalem, Israel, 4–7 October 2010. [Google Scholar]
- Chi, Y.; Lu, Y.M.; Chen, Y. Nonconvex Optimization Meets Low-Rank Matrix Factorization: An Overview. IEEE Trans. Signal Processing 2019, 67, 5239–5269. [Google Scholar] [CrossRef] [Green Version]
- Torr, P.H.S.; Murray, D.W. The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix. Int. J. Comput. Vis. 1997, 24, 271–300. [Google Scholar] [CrossRef]
- Russakoff, D.B.; Tomasi, C.; Rohlfing, T.; Maurer, C.R., Jr. Image Similarity Using Mutual Information of Regions. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; pp. 596–607. [Google Scholar]
- Zaragoza, J.; Tat-Jun, C.; Tran, Q.-H.; Brown, M.S.; Suter, D. As-Projective-as-Possible Image Stitching with Moving DLT. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1285–1298. [Google Scholar] [PubMed] [Green Version]
- Hu, T.; Zhang, H.; Shen, H.; Zhang, L. Robust Registration by Rank Minimization for Multiangle Hyper/Multispectral Remotely Sensed Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2443–2457. [Google Scholar] [CrossRef]
- Goshtasby, A. Piecewise Linear Mapping Functions for Image Registration. Pattern Recognit. 1986, 19, 459–466. [Google Scholar] [CrossRef]
- Han, Y.; Bovolo, F.; Bruzzone, L. An Approach to Fine Coregistration between Very High Resolution Multispectral Images Based on Registration Noise Distribution. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6650–6662. [Google Scholar] [CrossRef]
- Gharbia, R.; Ahmed, S.A.; Hassanien, A.E. Remote Sensing Image Registration Based on Particle Swarm Optimization and Mutual Information. In Advances in Intelligent Systems and Computing; Springer: New Delhi, India, 2015; pp. 399–408. [Google Scholar]
- Lin, Z.; Ganesh, A.; Wright, J.; Wu, L.; Chen, M.; Ma, Y. Fast Convex Optimization Algorithms for Exact Recovery of a Corrupted Low-Rank Matrix. 2009. Available online: https://www.ideals.illinois.edu/handle/2142/74352 (accessed on 20 January 2021).
- Lin, Z.; Chen, M.; Ma, Y. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices. arXiv 2010, arXiv:1009.5055. [Google Scholar]
- Yuan, X.-M.; Yang, J.-F. Sparse and Low Rank Matrix Decomposition via Alternating Direction Method. Preprint 2009, 12. [Google Scholar]

















| Type | Time | No. | Size | Res 1 | Characteristics | Preprocessing | BFM Method |
|---|---|---|---|---|---|---|---|
| Ecological reserve | 2015–2020 | 18 | 3600 × 3900 pixels | 0.8 m | Mountainous areas with high vegetation coverage; deciduous vegetation is widely distributed. | Geocoding alignment + ortho-rectification (30 m precision DEM) | SURF 6 × 6 block |
| Mine production | 2015–2021 | 18 | 2850 × 3300 pixels | 0.8 m | Large-scale mining and waste discharge; evergreen vegetation and deciduous vegetation are staggered. | Geocoding alignment + ortho-rectification (30 m precision DEM) | SIFT 3 × 3 block |
| Mine environmental treatment | 2014–2020 | 22 | 3900 × 4000 pixels | 0.8 m | Small-scale mining activities, greening treatment, deciduous vegetation is widely distributed | Geocoding alignment | SIFT 5 × 5 block |
| Ecological Reserve | Mine Production | Mine Environmental Treatment | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NCC | MI | RMSE/pixels | NCC | MI | RMSE/pixels | NCC | MI | RMSE/pixels | |
| Original | 0.28136 | 0.059138 | 0.37336 | 0.14756 | 0.026849 | 0.28831 | 0.28807 | 0.058247 | 0.27997 |
| RRM | 0.40549 | 0.10822 | 0.3533 | 0.27153 | 0.054601 | 0.26371 | 0.45068 | 0.13519 | 0.25229 |
| PLM | 0.50274 | 0.2535 | 0.31822 | 0.29541 | 0.093957 | 0.27233 | 0.49631 | 0.16344 | 0.24489 |
| APAP | 0.63317 | 0.32688 | 0.3533 | 0.34195 | 0.097451 | 0.25461 | 0.53916 | 0.19488 | 0.23318 |
| OFM | 0.6786 | 0.34853 | 0.30167 | 0.33511 | 0.09357 | 0.2557 | 0.50141 | 0.17111 | 0.24879 |
| LRC-BRE-BR | 0.68687 | 0.35448 | 0.31131 | 0.36022 | 0.10722 | 0.25249 | null | null | null |
| CCFR | 0.70928 | 0.39685 | 0.28171 | 0.38415 | 0.11548 | 0.24826 | 0.6413 | 0.30463 | 0.22609 |
| Type | Time | Sensor | No. | Size | Res 1 | Characteristics | Preprocessing |
|---|---|---|---|---|---|---|---|
| Mine production | 2014–2021 | GF-1 | 8 | 960 × 1200 pixels | 2 m | Large-scale underground mining, continuous discharge and leakage of mine waste. | Geocoding alignment, up sampling |
| GF-2 | 16 | 2400 × 3000 pixels | 0.8 m | Geocoding alignment |
| Ecological Reserve | |||
|---|---|---|---|
| NCC | MI | RMSE/pixels | |
| Original | 0.28861 | 0.095284 | 0.39303 |
| RRM | 0.30568 | 0.09869 | 0.39306 |
| PLM | 0.47723 | 0.29056 | 0.36538 |
| APAP | 0.50373 | 0.44417 | 0.39686 |
| OFM | 0.50852 | 0.41378 | 0.37514 |
| CCFR | 0.51342 | 0.44967 | 0.3638 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Luo, X.; Ma, Y.; Wang, C.; Wang, W.; Qian, X. Coarse-to-Fine Image Registration for Multi-Temporal High Resolution Remote Sensing Based on a Low-Rank Constraint. Remote Sens. 2022, 14, 573. https://doi.org/10.3390/rs14030573
Zhang P, Luo X, Ma Y, Wang C, Wang W, Qian X. Coarse-to-Fine Image Registration for Multi-Temporal High Resolution Remote Sensing Based on a Low-Rank Constraint. Remote Sensing. 2022; 14(3):573. https://doi.org/10.3390/rs14030573
Chicago/Turabian StyleZhang, Peijing, Xiaoyan Luo, Yan Ma, Chengyi Wang, Wei Wang, and Xu Qian. 2022. "Coarse-to-Fine Image Registration for Multi-Temporal High Resolution Remote Sensing Based on a Low-Rank Constraint" Remote Sensing 14, no. 3: 573. https://doi.org/10.3390/rs14030573
APA StyleZhang, P., Luo, X., Ma, Y., Wang, C., Wang, W., & Qian, X. (2022). Coarse-to-Fine Image Registration for Multi-Temporal High Resolution Remote Sensing Based on a Low-Rank Constraint. Remote Sensing, 14(3), 573. https://doi.org/10.3390/rs14030573








