The Extreme Heat Wave over Western North America in 2021: An Assessment by Means of Land Surface Temperature
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Areas: Selection of Urban Areas and Geographical/Climatic Characreristics
- (i)
- A subset of 28 cities (Table S1) for SUHI analysis using low spatial resolution but high temporal resolution sensor;
- (ii)
- A subset of 18 cities (Table S1) for SUHI analysis using high spatial resolution but low temporal resolution sensor;
- (iii)
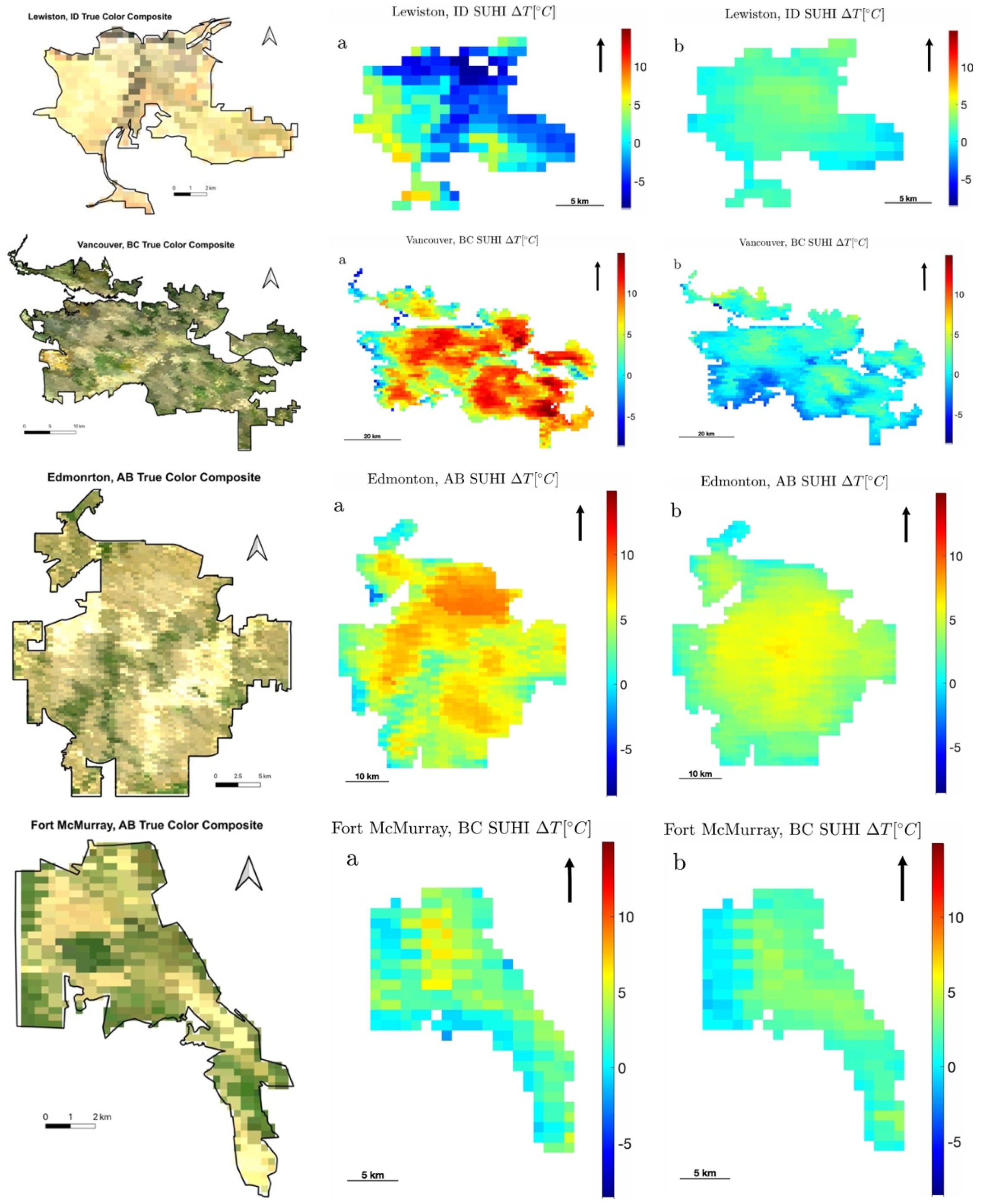
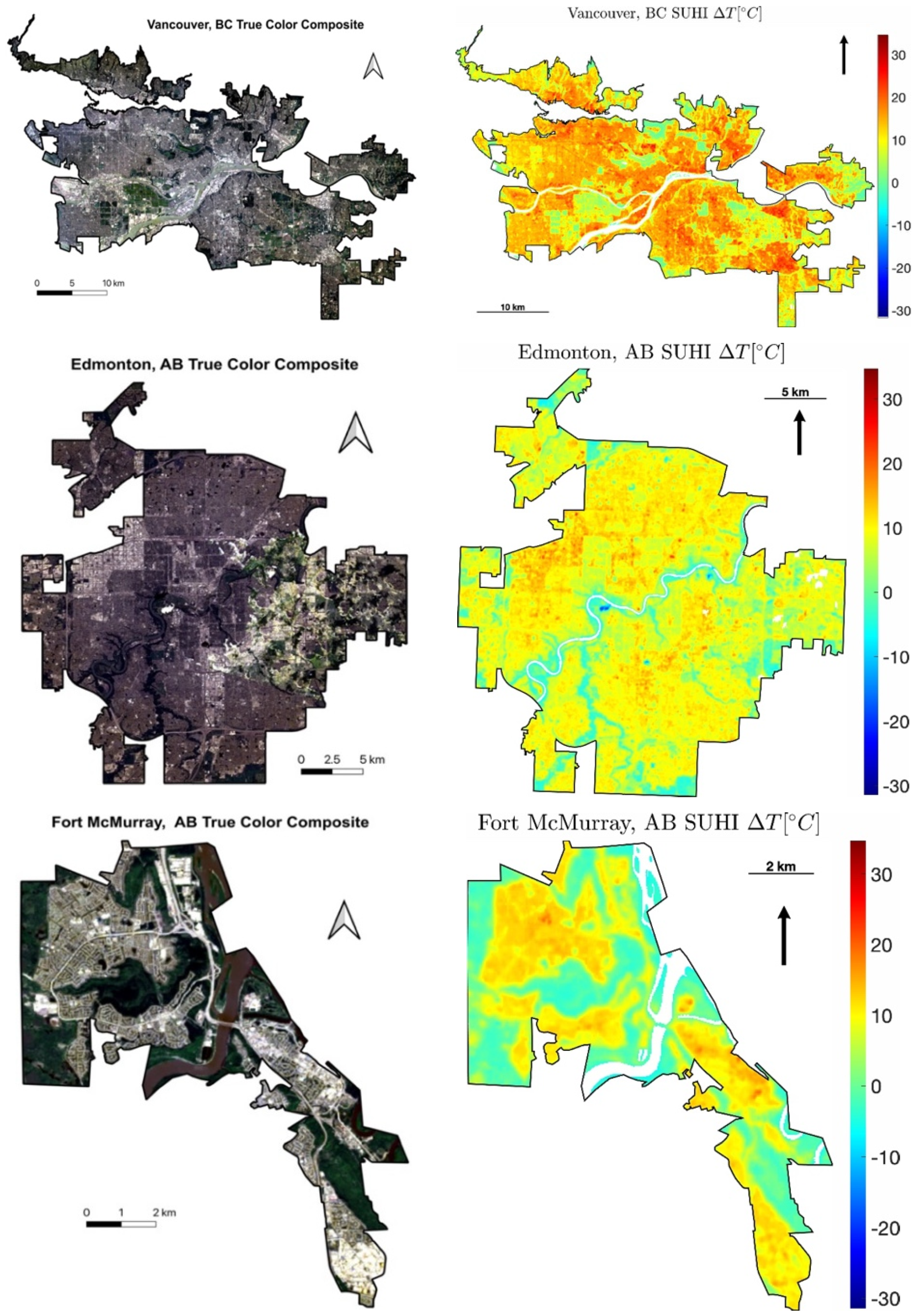
- A subset of four sample cities (Vancouver, Edmonton, Lewiston, and Fort McMurray) distributed across different latitudes to illustrate the spatial patterns of LST, SUHI, and thermal environment indicators.
2.2. Thermal Infrared Remote Sensing Data
2.2.1. MODIS Data
2.2.2. Landsat Data
2.3. Estimation of SUHI Intensity and UFTVI
2.4. Identification of LST Clusters
2.5. Data Processing Tools and Software
3. Results
3.1. Analysis of SUHI from MODIS Data
3.1.1. Maximum LSTs and SUHI Intensity during the 2021 HW
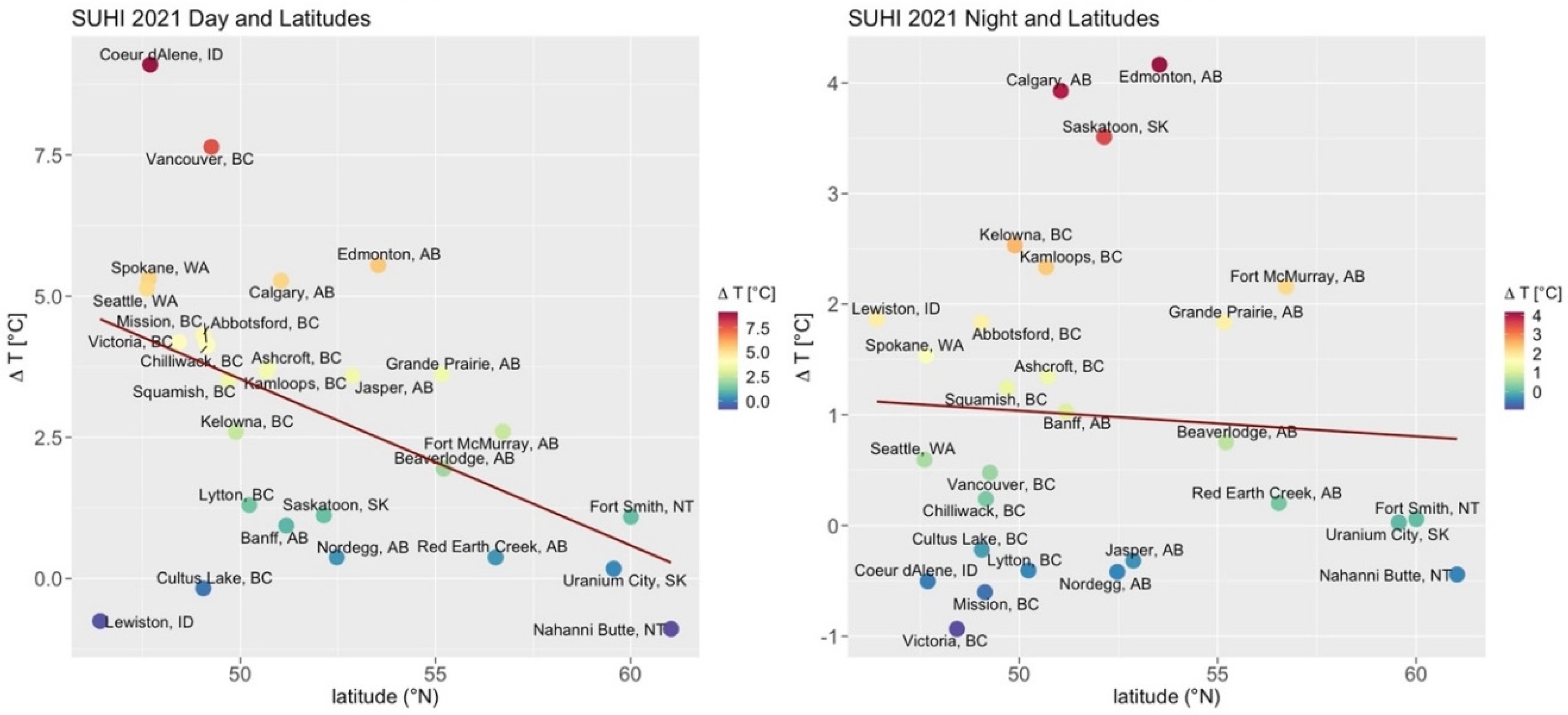
3.1.2. Latitudinal Variations on SUHI Intensity during the 2021 HW
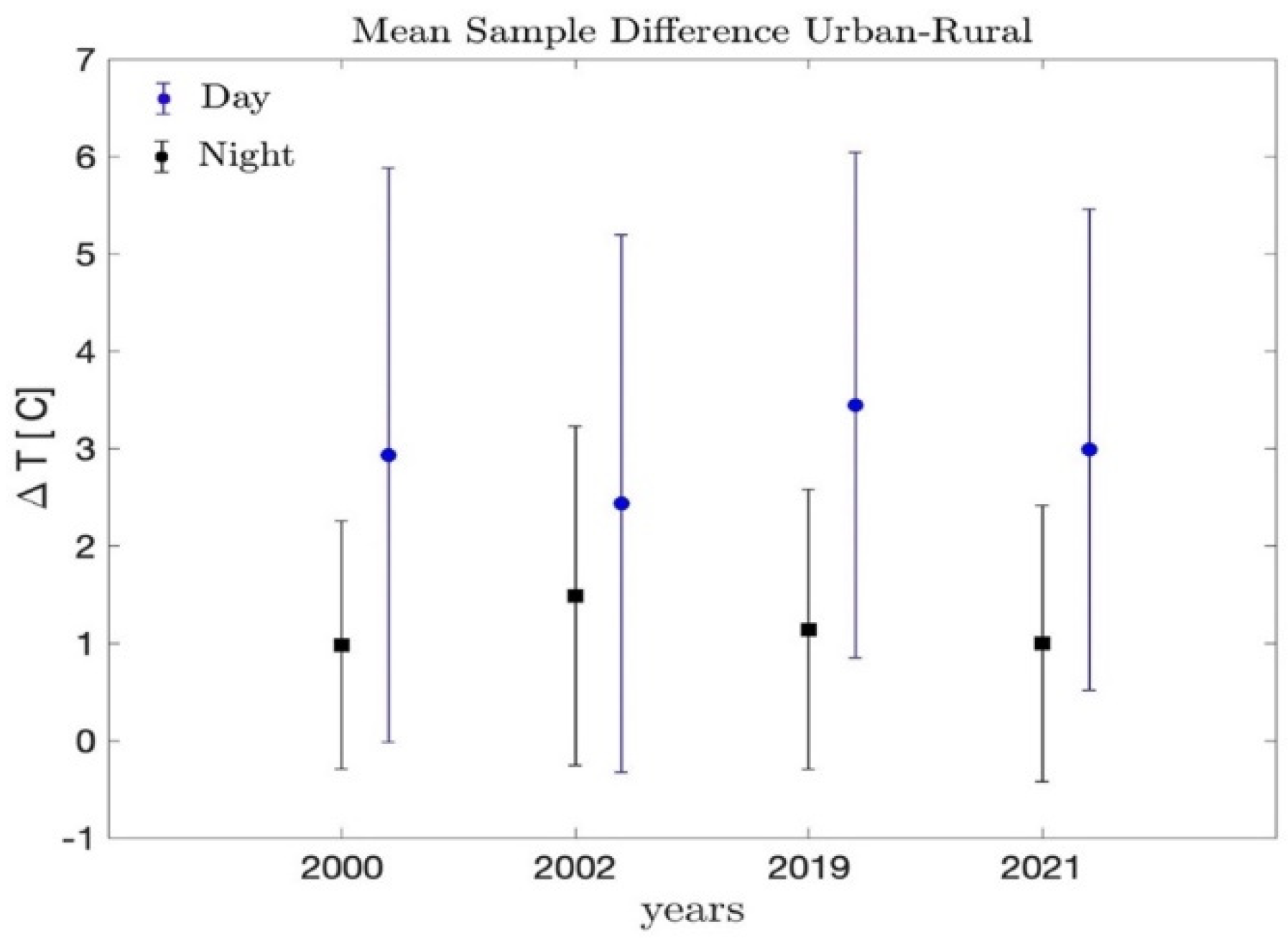
3.1.3. Interannual Variations on SUHI intensity
3.1.4. Spatial Patterns of SUHI Intensity
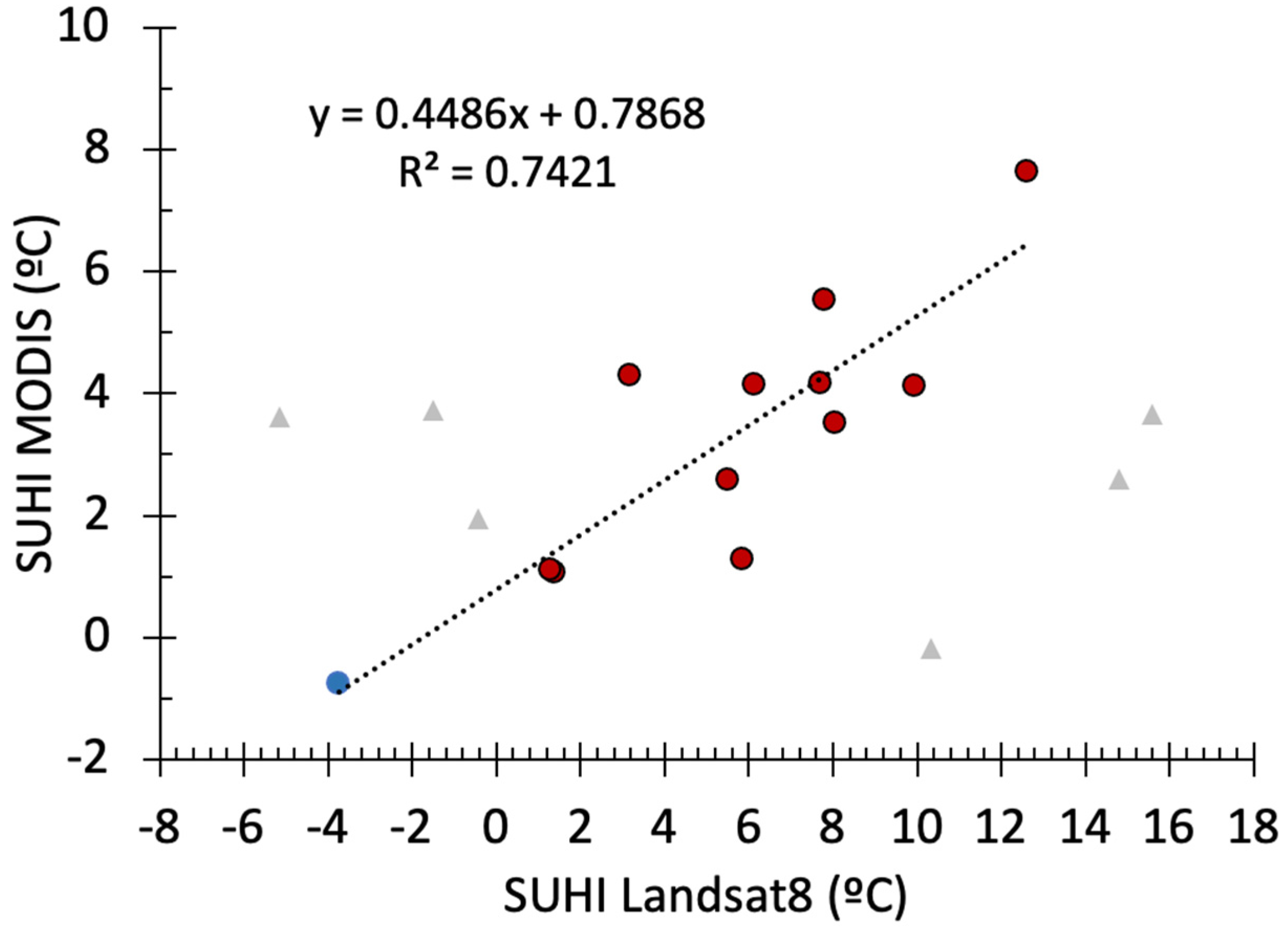
3.2. Analysis of SUHI from Landsat-8 Data
3.2.1. SUHI Intensity during the 2021 HW
3.2.2. Spatial Patterns of SUHI
3.2.3. Thermal Comfort Conditions and Spatial Clusters
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Robinson, P.J. On the definition of a heat wave. J. Appl. Meteorol. 2001, 40, 762–775. [Google Scholar] [CrossRef]
- Lee, E.; Bieda, R.; Shanmugasundaram, J.; Basara Richter, H. Land surface and atmospheric conditions associated with heat waves over the Chickasaw Nation in the South Central United States. J. Geophys. Res. Atmos. 2016, 121, 6284–6298. [Google Scholar] [CrossRef]
- Guo, Y.; Gasparrini, A.; Armstrong, B.; Li, S.; Tawatsupa, B.; Tobias, A.; Lavigne, E.; Coelho, M.d.Z.S.; Leone, M.; Pan, X.; et al. Global variation in the effects of ambient temperature on mortality: A systematic evaluation. Epidemiology 2014, 25, 781–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guirguis, K.; Gershunov, A.; Tardy, A.; Basu, R. The Impact of Recent Heat Waves on Human Health in California. J. Appl. Meteorol. Climatol. 2014, 53, 3–19. [Google Scholar] [CrossRef]
- Xia, Y.; Li, Y.; Guan, D.; Tinoco, D.M.; Xia, J.; Yan, Z.; Huo, H. Assessment of the economic impacts of heat waves: A case study of Nanjing, China. J. Clean. Prod. 2018, 171, 811–819. [Google Scholar] [CrossRef] [Green Version]
- Castillo, F.; Vargas, A.S.; Gilless, J.K.; Wehner, M. The Impact of Heat Waves on Agricultural Labor Productivity and Output. In Extreme Events and Climate Change: A Multidisciplanary Approach, 1st ed.; Castillo, F., Wehner, M., Stone, D.A., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2021; pp. 11–20. [Google Scholar] [CrossRef]
- Dobricic, S.; Russo, S.; Pozzoli1, L.; Wilson, J.; Vignati, E. Increasing occurrence of heat waves in the terrestrial Arctic. Environ. Res. Lett. 2020, 15, 024022. [Google Scholar] [CrossRef]
- Lloret, F.; Batllori, E. Climate-Induced Global Forest Shifts due to Heatwave-Drought. Ecol. Stud. 2021, 241, 155–186. [Google Scholar] [CrossRef]
- Lansu, E.M.; Heerwaarden, C.C.; Stegehuis, A.I.; Teuling, A.J. Atmospheric Aridity and Apparent Soil Moisture Drought in European Forest During Heat Waves. Geophys. Res. Lett. 2020, 47, e2020GL087091. [Google Scholar] [CrossRef] [Green Version]
- Sutanto, S.J.; Vitolo, C.; Di Napoli, C.; D’Andrea, M.; Van Lanen, H.A.J. Heatwaves, droughts, and fires: Exploring compound and cascading dry hazards at the pan-European scale. Environ. Int. 2020, 134, 105276. [Google Scholar] [CrossRef]
- Mozny, M.; Trnka, M.; Brázdil, R. Climate change driven changes of vegetation fires in the Czech Republic. Theor. Appl. Climatol. 2020, 143, 691–699. [Google Scholar] [CrossRef]
- Albright, T.P.; Pidgeon, A.M.; Rittenhouse, C.D.; Clayton, M.K.; Flather, C.H.; Culbert, P.D.; Radeloff, V.C. Heat waves measured with MODIS land surface temperature data predict changes in avian community structure. Remote Sens. Environ. 2011, 115, 245–254. [Google Scholar] [CrossRef] [Green Version]
- Parmesan, C.; Yohe, G. A globally coherent fingerprint of climate change impacts across natural systems. Nature 2003, 421, 37–42. [Google Scholar] [CrossRef]
- Wernberg, T. Marine Heatwave Drives Collapse of Kelp Forests in Western Australia. Ecol. Stud. 2021, 241, 325–343. [Google Scholar] [CrossRef]
- Coumou, D.; Rahmstorf, S. A decade of weather extremes. Nat. Clim. Chang. 2012, 2, 491–496. [Google Scholar] [CrossRef]
- Guo, X.; Huang, J.; Luo, Y.; Zhao, Z.; Xu, Y. Projection of heat waves over China for eight different global warming targets using 12 CMIP5 models. Theor. Appl. Climatol. 2016, 128, 507–522. [Google Scholar] [CrossRef]
- Wu, X.; Wang, L.; Yao, R.; Luo, M.; Li, X. Identifying the dominant driving factors of heat waves in the North China Plain. Atmos. Res. 2021, 252, 105458. [Google Scholar] [CrossRef]
- Theeuwes, N.E.; Steeneveld, G.-J.; Ronda, R.J.; Rotach, M.W.; Holtslag, A.A.M. Cool city mornings by urban heat. Environ. Res. Lett. 2015, 10, 114022. [Google Scholar] [CrossRef]
- Oke, T.R. City Size and the Urban Heat Island. Atmos. Environ. 1973, 7, 769–779. [Google Scholar] [CrossRef]
- Oke, T.R. The Energetic Basis of the Urban Heat Island. Q. J. R. Met. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Santamouris, M.; Papanikolaou, N.; Livada, I.; Koronakis, I.; Georgakis, C.; Argiriou, A.; Assimakopoulos, D. On the impact of urban climate on the energy consumption of buildings. Sol. Energy 2001, 70, 201–216. [Google Scholar] [CrossRef]
- Saaroni, H.; Ben-Dor, E.; Bitan, A.; Potchter, O. Spatial distribution and microscale characteristics of the urban heat island in Tel-Aviv, Israel. Landsc. Urban Plan. 2000, 48, 1–18. [Google Scholar] [CrossRef]
- Hart, M.A.; Sailor, D.J. Quantifying the influence of land-use and surface characteristics on spatial variability in the urban heat island. Theor. Appl. Climatol. 2009, 95, 397–406. [Google Scholar] [CrossRef]
- Founda, D.; Santamouris, M. Synergies between Urban Heat Island and Heat Waves in Athens (Greece), during an extremely hot summer (2012). Sci. Rep. 2017, 7, 10973. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zou, Z.; Yan, C.; Yu, L.; Jiang, X.; Ding, J.; Qin, L.; Qiu, G. Impacts of land use/ land cover types on interactions between urban heat island effects and heat waves. Build. Environ. 2021, 204, 108138. [Google Scholar] [CrossRef]
- Zhao, L.; Oppenheimer, M.; Zhu, Q.; Baldwin, J.W.; Ebi, K.L.; Bou-Zeid, E.; Liu, X. Interactions between urban heat islands and heat waves. Environ. Res. Lett. 2018, 13, 034003. [Google Scholar] [CrossRef]
- Pyrgou, A.; Hadjinicolaou, P.; Santamouris, M. Urban-rural moisture contrast: Regulator of the urban heat island and heatwaves’ synergy over a mediterranean city. Environ. Res. 2020, 182, 109102. [Google Scholar] [CrossRef] [PubMed]
- Shreevastava, A.; Prasanth, S.; Ramamurthy, P.; Rao, P.S.C. Scale-dependent response of the urban heat island to the European heatwave of 2018. Environ. Res. Lett. 2021, 16, 104021. [Google Scholar] [CrossRef]
- Kong, J.; Zhao, Y.; Carmeliet, J.; Lei, C. Urban Heat Island and Its Interaction with Heatwaves: A Review of Studies on Mesoscale. Sustainability 2021, 13, 10923. [Google Scholar] [CrossRef]
- Chapman, S.C.; Watkins, N.W.; Stainforth, D.A. Warming Trends in Summer Heatwaves. Geophys. Res. Lett. 2019, 46, 1634–1640. [Google Scholar] [CrossRef] [Green Version]
- Unkašević, M.; Tošić, I. Seasonal analysis of cold and heat waves in Serbia during the period 1949–2012. Theor. Appl. Climatol. 2014, 120, 29–40. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Bateni, S.M.; Entekhabi, D. Relative efficiency of land surface energy balance components. Water Resour. Res. 2012, 48, W04510. [Google Scholar] [CrossRef]
- Schwaab, J.; Meier, R.; Bürgi, C.; Mussetti, G.; Seneviratne, S.I.; Davin, E.L. The role of urban trees in reducing land surface temperatures in European cities. Nat. Commun. 2021, 12, 6763. [Google Scholar] [CrossRef] [PubMed]
- Bokaie, M.; Zarkesh, M.K.; Arasteh, P.D.; Hosseini, A. Assessment of Urban Heat Island based on the relationship between land surface temperature and Land Use/ Land Cover in Tehran. Sustain. Cities Soc. 2016, 23, 94–104. [Google Scholar] [CrossRef]
- Walawender, J.P.; Szymanowski, M.; Hajto, M.J.; Bokwa, A. Land Surface Temperature Patterns in the Urban Agglomeration of Krakow (Poland) Derived from Landsat-7/ETM+ Data. Pure Appl. Geophys. 2013, 171, 913–940. [Google Scholar] [CrossRef] [Green Version]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Martilli, A.; Krayenhoff, E.S.; Nazarian, N. Is the Urban Heat Island intensity relevant for heat mitigation studies? Urban Clim. 2020, 31, 100541. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z.; Xu, W.; Zheng, H. Spatial pattern of greenspace affects land surface temperature: Evidence from the heavily urbanized Beijing metropolitan area, China. Landsc. Ecol. 2012, 27, 887–898. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z. Relationship between land surface temperature and spatial pattern of greenspace: What are the effects of spatial resolution? Landsc. Urban Plan. 2013, 114, 1–8. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G.; Cadenasso, M.L. Does spatial configuration matter? Understanding the effects of land cover pattern on land surface temperature in urban landscapes. Landsc. Urban Plan. 2011, 102, 54–63. [Google Scholar] [CrossRef]
- Li, K.; Zhang, W. Directionally and spatially varying relationship between land surface temperature and land-use pattern considering wind direction: A case study in central China. Environ. Sci. Pollut. Res. 2021, 28, 44479–44493. [Google Scholar] [CrossRef]
- Rao, Y.; Dai, J.; Dai, D.; He, Q. Effect of urban growth pattern on land surface temperature in China: A multi-scale landscape analysis of 338 cities. Land Use Policy 2021, 103, 105314. [Google Scholar] [CrossRef]
- Abdulmana, S.; Lim, A.; Wongsai, S.; Wongsai, N. Land surface temperature and vegetation cover changes and their relationships in Taiwan from 2000 to 2020. Remote Sens. Appl. Soc. Environ. 2021, 24, 100636. [Google Scholar] [CrossRef]
- Effati, F.; Karimi, H.; Yavari, A. Investigating effects of land use and land cover patterns on land surface temperature using landscape metrics in the city of Tehran, Iran. Arab. J. Geosci. 2021, 14, 1240. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, J.; Yang, G.; Schlaberg, J. Reverse Thinking: A New Method from the Graph Perspective for Evaluating and Mitigating Regional Surface Heat Islands. Remote Sens. 2021, 13, 1127. [Google Scholar] [CrossRef]
- Forman, R.T.T. Land Mosaics: The Ecology of Landscapes and Regions; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Turner, M.G.; Gardner, R.H.; O’Neill, R.V. Landscape Ecology in Teory and Practice; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Southworth, J.; Munroe, D.; Nagendra, H. Land cover change and landscape fragmentation—Comparing the utility of continuous and discrete analyses for a western Honduras region. Agric. Ecosyst. Environ. 2004, 101, 185–205. [Google Scholar] [CrossRef]
- Wulder, M.; Boots, B. Local spatial autocorrelation characteristics of remotely sensed imagery assessed with the Getis statistic. Int. J. Remote Sens. 1998, 19, 2223–2231. [Google Scholar] [CrossRef]
- Fan, C.; Wang, Z. Spatiotemporal Characterization of Land Cover Impacts on Urban Warming: A Spatial Autocorrelation Approach. Remote Sens. 2020, 12, 1631. [Google Scholar] [CrossRef]
- Kumari, M.; Sarma, K.; Sharma, R. Using Moran’s I and GIS to study the spatial pattern of land surface temperature in relation to land use/cover around a thermal power plant in Singrauli district, Madhya Pradesh, India. Remote Sens. Appl. Soc. Environ. 2019, 15, 100239. [Google Scholar] [CrossRef]
- Portela, C.I.; Massi, K.G.; Rodrigues, T.; Alcântara, E. Impact of urban and industrial features on land surface temperature: Evidences from satellite thermal indices. Sustain. Cities Soc. 2020, 56, 102100. [Google Scholar] [CrossRef]
- Das Majumdar, D.; Biswas, A. Quantifying land surface temperature change from LISA clusters: An alternative approach to identifying urban land use transformation. Landsc. Urban Plan. 2016, 153, 51–65. [Google Scholar] [CrossRef]
- Wu, X.; Li, B.; Li, M.; Guo, M.; Zang, S.; Zhang, S. Examining the Relationship Between Spatial Configurations of Urban Impervious Surfaces and Land Surface Temperature. Chin. Geogr. Sci. 2019, 29, 568–578. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Onishi, A.; Chen, J.; Imura, H. Quantifying the cool island intensity of urban parks using ASTER and IKONOS data. Landsc. Urban Plan. 2010, 96, 224–231. [Google Scholar] [CrossRef]
- Shishegar, N. The Impacts of Green Areas on Mitigating Urban Heat Island Effect. Int. J. Environ. Sustain. 2014, 9, 119–130. [Google Scholar] [CrossRef]
- Ren, Z.; He, X.; Zheng, H.; Zhang, D.; Yu, X.; Shen, G.; Guo, R. Estimation of the Relationship between Urban Park Characteristics and Park Cool Island Intensity by Remote Sensing Data and Field Measurement. Forests 2013, 4, 868–886. [Google Scholar] [CrossRef] [Green Version]
- Ben-Dor, E.; Saaroni, H. Airborne video thermal radiometry as a tool for monitoring microscale structures of the urban heat island. Int. J. Remote Sens. 1997, 18, 3039–3053. [Google Scholar] [CrossRef]
- Shashua-Bar, L.; Hoffman, M.E. Vegetation as a climatic component in the design of an urban street An empirical model for predicting the cooling effect of urban green. Energy Build. 2000, 31, 221–235. [Google Scholar] [CrossRef]
- Shashua-Bar, L.; Potchter, O.; Bitan, A.; Boltansky, D.; Yaakov, Y. Microclimate modelling of street tree species effects within the varied urban morphology in the Mediterranean city of Tel Aviv. Israel. Int. J. Climatol. 2010, 30, 44–57. [Google Scholar] [CrossRef]
- Shashua-Bar, L.; Pearlmutter, D.; Erell, E. The influence of trees and grass on outdoor thermal comfort in a hot-arid environment. Int. J. Climatol. 2011, 31, 1498–1506. [Google Scholar] [CrossRef]
- Mijani, N.; Alavipanah, S.K.; Hamzeh, S.; Firozjaei, M.K.; Arsanjani, J.J. Modeling thermal comfort in different condition of mind using satellite images: An Ordered Weighted Averaging approach and a case study. Ecol. Indic. 2019, 104, 1–12. [Google Scholar] [CrossRef]
- Feng, L.; Zhao, M.; Zhou, Y.; Zhu, L.; Tian, H. The seasonal and annual impacts of landscape patterns on the urban thermal comfort using Landsat. Ecol. Indic. 2020, 110, 105798. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, T.; Gu, X.; Zhang, Y.; Chen, L. Land surface temperature retrieval from CBERS-02 IRMSS thermal infrared data and its applications in quantitative analysis of urban heat island effect. J. Remote Sens. 2006, 10, 789. [Google Scholar]
- Liu, L.; Zhang, Y. Urban Heat Island Analysis Using the Landsat TM Data and ASTER Data: A Case Study in Hong Kong. Remote Sens. 2011, 3, 1535–1552. [Google Scholar] [CrossRef] [Green Version]
- Naim, M.N.H.; Kafy, A.A. Assessment of urban thermal field variance index and defining the relationship between land cover and surface temperature in Chattogram city: A remote sensing and statistical approach. Environ. Chall. 2021, 4, 100107. [Google Scholar] [CrossRef]
- Singh, P.; Kikon, N.; Verma, P. Impact of land use change and urbanization on urban heat island in Lucknow city, Central India. A remote sensing based estimate. Sustain. Cities Soc. 2017, 32, 100–114. [Google Scholar] [CrossRef]
- Faisal, A.A.; Kafy, A.A.; Al Rakib, A.; Akter, K.S.; Jahir, D.M.A.; Sikdar, M.S.; Rahman, M.M. Assessing and predicting land use/land cover, land surface temperature and urban thermal field variance index using Landsat imagery for Dhaka Metropolitan area. Environ. Chall. 2021, 4, 100192. [Google Scholar] [CrossRef]
- Guha, S. Dynamic seasonal analysis on LST-NDVI relationship and ecological health of Raipur City, India. Ecosyst. Health Sustain. 2021, 7, 1927852. [Google Scholar] [CrossRef]
- Nguyen, T.; Lin, T.-H.; Chan, H.-P. The Environmental Effects of Urban Development in Hanoi, Vietna from Satellite and Meteorological Observations from 1999–2016. Sustainability 2019, 11, 1768. [Google Scholar] [CrossRef] [Green Version]
- Hung, T.; Uchihama, D.; Ochi, S.; Yasuoka, Y. Assessment with satellite data of the urban heat island effects in Asian mega cities. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 34–48. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature–vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Li, D.; Bou-Zeid, E. Synergistic Interactions between Urban Heat Islands and Heat Waves: The Impact in Cities Is Larger than the Sum of Its Parts. J. Appl. Meteorol. Climatol. 2013, 52, 2051–2064. [Google Scholar] [CrossRef] [Green Version]
- Mildrexler, D.J.; Zhao, M.; Cohen, W.B.; Running, S.W.; Song, X.P.; Jones, M.O. Thermal Anomalies Detect Critical Global Land Surface Changes. J. Appl. Meteorol. Climatol. 2018, 57, 391–411. [Google Scholar] [CrossRef]
- Yan, Y.; Mao, K.; Shi, J.; Piao, S.; Shen, X.; Dozier, J.; Bao, Q. Driving forces of land surface temperature anomalous changes in North America in 2002–2018. Sci. Rep. 2020, 10, 6931. [Google Scholar] [CrossRef] [PubMed]
- Ossola, A.; Jenerette, G.D.; McGrath, A.; Chow, W.; Hughes, L.; Leishman, M.R. Small vegetated patches greatly reduce urban surface temperature during a summer heatwave in Adelaide, Australia. Landsc. Urban Plan. 2021, 209, 104046. [Google Scholar] [CrossRef]
- Dousset, B.; Gourmelon, F.; Laaidi, K.; Zeghnoun, A.; Giraudet, E.; Bretin, P.; Vandentorren, S. Satellite monitoring of summer heat waves in the Paris metropolitan area. Int. J. Climatol. 2010, 31, 313–323. [Google Scholar] [CrossRef]
- Cheval, S.; Dumitrescu, A.; Bell, A. The urban heat island of Bucharest during the extreme high temperatures of July 2007. Theor. Appl. Climatol. 2009, 97, 391–401. [Google Scholar] [CrossRef]
- Tomlinson, C.J.; Chapman, L.; Thornes, J.E.; Baker, C.J. Derivation of Birmingham’s summer surface urban heat island from MODIS satellite images. Int. J. Climatol. 2012, 32, 214–224. [Google Scholar] [CrossRef] [Green Version]
- Rizvi, S.H.; Alam, K.; Iqbal, M.J. Spatio-temporal variations in urban heat island and its interaction with heat wave. J. Atmos. Sol.-Terr. Phys. 2019, 185, 50–57. [Google Scholar] [CrossRef]
- Zhou, Y.; Shepherd, J.M. Atlanta’s urban heat island under extreme heat conditions and potential mitigation strategies. Nat. Hazards 2010, 52, 639–668. [Google Scholar] [CrossRef]
- Zaitchik, B.F.; Macalady, A.K.; Bonneau, L.R.; Smith, R.B. Europe’s 2003 heat wave: A satellite view of impacts and land–atmosphere feedbacks. Int. J. Climatol. 2006, 26, 743–769. [Google Scholar] [CrossRef]
- Ward, K.; Lauf, S.; Kleinschmit, B.; Endlicher, W. Heat waves and urban heat islands in Europe: A review of relevant drivers. Sci. Total Environ. 2016, 569–570, 527–539. [Google Scholar] [CrossRef]
- Oliveira, A.; Lopes, A.; Correia, E.; Niza, S.; Soares, A. Heatwaves and Summer Urban Heat Islands: A Daily Cycle Approach to Unveil the Urban Thermal Signal Changes in Lisbon, Portugal. Atmosphere 2021, 12, 292. [Google Scholar] [CrossRef]
- Scott, A.A.; Waugh, D.W.; Zaitchik, B.F. Reduced Urban Heat Island intensity under warmer conditions. Environ. Res. Lett. 2018, 13, 064003. [Google Scholar] [CrossRef] [PubMed]
- Richard, Y.; Pohl, B.; Rega, M.; Pergaud, J.; Thevenin, T.; Emery, J.; Dudek, J.; Vairet, T.; Zito, S.; Chateau-Smith, C. Is Urban Heat Island intensity higher during hot spells and heat waves (Dijon, France, 2014–2019)? Urban Clim. 2021, 35, 100747. [Google Scholar] [CrossRef]
- Kumar, R.; Mishra, V. Decline in surface urban heat island intensity in India during heatwaves. Environ. Res. Commun. 2019, 1, 031001. [Google Scholar] [CrossRef] [Green Version]
- Chew, L.W.; Liu, X.; Li, X.-X.; Norford, L.K. Interaction between heat wave and urban heat island: A case study in a tropical coastal city, Singapore. Atmos. Res. 2021, 247, 105134. [Google Scholar] [CrossRef]
- Sjoukje, Y.P.; Kew, S.F.; van Oldenborgh, G.J.; Anslow, F.S.; Seneviratne, S.I.; Vautard, R.; Coumou, D.; Ebi, K.L.; Arrighi, J.; Singh, R.; et al. Rapid Attribution Analysis of the Extraordinary Heatwave on the Pacific Coast of the US and Canada June 2021. World Weather Attribution. Available online: https://www.worldweatherattribution.org/wp-content/uploads/NW-US-extreme-heat-2021-scientific-report-WWA.pdf (accessed on 3 September 2021).
- Zhou, D.; Xiao, J.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.; Sobrino, J. Satellite Remote Sensing of Surface Urban Heat Islands: Progress, Challenges, and Perspectives. Remote Sens. 2018, 11, 48. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://www.census.gov/geographies/mapping-files/time-series/geo/carto-boundary-file.2017.html (accessed on 8 September 2021).
- Available online: https://www12.statcan.gc.ca/census-recensement/2011/geo/bound-limit/bound-limit-2016-eng.cfm (accessed on 8 September 2021).
- Available online: https://lpdaac.usgs.gov/products/mod11a2v006/ (accessed on 8 September 2021).
- Available online: https://lpdaac.usgs.gov/products/mod09gav006/ (accessed on 11 November 2021).
- Available online: https://earthexplorer.usgs.gov (accessed on 8 September 2021).
- Roy, D.P.; Wulder, M.; Loveland, T.R.; Woodcock, C.; Allen, R.; Anderson, M.; Helder, D.; Irons, J.; Johnson, D.; Kennedy, R. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef] [Green Version]
- Xu, H. Modification of Normalized Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Ko, B.; Kim, H.; Nam, J. Classification of Potential Water Bodies Using Landsat 8 OLI and a Combination of Two Boosted Random Forest Classifiers. Sensors 2015, 15, 13763–13777. [Google Scholar] [CrossRef] [Green Version]
- USGS (United States Geological Survey). Landsat 8 Collection 2 (C2) Level 2 Science Product (L2SP) Guide; Department of the Interior US Geological Survey: Reston, VA, USA, 2020.
- Sobrino, J.A.; Irakulis, I. A Methodology for Comparing the Surface Urban Heat Island in Selected Urban Agglomerations Around the World from Sentinel-3 SLSTR Data. Remote Sens. 2020, 12, 2052. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Openshaw, S. Algorithm 9: Simulation of Autocorrelation for Aggregate Data. Environ. Plan. A Econ. Space 1980, 12, 1073–1081. [Google Scholar] [CrossRef]
- Goodchild, M.F. Spatial Autocorrelation; CATMOG 47; Geo Books: Norwich, UK, 1986. [Google Scholar]
- Zhou, X.; Lin, H. Geary’s, C. In Encyclopedia of GIS; Shekhar, S., Xiong, H., Zhou, X., Eds.; Springer: Cham, Switherland, 2017. [Google Scholar] [CrossRef]
- Bivand, R.; Pebesma, E.; Gomez-Rubio, V. Applied Spatial Data Analysis with R, 2nd ed.; Springer: New York, NY, USA, 2013; pp. 281–282. [Google Scholar]
- Bivand, R.; Wong, D.W.S. Comparing implementations of global and local indicators of spatial association. Test 2018, 27, 716–748. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association: LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- How Do I Use a Scale Factor with Landsat Level-2 Science Products? USGS Mapping, Remote Sensing and Geospatial Data. Available online: https://www.usgs.gov/faqs/how-do-i-use-a-scale-factor-landsat-level-2-science-products?qt-news_science_products=0#qt-news_science_products (accessed on 8 September 2021).
- QGIS Development Team. QGIS Version 3.18. Geographic Information System. Open-Source Geospatial Foundation Project. 2021. Available online: https://www.qgis.org/en/site/ (accessed on 9 August 2021).
- MathWorks. MATLAB ver. 2021b Computer Program; The MathWorks Inc.: Natick, MA, USA, 2021; Available online: https://www.mathworks.com/ (accessed on 9 August 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; Version 4.1.1.; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 9 August 2021).
- Bivand, R. Spdep: Spatial Dependence: Weighting Schemes, Statistics and Models. R Package Version 1.1-11. 2021. Available online: http://CRAN.R-project.org/package=spdep (accessed on 9 August 2021).
- Hijmans, R.J.; Van Etten, J. Raster: Geographic Analysis and Modeling with Raster Data. R Package Version 3.5-2. 2021. Available online: http://CRAN.R-project.org/package=raster (accessed on 9 August 2021).
- Tennekes, M. tmap: Thematic Maps in R. J. Stat. Softw. 2018, 84, 1–39. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://gis.ncdc.noaa.gov/maps/ncei/summaries/daily (accessed on 8 September 2021).
- Tan, J.; Yu, D.; Li, Q.; Tan, X.; Zhou, W. Spatial relationship between land-use/land-cover change and land surface temperature in the Dongting Lake area, China. Sci. Rep. 2020, 10, 9245. [Google Scholar] [CrossRef]
- Peng, X.; Wu, W.; Zheng, Y.; Sun, J.; Hu, T.; Wang, P. Correlation analysis of land surface temperature and topographic elements in Hangzhou, China. Sci. Rep. 2020, 10, 10451. [Google Scholar] [CrossRef]
- Li, H.; Zhou, Y.; Li, X.; Meng, L.; Wang, X.; Wu, S.; Sodoudi, S. A new method to quantify surface urban heat island intensity. Sci. Total Environ. 2018, 624, 262–272. [Google Scholar] [CrossRef] [PubMed]
- Stewart, I.D.; Oke, T.R. Local climate zones for urban temperature studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Bonafoni, S.; Keeratikasikorn, C. Land surface temperature and urban density: Multiyear modeling and relationship analysis using MODIS and Landsat data. Remote Sens. 2018, 10, 1471. [Google Scholar] [CrossRef] [Green Version]
- Sobrino, J.; Oltra-Carrió, R.; Sòria, G.; Jiménez-Muñoz, J.C.; Franch, B.; Hidalgo, V.; Mattar, C.; Julien, Y.; Cuenca, J.; Romaguera, M.; et al. Evaluation of the surface urban heat island effect in the city of Madrid by thermal remote sensing. Int. J. Remote Sens. 2013, 34, 3177. [Google Scholar] [CrossRef]
- Li, J.; Wang, F.; Fu, Y.; Guo, B.; Zhao, Y.; Yu, H. A Novel SUHI Referenced Estimation Method for Multicenters Urban Agglomeration using DMSP/OLS Nighttime Light Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1416–1425. [Google Scholar] [CrossRef]
- Peng, J.; Ma, J.; Liu, Q.; Liu, Y.; Hu, Y.; Li, Y.; Yue, Y. Spatial-temporal change of land surface temperature across 285 cities in China: An urban-rural contrast perspective. Sci. Total Environ. 2018, 635, 487–497. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef] [Green Version]
- Zhou, D.; Zhao, S.; Liu, S.; Zhang, L.; Zhu, C. Surface urban heat island in China’s 32 major cities: Spatial patterns and drivers. Remote Sens. Environ. 2014, 152, 51–61. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Gangodagamage, C.; Zhou, X.; Lin, H. Autocorrelation, Spatial. In Encyclopedia of GIS; Shekhar, S., Xiong, H., Eds.; Springer: Boston, MA, USA, 2008. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S. The gradient concept of landscape structure [Chapter 12]. In Issues and Perspectives in Landscape Ecology; Wiens, J.A., Moss, M.R., Eds.; Cambridge University Press: Cambridge, UK, 2005; pp. 112–119. [Google Scholar]
- Fan, C.; Myint, S. A comparison of spatial autocorrelation indices and landscape metrics in measuring urban landscape fragmentation. Landsc. Urban Plan. 2014, 121, 117–128. [Google Scholar] [CrossRef]
- Shao, G.; Wu, J. On the accuracy of landscape pattern analysis using remote sensing data. Landsc. Ecol. 2008, 23, 505–511. [Google Scholar] [CrossRef]

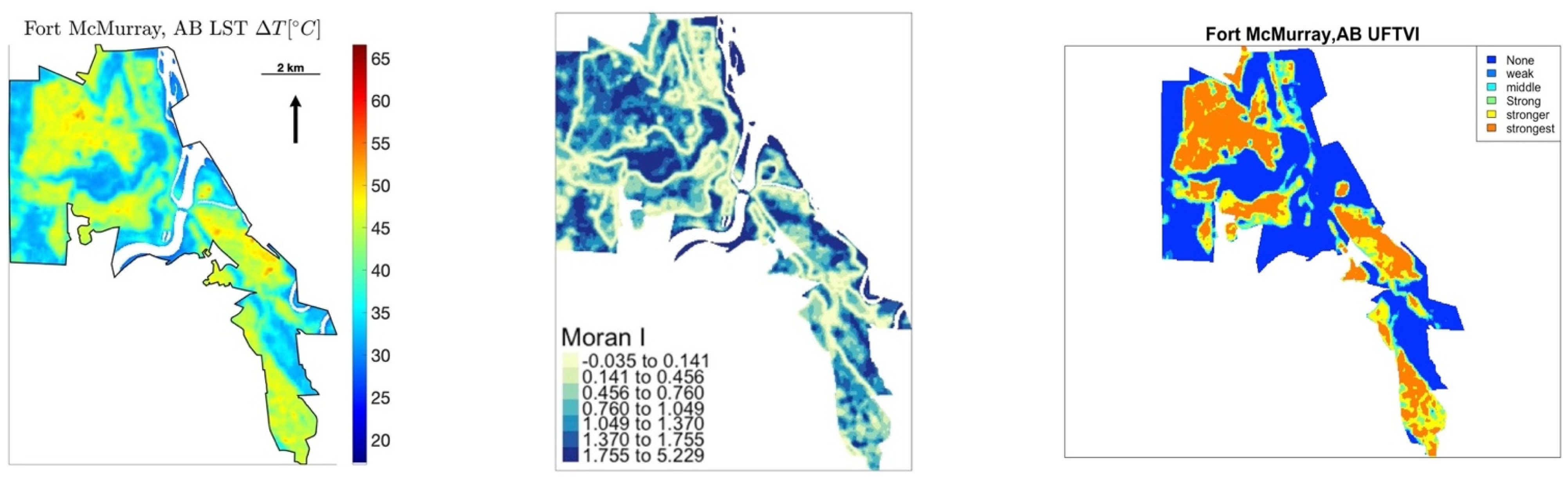
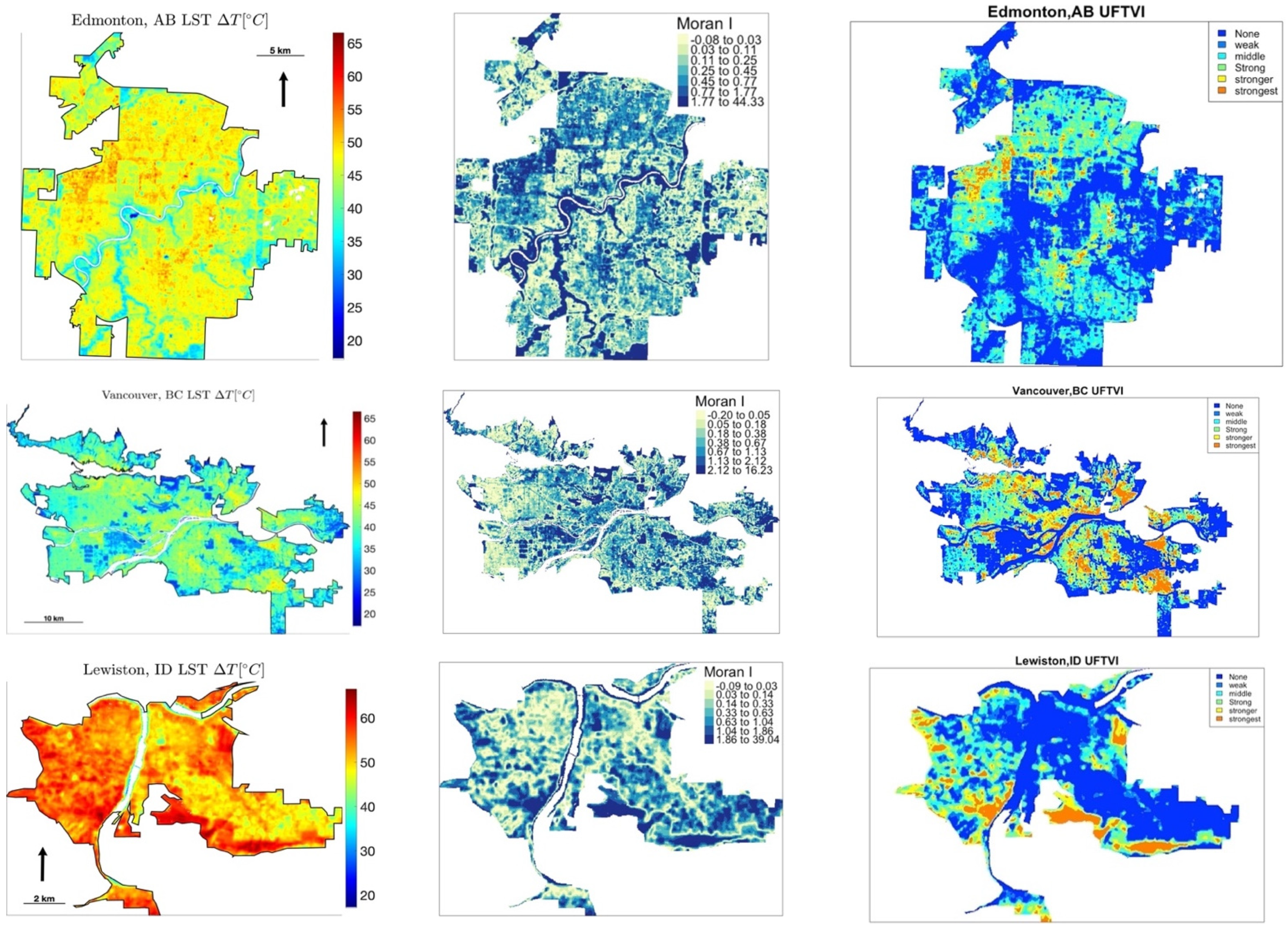
| UTFVI | UHI Phenomena | Ecological Evaluation Scale |
|---|---|---|
| <0 | None | Excellent |
| 0–0.005 | Weak | Good |
| 0.005–0.010 | Middle | Normal |
| 0.010–0.015 | Strong | Bad |
| 0.015–0.020 | Stronger | Worse |
| >0.020 | Strongest | Worst |
| City/Town | Country | Date | Max LST Day 1 km | Max LST Night 1 km | Difference Day Night |
|---|---|---|---|---|---|
| Seattle, WA | US | 26 June 2021 | 36.6 | 22.1 | 14.5 |
| Ashcroft, BC | Canada | 26 June 2021 | 49.6 | 28.7 | 21.0 |
| Abbotsford, BC | Canada | 26 June 2021 | 41.4 | 23.0 | 18.4 |
| Banff, AB | Canada | 26 June 2021 | 32.4 | 20.7 | 11.7 |
| Beaverlodge, AB | Canada | 26 June 2021 | 40.5 | 19.3 | 21.2 |
| Calgary, AB | Canada | 26 June 2021 | 39.8 | 20.2 | 19.6 |
| Chilliwack, BC | Canada | 26 June 2021 | 38.1 | 24.0 | 14.1 |
| Couer dAlene, ID | US | 26 June 2021 | 43.8 | 23.2 | 20.6 |
| Edmonton, AB | Canada | 26 June 2021 | 39.7 | 23 | 16.7 |
| Fort Mackmurray, AB | Canada | 26 June 2021 | 34.6 | 21.4 | 13.3 |
| Fort Smith, NT | Canada | 26 June 2021 | 30.2 | 19.4 | 10.8 |
| Grande Prairie, AB | Canada | 26 June 2021 | 39.2 | 21.2 | 18.0 |
| Jasper, AB | Canada | 26 June 2021 | 36.1 | 21.0 | 15.1 |
| Kamloops, BC | Canada | 26 June 2021 | 44.6 | 26.1 | 18.5 |
| Kelowna, BC | Canada | 26 June 2021 | 38.9 | 25.8 | 13.1 |
| Lewinston, ID | US | 26 June 2021 | 51.7 | 26.0 | 25.7 |
| Mission, BC | Canada | 26 June 2021 | 37.4 | 22.3 | 15.1 |
| Saskatoon, SK | Canada | 26 June 2021 | 40.1 | 21.4 | 18.7 |
| Spokane, WA | US | 26 June 2021 | 46.3 | 23.5 | 22.7 |
| Squamish, BC | Canada | 26 June 2021 | 32.5 | 22 | 10.5 |
| Vancouver, BC | Canada | 26 June 2021 | 37.6 | 22.3 | 15.3 |
| Victoria, BC | Canada | 26 June 2021 | 34.6 | 20.2 | 14.5 |
| Cultus Lake, BC | Canada | 26 June 2021 | 32.6 | 24.1 | 8.5 |
| Lytton, BC | Canada | 26 June 2021 | 37.9 | 26.4 | 11.6 |
| Nahanni Butte, NT | Canada | 26 June 2021 | 26.3 | 20.6 | 5.7 |
| Nordegg, AB | Canada | 26 June 2021 | 33.9 | 17.7 | 16.2 |
| Red Earth Creek, AB | Canada | 26 June 2021 | 34.0 | 21.0 | 13.0 |
| Uranium City, SK | Canada | 26 June 2021 | 30.1 | 18.4 | 11.7 |
| City/Town | Country | Mean Rural Day | Mean Urban Day | Diference Day | Mean Rural Night | Mean Urban Night | Diference Night |
|---|---|---|---|---|---|---|---|
| Spokane, WA | US | 41.0 | 46.3 | 5.3 | 22.0 | 23.5 | 1.5 |
| Edmonton, AB | Canada | 34.2 | 39.7 | 5.5 | 18.8 | 23.0 | 4.2 |
| Seattle, WA | US | 31.4 | 36.6 | 5.1 | 21.5 | 22.1 | 0.6 |
| Abbotsford, BC | Canada | 37.1 | 41.4 | 4.3 | 21.1 | 23.0 | 1.8 |
| Vancouver, BC | Canada | 30.0 | 37.6 | 7.6 | 21.9 | 22.3 | 0.5 |
| Chilliwack, BC | Canada | 33.9 | 38.1 | 4.1 | 23.8 | 24.0 | 0.2 |
| Mission, BC | Canada | 33.2 | 37.4 | 4.2 | 22.9 | 22.3 | −0.6 |
| Ashcroft, BC | Canada | 45.9 | 49.6 | 3.7 | 27.3 | 28.7 | 1.3 |
| Banff, AB | Canada | 31.5 | 32.4 | 0.9 | 19.7 | 20.7 | 1.0 |
| Beaverlodge, AB | Canada | 38.6 | 40.5 | 1.9 | 18.6 | 19.3 | 0.8 |
| Calgary, AB | Canada | 34.5 | 39.8 | 5.3 | 16.2 | 20.2 | 3.9 |
| Coeur dAlene, ID | US | 34.7 | 43.8 | 9.1 | 23.7 | 23.2 | −0.5 |
| Fort McMurray, AB | Canada | 32.0 | 34.6 | 2.6 | 19.2 | 21.4 | 2.2 |
| Fort Smith, NT | Canada | 29.1 | 30.2 | 1.1 | 19.3 | 19.4 | 0.1 |
| Grande Prairie, AB | Canada | 35.6 | 39.2 | 3.6 | 19.4 | 21.2 | 1.8 |
| Jasper, AB | Canada | 32.5 | 36.1 | 3.6 | 21.3 | 21.0 | −0.3 |
| Kamloops, BC | Canada | 41.0 | 44.6 | 3.7 | 23.8 | 26.1 | 2.3 |
| Kelowna, BC | Canada | 36.3 | 38.9 | 2.6 | 23.3 | 25.8 | 2.5 |
| Saskatoon, SK | Canada | 38.9 | 40.1 | 1.1 | 17.8 | 21.4 | 3.5 |
| Squamish, BC | Canada | 29.0 | 32.5 | 3.5 | 20.8 | 22.0 | 1.2 |
| Victoria, BC | Canada | 30.4 | 34.6 | 4.2 | 21.1 | 20.2 | −0.9 |
| Lewiston, ID | US | 52.4 | 51.7 | −0.8 | 24.1 | 26.0 | 1.9 |
| Cultus Lake, BC | Canada | 32.8 | 32.6 | −0.2 | 24.3 | 24.1 | −0.2 |
| Lytton, BC | Canada | 36.6 | 37.9 | 1.3 | 26.8 | 26.4 | −0.4 |
| Nahanni Butte, NT | Canada | 27.2 | 26.3 | −0.9 | 21.0 | 20.6 | −0.4 |
| Nordegg, AB | Canada | 33.6 | 33.9 | 0.4 | 18.1 | 17.7 | −0.4 |
| Red Earth Creek, AB | Canada | 33.6 | 34.0 | 0.4 | 20.8 | 21.0 | 0.2 |
| Uranium City, SK | Canada | 29.9 | 30.1 | 0.2 | 18.4 | 18.4 | 0.0 |
| Cities/Towns | LST Urban Mean | LST Rural Mean | SUHI |
|---|---|---|---|
| Abbotsford, BC | 38.8 | 35.6 | 3.17 |
| Ashcroft, BC | 50.0 | 51.5 | −1.49 |
| Beaverlodge, AB | 47.5 | 47.9 | −0.44 |
| Chilliwack, BC | 36.9 | 27.0 | 9.93 |
| Cultus_Lake, BC | 35.8 | 25.5 | 10.34 |
| Edmonton, AB | 45.6 | 37.8 | 7.79 |
| Fort_McMurray, AB | 39.9 | 34.4 | 5.49 |
| Fort_Smith, NT | 36.6 | 35.3 | 1.37 |
| Grande_Prairie, AB | 21.8 | 26.9 | −5.15 |
| Kamloops, BC | 43.2 | 27.6 | 15.57 |
| Kelowna, BC | 47.7 | 32.9 | 14.79 |
| Lewiston, ID | 53.3 | 57.0 | −3.75 |
| Lytton, BC | 45.8 | 40.0 | 5.84 |
| Mission, BC | 35.3 | 29.2 | 6.1 |
| Saskatoon, SK | 45.3 | 44.0 | 1.28 |
| Squamish, BC | 34.4 | 26.4 | 8.04 |
| Vancouver, BC | 38.6 | 25.9 | 12.61 |
| Victoria, BC | 34.7 | 27.0 | 7.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cotlier, G.I.; Jimenez, J.C. The Extreme Heat Wave over Western North America in 2021: An Assessment by Means of Land Surface Temperature. Remote Sens. 2022, 14, 561. https://doi.org/10.3390/rs14030561
Cotlier GI, Jimenez JC. The Extreme Heat Wave over Western North America in 2021: An Assessment by Means of Land Surface Temperature. Remote Sensing. 2022; 14(3):561. https://doi.org/10.3390/rs14030561
Chicago/Turabian StyleCotlier, Gabriel I., and Juan Carlos Jimenez. 2022. "The Extreme Heat Wave over Western North America in 2021: An Assessment by Means of Land Surface Temperature" Remote Sensing 14, no. 3: 561. https://doi.org/10.3390/rs14030561
APA StyleCotlier, G. I., & Jimenez, J. C. (2022). The Extreme Heat Wave over Western North America in 2021: An Assessment by Means of Land Surface Temperature. Remote Sensing, 14(3), 561. https://doi.org/10.3390/rs14030561








