Toward Real Hyperspectral Image Stripe Removal via Direction Constraint Hierarchical Feature Cascade Networks
Abstract
:1. Introduction
1.1. Model-Driven Destriping Method
1.2. Data-Driven Destriping Method
1.3. Contributes
- The training stripe samples for TRS-DCHC are both realistic and simulated data. On one hand, the model can process stripes with unknown distribution and structure. On the other hand, there is no need to thoroughly design the complicated stripe generation method; moreover, a blind destriping dataset can be obtained.
- In the stripe sample extraction and generation part, we mainly focus on spatial context information by adopting the strategy of extrapolating from local to global, and by proposing a constraint on the direction extraction strategy of points and lines, and lines and surfaces that extracts stripe samples from a global perspective.
- In the stripe removal part, we propose a multi-scale dense hierarchical feature cascading wavelet network through multi-scale feature extraction and multilevel feature fusion to obtain abundant information flow for the stripe component. In particular, we use the discrete wavelet transform (DWT) to explicitly decompose the input data into different frequency information as network input. This strategy combines the prior knowledge of an image with deep learning, which is more suitable for stripe removal. Moreover, it can alleviate the challenge of training, reduce information loss, and maintain spectrum consistency.
2. Materials and Methods
2.1. HSI Degradation Formula
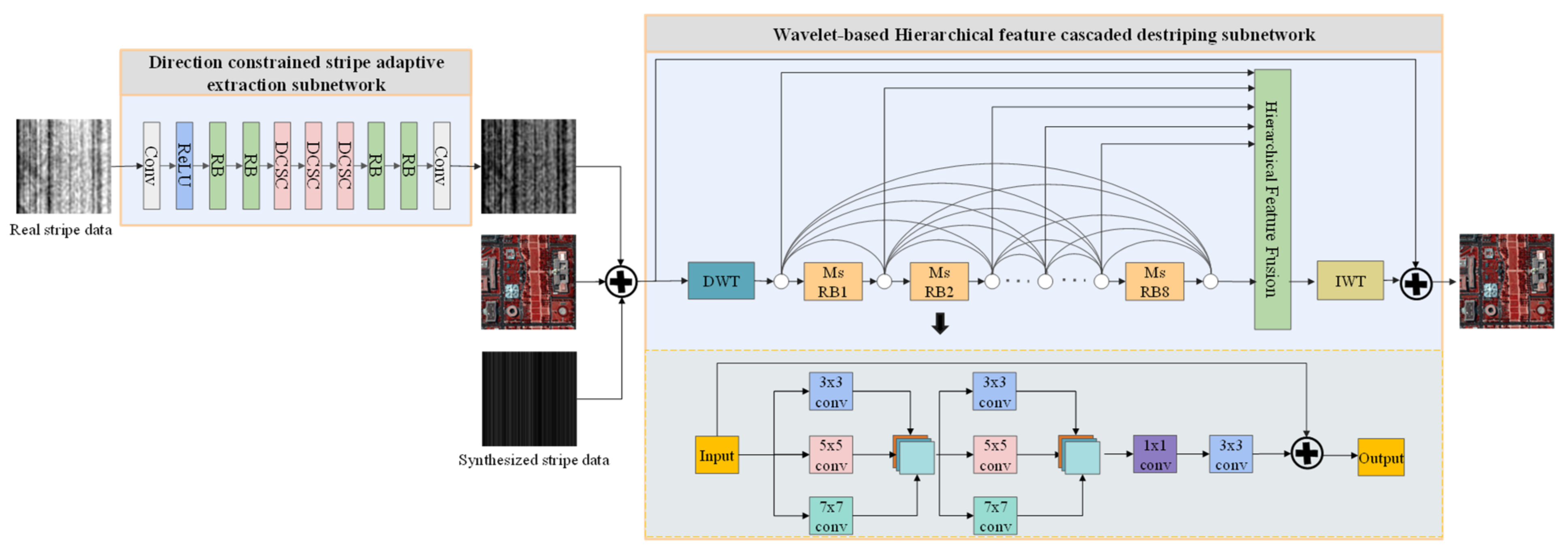
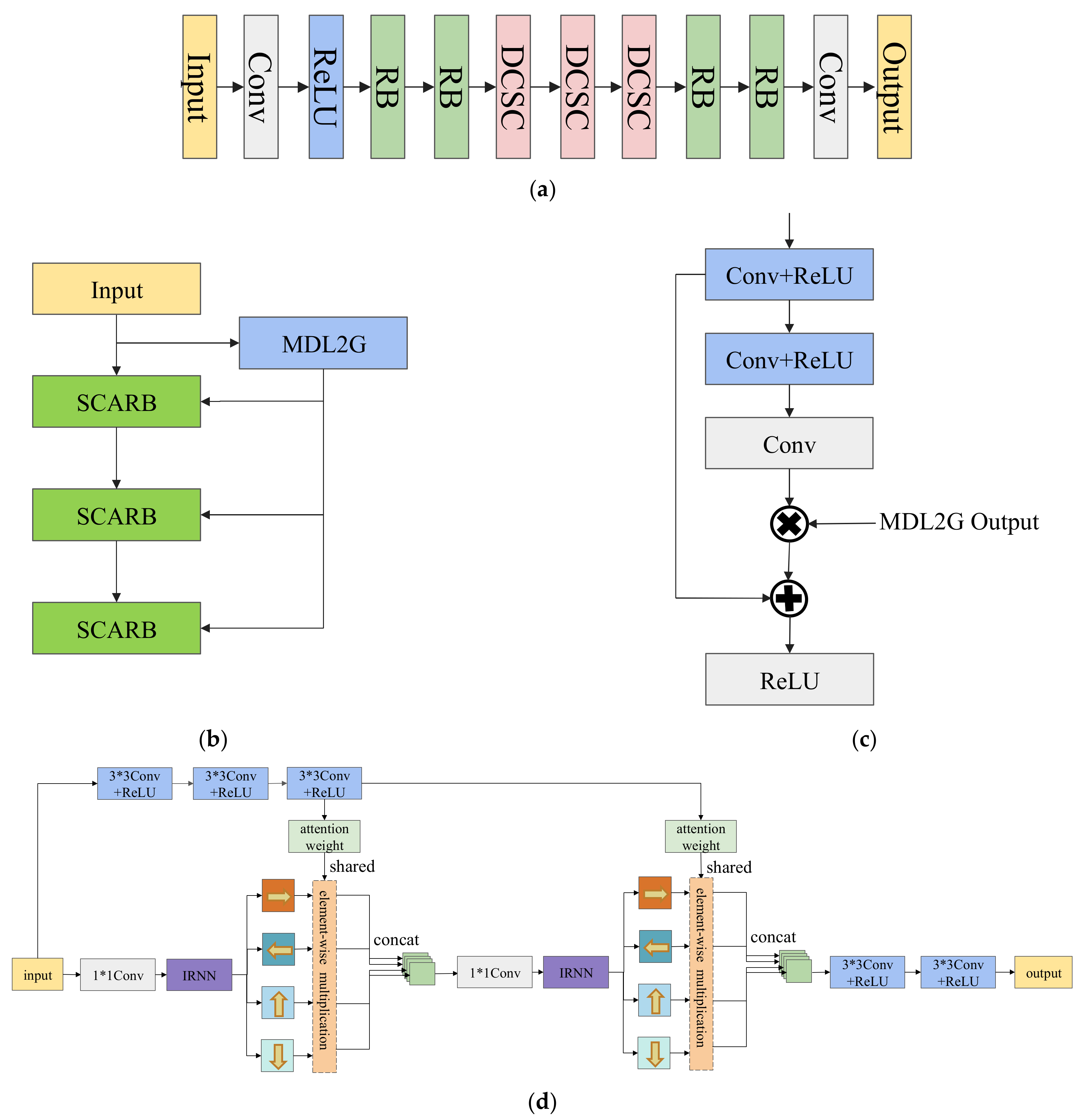
2.2. Direction Constrained Stripe Adaptive Unsupervised Extraction Subnetwork
2.3. Wavelet-Based Hierarchical Feature Cascaded Destriping Subnetwork
2.3.1. Wavelet Decomposition
2.3.2. Multi-Scale Hierarchical Feature Fusion
3. Experimental Results and Discussion
3.1. Experimental Datasets and Parameter Setting
3.2. Simulated Data Experimental Results and Analysis
3.3. Real Data Experimental Results and Analysis
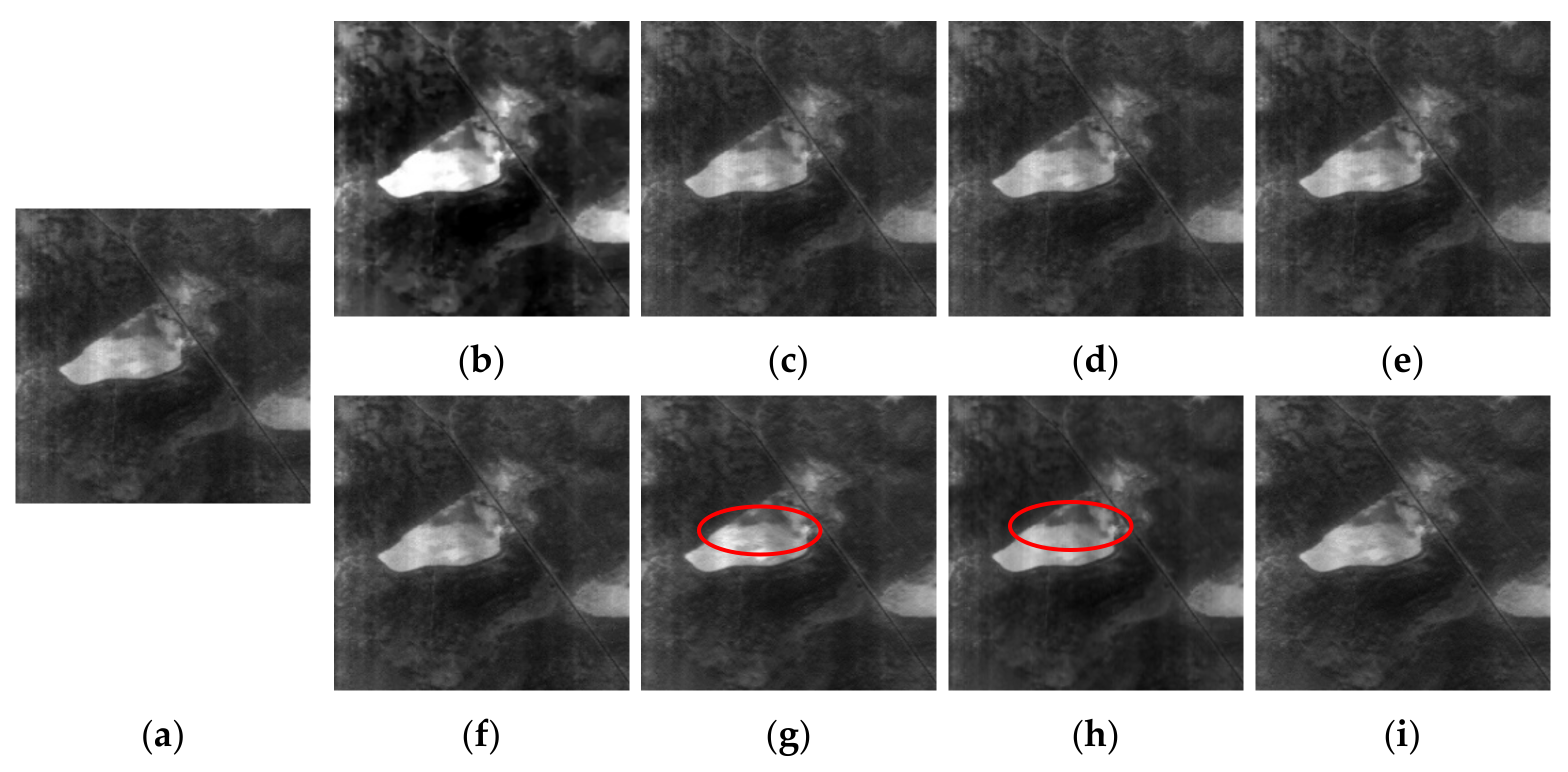
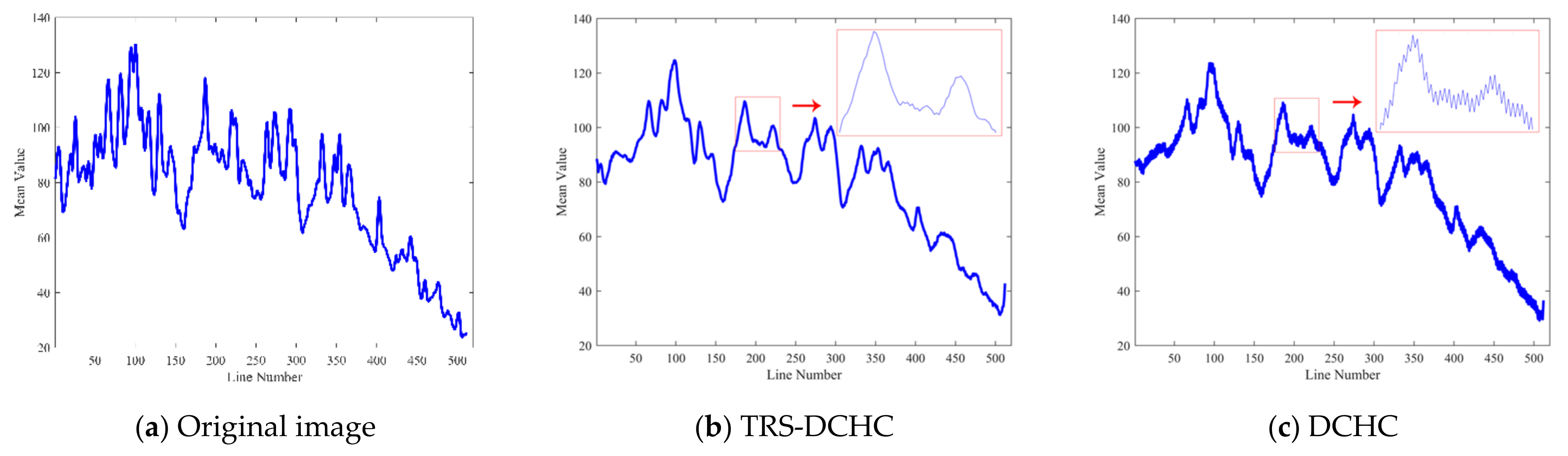
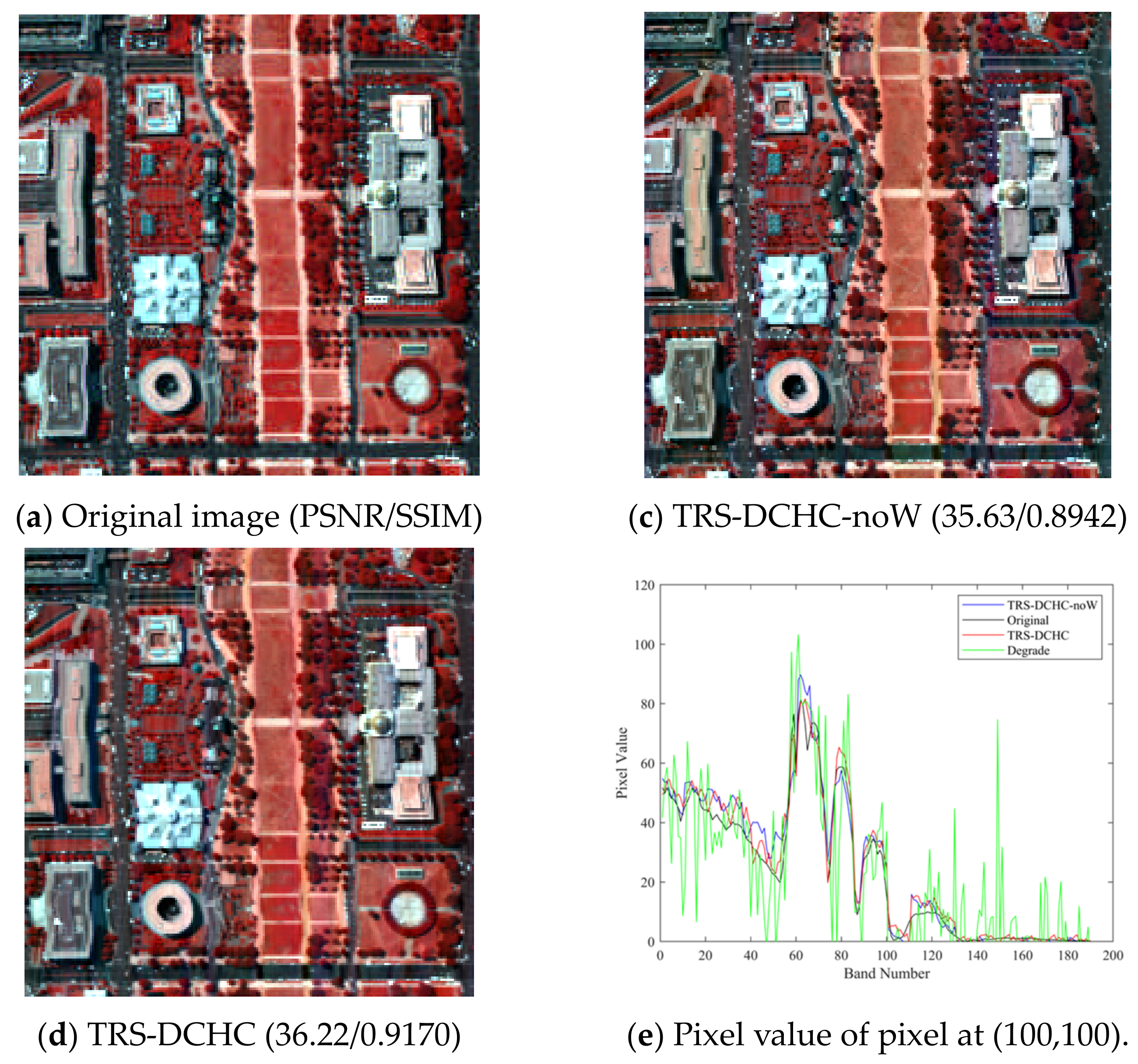
3.3.1. GF-5 HSI Dataset
3.3.2. Zhuhai-1 Dataset
3.3.3. Hyperion EO-1 Dataset
3.3.4. HYDICE Urban Data Set
4. Discussion
4.1. Effectiveness toward Real Data Training Strategy
4.2. Effectiveness of DWT
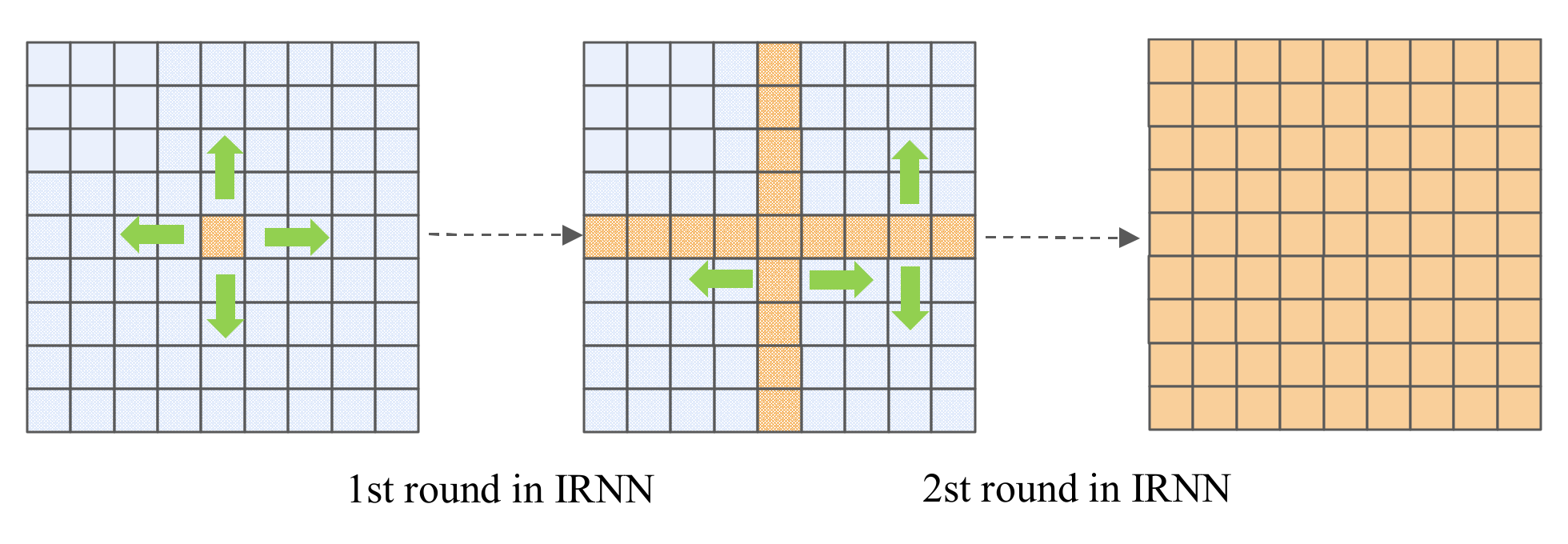
4.3. Analysis of Direction Constrained Stripe Adaptive Unsupervised Extraction Subnetwork
4.4. The Time Costs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HSI | hyperspectral imaging |
| CNNs | convolutional neural networks |
| TRS-DCHC | toward real HSI stripe removal via direction constraint hierarchical feature cascade network |
| PCA | principal component analysis |
| DWT | discrete wavelet transform |
| DCSC | direction constraint spatial context module |
| SCARB | spatial context aggregation residual block |
| MDL2G | multi-direction awarded local to global module |
| IRNN | image spatial recurrent neural network |
| TV | total variation |
| LL | approximation of DWT image |
| LH | horizontal detail |
| HL | vertical detail |
| HH | diagonal detail |
| MSE | mean square error |
| GF-5 | GaoFen-5 |
| AHSI | advanced hyperspectral imager |
| VNIR | visible and near-infrared |
| SWIR | shortwave infrared |
| CHEOS | China High-Resolution Earth Observation System |
| WDC | Washington DC Mall HSI dataset |
| ZhuHai-1 | Chinese ZhuHai-1 hyperspectral satellite |
| EO-1 | Earth Observing-1 |
| ASSTV | anisotropic spectral-spatial total variation |
| LRTV | total-variation-regularized low-rank matrix factorization |
| NGMeet | non-local meets global |
| LRMR | low-rank matrix recovery |
| TDL | tensor dictionary learning |
| HSI-DeNet | hyperspectral image restoration via convolutional neural |
| SGIDN | Satellite-ground integrated destriping network |
| PSNR | peak signal-to-noise ratio |
| SSIM | structural similarity |
| ICV | inverse coefficient of variation |
| MRD | mean relative deviation |
| DCHC | the TRS-DCHC without incorporated real data |
| TRS-DCHC-noW | the TRS-DCHC without DWT |
References
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C.-I. Feedback attention-based dense CNN for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 1–16. [Google Scholar] [CrossRef]
- Sun, X.; Qi, Y.; Gao, L.; Sun, X.; Qi, H.; Zhang, B.; Shen, T. Ensemble-based information retrieval with mass estimation for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2021, 1–23. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Shang, K.; Zhang, L.; Wang, S. Crop classification based on feature band set construction and object-oriented approach using hyperspectral images. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2016, 9, 4117–4128. [Google Scholar] [CrossRef]
- Song, M.; Shang, X.; Chang, C.-I. 3-D receiver operating characteristic analysis for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8093–8115. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Li, J.; Sun, F.; Zhang, L. Deep spatio-spectral Bayesian posterior for hyperspectral image non-i.i.d. noise removal. ISPRS J. Photogramm. Remote Sens. 2020, 164, 125–137. [Google Scholar] [CrossRef]
- Wan, Y.; Ma, A.; He, W.; Zhong, Y. Accurate multi-objective low-rank and sparse model for hyperspectral image denoising method. IEEE Trans. Evol. Comput. 2021. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, L.; He, W.; Zhang, L. Hyperspectral with image denoising total variation regularization and nonlocal low-rank tensor decomposition. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3071–3084. [Google Scholar] [CrossRef]
- Zheng, Y.-B.; Huang, T.-Z.; Zhao, X.-L.; Chen, Y.; He, W. Double-factor-regularized low-rank tensor factorization for mixed noise removal in hyperspectral image. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8450–8464. [Google Scholar] [CrossRef]
- Zhuang, L.; Fu, X.; Ng, M.K.; Bioucas-Dias, J.M. Hyperspectral image denoising based on global and nonlocal low-rank factorizations. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Zhang, H.; Cai, J.; He, W.; Shen, H.; Zhang, L. Double low-rank matrix decomposition for hyperspectral image denoising and destriping. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Fan, H.; Li, C.; Guo, Y.; Kuang, G.; Ma, J. Spatial-spectral total variation regularized low-rank tensor decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6196–6213. [Google Scholar] [CrossRef]
- Ye, M.; Qian, Y.; Zhou, J. Multitask sparse nonnegative matrix factorization for joint spectral-spatial hyperspectral imagery denoising. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2621–2639. [Google Scholar] [CrossRef] [Green Version]
- Rasti, B.; Sveinsson, J.R.; Ulfarsson, M.O.; Benediktsson, J.A. Hyperspectral image denoising using first order spectral roughness penalty in wavelet domain. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 2458–2467. [Google Scholar] [CrossRef]
- Chen, Y.; He, W.; Yokoya, N.; Huang, T.; Zhao, X. Nonlocal tensor-ring decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1348–1362. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, L.; Jiao, Y.; Tian, C.; Wang, C.; Zhang, Y. Intracluster structured low-rank matrix analysis method for hyperspectral denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 866–880. [Google Scholar] [CrossRef]
- Liu, N.; Li, W.; Tao, R.; Fowler, J.E. Wavelet-domain low-rank/group-sparse destriping for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10310–10321. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Q.; Chanussot, J.; Li, D. Hyperspectral image mixed noise removal based on multidirectional low-rank modeling and spatial-spectral total variation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 488–507. [Google Scholar] [CrossRef]
- Othman, H.; Qian, S.-E. Noise reduction of hyperspectral imagery using hybrid spatial-spectral derivative-domain wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2006, 44, 397–408. [Google Scholar] [CrossRef]
- Rasti, B.; Sveinsson, J.R.; Ulfarsson, M.O. Wavelet-based sparse reduced-rank regression for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6688–6698. [Google Scholar] [CrossRef]
- Chen, G.; Qian, S. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2011, 49, 973–980. [Google Scholar] [CrossRef]
- Song, J.; Jeong, J.-H.; Park, D.-S.; Kim, H.-H.; Seo, D.-C.; Ye, J.C. Unsupervised denoising for satellite imagery using wavelet directional CycleGAN. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6823–6839. [Google Scholar] [CrossRef]
- Cao, X.; Fu, X.; Xu, C.; Meng, D. Deep spatial-spectral global reasoning network for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Li, J.; Liu, X.; Shen, H.; Zhang, L. Hybrid noise removal in hyperspectral imagery with a spatial–spectral gradient network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7317–7329. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, W.; Wang, X.; Jin, S.; Zhang, L. Satellite-ground integrated destriping network: A new perspective for EO-1 Hyperion and Chinese hyperspectral satellite datasets. Remote Sens. Environ. 2020, 237, 111416. [Google Scholar] [CrossRef]
- Maffei, A.; Haut, J.M.; Paoletti, M.E.; Plaza, J.; Bruzzone, L.; Plaza, A. A single model CNN for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2516–2529. [Google Scholar] [CrossRef]
- Yuan, Y.; Ma, H.; Liu, G. Partial-DNet: A novel blind denoising model with noise intensity estimation for HSI. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Wang, X.; Luo, Z.; Li, W.; Hu, X.; Zhang, L.; Zhong, Y. A self-supervised denoising network for satellite-airborne-ground hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Dong, W.; Wang, H.; Wu, F.; Shi, G.; Li, X. Deep Spatial–spectral representation learning for hyperspectral image denoising. IEEE Trans. Comput. Imag. 2019, 5, 635–648. [Google Scholar] [CrossRef]
- Chang, Y.; Chen, M.; Yan, L.; Zhao, X.-L.; Li, Y.; Zhong, S. Toward universal stripe removal via wavelet-based deep convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2880–2897. [Google Scholar] [CrossRef]
- Liu, W.; Lee, J. A 3-D atrous convolution neural network for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5701–5715. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Zhong, S.; Liao, W. HSI-DeNet: Hyperspectral image restoration via convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 667–682. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, L.; Xu, M.; Zhang, T.; Lv, P.; Zhou, B.; Yang, X.; Pang, Y. Attention scaling for crowd counting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 4705–4714. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene seg-mentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 3146–3154. [Google Scholar]
- Lu, M.; Li, Z.-N.; Wang, Y.; Pan, G. Deep attention network for egocentric action recognition. IEEE Trans. Image Process. 2019, 28, 3703–3713. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, J.; Liu, L.; Zhu, F.; Shao, L. RANet: Ranking attention network for fast video object segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 3977–3986. [Google Scholar]
- Zhu, M.; Jiao, L.; Liu, F.; Yang, S.; Wang, J. Residual spectral-spatial attention network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 449–462. [Google Scholar] [CrossRef]
- Sun, H.; Zheng, X.; Lu, X. A supervised segmentation network for hyperspectral image classification. IEEE Trans. Image Process. 2021, 30, 2810–2825. [Google Scholar] [CrossRef] [PubMed]
- Xiang, P.; Song, J.; Qin, H.; Tan, W.; Li, H.; Zhou, H. Visual attention and background subtraction with adaptive weight for hyperspectral anomaly detection. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2021, 14, 2270–2283. [Google Scholar] [CrossRef]
- Marinelli, D.; Bovolo, F.; Bruzzone, L. A novel change detection method for multitemporal hyperspectral images based on binary hyperspectral change vectors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4913–4928. [Google Scholar] [CrossRef]
- Anwar, S.; Barnes, N. Real Image denoising with feature attention. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 3155–3164. [Google Scholar]
- Shi, Q.; Tang, X.; Yang, T.; Liu, R.; Zhang, L. Hyperspectral image denoising using a 3-D attention denoising network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1–16. [Google Scholar] [CrossRef]
- Hu, X.; Fu, C.-W.; Zhu, L.; Qin, J.; Heng, P.-A. Direction-aware spatial context features for shadow detection and removal. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2795–2808. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rudin, L.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Physica D. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Liu, L.; Liu, J.; Yuan, S.; Slabaugh, G.; Leonardis, A.; Zhou, W.; Tian, Q. Wavelet-based dual-branch network for image demoireing. In Proceedings of the IEEE/CVF European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; Available online: https://arxiv.org/pdf/2007.07173.pdf (accessed on 12 December 2021).
- Liu, P.; Zhang, H.; Zhang, K.; Lin, L.; Zuo, W. Multi-level wavelet-CNN for image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshop (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 773–782. [Google Scholar]
- Liu, Y.; Ma, L.; Zhao, Y.; Wang, N.; Qian, Y.; Li, W.; Gao, C.; Qiu, S.; Li, C. A spectrum extension approach for radiometric calibration of the advanced hyperspectral imager aboard the Gaofen-5 Satellite. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Si, M.; Tang, B.-H.; Li, Z.-L.; Nerry, F.; Zhang, X.; Shang, G. An artificial neuron network with parameterization scheme for estimating net surface shortwave radiation from satellite data under clear sky—Application to simulated GF-5 data set. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4262–4272. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Chang, Y.; Yan, L.; Fang, H.; Luo, C. Anisotropic spectral-spatial total variation model for multispectral remote sensing image destriping. IEEE Trans. Image Process. 2015, 24, 1852–1866. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 178–188. [Google Scholar] [CrossRef]
- He, W.; Yao, Q.; Li, C.; Yokoya, N.; Zhao, Q. Non-local meets global: An integrated paradigm for hyperspectral denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 6861–6870. [Google Scholar]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Peng, Y.; Meng, D.; Xu, Z.; Gao, C.; Yang, Y.; Zhang, B. Decomposable nonlocal tensor dictionary learning for multispectral image denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 2949–2956. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2014, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bouali, M.; Ladjal, S. Toward optimal destriping of MODIS data using a unidirectional variational model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L. A MAP-based algorithm for destriping and inpainting of remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1492–1502. [Google Scholar] [CrossRef]












| Dataset | |||||
|---|---|---|---|---|---|
| WDC | GF-5 | ZhuHai-1 | EO-1 | Urban | |
| Size | 1208 × 307 × 191 | 2008 × 2083 × 150/2008 × 2083 × 180 | 512 × 512 × 32 | 200 × 200 × 210 | 307 × 307 × 210 |
| Sensor | Hydice | AHSI | CMOS | Hyperion | Hydice |
| Case 1 | Case 2 | Case 3 | ||||
|---|---|---|---|---|---|---|
| MPSNR | MSSIM | MPSNR | MSSIM | MPSNR | MSSIM | |
| LRTV [50] | 30.21 | 0.8206 | 29.26 | 0.7661 | 25.37 | 0.6427 |
| LRMR [52] | 27.27 | 0.7102 | 28.91 | 0.7850 | 26.54 | 0.6771 |
| TDL [53] | 27.51 | 0.7099 | 27.81 | 0.7364 | 26.16 | 0.6555 |
| NGMeet [51] | 28.06 | 0.7434 | 33.64 | 0.8565 | 33.76 | 0.8703 |
| ASSTV [49] | 29.36 | 0.7542 | 32.63 | 0.8423 | 33.61 | 0.8626 |
| HSI-DeNet [31] | 36.17 | 0.9128 | 34.69 | 0.8974 | 33.84 | 0.8741 |
| SGIDN [24] | 35.97 | 0.9036 | 35.85 | 0.9002 | 34.33 | 0.8846 |
| DCHC | 42.83 | 0.9786 | 36.07 | 0.9013 | 36.86 | 0.9025 |
| TRS-DCHC-noW | 42.21 | 0.9675 | 35.63 | 0.8942 | 36.07 | 0.8870 |
| TRS-DCHC | 43.04 | 0.9867 | 36.22 | 0.9170 | 36.91 | 0.9078 |
| Images | Index | Methods | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| LRTV | LRMR | TDL | NGMeet | ASSTV | HSI-DeNet | SGIDN | DCHC | TRS-DCHC-noW | TRS-DCHC | ||
| GF-5 Scene 1 | MRD | 1.763 | 1.787 | 2.490 | 3.731 | 1.706 | 3.309 | 1.605 | 3.830 | 3.508 | 3.599 |
| ICV | 8.031 | 8.685 | 8.428 | 6.915 | 7.924 | 5.906 | 7.767 | 12.141 | 11.505 | 13.341 | |
| GF-5 Scene 2 | MRD | 0.778 | 0.555 | 3.218 | 3.838 | 1.002 | 1.101 | 1.506 | 0.539 | 0.630 | 0.522 |
| ICV | 2.590 | 2.772 | 2.912 | 3.334 | 2.333 | 2.226 | 1.945 | 3.326 | 3.491 | 3.863 | |
| GF-5 Scene 3 | MRD | 4.368 | 2.904 | 2.929 | 2.523 | 2.196 | 5.129 | 7.428 | 4.020 | 3.334 | 3.623 |
| ICV | 5.393 | 3.723 | 3.747 | 4.062 | 2.863 | 3.441 | 6.493 | 2.408 | 3.590 | 3.317 | |
| Zhuhai-1 Scene 1 | MRD | 1.804 | 2.176 | 1.961 | 1.539 | 1.382 | 1.415 | 2.697 | 2.052 | 1.126 | 0.960 |
| ICV | 5.335 | 4.996 | 4.525 | 4.872 | 5.170 | 4.434 | 4.012 | 5.120 | 5.377 | 5.443 | |
| Zhuhai-1 Scene 2 | MRD | 2.813 | 1.680 | 1.308 | 1.672 | 1.539 | 0.820 | 4.384 | 1.374 | 1.283 | 1.134 |
| ICV | 3.607 | 3.913 | 4.260 | 4.765 | 4.475 | 4.368 | 5.261 | 4.310 | 4.235 | 5.484 | |
| Hyperion EO-1 | MRD | 2.160 | 2.663 | 2.788 | 2.383 | 2.738 | 3.185 | 2.929 | 2.532 | 2.193 | 2.375 |
| ICV | 2.507 | 1.854 | 2.102 | 2.044 | 1.978 | 2.606 | 1.953 | 2.672 | 2.598 | 2.714 | |
| HYDICE Urban | MRD | 2.209 | 2.292 | 3.011 | 3.177 | 1.878 | 1.936 | 1.986 | 2.044 | 1.895 | 1.779 |
| ICV | 0.785 | 0.779 | 0.8992 | 0.729 | 0.754 | 1.118 | 0.688 | 0.795 | 1.051 | 1.387 | |
| Methods | ||||||||
|---|---|---|---|---|---|---|---|---|
| LRTV | LRMR | TDL | NGMeet | ASSTV | HSI-DeNet | SGIDN | TRS-DCHC | |
| Time costs (s) | 35.7 | 74.4 | 21.3 | 46.7 | 23.6 | 4.6 | 8.4 | 8.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Xu, M.; Jiang, Y.; Zhang, G.; Cui, H.; Deng, G.; Lu, Z. Toward Real Hyperspectral Image Stripe Removal via Direction Constraint Hierarchical Feature Cascade Networks. Remote Sens. 2022, 14, 467. https://doi.org/10.3390/rs14030467
Wang C, Xu M, Jiang Y, Zhang G, Cui H, Deng G, Lu Z. Toward Real Hyperspectral Image Stripe Removal via Direction Constraint Hierarchical Feature Cascade Networks. Remote Sensing. 2022; 14(3):467. https://doi.org/10.3390/rs14030467
Chicago/Turabian StyleWang, Chengjun, Miaozhong Xu, Yonghua Jiang, Guo Zhang, Hao Cui, Guohui Deng, and Zhongyuan Lu. 2022. "Toward Real Hyperspectral Image Stripe Removal via Direction Constraint Hierarchical Feature Cascade Networks" Remote Sensing 14, no. 3: 467. https://doi.org/10.3390/rs14030467
APA StyleWang, C., Xu, M., Jiang, Y., Zhang, G., Cui, H., Deng, G., & Lu, Z. (2022). Toward Real Hyperspectral Image Stripe Removal via Direction Constraint Hierarchical Feature Cascade Networks. Remote Sensing, 14(3), 467. https://doi.org/10.3390/rs14030467







