Measuring Height Difference Using Two-Way Satellite Time and Frequency Transfer
Abstract
1. Introduction
2. Methods
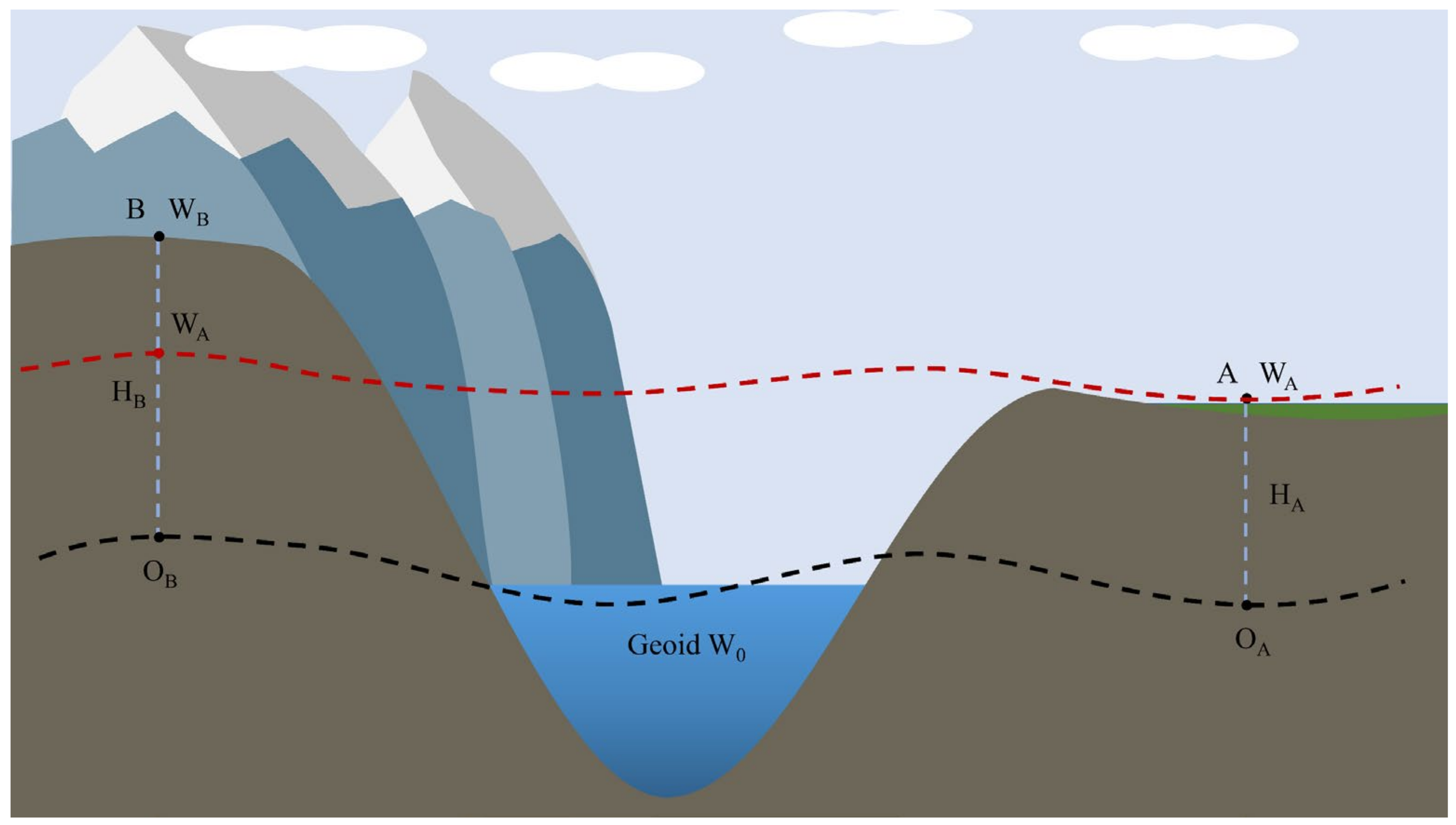
2.1. Height Measurement Based on Time Difference
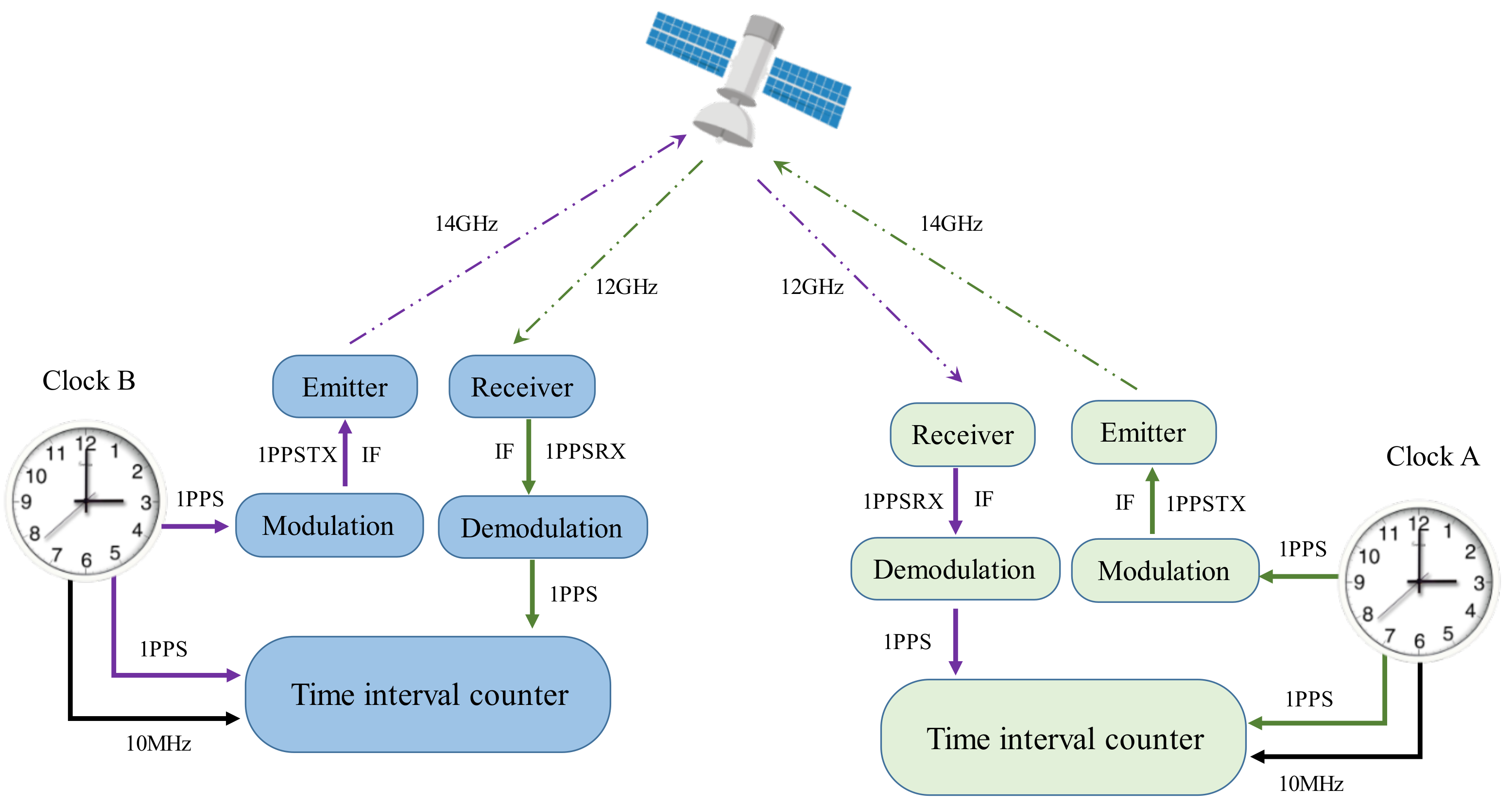
2.2. One Pulse Per Second (1 PPS) Signal
2.3. Transmission of 1 PPS Signal
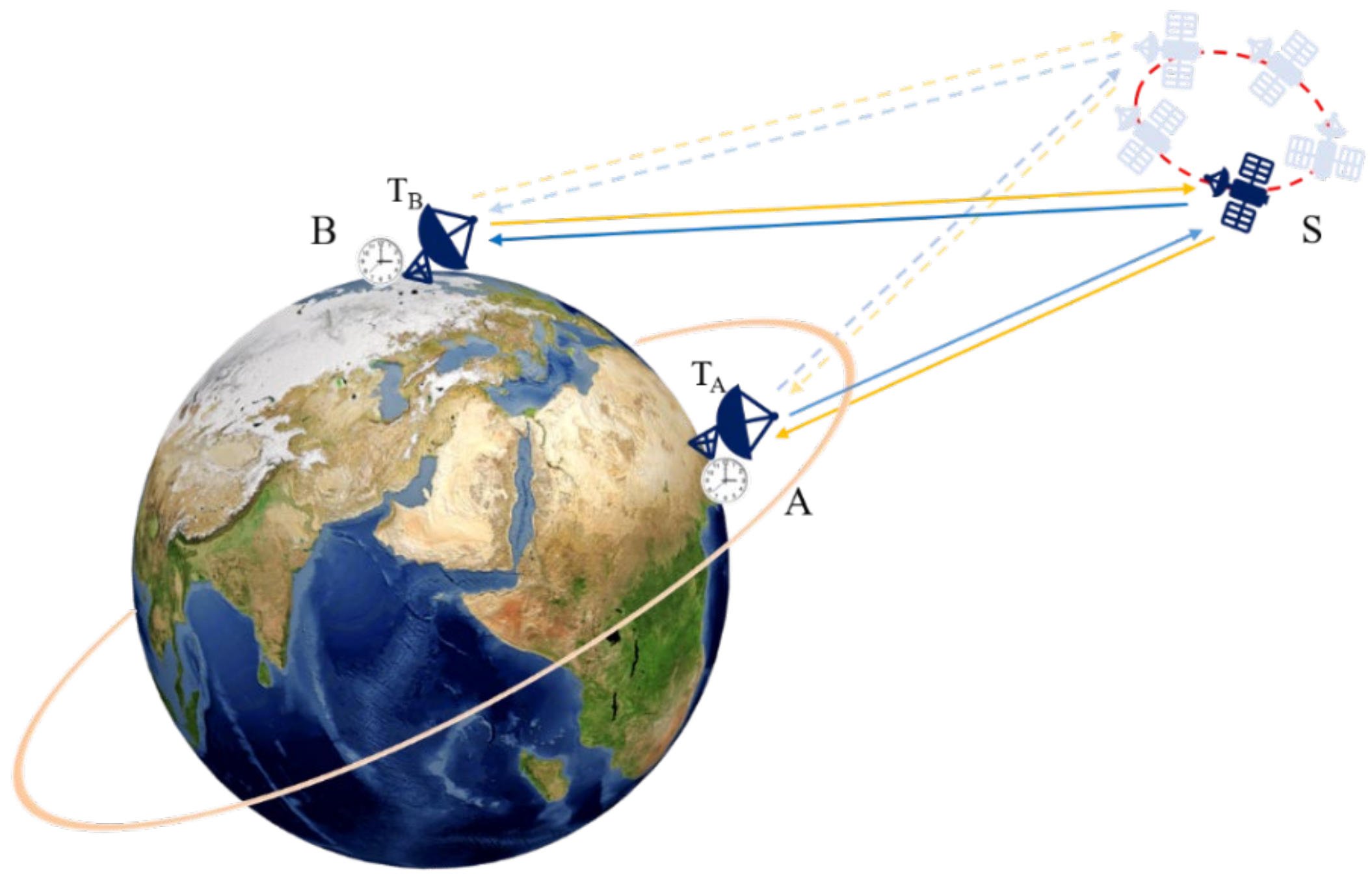
2.4. Time Difference Calculation in TWSTFT
3. Error Analysis and Corrections
3.1. Equipment Delay Error
3.2. Propagation Path Delay Error
3.3. Sagnac Effect Error
4. Experiments and Data Processing
4.1. Experiments
4.2. Data Processing
- (1)
- Through the data analysis with a large magnitude of change, we found that the data had some jumps, so we used fitting to restore them to the correct positions to ensure the continuity of all data.
- (2)
- To avoid the influence of outliers on the calculation results, we adopted 3σ criterion (PauTa criterion) to identify and eliminate outliers. The occasional outliers might be due to the fact that during its propagation, the radio frequency signal will suffer from various influences, which causes its distortion. Therefore, in the demodulation process, the sampling decision device cannot accurately reproduce the original 1 PPS signal, leading to outliers.
- (3)
- During continuous observation, some missing data may be caused by accidental failure of touch elements in TIC. We used linear interpolation to supplement the missing data.
- (4)
- We used singular spectrum analysis (SSA) [51] to remove periodic terms. This allows better extraction of trend items.
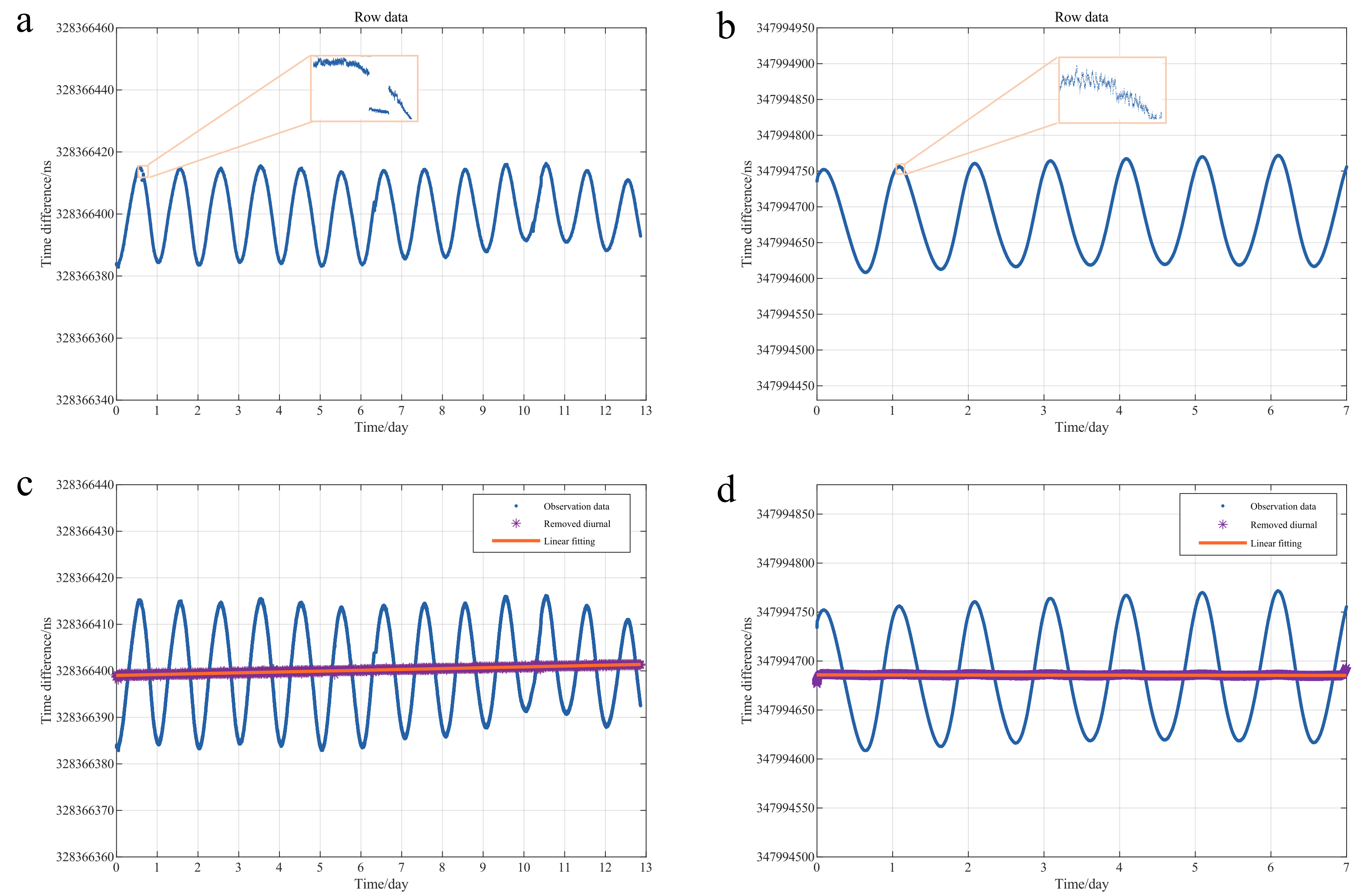
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Einstein, A. Die Feldgleichungen der Gravitation; Sitzungsberichte der Preussischen Akademie der Wissenschaften: Berlin, Germany, 1915; pp. 844–847. [Google Scholar]
- Takamoto, M.; Ushijima, I.; Ohmae, N.; Yahagi, T.; Kokado, K.; Shinkai, H.; Katori, H. Test of general relativity by a pair of transportable optical lattice clocks. Nat. Photonics 2020, 14, 411–415. [Google Scholar] [CrossRef]
- Grotti, J.; Koller, S.; Vogt, S.; Häfner, S.; Sterr, U.; Lisdat, C.; Denker, H.; Voigt, C.; Timmen, L.; Rolland, A.; et al. Geodesy and metrology with a transportable optical clock. Nat. Phys. 2018, 14, 437–441. [Google Scholar] [CrossRef]
- Bondarescu, R.; Bondarescu, M.; Hetényi, G.; Boschi, L.; Jetzer, P.; Balakrishna, J. Geophysical applicability of atomic clocks: Direct continental geoid mapping. Geophys. J. Int. 2012, 191, 78–82. [Google Scholar] [CrossRef]
- Shen, W.B.; Ning, J.; Chao, D.; Liu, J. A proposal on the test of general relativity by clock transportation experiments. Adv. Space Res. 2009, 43, 164–166. [Google Scholar] [CrossRef]
- Shen, W.; Chao, D.; Jin, B. On relativistic geoid. Boll Geod. Sci. Affini. 1993, 52, 207–216. [Google Scholar]
- Bjerhammar, A. On a relativistic geodesy. Bull. Géodésique 1985, 59, 207–220. [Google Scholar] [CrossRef]
- Chen, J.S.; Hankin, A.M.; Clements, E.R.; Chou, C.W.; Wineland, D.J.; Hume, D.B.; Leibrandt, D.R.; Brewer, S.M. An 27Al+ Quantum-Logic Clock with a Systematic Uncertainty below 10−18. Phys. Rev. Lett. 2019, 123, 33201. [Google Scholar]
- Poli, N.; Schioppo, M.; Vogt, S.; Falke, S.; Sterr, U.; Lisdat, C.; Tino, G.M. A transportable strontium optical lattice clock. Appl. Phys. B 2014, 117, 1107–1116. [Google Scholar] [CrossRef]
- Koller, S.B.; Grotti, J.; Vogt, S.; Al-Masoudi, A.; Dörscher, S.; Häfner, S.; Sterr, U.; Lisdat, C. Transportable Optical Lattice Clock with 7×10−17 Uncertainty. Phys. Rev. Lett. 2017, 118, 73601. [Google Scholar] [CrossRef] [PubMed]
- Rovera, G.D.; Abgrall, M.; Courde, C.; Exertier, P.; Fridelance, P.; Guillemot, P.; Laas-Bourez, M.; Martin, N.; Samain, E.; Sherwood, R.; et al. A direct comparison between two independently calibrated time transfer techniques: T2L2 and GPS Common-Views. J. Physics. Conf. Ser. 2016, 723, 12037. [Google Scholar] [CrossRef]
- Siu, S.; Wang, J.-L.; Tseng, W.-H.; Liao, C.-S.; Hu, H.-F. Primary reference time clocks performance monitoring using GNSS common-view technique in telecommunication networks. In Proceedings of the 2016 18th Asia-Pacific Network Operations and Management Symposium (APNOMS), Kanazawa, Japan, 5–7 October 2016; pp. 1–4. [Google Scholar]
- Hang, Y.; Hongbo, W.; Shengkang, Z.; Haifeng, W.; Fan, S.; Xueyun, W. Remote time and frequency transfer experiment based on BeiDou Common View. In Proceedings of the 2016 European Frequency and Time Forum (EFTF), York, UK, 4–7 April 2016; pp. 1–4. [Google Scholar]
- Petit, G.; Defraigne, P. The performance of GPS time and frequency transfer: Comment on ‘A detailed comparison of two continuous GPS carrier-phase time transfer techniques’. Metrologia 2016, 53, 1003–1008. [Google Scholar] [CrossRef]
- Lee, S.W.; Schutz, B.E.; Lee, C.; Yang, S.H. A study on the Common-View and All-in-View GPS time transfer using carrier-phase measurements. Metrologia 2008, 45, 156–167. [Google Scholar] [CrossRef]
- Kirchner, D. Two-way time transfer via communication satellites. Proc. IEEE 1991, 79, 983–990. [Google Scholar] [CrossRef]
- Steele, J.M.; Markowitz, W.; Lidback, C.A. Telstar Time Synchronization. IEEE Trans. Instrum. Meas. 1964, IM-13, 164–170. [Google Scholar] [CrossRef]
- Jiang, Z.; Konaté, H.; Lewandowski, W. Review and preview of two-way time transfer for UTC generation—From TWSTFT to TWOTFT. In Proceedings of the 2013 Joint European Frequency and Time Forum & International Frequency Control Symposium (EFTF/IFC), Prague, Czech Republic, 21–25 July 2013; pp. 501–504. [Google Scholar]
- Bauch, A. Time and frequency comparisons using radiofrequency signals from satellites. Comptes Rendus Phys. 2015, 16, 471–479. [Google Scholar] [CrossRef]
- Hanson, D.W. Fundamentals of two-way time transfers by satellite. In Proceedings of the 43rd Annual Symposium on Frequency Control, Denver, CO, USA, 31 May–2 June 1989; pp. 174–178. [Google Scholar]
- Imae, M.; Hosokawa, M.; Imamura, K.; Yukawa, H.; Shibuya, Y.; Kurihara, N.; Fisk, P.; Lawn, M.A.; Li, Z.; Li, H. Two-way satellite time and frequency transfer networks in Pacific Rim region. IEEE Trans. Instrum. Meas. 2002, 50, 559–562. [Google Scholar] [CrossRef]
- Fujieda, M.; Gotoh, T.; Nakagawa, F.; Tabuchi, R.; Aida, M.; Amagai, J. Carrier-phase-based two-way satellite time and frequency transfer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2625–2630. [Google Scholar] [CrossRef] [PubMed]
- Jing, W.; Wang, J.; Zhao, D.; Lu, X.; Wu, J. A measurement method of the GEO satellite local oscillator error. In Proceedings of the 2013 Joint European Frequency and Time Forum & International Frequency Control Symposium (EFTF/IFC), Prague, Czech Republic, 21–25 July 2013; pp. 339–342. [Google Scholar]
- Fujieda, M.; Yang, S.; Gotoh, T.; Hwang, S.; Hachisu, H.; Kim, H.; Lee, Y.K.; Tabuchi, R.; Ido, T.; Lee, W.; et al. Advanced Satellite-Based Frequency Transfer at the 10−16 Level. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 973–978. [Google Scholar] [CrossRef]
- Riedel, F.; Al-Masoudi, A.; Benkler, E.; Dörscher, S.; Gerginov, V.; Grebing, C.; Häfner, S.; Huntemann, N.; Lipphardt, B.; Lisdat, C.; et al. Direct comparisons of European primary and secondary frequency standards via satellite techniques. Metrologia 2020, 57, 45005. [Google Scholar] [CrossRef]
- Wu, K.; Shen, Z.; Shen, W.B.; Sun, X.; Wu, Y. A preliminary experiment of determining the geopotential difference using two hydrogen atomic clocks and TWSTFT technique. Geod. Geodyn. 2020, 11, 229–241. [Google Scholar] [CrossRef]
- Shen, W.; Sun, X.; Cai, C.; Wu, K.; Shen, Z. Geopotential determination based on a direct clock comparison using two-way satellite time and frequency transfer. Terr. Atmos. Ocean. Sci. 2019, 30, 21–31. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and cosmology: Principles and Applications of the General Theory of Relativity. Am. J. Phys. 1972, 41, 598–599. [Google Scholar] [CrossRef]
- Pavlis, N.; Weiss, M. The relativistic redshift with 3×10−17 uncertainty at NIST, Boulder, Colorado, USA. Metrologia 2003, 40, 66. [Google Scholar] [CrossRef][Green Version]
- Dittus, H.; Lämmerzahl, C.; Peters, A.; Schiller, S. OPTIS—A Satellite test of Special and General Relativity. Adv. Space Res. 2007, 39, 230–235. [Google Scholar] [CrossRef]
- Vessot, R.; Levine, M.; Mattison, E.; Blomberg, E.; Hoffman, T.; Nystrom, G.; Farrel, B.; Decher, R.; Eby, P.; Baugher, C. Test of Relativistic Gravitation with a Space-Borne Hydrogen Maser. Phys. Rev. Lett. 1981, 45, 2081–2084. [Google Scholar] [CrossRef]
- Shen, Z.; Shen, W.; Peng, Z.; Liu, T.; Zhang, S.; Chao, D. Formulation of Determining the Gravity Potential Difference Using Ultra-High Precise Clocks via Optical Fiber Frequency Transfer Technique. J. Earth Sci. China 2018, 30, 422–428. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; Freeman and Company: San Francisco, CA, USA, 1967. [Google Scholar]
- Saburi, Y.; Yamamoto, M.; Harada, K. High-precision time comparison via satellite and observed discrepancy of synchronization. IEEE Trans. Instrum. Meas. 1976, IM-25, 473–477. [Google Scholar] [CrossRef]
- Asami, K. An Algorithm to Improve the Performance of M-Channel Time-Interleaved A-D Converters. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2007, E90-A, 2846–2852. [Google Scholar] [CrossRef]
- Ridders, C. Accurate determination of threshold voltage levels of Schmitt trigger. IEEE Trans. Circuits Syst. 1985, 32, 969–970. [Google Scholar] [CrossRef]
- Dinan, E.H.; Jabbari, B. Spreading codes for direct sequence CDMA and wideband CDMA cellular networks. IEEE Commun. Mag. 1998, 36, 48–54. [Google Scholar] [CrossRef]
- Celano, T.P.; Francis, S.P.; Gifford, G.A. Continuous satellite two-way time transfer using commercial modems. In Proceedings of the 2000 IEEE/EIA International Frequency Control Symposium and Exhibition (Cat. No.00CH37052), Kansas City, MO, USA, 9 June 2000; pp. 607–611. [Google Scholar]
- Barrow, B.B. Error Probabilities for Telegraph Signals Transmitted on a Fading FM Carrier. Proc. IRE 1960, 48, 1613–1629. [Google Scholar] [CrossRef]
- Piester, D.; Bauch, A.; Becker, J.; Staliuniene, E.; Schlunegger, C. On measurement noise in the European TWSTFT network. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 1906–1912. [Google Scholar] [CrossRef] [PubMed]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- ITU-R. The Operational Use of Two-Way Satellite Time and Frequency Transfer Employing Pseudorandom Noise Codes. TF Series: Time Signals and Frequency Standards Emissions, Recommendation ITU-R TF.1153- 3 (08/2015), International Telcomunication Union. 2015. Available online: https://www.itu.int/rec/R-REC-TF.1153-4-201508-I/en (accessed on 5 September 2021).
- Lin, H.T.; Huang, Y.J.; Tseng, W.H.; Liao, C.S.; Chu, F.D. The TWSTFT links circling the world. In Proceedings of the 2014 IEEE International Frequency Control Symposium (FCS), Taipei, Taiwan, 19–22 May 2014; pp. 1–4. [Google Scholar]
- Hopfield, H.S. Tropospheric effect on electromagnetically measured range: Prediction from surface weather data. Radio Sci. 1971, 6, 357–367. [Google Scholar] [CrossRef]
- Sastamoinen, J. Atmospheric correction for troposphere and stratosphere in radio ranging of satellites, in the Use of Artifical Satellites for Geodesy. Geophys. Monogr. Ser. 1972, 15, 247–251. [Google Scholar]
- Penna, N.; Dodson, A.; Chen, W. Assessment of EGNOS Tropospheric Correction Model. J. Navigation. 2001, 54, 37–55. [Google Scholar] [CrossRef]
- Rose, J.A.R.; Watson, R.J.; Allain, D.J.; Mitchel, N.C. Ionospheric corrections for GPS time transfer. Radio Sci. 2014, 49, 196–206. [Google Scholar] [CrossRef]
- Tseng, W.; Feng, K.; Lin, S.; Lin, H.; Huang, Y.; Liao, C. Sagnac Effect and Diurnal Correction on Two-Way Satellite Time Transfer. IEEE Trans. Instrum. Meas. 2011, 60, 2298–2303. [Google Scholar] [CrossRef]
- Bidikar, B.; Rao, G.; Laveti, G. Sagnac Effect and SET Error Based Pseudorange Modeling for GPS Applications. Procedia Comput. Sci. 2016, 87, 172–177. [Google Scholar] [CrossRef]
- Hackman, C.; Levine, J. A Long-Term Comparison of GPS Carrierphase Frequency Transfer and Two-Way Satellite Time/Frequency Transfer. In Proceedings of the 38th Annual Precise Time and Time Interval (PTTI) Meeting, Reston, VA, USA, 7–9 December 2006; pp. 1–15. [Google Scholar]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Phys. D Nonlinear Phenom. 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Hocking, R. Methods and Applications of Linear Models. In Regression and the Analysis of Variance; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ascarrunz, F.G.; Jefferts, S.R.; Parker, T.E. Environmental effects on errors in two-way time transfer. In Proceedings of the 20th Biennial Conference on Precision Electromagnetic Measurements, Braunschweig, Germany, 17–21 June 1996; pp. 518–519. [Google Scholar]
- Ascarrunz, F.G.; Jefferts, S.R.; Parker, T.E. Earth station errors in two-way time and frequency transfer. IEEE Trans. Instrum. Meas. 1997, 46, 205–208. [Google Scholar] [CrossRef][Green Version]


| Error Sources | Error Magnitude/ps (Two-Way) | Correction Model | Residual Error/ps |
|---|---|---|---|
| Time interval counter delay | 10~100 | Zero-baseline calibration | 5 |
| Modems delay | 100 | Zero-baseline calibration | 10 |
| Satellite transparent transponder delay | 80 | Zero-baseline calibration | 10 |
| Transmission and receiving system delay | 200~500 | Zero-baseline calibration | 30 |
| Propagation path geometry delay | <10 | Neglected | <10 |
| Tropospheric delay | 10 | Neglected | 10 |
| Ionospheric delay | 100 | Model correction | <10 |
| Asymmetry of station and satellite position delay | 30 | Delay transmission compensation | <1 |
| Sagnac effect delay | 1~2 × 105 | Model correction | 10~100 |
| Geopotential Comparison | Zero-Baseline | |
|---|---|---|
| Slope | 2.11639 × 10−15 | −0.93617 × 10−15 |
| The uncertainty of the slope | 0.26 × 10−15 | 0.52 × 10−15 |
| Measured height difference between A and B (m) | 28.0 5.4 | |
| True value (m) | 22.8 | |
| Deviation (m) | 5.2 5.4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, P.; Shen, W.; Sun, X.; Cai, C.; Wu, K.; Shen, Z. Measuring Height Difference Using Two-Way Satellite Time and Frequency Transfer. Remote Sens. 2022, 14, 451. https://doi.org/10.3390/rs14030451
Cheng P, Shen W, Sun X, Cai C, Wu K, Shen Z. Measuring Height Difference Using Two-Way Satellite Time and Frequency Transfer. Remote Sensing. 2022; 14(3):451. https://doi.org/10.3390/rs14030451
Chicago/Turabian StyleCheng, Peng, Wenbin Shen, Xiao Sun, Chenghui Cai, Kuangchao Wu, and Ziyu Shen. 2022. "Measuring Height Difference Using Two-Way Satellite Time and Frequency Transfer" Remote Sensing 14, no. 3: 451. https://doi.org/10.3390/rs14030451
APA StyleCheng, P., Shen, W., Sun, X., Cai, C., Wu, K., & Shen, Z. (2022). Measuring Height Difference Using Two-Way Satellite Time and Frequency Transfer. Remote Sensing, 14(3), 451. https://doi.org/10.3390/rs14030451







