Abstract
In this paper, we present a study comparing the depth to diameter (d/D) ratio of small simple craters (200–1000 m) of an area between −88.5° to −90° latitude at the lunar south pole containing Permanent Shadowed Regions (PSRs) versus craters without PSRs. As PSRs can reach temperatures of 110 K and are capable of harboring volatiles, especially water ice, we analyzed the relationship of depth versus diameter ratios and its possible implications for harboring water ice. Variations in the d/D ratios can also be caused by other processes such as degradation, isostatic adjustment, or differences in surface properties. The conducted d/D ratio analysis suggests that a differentiation between craters containing PSRs versus craters without PSRs occurs. Thus, a possible direct relation between d/D ratio, PSRs, and water ice harboring might exist. Our results suggest that differences in the target’s surface properties may explain the obtained results. The resulting d/D ratios of craters with PSRs can help to select target areas for future In-Situ Resource Utilization (ISRU) missions.
1. Introduction
Volatile characterization on the lunar surface is ongoing research that started over 50 years ago. Watson et al. [1] suggested that ice might be trapped in Permanent Shadowed Regions (PSR) for short periods of time. Arnold [2] corroborated the idea of PSRs harboring volatiles, especially water ice, at the lunar south pole. Recent investigations also concur with this hypothesis (Nozette et al. [3], McClanahan et al. [4], and Susorney et al. [5]) however, others (Eke et al. [6], Haruyama et al. [7]) did not find any compelling results.
In polar regions, PSRs can be excellent cold trap candidates (Kokhanov et al. [8] and Rubanenko et al. [9]). Due to the low inclination of the spin axis of the Moon relative to the ecliptic (1.54°) and the extremely high topography in its south pole, PSRs can become excellent cold traps where ice might be present (Paige et al. [10]). Due to the lack of illumination, the characterization of water ice in these regions is mainly studied indirectly (e.g., relating PSR with low temperature) and by combining data from different instruments. A study by Mitrofanov et al. [11] registered a decrease of the neutron flux on the Lunar Exploration Neutron Detector (LEND) onboard the Lunar Reconnaissance Orbiter (LRO) in some PSR areas at the lunar south pole. This neutron flux decrease could be related to the volatile presence. In addition, Fisher et al. [12] found a positive correlation between reflectance measurements within PSRs, obtained by using the scattered sunlight from the inner crater walls, that the presence of ice might cause. Mitrofanov et al. [11] and Sanin et al. [13] registered a decrease of the neutron flux LEND, which might be related to possible traces of ice. The study Sanin et al. [14] showed that only three craters on the Moon, namely Shoemaker and Cabeus in the South and Rozhdestvensky in the North, had significant neutron suppression. Other PSRs were not showing relevant values, and some even showed an excess of neutron emission with respect to near-lit areas. Sanin et al. [14] concluded that except for the three craters mentioned above, no conclusive results could be extracted for the rest of PSRs. Furthermore, Fisher et al. [12] used reflectance measurements of the Lunar Orbiter Laser Altimeter (LOLA) tracks to find evidence for surface water ice. They found out that the reflectance increases with decreasing temperatures (around 110 K) which coincides with the presence of water ice. Finally, Hayne et al. [15] found a correlation between PSR crater temperatures and ultraviolet albedo spectra.
The Circular Polarization Ratio (CPR) is a measure of the quality of the reflected circularly-polarized radar signal. It is used to emphasize and ignore specific signals related to the texture of the reflecting material. Several studies on radar observation suggest that the CPR of the signal is directly related to the morphology of the radiating surface (Spudis et al. [16], Campbell et al. [17], and Thomson et al. [18]). Harmon et al. [19] identified that a high CPR (CPR > 1) in several locations of the south pole of Mercury coincided with areas where water ice might be present. This correlation was also found on Europa, Ganymede, and Callisto (Ostro et al. [20]). The problem of CPR is that a high CPR signal could also be produced by fresh regolith exposed to the surface, terrain ruggedness, and boulder distribution coinciding with the CPR scale (in the case of Mini-RF, 10 cm) (Baloga et al. [21]). Using CPR alone to characterize ice introduces significant uncertainties and needs to be supported by other data to eliminate possible false positives. On the Moon, several attempts to relate high CPR signatures with ice have been pursued, although no conclusive results have been achieved (Eke et al. [6] and Nozette et al. [3]). CPR was also found to have high signals in illuminated and shadowed areas, thus concluding that CPR depends on the morphology and nature of the terrain. Eke et al. [6] analyzed various polar craters and concluded that CPR alone is not sufficient to indicate the presence of ice. M-chi decompositions of radar sensors (Raney et al. [22]) is a recent technique used in surface analysis. By combining the Stokes products (Stokes and G. [23]) in an RGB composition, the backscattering behavior of the radar signal is shown in different colors. These colors reflect different characteristics of the surface (Raney et al. [24]). This RGB combination is helpful to identify the nature of high CPR signals inside craters, enhancing young fresh craters where ejecta and new material will return a high CPR value, thus allowing to discard the possibility of having ice.
The fact that PSRs are never directly illuminated makes it impossible to use an imaging spectrometer such as the Mineralogical Moon Mapper (M3) onboard Chandrayaan-1 (Pieters et al. [25]). However Li et al. [26] used scattered sunlight from crater walls within PSRs and analyzed spectra on those regions that showed consistency with the presence of ice. McCord et al. [27] detected absorption features outside PSRs from 2.8 to 3.0 μm, attributed to water. The bands near 2.8 μm in M3 are particularly sensitive to temperature, and images located at the lunar south pole need a specific temperature effect removal function (Combe et al. [28], Clark et al. [29]). Current temperature removal functions have been reported to be untrustworthy in images taken at the lunar south pole and might introduce uncertainty in the areas where water has absorption peaks in the spectra (Dr. Christian Wöhler, personal communication, May 2017). Furthermore, using the 3.0 μm band on M3 is inadvisable as it is too close to the detector boundary.
A crater’s topography with steep walls and the low elevation of the Sun in south polar regions make craters ideal candidates to contain PSRs (Mazarico et al. [30]). Zuber et al. [31] extensively studied the Shackleton crater (where more than 70% of the area is a PSR) in order to find possible water ice by analyzing Lunar Orbiter Laser Altimeter (LOLA) observations. The study shows a possible water ice occurrence on the crater’s floor, as such areas are brighter (at LOLA’s wavelength of 1064 nm) than their surroundings. However, results are unclear as the brightness might also be caused by space weathering. Most of the studies conducted in this region focused on large craters such as Shackleton (Haruyama et al. [7], Thomson et al. [18], and Nozette et al. [3]) and a smaller number of studies concentrated on small simple craters (Kereszturi and Steinmann [32], Daubar et al. [33], and Stopar et al. [34]).
The depth to diameter (d/D) ratio can be used to characterize crater age and evolutionary stage (Lagain et al. [35], Craddock et al. [36], and Robbins et al. [37]). Previous studies suggested that the d/D ratio for fresh primary craters is expected to be around 0.2 and decreases over time due to degradation (Elachi et al. [38] and Schultz et al. [39]). Recent studies also show d/D values from small simple craters to be slightly lower for fresh craters (∼0.1) than older ones. According to Stopar et al. [40], fresh simple craters are deeper than degraded craters regardless of their size. Changes in d/D are difficult to distinguish for minor and moderate crater degradations. Daubar et al. [33] suggest that small lunar craters are likely to be unrecognized secondary craters or some of those craters are primary craters that have undertaken degradation to similar shapes. In addition, small craters are less likely to show variation in surface heat flow after formation, making it easier to retain the possible volatiles carried by an impacting asteroid, as the crater’s surface temperature might not reach temperatures capable of changing the volatile state of matter (e.g., water ice’s sublimation temperature). If this hypothesis is true, small craters containing PSRs create an excellent environment for harboring water. Finally, according to Boyce et al. [41] slight variations in depths of small simple craters might be interpreted as volatile activity inside the crater. Stopar et al. [40], interprets the d/D ratio variations to be caused by other processes such as differences in target properties (e.g., layering, porosity, angle of repose, strength, fragmentation, cohesion, shear strength, and stratigraphy), resurfacing processes, or degradation.
This study focuses on the analysis of the depth to diameter characteristics of small simple craters that might contain water ice in a Region of Interest (RoI) at the lunar south pole between −88.5° to −90° latitude (Figure 1). This area (Figure 2) is a candidate landing site for future lunar exploration missions (De Rosa et al. [42], Kokhanov et al. [43], and Lemelin et al. [44]). The primary objective of our investigation is to analyze the d/D ratios small simple craters that fulfill good volatile harboring conditions on the Moon.
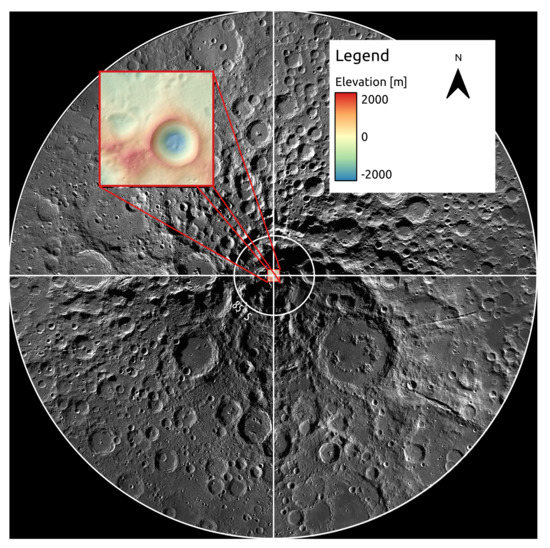
Figure 1.
Location of the Digital Terrain Model (DTM) within the south pole of the Moon. The elevation shows the extreme topography of the area.
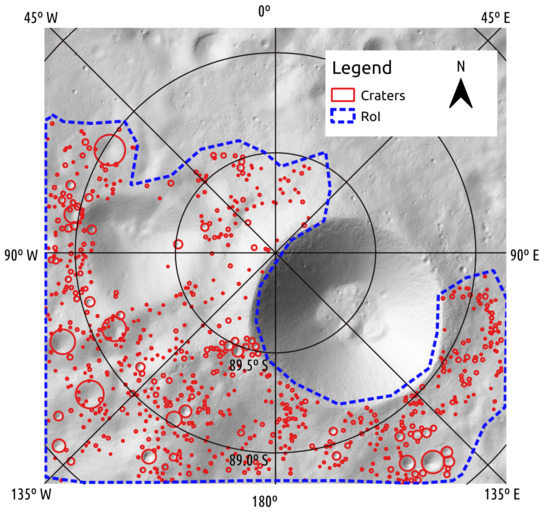
Figure 2.
Region of Interest (RoI) (blue) located at the lunar south pole with all the digitized craters (red) used in this study.
2. Data and Methods
The Lunar Reconnaissance Orbiter Camera (LROC) has a Wide Angle Camera (WAC) offering a resolution of 75 to 380 m and the Narrow Angle Camera (NAC) provides images with a full resolution of 0.5 m, both at an altitude of 50 km (Robinson et al. [45]). Previous studies (Boyce et al. [41] and Stopar et al. [40]) of d/D analysis focusing on small simple craters used the higher resolution available data. Several NAC and WAC images of the lunar south pole exist. However, due to the inclination of the rotation axis of the Moon and its extreme topography, most of the images only show large shadows. The presence of large shadows makes it almost impossible to create Digital Terrain Models (DTM) as stereophotogrammetry is not possible.
The Lunar Orbiter Laser Altimeter (LOLA) is a laser that creates a 65-m wide swath containing five laser dots with 10-m spacing along tracks (Robinson et al. [45]). DTMs using LOLA data are available on PDS. However, they contain artifacts (Gläser et al. [46] and Barker et al. [47]) that will influence the results of our study, especially the illumination.
In our study, we use a DTM provided by Gläser et al. [48] generated from Lunar Orbiter Laser Altimeter (LOLA) data (Figure 3). The DTM was co-registered using optical data from LROC NAC, has a resolution of 20 m per pixel, and covers the area from −88.5° to −90° S. We use the DTM to identify PSRs based on illumination conditions and digitize impact craters based on topography information.
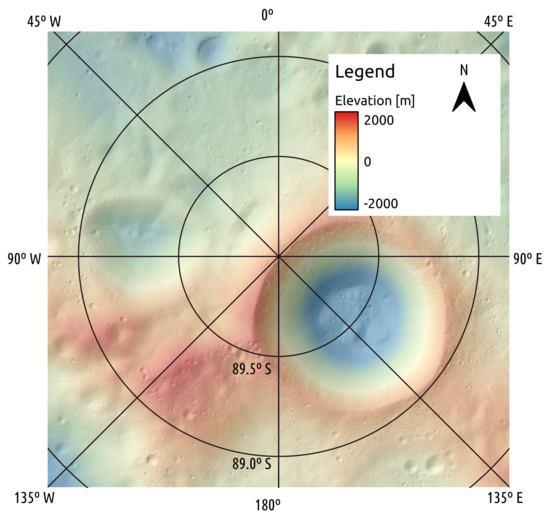
Figure 3.
Portion of the digital terrain model covering the RoI. The elevation of the terrain is shown in meters.
2.1. Illumination
DTMs are a common data source to compute illumination on the lunar south pole (Mazarico et al. [30], Bussey et al. [49], Noda et al. [50], and Gläser et al. [48]). Illumination conditions based on elevation data can be computed through ray tracing or the horizons method. Both methods rely on computing the elevation of the Sun at a given position and comparing it with the elevation of the highest elevated terrain along the line from the observer to the Sun. If the Sun has a higher elevation, the pixel where the observer is located is illuminated. In the other case, the observer will be in shadow (see Gläser et al. [46]).
The ray-tracing method (Noda et al. [50] and Bussey et al. [49]) compares the elevation of the Sun versus the elevation of the highest point in the terrain at a given time along the direction of the Sun from a location on the terrain. This method is convenient when short periods of time are analyzed. The computation is pursued for each pixel at every position of the Sun. Therefore, the number of calculations increases for a long period of time. Hence, this method is only recommended for periods ranging from a few hours to one year if an hourly time step is used.
The horizons method (Mazarico et al. [30] and Gläser et al. [46]) introduces a preprocessing step where the highest elevated points around all pixels on the terrain are computed. Although very time-consuming, this initial step allows computing the illumination quickly when analyzing multiple azimuths and more extended periods. The result is about 720 files corresponding to the horizon around all the pixels every 0.5°. Choosing this step size of 0.5° ensures that at least one azimuth direction lies within the Sun’s angular diameter of 0.53°. In our study, we used the horizons method, as described in Gläser et al. [46], to compute the illumination as it was more convenient for our analysis. We chose to create one file per azimuth as this will reduce the input/output operations, which are highly time-consuming while computing the illumination.
We computed illumination over a 20-year period, which covers the precession cycle (18.6 years) of the Moon, as the orientation of its rotational axis is not fixed. This allows us to average the amount of light received over certain areas that receive high illumination during certain times and are less illuminated during other periods. We also modeled the Sun as a disk and not a simple dot, allowing us to assign a fraction of the visible disk, thus getting closer to an accurate representation. The illumination is computed by comparing the Sun’s and Horizon’s elevations over a certain period and assigning an illumination value to each pixel.
To minimize the computation time, Marco Figuera [51] and Marco Figuera et al. [52] created an illumination computation method adapted to work on GPUs using parallel computation. The process reduced the computation time significantly, allowing to analyze illumination for larger areas and along a more extended period of time. The resulting PSRs are shown in Figure 4.
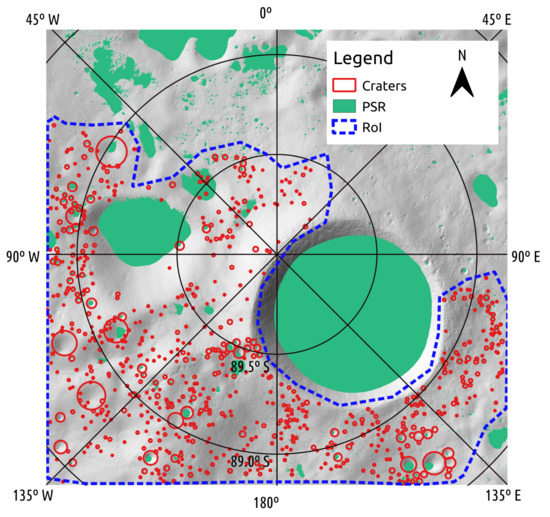
Figure 4.
Selected craters after filtering (red) with the Permanent Shadowed Regions (PSRS) (green) and the RoI (blue). One large PSR can cover several small craters.
2.2. Crater Selection
There are two methods to measure rim-to-rim diameter and rim-to-floor depth (Chappelow [53] and Stopar et al. [40]). One method uses DTMs, and the other the cast of shadows over craters. The shadow casting method is beneficial when craters are not nested, have clear and distinguishable rims, and the shadows lay within the crater (Chappelow [53] and Daubar et al. [33]). The second method for crater selection uses DTMs (Stopar et al. [40]). Using specific software, such as JMars (Christensen et al. [54]) and CraterTools (Kneissl et al. [55]), we can compute the rim-to-rim diameter and rim-to-floor depth. CraterTools is a toolbox running on ArcGIS and JMars is a java-based GIS client allowing the user to digitize craters in a straightforward way by selecting a fixed circle and hovering it over same-sized craters. The results can be stored as a shapefile for later visualization in JMars or other GIS clients. The results can also be exported for further analysis in CraterStats (Michael and Neukum [56]). One of the main drawbacks of JMars is that the diameters of the circles have to be previously selected by hand and fitted to the craters. This makes the results to be approximated and not as precise as with CraterTools. In conclusion, the overall speed and accuracy drove the choice of CraterTools over JMars. As mentioned in Section 2, NAC images of the lunar south pole are mostly covered by shadows. Therefore, the DTM method using CraterTools was preferred over the shadow-casting method.
To enhance the crater rims in the DTM to better digitize them, we computed a series of hillshaded reliefs locating the Sun at different angles and constant elevation. This was necessary as some of the craters at the lightly sloped areas faces are otherwise challenging to identify. The hillshades were computed using the GDAL library with a constant elevation of the Sun of 45° above the horizon and 45, 135, 225, and 315° azimuth, respectively. A hillshade at every 90° azimuth was considered sufficient to appreciate differences between the scenes. Once the hillshades were computed, we overlapped them with the DTM in ArcGIS and gave them a 50% transparency to help distinguish the craters.
To digitize the craters, we divided the region of interest, located in the south-westernmost part of the DTM, into smaller squared areas. The process starts by selecting one area, loading one hillshade, and digitizing all the visible craters, and repeating the process for the rest of the areas. In case a crater was not clearly visible, all the hillshades were loaded at the same time. If the crater edges were still not visible, the crater was not digitized.
In our study, we used CraterTools by drawing three points on the crater rim or by selecting two points along the crater’s diameter. While the second method seems faster due to fewer points needed, better results are achieved when using the first. CraterTools stores the selected craters in a shapefile containing the diameter, longitude, and latitude of each crater.
2.3. Depth and Diameter Measurement
To derive the depth of the craters, we measured the highest elevated point on a crater’s rim and the lowest elevated point on a crater’s floor, using the raster calculator of ArcGIS. Craters on very steep areas (>25°) were discarded as the lowest point could not reflect the actual depth of the crater. Subtracting these two measurements, we computed the range of each crater and later included them into the craters table.
As mentioned in Robbins et al. [57], diameters of craters must be at least 10 pixels across as artifacts may occur within this distance. Taking the DTM’s resolution of 20 m per pixel, the minimum diameter considered was 200 m. We digitized a total of 3317 craters and discarded 2564 after applying filters (slope <25° and diameter between 200 and 1000 m) leaving us with a total of 753 craters. Using ArcGIS’s intersection tool, we selected the craters containing PSR regions and those without PSRs (Figure 4).
2.4. Uncertainties
The method used to select craters has a random error derived from measured crater diameters and depths. In order to evaluate the error, we conducted an experiment consisting of repetitively measuring diameters and depths. We divided the craters into groups of 100-m diameter steps, such that we had eight groups ranging from 200 m to 1000 m. We selected two craters randomly from each group and measured the diameter and depth three times.
The results and statistics of the experiment are shown in Table 1. The maximum standard deviation of diameters is 0.76 m for a crater diameter of 523.41 m with an associated error of 0.15%. However, the depth standard deviation of the crater is 0.01% for a depth of 112.21 m. For the depths, the maximum standard deviation is 0.08 m for a depth of 198.01 m, and a percentage of the standard deviation of 0.04%. The analysis shows good agreement with the values that were digitized.

Table 1.
Crater statistics used in the uncertainties experiment.
3. Results
The results from the d/D measurement of craters containing PSRs vs. craters not containing PSRs are shown in Figure 5. Figure 5A shows the histogram grouped in d/D ratios of craters containing PSRs (blue) and not containing PSRs (orange). The results show that the average d/D ratio is smaller for craters with PSRs (d/D∼0.16) than without PSRs (d/D∼0.22).
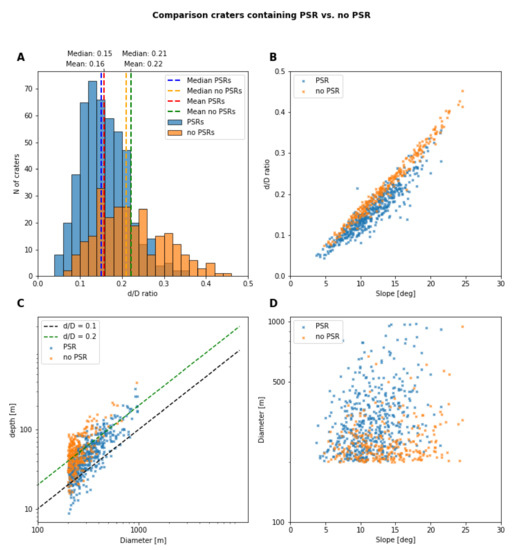
Figure 5.
Comparison of craters containing PSRs and without PSRs. (A) Histogram of all d/D values measured within our RoI. Craters with PSRs in their interior are shown in blue with a peak around 0.16. Craters without PSRs are shown in orange with a peak at 0.22. (B) Average slopes and d/D ratio seem to show a strong correlation between wall slope and d/D ratio where the deepest craters have the steepest slopes. Craters with PSR tend to accumulate in the area with a low d/D ratio and low slope. (C) The average ratio for craters containing PSRs is approximately 0.1 which appears to be of an older age in comparison with the craters without PSRs. (D) Average slopes with respect to the diameter of the craters. Craters containing PSRs are normally characterized by low slope walls even for larger diameters, making them shallower. Craters with no PSRs are on average smaller in diameters but contain steeper slopes.
Figure 5B shows the slope versus the d/D ratio and a strong correlation between the wall slope and d/D ratio where the deepest craters have the steepest slopes. Craters without PSRs follow the expected trend of increasing the slope with an increasing d/D ratio. Craters with PSRs cluster at slopes smaller than 20°, denoting a possible increased shallowness of the crater profile.
Figure 5C shows the depth versus diameter on a logarithmic scale. Although craters from both categories overlap, especially at a small diameter and depth, two distinguished classes can be identified. In general, we can see that craters in both groups tend to decrease their d/D ratio at around 400 m in diameter, whereas larger craters cluster around 0.2. This observation is consistent with the studies from Stopar et al. [40] and Fassett et al. [58].
According to Figure 5D, craters containing PSRs concentrate in the low slope region with an increasing diameter, whereas craters with no PSRs are primarily in the 200–300-m diameter range but with greater average slopes.
In general, our analysis shows that craters containing PSRs tend to be shallower than those without PSRs. Furthermore, craters with PSRs have lower slopes but higher variability than craters with no PSRs, which tend to follow a more linear trend (Figure 5B).
We conducted a two-sided two-sample hypothesis testing to determine whether the difference between the two groups of craters is statistically significant. Several statistical tests can be performed for two-sample testing, for example, the Kolmogorov–Smirnov test, Student’s t-test, or Mann–Whitney U test. Our study applies the Mann–Whitney U test since it is less sensitive to the different numbers of craters in the two populations (MacFarland et al. [59]). The null hypothesis () is that the d/D ratios in the two groups of craters are equal, whereas our alternate hypothesis () states a difference in d/D ratios between the two groups. We obtained a p-value smaller than 0.01, which is statistically significant (). We also ran the Mann–Whitney U test based on diameter ranges to see if the differences are also significant. We found craters with diameters smaller than 399 m and from 500 m to 599 m to be significant. However the remaining ranges have a p-value above 0.01. This is most likely caused by a very unbalanced population of craters containing PSRs vs. no PSRs in the range 400 m to 499 m. In the case of crater with a range of 700 m to 899 m, it might be due to a lack of no PSRs craters. Therefore, we can conclude that the d/D ratios of the craters, especially smaller than 400 m in diameter, containing PSRs are significantly different from the d/D ratios of craters without PSRs.
4. Discussion
We analyzed the d/D ratios of small simple craters at the lunar south pole. Our results show a close correlation between slopes and d/D ratios. In general, craters containing PSRs have average d/D ratios of about 0.16, whereas those without PSRs have average d/D ratios spanning from 0.20 to 0.23. Similarly, craters with and without PSRs form two distinguishable groups based on the slope gradients. Craters with PSRs are usually sparse and cluster at slopes lower than 20°, whereas craters without PSRs follow a linear tendency when increasing the slope. The same two groupings can be seen on the depth vs. diameter logarithmic plots. Craters without PSRs cluster around smaller diameters and are closer to d/D ratios of 0.2. On the contrary, craters with PSRs have a smaller d/D ratio of 0.1. Furthermore, the statistical test confirms the differences in d/D ratios between the two groups of craters. Our results support those obtained by Stopar et al. [40], Fassett et al. [58], and Kokhanov et al. [8], who used a different source DTM and included craters smaller than 200 m in diameter.
The difference in d/D ratios between craters containing PSRs and craters containing no PSRs can be caused by various processes related to diffusive crater degradation and target properties. For example, if PSRs contain a subsurface layer of ice, the surface dynamics should be different since the surface material would be harder than the regolith. Therefore, a subsurface layer of ice could cause a lower d/D ratio, as observed of craters containing PSRs. Furthermore, the flatter average slopes on craters containing PSRs coincide with McClanahan et al. [4], who observed that craters with an average wall slope of less than 20° are more likely to bound ice on the surface. Accordingly, if a layer of ice were present in these regions, we would expect the d/D ratio and the crater topography between the populations to be as distinguishable as we observed. However, different states of diffusive degradation due to crater age could show a similar effect (Fassett et al. [58]). If geologic units on craters containing PSRs would be significantly older, we would also expect lower d/D ratios and shallower crater slopes. However, since PSRs in the RoI are not located on unambiguously distinguishable geologic units, we can not study the effect of different degradation states on our interpretations using the given method. This would require further investigation and a detailed geologic analysis of the area.
As some craters containing PSRs might have temperatures not rising above the water ice sublimation temperature (110K), and they have, on average, a slope below the angle of repose, if any water ice exists, those craters fulfilling these constraints have the best morphological conditions to harbor water ice. However, according to the derived temperature maps from Paige et al. [10], the majority of the craters within the studied RoI are located in an area with temperatures, on average, that are above the water ice sublimation temperature. As the spatial resolution of Diviner ranges from 200 m to 1.3 km, small craters with PSRs might not be included in the map from Paige et al. [10]. Using the derived Diviner temperatures as a proxy in the crater diameter ranges used in this study is not sufficient enough to discard the craters containing PSRs as not suitable for harboring water ice. Therefore, the majority of the analyzed craters can be candidates for harboring water ice in its interior.
We also considered a possible bias of the results caused by secondary craters. However, it is challenging to unambiguously distinguish between primary and secondary craters in this region because secondaries do not appear in apparent clusters or rays. As we excluded an area encompassing two large impact structures from the analysis, a randomness analysis would most likely indicate a non-random crater distribution, even if no contamination was present. Since we assume that possible contamination by secondaries would affect craters containing PSRs and craters not containing PSRs to a similar degree and we observe d/D ratios between both populations are statistically distinguishable, we conclude that secondary contamination only marginally affects the results.
The analyzed area has been proposed as a candidate landing area for several missions, both from agencies and the private sector. The possibility of accessing a water ice source could lead, for example, to permanent lunar bases or refueling options. Moreover, as the craters containing PSRs are shallower with a slope that is generally below the maximum operational slope of a rover (<25°), this makes the analyzed craters perfect candidates for an In-Situ Resource Utilization (ISRU) mission.
5. Conclusions
- We analyzed the d/D ratio of 753 craters with a diameter between 200 and 1000 m and a slope smaller than 25° at the lunar south pole and groupped the craters in two groups: Craters containing PSRs and without PSRs;
- d/D ratios of craters containing PSRs vs. without PSRs, cluster in two distinct groups, which implies that the two groups might have some geomorphological differences;
- The results from the Mann–Whitney U statistical test support the hypothesis that two distinct groups exist;
- Possible secondary craters contamination will affect both crater population, therefore the contamination will only marginally affect the global results;
- The difference in d/D ratios can be caused by a subsurface ice layer present within the PSRs. However, we cannot discard the influence of diffusive crater degradation or different geological units.
Author Contributions
Conceptualization, R.M.F. and A.P.R.; methodology, R.M.F. and C.R.; software, R.M.F.; validation, R.M.F., C.R., A.P.R. and V.U.; formal analysis, R.M.F. and C.R.; investigation, R.M.F., C.R. and A.P.R.; resources, A.P.R.; data curation, R.M.F.; writing—original draft preparation, R.M.F.; writing—review and editing, R.M.F., C.R., A.P.R. and V.U.; visualization, R.M.F.; supervision, A.P.R.; project administration, A.P.R.; funding acquisition, A.P.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 654367 (EarthServer-2).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Craters Data and script for the statistical test are available at https://zenodo.org/record/5779260, accessed on 15 December 2021. PSR data is available at https://zenodo.org/record/5777265, accessed on 15 December 2021, and TUB-Light software is available at https://zenodo.org/record/5777269, accessed on 15 December 2021.
Acknowledgments
Christian Riedel was supported by Deutsche Forschungsgemeinschaft’s SFB-TRR 170-A03 and SFB 1294-Z03 projects. We thank Philipp Gläser for providing the DTM used in this study as well as very constructive discussions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Watson, K.; Murray, B.C.; Brown, H. The behavior of volatiles on the lunar surface. J. Geophys. Res. 1961, 66, 3033–3045. [Google Scholar] [CrossRef]
- Arnold, J.R. Ice in the lunar polar regions. J. Geophys. Res. 1979, 84, 5659. [Google Scholar] [CrossRef]
- Nozette, S.; Spudis, P.D.; Robinson, M.S.; Bussey, D.B.J.; Lichtenberg, C.; Bonner, R. Integration of Lunar Polar Remote-Sensing Data Sets: Evidence for Ice at the Lunar South Pole. J. Geophys. Res. 2001, 106, 253–266. [Google Scholar] [CrossRef]
- McClanahan, T.; Mitrofanov, I.; Boynton, W.; Chin, G.; Bodnarik, J.; Droege, G.; Evans, L.; Golovin, D.; Hamara, D.; Harshman, K.; et al. Evidence for the sequestration of hydrogen-bearing volatiles towards the Moon’s southern pole-facing slopes. Icarus 2015, 255, 88–99. [Google Scholar] [CrossRef]
- Susorney, H.C.; Ernst, C.M.; Chabot, N.L.; Deutsch, A.N.; Barnouin, O.S. Morphometry and Temperature of Simple Craters in Mercury’s Northern Hemisphere: Implications for Stability of Water Ice. Planet. Sci. J. 2021, 2, 97. [Google Scholar] [CrossRef]
- Eke, V.R.; Bartram, S.A.; Lane, D.A.; Smith, D.; Teodoro, L.F. Lunar polar craters—Icy, rough or just sloping? Icarus 2014, 241, 66–78. [Google Scholar] [CrossRef][Green Version]
- Haruyama, J.; Ohtake, M.; Matsunaga, T.; Morota, T.; Honda, C.; Yokota, Y.; Pieters, C.M.; Hara, S.; Hioki, K.; Saiki, K.; et al. Lack of Exposed Ice Inside Lunar South Pole Shackleton Crater. Science 2008, 322, 938–939. [Google Scholar] [CrossRef] [PubMed]
- Kokhanov, A.A.; Kreslavsky, M.A.; Karachevtseva, I.P. Small impact craters in the polar regions of the Moon: Peculiarities of morphometric characteristics. Sol. Syst. Res. 2015, 49, 295–302. [Google Scholar] [CrossRef]
- Rubanenko, L.; Venkatraman, J.; Paige, D.A. Thick ice deposits in shallow simple craters on the Moon and Mercury. Nat. Geosci. 2019, 12, 597–601. [Google Scholar] [CrossRef]
- Paige, D.A.; Siegler, M.A.; Zhang, J.A.; Hayne, P.O.; Foote, E.J.; Bennett, K.A.; Vasavada, A.R.; Greenhagen, B.T.; Schofield, J.T.; McCleese, D.J.; et al. Diviner Lunar Radiometer Observations of Cold Traps in the Moon’s South Polar Region. Science 2010, 330, 479–482. [Google Scholar] [CrossRef]
- Mitrofanov, I.G.; Sanin, A.B.; Boynton, W.V.; Chin, G.; Garvin, J.B.; Golovin, D.; Evans, L.G.; Harshman, K.; Kozyrev, A.S.; Litvak, M.L.; et al. Hydrogen Mapping of the Lunar South Pole Using the LRO Neutron Detector Experiment LEND. Science 2010, 330, 483–486. [Google Scholar] [CrossRef]
- Fisher, E.A.; Lucey, P.G.; Lemelin, M.; Greenhagen, B.T.; Siegler, M.A.; Mazarico, E.; Aharonson, O.; Williams, J.-P.; Hayne, P.O.; Neumann, G.A.; et al. Evidence for surface water ice in the lunar polar regions using reflectance measurements from the Lunar Orbiter Laser Altimeter and temperature measurements from the Diviner Lunar Radiometer Experiment. Icarus 2017, 292, 74–85. [Google Scholar] [CrossRef]
- Sanin, A.B.; Mitrofanov, I.G.; Litvak, M.L.; Malakhov, A.; Boynton, W.V.; Chin, G.; Droege, G.; Evans, L.G.; Garvin, J.; Golovin, D.V.; et al. Testing lunar permanently shadowed regions for water ice: LEND results from LRO. J. Geophys. Res. Planets 2012, 117, E12. [Google Scholar] [CrossRef]
- Sanin, A.; Mitrofanov, I.; Litvak, M.; Bakhtin, B.; Bodnarik, J.; Boynton, W.; Chin, G.; Evans, L.; Harshman, K.; Fedosov, F.; et al. Hydrogen distribution in the lunar polar regions. Icarus 2017, 283, 20–30. [Google Scholar] [CrossRef]
- Hayne, P.O.; Hendrix, A.; Sefton-Nash, E.; Siegler, M.A.; Lucey, P.G.; Retherford, K.D.; Williams, J.-P.; Greenhagen, B.T.; Paige, D.A. Evidence for exposed water ice in the Moon’s south polar regions from Lunar Reconnaissance Orbiter ultraviolet albedo and temperature measurements. Icarus 2015, 255, 58–69. [Google Scholar] [CrossRef]
- Spudis, P.; Bussey, D.; Baloga, S.; Cahill, J.; Glaze, L.; Patterson, G.; Raney, R.; Thompson, T.; Thomson, B.; Ustinov, E. Evidence for water ice on the Moon: Results for anomalous polar craters from the LRO Mini-RF imaging radar. J. Geophys. Res. Planets 2013, 118, 2016–2029. [Google Scholar] [CrossRef]
- Campbell, B.; Campbell, D.; Ler, J.; Hine, A.; Nolan, M.; Perillat, P. Radar imaging of the lunar poles. Nature 2003, 426, 137–138. [Google Scholar] [CrossRef] [PubMed]
- Thomson, B.J.; Bussey, D.B.J.; Neish, C.D.; Cahill, J.T.S.; Heggy, E.; Kirk, R.L.; Patterson, G.W.; Raney, R.K.; Spudis, P.D.; Thompson, T.W.; et al. An upper limit for ice in Shackleton crater as revealed by LRO Mini-RF orbital radar. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Harmon, J.K.; Slade, M.A.; Vélez, R.A.; Crespo, A.; Dryer, M.J.; Johnson, J.M. Radar mapping of Mercury’s polar anomalies. Nature 1994, 369, 213–215. [Google Scholar] [CrossRef]
- Ostro, S.J.; Campbell, D.B.; Simpson, R.A.; Hudson, R.S.; Chandler, J.F.; Rosema, K.D.; Shapiro, I.I.; Standish, E.M.; Winkler, R.; Yeomans, D.K.; et al. Europa, Ganymede, and Callisto: New radar results from Arecibo and Goldstone. J. Geophys. Res. 1992, 97, 227. [Google Scholar] [CrossRef]
- Baloga, S.M.; Glaze, L.S.; Spudis, P.D. Inferred Lunar Boulder Distributions at Decimeter Scales. In Proceedings of the 43rd Lunar and Planetary Science Conference, Woodlands, TX, USA, 19–23 March 2012; LPI Contribution No. 1659, id.1647. Volume 43. [Google Scholar]
- Raney, R.K.; Cahill, J.T.S.; Patterson, G.W.; Bussey, D.B.J. The m-chi decomposition of hybrid dual-polarimetric radar data with application to lunar craters. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef]
- Stokes, G.G. On the Composition and Resolution of Streams of Polarized Light from different Sources. Trans. Camb. Philos. Soc. 1851, 9, 399. [Google Scholar]
- Raney, R.K.; Cahill, J.T.S.; Patterson, G.W.; Bussey, D.B.J.; Team, M.-R. Characterization of Lunar Craters Using M-Chi Decompositions of Mini-RF Radar Data. In Proceedings of the 43rd Lunar and Planetary Science Conference, Woodlands, TX, USA, 19–23 March 2012; LPI Contribution No. 1659, id.2676. Volume 43. [Google Scholar]
- Pieters, C.M.; Boardman, J.; Buratti, B.; Chatterjee, A.; Clark, R.; Glavich, T.; Green, R.; Head Iii, J.; Isaacson, P.; Malaret, E.; et al. The Moon Mineralogy Mapper (M 3) on Chandrayaan-1. Curr. Sci. 2009, 96. [Google Scholar] [CrossRef]
- Li, S.; Lucey, P.G.; Milliken, R.E.; Hayne, P.O.; Fisher, E.; Williams, J.P.; Hurley, D.M.; Elphic, R.C. Direct evidence of surface exposed water ice in the lunar polar regions. Proc. Natl. Acad. Sci. USA 2018, 115, 8907–8912. [Google Scholar] [CrossRef] [PubMed]
- McCord, T.B.; Taylor, L.A.; Combe, J.-P.; Kramer, G.; Pieters, C.M.; Sunshine, J.M.; Clark, R.N. Sources and physical processes responsible for OH/H2O in the lunar soil as revealed by the Moon Mineralogy Mapper (M3). J. Geophys. Res. 2011, 116, E00G05. [Google Scholar] [CrossRef]
- Combe, J.; Mccord, T.B.; Hayne, P.O.; Paige, D.A. Mapping of Lunar Volatiles with Moon Mineralogy Mapper Spectra: A Challenge Due to Thermal Emission. In EPSC Abstracts Vol. 6, EPSC-DPS2011-1644. 2011, pp. 8–9. Available online: https://meetingorganizer.copernicus.org/EPSC-DPS2011/EPSC-DPS2011-1644.pdf (accessed on 5 November 2021).
- Clark, R.; Pieters, C.M.; Green, R.O.; Science, T.M. Thermal removal from moon mineralogy mapper (M3) data. In Proceedings of the 40th Lunar and Planetary Science Conference, Woodlands, TX, USA, 23–27 March 2009. [Google Scholar]
- Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T.; Torrence, M.H. Illumination conditions of the lunar polar regions using LOLA topography. Icarus 2011, 211, 1066–1081. [Google Scholar] [CrossRef]
- Zuber, M.T.; Head, J.W.; Smith, D.E.; Neumann, G.A.; Mazarico, E.; Torrence, M.H.; Aharonson, O.; Tye, A.R.; Fassett, C.I.; Rosenburg, M.A.; et al. Constraints on the volatile distribution within Shackleton crater at the lunar south pole. Nature 2012, 486, 378–381. [Google Scholar] [CrossRef]
- Kereszturi, A.; Steinmann, V. Characteristics of small young lunar impact craters focusing on current production and degradation on the Moon. Planet. Space Sci. 2017, 148, 12–27. [Google Scholar] [CrossRef]
- Daubar, I.J.; Atwood-Stone, C.; Byrne, S.; McEwen, A.S.; Russell, P.S. The morphology of small fresh craters on Mars and the Moon. J. Geophys. Res. Planets 2014, 119, 2620–2639. [Google Scholar] [CrossRef]
- Stopar, J.D.; Robinson, M.S.; Speyerer, E.J.; Burns, K.; Gengl, H. Regolith characterization using lroc nac digital elevation models of small lunar craters. In Proceedings of the 43rd Lunar and Planetary Science Conference, Woodlands, TX, USA, 19–23 March 2012. [Google Scholar]
- Lagain, A.; Benedix, G.K.; Servis, K.; Baratoux, D.; Doucet, L.S.; Rajšic, A.; Devillepoix, H.A.R.; Bland, P.A.; Towner, M.C.; Sansom, E.K.; et al. The Tharsis mantle source of depleted shergottites revealed by 90 million impact craters. Nat. Commun. 2021, 12, 6352. [Google Scholar] [CrossRef]
- Craddock, R.A.; Howard, A.D. Simulated degradation of lunar impact craters and a new method for age dating farside mare deposits. J. Geophys. Res. Planets 2000, 105, 20387–20401. [Google Scholar] [CrossRef]
- Robbins, S.J.; Watters, W.A.; Chappelow, J.E.; Bray, V.J.; Daubar, I.J.; Craddock, R.A.; Beyer, R.A.; Landis, M.; Ostrach, L.R.; Tornabene, L.; et al. Measuring impact crater depth throughout the solar system. Meteorit. Planet. Sci. 2018, 53, 583–637. [Google Scholar] [CrossRef]
- Elachi, C.; Kobrick, M.; Roth, L.; Tiernan, M.; Brown, W.E. Local lunar topography from the Apollo 17 Alse radar imagery and altimetry. Moon 1976, 15, 119–131. [Google Scholar] [CrossRef]
- Schultz, P.H.; Gault, D.; Greeley, R. Interpreting statistics of small lunar craters. In Proceedings of the Lunar Science Conference, Houston, TX, USA, 14–18 March 1977; Proceedings Volume 3. (A78-41551 18-91). Pergamon Press, Inc.: New York, NY, USA, 1977; Volume 8, pp. 3539–3564. [Google Scholar]
- Stopar, J.D.; Robinson, M.S.; Barnouin, O.S.; McEwen, A.S.; Speyerer, E.J.; Henriksen, M.R.; Sutton, S.S. Relative depths of simple craters and the nature of the lunar regolith. Icarus 2017, 298, 34–48. [Google Scholar] [CrossRef]
- Boyce, J.M.; Mouginis-Mark, P.; Garbeil, H. Ancient oceans in the northern lowlands of Mars: Evidence from impact crater depth/diameter relationships. J. Geophys. Res. Planets 2005, 110. [Google Scholar] [CrossRef]
- De Rosa, D.; Bussey, B.; Cahill, J.T.; Lutz, T.; Crawford, I.A.; Hackwill, T.; Gasselt, S.V.; Neukum, G.; Witte, L.; McGovern, A.; et al. Characterisation of potential landing sites for the European Space Agency’s Lunar Lander project. Planet. Space Sci. 2012, 74, 224–246. [Google Scholar] [CrossRef]
- Kokhanov, A.; Karachevtseva, I.; Zubarev, A.; Patraty, V.; Rodionova, Z.; Oberst, J. Mapping of potential lunar landing areas using LRO and SELENE data. Planet. Space Sci. 2017. [Google Scholar] [CrossRef]
- Lemelin, M.; Blair, D.M.; Roberts, C.E.; Runyon, K.D.; Nowka, D.; Kring, D.A. High-priority lunar landing sites for in situ and sample return studies of polar volatiles. Planet. Space Sci. 2014, 101, 149–161. [Google Scholar] [CrossRef]
- Robinson, M.; Brylow, S.; Tschimmel, M.; Humm, D.; Lawrence, S.; Thomas, P.; Denevi, B.; Bowman-cisneros, E.; Zerr, J.; Ravine, M.; et al. Lunar Reconnaissance Orbiter Camera (LROC) Instrument Overview. Space Sci. Rev. 2010, 150, 81–124. [Google Scholar] [CrossRef]
- Gläser, P.; Scholten, F.; De Rosa, D.; Marco Figuera, R.; Oberst, J.; Mazarico, E.; Neumann, G.A.; Robinson, M.S. Illumination conditions at the lunar south pole using high resolution digital terrain models from lola. Icarus 2014, 243, 78–90. [Google Scholar] [CrossRef]
- Barker, M.; Mazarico, E.; Neumann, G.; Zuber, M.; Haruyama, J.; Smith, D. A new lunar digital elevation model from the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. Icarus 2016, 273, 346–355. [Google Scholar] [CrossRef]
- Gläser, P.; Haase, I.; Oberst, J.; Neumann, G. Co-registration of laser altimeter tracks with digital terrain models and applications in planetary science. Planet. Space Sci. 2013, 89, 111–117. [Google Scholar] [CrossRef]
- Bussey, D.B.J.; McGovern, J.A.; Spudis, P.D.; Neish, C.D.; Noda, H.; Ishihara, Y.; Sørensen, S.A. Illumination conditions of the south pole of the Moon derived using Kaguya topography. Icarus 2010, 208, 558–564. [Google Scholar] [CrossRef]
- Noda, H.; Araki, H.; Goossens, S.; Ishihara, Y.; Matsumoto, K.; Tazawa, S.; Kawano, N.; Sasaki, S. Illumination conditions at the lunar polar regions by KAGUYA(SELENE) laser altimeter. Geophys. Res. Lett. 2008, 35, L24203. [Google Scholar] [CrossRef]
- Marco Figuera, R. Analysis of Illumination Conditions at the Lunar South Pole Using Parallel Computing Techniques. Master’s Thesis, Technische Universität Berlin, Berlin, Germany, 2014. [Google Scholar]
- Marco Figuera, R.; Gläser, P.; Oberst, J.; De Rosa, D. Calculation of illumination conditions at the lunar south pole—Parallel programming approach. In Proceedings of the European Planetary Science Congress 2014, Cascais, Portugal, 7–12 September 2014; Volume 9, p. EPSC2014-476. [Google Scholar]
- Chappelow, J.E. Simple impact crater shape determination from shadows. Meteorit. Planet. Sci. 2013, 48, 1863–1872. [Google Scholar] [CrossRef]
- Christensen, P.R.; Engle, E.; Anwar, S.; Dickenshied, S.; Noss, D.; Gorelick, N.; Weiss-Malik, M. JMARS—A Planetary GIS. In Proceedings of the American Geophysical Union, Fall Meeting 2009, San Francisco, CA, USA, 13–18 December 2009; Available online: https://ui.adsabs.harvard.edu/abs/2009AGUFMIN22A..06C/abstract (accessed on 5 November 2021).
- Kneissl, T.; van Gasselt, S.; Neukum, G. Map-projection-independent crater size-frequency determination in GIS environments—New software tool for ArcGIS. Planet. Space Sci. 2011, 59, 1243–1254. [Google Scholar] [CrossRef]
- Michael, G.; Neukum, G. Planetary surface dating from crater size–frequency distribution measurements: Partial resurfacing events and statistical age uncertainty. Earth Planet. Sci. Lett. 2010, 294, 223–229. [Google Scholar] [CrossRef]
- Robbins, S.; Antonenko, I.; Kirchoff, M.; Chapman, C.; Fassett, C.; Herrick, R.; Singer, K.; Zanetti, M.; Lehan, C.; Huang, D.; et al. The variability of crater identification among expert and community crater analysts. Icarus 2014, 234, 109–131. [Google Scholar] [CrossRef]
- Fassett, C.; Thomson, B. Crater degradation on the lunar maria: Topographic diffusion and the rate of erosion on the Moon. J. Geophys. Res. Planets 2014, 119, 2255–2271. [Google Scholar] [CrossRef]
- MacFarland, T.W.; Yates, J.M. Mann–Whitney U Test. In Introduction to Nonparametric Statistics for the Biological Sciences Using R; Springer: Berlin/Heidelberg, Germany, 2016; pp. 103–132. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).