The Joint Assimilation of Remotely Sensed Leaf Area Index and Surface Soil Moisture into a Land Surface Model
Abstract
:1. Introduction
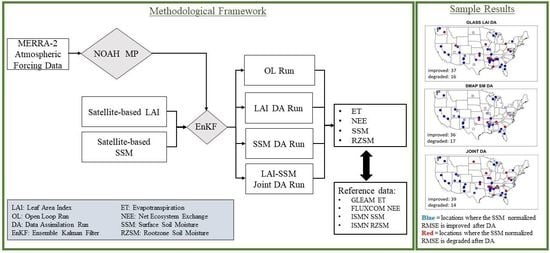
2. Materials and Methods
2.1. The Noah-MP Land Surface Model
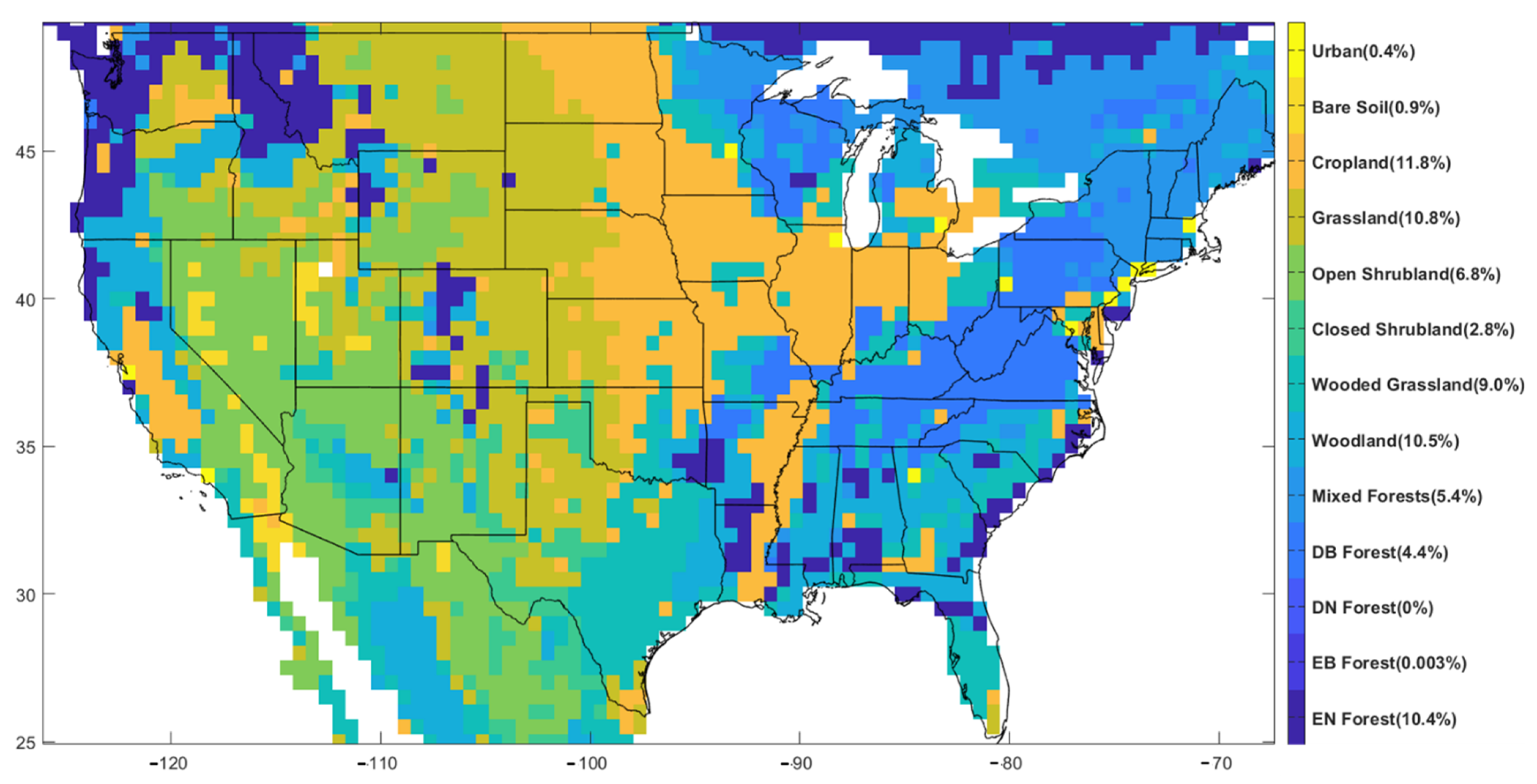
2.2. Satellite-Based Observations
2.3. Validation Dataset
2.4. The Data Assimilation System
2.5. System Evaluation
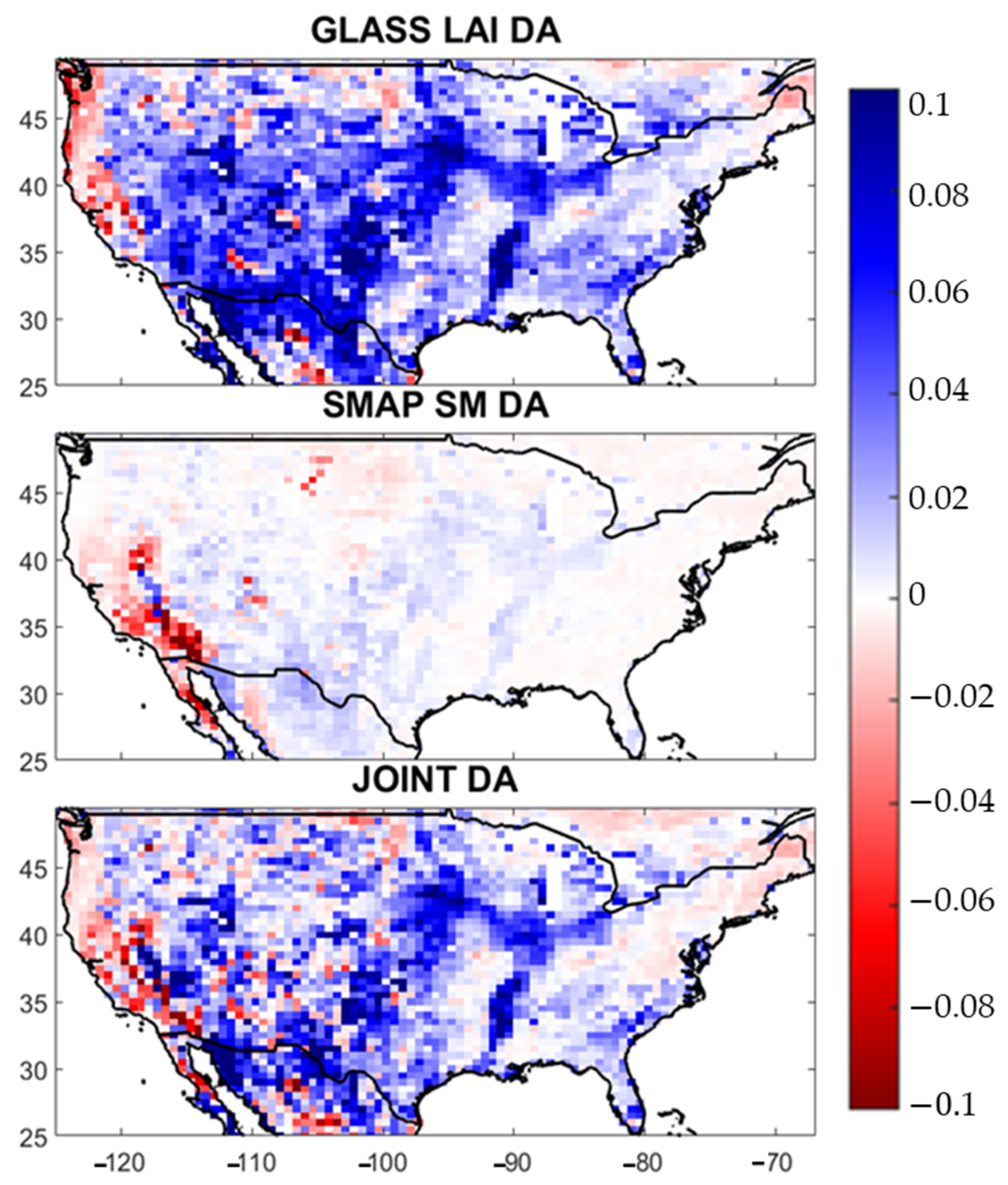
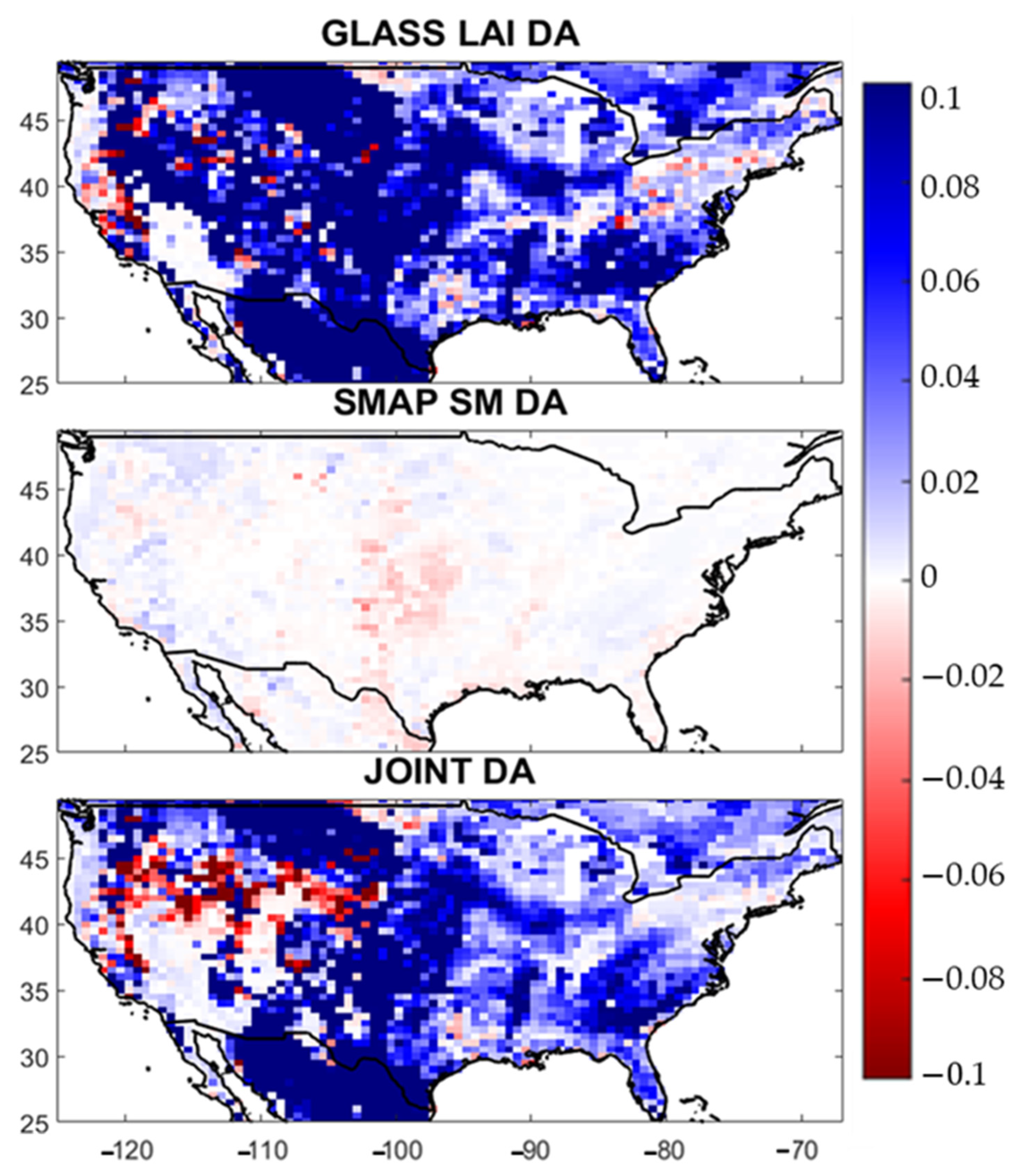
3. Results
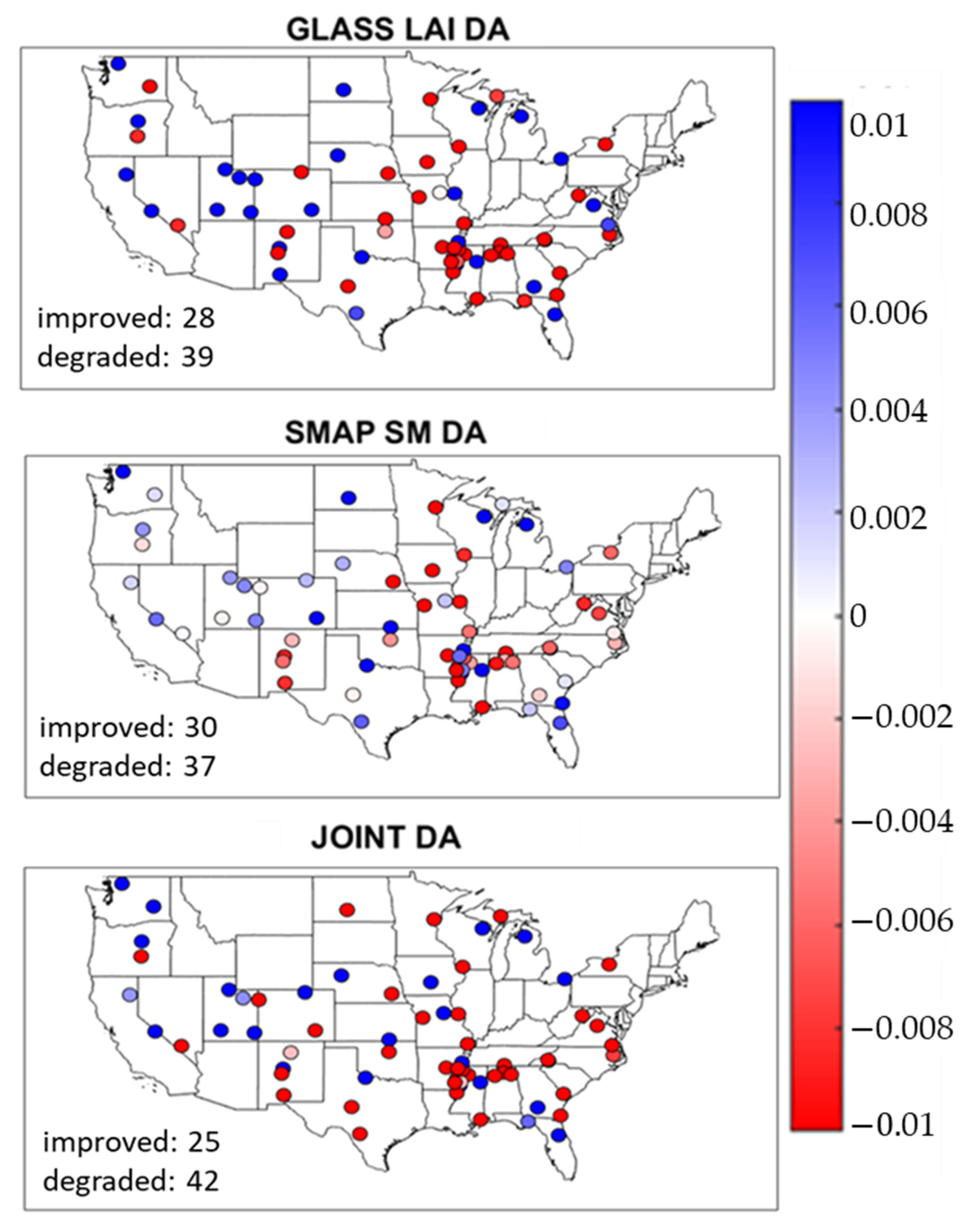
3.1. Impact of Data Assimilation
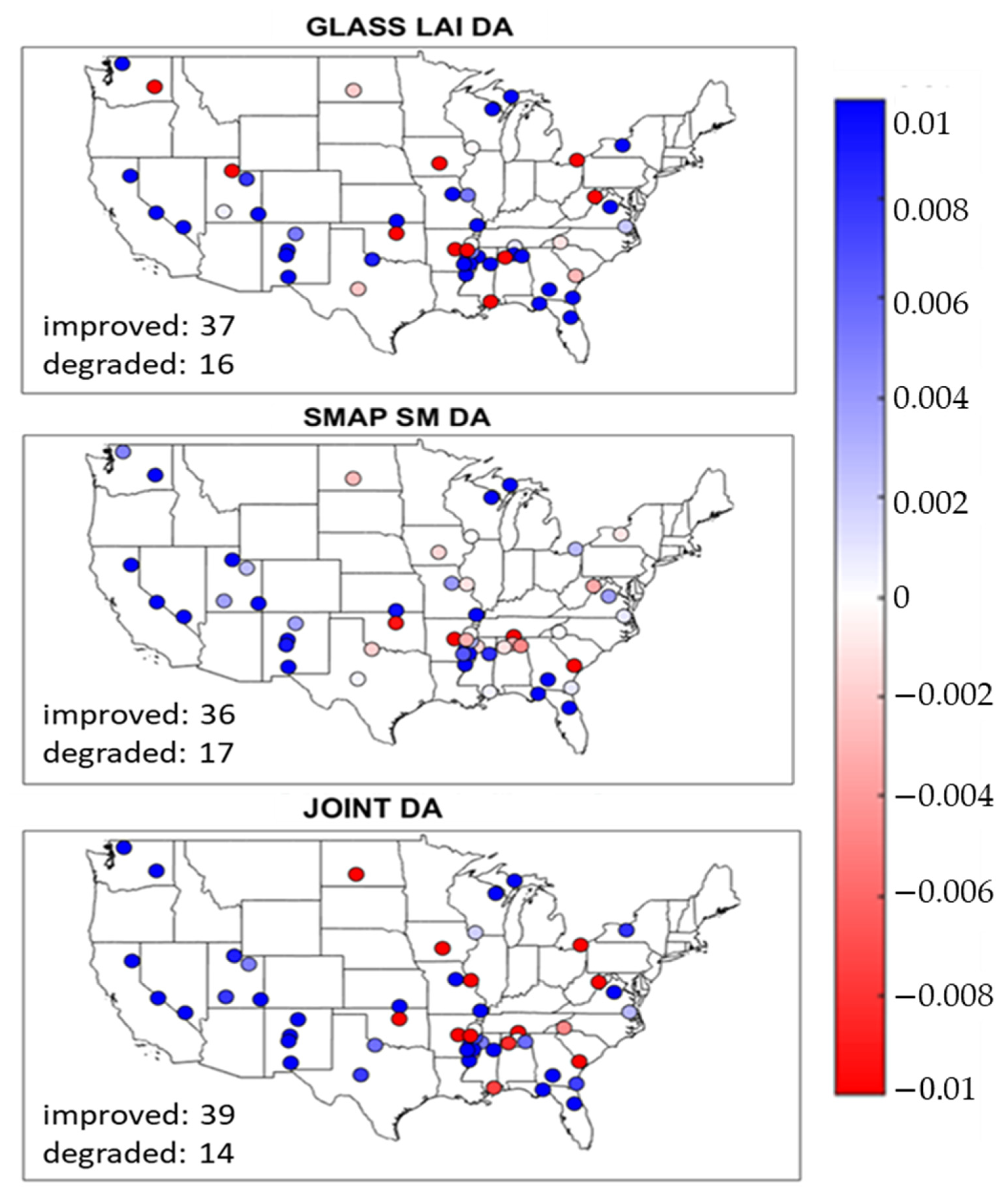
3.2. Validation of ET
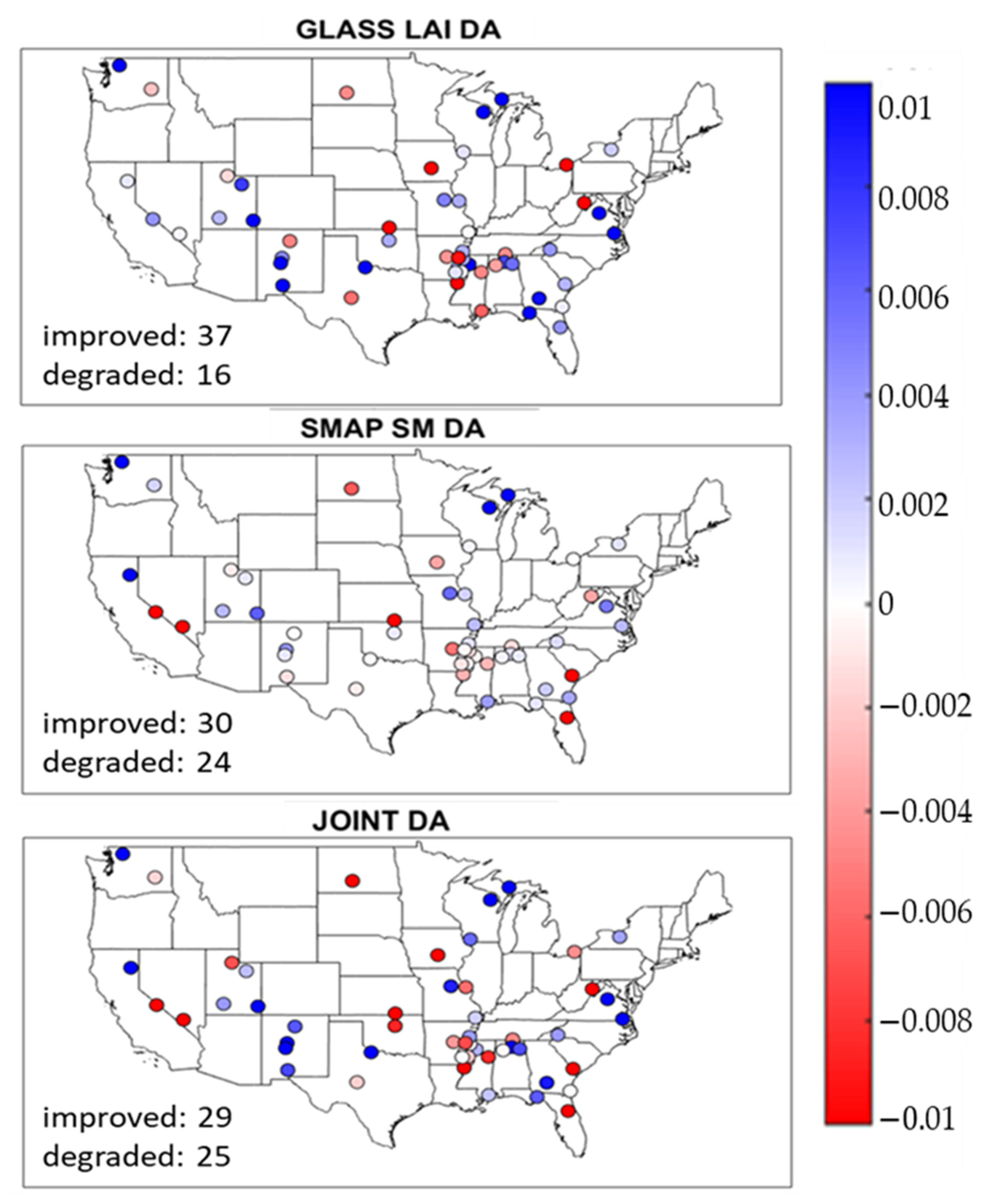
3.3. Validation of NEE
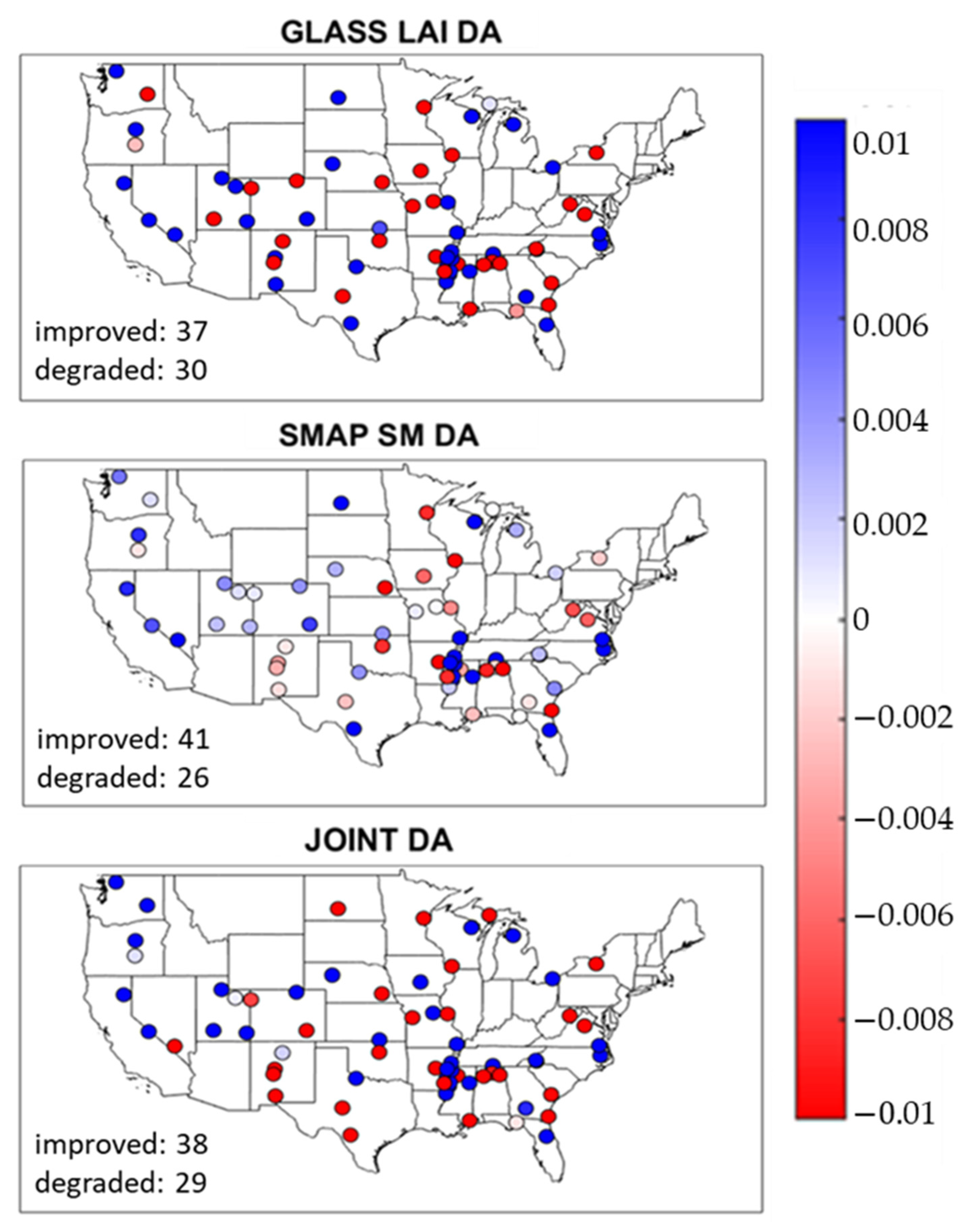
3.4. Validation of Soil Moisture
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumi-Boateng, B.; Mireku-Gyimah, D.; Duker, A.A. A Spatio-Temporal Based Estimation of Vegetation Changes in the Tarkwa Mining Area of Ghana. Res. J. Environ. Earth Sci. 2012, 4, 215–229. [Google Scholar]
- Betts, A.K.; Ball, J.H. FIFE Surface Climate and Site-Average Dataset 1987–89. J. Atmos. Sci. 1998, 55, 1091–1108. [Google Scholar] [CrossRef] [Green Version]
- Maggioni, V.; Houser, P.R. Soil Moisture Data Assimilation. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications; Springer: Berlin, Germany, 2017; Volume 3, pp. 195–217. [Google Scholar]
- Wullschleger, S.D.; Epstein, H.E.; Box, E.O.; Euskirchen, E.S.; Goswami, S.; Iversen, C.M.; Kattge, J.; Norby, R.J.; van Bodegom, P.M.; Xu, X. Plant functional types in Earth system models: Past experiences and future directions for application of dynamic vegetation models in high-latitude ecosystems. Ann. Bot. 2014, 114, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Clark, D.B.; Mercado, L.M.; Sitch, S.; Jones, C.D.; Gedney, N.; Best, M.J.; Pryor, M.; Rooney, G.G.; Essery, R.L.H.; Blyth, E.; et al. The Joint UK Land Environment Simulator (JULES), model description—Part 2: Carbon fluxes and vegetation dynamics. Geosci. Model Dev. 2011, 4, 701–722. [Google Scholar] [CrossRef] [Green Version]
- Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G.; et al. The Common Land Model. Bull. Am. Meteorol. Soc. 2003, 84, 1013–1024. [Google Scholar] [CrossRef] [Green Version]
- Niu, G.-Y.; Yang, Z.-L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Bonan, B.; Albergel, C.; Zheng, Y.; Barbu, A.L.; Fairbairn, D.; Munier, S.; Calvet, J.-C. An Ensemble Square Root Filter for the Joint Assimilation of Surface Soil Moiture and Leaf Area Index within LDAS-Monde: Application over the Euro-Mediterranean Region. Hydrol. Earth Syst. Sci. 2020, 24, 325–347. [Google Scholar] [CrossRef] [Green Version]
- Rahman, A.; Zhang, X.; Xue, Y.; Houser, P.; Sauer, T.; Kumar, S.; Mocko, D.; Maggioni, V. A synthetic experiment to investigate the potential of assimilating LAI through direct insertion in a land surface model. J. Hydrol. X 2020, 9, 100063. [Google Scholar] [CrossRef]
- Rees, W.G.; Danks, F.S. Derivation and assessment of vegetation maps for reindeer pasture analysis in Arctic European Russia. Polar Rec. 2007, 43, 290–304. [Google Scholar] [CrossRef]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Reichle, R.H. Data assimilation methods in the Earth sciences. Adv. Water Resour. 2008, 31, 1411–1418. [Google Scholar] [CrossRef]
- Reichle, R.H.; Crow, W.T.; Keppenne, C.L. An adaptive ensemble Kalman filter for soil moisture data assimilation: Adaptive ensemble filter for soil moisture assimilation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 1994, 99, 10143. [Google Scholar] [CrossRef]
- García-Pintado, J.; Neal, J.C.; Mason, D.C.; Dance, S.L.; Bates, P.D. Scheduling satellite-based SAR acquisition for sequential assimilation of water level observations into flood modelling. J. Hydrol. 2013, 495, 252–266. [Google Scholar] [CrossRef] [Green Version]
- Reichle, R.H.; Walker, J.P.; Koster, R.D.; Houser, P.R. Extended versus Ensemble Kalman Filtering for Land Data Assimilation. J. Hydrometeorol. 2002, 3, 728–740. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Koster, R.D.; Guo, Z.; Yang, R.; Dirmeyer, P.A.; Mitchell, K.; Puma, M.J. On the Nature of Soil Moisture in Land Surface Models. J. Clim. 2009, 22, 4322–4335. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.V.; Reichle, R.H.; Peters-Lidard, C.D.; Koster, R.D.; Zhan, X.; Crow, W.T.; Eylander, J.B.; Houser, P.R. A land surface data assimilation framework using the land information system: Description and applications. Adv. Water Resour. 2008, 31, 1419–1432. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Mocko, D.; Reichle, R.; Liu, Y.; Arsenault, K.R.; Xia, Y.; Ek, M.; Riggs, G.; Livneh, B.; et al. Assimilation of Remotely Sensed Soil Moisture and Snow Depth Retrievals for Drought Estimation. J. Hydrometeorol. 2014, 15, 2446–2469. [Google Scholar] [CrossRef]
- Leach, J.M.; Coulibaly, P. Soil moisture assimilation in urban watersheds: A method to identify the limiting imperviousness threshold based on watershed characteristics. J. Hydrol. 2020, 587, 124958. [Google Scholar] [CrossRef]
- Lievens, H.; Tomer, S.K.; Al Bitar, A.; De Lannoy, G.J.M.; Drusch, M.; Dumedah, G.; Hendricks Franssen, H.-J.; Kerr, Y.H.; Martens, B.; Pan, M.; et al. SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia. Remote Sens. Environ. 2015, 168, 146–162. [Google Scholar] [CrossRef]
- Kumar, S.V.; Mocko, D.M.; Wang, S.; Peters-Lidard, C.D.; Borak, J. Assimilation of remotely sensed Leaf Area Index into the Noah-MP land surface model: Impacts on water and carbon fluxes and states over the Continental U.S. J. Hydrometeorol. 2019, 20, 1359–1377. [Google Scholar] [CrossRef]
- Ling, X.L.; Fu, C.B.; Guo, W.D.; Yang, Z.-L. Assimilation of Remotely Sensed LAI Into CLM4CN Using DART. J. Adv. Model. Earth Syst. 2019, 11, 2768–2786. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Maggioni, V.; Rahman, A.; Houser, P.; Xue, Y.; Sauer, T.; Kumar, S.; Mocko, D. The influence of assimilating leaf area index in a land surface model on global water fluxes and storages. Hydrol. Earth Syst. Sci. 2020, 24, 3775–3788. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, P.; Sun, H.; Zhang, S.; Li, L. Assimilation of Leaf Area Index and Surface Soil Moisture With the CERES-Wheat Model for Winter Wheat Yield Estimation Using a Particle Filter Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1303–1316. [Google Scholar] [CrossRef]
- Pan, H.; Chen, Z.; de Wit, A.; Ren, J. Joint Assimilation of Leaf Area Index and Soil Moisture from Sentinel-1 and Sentinel-2 Data into the WOFOST Model for Winter Wheat Yield Estimation. Sensors 2019, 19, 3161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Albergel, C.; Calvet, J.-C.; Gibelin, A.-L.; Lafont, S.; Roujean, J.-L.; Berne, C.; Traullé, O.; Fritz, N. Observed and modelled ecosystem respiration and gross primary production of a grassland in southwestern France. Biogeosciences 2010, 7, 1657–1668. [Google Scholar] [CrossRef] [Green Version]
- Noilhan, J.; Mahfouf, J.-F. The ISBA land surface parameterisation scheme. Glob. Planet. Chang. 1996, 13, 145–159. [Google Scholar] [CrossRef]
- Albergel, C.; Zheng, Y.; Bonan, B.; Dutra, E.; Rodríguez-Fernández, N.; Munier, S.; Draper, C.; de Rosnay, P.; Muñoz-Sabater, J.; Balsamo, G.; et al. Data assimilation for continuous global assessment of severe conditions over terrestrial surfaces. Hydrol. Earth Syst. Sci. 2020, 24, 4291–4316. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L. An observation-based formulation of snow cover fraction and its evaluation over large North American river basins. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Ball, J.T.; Woodrow, I.E.; Berry, J.A. A Model Predicting Stomatal Conductance and its Contribution to the Control of Photosynthesis under Different Environmental Conditions. In Progress in Photosynthesis Research; Biggins, J., Ed.; Springer: Dordrecht, The Netherlands, 1987; pp. 221–224. ISBN 978-94-017-0521-9. [Google Scholar]
- Niu, G.-Y.; Yang, Z.-L. Effects of vegetation canopy processes on snow surface energy and mass balances: CANOPY EFFECTS ON SNOW PROCESSES. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Kumar, S.; Peterslidard, C.; Tian, Y.; Houser, P.; Geiger, J.; Olden, S.; Lighty, L.; Eastman, J.; Doty, B.; Dirmeyer, P. Land information system: An interoperable framework for high resolution land surface modeling. Environ. Model. Softw. 2006, 21, 1402–1415. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product From Time-Series MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Sadri, S.; Pan, M.; Wada, Y.; Vergopolan, N.; Sheffield, J.; Famiglietti, J.S.; Kerr, Y.; Wood, E. A global near-real-time soil moisture index monitor for food security using integrated SMOS and SMAP. Remote Sens. Environ. 2020, 246, 111864. [Google Scholar] [CrossRef]
- ONeill, P. SMAP L2 Radiometer Half-Orbit 36 km EASE-Grid Soil Moisture. Distrib. Act. Arch. Cent. 2016, 4. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Jiang, S.; Wei, L.; Ren, L.; Xu, C.-Y.; Zhong, F.; Wang, M.; Zhang, L.; Yuan, F.; Liu, Y. Utility of integrated IMERG precipitation and GLEAM potential evapotranspiration products for drought monitoring over mainland China. Atmos. Res. 2021, 247, 105141. [Google Scholar] [CrossRef]
- Jin, X.; Jin, Y. Calibration of a Distributed Hydrological Model in a Data-Scarce Basin Based on GLEAM Datasets. Water 2020, 12, 897. [Google Scholar] [CrossRef] [Green Version]
- Birch, L.; Schwalm, C.R.; Natali, S.; Lombardozzi, D.; Keppel-Aleks, G.; Watts, J.; Lin, X.; Zona, D.; Oechel, W.; Sachs, T.; et al. Addressing biases in Arctic–boreal carbon cycling in the Community Land Model Version 5. Geosci. Model Dev. 2021, 14, 3361–3382. [Google Scholar] [CrossRef]
- Luo, X.; Croft, H.; Chen, J.M.; He, L.; Keenan, T.F. Improved estimates of global terrestrial photosynthesis using information on leaf chlorophyll content. Glob. Chang. Biol. 2019, 25, 2499–2514. [Google Scholar] [CrossRef] [Green Version]
- Brust, C.; Kimball, J.S.; Maneta, M.P.; Jencso, K.; He, M.; Reichle, R.H. Using SMAP Level-4 soil moisture to constrain MOD16 evapotranspiration over the contiguous USA. Remote Sens. Environ. 2021, 255, 112277. [Google Scholar] [CrossRef]
- Feng, X.; Fu, B.; Zhang, Y.; Pan, N.; Zeng, Z.; Tian, H.; Lyu, Y.; Chen, Y.; Ciais, P.; Wang, Y.; et al. Recent leveling off of vegetation greenness and primary production reveals the increasing soil water limitations on the greening Earth. Sci. Bull. 2021, 66, 1462–1471. [Google Scholar] [CrossRef]
- Pascolini-Campbell, M.A.; Reager, J.T.; Fisher, J.B. GRACE-based Mass Conservation as a Validation Target for Basin-Scale Evapotranspiration in the Contiguous United States. Water Resour. Res. 2020, 56, e2019WR026594. [Google Scholar] [CrossRef]
- Jung, M.; Koirala, S.; Weber, U.; Ichii, K.; Gans, F.; Camps-Valls, G.; Papale, D.; Schwalm, C.; Tramontana, G.; Reichstein, M. The FLUXCOM ensemble of global land-atmosphere energy fluxes. Sci. Data 2019, 6, 74. [Google Scholar] [CrossRef] [Green Version]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting carbon dioxide and energy fluxes across global FLUXNET sites withregression algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, W.A.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef] [Green Version]
- Fang, B.; Lakshmi, V.; Bindlish, R.; Jackson, T. AMSR2 Soil Moisture Downscaling Using Temperature and Vegetation Data. Remote Sens. 2018, 10, 1575. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Parinussa, R.M.; Liu, Y.Y.; Johnson, F.M.; Sharma, A. A framework for combining multiple soil moisture retrievals based on maximizing temporal correlation. Geophys. Res. Lett. 2015, 42, 6662–6670. [Google Scholar] [CrossRef]
- Katzfuss, M.; Stroud, J.R.; Wikle, C.K. Understanding the Ensemble Kalman Filter. Am. Stat. 2016, 70, 350–357. [Google Scholar] [CrossRef]
- Pan, M.; Wood, E.F. Data Assimilation for Estimating the Terrestrial Water Budget Using a Constrained Ensemble Kalman Filter. J. Hydrometeorol. 2006, 7, 534–547. [Google Scholar] [CrossRef]
- Reichle, R.H. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef] [Green Version]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Nikolopoulos, E.I.; Anagnostou, E.N.; Quintana-Seguí, P.; Barella-Ortiz, A. A nonparametric statistical technique for combining global precipitation datasets: Development and hydrological evaluation over the Iberian Peninsula. Hydrol. Earth Syst. Sci. 2018, 22, 1371–1389. [Google Scholar] [CrossRef] [Green Version]
- Falck, A.S.; Maggioni, V.; Tomasella, J.; Diniz, F.L.R.; Mei, Y.; Beneti, C.A.; Herdies, D.L.; Neundorf, R.; Caram, R.O.; Rodriguez, D.A. Improving the use of ground-based radar rainfall data for monitoring and predicting floods in the Iguaçu river basin. J. Hydrol. 2018, 567, 626–636. [Google Scholar] [CrossRef]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance Metrics for Soil Moisture Retrievals and Application Requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Han, S.-C.; Yeo, I.-Y.; Dong, J.; Steele-Dunne, S.C.; Willgoose, G.; Walker, J.P. Multivariate data assimilation of GRACE, SMOS, SMAP measurements for improved regional soil moisture and groundwater storage estimates. Adv. Water Resour. 2020, 135, 103477. [Google Scholar] [CrossRef]
- Kolassa, J.; Reichle, R.; Liu, Q.; Cosh, M.; Bosch, D.; Caldwell, T.; Colliander, A.; Holifield Collins, C.; Jackson, T.; Livingston, S.; et al. Data Assimilation to Extract Soil Moisture Information from SMAP Observations. Remote Sens. 2017, 9, 1179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rouf, T.; Girotto, M.; Houser, P.; Maggioni, V. Assimilating satellite-based soil moisture observations in a land surface model: The effect of spatial resolution. J. Hydrol. X 2021, 13, 100105. [Google Scholar] [CrossRef]
- Shellito, P.J.; Small, E.E.; Colliander, A.; Bindlish, R.; Cosh, M.H.; Berg, A.A.; Bosch, D.D.; Caldwell, T.G.; Goodrich, D.C.; McNairn, H.; et al. SMAP soil moisture drying more rapid than observed in situ following rainfall events: SMAP SOIL MOISTURE DRYING. Geophys. Res. Lett. 2016, 43, 8068–8075. [Google Scholar] [CrossRef] [Green Version]
- Walther, S.; Duveiller, G.; Jung, M.; Guanter, L.; Cescatti, A.; Camps-Valls, G. Satellite Observations of the Contrasting Response of Trees and Grasses to Variations in Water Availability. Geophys. Res. Lett. 2019, 46, 1429–1440. [Google Scholar] [CrossRef] [Green Version]
- Rahman, A.; Zhang, X.; Houser, P.; Sauer, T.; Maggioni, V. Global Assimilation of Remotely Sensed Leaf Area Index: The Impact of Updating More State Variables Within a Land Surface Model. Front. Water 2022, 3, 789352. [Google Scholar] [CrossRef]
- Maggioni, V.; Reichle, R.H.; Anagnostou, E.N. The Impact of Rainfall Error Characterization on the Estimation of Soil Moisture Fields in a Land Data Assimilation System. J. Hydrometeorol. 2012, 13, 1107–1118. [Google Scholar] [CrossRef]


| Dataset | Spatial Resolution | Temporal Resolution | Temporal Extent | |
|---|---|---|---|---|
| Atmospheric forcing | MERRA-2 | 0.500°/0.625°, lat/lon | Hourly | 1980–present |
| Satellite observations | GLASS | 0.05° | 8 days | 2000–2018 |
| SMAP | 36 km | Daily | April 2015–present | |
| GLEAM | 0.25° | Daily | 2003–2018 | |
| Validation | FLUXCOM | 0.50° | Daily | 1980–2018 |
| ISMN | Point data | Hourly | Varies at each station |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, A.; Maggioni, V.; Zhang, X.; Houser, P.; Sauer, T.; Mocko, D.M. The Joint Assimilation of Remotely Sensed Leaf Area Index and Surface Soil Moisture into a Land Surface Model. Remote Sens. 2022, 14, 437. https://doi.org/10.3390/rs14030437
Rahman A, Maggioni V, Zhang X, Houser P, Sauer T, Mocko DM. The Joint Assimilation of Remotely Sensed Leaf Area Index and Surface Soil Moisture into a Land Surface Model. Remote Sensing. 2022; 14(3):437. https://doi.org/10.3390/rs14030437
Chicago/Turabian StyleRahman, Azbina, Viviana Maggioni, Xinxuan Zhang, Paul Houser, Timothy Sauer, and David M. Mocko. 2022. "The Joint Assimilation of Remotely Sensed Leaf Area Index and Surface Soil Moisture into a Land Surface Model" Remote Sensing 14, no. 3: 437. https://doi.org/10.3390/rs14030437
APA StyleRahman, A., Maggioni, V., Zhang, X., Houser, P., Sauer, T., & Mocko, D. M. (2022). The Joint Assimilation of Remotely Sensed Leaf Area Index and Surface Soil Moisture into a Land Surface Model. Remote Sensing, 14(3), 437. https://doi.org/10.3390/rs14030437