Development and Assessment of Seasonal Rainfall Forecasting Models for the Bani and the Senegal Basins by Identifying the Best Predictive Teleconnection
Abstract
1. Introduction
2. Materials and Methods
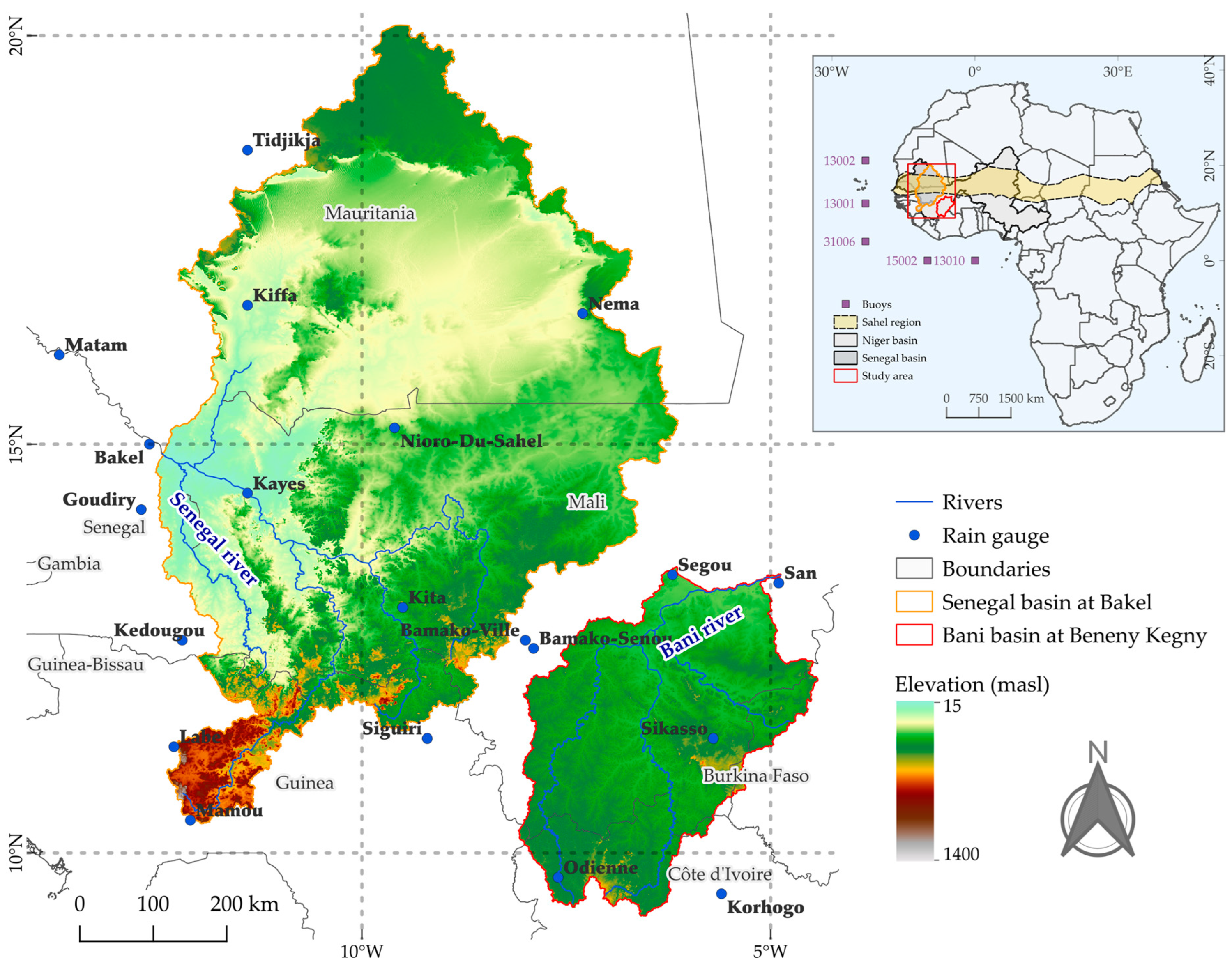
2.1. Description of the Study Region
2.2. Input Data
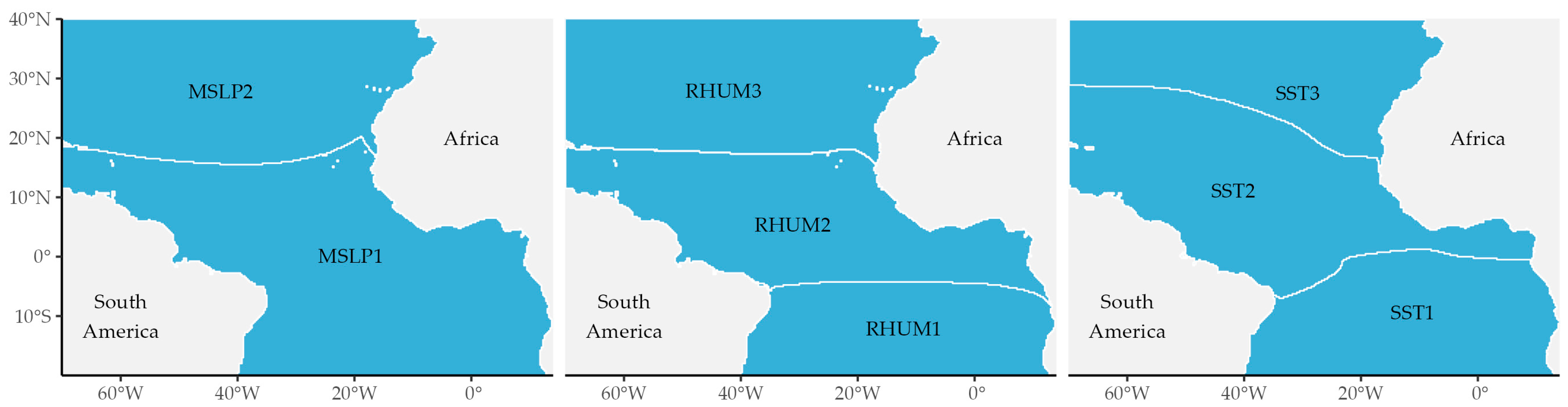
2.3. Ocean-WAM Teleconnections
2.4. Forecasting Models
2.5. Model Assessment
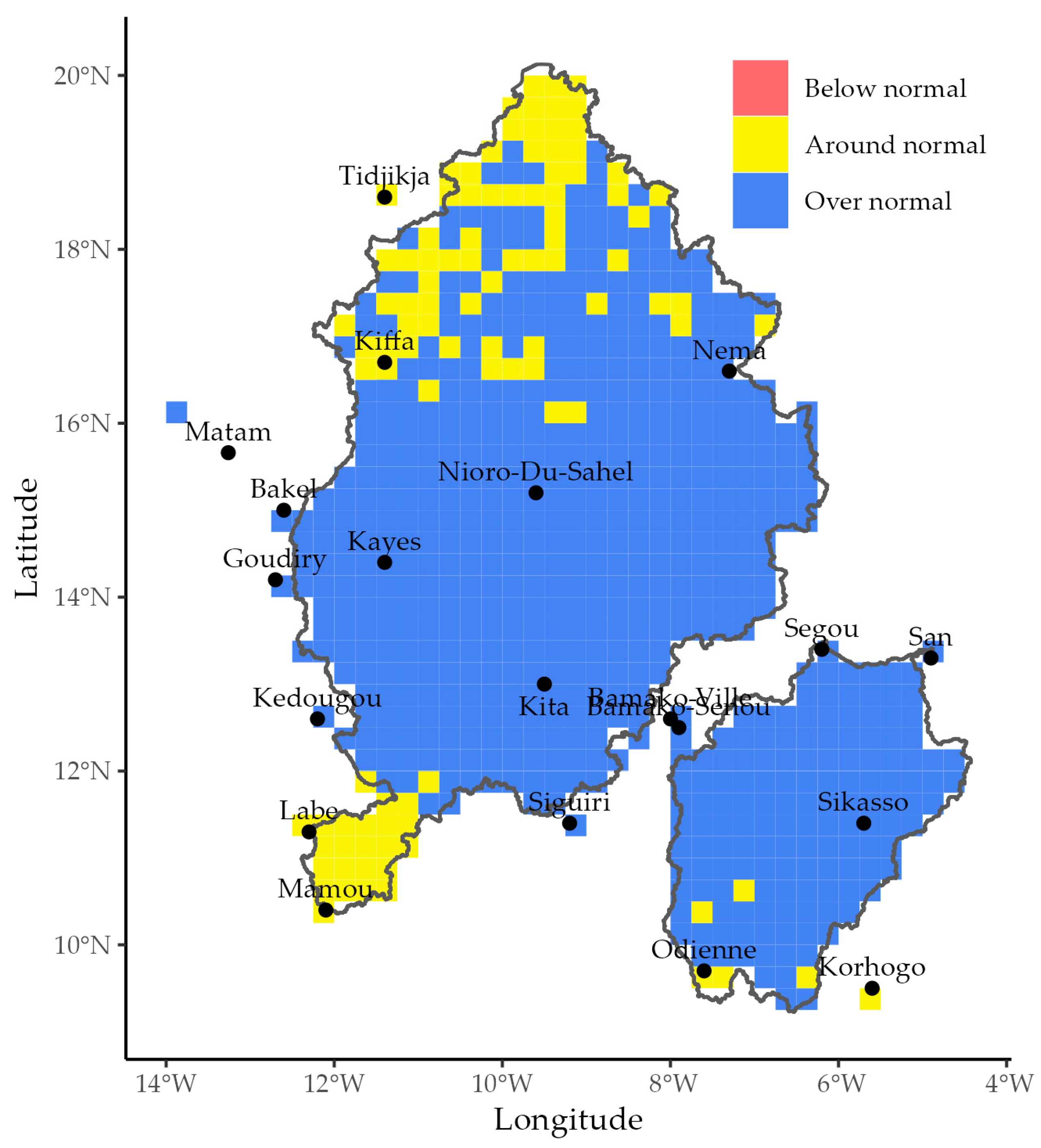
3. Results
3.1. Validation of Satellite Products
3.2. Classification of the Atlantic Variables
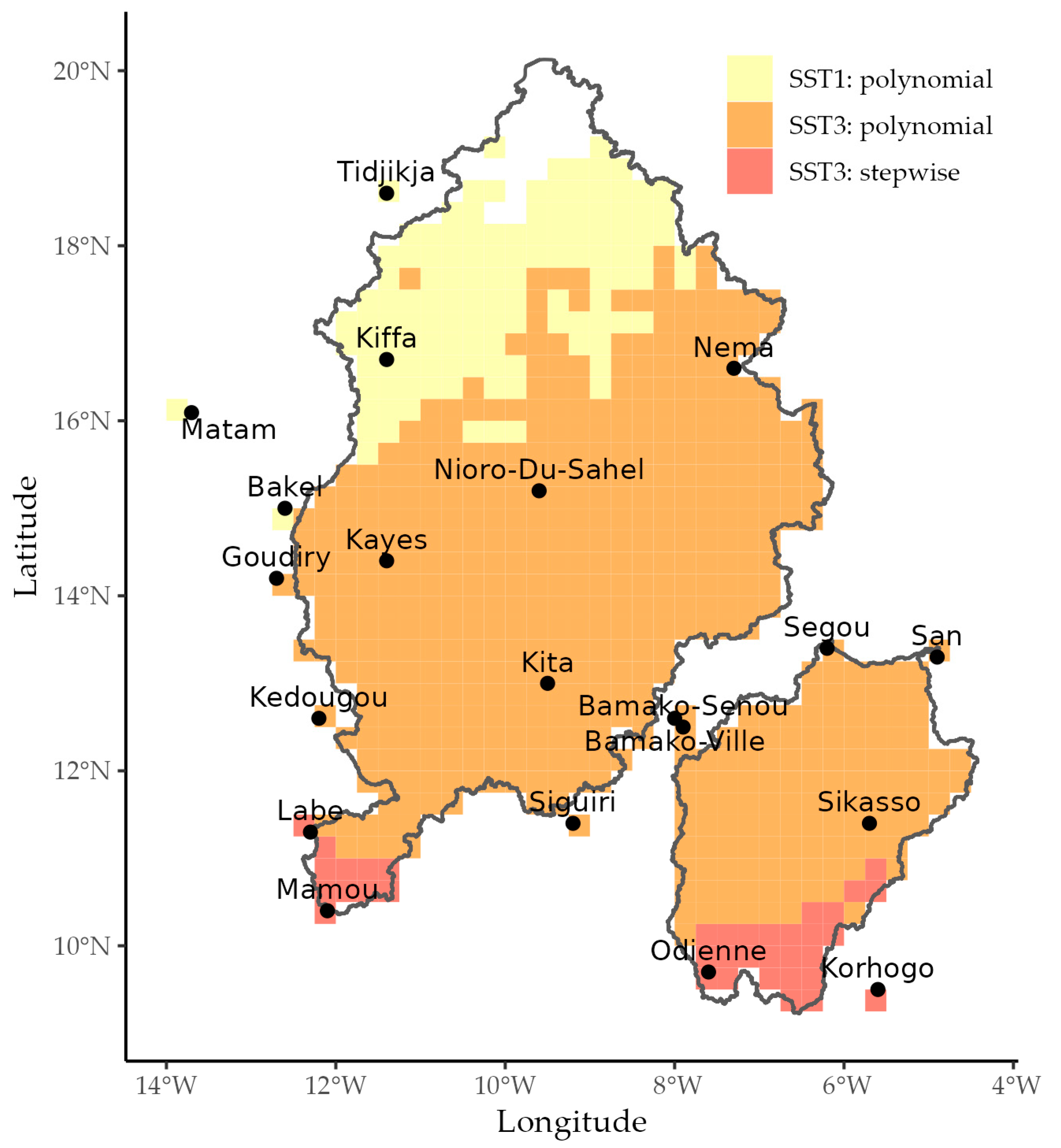
3.3. Selection of Forecast Models
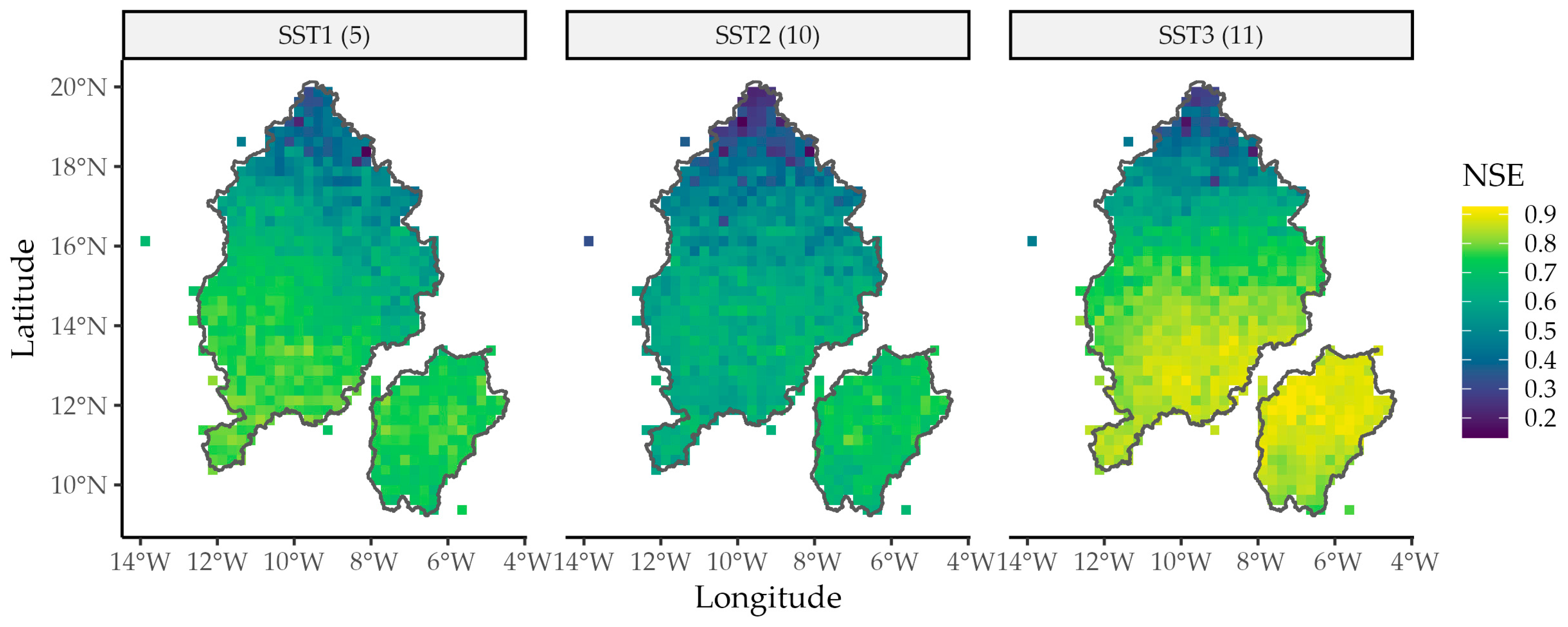
3.4. Comparison of the Forecasts with the Reference Rainfall
4. Discussion
4.1. Rainfall Distribution
4.2. Atlantic Regions
4.3. Rainfall Forecasts
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Year | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. | Total |
| 1983 | - | - | - | - | - | - | - | - | - | - | - | 0 | - |
| 1984 | 0 | 0 | 0 | 0 | 26.1 | 82.4 | 133.6 | 152 | 96.7 | 35.4 | 0 | 0 | 526 |
| 1985 | 0 | 0 | 0 | 0 | 19 | 78.2 | 127.7 | 140.8 | 92.1 | 34.6 | 0 | 0 | 492 |
| 1986 | 0 | 0 | 0 | 0 | 38.1 | 106.3 | 153.8 | 157.1 | 90.9 | 29.3 | 0 | 0 | 576 |
| 1987 | 0 | 0 | 0 | 0 | 33.5 | 98.8 | 159 | 135.2 | 82.7 | 36.6 | 0 | 0 | 546 |
| 1988 | 0 | 0 | 0 | 0 | 37.6 | 117 | 162.5 | 174.1 | 108.6 | 37.1 | 0 | 0 | 637 |
| 1989 | 0 | 0 | 0 | 0 | 40.9 | 101.8 | 174.6 | 162.1 | 107.1 | 37.9 | 0 | 0 | 624 |
| 1990 | 0 | 0 | 0 | 0 | 57.1 | 131.2 | 189.3 | 158.9 | 95.5 | 36.1 | 0 | 0 | 668 |
| 1991 | 0 | 0 | 0 | 0 | 36.9 | 126 | 182.5 | 194.7 | 117.8 | 48.4 | 11.7 | 0 | 718 |
| 1992 | 0 | 0 | 0 | 0 | 37.9 | 115.8 | 195.4 | 182.9 | 100.9 | 42 | 10.6 | 0 | 686 |
| 1993 | 0 | 0 | 0 | 0 | 33.8 | 98.7 | 170.2 | 160.2 | 89.1 | 30.7 | 10.2 | 0 | 593 |
| 1994 | 0 | 0 | 0 | 0 | 31.6 | 85.6 | 154.1 | 161 | 93.7 | 35.5 | 0 | 0 | 562 |
| 1995 | 0 | 0 | 0 | 0 | 37.2 | 111.6 | 166.7 | 167.6 | 108.4 | 51.9 | 13.3 | 0 | 657 |
| 1996 | 0 | 0 | 0 | 10.4 | 54.8 | 133.8 | 186.5 | 170.2 | 111.9 | 44.9 | 0 | 0 | 712 |
| 1997 | 0 | 0 | 0 | 0 | 29.5 | 91 | 163.9 | 171.1 | 111.7 | 46.6 | 0 | 0 | 614 |
| 1998 | 0 | 0 | 0 | 0 | 34.2 | 100.9 | 171.8 | 173.1 | 111.7 | 45.2 | 10.9 | 0 | 648 |
| 1999 | 0 | 0 | 0 | 0 | 47.5 | 118.8 | 184.1 | 186.6 | 125.5 | 71.4 | 19.1 | 0 | 753 |
| 2000 | 0 | 0 | 0 | 10.5 | 42.7 | 129.6 | 201.4 | 195.1 | 122.2 | 47.8 | 11.4 | 0 | 761 |
| 2001 | 0 | 0 | 0 | 0 | 45.2 | 111.8 | 165.4 | 171.3 | 118.1 | 51.3 | 11.3 | 0 | 674 |
| 2002 | 0 | 0 | 0 | 0 | 40.2 | 117.1 | 198.7 | 196.2 | 135.2 | 52 | 13 | 0 | 752 |
| 2003 | 0 | 0 | 0 | 0 | 34.2 | 92.9 | 160.8 | 165.6 | 110.3 | 48.4 | 13.2 | 0 | 625 |
| 2004 | 0 | 0 | 0 | 0 | 54.4 | 151.5 | 219.2 | 203.5 | 126.5 | 52.3 | 14.5 | 0 | 822 |
| 2005 | 0 | 0 | 0 | 0 | 54.7 | 132.6 | 207.5 | 186.1 | 122.3 | 54.5 | 15.3 | 0 | 773 |
| 2006 | 0 | 0 | 0 | 0 | 38.3 | 122.4 | 180.3 | 177.5 | 114.7 | 51 | 14.2 | 0 | 698 |
| 2007 | 0 | 0 | 0 | 0 | 43.6 | 120.9 | 194.4 | 182 | 121.7 | 59.8 | 14.7 | 0 | 737 |
| 2008 | 0 | 0 | 0 | 0 | 33.7 | 102.3 | 152.8 | 152.6 | 111.1 | 50.6 | 13.6 | 0 | 617 |
| 2009 | 0 | 0 | 0 | 0 | 53 | 129.9 | 188.5 | 190.1 | 116.8 | 45.5 | 10.3 | 0 | 734 |
| 2010 | 0 | 0 | 0 | 0 | 48.9 | 132.1 | 202.8 | 190.3 | 130.2 | 58.3 | 14.1 | 0 | 777 |
| 2011 | 0 | 0 | 0 | 0 | 37.6 | 121 | 184.8 | 179.4 | 124.8 | 57.9 | 12.1 | 0 | 718 |
| 2012 | 0 | 0 | 0 | 0 | 41.4 | 107.2 | 165.6 | 190.6 | 126.8 | 47.1 | 12.9 | 0 | 692 |
| 2013 | 0 | 0 | 0 | 0 | 48.1 | 117.6 | 211.2 | 198.3 | 121.3 | 47.8 | 11.7 | 0 | 756 |
| 2014 | 0 | 0 | 0 | 0 | 37.8 | 126.7 | 182.1 | 175.7 | 125.2 | 53.4 | 12.5 | 0 | 713 |
| 2015 | 0 | 0 | 0 | 0 | 41.1 | 126.1 | 190.6 | 200.2 | 134.7 | 60.2 | 13.4 | 0 | 766 |
| 2016 | 0 | 0 | 0 | 0 | 52.5 | 148.2 | 207.4 | 211.9 | 136.1 | 55.2 | 15.8 | 0 | 827 |
| 2017 | 0 | 0 | 0 | 11.5 | 52.2 | 121.8 | 187.3 | 183.4 | 123.7 | 58.5 | 16.2 | 0 | 755 |
| 2018 | 0 | 0 | 0 | 0 | 49.6 | 126.6 | 193 | 183.1 | 134.1 | 68.7 | 21.9 | 0 | 777 |
| 2019 | 0 | 0 | 0 | 10.1 | 47.6 | 111.9 | 178.9 | 194.1 | 121.2 | 48.6 | 14.2 | 0 | 727 |
| 2020 | 0 | 0 | 0 | 0 | 48.7 | 125.7 | 209.3 | 196.1 | 121.7 | 56.7 | 17.9 | 0 | 776 |
| Name | Year | CDR | FRC | ER | Name | Year | CDR | FRC | ER |
|---|---|---|---|---|---|---|---|---|---|
| Bakel | 2017 | 519 | 613 | 18.1 | Korhogo | 2017 | 846 | 996 | 17.7 |
| Bakel | 2018 | 596 | 639 | 7.2 | Korhogo | 2018 | 1043 | 1013 | 2.9 |
| Bakel | 2019 | 530 | 591 | 11.5 | Korhogo | 2019 | 1141 | 976 | 14.5 |
| Bakel | 2020 | 722 | 643 | 10.9 | Korhogo | 2020 | 935 | 1008 | 7.8 |
| Bakel | 2021 | 581 | 653 | 12.4 | Korhogo | 2021 | 904 | 1016 | 12.4 |
| Bamako-Senou | 2017 | 950 | 1057 | 11.3 | Mamou | 2017 | 1801 | 1734 | 3.7 |
| Bamako-Senou | 2018 | 1015 | 1096 | 8.0 | Mamou | 2018 | 1497 | 1764 | 17.8 |
| Bamako-Senou | 2019 | 1318 | 1022 | 22.5 | Mamou | 2019 | 1743 | 1698 | 2.6 |
| Bamako-Senou | 2020 | 1219 | 1100 | 9.8 | Mamou | 2020 | 1624 | 1753 | 7.9 |
| Bamako-Senou | 2021 | 1246 | 1116 | 10.4 | Mamou | 2021 | 1692 | 1765 | 4.3 |
| Bamako-Ville | 2017 | 908 | 1011 | 11.3 | Matam | 2017 | 298 | 354 | 18.8 |
| Bamako-Ville | 2018 | 963 | 1050 | 9.0 | Matam | 2018 | 303 | 370 | 22.1 |
| Bamako-Ville | 2019 | 1236 | 977 | 21.0 | Matam | 2019 | 260 | 340 | 30.8 |
| Bamako-Ville | 2020 | 1184 | 1053 | 11.1 | Matam | 2020 | 492 | 373 | 24.2 |
| Bamako-Ville | 2021 | 1150 | 1069 | 7.0 | Matam | 2021 | 425 | 380 | 10.6 |
| Goudiry | 2017 | 717 | 781 | 8.9 | Odienne | 2017 | 1230 | 1365 | 11.0 |
| Goudiry | 2018 | 730 | 813 | 11.4 | Odienne | 2018 | 1395 | 1397 | 0.1 |
| Goudiry | 2019 | 686 | 754 | 9.9 | Odienne | 2019 | 1668 | 1332 | 20.1 |
| Goudiry | 2020 | 755 | 817 | 8.2 | Odienne | 2020 | 1463 | 1394 | 4.7 |
| Goudiry | 2021 | 780 | 830 | 6.4 | Odienne | 2021 | 1441 | 1407 | 2.4 |
| Kayes | 2017 | 780 | 815 | 4.5 | San | 2017 | 742 | 790 | 6.5 |
| Kayes | 2018 | 794 | 851 | 7.2 | San | 2018 | 855 | 824 | 3.6 |
| Kayes | 2019 | 797 | 784 | 1.6 | San | 2019 | 826 | 761 | 7.9 |
| Kayes | 2020 | 896 | 857 | 4.4 | San | 2020 | 917 | 829 | 9.6 |
| Kayes | 2021 | 834 | 871 | 4.4 | San | 2021 | 722 | 843 | 16.8 |
| Kedougou | 2017 | 1223 | 1261 | 3.1 | Siguiri | 2017 | 1068 | 1282 | 20.0 |
| Kedougou | 2018 | 1112 | 1307 | 17.5 | Siguiri | 2018 | 1193 | 1321 | 10.7 |
| Kedougou | 2019 | 1254 | 1220 | 2.7 | Siguiri | 2019 | 1291 | 1245 | 3.6 |
| Kedougou | 2020 | 1220 | 1310 | 7.4 | Siguiri | 2020 | 1277 | 1321 | 3.4 |
| Kedougou | 2021 | 1210 | 1329 | 9.8 | Siguiri | 2021 | 1413 | 1337 | 5.4 |
| Kiffa | 2017 | 343 | 321 | 6.4 | Sikasso | 2017 | 988 | 1105 | 11.8 |
| Kiffa | 2018 | 328 | 336 | 2.4 | Sikasso | 2018 | 1252 | 1141 | 8.9 |
| Kiffa | 2019 | 265 | 309 | 16.6 | Sikasso | 2019 | 1168 | 1072 | 8.2 |
| Kiffa | 2020 | 444 | 339 | 23.6 | Sikasso | 2020 | 1172 | 1142 | 2.6 |
| Kiffa | 2021 | 308 | 345 | 12.0 | Sikasso | 2021 | 1123 | 1157 | 3.0 |
| Kita | 2017 | 1024 | 1138 | 11.1 | Tidjikja | 2017 | 103 | 133 | 29.1 |
| Kita | 2018 | 1116 | 1182 | 5.9 | Tidjikja | 2018 | 106 | 140 | 32.1 |
| Kita | 2019 | 1288 | 1100 | 14.6 | Tidjikja | 2019 | 74 | 128 | 73.0 |
| Kita | 2020 | 1352 | 1186 | 12.3 | Tidjikja | 2020 | 182 | 141 | 22.5 |
| Kita | 2021 | 1219 | 1204 | 1.2 | Tidjikja | 2021 | 60 | 143 | 138.3 |
References
- Agnew, C.T.; Chappell, A. Drought in the Sahel. Geo J. 1999, 48, 299–311. [Google Scholar]
- Gado Djibo, A.; Karambiri, H.; Seidou, O.; Sittichok, K.; Philippon, N.; Paturel, J.; Saley, H. Linear and Non-Linear Approaches for Statistical Seasonal Rainfall Forecast in the Sirba Watershed Region (SAHEL). Climate 2015, 3, 727–752. [Google Scholar] [CrossRef]
- Nicholson, S.E. The West African Sahel: A Review of Recent Studies on the Rainfall Regime and Its Interannual Variability. ISRN Meteorol. 2013, 2013, 32. [Google Scholar] [CrossRef]
- Folland, C.; Owen, J.; Ward, M.N.; Colman, A. Prediction of Seasonal Rainfall in the Sahel Region Using Empirical and Dynamical Methods. J. Forecast. 1991, 10, 21–56. [Google Scholar] [CrossRef]
- Samimi, C.; Fink, A.H.; Paeth, H. The 2007 Flood in the Sahel: Causes, Characteristics and Its Presentation in the Media and FEWS NET. Nat. Hazards Earth Syst. Sci. 2012, 12, 313–325. [Google Scholar] [CrossRef]
- Biasutti, M. Rainfall Trends in the African Sahel: Characteristics, Processes, and Causes. WIREs Clim. Change 2019, 10, e591. [Google Scholar] [CrossRef]
- Thorncroft, C.; Lamb, P. The West African Monsoon. In The Global Monsoon System: Research and Forecast; Chang, C.-P., Bin, W., Lau, N.-C.G., Eds.; World Meteorological Organization: Geneva, Switzerland, 2005; pp. 239–250. [Google Scholar]
- Bâ, K.; Balcázar, L.; Diaz, V.; Ortiz, F.; Gómez-Albores, M.; Díaz-Delgado, C. Hydrological Evaluation of PERSIANN-CDR Rainfall over Upper Senegal River and Bani River Basins. Remote Sens. 2018, 10, 1884. [Google Scholar] [CrossRef]
- Vischel, T.; Panthou, G.; Peyrillé, P.; Roehrig, R.; Quantin, G.; Lebel, T.; Wilcox, C.; Beucher, F.; Budiarti, M. Precipitation Extremes in the West African Sahel: Recent Evolution and Physical Mechanisms. In Tropical Extremes: Natural Variability and Trends; Venugopal, V., Sukhatme, J., Murtugudde, R., Roca, R., Eds.; Elsevier: Amsterdam, The Netherlands; Oxford, UK; Cambridge, MA, USA, 2019; ISBN 978-0-12-809248-4. [Google Scholar]
- Lebel, T.; Cappelaere, B.; Galle, S.; Hanan, N.; Kergoat, L.; Levis, S.; Vieux, B.; Descroix, L.; Gosset, M.; Mougin, E.; et al. AMMA-CATCH Studies in the Sahelian Region of West-Africa: An Overview. J. Hydrol. 2009, 375, 3–13. [Google Scholar] [CrossRef]
- Redelsperger, J.-L.; Lebel, T. Surface Processes and Water Cycle in West Africa, Studied from the AMMA-CATCH Observing System. J. Hydrol. 2009, 375, 298. [Google Scholar] [CrossRef]
- Sittichok, K. Improving Seasonal Rainfall and Streamflow Forecasting in the Sahel Region via Better Predictor Selection, Uncertainty Quantification and Forecast Economic Value Assessmen; University of Ottawa: Ottawa, Canada, 2015. [Google Scholar]
- Sittichok, K.; Djibo, A.G.; Seidou, O.; Saley, H.M.; Karambiri, H.; Paturel, J. Statistical Seasonal Rainfall and Streamflow Forecasting for the Sirba Watershed, West Africa, Using Sea-Surface Temperatures. Hydrol. Sci. J. 2016, 61, 805–815. [Google Scholar] [CrossRef]
- PRESASS. Prévisions Saisonnières des Caractéristiques Agro-Hydro-Climatiques de la Saison des Pluies pour les Zones Soudaniennes et Sahéliennes (PRSEASS—2021); The AGRHYMET Regional Center: Niamey, Niger, 2021. [Google Scholar]
- PRESASS. Forum 2022 des Prévisions Saisonnières des Caractéristiques Agro-Hydro-Climatiques de La Saison des Pluies pour les Zones Soudanienne et Sahélienne (PRSEASS, 2022); The AGRHYMET Regional Center: Niamey, Niger, 2022. [Google Scholar]
- Pirret, J.S.R.; Daron, J.D.; Bett, P.E.; Fournier, N.; Foamouhoue, A.K. Assessing the Skill and Reliability of Seasonal Climate Forecasts in Sahelian West Africa. Weather. Forecast. 2020, 35, 1035–1050. [Google Scholar] [CrossRef]
- Ashouri, H.; Nguyen, P.; Thorstensen, A.; Hsu, K.; Sorooshian, S.; Braithwaite, D. Assessing the Efficacy of High-Resolution Satellite-Based PERSIANN-CDR Precipitation Product in Simulating Streamflow. J. Hydrometeorol. 2016, 17, 2061–2076. [Google Scholar] [CrossRef]
- World Bank. Transforming Agriculture in the Sahel: What Would It Take? Available online: https://www.preventionweb.net/publication/transforming-agriculture-sahel-what-would-it-take (accessed on 30 July 2022).
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled Seamless SRTM Data V4. Available online: https://srtm.csi.cgiar.org/ (accessed on 30 July 2022).
- Bâ, K.M.; Díaz-Delgado, C.; Quentin, E.; Guerra-Cobián, V.H.; Ojeda-Chihuahua, J.I.; Cârsteanu, A.A.; Franco-Plata, R. Hydrological Modeling of Large Watersheds: Case Study of the Senegal River, West Africa. Tecnol. Cienc. Agua 2013, 4, 129–136. [Google Scholar]
- Chaibou Begou, J.; Jomaa, S.; Benabdallah, S.; Bazie, P.; Afouda, A.; Rode, M. Multi-Site Validation of the SWAT Model on the Bani Catchment: Model Performance and Predictive Uncertainty. Water 2016, 8, 178. [Google Scholar] [CrossRef]
- GlobCover. Global Land Cover Map. Available online: http://due.esrin.esa.int/page_globcover.php (accessed on 23 March 2021).
- Bontemps, S.; Defourny, P.; Van Bogaert, E.; Arino, O.; Kalogirou, V.; Ramos Perez, J. GLOBCOVER 2009—Product Description and Validation Report; Université Catholique de Louvain (UCLouvain): Louvain-la-Nueve, Belgium, 2009. [Google Scholar]
- Bâ, K.; Diaz-Mercado, V.; Gómez Albores, M.; Díaz-Delgado, C.; Nájera, N.; Seidou, O.; Ortiz, F. Spatially Distributed Hydrological Modelling of a Western Africa Basin. In Proceedings of the 13th International Conference on Hydroinformatics, Palermo, Italy, 1–5 July 2018; pp. 343–350. [Google Scholar]
- Bâ, K.; Diaz-Mercado, V.; Balcázar, L.; Ortiz, F.; Gómez Albores, M.; Díaz-Delgado, C. Performance Evaluation of Satellite Precipitation and Its Use for Distributed Hydrological Modelling on Western Africa Basins. In Proceedings of the 3rd International Conference on African Large River Basin Hydrology (ICALRBH), Algiers, Algeria, 6–9 May 2018. [Google Scholar]
- Serrat-Capdevila, A.; Merino, M.; Valdes, J.; Durcik, M. Evaluation of the Performance of Three Satellite Precipitation Products over Africa. Remote Sens. 2016, 8, 836. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Stepaniak, D.P. Indices of El Niño Evolution. J. Climate 2001, 14, 1697–1701. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q.J.R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) System. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Bourlès, B.; Araujo, M.; McPhaden, M.J.; Brandt, P.; Foltz, G.R.; Lumpkin, R.; Giordani, H.; Hernandez, F.; Lefèvre, N.; Nobre, P.; et al. PIRATA: A Sustained Observing System for Tropical Atlantic Climate Research and Forecasting. Earth Space Sci. 2019, 6, 577–616. [Google Scholar] [CrossRef]
- Gado Djibo, A.; Seidou, O.; Karambiri, H.; Sittichok, K.; Paturel, J.E.; Moussa Saley, H. Development and Assessment of Non-Linear and Non-Stationary Seasonal Rainfall Forecast Models for the Sirba Watershed, West Africa. J. Hydrol. Reg. Stud. 2015, 4, 134–152. [Google Scholar] [CrossRef]
- Foltz, G.R.; Brandt, P.; Richter, I.; Rodríguez-Fonseca, B.; Hernandez, F.; Dengler, M.; Rodrigues, R.R.; Schmidt, J.O.; Yu, L.; Lefevre, N.; et al. The Tropical Atlantic Observing System. Front. Mar. Sci. 2019, 6, 206. [Google Scholar] [CrossRef]
- Linting, M.; Meulman, J.J.; Groenen, P.J.F.; van der Koojj, A.J. Nonlinear Principal Components Analysis: Introduction and Application. Psychol. Methods 2007, 12, 336–358. [Google Scholar] [CrossRef] [PubMed]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis, Wiley Series in Probability and Statistics; 1st ed.; Wiley: Hoboken, NJ, USA, 2011; ISBN 978-0-470-74991-3. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill: New York, NY, USA, 2004; Volume 29, ISBN ISBN 0-07-238688-6. [Google Scholar]
- Leach, L.F.; Henson, R. The Use and Impact of Adjusted R2 Effects in Published Regression Research. Mult. Linear Regres. Viewp. 2007, 33, 1–11. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Sorooshian, S.; Duan, Q.; Gupta, V.K. Calibration of Rainfall-Runoff Models: Application of Global Optimization to the Sacramento Soil Moisture Accounting Model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]
- Moriasi, D.; Gitau, M.W.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Janicot, S.; Trzaska, S.; Poccard, I. Summer Sahel-ENSO Teleconnection and Decadal Time Scale SST Variations. Clim. Dyn. 2001, 18, 303–320. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Tucker, C.J.; Ba, M.B. Desertification, Drought, and Surface Vegetation: An Example from the West African Sahel. Bull. Amer. Meteor. Soc. 1998, 79, 815–829. [Google Scholar] [CrossRef]
- Garric, G.; Douville, H.; Déqué, M. Prospects for Improved Seasonal Predictions of Monsoon Precipitation over Sahel. Int. J. Climatol. 2002, 22, 331–345. [Google Scholar] [CrossRef]


| Rain Gauge | R2 | PBIAS (%) | MAE (mm) | N° of Data |
|---|---|---|---|---|
| Tidjikja | 0.672 | 13.2 | 10.0 | 104 |
| Kiffa | 0.600 | −0.1 | 21.0 | 115 |
| Nema | 0.510 | 9.0 | 23.0 | 116 |
| Matam | 0.538 | 2.3 | 28.0 | 120 |
| Nioro-Du-Sahel | 0.764 | 15.4 | 24.0 | 122 |
| Bakel | 0.756 | 3.2 | 30.0 | 159 |
| Kayes | 0.779 | 16.7 | 29.0 | 122 |
| Goudiry | 0.688 | 18.2 | 36.0 | 140 |
| Segou | 0.833 | 11.0 | 26.0 | 169 |
| San | 0.858 | 2.8 | 22.0 | 168 |
| Kita | 0.879 | 13.7 | 30.0 | 142 |
| Kedougou | 0.682 | 4.7 | 51.0 | 156 |
| Bamako-Ville | 0.817 | 0.8 | 34.0 | 140 |
| Bamako-Senou | 0.838 | 8.2 | 30.0 | 183 |
| Labe | 0.825 | 25.0 | 58.0 | 204 |
| Siguiri | 0.784 | 9.8 | 40.0 | 190 |
| Sikasso | 0.85 | −1.7 | 29.0 | 202 |
| Mamou | 0.815 | 11.1 | 49.0 | 246 |
| Odienne | 0.827 | 4.1 | 35.0 | 120 |
| Korhogo | 0.717 | −9.2 | 38.0 | 95 |
| Buoys | R2 | PBIAS (%) | MAE (°C) | N° of Data |
|---|---|---|---|---|
| 13001 | 0.977 | −1.30 | 0.36 | 127 |
| 13002 | 0.991 | −0.80 | 0.23 | 128 |
| 13010 | 0.983 | −1.40 | 0.38 | 194 |
| 15002 | 0.987 | −0.90 | 0.27 | 198 |
| 31006 | 0.928 | −0.60 | 0.20 | 137 |
| Rain Gauges | Models | |||
|---|---|---|---|---|
| Linear (lm) | Polynomial (Poly) | Exponential (nls) | Stepwise Regression | |
| Tidjikja | - | - | - | - |
| Kiffa | 0.509 | 0.629 | 0.627 | 0.610 |
| Nema | 0.541 | 0.685 | 0.674 | 0.585 |
| Matam | 0.501 | 0.673 | 0.674 | 0.617 |
| Nioro-Du-Sahel | 0.647 | 0.767 | 0.707 | 0.714 |
| Bakel | 0.645 | 0.752 | 0.677 | 0.676 |
| Kayes | 0.682 | 0.754 | 0.705 | 0.741 |
| Goudiry | 0.730 | 0.820 | 0.726 | 0.792 |
| Segou | 0.696 | 0.843 | 0.839 | 0.703 |
| San | 0.743 | 0.879 | 0.873 | 0.765 |
| Kita | 0.782 | 0.872 | 0.838 | 0.802 |
| Kedougou | 0.762 | 0.821 | 0.790 | 0.821 |
| Bamako-Ville | 0.772 | 0.865 | 0.855 | 0.791 |
| Bamako-Senou | 0.770 | 0.833 | 0.820 | 0.794 |
| Labe | 0.836 | 0.853 | 0.812 | 0.837 |
| Siguiri | 0.816 | 0.860 | 0.826 | 0.837 |
| Sikasso | 0.869 | 0.905 | 0.888 | 0.889 |
| Mamou | 0.815 | 0.815 | 0.755 | 0.842 |
| Odienne | 0.786 | 0.808 | 0.787 | 0.817 |
| Korhogo | 0.776 | 0.776 | 0.731 | 0.828 |
| Year | Labe | Nema | Nioro-Du-Sahel | Segou | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CDR | FRC | RE | CDR | FRC | RE | CDR | FRC | RE | CDR | FRC | RE | |
| 2017 | 1726.7 | 1815.4 | 5.1 | 312.4 | 295.5 | 5.4 | 571.8 | 618.2 | 8.1 | 781.7 | 795.1 | 1.7 |
| 2018 | 1595.0 | 1863.4 | 16.8 | 380.8 | 311.4 | 18.2 | 689.4 | 648.0 | 6.0 | 759.5 | 830.5 | 9.3 |
| 2019 | 1989.0 | 1767.4 | 11.1 | 262.7 | 282.8 | 7.7 | 661.4 | 593.7 | 10.2 | 907.8 | 765.4 | 15.7 |
| 2020 | 1682.7 | 1859.6 | 10.5 | 336.5 | 315 | 6.4 | 772.9 | 653.5 | 15.4 | 910.3 | 836.2 | 8.1 |
| 2021 | 1802.5 | 1879.0 | 4.2 | 231.9 | 321.4 | 38.6 | 609.3 | 665.5 | 9.2 | 841.8 | 850.6 | 1.0 |
| Author | Data/Location | Sources and Characteristics | Models (Rainfall Forecast) | Lag (Months) | Efficiency |
|---|---|---|---|---|---|
| In this study | Atlantic SST (0.25° × 0.25°), PCA cluster analysis/Bani basin | ERA5 | Second-order polynomial | 11 | SST: NSE mean = 0.867 SST: NSE max = 0.926 SST: NSE min = 0.751 |
| In this study | Atlantic SST (0.25° × 0.25°), PCA cluster analysis/Senegal basin | ERA5 | Second-order polynomial | 11 | SST: NSE mean = 0.711 SST: NSE max = 0.916 SST: NSE min = 0.133 |
| Sittichok et al. [12,13] | Atlantic and Pacific SST/(2° × 2°), combination of regression, PCA and ACC/Sirba basin | Meteorology and Water Resource Centre of Ceara State, Brazil | Stepwise regression | 5 12 | Atlantic SST NSE = 0.231 Pacific SST NSE = 0.387 |
| Gado Djibo et al. [2] | SLP, RHUM, Ta, zonal wind and meridional wind/Sirba basin | NCEP- DOE Reanalysis (NOAA), 2.5° × 2.5° | Linear | SLP: 0 RHUM: 8 Ta: 7 VWIND: 8 UWIND: 7 SST: 12 | SLP: NSE = 0.46 RHUM: NSE = 0.52 Ta: NSE = 0.53 VWIND: NSE = 0.28 UWIND: NSE = 0.32 SST: NSE = 0.34 |
| Non-linear | SLP: 9 RHUM: 7 Ta: 8 | SLP: NSE = 0.31 RHUM: NSE = 0.36 Ta: NSE = 0.45 | |||
| Gado Djibo et al. [31] | Ta, SLP, RHUM | Climatic Research Unit | Linear | Ta: 14 SLP: 0 RHUM: 8 | Ta: NSE = 0.76 SLP: NSE = 46 RHUM: NSE = 0.52 |
| Garric et al. [44] | Gulf of Guinea SST | CRU, NCEP/NCAR, ECMWF) | Linear, stepwise regression | 12 | SST: r = 0.67 |
| Folland et al. [4] | SST | Meteorological Office Historical Sea Surface Temperature data set version 3 (MOHSST3) | Stepwise regression Linear Discriminant | 1 | SST: r = 0.54 SST: r = 0.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balcázar, L.; Bâ, K.M.; Díaz-Delgado, C.; Gómez-Albores, M.A.; Gaona, G.; Minga-León, S. Development and Assessment of Seasonal Rainfall Forecasting Models for the Bani and the Senegal Basins by Identifying the Best Predictive Teleconnection. Remote Sens. 2022, 14, 6397. https://doi.org/10.3390/rs14246397
Balcázar L, Bâ KM, Díaz-Delgado C, Gómez-Albores MA, Gaona G, Minga-León S. Development and Assessment of Seasonal Rainfall Forecasting Models for the Bani and the Senegal Basins by Identifying the Best Predictive Teleconnection. Remote Sensing. 2022; 14(24):6397. https://doi.org/10.3390/rs14246397
Chicago/Turabian StyleBalcázar, Luis, Khalidou M. Bâ, Carlos Díaz-Delgado, Miguel A. Gómez-Albores, Gabriel Gaona, and Saula Minga-León. 2022. "Development and Assessment of Seasonal Rainfall Forecasting Models for the Bani and the Senegal Basins by Identifying the Best Predictive Teleconnection" Remote Sensing 14, no. 24: 6397. https://doi.org/10.3390/rs14246397
APA StyleBalcázar, L., Bâ, K. M., Díaz-Delgado, C., Gómez-Albores, M. A., Gaona, G., & Minga-León, S. (2022). Development and Assessment of Seasonal Rainfall Forecasting Models for the Bani and the Senegal Basins by Identifying the Best Predictive Teleconnection. Remote Sensing, 14(24), 6397. https://doi.org/10.3390/rs14246397






