A Large-Scale Invariant Matching Method Based on DeepSpace-ScaleNet for Small Celestial Body Exploration
Abstract
1. Introduction
- (1)
- As far as we know, we are the first to propose a solution to the problem of matching images of SCB with large-scale variations.
- (2)
- We have creatively used scale estimation networks in SCB image matching and designed DeepSpace-ScaleNet by using the architecture of Transformer. This is unprecedented in previous SCB matching methods.
- (3)
- We designed the novel GA-DenseASPP module and CADP module in DeepSpace-ScaleNet, which can improve the performance of the algorithm.
- (4)
- We created the first simulated SCB dataset named Virtual SCB Dataset in the field, which can be applied to image matching, relative localization and more.
2. Related Work
2.1. Local Feature Extraction and Matching
2.2. Image Scale Estimation
2.3. Multi-Scale Modules
3. Methods
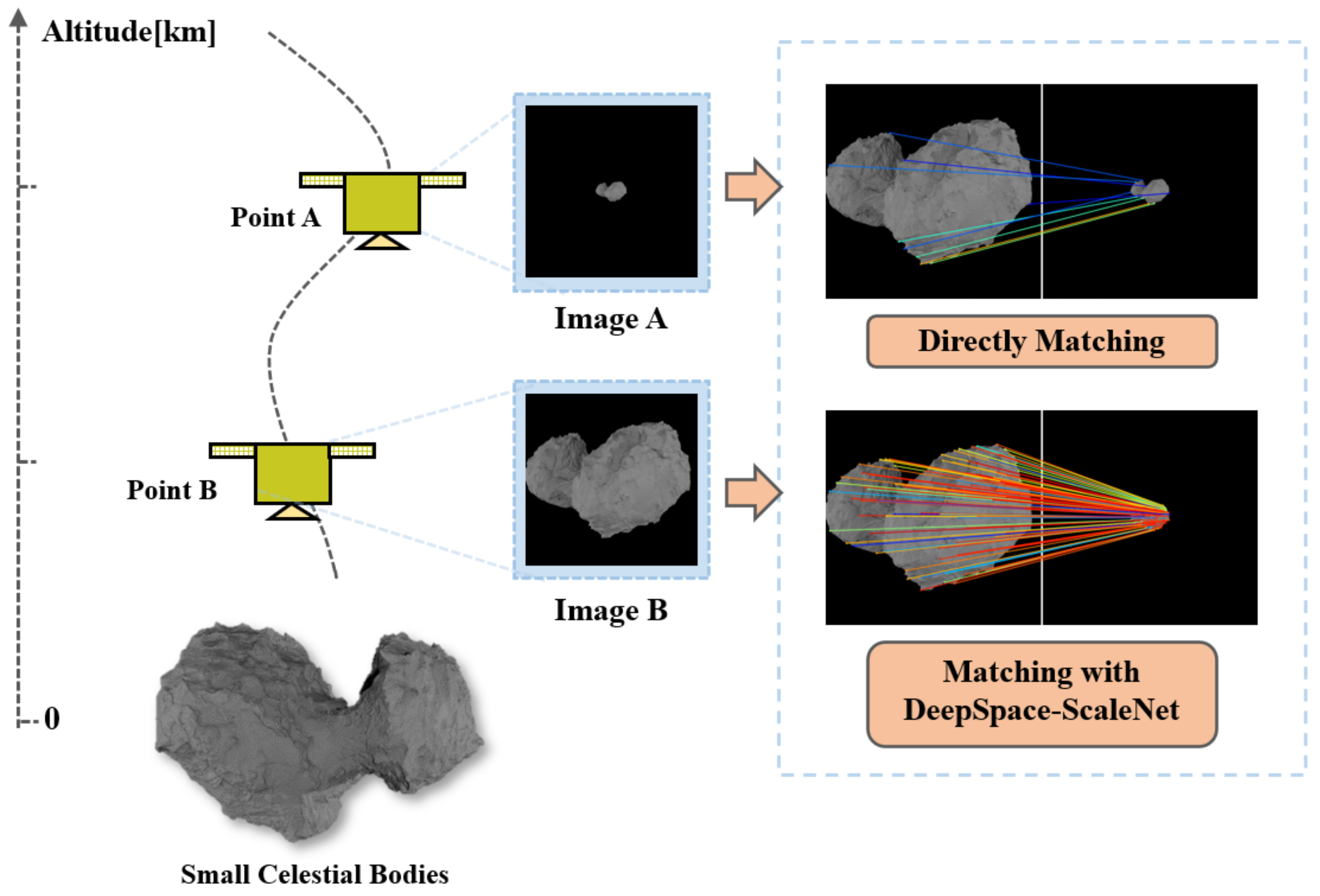
3.1. Large-Scale Invariant Method for SCB Image Matching
3.2. Scale Distributions
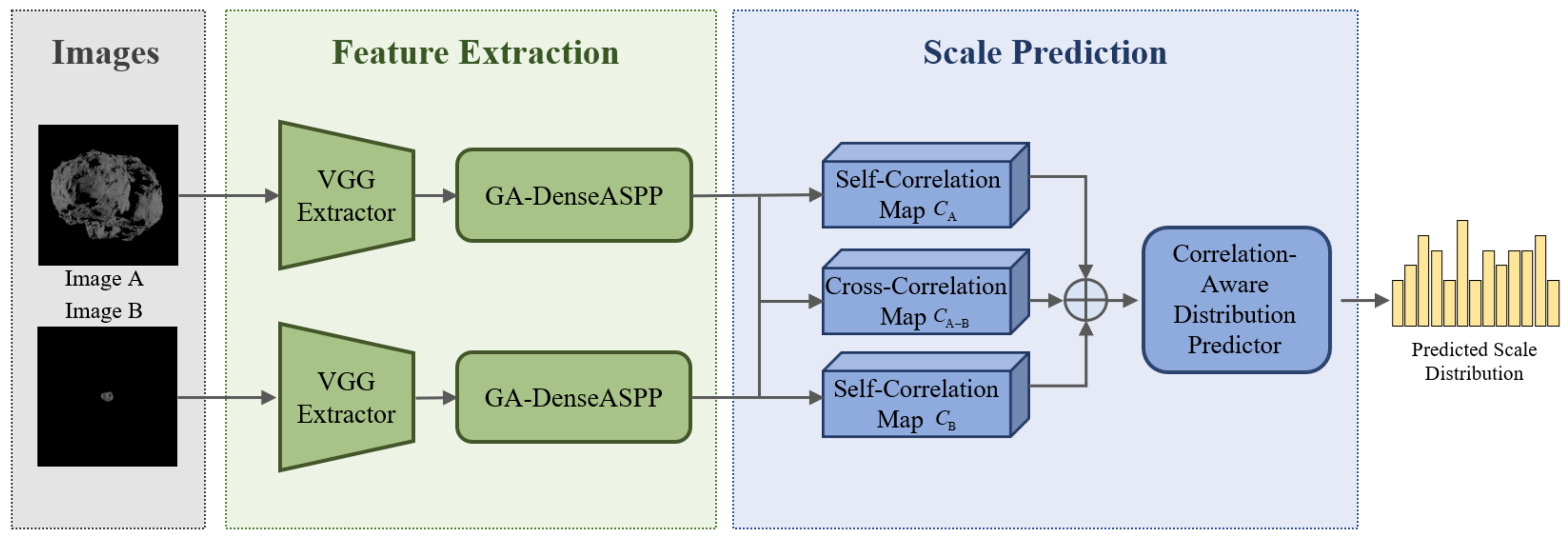
3.3. DeepSpace-ScaleNet
3.3.1. Deepspace-Scalenet Architecture
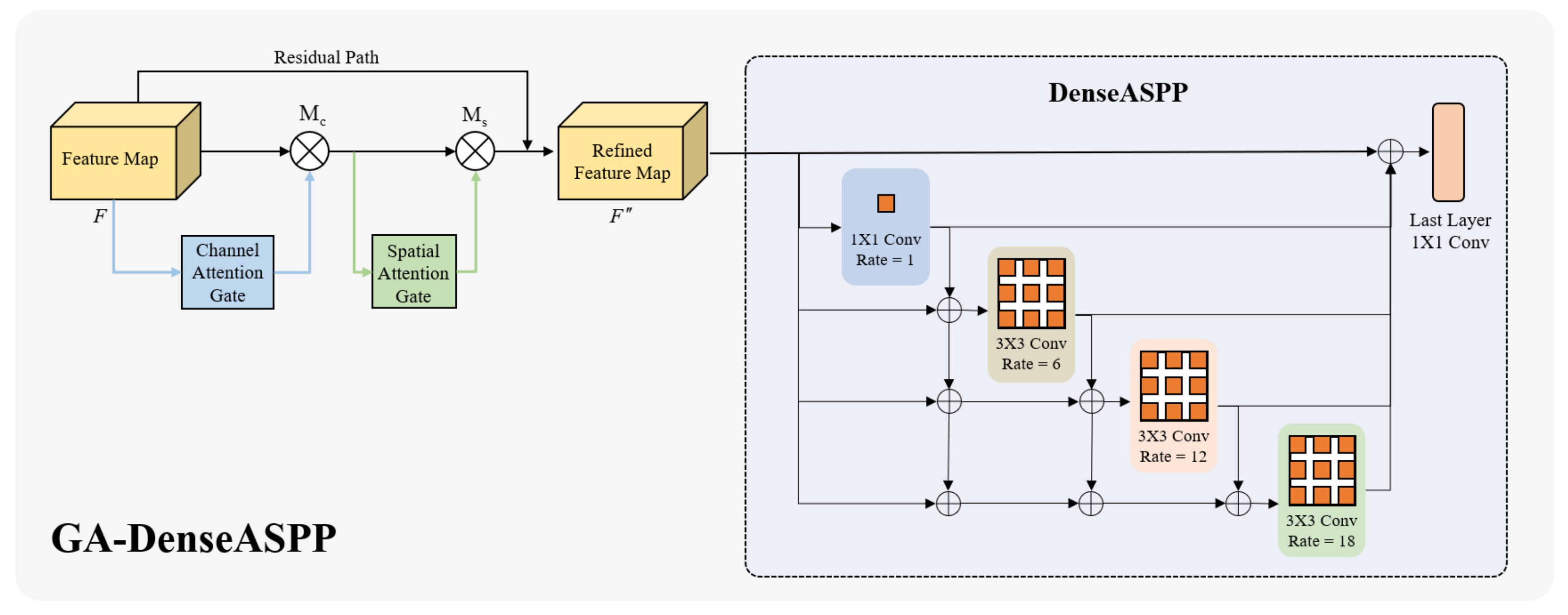
3.3.2. Global Attention-DenseASPP (GA-DenseASPP)
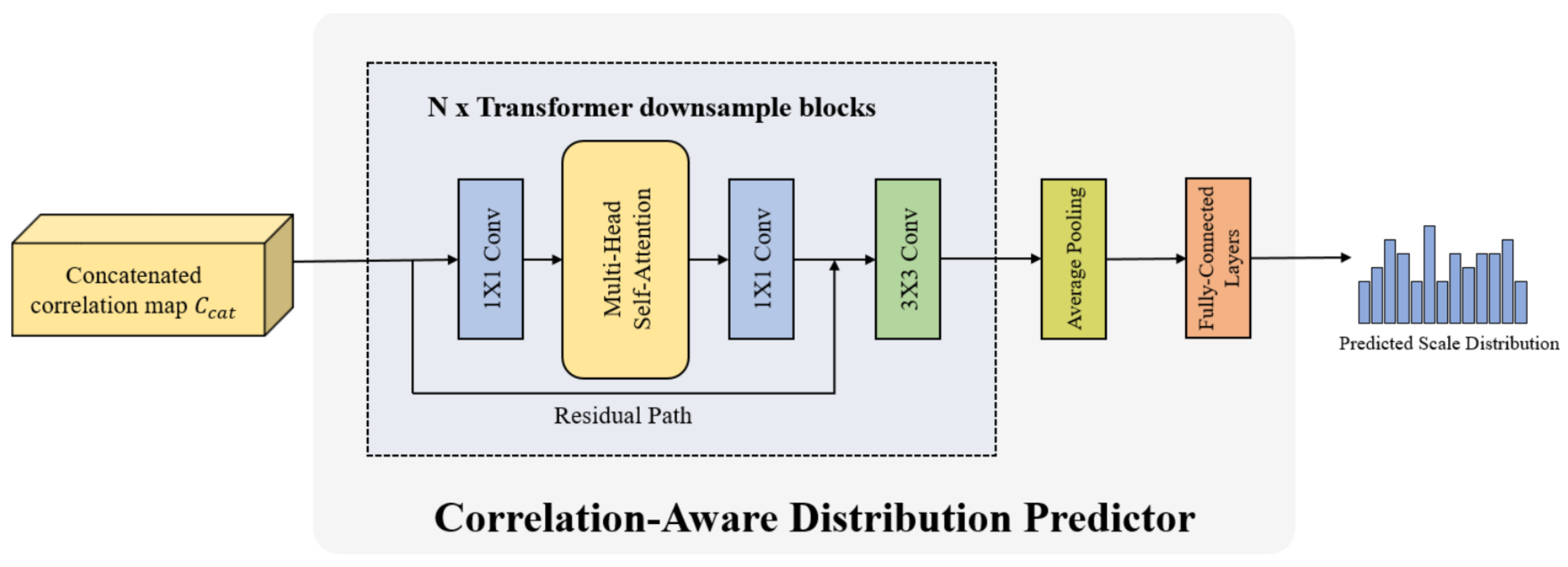
3.3.3. Correlation-aware Distribution Predictor (CADP)
3.3.4. Loss Function
3.3.5. Learning Rate and Optimizer
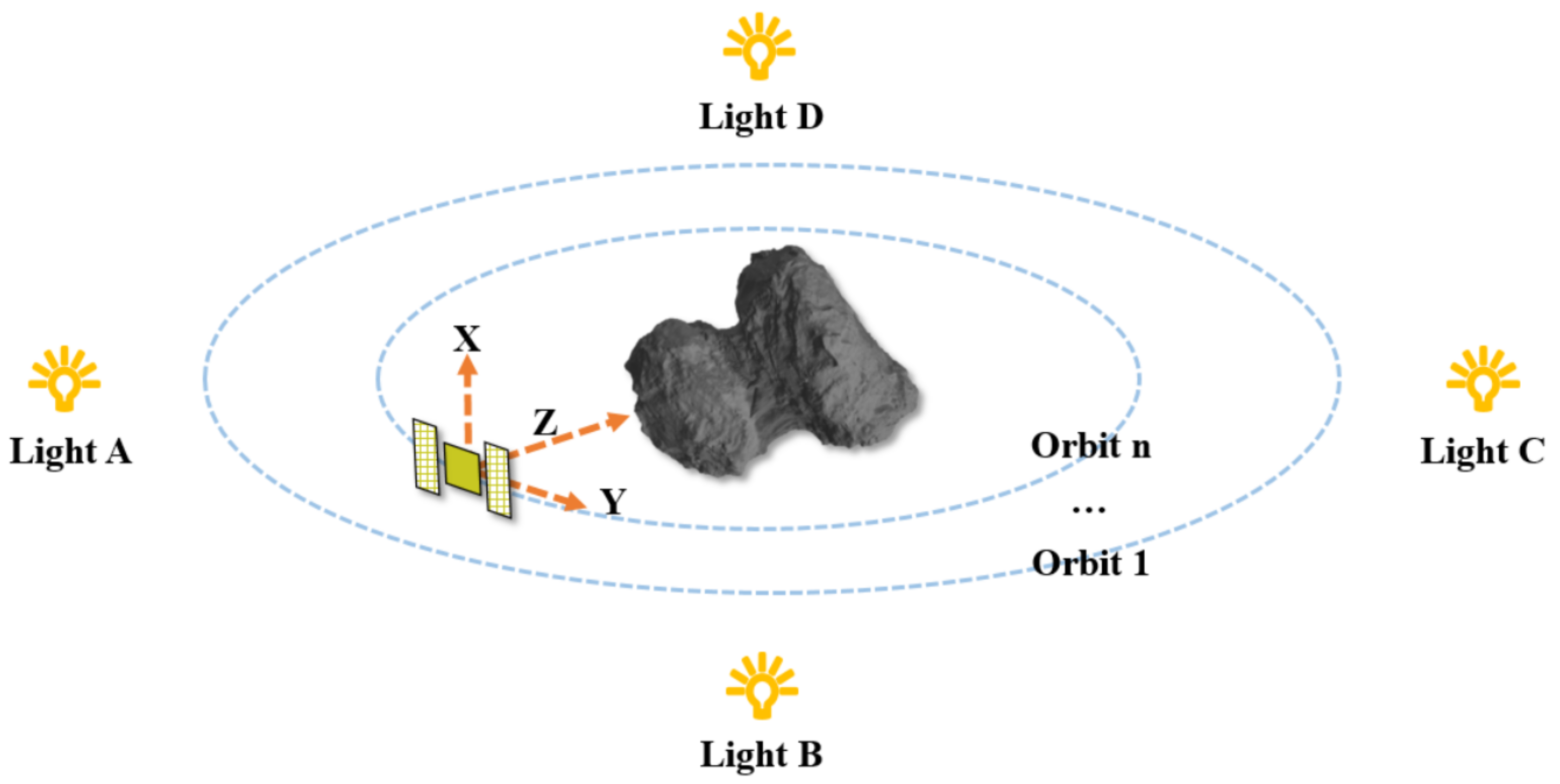
4. Virtual SCB Dataset
5. Experiments and Results
5.1. Implementation Details
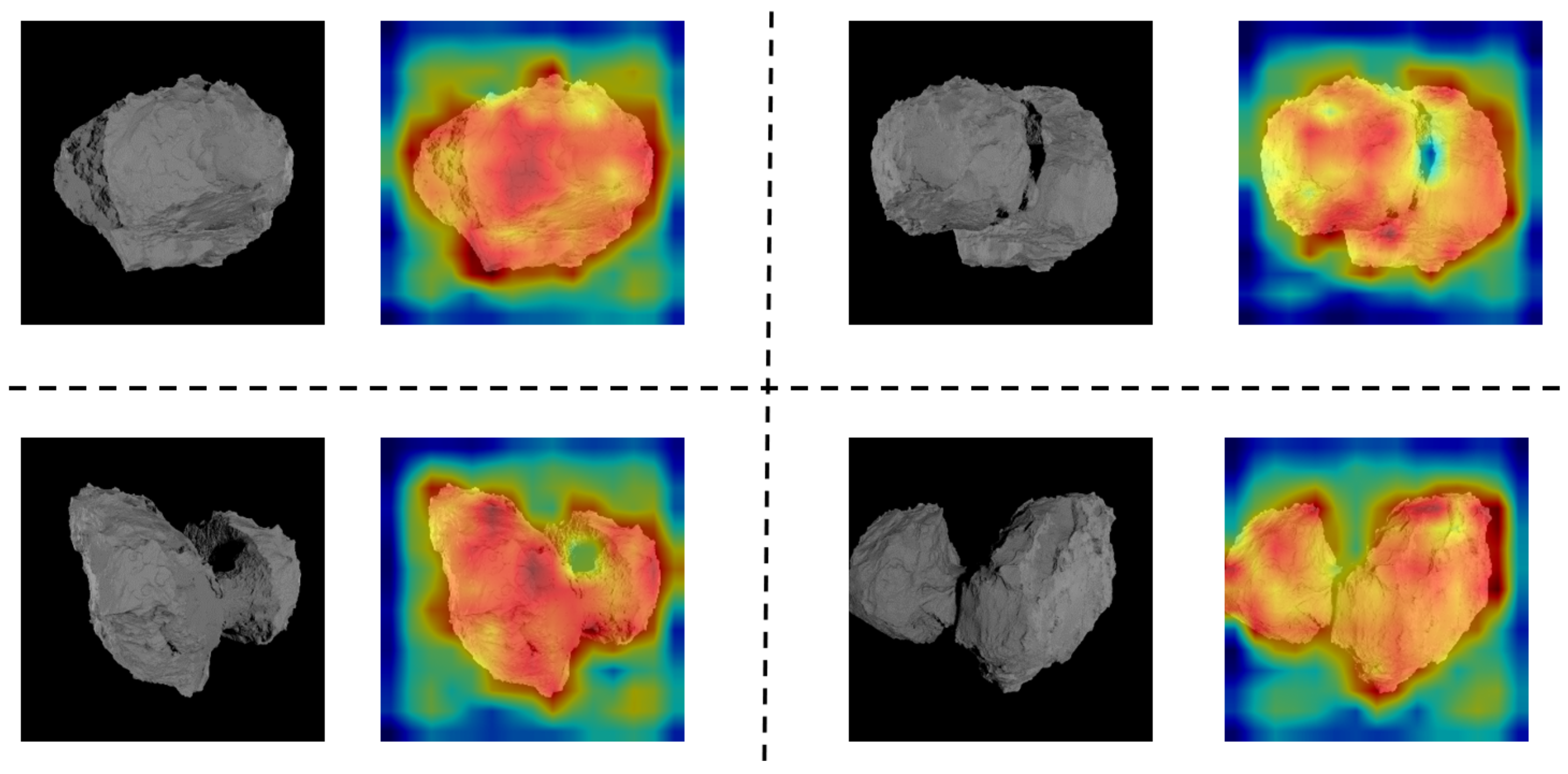
5.2. Image Scale Estimation
5.3. Ablation Study
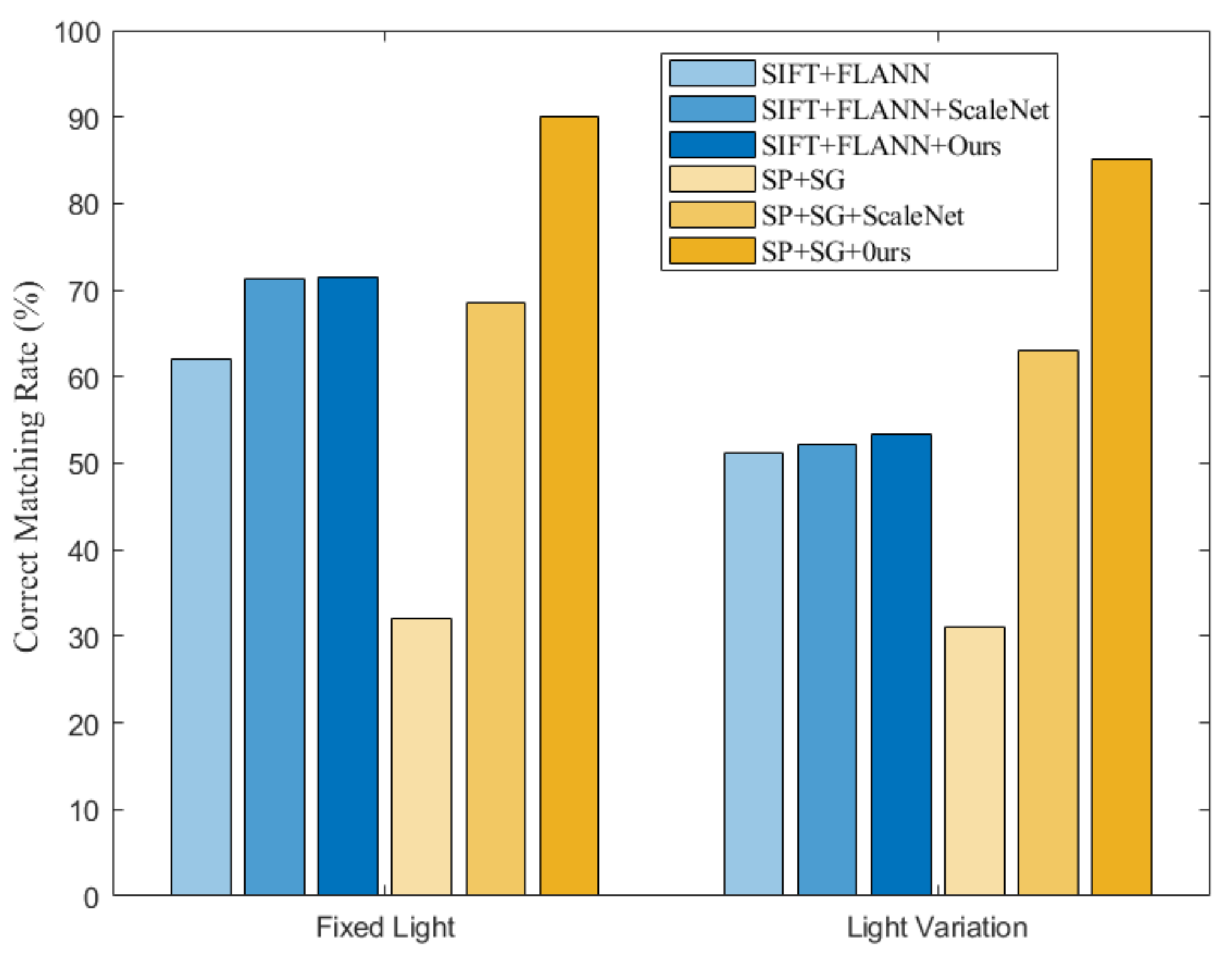
5.4. Image Matching
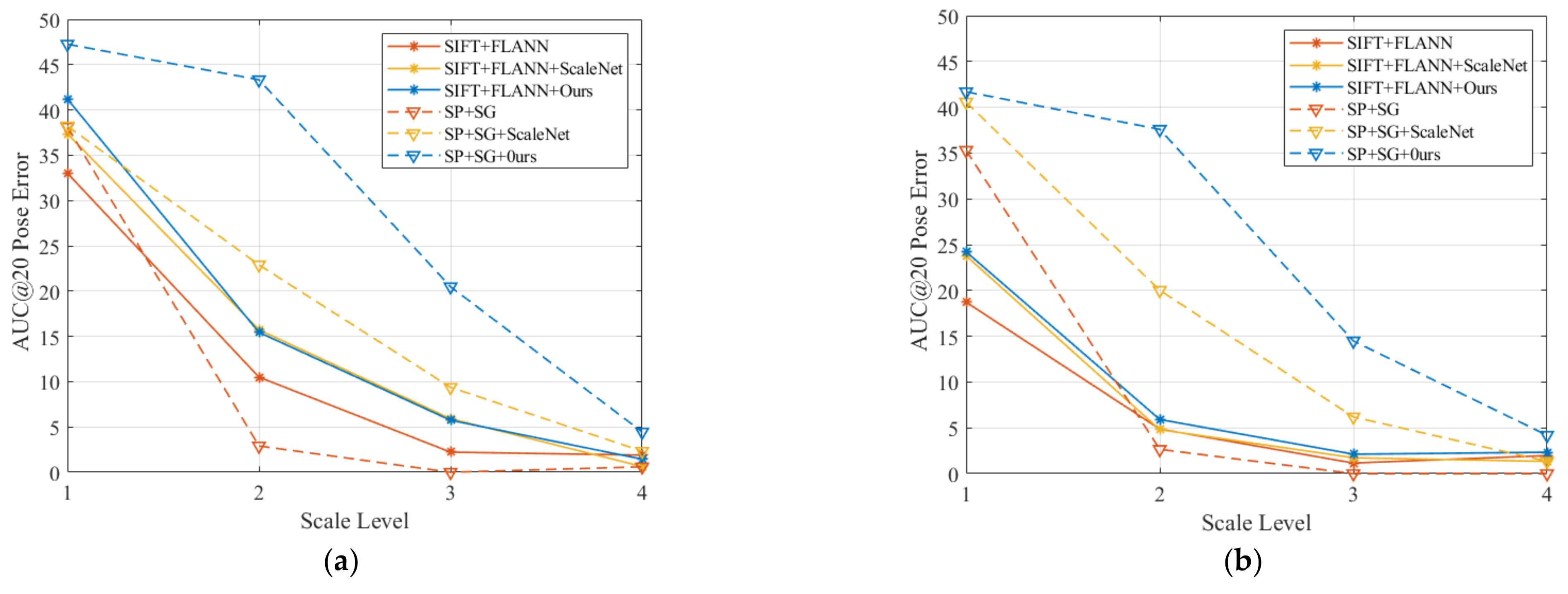
5.5. Relative Pose Estimation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

Appendix B
| Research Field in Deepspace Exploration | Related Work | The Advantages | The Disadvantages | Our Contributions (Proposing a New Method) |
|---|---|---|---|---|
| Image Local Feature Extraction And Matching | SIFT [24] + FLANN [27] | A robust performance to scale changes | Not available when scene lighting changes dramatically | More robust to changes in light |
| SuperPoint [12] + SuperGlue [13] | A robust performance to changes in light | Inability to adapt to large-scale changes | More robust to large-scale changes | |
| Pattern matching based on meteorite craters, etc. [9,10,11] | Suitable for SCB Scenarios | Deactivated when there are no craters in the field of view | No requirement for craters, rocks, etc., in the field of view, and a wide range of application | |
| Estimation Of Image Scale Ratio | ScaleNet [14] | Valid for most scale changes | Low accuracy in deep space scenes | Higher accuracy of scale estimation in deep space scenes |
| Multi-scale Modules | Image feature pyramids [16,17,41,42,43,44] | Ability to overcome scale changes | Limits to computational efficiency | More lightweight |
| ASPP [50,51,52,53] | Ability to extract multi-scale features in the network | Limited by deeper features | Better extraction of large-scale scene features |
References
- Ge, D.; Cui, P.; Zhu, S. Recent development of autonomous GNC technologies for small celestial body descent and landing. Prog. Aerosp. Sci. 2019, 110, 100551. [Google Scholar] [CrossRef]
- Song, J.; Rondao, D.; Aouf, N. Deep learning-based spacecraft relative navigation methods: A survey. Acta Astronaut. 2022, 191, 22–40. [Google Scholar] [CrossRef]
- Ye, M.; Li, F.; Yan, J.; Hérique, A.; Kofman, W.; Rogez, Y.; Andert, T.P.; Guo, X.; Barriot, J.P. Rosetta Consert Data as a Testbed for in Situ Navigation of Space Probes and Radiosciences in Orbit/Escort Phases for Small Bodies of the Solar System. Remote Sens. 2021, 13, 3747. [Google Scholar] [CrossRef]
- Zhong, W.; Jiang, J.; Ma, Y. L2AMF-Net: An L2-Normed Attention and Multi-Scale Fusion Network for Lunar Image Patch Matching. Remote Sens. 2022, 14, 5156. [Google Scholar] [CrossRef]
- Anzai, Y.; Yairi, T.; Takeishi, N.; Tsuda, Y.; Ogawa, N. Visual localization for asteroid touchdown operation based on local image features. Astrodynamics 2020, 4, 149–161. [Google Scholar] [CrossRef]
- de Santayana, R.P.; Lauer, M. Optical measurements for rosetta navigation near the comet. In Proceedings of the 25th International Symposium on Space Flight Dynamics (ISSFD), Munich, Germany, 19–23 October 2015. [Google Scholar]
- Takeishi, N.; Tanimoto, A.; Yairi, T.; Tsuda, Y.; Terui, F.; Ogawa, N.; Mimasu, Y. Evaluation of Interest-Region Detectors and Descriptors for Automatic Landmark Tracking on Asteroids. Trans. Jpn. Soc. Aeronaut. Space Sci. 2015, 58, 45–53. [Google Scholar] [CrossRef]
- Shao, W.; Cao, L.; Guo, W.; Xie, J.; Gu, T. Visual navigation algorithm based on line geomorphic feature matching for Mars landing. Acta Astronaut. 2020, 173, 383–391. [Google Scholar] [CrossRef]
- DeLatte, D.M.; Crites, S.T.; Guttenberg, N.; Yairi, T. Automated crater detection algorithms from a machine learning perspective in the convolutional neural network era. Adv. Space Res. 2019, 64, 1615–1628. [Google Scholar] [CrossRef]
- Cheng, Y.; Johnson, A.E.; Matthies, L.H.; Olson, C.F. Optical landmark detection for spacecraft navigation. Adv. Astronaut. Sci. 2003, 114, 1785–1803. [Google Scholar]
- Kim, J.R.; Muller, J.-P.; van Gasselt, S.; Morley, J.G.; Neukum, G. Automated crater detection, a new tool for Mars cartography and chronology. Photogramm. Eng. Remote Sens. 2005, 71, 1205–1217. [Google Scholar] [CrossRef]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar]
- Sarlin, P.E.; Detone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–29 June 2020; pp. 4938–4947. [Google Scholar]
- Barroso-Laguna, A.; Tian, Y.; Mikolajczyk, K. ScaleNet: A Shallow Architecture for Scale Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2022; pp. 12808–12818. [Google Scholar]
- Fu, Y.; Zhang, P.; Liu, B.; Rong, Z.; Wu, Y. Learning to Reduce Scale Differences for Large-Scale Invariant Image Matching. IEEE Trans. Circuits Syst. Video Technol. 2022, 61, 583–592. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Ghiasi, G.; Fowlkes, C.C. Laplacian Pyramid Reconstruction and Refinement for Semantic Segmentation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 519–534. [Google Scholar]
- Zhou, L.; Zhu, S.; Shen, T.; Wang, J.; Fang, T.; Quan, L. Progressive large-scale-invariant image matching in scale space. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2362–2371. [Google Scholar]
- Rau, A.; Garcia-Hernando, G.; Stoyanov, D.; Brostow, G.J.; Turmukhambetov, D. Predicting visual overlap of images through interpretable non-metric box embeddings. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 629–646. [Google Scholar]
- Jiang, X.; Ma, J.; Xiao, G.; Shao, Z.; Guo, X. A review of multimodal image matching: Methods and applications. Inf. Fusion 2021, 73, 22–71. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image matching from handcrafted to deep features: A survey. Int. J. Comput. Vis. 2021, 129, 23–79. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A combined corner and edge detector. Alvey Vis. Conf. 1988, 15, 10–5244. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin, Heidelberg, 2006; pp. 430–443. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar] [CrossRef]
- Yang, L.; Huang, Q.; Li, X.; Yuan, Y. Dynamic-scale grid structure with weighted-scoring strategy for fast feature matching. Appl. Intell. 2022, 52, 10576–10590. [Google Scholar] [CrossRef]
- Laguna, A.B.; Riba, E.; Ponsa, D.; Mikolajczyk, K. Key.Net: Keypoint Detection by Handcrafted and Learned CNN Filters. Proc. IEEE Int. Conf. Comput. Vis. 2019, 2019, 5835–5843. [Google Scholar] [CrossRef]
- Ono, Y.; Fua, P.; Trulls, E.; Yi, K.M. LF-Net: Learning Local Features from Images. Adv. Neural Inf. Process. Syst. 2018, 2018, 6234–6244. [Google Scholar]
- Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector-free local feature matching with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 21–24 June 2021; pp. 8922–8931. [Google Scholar]
- Shao, W.; Gu, T.; Ma, Y.; Xie, J.; Cao, L. A Novel Approach to Visual Navigation Based on Feature Line Correspondences for Precision Landing. J. Navig. 2018, 71, 1413–1430. [Google Scholar] [CrossRef]
- Matthies, L.; Huertas, A.; Cheng, Y.; Johnson, A. Stereo Vision and Shadow Analysis for Landing Hazard Detection. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 2735–2742. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, X.; Ye, Z.; Xie, H.; Liu, S.; Xu, X.; Tong, X. Robust Template Feature Matching Method Using Motion-Constrained DCF Designed for Visual Navigation in Asteroid Landing. Astrodynamics 2023, 7, 83–99. [Google Scholar] [CrossRef]
- Johnson, A.E.; Cheng, Y.; Matthies, L.H. Machine vision for autonomous small body navigation. In Proceedings of the 2000 IEEE Aerospace Conference. Proceedings (Cat. No. 00TH8484), Big Sky, MT, USA, 25 March 2000; Volume 7, pp. 661–671. [Google Scholar]
- Cocaud, C.; Kubota, T. SLAM-based navigation scheme for pinpoint landing on small celestial body. Adv. Robot. 2012, 26, 1747–1770. [Google Scholar] [CrossRef]
- Cheng, Y.; Miller, J.K. Autonomous landmark based spacecraft navigation system. In Proceedings of the 2003 AAS/AIAA Astrodynamics Specialist Conference, Big Sky, MT, USA, 13–17 August 2003. [Google Scholar]
- Yu, M.; Cui, H.; Tian, Y. A new approach based on crater detection and matching for visual navigation in planetary landing. Adv. Space Res. 2014, 53, 1810–1821. [Google Scholar] [CrossRef]
- Cui, P.; Gao, X.; Zhu, S.; Shao, W. Visual Navigation Using Edge Curve Matching for Pinpoint Planetary Landing. Acta Astronaut. 2018, 146, 171–180. [Google Scholar] [CrossRef]
- Tian, Y.; Yu, M. A novel crater recognition based visual navigation approach for asteroid precise pin-point landing. Aerosp. Sci. Technol. 2017, 70, 1–9. [Google Scholar] [CrossRef]
- Xiao, T.; Liu, Y.; Zhou, B.; Jiang, Y.; Sun, J. Unified Perceptual Parsing for Scene Understanding. In Proceedings of the Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 418–434. [Google Scholar]
- Eigen, D.; Fergus, R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2650–2658. [Google Scholar]
- Farabet, C.; Couprie, C.; Najman, L.; LeCun, Y. Learning Hierarchical Features for Scene Labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1915–1929. [Google Scholar] [CrossRef]
- Lin, G.; Shen, C.; Van Den Hengel, A.; Reid, I. Efficient piecewise training of deep structured models for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3194–3203. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Pohlen, T.; Hermans, A.; Mathias, M.; Leibe, B. Full-resolution residual networks for semantic segmentation in street scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4151–4160. [Google Scholar]
- Amirul Islam, M.; Rochan, M.; Bruce, N.D.B.; Wang, Y. Gated feedback refinement network for dense image labeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3751–3759. [Google Scholar]
- Oktay, O.; Schlemper, J.; Le Folgoc, L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:arXiv1804.03999. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected Crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Zhao, X.; Pang, Y.; Zhang, L.; Lu, H.; Zhang, L. Suppress and balance: A simple gated network for salient object detection. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 35–51. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Zhu, X.; Hu, H.; Lin, S.; Dai, J. Deformable Convnets V2: More Deformable, Better Results. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9300–9308. [Google Scholar]
- Liu, S.; Huang, D. Receptive field block net for accurate and fast object detection. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 385–400. [Google Scholar]
- Zhao, X.; Zhang, L.; Pang, Y.; Lu, H.; Zhang, L. A single stream network for robust and real-time RGB-D salient object detection. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 646–662. [Google Scholar]
- Rocco, I.; Arandjelovic, R.; Sivic, J. Convolutional neural network architecture for geometric matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6148–6157. [Google Scholar]
- Liu, Y.; Shao, Z.; Hoffmann, N. Global Attention Mechanism: Retain Information to Enhance Channel-Spatial Interactions. arXiv 2021, arXiv:2112.05561. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. Cbam: Convolutional Block Attention Module. In Proceedings of the Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Park, J.; Woo, S.; Lee, J.-Y.; Kweon, I.S. Bam: Bottleneck Attention Module. arXiv 2018, arXiv:1807.06514. [Google Scholar]
- Misra, D.; Nalamada, T.; Arasanipalai, A.U.; Hou, Q. Rotate to Attend: Convolutional Triplet Attention Module. In Proceedings of the Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Virtual, 5–9 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 3139–3148. [Google Scholar]
- Fukui, H.; Hirakawa, T.; Yamashita, T.; Fujiyoshi, H. Attention branch network: Learning of attention mechanism for visual explanation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 10705–10714. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Srinivas, A.; Lin, T.-Y.; Parmar, N.; Shlens, J.; Abbeel, P.; Vaswani, A. Bottleneck Transformers for Visual Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 16519–16529. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. International conference on machine learning. PMLR 2015, 37, 448–456. [Google Scholar]
- Glassmeier, K.H.; Boehnhardt, H.; Koschny, D.; Kührt, E.; Richter, I. The Rosetta Mission: Flying towards the Origin of the Solar System. Space Sci. Rev. 2007, 128, 1–21. [Google Scholar] [CrossRef]
- Saiki, T.; Takei, Y.; Fujii, A.; Kikuchi, S.; Terui, F.; Mimasu, Y.; Ogawa, N.; Ono, G.; Yoshikawa, K.; Tanaka, S. Overview of the Hayabusa2 Asteroid Proximity Operations. In Hayabusa2 Asteroid Sample Return Mission; Elsevier: Amsterdam, The Netherlands, 2022; pp. 113–136. [Google Scholar]
- Qin, X.; Zhang, Z.; Huang, C.; Dehghan, M.; Zaiane, O.R.; Jagersand, M. U2-Net: Going deeper with nested U-structure for salient object detection. Pattern Recognit. 2020, 106, 107404. [Google Scholar] [CrossRef]





| Scale Ratio Range | All | ||||
|---|---|---|---|---|---|
| Number of Pairs | 9145 | 2276 | 3349 | 2265 | 755 |
| Proportion | 100% | 30.4% | 36.6% | 24.8% | 8.3% |
| Model | All | ||||
|---|---|---|---|---|---|
| BoundingBoxes Algorithm | 1.184/0.280 | 0.036/0.044 | 0.075/0.150 | 1.966/0.423 | 7.556/1.233 |
| ScaleNet | 0.793/0.173 | 0.104/0.116 | 0.118/0.130 | 1.519/0.183 | 3.933/0.517 |
| DeepSpace-ScaleNet | 0.203/0.052 | 0.047/0.053 | 0.075/0.046 | 0.410/0.049 | 0.693/0.085 |
| Image Pairs | Ground-Truth | BoundingBoxes Algorithm | ScaleNet | DeepSpace-ScaleNet | |
|---|---|---|---|---|---|
| (a) |   | 1.15 | 1.14 | 1.32 | 1.16 |
| (b) |   | 8 | 8.29 | 7.23 | 8.06 |
| (c) |   | 13.5 | 13.43 | 11.49 | 13.53 |
| (d) |   | 18 | 13.07 | 12.75 | 18.02 |
| Average Absolute Discrepancy | Average L1 Discrepancy | |
|---|---|---|
| DeepSpace-ScaleNet w/o GA-DenseASPP | 0.236 | 0.057 |
| DeepSpace-ScaleNet w/o CADP | 0.237 | 0.061 |
| DeepSpace-ScaleNet | 0.203 | 0.052 |
| AUC@5 | AUC@10 | AUC@20 | |
|---|---|---|---|
| SIFT + FLANN | 4.46 | 7.88 | 14.05 |
| SIFT + FLANN + ScaleNet | 5.32 (19.34%↑) | 9.69 (23.02%↑) | 18.06 (28.56%↑) |
| SIFT + FLANN + Ours | 5.55 (24.41%↑) | 10.50 (33.27%↑) | 19.10 (35.96%↑) |
| SP + SG | 3.65 | 6.73 | 12.31 |
| SP + SG + ScaleNet | 4.97 (36.25%↑) | 10.56 (56.90%↑) | 21.84 (77.44%↑) |
| SP + SG + Ours | 8.55 (134.25%↑) | 16.96 (152.01%↑) | 34.74 (182.21%↑) |
| AUC@5 | AUC@10 | AUC@20 | |
|---|---|---|---|
| SIFT + FLANN | 2.29 | 4.19 | 7.59 |
| SIFT + FLANN + ScaleNet | 3.03 (32.29%↑) | 5.18 (23.68%↑) | 9.18 (20.93%↑) |
| SIFT + FLANN + Ours | 3.07 (34.18%↑) | 5.63 (34.51%↑) | 9.87 (29.99%↑) |
| SP + SG | 3.58 | 6.43 | 11.36 |
| SP + SG + ScaleNet | 5.23 (46.20%↑) | 10.42 (62.05%↑) | 20.63 (81.56%↑) |
| SP + SG + Ours | 6.97 (94.79%↑) | 13.96 (117.10%↑) | 29.42 (158.93%↑) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, M.; Lu, W.; Niu, W.; Peng, X.; Yang, Z. A Large-Scale Invariant Matching Method Based on DeepSpace-ScaleNet for Small Celestial Body Exploration. Remote Sens. 2022, 14, 6339. https://doi.org/10.3390/rs14246339
Fan M, Lu W, Niu W, Peng X, Yang Z. A Large-Scale Invariant Matching Method Based on DeepSpace-ScaleNet for Small Celestial Body Exploration. Remote Sensing. 2022; 14(24):6339. https://doi.org/10.3390/rs14246339
Chicago/Turabian StyleFan, Mingrui, Wenlong Lu, Wenlong Niu, Xiaodong Peng, and Zhen Yang. 2022. "A Large-Scale Invariant Matching Method Based on DeepSpace-ScaleNet for Small Celestial Body Exploration" Remote Sensing 14, no. 24: 6339. https://doi.org/10.3390/rs14246339
APA StyleFan, M., Lu, W., Niu, W., Peng, X., & Yang, Z. (2022). A Large-Scale Invariant Matching Method Based on DeepSpace-ScaleNet for Small Celestial Body Exploration. Remote Sensing, 14(24), 6339. https://doi.org/10.3390/rs14246339





