Multispectral Characteristics of Glacier Surface Facies (Chandra-Bhaga Basin, Himalaya, and Ny-Ålesund, Svalbard) through Investigations of Pixel and Object-Based Mapping Using Variable Processing Routines
Abstract
1. Introduction
2. Study Area and Data Used
3. Research Methodology
3.1. Summary of the Experiment
3.2. The Preprocessing Routines
3.2.1. Atmospheric Correction
3.2.2. Pansharpening and Glacier Boundary Digitization
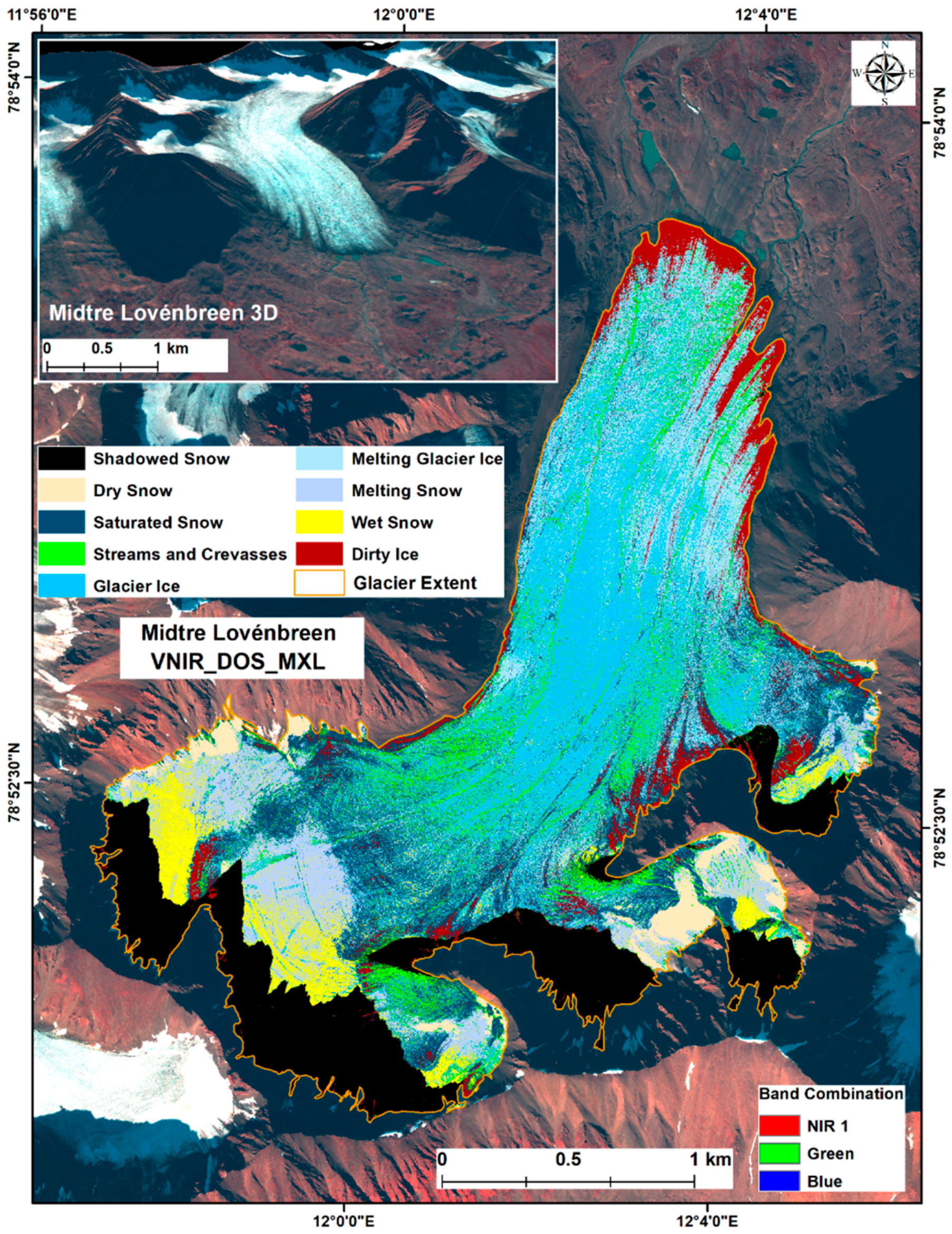
3.2.3. Identifying Glacier Surface Facies
3.3. Mapping Facies Using Conventional and Advanced Pixel-Based Image Analysis (PBIA)
3.4. Mapping Facies Using a Geographic Object-Based Image Analysis (GEOBIA)
3.4.1. Multiresolution Segmentation
3.4.2. Object Features and Rule Sets
3.5. Accuracy Assessment
4. Results and Discussion
4.1. Pixel-Based Image Analysis
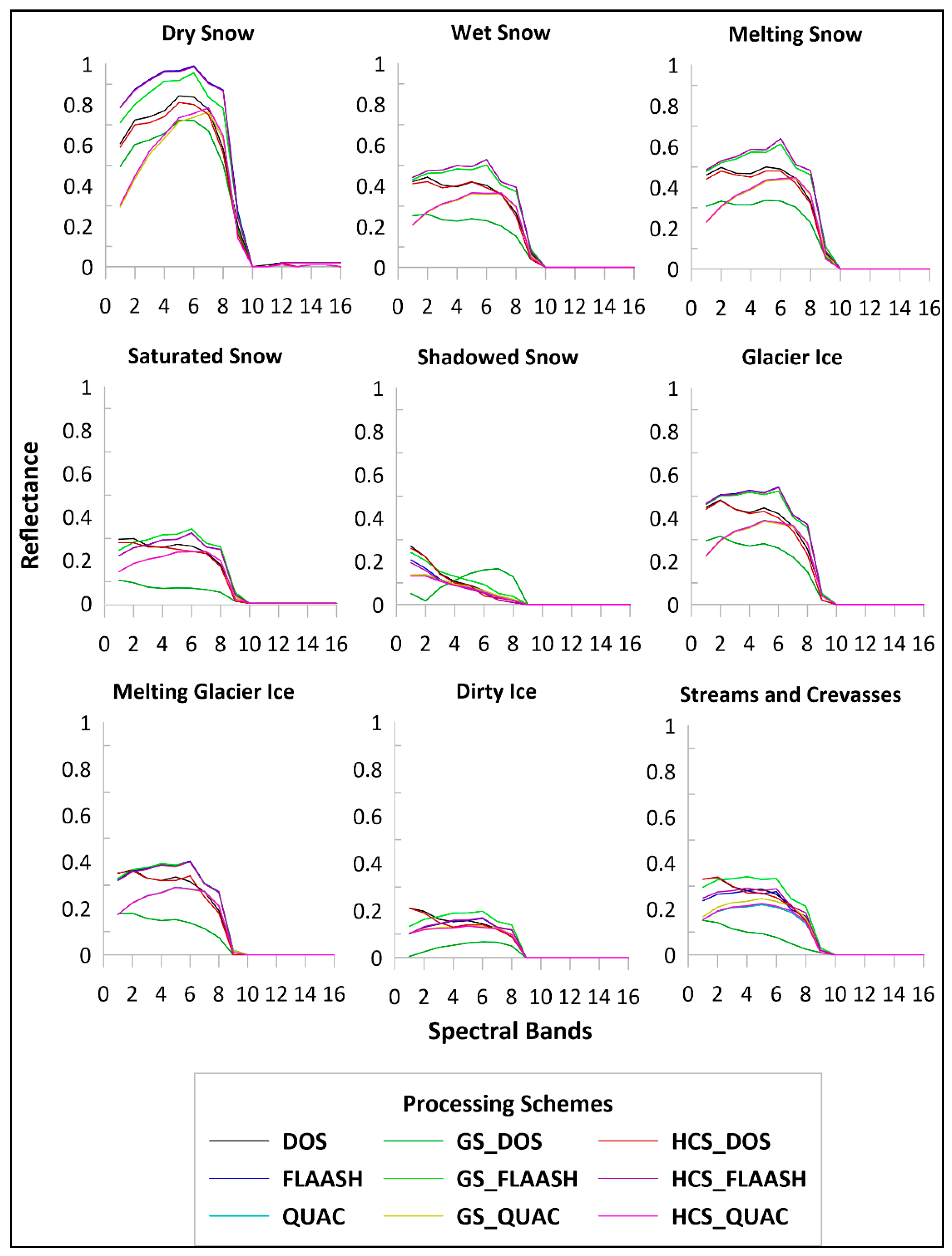
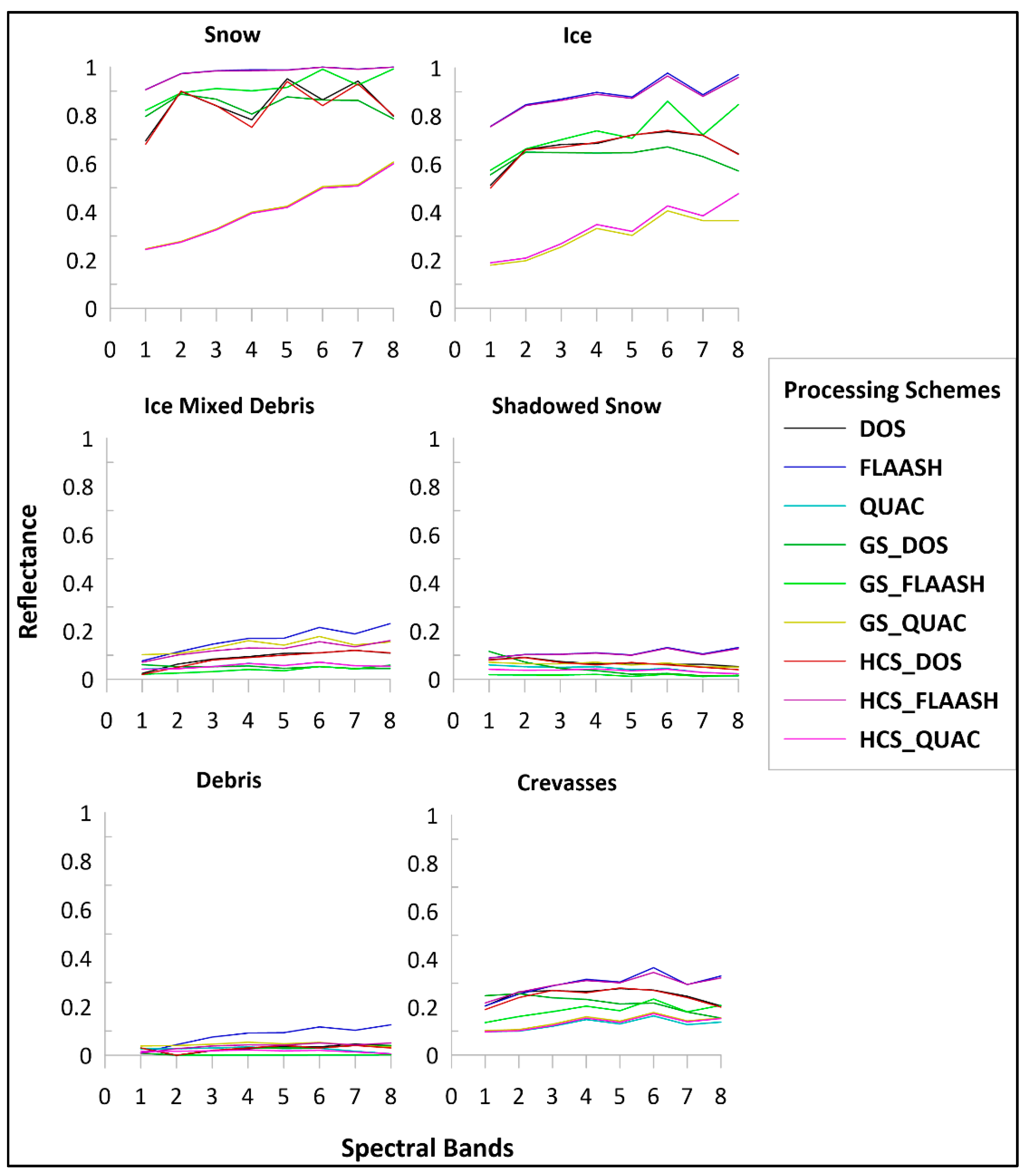
4.1.1. Effect of Atmospheric Corrections on PBIA
4.1.2. Effect of Pansharpening on PBIA
4.2. Geographic Object-Based Image Analysis
4.2.1. Effect of Atmospheric Corrections on GEOBIA
4.2.2. Effect of Pansharpening on GEOBIA
4.3. Discussion
4.3.1. Manifestation of Facies
4.3.2. Variations in the Best Performance
4.4. Comparative Analysis
Comparative Analysis of WV-2/3 Spectral Performance
4.5. Final Inferences and Recommendations
4.6. Significances and Limitations
Future Directions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Braun, M.; Schuler, T.V.; Hock, R.; Brown, I.; Jackson, M. Comparison of remote sensing derived glacier facies maps with distributed mass balance modelling at Engabreen, Northern Norway. IAHS Publ. Ser. Proc. Rep. 2007, 318, 126–134. [Google Scholar]
- Luis, A.J.; Singh, S. High-resolution multispectral mapping facies on glacier surface in the Arctic using World, View-3 data. Czech Polar Rep. 2020, 10, 23–36. [Google Scholar] [CrossRef]
- Jawak, S.D.; Wankhede, S.F.; Luis, A.J. Explorative Study on Mapping Surface Facies of Selected Glaciers from Chandra Basin, Himalaya Using World, View-2 Data. Remote Sens. 2019, 11, 1207. [Google Scholar] [CrossRef]
- Jawak, S.D.; Wankhede, S.F.; Luis, A.J.; Pandit, P.H.; Kumar, S. Implementing an object-based multi-index protocol for mapping surface glacier facies from Chandra-Bhaga basin, Himalaya. Czech Polar Rep. 2019, 9, 125–140. [Google Scholar] [CrossRef]
- Keshri, A.K.; Shukla, A.; Gupta, R.P. ASTER ratio indices for supraglacial terrain mapping. Int. J. Remote Sens. 2009, 30, 519–524. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Joshi, P.; Snehmani; Singh, M.; Sam, L.; Gupta, R. Mapping debris-covered glaciers and identifying factors affecting the accuracy. Cold Reg. Sci. Technol. 2014, 106–107, 161–174. [Google Scholar] [CrossRef]
- Pope, A.; Rees, W.G. Impact of spatial, spectral, and radiometric properties of multispectral imagers on glacier surface classification. Remote Sens. Environ. 2014, 141, 1–13. [Google Scholar] [CrossRef]
- Kundu, S.; Chakraborty, M. Delineation of glacial zones of Gangotri and other glaciers of Central Himalaya using RISAT-1 C-band dual-pol SAR. Int. J. Remote Sens. 2015, 36, 1529–1550. [Google Scholar] [CrossRef]
- Robson, B.; Nuth, C.; Dahl, S.; Hölbling, D.; Strozzi, T.; Nielsen, P. Automated classification of debris-covered glaciers combining optical, SAR and topographic data in an object-based environment. Remote Sens. Environ. 2015, 170, 372–387. [Google Scholar] [CrossRef]
- Gore, A.; Mani, S.; Shekhar, C.; Ganju, A. Glacier surface characteristics derivation and monitoring using Hyperspectral datasets: A case study of Gepang Gath glacier, Western Himalaya. Geocarto Int. 2017, 34, 23–42. [Google Scholar] [CrossRef]
- Yousuf, B.; Shukla, A.; Arora, M.K.; Jasrotia, A.S. Glacier facies characterization using optical satellite data: Impacts of radiometric resolution, seasonality, and surface morphology. Prog. Phys. Geogr. Earth Environ. 2019, 43, 473–495. [Google Scholar] [CrossRef]
- Foster, L.A.; Brock, B.W.; Cutler, M.E.J.; Diotri, F. A physically based method for estimating supraglacial debris thickness from thermal band remote-sensing data. J. Glaciol. 2012, 58, 677–691. [Google Scholar] [CrossRef]
- Zhang, Y.; Hirabayashi, Y.; Fujita, K.; Liu, S.; Liu, Q. Heterogeneity in supraglacial debris thickness and its role in glacier mass changes of the Mount Gongga. Sci. China Earth Sci. 2015, 59, 170–184. [Google Scholar] [CrossRef]
- Pandey, A.; Rai, A.; Gupta, S.K.; Shukla, D.P.; Dimri, A. Integrated approach for effective debris mapping in glacierized regions of Chandra River Basin, Western Himalayas, India. Sci. Total Environ. 2021, 779, 146492. [Google Scholar] [CrossRef]
- Winsvold, S.H.; Kaab, A.; Nuth, C. Regional Glacier Mapping Using Optical Satellite Data Time Series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3698–3711. [Google Scholar] [CrossRef]
- Pope, A.; Rees, G. Using in situ spectra to explore Landsat classification of glacier surfaces. Int. J. Appl. Earth Obs. Geoinf. 2014, 27, 42–52. [Google Scholar] [CrossRef]
- Paul, F.; Winsvold, S.H.; Kääb, A.; Nagler, T.; Schwaizer, G. Glacier Remote Sensing Using Sentinel-2. Part II: Mapping Glacier Extents and Surface Facies, and Comparison to Landsat 8. Remote Sens. 2016, 8, 575. [Google Scholar] [CrossRef]
- Jawak, S.D.; Wankhede, S.F.; Luis, A.J.; Balakrishna, K. Impact of Image-Processing Routines on Mapping Glacier Surface Facies from Svalbard and the Himalayas Using Pixel-Based Methods. Remote Sens. 2022, 14, 1414. [Google Scholar] [CrossRef]
- Jensen, J.R.; Lulla, K. Introductory digital image processing: A remote sensing perspective. Geocarto Int. 1987, 2, 65. [Google Scholar] [CrossRef]
- Arbiol, R.; Zhang, Y.; i Comellas, V.P. Advanced classification techniques: A review. Rev. Catalana Geogr. 2007, 12, 31. [Google Scholar]
- Weih, R.C.; Riggan, N.D. Object-based classification vs. pixel-based classification: Comparative importance of multi-resolution imagery. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2010, 38, C7. [Google Scholar]
- Mitkari, K.V.; Arora, M.K.; Tiwari, R.K.; Sofat, S.; Gusain, H.S.; Tiwari, S.P. Large-Scale Debris Cover Glacier Mapping Using Multisource Object-Based Image Analysis Approach. Remote Sens. 2022, 14, 3202. [Google Scholar] [CrossRef]
- Sharda, S.; Srivastava, M. Classification of Siachen Glacier Using Object-Based Image Analysis. In Proceedings of the 2018 International Conference on Intelligent Circuits and Systems (ICICS), Phagwara, India, 19–20 April 2018. [Google Scholar]
- Gao, B.C.; Davis, C.; Goetz, A. A review of atmospheric correction techniques for hyperspectral remote sensing of land surfaces and ocean color. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 1979–1981. [Google Scholar] [CrossRef]
- Lee, K.H.; Yum, J.M. A Review on Atmospheric Correction Technique Using Satellite Remote Sensing. Korean J. Remote Sens. 2019, 35, 1011–1030. [Google Scholar] [CrossRef]
- Gao, B.C.; Montes, M.J.; Davis, C.O.; Goetz, A.F. Atmospheric correction algorithms for hyperspectral remote sensing data of land and ocean. Remote Sens. Environ. 2009, 113, S17–S24. [Google Scholar] [CrossRef]
- Guo, Y.; Zeng, F. Asstmospheric correction comparison of SPOT-5 image based on model FLAASH and model QUAC. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 21–23. [Google Scholar]
- Nazeer, M.; Nichol, J.E.; Yung, Y.K. Evaluation of atmospheric correction models and Landsat surface reflectance product in an urban coastal environment. Int. J. Remote Sens. 2014, 35, 6271–6291. [Google Scholar] [CrossRef]
- Mandanici, E.; Franci, F.; Bitelli, G.; Agapiou, A.; Alexakis, D.; Hadjimitsis, D.G. Comparison between empirical and physically based models of atmospheric correction. In Proceedings of the Third International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2015), Paphos, Cyprus, 16–19 March 2015; Volume 9535, pp. 110–119. [Google Scholar] [CrossRef]
- Eugenio, F.; Marcello, J.; Martin, J.; Rodríguez-Esparragón, D. Benthic Habitat Mapping Using Multispectral High-Resolution Imagery: Evaluation of Shallow Water Atmospheric Correction Techniques. Sensors 2017, 17, 2639. [Google Scholar] [CrossRef]
- Karimi, N.; Farokhnia, A.; Karimi, L.; Eftekhari, M.; Ghalkhani, H. Combining optical and thermal remote sensing data for mapping debris-covered glaciers (Alamkouh Glaciers, Iran). Cold Reg. Sci. Technol. 2012, 71, 73–83. [Google Scholar] [CrossRef]
- Albert, T.H. Evaluation of Remote Sensing Techniques for Ice-Area Classification Applied to the Tropical Quelccaya Ice Cap, Peru. Polar Geogr. 2002, 26, 210–226. [Google Scholar] [CrossRef]
- Guo, Z.; Geng, L.; Shen, B.; Wu, Y.; Chen, A.; Wang, N. Spatiotemporal Variability in the Glacier Snowline Altitude across High Mountain Asia and Potential Driving Factors. Remote Sens. 2021, 13, 425. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Alparone, L.; Aiazzi, B.; Baronti, S. Pan-sharpening of multispectral images: A critical review and comparison. In Proceedings of the IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, Y.; Li, B. Recent advances in pansharpening and key problems in applications. Int. J. Image Data Fusion 2014, 5, 175–195. [Google Scholar] [CrossRef]
- Snehmani, A.G.; Ganju, A.; Kumar, S.; Srivastava, P.K.; Hari Ram, R.P. A comparative analysis of pansharpening techniques on Quick, Bird and World, View-3 images. Geocarto Int. 2016, 32, 1268–1284. [Google Scholar] [CrossRef]
- Jawak, S.D.; Wankhede, S.F.; Luis, A.J.; Balakrishna, K. Effect of Image-Processing Routines on Geographic Object-Based Image Analysis for Mapping Glacier Surface Facies from Svalbard and the Himalayas. Remote Sens. 2022, 14, 4403. [Google Scholar] [CrossRef]
- Isaksen, K.; Nordli, Ø.; Førland, E.J.; Lupikasza, E.; Eastwood, S.; Niedźwiedź, T. Recent warming on Spitsbergen—Influence of atmospheric circulation and sea ice cover. J. Geophys. Res. Atmos. 2016, 121, 121. [Google Scholar] [CrossRef]
- Pandey, P.; Ali, S.N.; Ramanathan, A.L.; Venkataraman, G. Regional representation of glaciers in Chandra Basin region, western Himalaya, India. Geosci. Front. 2017, 8, 841–850. [Google Scholar] [CrossRef][Green Version]
- Pandey, P.; Venkataraman, G. Changes in the glaciers of Chandra–Bhaga basin, Himachal Himalaya, India, between 1980 and 2010 measured using remote sensing. Int. J. Remote Sens. 2013, 34, 5584–5597. [Google Scholar] [CrossRef]
- Raup, B.; Racoviteanu, A.; Khalsa, S.J.; Helm, C.; Armstrong, R.; Arnaud, Y. The GLIMS geospatial glacier database: A new tool for studying glacier change. Glob. Planet. Chang. 2007, 56, 101–110. [Google Scholar] [CrossRef]
- Digital Globe Product Details. Available online: https://www.geosoluciones.cl/documentos/worldview/Digital,Globe-Core-Imagery-Products-Guide.pdf (accessed on 20 February 2020).
- ASTER GDEM v2. Available online: Gdex.cr.usgs.gov/gdex/ (accessed on 2 February 2017).
- Arctic DEM. Available online: www.pgc.umn.edu/data/arcticdem/ (accessed on 21 January 2019).
- Porter, C.; Morin, P.; Howat, I.; Noh, M.-J.; Bates, B.; Peterman, K.; Keesey, S.; Schlenk, M.; Gardiner, J.; Tomko, K.; et al. “ArcticDEM”, Harvard Dataverse, V1. 2018. Available online: https://www.pgc.umn.edu/data/arcticdem/ (accessed on 13 March 2022).
- Radiative Transfer Code. Available online: https://www.harrisgeospatial.com/docs/backgroundflaash.html (accessed on 17 February 2017).
- Atmospheric Correction User Guide. Available online: https://www.l3harrisgeospatial.com/portals/0/pdfs/envi/Flaash_Module.pdf (accessed on 17 February 2017).
- Kaufman, Y.; Wald, A.; Remer, L.; Gao, B.-C.; Li, R.-R.; Flynn, L. The MODIS 2.1-μm channel-correlation with visible reflectance for use in remote sensing of aerosol. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1286–1298. [Google Scholar] [CrossRef]
- Abreu, L.W.; Anderson, G.P. The MODTRAN 2/3 report and LOWTRAN 7 model. Contract 1996, 19628, 132. [Google Scholar]
- Teillet, P.; Fedosejevs, G. On the Dark Target Approach to Atmospheric Correction of Remotely Sensed Data. Can. J. Remote Sens. 1995, 21, 374–387. [Google Scholar] [CrossRef]
- Zhang, Z.; He, G.; Zhang, X.; Long, T.; Wang, G.; Wang, M. A coupled atmospheric and topographic correction algorithm for remotely sensed satellite imagery over mountainous terrain. GISci. Remote Sens. 2017, 55, 400–416. [Google Scholar] [CrossRef]
- Rumora, L.; Miler, M.; Medak, D. Impact of Various Atmospheric Corrections on Sentinel-2 Land Cover Classification Accuracy Using Machine Learning Classifiers. ISPRS Int. J. Geo-Inform. 2020, 9, 277. [Google Scholar] [CrossRef]
- Bernstein, L.S.; Jin, X.; Gregor, B.; Adler-Golden, S.M. Quick atmospheric correction code: Algorithm description and recent upgrades. Opt. Eng. 2012, 51, 111719. [Google Scholar] [CrossRef]
- Pushparaj, J.; Hegde, A.V. Evaluation of pan-sharpening methods for spatial and spectral quality. Appl. Geomat. 2016, 9, 1–12. [Google Scholar] [CrossRef]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
- Bhardwaj, A.; Joshi, P.; Snehmani; Sam, L.; Singh, M.; Singh, S.; Kumar, R. Applicability of Landsat 8 data for characterizing glacier facies and supraglacial debris. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 51–64. [Google Scholar] [CrossRef]
- De Angelis, H.; Rau, F.; Skvarca, P. Snow zonation on Hielo Patagónico Sur, Southern Patagonia, derived from Landsat 5 TM data. Glob. Planet. Chang. 2007, 59, 149–158. [Google Scholar] [CrossRef]
- Shukla, A.; Ali, I. A hierarchical knowledge-based classification for glacier terrain mapping: A case study from Kolahoi Glacier, Kashmir Himalaya. Ann. Glaciol. 2016, 57, 1–10. [Google Scholar] [CrossRef]
- Baatz, M.; Schape, A. Multiresolution Segmentation: An Optimization Approach for High Quality Multi-Scale Image Segmentation. In Angewandte Geographische Informations-Verarbeitung, XII; Strobl, J., Blaschke, T., Griesbner, G., Eds.; Wichmann Verlag: Heidelberg/Karlsruhe, Germany, 2000; pp. 12–23. [Google Scholar]
- Han, Y.; Javed, A.; Jung, S.; Liu, S. Object-Based Change Detection of Very High Resolution Images by Fusing Pixel-Based Change Detection Results Using Weighted Dempster–Shafer Theory. Remote Sens. 2020, 12, 983. [Google Scholar] [CrossRef]
- Trimble GmbH. eCognition Developer 9.0 User Guide; Trimble Germany GmbH: Munich, Germany, 2014. [Google Scholar]
- Richards, J.A. Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Maxwell, A.E.; Warner, T.A. Thematic Classification Accuracy Assessment with Inherently Uncertain Boundaries: An Argument for Center-Weighted Accuracy Assessment Metrics. Remote Sens. 2020, 12, 1905. [Google Scholar] [CrossRef]
- Mölg, N.; Bolch, T.; Rastner, P.; Strozzi, T.; Paul, F. A consistent glacier inventory for Karakoram and Pamir derived from Landsat data: Distribution of debris cover and mapping challenges. Earth Syst. Sci. Data 2018, 10, 1807–1827. [Google Scholar] [CrossRef]
- Garg, V.; Thakur, P.K.; Rajak, D.R.; Aggarwal, S.P.; Kumar, P. Spatio-temporal changes in radar zones and ELA estimation of glaciers in Ny-Ålesund using Sentinel-1 SAR. Polar Sci. 2022, 31, 100786. [Google Scholar] [CrossRef]
- Casacchia, R.; Lauta, F.; Salvatori, R.; Cagnati, A.; Valt, M.; Ørbæk, J.B. Radiometric investigation of different snow covers in Svalbard. Polar Res. 2001, 20, 13–22. [Google Scholar] [CrossRef][Green Version]
- Snapir, B.; Momblanch, A.; Jain, S.K.; Waine, T.W.; Holman, I.P. A method for monthly mapping of wet and dry snow using Sentinel-1 and MODIS: Application to a Himalayan river basin. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 222–230. [Google Scholar] [CrossRef]
- Karbou, F.; Veyssière, G.; Coleou, C.; Dufour, A.; Gouttevin, I.; Durand, P.; Gascoin, S.; Grizonnet, M. Monitoring Wet Snow Over an Alpine Region Using Sentinel-1 Observations. Remote Sens. 2021, 13, 381. [Google Scholar] [CrossRef]
- Nagajothi, V.; Geetha, P.M.; Sharma, P.; Krishnaveni, D. Classification of Dry/Wet Snow Using Sentinel-2 High Spatial Resolution Optical Data. In Intelligent Data Engineering and Analytics; Springer: Singapore, 2021; pp. 1–9. [Google Scholar] [CrossRef]
- Yousuf, B.; Shukla, A.; Arora, M.K. Temporal Variability of the Satopanth Glacier Facies at Sub-pixel Scale, Garhwal Himalaya, India. In Mountain Landscapes in Transition; Springer: Cham, Switzerland, 2022; pp. 207–218. [Google Scholar] [CrossRef]
- Ji, X.; Chen, Y.; Tong, L.; Jia, M.; Tan, L.; Fan, S. Area retrieval of melting snow in alpine areas. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3991–3993. [Google Scholar] [CrossRef]
- Vickers, H.; Malnes, E.; Eckerstorfer, M. A Synthetic Aperture Radar Based Method for Long Term Monitoring of Seasonal Snowmelt and Wintertime Rain-On-Snow Events in Svalbard. Front. Earth Sci. 2022, 10, 2296–6463. [Google Scholar] [CrossRef]
- Aggarwal, S.P.; Thakur, P.K.; Nikam, B.R.; Garg, V. Integrated approach for snowmelt run-off estimation using temperature index model, remote sensing and GIS. Curr. Sci. 2014, 106, 397–407. [Google Scholar]
- Liang, D.; Guo, H.; Zhang, L.; Cheng, Y.; Zhu, Q.; Liu, X. Time-series snowmelt detection over the Antarctic using Sentinel-1 SAR images on Google Earth Engine. Remote Sens. Environ. 2021, 256, 112318. [Google Scholar] [CrossRef]
- Mendes, C.W., Jr.; Arigony, N.J.; Hillebrand, F.L.; De Freitas, M.W.D.; Costi, J.; Simões, J.C. Snowmelt retrieval algorithm for the Antarctic Peninsula using SAR imageries. An. Acad. Bras. Cienc. 2022, 94, e20210217. [Google Scholar] [CrossRef]
- Paterson, W.S.B. The Physics of Glaciers; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Hinkler, J.; Ørbæk, J.B.; Hansen, B.U. Detection of spatial, temporal, and spectral surface changes in the Ny-Ålesund area 79° N, Svalbard, using a low cost multispectral camera in combination with spectroradiometer measurements. Phys. Chem. Earth Parts A/B/C 2003, 28, 1229–1239. [Google Scholar] [CrossRef]
- Prieur, C.; Rabatel, A.; Thomas, J.-B.; Farup, I.; Chanussot, J. Machine Learning Approaches to Automatically Detect Glacier Snow Lines on Multi-Spectral Satellite Images. Remote Sens. 2022, 14, 3868. [Google Scholar] [CrossRef]
- Azzoni, R.S.; Fugazza, D.; Zerboni, A.; Senese, A.; D’Agata, C.; Maragno, D.; Carzaniga, A.; Cernuschi, M.; Diolaiuti, G.A. Evaluating high-resolution remote sensing data for reconstructing the recent evolution of supra glacial debris: A study in the Central Alps (Stelvio Park, Italy). Prog. Phys. Geogr. Earth Environ. 2018, 42, 3–23. [Google Scholar] [CrossRef]
- Alifu, H.; Johnson, B.A.; Tateishi, R. Delineation of Debris-Covered Glaciers Based on a Combination of Geomorphometric Parameters and a TIR/NIR/SWIR Band Ratio. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 781–792. [Google Scholar] [CrossRef]
- Ambinakudige, S.; Intsiful, A. Estimation of area and volume change in the glaciers of the Columbia Icefield, Canada using machine learning algorithms and Landsat images. Remote Sens. Appl. Soc. Environ. 2022, 26, 100732. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Fyffe, C.L.; Woodget, A.S.; Kirkbride, M.P.; Deline, P.; Westoby, M.J.; Brock, B.W. Processes at the margins of supraglacial debris cover: Quantifying dirty ice ablation and debris redistribution. Earth Surf. Process. Landf. 2020, 45, 2272–2290. [Google Scholar] [CrossRef]
- Chandler, D.M.; Alcock, J.D.; Wadham, J.L.; Mackie, S.L.; Telling, J. Seasonal changes of ice surface characteristics and productivity in the ablation zone of the Greenland Ice Sheet. Cryosphere 2015, 9, 487–504. [Google Scholar] [CrossRef]
- Østrem, G. Ice melting under a thin layer of moraine, and the existence of ice cores in moraine ridges. Geogr. Ann. 1959, 41, 228–230. [Google Scholar] [CrossRef]
- Østrem, G. Problems of dating ice-cored moraines. Geogr. Ann. Ser. A Phys. Geogr. 1965, 47, 1–38. [Google Scholar] [CrossRef]
- Haq, M.A.; Alshehri, M.; Rahaman, G.; Ghosh, A.; Baral, P.; Shekhar, C. Snow and glacial feature identification using Hyperion dataset and machine learning algorithms. Arab. J. Geosci. 2021, 14, 1525. [Google Scholar] [CrossRef]
- Croot, D.G.; Sharp, R.P. Living ice. Understanding glaciers and glaciation. Geogr. J. 2006, 155, 410. [Google Scholar] [CrossRef]
- Florath, J.; Keller, S.; Abarca-del-Rio, R.; Hinz, S.; Staub, G.; Weinmann, M. Glacier Monitoring Based on Multi-Spectral and Multi-Temporal Satellite Data: A Case Study for Classification with Respect to Different Snow and Ice Types. Remote Sens. 2022, 14, 845. [Google Scholar] [CrossRef]
- Bennett, M. Glaciers and Glaciation; Benn, D.I., Evans, D.J.A., Eds.; Boreas: London, UK, 2011. [Google Scholar] [CrossRef]
- Pandey, A.; Rai, A.; Gupta, S.K.; Shukla, D.P. Hierarchical Knowledge Based Classification (Hkbc) On Sentinel-2a Data for Glacier Mapping of Bhaga River Basin, Northwest Himalaya. Red 2017, 10, 665. [Google Scholar]
- Ali, I.; Shukla, A.; Romshoo, S. Assessing linkages between spatial facies changes and dimensional variations of glaciers in the upper Indus Basin, western Himalaya. Geomorphology 2017, 284, 115–129. [Google Scholar] [CrossRef]
- Shukla, A.; Gupta, R.; Arora, M. Estimation of debris cover and its temporal variation using optical satellite sensor data: A case study in Chenab basin, Himalaya. J. Glaciol. 2009, 55, 444–452. [Google Scholar] [CrossRef]
- Shukla, A.; Arora, M.; Gupta, R. Synergistic approach for mapping debris-covered glaciers using optical–thermal remote sensing data with inputs from geomorphometric parameters. Remote Sens. Environ. 2010, 114, 1378–1387. [Google Scholar] [CrossRef]
- Ghosh, S.; Pandey, A.C.; Nathawat, M.S. Mapping of debris-covered glaciers in parts of the Greater Himalaya Range, Ladakh, western Himalaya, using remote sensing and GIS. J. Appl. Remote Sens. 2014, 8, 083579. [Google Scholar] [CrossRef]
- Fleischer, F.; Otto, J.C.; Junker, R.R.; Hölbling, D. Evolution of debris cover on glaciers of the Eastern Alps, Austria, between 1996 and 2015. Earth Surf. Process. Landf. 2021, 46, 1673–1691. [Google Scholar] [CrossRef]
- Kirkbride, M.P. Debris-Covered Glaciers. In Encyclopedia of Snow, Ice and Glaciers; Singh, V.P., Singh, P., Haritashya, U.K., Eds.; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar] [CrossRef]
- Shrestha, R.; Kayastha, R.B.; Kayastha, R. Effect of debris on seasonal ice melt (2016−2018) on Ponkar Glacier, Manang, Nepal. Sci. Cold Arid. Reg. 2020, 12, 261–271. [Google Scholar] [CrossRef]
- Pratibha, S.; Kulkarni, A.V. Decadal change in supraglacial debris cover in Baspa basin, Western Himalaya. Curr. Sci. 2018, 114, 792–799. [Google Scholar] [CrossRef]
- Gibson, M.J.; Glasser, N.F.; Quincey, D.J.; Mayer, C.; Rowan, A.V.; Irvine-Fynn, T.D. Temporal variations in supraglacial debris distribution on Baltoro Glacier, Karakoram between 2001 and 2012. Geomorphology 2017, 295, 572–585. [Google Scholar] [CrossRef]
- Nicholson, L.I.; McCarthy, M.; Pritchard, H.D.; Willis, I. Supraglacial debris thickness variability: Impact on ablation and relation to terrain properties. Cryosphere 2018, 12, 3719–3734. [Google Scholar] [CrossRef]
- Racoviteanu, A.E.; Nicholson, L.; Glasser, N.F. Surface composition of debris-covered glaciers across the Himalaya using linear spectral unmixing of Landsat 8 OLI imagery. Cryosphere 2021, 15, 4557–4588. [Google Scholar] [CrossRef]
- Kaushik, S.; Singh, T.; Bhardwaj, A.; Joshi, P.K.; Dietz, A.J. Automated Delineation of Supraglacial Debris Cover Using Deep Learning and Multisource Remote Sensing Data. Remote Sens. 2022, 14, 1352. [Google Scholar] [CrossRef]
- Jawak, S.D.; Jadhav, A.; Luis, A.J. Object-oriented feature extraction approach for mapping supraglacial debris in Schirmacher Oasis using very high-resolution satellite data. In Land Surface and Cryosphere Remote Sensing III; SPIE: Bellingham, WA, USA, 2016; Volume 9877, pp. 337–345. [Google Scholar] [CrossRef]
- Bennett, M.M.; Glasser, N.F. (Eds.) Glacial Geology: Ice Sheets and Landforms; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Colgan, W.; Rajaram, H.; Abdalati, W.; McCutchan, C.; Mottram, R.; Moussavi, M.S.; Grigsby, S. Glacier crevasses: Observations, models, and mass balance implications. Rev. Geophys. 2016, 54, 119–161. [Google Scholar] [CrossRef]
- Chen, F. Comparing Methods for Segmenting Supra-Glacial Lakes and Surface Features in the Mount Everest Region of the Himalayas Using Chinese GaoFen-3 SAR Images. Remote Sens. 2021, 13, 2429. [Google Scholar] [CrossRef]
- Singh, K.K.; Negi, H.S.; Ganju, A.; Kulkarni, A.V.; Kumar, A.; Mishra, V.D.; Kumar, S. Crevasses detection in Himalayan glaciers using ground-penetrating radar. Curr. Sci. 2013, 105, 1288–1295. [Google Scholar]
- Taurisano, A.; Tronstad, S.; Brandt, O.; Kohler, J. On the use of ground penetrating radar for detecting and reducing crevasse-hazard in Dronning Maud Land, Antarctica. Cold Reg. Sci. Technol. 2006, 45, 166–177. [Google Scholar] [CrossRef]
- Hao, S.; Cui, Y.; Wang, J. Segmentation Scale Effect Analysis in the Object-Oriented Method of High-Spatial-Resolution Image Classification. Sensors 2021, 21, 7935. [Google Scholar] [CrossRef]
- Hossain, M.D.; Chen, D.M. Segmentation for Object-based Image analysis (OBIA): A review of algorithm and challenges from remote sensing perspective. ISPRS J. Photogram. Remote Sens. 2019, 150, 115–134. [Google Scholar] [CrossRef]
- Arifjanov, A.M.; Akmalov, S.B.; Apakhodjaeva, T.U.; Tojikhodjaeva, D.S. Comparison Of Pixel To Pixel And Object Based Image Analysis with using Worldview-2 Satellite Images of Yangiobod Village of Syrdarya Province. Интеркартo. Интергис 2020, 26, 313–321. [Google Scholar] [CrossRef]
- Kucharczyk, M.; Hay, G.J.; Ghaffarian, S.; Hugenholtz, C.H. Geographic Object-Based Image Analysis: A Primer and Future Directions. Remote Sens. 2020, 12, 2012. [Google Scholar] [CrossRef]
- Arundel, S.T. Pairing semantics and object-based image analysis for national terrain mapping—A first-case scenario of cirques. In Proceedings of the GEOBIA 2016: Solutions and synergies, Enschede, The Netherlands, 14–16 September 2016; University of Twente Faculty of Geo-Information and Earth Observation (ITC): Enschede, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Garajeh, M.K.; Blaschke, T.; Lakes, T. An object based image analysis applied for volcanic and glacial landforms mapping in Sahand Mountain, Iran. Catena 2021, 198, 105073. [Google Scholar] [CrossRef]
- Robb, C.; Willis, I.; Arnold, N.; Guðmundsson, S. A semi-automated method for mapping glacial geomorphology tested at Breiðamerkurjökull, Iceland. Remote Sens. Environ. 2015, 163, 80–90. [Google Scholar] [CrossRef]
- Dabiri, Z.; Hölbling, D.; Abad, L.; Prasicek, G.; Argentin, A.L.; Tsai, T.T. An Object-Based Approach for Monitoring the Evolution of Landslide-dammed Lakes and Detecting Triggering Landslides in Taiwan. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 103–108. [Google Scholar] [CrossRef]
- Farhan, S.B.; Kainat, M.; Shahzad, A.; Aziz, A.; Kazmi, S.J.H.; Shaikh, S.; Zhang, Y.; Gao, H.; Javed, M.N.; Zamir, U.B. Discrimination of Seasonal Snow Cover in Astore Basin, Western Himalaya using Fuzzy Membership Function of Object-Based Classification. Int. J. Econ. Environ. Geol. 2019, 9, 20–25. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.A.; Shea, J.M.; Pellicciotti, F.; De Jong, S.M.; Immerzeel, W.W. Object-based analysis of unmanned aerial vehicle imagery to map and characterise surface features on a debris-covered glacier. Remote Sens. Environ. 2016, 186, 581–595. [Google Scholar] [CrossRef]
- Podgórski, J.; Pętlicki, M. Detailed Lacustrine Calving Iceberg Inventory from Very High Resolution Optical Imagery and Object-Based Image Analysis. Remote Sens. 2020, 12, 1807. [Google Scholar] [CrossRef]
- Dabiri, Z.; Hölbling, D.; Abad, L.; Guðmundsson, S. Comparing the Applicability of Sentinel-1 and Sentinel-2 for Mapping the Evolution of Ice-marginal Lakes in Southeast Iceland. GI_Forum 2021, 9, 46–52. [Google Scholar] [CrossRef]
- Rendenieks, Z.; Nita, M.D.; Nikodemus, O.; Radeloff, V.C. Half a century of forest cover change along the Latvian-Russian border captured by object-based image analysis of Corona and Landsat TM/OLI data. Remote Sens. Environ. 2020, 249, 112010. [Google Scholar] [CrossRef]
- Pandey, P.; Kulkarni, A.V.; Venkataraman, G. Remote sensing study of snowline altitude at the end of melting season, Chandra-Bhaga basin, Himachal Pradesh, 1980–2007. Geocarto Int. 2013, 28, 311–322. [Google Scholar] [CrossRef]
- Rathore, B.P.; Singh, S.K.; Jani, P.; Bahuguna, I.M.; Brahmbhatt, R.; Rajawat, A.S.; Randhawa, S.S.; Vyas, A. Monitoring of snow cover variability in Chenab Basin using IRS AWiFS sensor. J. Indian Soc. Remote Sens. 2018, 46, 1497–1506. [Google Scholar] [CrossRef]
- Sahu, R.; Gupta, R.D. Snow cover area analysis and its relation with climate variability in Chandra basin, Western Himalaya, during 2001–2017 using MODIS and ERA5 data. Environ. Monit. Assess. 2020, 192, 489. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, N.; Watanabe, F.; Rodrigues, T.; Alcântara, E. Atmospheric correction issues for retrieving total suspended matter concentrations in inland waters using OLI/Landsat-8 image. Adv. Space Res. 2017, 59, 2335–2348. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Binding, C.E.; Jerome, J.H.; Bukata, R.P.; Booty, W.G. Suspended particulate matter in Lake Erie derived from MODIS aquatic colour imagery. Int. J. Remote Sens. 2010, 31, 5239–5255. [Google Scholar] [CrossRef]
- Chakouri, M.; Lhissou, R.; El Harti, A.; Maimouni, S.; Adiri, Z. Assessment of the image-based atmospheric correction of multispectral satellite images for geological mapping in arid and semi-arid regions. Remote Sens. Appl. Soc. Environ. 2020, 20, 100420. [Google Scholar] [CrossRef]
- Saini, V.; Tiwari, R.; Gupta, R. Comparison of FLAASH and QUAC Atmospheric Correction Methods for Resourcesat-2 LISS-IV Data. In Proceedings of the SPIE, Earth Observing Missions and Sensors: Development, Implementation, and Characterization IV, New Delhi, India, 2 May 2016. [Google Scholar]
- Marcello, J.; Eugenio, F.; Perdomo, U.; Medina, A. Assessment of Atmospheric Algorithms to Retrieve Vegetation in Natural Protected Areas Using Multispectral High Resolution Imagery. Sensors 2016, 16, 1624. [Google Scholar] [CrossRef]
- Casey, K.A.; Kääb, A.; Benn, D.I. Geochemical characterization of supraglacial debris via in situ and optical remote sensing methods: A case study in Khumbu Himalaya, Nepal. Cryosphere 2012, 6, 85–100. [Google Scholar] [CrossRef]
- Rastner, P.; Bolch, T.; Notarnicola, C.; Paul, F. A Comparison of Pixel-and Object-Based Glacier Classification with Optical Satellite Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 853–862. [Google Scholar] [CrossRef]
- Longbotham, N.; Pacifici, F.; Malitz, S.; Baugh, W.; Camps-Valls, G. Measuring the spatial and spectral performance of WorldView-3. In Hyperspectral Imaging and Sounding of the Environment; Optica Publishing Group: Washington, DC, USA, 2015; p. HW3B-2. [Google Scholar] [CrossRef]
- Collin, A.; Andel, M.; James, D.; Claudet, J. The superspectral/hyperspatial worldview-3 as the link between spaceborne hyperspectral and airborne hyperspatial sensors: The case study of the complex tropical coast. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 1849–1854. [Google Scholar] [CrossRef]
- Ye, B.; Tian, S.; Ge, J.; Sun, Y. Assessment of WorldView-3 Data for Lithological Mapping. Remote Sens. 2017, 9, 1132. [Google Scholar] [CrossRef]
- Sun, Y.; Tian, S.; Di, B. Extracting mineral alteration information using WorldView-3 data. Geosci. Front. 2017, 8, 1051–1062. [Google Scholar] [CrossRef]
- Asadzadeh, S.; de Souza Filho, C.R. Investigating the capability of WorldView-3 superspectral data for direct hydrocarbon detection. Remote Sens. Environ. 2016, 173, 162–173. [Google Scholar] [CrossRef]
- Mars, J.C. Mineral and lithologic mapping capability of WorldView 3 data at Mountain Pass, California, using true-and false-color composite images, band ratios, and logical operator algorithms. Econ. Geol. 2018, 113, 1587–1601. [Google Scholar] [CrossRef]
- Kruse, F.A.; Baugh, W.M.; Perry, S.L. Validation of DigitalGlobe WorldView-3 Earth imaging satellite shortwave infrared bands for mineral mapping. J. Appl. Remote Sens. 2015, 9, 096044. [Google Scholar] [CrossRef]
- Hunt Jr, E.R.; Daughtry, C.S.; Li, L. Feasibility of estimating leaf water content using spectral indices from WorldView-3’s near-infrared and shortwave infrared bands. Int. J. Remote Sens. 2016, 37, 388–402. [Google Scholar] [CrossRef]
- Eckert, S. Improved Forest biomass and carbon estimations using texture measures from WorldView-2 satellite data. Remote Sens. 2012, 4, 810–829. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M. Testing the capabilities of the new WorldView-3 space-borne sensor’s red-edge spectral band in discriminating and mapping complex grassland management treatments. Int. J. Remote Sens. 2017, 38, 1–22. [Google Scholar] [CrossRef]
- Pu, R.; Gong, P.; Biging, G.S.; Larrieu, M.R. Extraction of red edge optical parameters from Hyperion data for estimation of forest leaf area index. IEEE Trans. Geosci. Remote Sens. 2003, 41, 916–921. [Google Scholar] [CrossRef]
- Upadhyay, P.; Ghosh, S.K.; Kumar, A.; Roy, P.S.; Gilbert, I. Effect on specific crop mapping using WorldView-2 multispectral add-on bands: Soft classification approach. J. Appl. Remote Sens. 2012, 6, 063524. [Google Scholar] [CrossRef]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree Species Classification with Random Forest Using Very High Spatial Resolution 8-Band WorldView-2 Satellite Data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Marshall, V.; Lewis, M.; Ostendorf, B. Do additional bands (coastal, NIR-2, red-edge and yellow) in WorldView-2 multispectral imagery improve discrimination of an Invasive Tussock, Buffel Grass (Cenchrus Ciliaris). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, B8. [Google Scholar] [CrossRef]
- Heenkenda, M.K.; Joyce, K.E.; Maier, S.W.; Bartolo, R. Mangrove Species Identification: Comparing WorldView-2 with Aerial Photographs. Remote Sens. 2014, 6, 6064–6088. [Google Scholar] [CrossRef]
- Collin, A.; Hench, J.L. Towards Deeper Measurements of Tropical Reefscape Structure Using the WorldView-2 Spaceborne Sensor. Remote Sens. 2012, 4, 1425–1447. [Google Scholar] [CrossRef]
- Malinowski, R.; Groom, G.; Schwanghart, W.; Heckrath, G. Detection and Delineation of Localized Flooding from WorldView-2 Multispectral Data. Remote Sens. 2015, 7, 14853–14875. [Google Scholar] [CrossRef]
- Shahi, K.; Shafri, H.Z.; Taherzadeh, E.; Mansor, S.; Muniandy, R. A novel spectral index to automatically extract road networks from WorldView-2 satellite imagery. Egypt. J. Remote Sens. Space Sci. 2015, 18, 27–33. [Google Scholar] [CrossRef]
- Abriha, D.; Kovács, Z.; Ninsawat, S.; Bertalan, L.; Balázs, B.; Szabó, S. Identification of roofing materials with Discriminant Function Analysis and Random Forest classifiers on pan-sharpened WorldView-2 imagery–a comparison. Hung. Geogr. Bull. 2018, 67, 375–392. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Gupta, R.P.; Gens, R.; Prakash, A. Use of optical, thermal and microwave imagery for debris characterization in Bara-Shigri glacier, Himalayas, India. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 4422–4425. [Google Scholar] [CrossRef]
- Bühler, Y.; Meier, L.; Meister, R. Continuous, high resolution snow surface type mapping in high alpine terrain using WorldView-2 data. Digit. Globe 2011, 6. Available online: https://www.researchgate.net/profile/Roland-Meister-3/publication/267859153_Continuous_high_resolution_snow_surface_type_mapping_in_high_alpine_terrain_using_WorldView-2_data/links/547370c10cf2d67fc0373851/Continuous-high-resolution-snow-surface-type-mapping-in-high-alpine-terrain-using-WorldView-2-data.pdf (accessed on 16 August 2022).
- Jawak, S.D.; Khopkar, P.S.; Jadhav, S.P.; Luis, A.J. Customization of Normalized Difference Snow Index for Extraction of Snow Cover from Cryospheric Surface Using WorldView-2 Data. In Proceedings of the AGSE International Conference, Ahmedabad, India, 16–19 December 2013; pp. 16–19. Available online: https://www.researchgate.net/profile/Shridhar-Jawak/publication/270890440_Customization_of_Normalized_Difference_of_Snow_Index_NDSI_for_extraction_of_snow_andor_ice_cover_from_cryospheric_surface_using_WorldView-2_data/links/55279bb80cf229e6d6362dd3/Customization-of-Normalized-Difference-of-Snow-Index-NDSI-for-extraction-of-snow-and-or-ice-cover-from-cryospheric-surface-using-WorldView-2-data.pdf (accessed on 16 August 2022).
- Gray, A.; Krolikowski, M.; Fretwell, P.; Convey, P.; Peck, L.S.; Mendelova, M.; Smith, A.G.; Davey, M.P. Remote sensing phenology of Antarctic green and red snow algae using WorldView satellites. Front. Plant Sci. 2021, 12, 877. [Google Scholar] [CrossRef]
- Arroyo, L.A.; Johansen, K.; Armston, J.; Phinn, S. Integration of LiDAR and QuickBird imagery for mapping riparian biophysical parameters and land cover types in Australian tropical savannas. For. Ecol. Manag. 2010, 259, 598–606. [Google Scholar] [CrossRef]
- Gardin, S.; Van Laere, S.M.J.; Van Coillie, F.M.B.; Anseel, F.; Duyck, W.; De Wulf, R.R.; Verbeke, L.P.C. Remote sensing meets psychology: A concept for operator performance assessment. Remote Sens. Lett. 2011, 2, 251–257. [Google Scholar] [CrossRef]
- Shafri, H.Z.M.; Anuar, M.I.; Saripan, M.I. Modified vegetation indices for Ganoderma disease detection in oil palm from field spectroradiometer data. J. Appl. Remote Sens. 2009, 3, 033556. [Google Scholar] [CrossRef]
- Samsudin, S.H.; Shafri, H.Z.; Hamedianfar, A. Development of spectral indices for roofing material condition status detection using field spectroscopy and WorldView-3 data. J. Appl. Remote Sens. 2016, 10, 025021. [Google Scholar] [CrossRef]
- Vivone, G.; Chanussot, J. Fusion of short-wave infrared and visible near-infrared WorldView-3 data. Inf. Fusion 2020, 61, 71–83. [Google Scholar] [CrossRef]
- Clark, R.N.; Swayze, G.A.; Livo, K.E.; Kokaly, R.F.; Sutley, S.J.; Dalton, J.B.; McDougal, R.R.; Gent, C.A. Imaging spectroscopy: Earth and planetary remote sensing with the USGS Tetracorder and expert systems. J. Geophys. Res. Planets 2003, 108, E12. [Google Scholar] [CrossRef]
- Swayze, G.A.; Clark, R.N.; Goetz, A.F.; Livo, K.E.; Breit, G.N.; Kruse, F.A.; Sutley, S.J.; Snee, L.W.; Lowers, H.A.; Post, J.L.; et al. Mapping advanced argillic alteration at Cuprite, Nevada, using imaging spectroscopy. Econ. Geol. 2014, 109, 1179–1221. [Google Scholar] [CrossRef]

| Worldview-2 (WV-2): 16 October 2014 | WorldView-3 (WV-3): 10 August 2016 | ||||
|---|---|---|---|---|---|
| Name | Wavelength (µm) | GSD | Name | Wavelength (µm) | GSD |
| PAN | 0.45–0.80 | 0.46 m | PAN | 0.45–0.80 | 0.31 m |
| Coastal | 0.40–0.45 | 1.84 m | Coastal | 0.40–0.45 | 1.24 m |
| Blue | 0.45–0.51 | Blue | 0.45–0.51 | ||
| Green | 0.51–0.58 | Green | 0.51–0.58 | ||
| Yellow | 0.58–0.62 | Yellow | 0.58–0.62 | ||
| Red | 0.63–0.69 | Red | 0.63–0.69 | ||
| Red Edge | 0.70–0.74 | Red Edge | 0.70–0.74 | ||
| NIR 1 | 0.77–0.89 | NIR 1 | 0.77–0.89 | ||
| NIR 2 | 0.86–1.04 | NIR 2 | 0.86–1.04 | ||
| SWIR 1 | 1.19–1.22 | 3.7 m | |||
| SWIR 2 | 1.55–1.59 | ||||
| SWIR 3 | 1.64–1.68 | ||||
| SWIR 4 | 1.71–1.75 | ||||
| SWIR 5 | 2.14–2.18 | ||||
| SWIR 6 | 2.18–2.22 | ||||
| SWIR 7 | 2.23–2.28 | ||||
| SWIR 8 | 2.29–2.36 | ||||
| Parameter | Chandra–Bhaga Basin | Ny-Ålesund | Computation |
|---|---|---|---|
| Flight date | 16 October 2014 | 10 August 2018 | Imagery metadata |
| Scene center location | Lat: 32.5324 Long: 77.4175 | Lat: 78.8816 Long: 12.0734 | Automatic computation |
| GMT | 5.6825 | 12.7456 | User-defined |
| Sensor altitude (km) | 770 | 770 | Automatic computation |
| View zenith angle (degrees) | 180.00 | 180.00 | Automatic computation |
| Initial visibility (km) | 40.00 | 40.00 | User-defined |
| Atmospheric model | 1 (Tropical) | 4 (Subarctic Summer) | User-defined [49] |
| Aerosol model | 6 (Tropospheric) | 4 (Maritime) | User-defined [49] |
| Water column multiplier | 1.00 | 1.00 | Automatic computation |
| Pixel size (m) | 2.00 | 0.90 | Automatic computation |
| Aerosol scale height | 1.50 | 1.50 | Automatic computation |
| CO2 mixing ratio (ppm) | 390.00 | 390.00 | Automatic computation |
| Wavelengths | Mean at-Sensor Reflectance of Selected Dark Pixels | |
|---|---|---|
| Ny-Ålesund | Chandra–Bhaga Basin | |
| Coastal | 0.09 | 0.17 |
| Blue | 0.06 | 0.14 |
| Green | 0.04 | 0.11 |
| Yellow | 0.03 | 0.09 |
| Red | 0.03 | 0.08 |
| Red Edge | 0.02 | 0.08 |
| NIR1 | 0.01 | 0.06 |
| NIR2 | 0.01 | 0.06 |
| SWIR 1 | 0.00 | -- |
| SWIR 2 | 0.00 | -- |
| SWIR 3 | 0.00 | -- |
| SWIR 4 | 0.00 | -- |
| SWIR 5 | 0.00 | -- |
| SWIR 6 | 0.00 | -- |
| SWIR 7 | 0.00 | -- |
| SWIR 8 | 0.00 | -- |
| Layer Weights | |||||||
|---|---|---|---|---|---|---|---|
| VNIR_SWIR | Value | VNIR | Value | BGRN1 | Value | CYRN2 | Value |
| Coastal | 1 | Coastal | 1 | Coastal | 1 | ||
| Blue | 2 | Blue | 2 | Blue | 2 | ||
| Green | 2 | Green | 2 | Green | 2 | ||
| Yellow | 2 | Yellow | 2 | Yellow | 2 | ||
| Red | 1 | Red | 1 | Red | 1 | ||
| Red Edge | 2 | Red Edge | 2 | Red Edge | 2 | ||
| NIR 1 | 3 | NIR 1 | 3 | NIR 1 | 3 | ||
| NIR 2 | 1 | NIR 2 | 1 | NIR 2 | 1 | ||
| SWIR 1 | 1 | ||||||
| SWIR 2 | 1 | ||||||
| SWIR 3 | 1 | ||||||
| SWIR 4 | 1 | ||||||
| SWIR 5 | 1 | ||||||
| SWIR 6 | 1 | ||||||
| SWIR 7 | 1 | ||||||
| SWIR 8 | 1 | ||||||
| Common Object Parameters | Value | ||||||
| Scale | 5 | ||||||
| Shape | 0.9 | ||||||
| Compactness | 0.4 | ||||||
| Rule Sets | Type of Feature | Feature Name | Features Tested in This Study |
|---|---|---|---|
| Rule Set 1 and 3 | Object Features: Layer Values | Mean Value per Layer/Band | Coastal, Blue, Green, Yellow, Red, Red Edge, NIR 1, NIR 2, SWIR 1, Brightness, Max. difference |
| Rule Set 2 and 3 | Object Features: Layer Values | Quantile (50th percentile) | Quantile (Coastal), Quantile (Coastal), Quantile (Blue), Quantile (Green), Quantile (Yellow), Quantile (Red), Quantile (Red Edge), Quantile (NIR 1), Quantile (NIR 2), Quantile (NIR 2), Quantile (SWIR 1) |
| Rule Set 2 and 3 | Object Features: Layer Values: Pixel-Based | Standard Deviation | Coastal, Blue, Green, Yellow, Red, Red Edge, NIR 1, NIR 2, SWIR 1 |
| Rule Set 2 and 3 | Object Features: Layer Values: Pixel-Based | Minimum Pixel Value | Coastal, Blue, Green, Yellow, Red, Red Edge, NIR 1, NIR 2, SWIR 1 |
| Rule Set 2 and 3 | Object Features: Layer Values: Pixel-Based | Maximum Pixel Value | Coastal, Blue, Green, Yellow, Red, Red Edge, NIR 1, NIR 2, SWIR 1 |
| Rule Set 2 and 3 | Object Features: Layer Values: Pixel-Based | Edge Contrast of Neighbor Pixels | Coastal (3), Blue (3), Green (3), Yellow (3), Red (3), Red Edge (3), NIR 1 (3), NIR 2 (3), SWIR 1 (3) |
| All three rule sets | Object Features: Thematic Attributes | Number of Overlapping Thematic Objects | Manual Digitized Layer of Shadowed Snow |
| Rule Set 2 and 3 | Class-Related Features: Relations to Neighbor Objects | Relative Border To | Classified Objects |
| Rule Set 1 and 3 | Object Features: Customized Features | Arithmetic Feature | Customized Ratios (using Mean Value) R_RE = (Red/Red Edge) CB_CB = (Coastal − Blue)/(Coastal + Blue) G_C = (Green)/(Coastal) RC_RG = (Red/Coastal) * (Red/Green) Max_Min_RE = (Max. pixel value Red Edge − Min. pixel value Red Edge) Y_C = (Yellow/Coastal) C_G = (Coastal/Green) R_C = (Red/Coastal) C_N1 = (Coastal/NIR 1) G_RE = (Green/Red Edge) R_B = (Red/Blue) R_G = (Red/Green) N2_Y = (NIR 2/Yellow) N1_R = (NIR 1/Red) N1_N2 = (NIR 1/NIR 2) CN2_CN2 = (Coastal − NIR 2)/(Coastal + NIR 2) N1N2_N1N2 = (NIR 1 − NIR 2)/(NIR 1 + NIR 2) BN1_BS1 = (Blue − NIR 1)/(Blue + SWIR 1) GN1_GS1 = (Green − NIR 1)/(Green + SWIR 1) N1S1 = (NIR 1 − SWIR 1)/(NIR 1 + SWIR 1) |
| Classifier | Spectral Band Combinations | Average | |||
|---|---|---|---|---|---|
| BGRN1 | CYRN2 | VNIR | VNIR_SWIR | ||
| ACE | 0.35 | 0.34 | 0.37 | 0.36 | 0.36 |
| CEM | 0.23 | 0.22 | 0.23 | 0.22 | 0.23 |
| MF | 0.13 | 0.22 | 0.25 | 0.23 | 0.21 |
| MTMF | 0.10 | 0.12 | 0.15 | 0.14 | 0.13 |
| MTTCIMF | 0.10 | 0.10 | 0.12 | 0.12 | 0.11 |
| OSP | 0.14 | 0.09 | 0.12 | 0.12 | 0.12 |
| TCIMF | 0.39 | 0.13 | 0.16 | 0.16 | 0.21 |
| MHD | 0.48 | 0.38 | 0.42 | 0.41 | 0.42 |
| MXL | 0.29 | 0.47 | 0.50 | 0.49 | 0.44 |
| MD | 0.22 | 0.27 | 0.31 | 0.30 | 0.28 |
| SAM | 0.44 | 0.21 | 0.25 | 0.25 | 0.29 |
| WTA | 0.44 | 0.43 | 0.46 | 0.45 | 0.45 |
| Classifier | Comparison between Atmospheric Corrections Using Overall Accuracy | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BGRN1 | CYRN2 | VNIR | VNIR_SWIR | |||||||||
| DOS | FLAASH | QUAC | DOS | FLAASH | QUAC | DOS | FLAASH | QUAC | DOS | FLAASH | QUAC | |
| ACE | 0.60 | 0.47 | 0.55 | 0.60 | 0.46 | 0.55 | 0.63 | 0.47 | 0.59 | 0.62 | 0.46 | 0.58 |
| CEM | 0.53 | 0.36 | 0.35 | 0.51 | 0.35 | 0.35 | 0.55 | 0.38 | 0.37 | 0.52 | 0.37 | 0.36 |
| MF | 0.53 | 0.36 | 0.31 | 0.52 | 0.36 | 0.30 | 0.55 | 0.38 | 0.31 | 0.53 | 0.37 | 0.31 |
| MTMF | 0.22 | 0.15 | 0.05 | 0.21 | 0.14 | 0.05 | 0.24 | 0.17 | 0.07 | 0.23 | 0.16 | 0.06 |
| MTTCIMF | 0.01 | 0.01 | 0.14 | 0.01 | 0.01 | 0.14 | 0.02 | 0.01 | 0.16 | 0.02 | 0.01 | 0.15 |
| OSP | 0.28 | 0.11 | 0.17 | 0.27 | 0.10 | 0.16 | 0.29 | 0.13 | 0.19 | 0.28 | 0.13 | 0.19 |
| TCIMF | 0.21 | 0.11 | 0.22 | 0.20 | 0.10 | 0.19 | 0.24 | 0.12 | 0.25 | 0.22 | 0.11 | 0.24 |
| MHD | 0.70 | 0.61 | 0.66 | 0.68 | 0.59 | 0.64 | 0.70 | 0.61 | 0.66 | 0.70 | 0.59 | 0.65 |
| MXL | 0.75 | 0.66 | 0.76 | 0.75 | 0.67 | 0.77 | 0.78 | 0.73 | 0.79 | 0.77 | 0.73 | 0.79 |
| MD | 0.62 | 0.61 | 0.46 | 0.61 | 0.60 | 0.45 | 0.64 | 0.64 | 0.48 | 0.62 | 0.63 | 0.48 |
| SAM | 0.44 | 0.33 | 0.37 | 0.43 | 0.32 | 0.36 | 0.46 | 0.35 | 0.38 | 0.45 | 0.34 | 0.37 |
| WTA | 0.79 | 0.72 | 0.71 | 0.77 | 0.73 | 0.71 | 0.81 | 0.73 | 0.73 | 0.78 | 0.73 | 0.72 |
| Classifier | Comparison between Pansharpening Methods Using Error Rate | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BGRN1 | CYRN2 | VNIR | VNIR_SWIR | |||||||||
| NP | GS | HCS | NP | GS | HCS | NP | GS | HCS | NP | GS | HCS | |
| ACE | 0.46 | 0.74 | 0.66 | 0.46 | 0.74 | 0.67 | 0.44 | 0.72 | 0.63 | 0.45 | 0.72 | 0.65 |
| CEM | 0.59 | 0.81 | 0.76 | 0.60 | 0.81 | 0.78 | 0.57 | 0.80 | 0.74 | 0.59 | 0.81 | 0.74 |
| MF | 0.60 | 0.82 | 0.73 | 0.61 | 0.82 | 0.74 | 0.59 | 0.80 | 0.71 | 0.60 | 0.80 | 0.71 |
| MTMF | 0.86 | 0.85 | 0.81 | 0.87 | 0.86 | 0.81 | 0.85 | 0.82 | 0.78 | 0.85 | 0.83 | 0.79 |
| MTTCIMF | 0.95 | 0.91 | 0.73 | 0.95 | 0.92 | 0.74 | 0.94 | 0.89 | 0.71 | 0.94 | 0.90 | 0.72 |
| OSP | 0.82 | 0.87 | 0.84 | 0.83 | 0.89 | 0.85 | 0.80 | 0.86 | 0.82 | 0.80 | 0.86 | 0.83 |
| TCIMF | 0.82 | 0.87 | 0.77 | 0.84 | 0.88 | 0.78 | 0.80 | 0.85 | 0.75 | 0.81 | 0.86 | 0.76 |
| MHD | 0.35 | 0.66 | 0.56 | 0.36 | 0.67 | 0.58 | 0.35 | 0.66 | 0.56 | 0.36 | 0.67 | 0.58 |
| MXL | 0.28 | 0.62 | 0.60 | 0.27 | 0.62 | 0.61 | 0.24 | 0.59 | 0.57 | 0.24 | 0.60 | 0.58 |
| MD | 0.44 | 0.78 | 0.76 | 0.45 | 0.78 | 0.77 | 0.42 | 0.76 | 0.77 | 0.43 | 0.77 | 0.78 |
| SAM | 0.62 | 0.81 | 0.83 | 0.63 | 0.82 | 0.83 | 0.61 | 0.80 | 0.81 | 0.62 | 0.81 | 0.82 |
| WTA | 0.26 | 0.62 | 0.63 | 0.27 | 0.61 | 0.60 | 0.25 | 0.62 | 0.61 | 0.26 | 0.63 | 0.62 |
| Rule Sets | Spectral Band Combinations | Average | |||
|---|---|---|---|---|---|
| BGRN1 | CYRN2 | VNIR | VNIR_SWIR | ||
| Rule Set 1 | 0.75 | 0.73 | 0.77 | 0.73 | 0.75 |
| Rule Set 2 | 0.73 | 0.72 | 0.75 | 0.72 | 0.73 |
| Rule Set 3 | 0.86 | 0.85 | 0.86 | 0.85 | 0.85 |
| Classifier | Comparison between Atmospheric Corrections Using Overall Accuracy | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BGRN1 | CYRN2 | VNIR | VNIR_SWIR | |||||||||
| DOS | FLAASH | QUAC | DOS | FLAASH | QUAC | DOS | FLAASH | QUAC | DOS | FLAASH | QUAC | |
| Rule Set 1 | 0.73 | 0.81 | 0.77 | 0.72 | 0.79 | 0.76 | 0.77 | 0.81 | 0.78 | 0.72 | 0.79 | 0.76 |
| Rule Set 2 | 0.83 | 0.75 | 0.84 | 0.82 | 0.76 | 0.83 | 0.85 | 0.77 | 0.84 | 0.82 | 0.76 | 0.83 |
| Rule Set 3 | 0.87 | 0.84 | 0.87 | 0.86 | 0.84 | 0.87 | 0.87 | 0.84 | 0.87 | 0.86 | 0.84 | 0.87 |
| Classifier | Comparison between Pansharpening Methods Using Error Rate | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BGRN1 | CYRN2 | VNIR | VNIR_SWIR | |||||||||
| NP | GS | HCS | NP | GS | HCS | NP | GS | HCS | NP | GS | HCS | |
| Rule Set 1 | 0.24 | 0.24 | 0.24 | 0.25 | 0.24 | 0.26 | 0.25 | 0.24 | 0.23 | 0.25 | 0.24 | 0.26 |
| Rule Set 2 | 0.20 | 0.26 | 0.33 | 0.20 | 0.27 | 0.35 | 0.20 | 0.25 | 0.32 | 0.20 | 0.27 | 0.35 |
| Rule Set 3 | 0.15 | 0.14 | 0.16 | 0.15 | 0.14 | 0.15 | 0.15 | 0.14 | 0.14 | 0.15 | 0.14 | 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jawak, S.D.; Wankhede, S.F.; Luis, A.J.; Balakrishna, K. Multispectral Characteristics of Glacier Surface Facies (Chandra-Bhaga Basin, Himalaya, and Ny-Ålesund, Svalbard) through Investigations of Pixel and Object-Based Mapping Using Variable Processing Routines. Remote Sens. 2022, 14, 6311. https://doi.org/10.3390/rs14246311
Jawak SD, Wankhede SF, Luis AJ, Balakrishna K. Multispectral Characteristics of Glacier Surface Facies (Chandra-Bhaga Basin, Himalaya, and Ny-Ålesund, Svalbard) through Investigations of Pixel and Object-Based Mapping Using Variable Processing Routines. Remote Sensing. 2022; 14(24):6311. https://doi.org/10.3390/rs14246311
Chicago/Turabian StyleJawak, Shridhar D., Sagar F. Wankhede, Alvarinho J. Luis, and Keshava Balakrishna. 2022. "Multispectral Characteristics of Glacier Surface Facies (Chandra-Bhaga Basin, Himalaya, and Ny-Ålesund, Svalbard) through Investigations of Pixel and Object-Based Mapping Using Variable Processing Routines" Remote Sensing 14, no. 24: 6311. https://doi.org/10.3390/rs14246311
APA StyleJawak, S. D., Wankhede, S. F., Luis, A. J., & Balakrishna, K. (2022). Multispectral Characteristics of Glacier Surface Facies (Chandra-Bhaga Basin, Himalaya, and Ny-Ålesund, Svalbard) through Investigations of Pixel and Object-Based Mapping Using Variable Processing Routines. Remote Sensing, 14(24), 6311. https://doi.org/10.3390/rs14246311








