AdaSplats: Adaptive Splatting of Point Clouds for Accurate 3D Modeling and Real-Time High-Fidelity LiDAR Simulation
Abstract
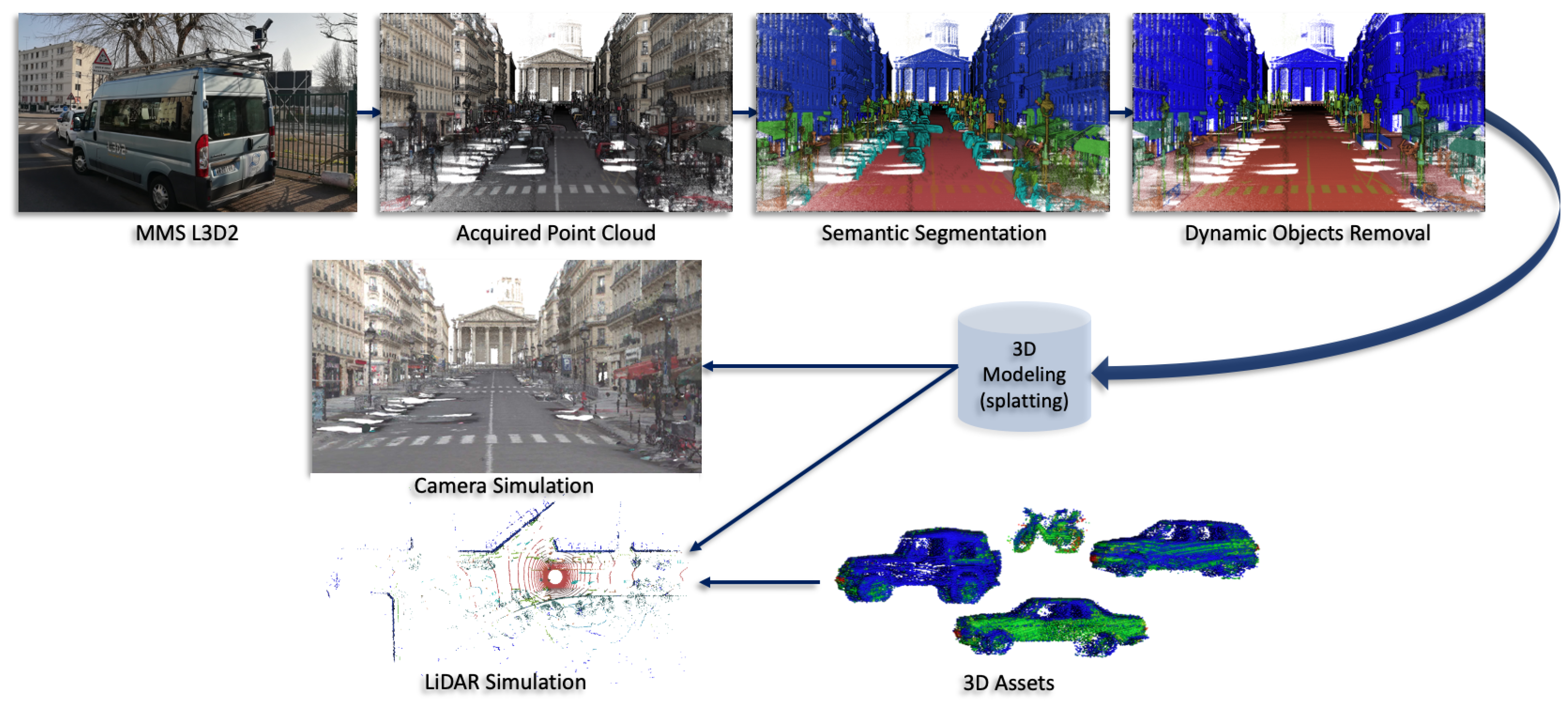
1. Introduction
- AdaSplats: a novel adaptive splatting approach for accurate 3D geometry modeling of large outdoor noisy point clouds;
- Splat-based point cloud resampling, dealing with highly varying densities and scalable to large data;
- Faster-than-real-time GPU ray casting in the splat model for LiDAR sensor simulation and rendering;
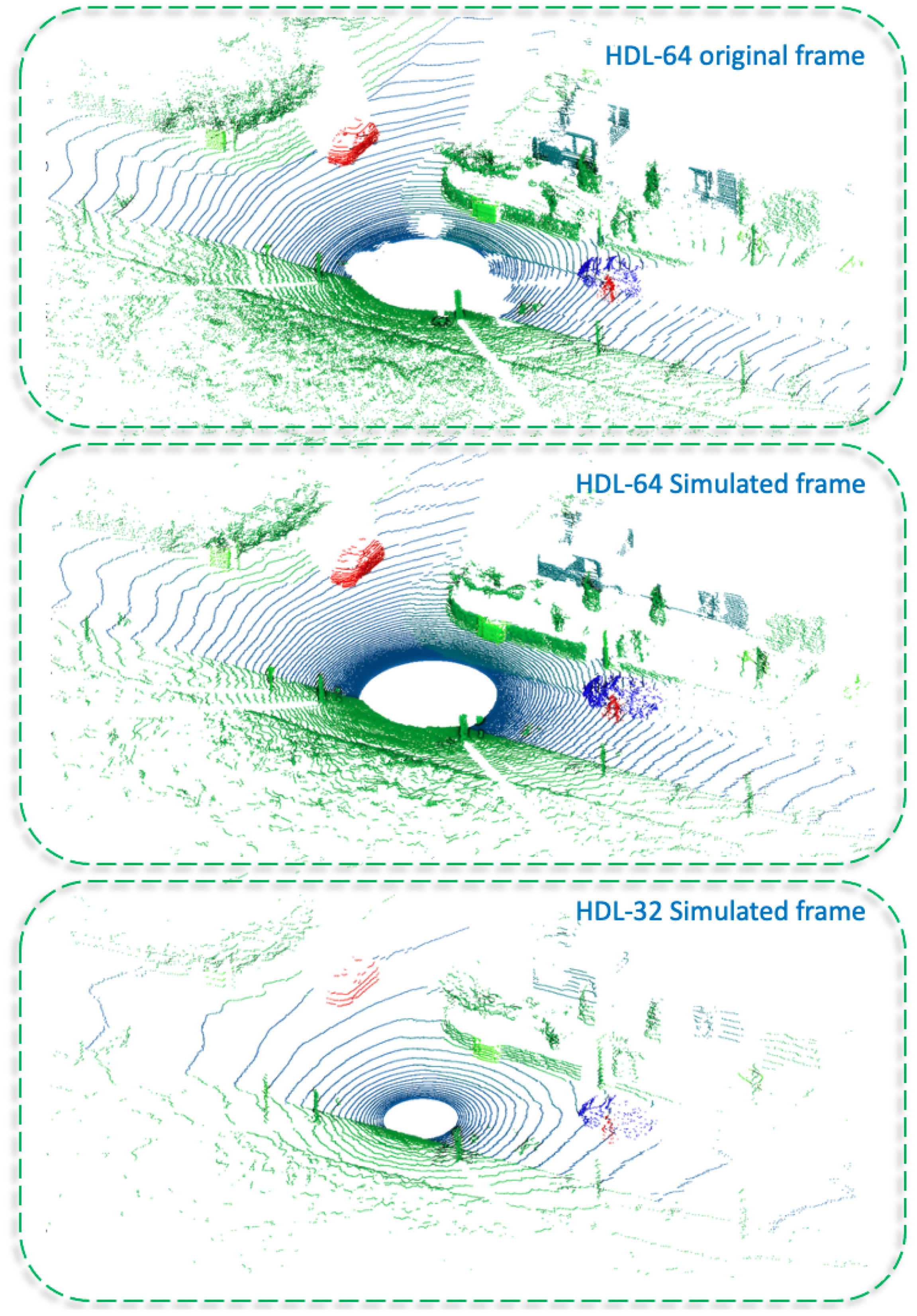
- SimKITTI32: a dataset simulating a Velodyne HDL-32 inside a sequence of SemanticKITTI dataset [18]. It is publicly available at: https://npm3d.fr/simkitti32 (accessed on 5 December 2022).
2. Related Works
2.1. Surface Reconstruction
2.1.1. Volumetric Segmentation
2.1.2. Volumetric Fusion
2.2. Point-Based Surface Modeling
2.2.1. Splatting
High-Quality Rendering
Advanced Shading
2.2.2. Splats Ray Tracing
2.3. Neural Radiance Fields
2.4. Resampling
2.5. LiDAR Simulation
2.5.1. Volumetric Scene Representation
2.5.2. Splat-Based Scene Representation
2.5.3. Mesh-Based Scene Representation
2.5.4. Real-Time LiDAR Simulation
3. Adaptive Splatting
3.1. Basic Splatting
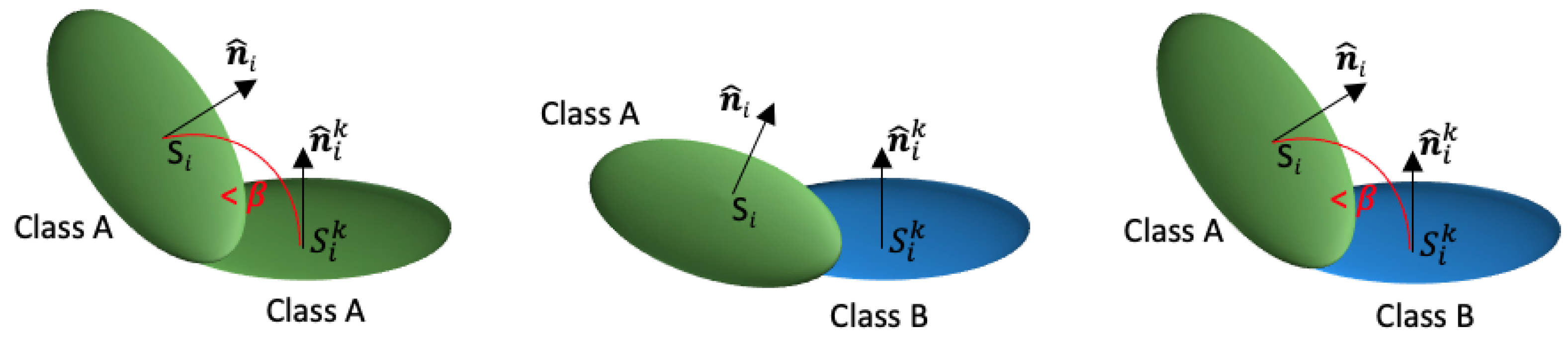
3.2. Adaptive Splatting
- Ground: road and sidewalk;
- Surface: buildings and other similar classes that locally resemble a surface;
- Linear: poles, traffic signs, and similar objects;
- Non-surface: vegetation, fences, and similar objects.
- Ground: = 120, , ;
- Surface: = 40, , (no change compared to basic splat);
- Linear: = 13, , ;
- Non-surface: = 10, , .
3.3. Adaptive Splatting Using Local Descriptors
- Ground and surface using the planarity descriptor;
- Linear using the linearity descriptor;
- Non-surface using the sphericity descriptor.
3.4. Splat-Based Resampling and Denoising
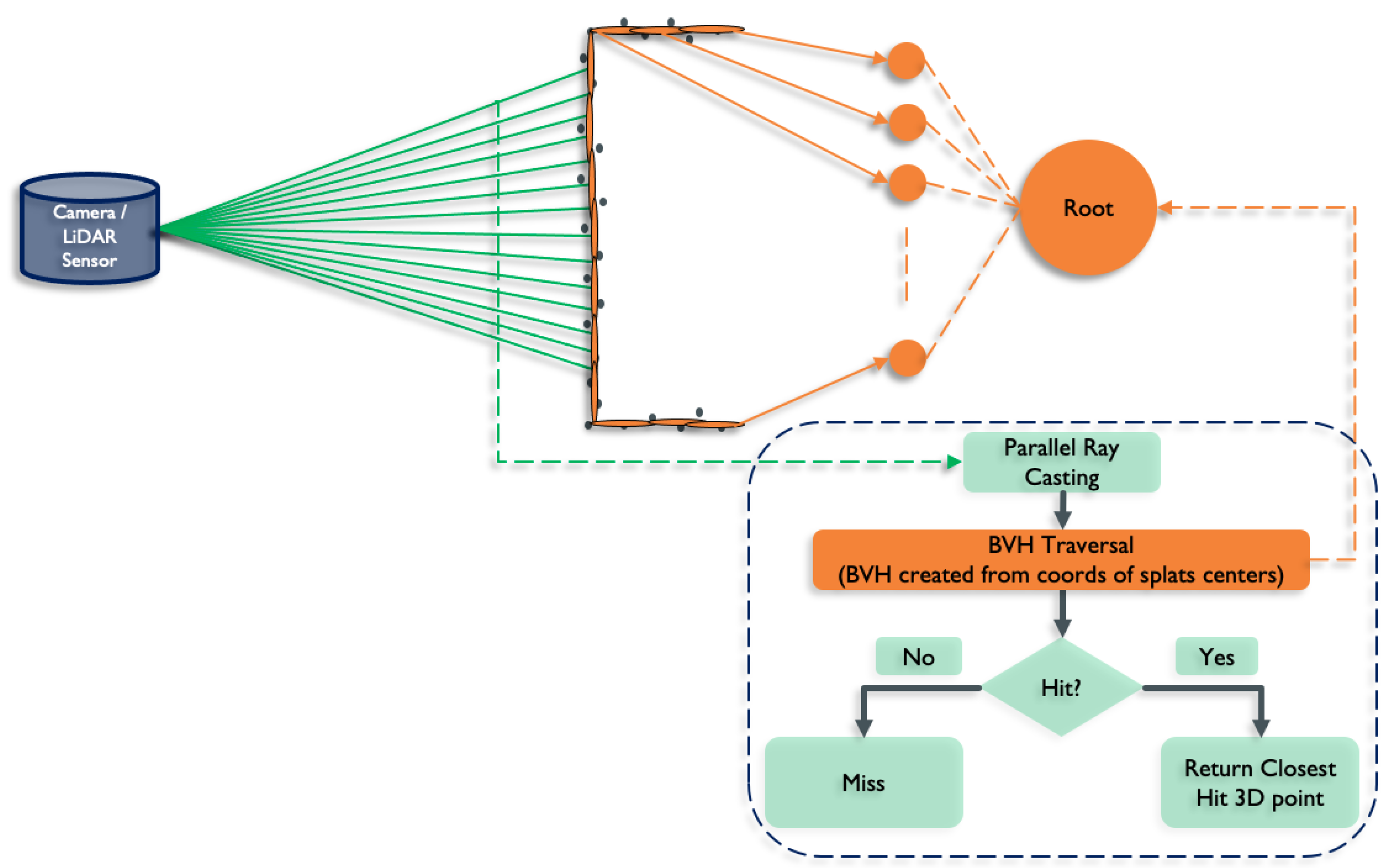
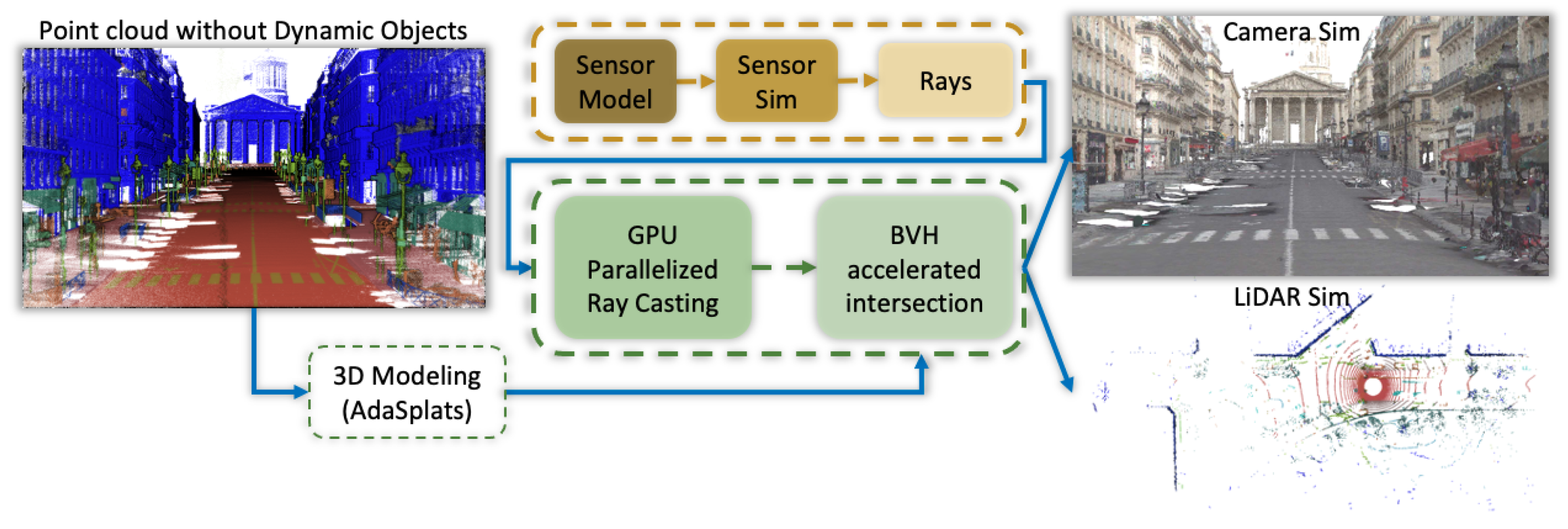
4. Splat Ray Tracing
4.1. Ray–Splat Intersection
4.2. OptiX
5. LiDAR Simulation
5.1. Firing Sequence Simulation
5.1.1. Velodyne HDL-32
5.1.2. Velodyne HDL-64
5.1.3. Firing Sequence Rays Generation
6. Experiments and Results
6.1. Experiments
6.1.1. Surface Representation
6.1.2. Datasets
Paris-Carla-3D
SemanticKITTI
M-City
6.2. New Trajectory Simulation
Evaluation Metric for LiDAR Simulation
6.3. Results
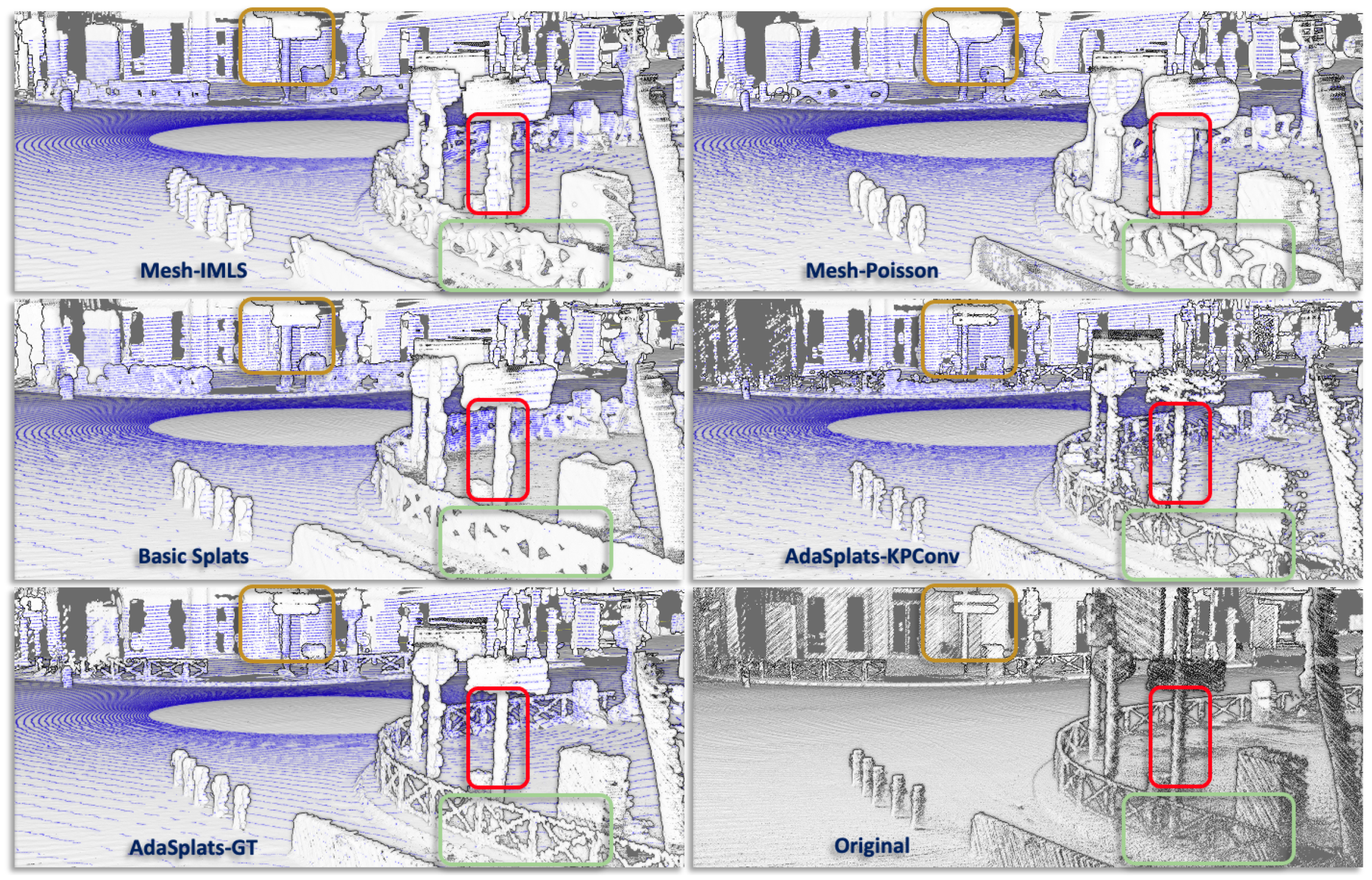
6.3.1. Paris-Carla-3D
6.3.2. SemanticKITTI
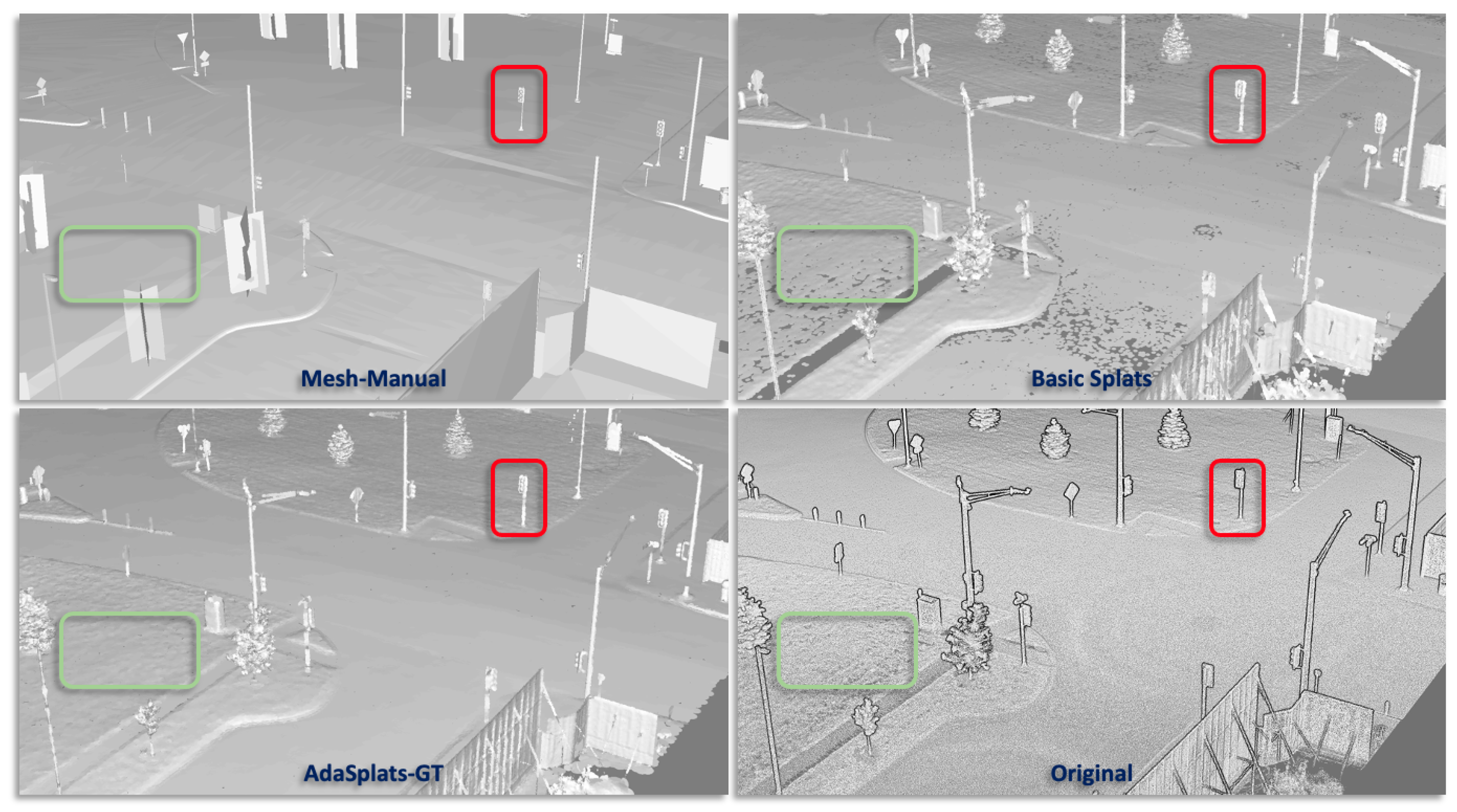
6.3.3. M-City
6.3.4. SimKITTI32
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dosovitskiy, A.; Ros, G.; Codevilla, F.; Lopez, A.; Koltun, V. CARLA: An Open Urban Driving Simulator. In Proceedings of the 1st Annual Conference on Robot Learning, Mountain View, CA, USA, 13–15 November 2017; pp. 1–16. [Google Scholar]
- Fang, J.; Zhou, D.; Yan, F.; Zhao, T.; Zhang, F.; Ma, Y.; Wang, L.; Yang, R. Augmented LiDAR Simulator for Autonomous Driving. IEEE Robot. Autom. Lett. 2020, 5, 1931–1938. [Google Scholar] [CrossRef]
- Manivasagam, S.; Wang, S.; Wong, K.; Zeng, W.; Sazanovich, M.; Tan, S.; Yang, B.; Ma, W.C.; Urtasun, R. LiDARsim: Realistic LiDAR Simulation by Leveraging the Real World. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11164–11173. [Google Scholar] [CrossRef]
- Zwicker, M.; Pfister, H.; van Baar, J.; Gross, M. Surface Splatting. In Proceedings of the SIGGRAPH ’01—28th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 1 August 2001; pp. 371–378. [Google Scholar] [CrossRef]
- Pfister, H.; Zwicker, M.; van Baar, J.; Gross, M. Surfels: Surface Elements as Rendering Primitives. In Proceedings of the SIGGRAPH ’00—27th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 1 July 2000; pp. 335–342. [Google Scholar] [CrossRef]
- Levoy, M.; Whitted, T. The Use of Points as a Display Primitive. 2000. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=3a6aa5ef72eeef9543695b3cc70f72576fc1651f (accessed on 5 December 2022).
- Hoppe, H.; DeRose, T.; Duchamp, T.; McDonald, J.; Stuetzle, W. Surface Reconstruction from Unorganized Points. In Proceedings of the SIGGRAPH ’92—19th Annual Conference on Computer Graphics and Interactive Techniques, Chicago, IL, USA, 27–31 July 1992; pp. 71–78. [Google Scholar] [CrossRef]
- Kolluri, R. Provably Good Moving Least Squares. ACM Trans. Algorithms 2008, 4, 1–25. [Google Scholar] [CrossRef]
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson Surface Reconstruction. In Proceedings of the Fourth Eurographics Symposium on Geometry Processing, Cagliari, Italy, 26–28 June 2006; pp. 61–70. [Google Scholar]
- Devaux, A.; Brédif, M. Realtime Projective Multi-Texturing of Pointclouds and Meshes for a Realistic Street-View Web Navigation. In Proceedings of the 21st International Conference on Web3D Technology, Anaheim, CA, USA, 22–24 July 2016; pp. 105–108. [Google Scholar] [CrossRef]
- Pagés, R.; García, S.; Berjón, D.; Morán, F. SPLASH: A Hybrid 3D Modeling/Rendering Approach Mixing Splats and Meshes. In Proceedings of the 20th International Conference on 3D Web Technology, Heraklion, Greece, 18–21 June 2015; pp. 231–234. [Google Scholar] [CrossRef]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L. KPConv: Flexible and Deformable Convolution for Point Clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6410–6419. [Google Scholar] [CrossRef]
- Landrieu, L.; Simonovsky, M. Large-Scale Point Cloud Semantic Segmentation with Superpoint Graphs. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar] [CrossRef]
- Boulch, A.; Puy, G.; Marlet, R. FKAConv: Feature-Kernel Alignment for Point Cloud Convolutions. In Proceedings of the 15th Asian Conference on Computer Vision (ACCV 2020), Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Choy, C.; Gwak, J.; Savarese, S. 4D Spatio-Temporal ConvNets: Minkowski Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3075–3084. [Google Scholar]
- Roynard, X.; Deschaud, J.E.; Goulette, F. Paris-Lille-3D: A large and high-quality ground-truth urban point cloud dataset for automatic segmentation and classification. Int. J. Robot. Res. 2018, 37, 545–557. [Google Scholar] [CrossRef]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. SEMANTIC3D.NET: A new large-scale point cloud classification benchmark. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2017, IV-1-W1, 91–98. [Google Scholar] [CrossRef]
- Behley, J.; Garbade, M.; Milioto, A.; Quenzel, J.; Behnke, S.; Stachniss, C.; Gall, J. SemanticKITTI: A Dataset for Semantic Scene Understanding of LiDAR Sequences. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9296–9306. [Google Scholar] [CrossRef]
- Deschaud, J.E.; Duque, D.; Richa, J.P.; Velasco-Forero, S.; Marcotegui, B.; Goulette, F. Paris-CARLA-3D: A Real and Synthetic Outdoor Point Cloud Dataset for Challenging Tasks in 3D Mapping. Remote Sens. 2021, 13, 4713. [Google Scholar] [CrossRef]
- Alexa, M.; Behr, J.; Cohen-Or, D.; Fleishman, S.; Levin, D.; Silva, C. Computing and rendering point set surfaces. IEEE Trans. Vis. Comput. Graph. 2003, 9, 3–15. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, T.; Cao, J.; Zhang, Y.J.; Wang, C. Point cloud resampling using centroidal Voronoi tessellation methods. Comput.-Aided Des. 2018, 102, 12–21. [Google Scholar] [CrossRef]
- Yu, L.; Li, X.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. PU-Net: Point Cloud Upsampling Network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2790–2799. [Google Scholar] [CrossRef]
- Zhou, K.; Dong, M.; Arslanturk, S. “Zero Shot” Point Cloud Upsampling. In Proceedings of the 2022 IEEE International Conference on Multimedia and Expo (ICME), Taipei, Taiwan, 18–22 July 2022. [Google Scholar]
- Chen, Y.; Yang, B.; Liang, M.; Urtasun, R. Learning Joint 2D-3D Representations for Depth Completion. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 10022–10031. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, X.; Shi, J.; Zhang, G.; Bao, H.; Li, H. Depth Completion from Sparse LiDAR Data with Depth-Normal Constraints. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2811–2820. [Google Scholar] [CrossRef]
- Linsen, L.; Müller, K.; Rosenthal, P. Splat-based Ray Tracing of Point Clouds. J. WSCG 2007, 15, 51–58. [Google Scholar]
- Mitra, N.J.; Nguyen, A. Estimating Surface Normals in Noisy Point Cloud Data. In Proceedings of the Nineteenth Annual Symposium on Computational Geometry, San Diego, CA, USA, 8–10 June 2003; pp. 322–328. [Google Scholar] [CrossRef]
- Dey, T.; Li, G.; Sun, J. Normal estimation for point clouds: A comparison study for a Voronoi based method. In Proceedings of the Eurographics/IEEE VGTC Symposium Point-Based Graphics, Stony Brook, NY, USA, 21–22 June 2005; pp. 39–46. [Google Scholar] [CrossRef]
- Boulch, A.; Marlet, R. Fast and Robust Normal Estimation for Point Clouds with Sharp Features. Comput. Graph. Forum 2012, 31, 1765–1774. [Google Scholar] [CrossRef]
- Zhao, R.; Pang, M.; Liu, C.; Zhang, Y. Robust Normal Estimation for 3D LiDAR Point Clouds in Urban Environments. Sensors 2019, 19, 1248. [Google Scholar] [CrossRef]
- Lorensen, W.E.; Cline, H.E. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. SIGGRAPH Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Kazhdan, M.; Hoppe, H. Screened Poisson Surface Reconstruction. ACM Trans. Graph. 2013, 32, 2487237. [Google Scholar] [CrossRef]
- Caraffa, L.; Brédif, M.; Vallet, B. 3D Octree Based Watertight Mesh Generation from Ubiquitous Data. ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2015, 2015, 613–617. [Google Scholar] [CrossRef]
- Caraffa, L.; Brédif, M.; Vallet, B. 3D Watertight Mesh Generation with Uncertainties from Ubiquitous Data. In Computer Vision—ACCV 2016; Lai, S.H., Lepetit, V., Nishino, K., Sato, Y., Eds.; Springer: Cham, Switzerland, 2017; pp. 377–391. [Google Scholar]
- Caraffa, L.; Marchand, Y.; Brédif, M.; Vallet, B. Efficiently Distributed Watertight Surface Reconstruction. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 1432–1441. [Google Scholar] [CrossRef]
- Soheilian, B.; Tournaire, O.; Paparoditis, N.; Vallet, B.; Papelard, J.P. Generation of an integrated 3D city model with visual landmarks for autonomous navigation in dense urban areas. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium (IV), Gold Coast City, Australia, 23 June 2013; pp. 304–309. [Google Scholar] [CrossRef]
- Demantke, J.; Vallet, B.; Paparoditis, N. Facade Reconstruction with Generalized 2.5d Grids. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2013, II-5/W2, 67–72. [Google Scholar] [CrossRef]
- Boussaha, M.; Fernandez-Moral, E.; Vallet, B.; Rives, P. On the production of semantic and textured 3d meshes of large scale urban environments from mobile mapping images and lidar scans. In Proceedings of the RFIAP 2018, Reconnaissance des Formes, Image, Apprentissage et Perception, Marne la Vallee, France, 26–28 June 2018. [Google Scholar]
- Peng, S.; Niemeyer, M.; Mescheder, L.; Pollefeys, M.; Geiger, A. Convolutional Occupancy Networks. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 523–540. [Google Scholar]
- Ummenhofer, B.; Koltun, V. Adaptive Surface Reconstruction with Multiscale Convolutional Kernels. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 5631–5640. [Google Scholar] [CrossRef]
- Curless, B.; Levoy, M. A Volumetric Method for Building Complex Models from Range Images. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 4–9 August 1996; pp. 303–312. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. QSplat: A Multiresolution Point Rendering System for Large Meshes. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; pp. 343–352. [Google Scholar] [CrossRef]
- Botsch, M.; Kobbelt, L. High-Quality Point-Based Rendering on Modern GPUs. In Proceedings of the 11th Pacific Conference on Computer Graphics and Applications, Canmore, AB, Canada, 8–10 October 2003; p. 335. [Google Scholar]
- Botsch, M.; Hornung, A.; Zwicker, M.; Kobbelt, L. High-quality surface splatting on today’s GPUs. In Proceedings of the Eurographics/IEEE VGTC Symposium Point-Based Graphics, Stony Brook, NY, USA, 21–22 June 2005; pp. 17–141. [Google Scholar] [CrossRef]
- Wu, J.; Kobbelt, L. Optimized Sub-Sampling of Point Sets for Surface Splatting. Comput. Graph. Forum 2004, 23, 643–652. [Google Scholar] [CrossRef]
- Botsch, M.; Spernat, M.; Kobbelt, L. Phong Splatting. In Proceedings of the First Eurographics Conference on Point-Based Graphics, Los Angeles, CA, USA, 10–11 August 2004; pp. 25–32. [Google Scholar]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. Commun. ACM 2020, 65, 99–106. [Google Scholar] [CrossRef]
- Garbin, S.J.; Kowalski, M.; Johnson, M.; Shotton, J.; Valentin, J. Fastnerf: High-fidelity neural rendering at 200fps. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 14346–14355. [Google Scholar]
- Hedman, P.; Srinivasan, P.P.; Mildenhall, B.; Barron, J.T.; Debevec, P.E. Baking Neural Radiance Fields for Real-Time View Synthesis. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11 October 2021; pp. 5855–5864. [Google Scholar]
- Liu, L.; Gu, J.; Lin, K.Z.; Chua, T.S.; Theobalt, C. Neural Sparse Voxel Fields. NeurIPS 2020, 33, 1–13. [Google Scholar]
- Rebain, D.; Jiang, W.; Yazdani, S.; Li, K.; Yi, K.M.; Tagliasacchi, A. DeRF: Decomposed Radiance Fields. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 14148–14156. [Google Scholar]
- Reiser, C.; Peng, S.; Liao, Y.; Geiger, A. KiloNeRF: Speeding up Neural Radiance Fields with Thousands of Tiny MLPs. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11 October 2021; pp. 14315–14325. [Google Scholar] [CrossRef]
- Maglo, A.; Lavoué, G.; Dupont, F.; Hudelot, C. 3D Mesh Compression: Survey, Comparisons, and Emerging Trends. ACM Comput. Surv. 2015, 47, 2693443. [Google Scholar] [CrossRef]
- Gschwandtner, M.; Kwitt, R.; Uhl, A.; Pree, W. BlenSor: Blender Sensor Simulation Toolbox. In Advances in Visual Computing; Bebis, G., Boyle, R., Parvin, B., Koracin, D., Wang, S., Kyungnam, K., Benes, B., Moreland, K., Borst, C., DiVerdi, S., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 199–208. [Google Scholar]
- Wu, B.; Wan, A.; Yue, X.; Keutzer, K. SqueezeSeg: Convolutional Neural Nets with Recurrent CRF for Real-Time Road-Object Segmentation from 3D LiDAR Point Cloud. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1887–1893. [Google Scholar] [CrossRef]
- Hurl, B.; Czarnecki, K.; Waslander, S. Precise Synthetic Image and LiDAR (PreSIL) Dataset for Autonomous Vehicle Perception. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 2522–2529. [Google Scholar] [CrossRef]
- Yue, X.; Wu, B.; Seshia, S.A.; Keutzer, K.; Sangiovanni-Vincentelli, A.L. A LiDAR Point Cloud Generator: From a Virtual World to Autonomous Driving. In Proceedings of the 2018 ACM on International Conference on Multimedia Retrieval, Yokohama, Japan, 11–14 June 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 458–464. [Google Scholar] [CrossRef]
- Wu, B.; Zhou, X.; Zhao, S.; Yue, X.; Keutzer, K. SqueezeSegV2: Improved Model Structure and Unsupervised Domain Adaptation for Road-Object Segmentation from a LiDAR Point Cloud. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4376–4382. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, Y.; Li, B.; Wu, B.; Gao, Y.; Xu, P.; Darrell, T.; Keutzer, K. ePointDA: An End-to-End Simulation-to-Real Domain Adaptation Framework for LiDAR Point Cloud Segmentation. arXiv 2020, arXiv:2009.03456. [Google Scholar] [CrossRef]
- Deschaud, J.E.; Prasser, D.; Dias, M.F.; Browning, B.; Rander, P. Automatic data driven vegetation modeling for lidar simulation. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–19 May 2012; pp. 5030–5036. [Google Scholar] [CrossRef]
- Tallavajhula, A.; Mericli, C.; Kelly, A. Off-Road Lidar Simulation with Data-Driven Terrain Primitives. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 7470–7477. [Google Scholar] [CrossRef]
- Wald, I.; Woop, S.; Benthin, C.; Johnson, G.S.; Ernst, M. Embree: A Kernel Framework for Efficient CPU Ray Tracing. ACM Trans. Graph. 2014, 33, 2601199. [Google Scholar] [CrossRef]
- Marchand, Y.; Vallet, B.; Caraffa, L. Evaluating Surface Mesh Reconstruction of Open Scenes. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 43, 369–376. [Google Scholar] [CrossRef]
- Parker, S.G.; Bigler, J.; Dietrich, A.; Friedrich, H.; Hoberock, J.; Luebke, D.; McAllister, D.; McGuire, M.; Morley, K.; Robison, A.; et al. OptiX: A General Purpose Ray Tracing Engine. ACM Trans. Graph. 2010, 29, 1778803. [Google Scholar] [CrossRef]
- Demantké, J.; Mallet, C.; David, N.; Vallet, B. Dimensionality Based Scale Selection in 3d LIDAR Point Clouds. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 3812, 97–102. [Google Scholar] [CrossRef]
- Deschaud, J.E. IMLS-SLAM: Scan-to-Model Matching Based on 3D Data. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2480–2485. [Google Scholar]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuScenes: A Multimodal Dataset for Autonomous Driving. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11618–11628. [Google Scholar] [CrossRef]






| Model | Gen T | Gen Prim | Render Freq | LiDAR Freq | C2C |
|---|---|---|---|---|---|
| (in s) | (#) | (in Hz) | (in Hz) | (in cm) | |
| Mesh–Poisson | 797 | 5.20M | 1000 Hz | 232 Hz | 2.3 cm |
| Mesh–IMLS | 3216 | 6.32M | 920 Hz | 233 Hz | 2.0 cm |
| Basic Splats | 200 | 5.40M | 100 Hz | 135 Hz | 2.3 cm |
| AdaSplats-Descr | 344 | 3.90M | 160 Hz | 181 Hz | 2.3 cm |
| AdaSplats-KPConv | 1064 | 1.75M | 240 Hz | 203 Hz | 2.2 cm |
| AdaSplats-GT | 451 | 1.72M | 250 Hz | 205 Hz | 1.97 cm |
| Model | Gen T | Gen Prim | Sim Freq | C2C |
|---|---|---|---|---|
| (in s) | (#) | (in Hz) | (in cm) | |
| AdaSplats-GT no resampling | 169 | 2.84M | 180 Hz | 1.99 cm |
| AdaSplats-GT | 451 | 1.72M | 205 Hz | 1.97 cm |
| Model | Fences | Poles | Traffic Signs | Average |
|---|---|---|---|---|
| Mesh–Poisson | 5.9 | 6.1 | 6.7 | 6.2 |
| Mesh–IMLS | 4.6 | 3.5 | 2.9 | 3.7 |
| Basic Splats | 4.7 | 4.3 | 3.4 | 4.1 |
| AdaSplats-Descr | 4.1 | 3.7 | 2.9 | 3.2 |
| AdaSplats-KPConv | 5.5 | 2.1 | 1.1 | 2.9 |
| AdaSplats-GT | 2.4 | 2.3 | 1.8 | 2.2 |
| Model | Fences | Poles | Traffic Signs | Average |
|---|---|---|---|---|
| AdaSplats-GT no resampling | 2.5 | 2.4 | 1.8 | 2.3 |
| AdaSplats-GT | 2.4 | 2.3 | 1.8 | 2.2 |
| Model | Gen T | Gen Prim | Render Freq | LiDAR Freq | C2C |
|---|---|---|---|---|---|
| (in s) | (#) | (in Hz) | (in Hz) | (in cm) | |
| Mesh–Poisson | 796 | 5.97M | 1050 Hz | 229 Hz | 2.6 cm |
| Mesh–IMLS | 1380 | 7.05M | 1020 Hz | 222 Hz | 3.0 cm |
| Basic Splats | 185 | 7.77M | 170 Hz | 144 Hz | 2.6 cm |
| AdaSplats-Descr | 416 | 6.69M | 200 Hz | 156 Hz | 2.2 cm |
| AdaSplats-KPConv | 1166 | 6.11M | 220 Hz | 157 Hz | 2.2 cm |
| AdaSplats-GT | 544 | 4.56M | 240 Hz | 180 Hz | 2.0 cm |
| Model | Gen T | Gen Prim | Render Freq | LiDAR Freq | C2C |
|---|---|---|---|---|---|
| (in s) | (#) | (in Hz) | (in Hz) | (in cm) | |
| Mesh–Manual | 1 month | 71.5K | 1930 Hz | 259 Hz | 7.0 cm |
| Basic Splats | 199 | 5.82M | 140 Hz | 110 Hz | 1.7 cm |
| AdaSplats-Descr | 480 | 3.92M | 290 Hz | 129 Hz | 1.6 cm |
| AdaSplats-GT | 513 | 3.01M | 440 Hz | 204 Hz | 1.5 cm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richa, J.P.; Deschaud, J.-E.; Goulette, F.; Dalmasso, N. AdaSplats: Adaptive Splatting of Point Clouds for Accurate 3D Modeling and Real-Time High-Fidelity LiDAR Simulation. Remote Sens. 2022, 14, 6262. https://doi.org/10.3390/rs14246262
Richa JP, Deschaud J-E, Goulette F, Dalmasso N. AdaSplats: Adaptive Splatting of Point Clouds for Accurate 3D Modeling and Real-Time High-Fidelity LiDAR Simulation. Remote Sensing. 2022; 14(24):6262. https://doi.org/10.3390/rs14246262
Chicago/Turabian StyleRicha, Jean Pierre, Jean-Emmanuel Deschaud, François Goulette, and Nicolas Dalmasso. 2022. "AdaSplats: Adaptive Splatting of Point Clouds for Accurate 3D Modeling and Real-Time High-Fidelity LiDAR Simulation" Remote Sensing 14, no. 24: 6262. https://doi.org/10.3390/rs14246262
APA StyleRicha, J. P., Deschaud, J.-E., Goulette, F., & Dalmasso, N. (2022). AdaSplats: Adaptive Splatting of Point Clouds for Accurate 3D Modeling and Real-Time High-Fidelity LiDAR Simulation. Remote Sensing, 14(24), 6262. https://doi.org/10.3390/rs14246262








