Abstract
Various biotic and abiotic stresses are causing decline in forest health globally. Presently, one of the major biotic stress agents in Europe is the European spruce bark beetle (Ips typographus L.) which is increasingly causing widespread tree mortality in northern latitudes as a consequence of the warming climate. Remote sensing using unoccupied aerial systems (UAS) together with evolving machine learning techniques provide a powerful tool for fast-response monitoring of forest health. The aim of this study was to investigate the performance of a deep one-stage object detection neural network in the detection of damage by I. typographus in Norway spruce trees using UAS RGB images. A Scaled-YOLOv4 (You Only Look Once) network was implemented and trained for tree health analysis. Datasets for model training were collected during 2013–2020 from three different areas, using four different RGB cameras, and under varying weather conditions. Different model training options were evaluated, including two different symptom rules, different partitions of the dataset, fine-tuning, and hyperparameter optimization. Our study showed that the network was able to detect and classify spruce trees that had visually separable crown symptoms, but it failed to separate spruce trees with stem symptoms and a green crown from healthy spruce trees. For the best model, the overall F-score was 89%, and the F-scores for the healthy, infested, and dead trees were 90%, 79%, and 98%, respectively. The method adapted well to the diverse dataset, and the processing results with different options were consistent. The results indicated that the proposed method could enable implementation of low-cost tools for management of I. typographus outbreaks.
1. Introduction
Various biotic and abiotic stresses are increasingly causing degradation of forest health all over the world. Presently, one of the major biotic threats to forest health in Europe is the European spruce bark beetle (Ips typographus L.) that infests Norway spruce (Picea abies L.). The insect pest has already caused vast tree mortality in Central Europe, southern Sweden, and Russia. Due to the temperature-dependent development of the bark beetle, its population is increasing in northern latitudes, where the warming climate provides opportunities for the development of additional generations during a single growing season [1,2]. It is important to develop technologies for detecting and monitoring the trees attacked by bark beetle to be able to develop efficient tools for their management.
The first signs of bark beetle infestation are small entry holes on the tree stem and wood dust at the base of the tree, as well as resin flow deriving from the entry holes of the bark beetle, which acts as a defense mechanism for the tree [3]. This first stage of infestation is called a green attack, as no visual changes can yet be seen in the foliage. As the infestation proceeds, the tree crown changes in color from green to yellowish, then reddish-brown, and finally gray as the tree dies and loses its needles [4]. Infested trees are traditionally identified by their stem and crown symptoms in laborious and costly field surveys, but crown discoloration and defoliation can also be observed from above the canopy. Therefore, remote sensing using satellites and unoccupied aerial systems (UAS) offer tools to develop procedures for bark beetle monitoring [5].
Satellite remote sensing provides opportunities for developing a global tool for bark beetle monitoring; Sentinel-2 in particular is a highly interesting constellation for monitoring forest health, as it provides open-source data with a short revisit time [4,6,7]. The challenge with Sentinel-2 is the relatively poor spatial resolution of 10 m × 10 m or lower, which is not sufficient for identifying damage at the individual tree level. UAS remote sensing has been increasingly used for forest insect pest and disease monitoring at the individual tree level. A recent review [8] showed that among sensor types, multispectral and red–green–blue (RGB) cameras have been the most popular, whereas random forest (RF) and deep learning (DL) classifiers have been the most commonly used analysis methods. According to the review, pine wilt disease and bark beetles have been the most studied biotic stress agents using UAS.
An UAS with a hyperspectral camera was used to identify different stages of bark beetle infestation in Finnish conditions [5,9]. An overall recall of 81% and class wise recall values of 86%, 67%, and 81% for healthy, infested, and dead spruce trees, respectively, were obtained using a support vector machine (SVM) classifier. In a multi-temporal study in the Czech Republic, UAS data collections were carried out at four timepoints in a year using low-cost RGB and near-infrared (NIR) sensors to detect different stages of attack [10]. The classification was done to separate healthy and infested trees; dead trees were excluded from the classification. The results showed that the classification using the early summer data had more misclassifications than when using data collected later in the summer. This indicated that as the changes in vegetation indices grew during the summer, the classification algorithm performed better in distinguishing healthy and infested trees. During the late summer season, the overall accuracy was 78%. Consistently, a study using spring and fall data in Finland showed that classification of the different health stages was more accurate at the end of the summer season, giving a recall of 71%, 78.6%, and 99% for healthy, declined, and dead spruce trees, respectively, and an overall recall of 87% [11].
The above studies represent classical object-based machine learning analysis with hand-crafted features, whereas recently, novel deep neural network techniques are being increasingly used for forest health studies. There are a few studies on bark beetle detection. Several versions of You Only Look Once (YOLO) [12] (YOLOv2, YOLOv3, and YOLOv4) and UAS RGB images were used to detect and classify Norway spruce trees infested by bark beetles into four categories: green, yellow, red, and gray based on canopy color in [13]. The best model provided a mean average precision of 94%, precision of 95%, and recall of 76% for unseen test data. Three convolutional neural network (CNN) classifiers and RF using a multispectral UAS image dataset were compared in [14]. Four categories were used: pine trees, spruce trees with advanced decline with yellow needles, spruce trees under green attack, and non-infested spruce trees. The best model provided an overall F-score of 84%, and F-scores of 78%, 83%, and 79% for the classes healthy, green-attacked, and infested spruce trees. When using a combined infested class, the best F-scores were 96% and 83% for infested and healthy spruce trees, respectively. Several studies have developed deep learning techniques for UAS RGB images in the context of managing pine wilt disease. Comparison of Faster Region-based Convolutional Neural Network (Faster R-CNN) and YOLOv3 showed the methods had similar precision, but the YOLO-based models had a smaller size and faster processing speed [15]. Recent studies have implemented YOLOv3 for object detection with a focus on minimizing the omission error [16], a lightweight improved YOLOv4-Tiny based method suitable for edge computing [17], and an enhanced version of YOLOv4 providing more efficient model optimization and an improved accuracy [18].
The previous results have shown that remote sensing using UAS RGB images and deep one-stage object detection neural networks is a promising tool for detecting damages by I. typographus. Still, there are many questions concerning the utilization of these techniques. Previous studies with YOLO-networks have used datasets collected in Central Europe, where the outbreak dynamics differ significantly from the situation in northern latitudes, where the epidemic is in its early stages. From the operational point of view, an important question is how the methodology adapts to the variability of the input data. Previous studies have used crown color symptoms to categorize reference trees; therefore, it is a question of whether stem symptoms cause crown symptoms that can be detected from UAS RGB images using CNN techniques.
The aim of this research was to investigate the performance of a deep one-stage object detection neural network in the detection of damages by I. typographus using UAS RGB images. Our detailed research questions include: (1) What is the performance of the methods in our study areas? (2) How should different field symptom observations be utilized in generation of the ground truth? (3) Does the method work with a diverse dataset collected during several years, in different areas, and with different systems? (4) How should the models be trained? To investigate these questions, a state-of-the-art deep one-stage object detection neural network YOLOv4-p5 for performing analysis of health status of spruce trees from UAS RGB images was implemented and its performance was assessed. The results will contribute to our overall development objective of implementing efficient remote sensing tools for bark beetle management.
2. Materials and Methods
2.1. Study Areas and Reference Data
The study areas were in Helsinki and Lahti in Southern Finland, and in Ruokolahti in South-Eastern Finland, as shown in Figure 1. There were seven study sites in total: Paloheinä (PH) in the Helsinki city central park (60°15′25.200″N, 24°55′19.200″E), Kerinkallio (KK) and Mukkula (MK) in Lahti (60°59′16.080″N, 25°41′2.040″E), and Murtomäki (MM), Paajasensalo (PS), Ryhmälehdonmäki (RM) and Viitalampi (VL) in Ruokolahti (61°29′21.840″N, 29°3′0.720″E) (Figure 2). The study sites are dominated by mature Norway spruce and were known to have ongoing infestations by I. typographus. The datasets were collected during several years using RGB cameras mounted on different UASs: Lahti in autumn 2013, Ruokolahti in autumn 2015, 2016, 2019, and 2020, and Helsinki in spring and autumn 2020. Details about the Lahti dataset are given in [5] and the Helsinki dataset in [11].
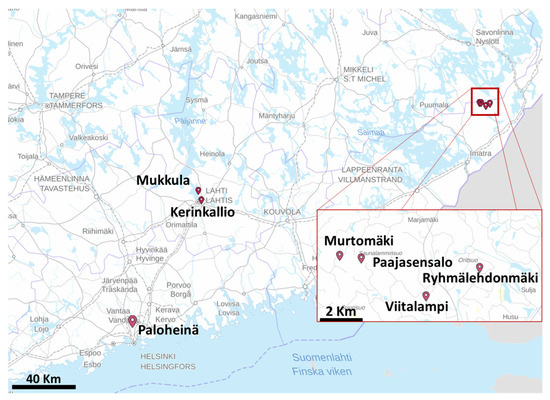
Figure 1.
Locations of the seven test areas. Background map contains data from the National Land Survey of Finland Topographic Database.

Figure 2.
UAS RGB orthomosaics of the test areas from (a) Murtomäki, (b) Paajasensalo, (c) Ryhmälehdonmäki, (d) Viitalampi, (e) Mukkula, (f) Kerinkallio, and (g) Paloheinä. Coordinate system: ETRS-TM35FIN.
Tree health data was collected by experts by evaluating and classifying various symptoms in field surveys. All symptoms were rated on a discrete numerical scale representing the severity of the symptom (Table 1).

Table 1.
Symptom scoring. The Ruokolahti and Lahti scoring is based on [19] and the Paloheinä scoring on [11].
In Lahti and Ruokolahti, circular sampling plots were established, and all trees within a plot were surveyed using the approach developed in [19]. The center of each plot was located with a Trimble Geo XT GPS-device (Trimble Navigation Ltd., Sunnyvale, CA, USA). Individual trees were located by measuring the distance and azimuth to each tree from the plot center. The radius of the plots was 5 m in the Ruokolahti datasets from 2015 and 2016, and 10 m in all other Ruokolahti and Lahti datasets. Within a sampling plot, the tree species, diameter at breast height (DBH) and height of each tree was recorded. For spruce trees, five symptoms indicative of bark beetle infestation were recorded: crown discoloration, defoliation, bark beetle entry and exit holes in the trunk, resin flow spots, and declined bark condition. The original scoring was 1–4 for discoloration and defoliation and 1–3 for holes, resin flow, and bark condition.
In Paloheinä, instead of using sampling plots, health data was recorded for selected individual spruce trees dispersed throughout the area, aiming for a uniform distribution of different health statuses [11]. The positions of the trees were obtained from orthophotos collected before tree selection. The recorded health symptoms were crown color, defoliation, resin flow, bark damage, and decreased canopy height; the scoring was 0–5 for the crown color, 0–4 for defoliation, and 0–2 for resin flow and bark damage.
The scoring scales were slightly different in these two schemes, so they were scaled to the same range (Table 1). The scoring for entry and exit holes and canopy height are not shown, because they were not evaluated for both areas and therefore were not used in scoring. There were altogether 1616 reference spruce trees and 1743 trees in total.
Two symptom rules were considered: one based only on the crown color, and another based on both crown and trunk symptoms. Previous studies have already shown that the classification is successful when there are visible crown symptoms [9,13], but it is also of interest to study whether the spruce trees with green crowns and stem symptoms could be distinguished from the healthy green spruce trees with the proposed method.
Symptom rule A: The crown color was used to classify the spruce trees into classes healthy, infested, and dead. Only spruce trees were labeled; other trees were considered background. In the Lahti and Ruokolahti datasets, green spruce trees were labeled as healthy, yellowish and reddish as infested, and gray as dead. In the Paloheinä datasets, green and faded green spruce trees were labeled as healthy, yellowish, yellow, and reddish/brown as infested, and gray as dead. Green attack was not included as a separate class in this study, because the field surveys were performed mostly late in the summer, when there was not a significant amount of trees in this phase.
Symptom rule B: A health index for the reference trees was calculated using a modified version of the equation initially presented in [11]:
The trees with reddish, brown, or gray color were classified as dead. Trees with a Health_index of two or lower were classified as healthy and those with a Health_index greater than two as infested.
Health_index = 1.5(Color + Defoliation) + Resin flow + Bark damage.
The number of trees in each class is presented in Table 2. With symptom rule A, the class healthy was the largest and the class infested the smallest; particularly the class infested was small in Lahti and Ruokolahti, with 14 and 17 trees, respectively. With symptom rule B, the class distribution was more even. In Lahti and Ruokolahti, many trees classified as healthy using rule A were moved to the class infested. These were trees that had a green or faded green crown color despite having stem symptoms.

Table 2.
Number of trees in each area with symptom rules A and B.
The class distribution represented well the outbreak status in the areas. In Paloheinä, the outbreak was at an active state, with many fresh infestations and high mortality. In Ruokolahti, the high number of dead spruce trees indicated a strong earlier colonization pressure; the portion of freshly infested reference trees was small due to an overridden outbreak peak. The fact that several trees with trunk symptoms had green crowns was due to either low population densities or an early phase of colonization.
2.2. Remote Sensing Datasets
Remote sensing images were collected during the field inspections in 2013–2020 (Table 3). Different RGB cameras and multirotor UASs were used in different years. The cameras included the Samsung NX1000 (20.3 megapixels 23.5 × 15.7 mm CMOS sensor and 16 mm lens), Samsung NX300 (20.3 megapixels 23.5 × 15.7 CMOS sensor and 16 mm lens), Sony A7R (36.4 megapixels 35.9 × 24 mm CMOS sensor and 28 mm lens), and Sony A7R II (42.4 megapixels 35.9 × 24 mm CMOS sensor and 35 mm lens) operated in single and dual camera modes. The flying altitudes were 90–140 m. Datasets were collected under cloudy, sunny, and varying conditions.

Table 3.
Details of the remote sensing datasets. (FA: Flying altitude; GSD: Ground Sample Distance; PH: Paloheinä, KK: Kerinkallio, MK: Mukkula, MM: Murtomäki, PS: Paajasensalo, RM: Ryhmälehdonmäki, VL: Viitalampi).
Orthophotos were calculated with ground sample distances (GSDs) of 2.4–6 cm with the Agisoft Metashape software using methods described in [20]. The images were scaled to a digital number range of 0–255 without further radiometric calibration.
Annotated datasets were created using the orthophotos and reference trees. Tree crown segmentations were made to determine the extent of individual reference treetops (Figure 3). For the Paloheinä dataset, this was done by automatically segmenting airborne laser scanning (ALS) data provided by the city of Helsinki and visually checking potential fallen trees by comparing segments to orthophotos [11]. Segmentations for Lahti and Ruokolahti data were made manually using the orthophotos and height data. Finally, bounding boxes were created around each segmented tree. The ground-surveyed reference tree coordinates in the Lahti and Ruokolahti datasets did not match perfectly with the tree positions in the orthophotos; the displacements were corrected during the manual segmentation process. The Paloheinä reference trees were initially located in the orthophotos.

Figure 3.
Examples of input images based on (a) sample sites in Lahti and Ruokolahti and (b) randomly selected trees in Paloheinä. Tree crown segments (red) and bounding boxes (blue) are shown overlaid on the images.
As the YOLOv4-p5 network can only process images up to a certain size without loss of information, the orthophotos were divided into several smaller images. For the Lahti and Ruokolahti areas, rectangular images corresponding roughly to the sample sites were cropped (Figure 3a). Possible unlabeled trees in the perimeters of the plots were removed by replacing them with zero-value pixels. In the Paloheinä area, individual reference trees were spread over the area. In this case, convex hulls for the tree crown segments with an additional 0.5 m buffer around them were created and the resulting shapes were cut from the orthoimages. Cropped images with a black background were then created (Figure 3b). The resulting images were not as realistic as the sampling plot images, as the trees were not surrounded by normal forest vegetation.
2.3. YOLOv4-p5 Implementation
The original YOLO network was published in 2016 [12]. It learns to detect the location and class of objects in an image. As a supervised deep learning approach, it requires lots of labeled training data to learn the task. Since the first YOLO release [12], several refined network versions have been presented, for example, YOLOv2 [21], YOLOv3 [22], and YOLOv4 [23]. Scaled-YOLOv4 [24], specifically its version YOLOv4-p5 which has been scaled up from YOLOv4, was used in this study. It has a deeper network than YOLOv4, and its input size (896 × 896 pixels) is larger than that of YOLOv4 (608 × 608 pixels). Scaled-YOLOv4 builds on the earlier YOLO models, as well as the Ultralytics YOLOv3 implementation [25], their YOLOv5 [26], and concepts from other neural networks.
Scaled-YOLOv4 consists of a backbone network, a neck, and a detection head [24]. The backbone is a CNN that extracts hierarchical features from three-band input images. The neck consists of add-on blocks that combine information from the feature maps at different levels. Finally, the detection head predicts object locations and their classes based on the combined features. It predicts a fixed number of bounding boxes, outputting for each the coordinates of the box center, the width and height of the box, an objectness score, and a class probability for each possible class [24,27]. The objectness score estimates the probability of the box containing an object of any class, while the class probabilities represent the conditional probability of the box containing an object of a specific class, given that it contains some object [12,21].
The network is trained by minimizing the error between its outputs and the ground-truth labels for a set of training images. The error is measured by a loss function (Equation (2)), which is the weighted sum of objectness (Lobj), classification (Lcls), and bounding box (Lbb) losses:
where λ1, λ2, and λ3 are the respective weights for objectness, classification, and bounding box loss. Binary cross-entropy (BCE) loss is used for the objectness and classification losses, and Complete IoU loss [28] for the bounding box loss. Training is done using mini-batch gradient descent (PyTorch SGD optimizer) with Nesterov momentum [29,30], weight decay, and a cosine learning rate scheduler. The network is trained for a chosen number of epochs. An exponential moving average (EMA) of the model weights is maintained during training, and the EMA model with the best performance on the validation set is chosen as the final model [27]. The performance is evaluated using the fitness score
where AP indicates average precision; AP@0.5 and AP@0.5:0.95 are defined in Section 2.4.
L = λ1Lobj + λ2Lcls + λ3Lbb,
0.1 AP@0.5 + 0.9 AP@0.5:0.95,
Models were not trained from scratch but by fine-tuning a pre-trained model. Fine-tuning refers to taking a model trained for one task and continuing its training using another dataset. This way, the knowledge learned for a more general task may be used as a starting point for learning a specific task. This can be beneficial when only a limited amount of data is available for the task at hand. All layers of the network may be fine-tuned, or some may be frozen before training. As a starting point for training, a pre-trained YOLOv4-p5 was used; it had been trained on the COCO 2017 object detection dataset, which contains 118,000 training and 5000 validation images with labeled instances from 80 common object classes [31]. Additionally, models were fine-tuned for different subareas by first fine-tuning the COCO-trained model on the full tree health dataset, and then further fine-tuning the model with data from one subarea. All the layers of the network were fine-tuned.
Training details can be adjusted by changing the model hyperparameters. Models were initially trained using the default hyperparameters, then the hyperparameters for two different models were optimized. The hyperparameters control details of the optimization algorithm, loss function, and data augmentation. The initial learning rate, momentum, and weight decay parameters affect the optimization algorithm, while the objectness, classification, and bounding box loss gains adjust the contribution of each component loss to the total loss. The BCE loss positive weights for the objectness and classification losses control the influence of positive samples on these losses. The anchor-multiple threshold controls the matching of predicted and ground-truth bounding boxes when computing loss. The Focal loss gamma is a parameter of focal loss [32], which can optionally be used in place of BCE loss. The remaining hyperparameters control data augmentation during training.
Scaled-YOLOv4 uses a set of data augmentation techniques on the training set to improve performance. Data augmentation provides more data for training and creates new types of examples, which helps learning. The dataset is augmented by combining multiple images into one training image using a mosaic technique [26] and MixUp augmentation [33], and then applying standard photometric and geometric distortions: random hue-saturation-value (HSV) changes, translation, scaling, and flipping. Additional augmentation options include rotation, shear, and perspective shifts. Each augmentation hyperparameter controls the probability or possible range of one augmentation method.
The hyperparameters were optimized for two of the models using a genetic algorithm (e.g., [34]) available in the Scaled-YOLOv4 implementation [27]. In each generation, the model was trained for 70 epochs, and hyperparameters were tuned by selection and mutation according to the performance on the validation set. The performance was measured with the fitness score (Equation (3)). The genetic algorithm was run for 300 generations. The hyperparameters were initialized with the default values, except those with default value 0 (details are given in Section 3.1).
When making detections with the trained model, Scaled-YOLOv4 applies some post-processing to its outputs. Non-maximum suppression (NMS) is used to remove redundant detections: it compares the confidence scores of overlapping boxes of the same class and removes the predictions with lower confidence. The model also uses a confidence threshold (CT) to filter the outputs, removing predictions with a score lower than the threshold. In this study, the confidence threshold was selected by balancing the precision and recall values on the validation dataset, and it varied from 0.1 to 0.6 for the different models.
The official PyTorch implementation of YOLOv4-p5 [27] was used. The code was run inside a Docker container created from the NVIDIA PyTorch container image, release 20.06 [35]. The container was an Ubuntu 18.04 environment with Python 3.6, PyTorch 1.6.0a0+9907a3e, and NVIDIA CUDA 11.0.167. For full details, see [35]. The host system was a desktop computer with an Ubuntu 18.04 operating system and a NVIDIA GeForce GTX 1080 Ti (11 GB) graphics processing unit (GPU).
Multiple trained YOLOv4-p5 models were produced by varying the training data, symptom rule, and hyperparameters (Table 4). A batch size of four was used for training. The impact of hyperparameter optimization was evaluated for two models (trFull-syrA-hyopt, trFull-syrB-hyopt). The models trained with the full data (all areas combined) as well as using separately the subareas Paloheinä (PH) and Lahti/Ruokolahti (LR) data were evaluated. Three different model options were evaluated in the subareas: (1) training the model with the full data and testing with the subarea test data (trFull-syrA-PHtest, trFull-syrA-LRtest), (2) training and testing the model using only the subarea data (trPH-syrA, trLR-syrA), and (3) initial training using the full datasets and fine-tuning and testing using the subarea data (trFull-syrA-PHft, trFull-syrA-LRft) (in the previous, for the sake of clarity the models are given only for symptom rule A; evaluations were made similarly for symptom rule B).

Table 4.
Models evaluated, PH: Paloheinä, LR: Lahti/Ruokolahti.
The full dataset was divided randomly into training, validation, and test datasets. 20% of the images were reserved for testing, and the remaining 80% were divided 80:20 into training and validation datasets, respectively. The subarea datasets were created after the division by removing the images from other areas from each dataset. Summary of the samples in the training dataset is given in Table 5 and in the validation and testing datasets in Table 6.

Table 5.
Sizes of the training datasets for different models given in Table 4. The size and class distribution of the dataset is determined by the area (trFull, trPH, and trLR) and the symptom rule (syrA and syrB).

Table 6.
Validation (Val) and testing (Test) datasets for models given in Table 4. The size and class distribution of the dataset is determined by the area (trFull, trPH, and trLR) and the symptom rule (syrA and syrB).
2.4. Performance Assessment
The trained models were evaluated using test datasets that consist of labeled data not used in training (see Table 6). To determine whether a predicted box correctly detects an object, it is compared to the ground-truth (GT) labels. A prediction is considered correct, or true positive (TP), if its Intersection over Union (IoU) [36] with a ground-truth box of the same class is greater than a chosen threshold; IoU threshold 0.5 was used in this study. If a prediction overlaps with multiple ground-truth boxes by more than the threshold, it is considered to predict the ground-truth object that it has the highest IoU with. The predictions that do not overlap a GT box of the same class by more than the threshold are considered false positives (FP). FPs are thus caused by location and classification errors.
Detection results of the trained model were evaluated with the metrics precision, recall, F-score, and average precision (AP) [36]. Precision and recall are calculated using a TP IoU threshold 0.5. Precision is defined as the fraction of predictions that are correct:
precision = TP/(TP + FP).
Recall is the fraction of ground-truth objects that were identified correctly, i.e.,
where FN indicates the number of false negative detections. Precision and recall may be adjusted by changing the confidence threshold. Recall decreases as the confidence threshold increases, while precision may increase or decrease. The F-score [36] is a harmonic mean of precision and recall:
recall = TP/(TP + FN),
F-score = 2·precision·recall/(precision + recall).
A precision-recall curve may be plotted by plotting precision against recall at different confidence thresholds from 0 to 1. An ideal object detector has high precision at all recall levels, and thus the area under the curve (AUC) is close to 1. AP is an estimate of the AUC, computed at a chosen true positive IoU threshold [36]. AP at IoU threshold 0.5 (AP@0.5) and the mean of APs at 10 equally spaced IoU thresholds from 0.5 to 0.95 (AP@0.5:0.95) were computed for the different classes. The term mean average precision (mAP) refers here to the mean of APs of the different classes; in other works, it is sometimes also used interchangeably with AP, or to denote the average over different IoU thresholds. Overall precision, recall, mAP@0.5, and mAP@0.5:0.95 were computed as the mean of the class-wise results.
3. Results
3.1. Hyperparameter Optimization
Hyperparameter optimization was done for the models trained using full datasets with symptom rules A and B. The final optimized values and the visualization of the parameter evolution show that the hyperparameters adjusted quite close to the default values (Table 7, Figure 4, Appendix A). For parameters such as the “classification loss gain” and the “translation fraction”, the optimized value clearly resulted in higher fitness, while for some parameters, the result of the evolution was not as clear (e.g., the initial learning rate) (Figure 4). The chosen initial values greatly influenced the results, as most hyperparameters only explored a narrow region of their possible range during the evolution. The three parameters with the greatest changes were the “image MixUp probability”, “initial learning rate” and “classification BCE loss positive weight” for symptom rule A, and λ1., λ2, and λ3 for symptom rule B. The evolution of all parameters is presented in Appendix A; results for the optimization algorithm and loss function hyperparameters are in Figure A1 and results for the augmentation hyperparameters are in Figure A2.

Table 7.
Default, initial, and optimized values of hyperparameters; syr: Symptom rule.
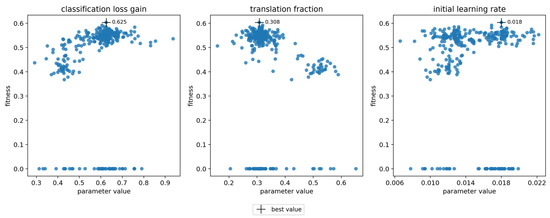
Figure 4.
Evolution of hyperparameters “classification loss gain”, “translation fraction”, and “initial learning rate” for symptom rule A. Each subplot shows the evolution of one parameter, with its value on the x-axis and fitness on the y-axis. The cross indicates the chosen optimal value.
3.2. Training
The training statistics for the full dataset with symptom rule A (trFull-syrA) showed that the training was successful; the validation metrics stabilized at approximately 100 epochs, while the training losses continued decreasing (Figure 5). Figures for the rest of the models are given in Appendix B and most of them show similar behavior. However, the metrics for the fine-tuned subarea models (trFull-syrA-PHft, trFull-syrA-LRft) were different: as the initial models were already well trained with the full dataset, consistently with the expectations, the additional training with the subarea data did not result in significant changes to the model (see details in Appendix B: trFull-syrA-PHft (Figure A5), trFull-syrA-LRft (Figure A7), trFull-syrB-PHft (Figure A13), trFull-syrB-LRft (Figure A15)).
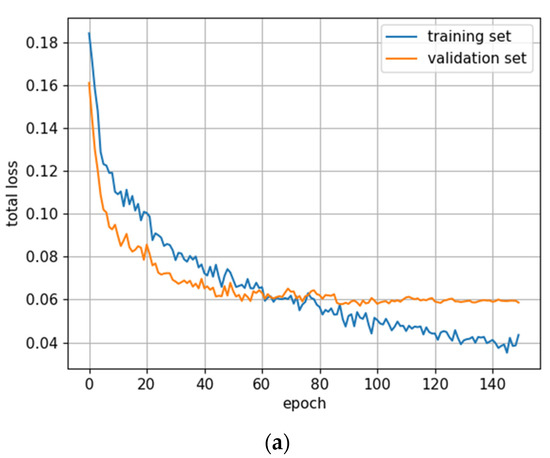
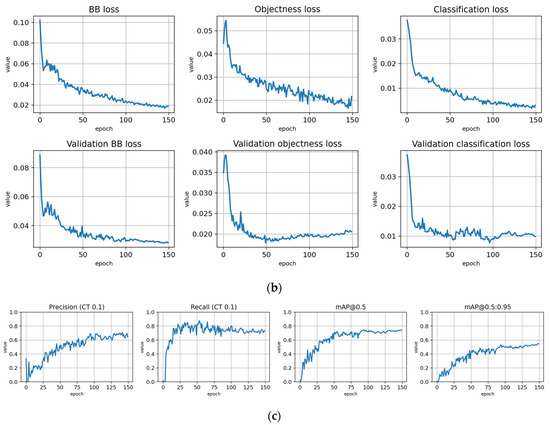
Figure 5.
Training statistics for the full dataset with symptom rule A (model: trFull-syrA). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5, and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
3.3. Performance Analysis for Symptom Rule A
Symptom rule A classified spruce trees into classes healthy, infested, and dead based on the crown color. The performance on the test data as well as the chosen confidence thresholds and the numbers of training, validation, and testing samples used in each model are given in Table 8.

Table 8.
Model testing results for symptom rule A. N-reference: Numbers of reference trees for training (Tr), validation (Va), and testing (Te). CT: Confidence threshold.
The best results for the full dataset were obtained when using the optimized hyperparameters (model: trFull-syrA-hyopt); the F-score and AP@0.5 metrics were 0.732 and 0.762, respectively. Considering the different classes, the best results were obtained for the dead trees (F-score: 0.840, AP@0.5: 0.841), followed by the healthy trees (F-score: 0.804, AP@0.5: 0.809). The infested trees were the most difficult to detect; the F-score and AP@0.5 were 0.547 and 0.635, respectively.
In the subarea evaluations, the best results were obtained for the Paloheinä subarea. The overall F-scores were 0.803, 0.827, and 0.793 for the full model (trFull-syrA-PHtest), the fine-tuned model (trFull-syrA-PHft), and the model trained with only Paloheinä data (trPH-syrA), respectively. Thus, results were better when the full dataset was utilized in training than when using only the Paloheinä subarea dataset. The fine-tuned model (trFull-syrA-PHft) provided the best result, with F-scores of 0.917, 0.689, and 0.871, respectively for the healthy, infested, and dead classes. The full model (trFull-syrA-PHtest) provided nearly as good results as the fine-tuned model.
Results for the subarea Lahti/Ruokolahti were weaker. The overall F-scores were 0.637, 0.593, and 0.588 for the full model (trFull-syrA-LRtest), the fine-tuned model (trFull-syrA-LRft), and the model trained with the subarea data (trLR-syrA), respectively. The infested class had very poor performance, although the result could not be considered reliable as there were only four test samples. For the healthy and dead classes, the best F-scores were 0.753 and 0.847, respectively, for the model trained with the Lahti/Ruokolahti subarea dataset (trLR-syrA); for the infested class, the full model (trFull-syrA-LRtest) had the best results. However, results of all models were similar, with differences in F-scores of less than 4% for classes healthy and dead.
We also tested training single-class models for the infested and dead trees using the full data and symptom rule A. For the infested class, the results were slightly better for the single-class model than for the three-class model; the F-scores were 0.665 vs. 0.578 and the AP@0.5 values 0.678 vs. 0.602 for the infested-class model and the infested class in the trFull-syrA model, respectively. A single-class model provided slightly better results also for the dead trees; the F-scores were 0.843 vs. 0.827, and the AP@0.5 values were 0.811 vs. 0.822 for the single-class and three-class models, respectively.
The use of optimized hyperparameters with the symptom rule A full model (trFull-syrA-hyopt) resulted in minor improvements, e.g., the overall AP@0.5 improved by 3% and the overall F-score did not improve.
The confidence threshold of each trained model was individually selected to balance the precision and recall to similar levels. The CT values were the highest, 0.3 to 0.6, for the Paloheinä subarea; in other areas, values 0.1 to 0.3 were used (Table 8).
3.4. Performance Analysis for Symptom Rule B
Symptom rule B considered the stem and crown symptoms to classify spruce trees into health classes. Results on the test set are given in Table 9.

Table 9.
Model testing results for symptom rule B. N-reference: Numbers of reference trees for training (Tr), validation (Va), and testing (Te). CT: Confidence threshold.
For the full dataset, the best results were obtained with the default hyperparameters (trFull-syrB); the F-score and AP@0.5 were 0.701 and 0.719, respectively. Considering the different classes, the best results were obtained for the dead trees (F-score: 0.869, AP@0.5: 0.878) followed by the healthy trees (F-score: 0.664, AP@0.5 0.733); the infested class had the poorest performance (F-score: 0.570, AP@0.5: 0.547). The hyperparameter optimization did not notably impact the results: the changes in the overall AP@0.5 and F-score were less than one percent (trFull-syrB-hyopt).
In the Paloheinä subarea, the best results were obtained with the full model (trFull-syrB-PHtest); the overall AP@0.5 was 0.9 and the F-score 0.892. For the healthy, infested, and dead classes, this model provided AP@0.5 values of 0.924, 0.799, and 0.977, respectively, and F-scores of 0.904, 0.792, and 0.981, respectively. Fine-tuning the full model further with the Paloheinä data did not improve its performance: its final F-score was 0.865. The model trained with the Paloheinä data alone performed poorest, with an F-score of 0.822.
Results were poor for the healthy and infested classes in the subarea Lahti/Ruokolahti. In this dataset, symptom rule B assigned most of the reference spruce trees with a green crown to the class infested due to their stem symptoms and defoliation status. The object detection method struggled to find differences between the resulting healthy and infested classes. The results were similar for all three models tested on the subarea. The dead class was detected best, with F-scores of 0.81–0.83.
Similar to symptom rule A, the confidence threshold was set highest, 0.6–0.7, for the Paloheinä subarea models; other models had confidence threshold values of 0.1–0.2.
Examples of detection results are shown in Figure 6 and Figure 7. The detections with model trPH-syrB in Figure 7b include a classification error; in Figure 7c the corresponding tree is correctly classified with model trFull-syrB-PHtest.

Figure 6.
Examples of detection results in the Ruokolahti s%ubarea. (a) Ground-truth labels and (b) YOLO results using the trFull-syrA model. Colors: green: healthy, gray: dead.

Figure 7.
Examples of detection results in the Paloheinä subarea and illustration of improvements gained when using the full dataset for model training. (a) Ground-truth labels, (b) YOLO results using a model trained with the Paloheinä dataset (trPH-syrB) including a misclassified tree, and (c) YOLO results using a model trained with the full dataset (trFull-syrB-PHtest) with correct results. Colors: green: healthy, orange: infested, gray: dead.
4. Discussion
4.1. Assessment of Results
A YOLOv4-p5 one-stage object detection network was successfully applied for the analysis of spruce health in the study areas. The best results were obtained in the Paloheinä subarea; the overall AP@0.5 was 0.9 and the F-score 0.892. For the classes healthy, infested, and dead, the best F-scores were 0.904, 0.792, and 0.981, respectively. However, in the more challenging Lahti/Ruokolahti subarea, the results were clearly poorer, particularly considering the identification of infested trees. The dead class had the most consistent performance; the F-score was always above 0.8, and at best was 0.98. This is likely due to the dead trees being spectrally relatively stable objects that differ significantly from the other classes. In addition, many dead trees were present in the training dataset. Particularly the Paloheinä subarea results were consistent with earlier results of YOLOv4 in a study area in Bulgaria (mAP: 0.94, precision: 0.95, recall: 0.76, F-score: 0.84) [13]; the conditions in the Paloheinä subarea resembled this area, as it had an active outbreak with many trees from different health classes. These results confirmed that YOLO provided good detection accuracies when symptoms were visible, and the training data was large.
Compared to the results of a study using multispectral images and a deep learning classifier [14], our results were slightly weaker. In [14], the average F-score was 0.84 and the class-wise F-scores 0.79, 0.83, and 0.78, respectively, for infested spruce trees with a yellow crown, spruce trees under green attack, and healthy spruce trees. When using two classes, infested (combined class) and healthy spruce trees, the F-scores were 0.94 and 0.83, respectively. The better performance compared to our work was expected, because multispectral images providing more detailed spectral information were used, and individual trees were identified in a pre-processing step before applying the classifier to each tree.
Some of the test areas used in this study have been investigated in previous papers. Our best results with YOLOv4-p5 (see above) were slightly better than the results obtained using UAS multispectral imagery and a RF classifier in the Paloheinä subarea [11]. In the latter case, the overall RF recall values were 0.74 and 0.87 for spring and fall datasets, respectively. The class-wise recall for the healthy, declined, and dead spruce trees was respectively 0.654, 0.511, and 0.956 for the spring data, and 0.885, 0.654, and 0.992 for the fall data, respectively. In an earlier study in the Lahti area (Mukkula and Kerinkallio), hyperspectral UAS images and a support vector machine (SVM) classifier were used [9]. The best UAS classification result was an overall recall of 0.81, and recall of 0.86, 0.67, and 0.81 for the classes healthy, infested, and dead, respectively, using leave-one-out validation. The differences in our object detection approach and the above classification processing chains have impacts on the comparability of the results as well as on the operational aspects. The classifier-based methods had a separate tree delineation step (no machine learning) before classification, whereas the YOLO-based method performs detection and classification simultaneously. The above studies used hyperspectral or multispectral data and handcrafted features were calculated for each tree. Therefore, the proposed YOLO-based method was a cheaper and more efficient approach because it had fewer processing steps and used a consumer-grade off-the-shelf RGB camera and automatic feature extraction. However, it is relevant to notice that in the Paloheinä dataset the data was not quite realistic, as the reference images had a masked black background due to the randomized approach used in the field data capture. Henceforth, the detection results are potentially optimistic in this area, whereas the classification performance is representative and comparable to classification techniques.
4.2. Characterization of the Tree Health
Two symptom rules were used to characterize the tree health, namely A: visual analysis of the tree crown color during the field inspection, and B: a health index calculated using both crown and stem symptoms collected in the field. In practice, this leads to differences in the ground-truth classes of the trees. When using symptom rule A, the number of trees with yellow/yellowish or red color (class infested) was 17, 14, and 90 for the Ruokolahti, Lahti, and Paloheinä areas, respectively (Table 2). When using symptom rule B, the number of reference trees in the infested class was 314, 46, and 122 for the same areas, respectively. Thus, the transfer of trees from the healthy to the infested class was extensive in Ruokolahti, relatively large in Lahti, and relatively minor in Paloheinä.
In the Paloheinä dataset, slightly better results were obtained when using symptom rule B. The greatest difference between rules A and B appeared in the results of the infested class, e.g., the F-score was 15% better for rule B; the average difference in the F-scores was 8%. This thus indicated that the symptom rule B provided slightly better consistency between the ground truth and images. Conversely, in the Lahti/Ruokolahti subarea, symptom rule B did not provide adequate differentiation between the healthy and infested classes. A large portion of the reference trees had green crowns and stem symptoms; these could not be correctly detected from the RGB images as infested trees. Symptom rule A provided acceptable results for the classes healthy and dead, but the infested class was too small to provide reliable results in this subarea.
The results confirmed that the YOLOv4-p5 model and RGB images were promising for the classification of tree health when there were visible color symptoms in the crowns. However, in the Lahti/Ruokolahti subarea, the results with YOLOv4-p5 were poor when green-colored trees were separated into the healthy and infested classes based on stem and crown symptoms. The multi-year dataset revealed that many of the trees that had low or moderate stem symptoms managed to recover from the attack, possibly due to higher resistance or a low population density (Section 2.1). It is questionable whether these trees were in the green attack phase during data collection and whether the stem symptoms would spread to the crowns. On the other hand, good results in the Paloheinä subarea and in studies in Central Europe [13,14] could be explained by high population densities that may have caused more pronounced crown symptoms. These aspects should be evaluated in future research. Furthermore, future studies should evaluate if multispectral or hyperspectral images would provide better performances in the difficult cases with an early attack phase or low numbers of beetles, when the impact is not visible in the crown.
4.3. Evaluation of Model Training
Different options of model training were evaluated, including hyperparameter optimization, comparisons of the use of the full dataset or subarea datasets, and different fine-tuning options.
Optimization of the hyperparameters had a minor impact on the results compared to the default parameters. A potential explanation can be the heuristic nature of the optimization approach, as it does not guarantee the true optimality of the obtained hyperparameters. Furthermore, the chosen initial values likely influenced the results significantly. The limited size of the training and validation datasets may also have an impact. On the other hand, the default hyperparameters could have been suitable for the task, in which case further optimization would not have had a significant effect on the results. In the referred studies [13,15,16], the researchers have not mentioned hyperparameter optimization; results of this study did not reveal any concerns regarding the use of default hyperparameters.
Performance of the models trained using the full diverse dataset and the models trained using the subarea datasets was compared. The utilization of the full dataset provided better results, which indicated that the method could utilize the diverse data.
Options for utilizing the full data in training an area-specific detector were studied by evaluating different approaches for fine-tuning: (a) using the weights based on the COCO-dataset [31] and fine-tuning with the subarea data, and (b) fine-tuning the COCO-dataset weights first with the full dataset and then further with the subarea data. In the Paloheinä subarea, the latter approach provided 3% better AP@0.5 and 4–5% better F-score for the symptom rules A and B. In the Lahti/Ruokolahti dataset, the difference was smaller, perhaps due to the larger reference data for the healthy and dead classes, i.e., the subarea dataset alone was probably of sufficient size for model training. Another possibility is that the easier, more pre-processed Paloheinä data did not provide useful information for making detection in the Lahti/Ruokolahti subarea. Furthermore, the models trained with the full dataset also provided good results in the subareas without further fine-tuning. In the cases of fine-tuning, the observations that were used for fine-tuning were already applied during the full model building, which might be one reason for small improvements in the fine-tuning process. Nevertheless, the results were promising and suggested that initial models could be trained with existing large datasets and used as such or subsequently fine-tuned with area-specific data. This will be a highly interesting option for future developments and should be validated in future studies. Furthermore, these results indicated that the method adapted to the diverse dataset.
This study aimed to optimize the overall performance of the detection results. This was carried out by using such confidence thresholds that recall and precision were at similar levels. By changing the confidence threshold, we could e.g., obtain a very high detection rate of infested trees, but with the cost of many false alarms. In the practical application, the trade-off between recall and precision could be done according to the user preferences.
4.4. Contribution and Further Research
Our study made three important contributions considering the utilization of deep one-stage object detection in tree health analysis. First, multiple datasets collected in different environments, during several years, using different UAS systems, and at different phases of outbreak dynamics of I. typographus were used. The method robustly adapted to the diverse datasets. Second, two different symptom rules for categorization of tree health were evaluated. The results confirmed that YOLOv4-p5 and RGB images produced good results when there were visible crown color symptoms, thus the proposed technique is suitable for this kind of analysis. Third, different processing options and hyperparameter optimization were evaluated. The results did not show clear advantages of tuning the hyperparameters. The model fine-tuning was shown to work in this specific UAS remote sensing application. All evaluations showed consistent behavior and indicated that it was advantageous to utilize the full diverse dataset, instead of training models separately using the subarea datasets.
The results were encouraging considering setting up low-cost monitoring systems for bark beetle management. Using UAS and RGB cameras, it is possible to build low-cost remote sensing tools, including also crowdsourcing-based approaches. The proposed technique was shown to provide acceptable results for detecting health classes based on visible crown color symptoms, i.e., healthy, infested, and dead spruce trees. The performance is at the level that enables the monitoring of tree health decline and finding new outbreak areas. However, for sanitary logging purposes, possibly more sensitive remote sensing techniques, such as e.g., hyperspectral imaging and deep classifier networks, might be required in order to find spruce trees at the early green attack phase. We expect that the conclusions are generalizable also to other regions, however, area-specific datasets are needed to fine-tune the models.
This study did not consider the early green attack phase of infestation; more specifically, the green attack data was not collected in the field inspection. An important need for the future is to increase the size and diversity of the annotated datasets to create a big dataset for analysis and for training deep learning methods to their full potential. It will be relevant to collect materials and study the performance of different techniques (RGB, multispectral or hyperspectral cameras) for the detection of green attack, as well as to collect data from more complex environments with mixed forests.
The future objective will be to deploy efficient remote sensing methods for large-scale operational monitoring of bark beetle outbreaks, which will require the implementation of an efficient pipeline from data collection to alarms and decision support. Such a system can have different functions, e.g., monitoring the spread, or early warnings and guidance for sanitary logging. As discussed above, different sensing techniques might be required for different purposes. For each operation, a schedule should be defined to produce data in time to support decision making. For example, satellites could produce global or countrywide data of tree health, individual tree level information about the spread of the infestation could be produced every spring or autumn with UAS RGB cameras, whereas precise information about trees with green attack could be produced soon after swarming of the pests. Three common steps in the practical implementation include the following. Firstly, the system should take care of steps of image calibration, georeferencing, and transforming into a form ingestible by the algorithm. Secondly, it is necessary to optimize algorithms for fast and reliable detection of infested trees. Computational aspects were not considered in this study. From a technical point of view, different optimized network structures have already been demonstrated suitable even for real-time onboard edge processing [17,18]. The third aspect is related to model training; our results indicate that using all available datasets and continuous fine-tuning is a potential approach for this task.
5. Conclusions
A methodology to detect individual spruce trees and their health status using a one-stage object detection network YOLOv4-p5 was implemented in this study. Various models were trained using different datasets and model training options. The datasets were collected during 2013–2020 in three geographic regions and they represented different stages and population densities of bark beetle outbreaks. Images were captured using several UAS-based RGB camera systems, and health data was obtained by evaluating crown and stem symptoms in field inspections.
The YOLOv4-p5 model trained using all datasets combined, had an overall F-score of 73% and class-specific F-scores of 80%, 55%, and 84% for the healthy, infested, and dead classes, respectively. Correspondingly, in the subarea with a good distribution of all three health classes and clear crown symptoms, the overall F-score was 89% and the class-wise F-scores were 90%, 79%, and 98%, respectively. The analysis of infested trees was challenging in two of the areas due to the small number of infested trees and the fact that there were many trees with stem symptoms but a green crown color; the YOLOv4-p5 model had poorer performance in those areas. The dead trees could be detected in all evaluated models with an F-score greater than 80% and at best with an F-score of 98%. The method adapted well to the diverse dataset and the results were consistent with different processing options. An interesting result was that the utilization of the diverse dataset in model training was advantageous in comparison to training models using only a subarea dataset.
As a broader impact, it was concluded that the UAS RGB images and YOLO-based object detection method could be utilized as a low-cost tool for the monitoring and management of I. typographus outbreaks. Once in use, models could be continuously updated and fine-tuned with new data to improve their performance. The complete monitoring system could potentially include global or countrywide monitoring using satellite images, local area monitoring with low cost UAS RGB systems, and for real-time decision support, such as sanitary logging, use even more sensitive techniques such as multispectral or hyperspectral imaging.
Author Contributions
Conceptualization, E.H., P.L.-S.; methodology, H.K., E.H., K.K.; software, H.K.; validation, H.K., E.H.; formal analysis, H.K.; investigation, H.K., E.H.; resources, P.L.-S., S.J., R.N., T.H., N.K., R.A.O., M.P.-A., J.T., M.Ö.; data curation, H.K., S.J., J.T., R.N., N.K., R.A.O.; writing—original draft preparation, H.K., E.H.; writing—review and editing, H.K., E.H., P.L.-S., S.J., R.N., T.H., K.K., N.K., R.A.O., M.P.-A., I.P., J.T., M.Ö.; visualization, H.K., R.A.O.; supervision, E.H., P.L.-S., S.J., I.P., R.N.; project administration, E.H., P.L.-S.; funding acquisition, E.H., P.L.-S., I.P., S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Academy of Finland under grants 327861, 327862 and 330422, by the Ministry of Agriculture and Forestry of Finland with the projects MONITUHO (no. 647/03.02.06.00/2018), SPRUCERISK (no. VN/5292/2021) and MMM_UNITE (no. VN/3482/2021) and by Maj and Tor Nessling Foundation with IPSCAR project (no. 2014462). This study has been performed with affiliation to the Academy of Finland Flagship Forest–Human–Machine Interplay—Building Resilience, Redefining Value Networks and Enabling Meaningful Experiences (UNITE) (decision no. 337127).
Data Availability Statement
Data sharing is not applicable to this article.
Acknowledgments
Authors are grateful to Anna-Maaria Särkkä, City of Lahti, for her cooperation. We also would like to express our thanks to Maarit Sallinen, Tornator Ltd., for enabling the study in Ruokolahti, as well as the City of Helsinki and Juha Raisio and Vesa Koskikallio for their support in the Paloheinä area.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
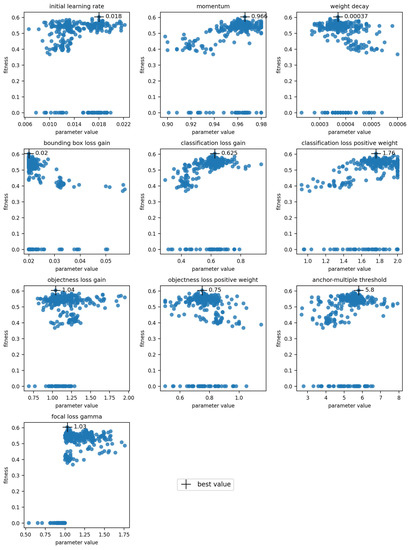
Figure A1.
Evolution of the optimization algorithm and loss function hyperparameters for symptom rule A. Each subplot shows the tested values of one hyperparameter (parameter name given in the plot title), with its value on the x-axis and fitness on the y-axis. The cross indicates the chosen optimal value.
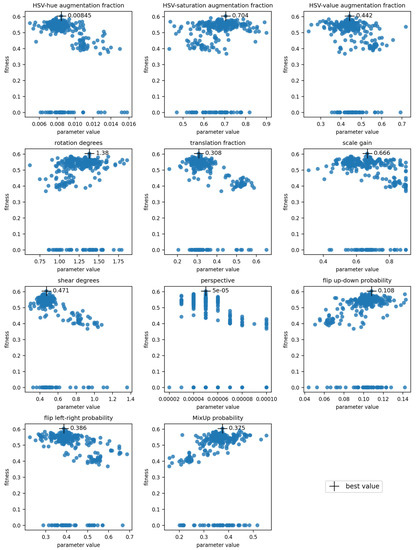
Figure A2.
Evolution of the augmentation hyperparameters for symptom rule A. Each subplot shows the tested values of one hyperparameter (parameter name given in the plot title), with its value on the x-axis and fitness on the y-axis. The cross indicates the chosen optimal value.
Appendix B
The loss curves and validation metrics for each trained model are presented in Figure A3, Figure A4, Figure A5, Figure A6, Figure A7, Figure A8, Figure A9, Figure A10, Figure A11, Figure A12, Figure A13, Figure A14 and Figure A15. The models are explained in Table 4.
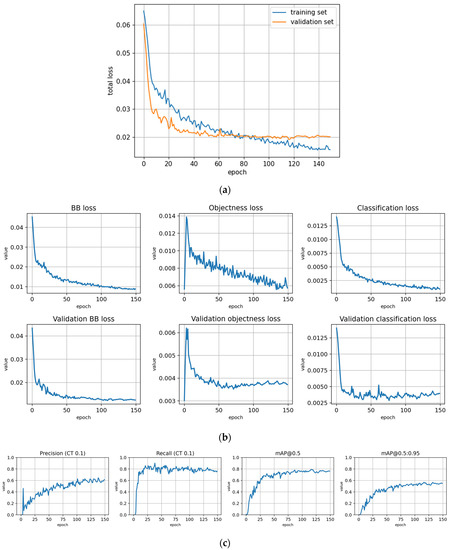
Figure A3.
Training with the Full dataset using classification rule A and optimized hyperparameters (model: trFull-syrA-hyopt). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5, and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
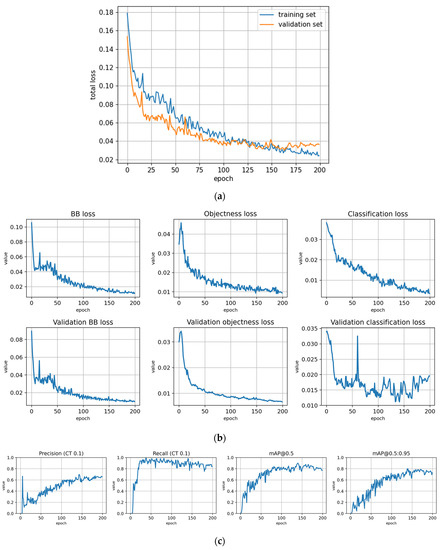
Figure A4.
Training with the Paloheinä dataset using symptom rule A (model: trPH-syrA). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5 and mAP@0.5:0.95 are presented for the validation dataset with CT: confidence threshold.
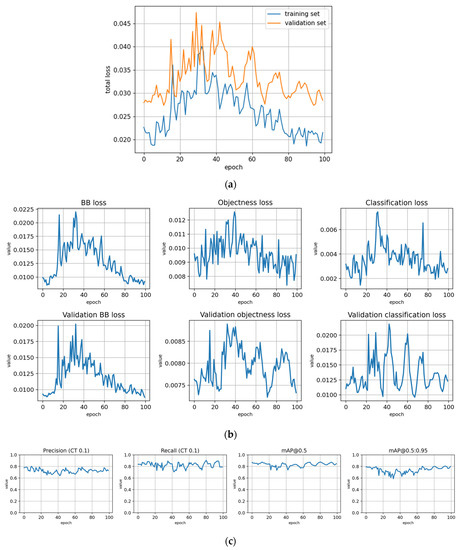
Figure A5.
Fine-tuning the trFull-syrA model with the Paloheinä dataset using symptom rule A (model: trFull-syrA-PHft). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB loss), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5 and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
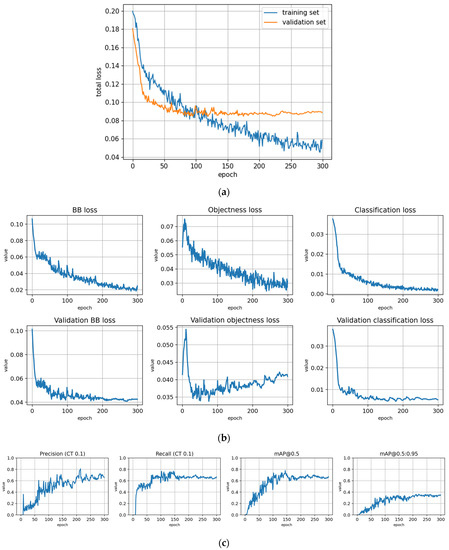
Figure A6.
Training with the Lahti-Ruokolahti dataset using symptom rule A (model: trLR-syrA). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB loss), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5 and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
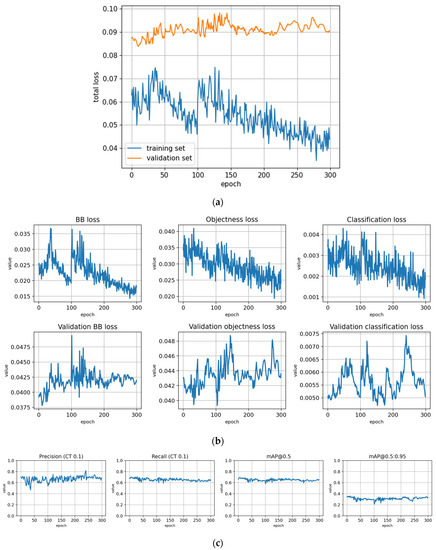
Figure A7.
Fine-tuning the trFull-syrA model with the Lahti-Ruokolahti dataset using symptom rule A (model: trFull-syrA-LRft). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB loss), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5, and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
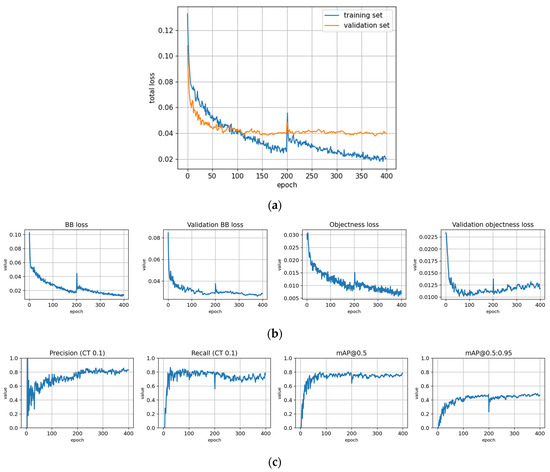
Figure A8.
Training to detect dead trees with the Full dataset using symptom rule A (model: syrA-dead). (a) Total loss on the training and validation datasets during training. (b) Loss of components during training. Bounding box (BB loss), objectness, and classification losses are given for the training and validation datasets. (c) Precision, Recall, mAP@0.5 and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
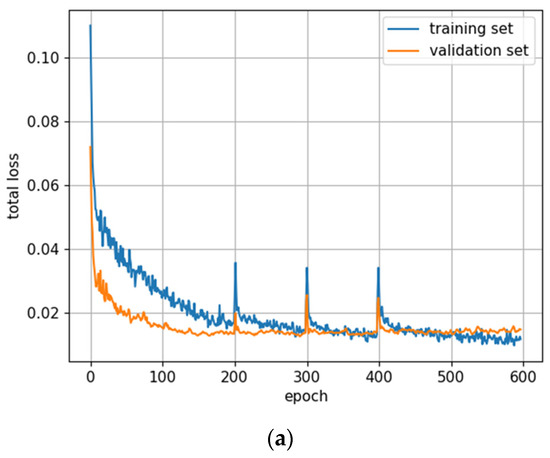
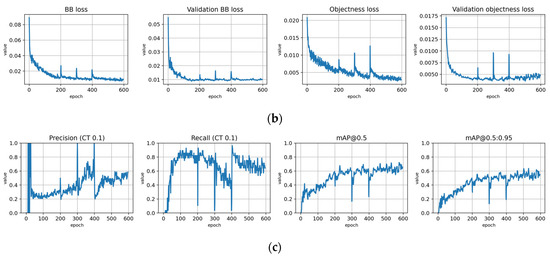
Figure A9.
Training to detect infested trees with the Full dataset using symptom rule A (model: syrA-infested). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB loss), objectness, and classification losses are given for the training and validation datasets. (c) Precision, Recall, mAP@0.5, and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
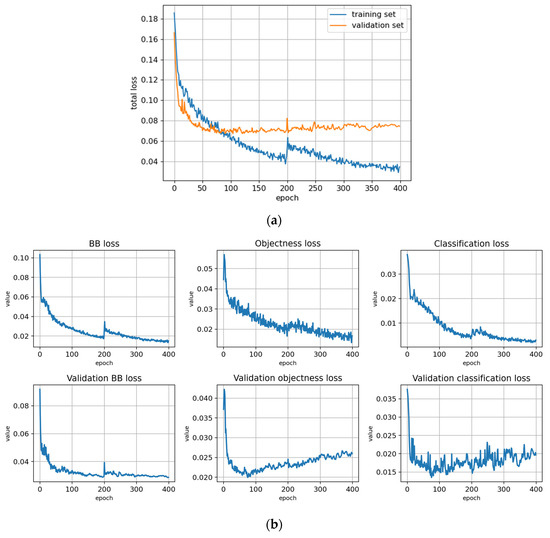
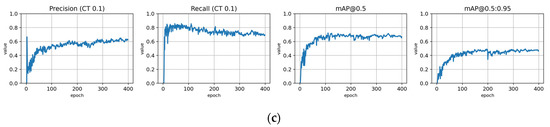
Figure A10.
Training with the Full dataset using symptom rule B (model: trFull-syrB). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB loss), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5, and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
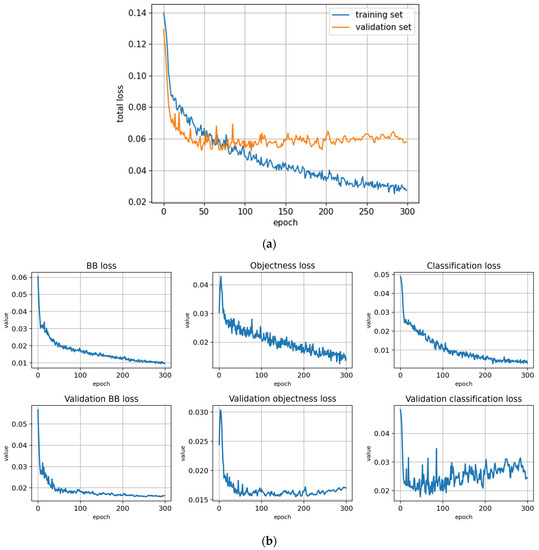
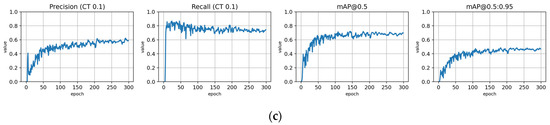
Figure A11.
Training with the Full dataset using symptom rule B and optimized hyperparameters (model: trFull-syrB-hyopt). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB loss), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5, and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
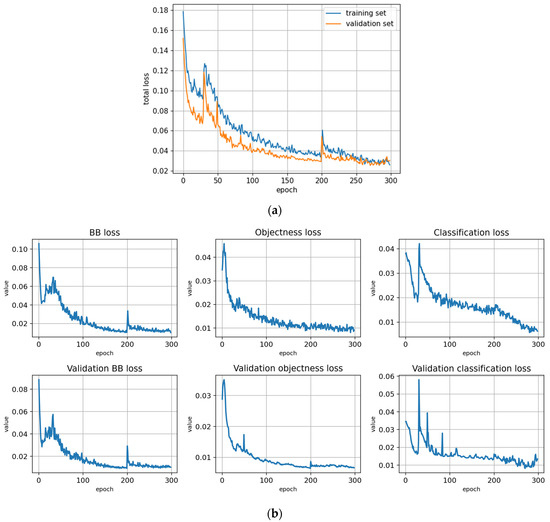
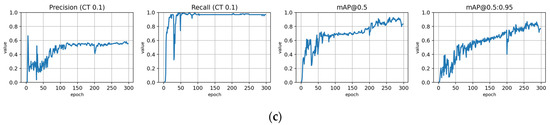
Figure A12.
Training with the Paloheinä dataset using symptom rule B (model: trPH-syrB). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB loss), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5 and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
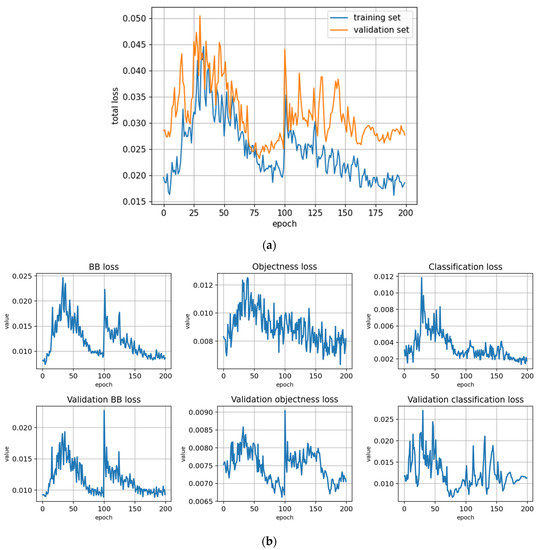
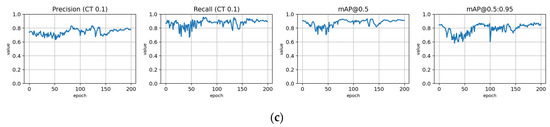
Figure A13.
Fine-tuning the trFull-clrB model with the Paloheinä dataset using symptom rule B (model: trFull-syrB-PHft). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB loss), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5, and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
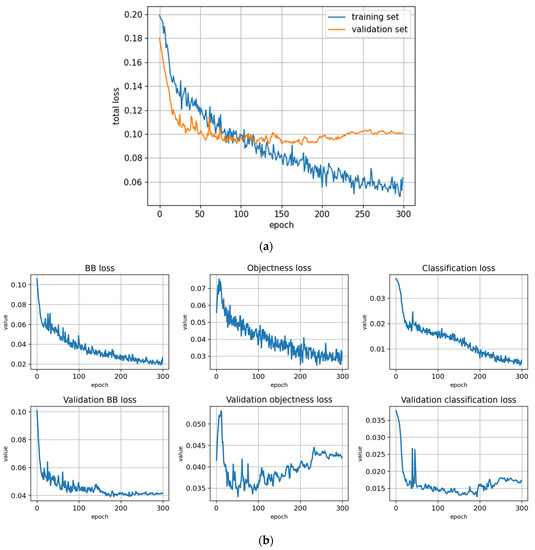
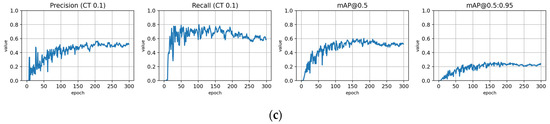
Figure A14.
Training with the Lahti-Ruokolahti dataset using symptom rule B (trLR-syrB). (a) Total loss on the training and validation datasets during training. (b) Loss of components during training. Bounding box (BB loss), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5, and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
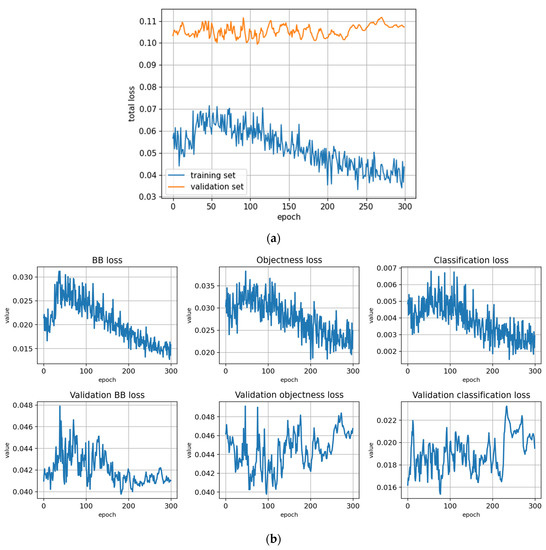
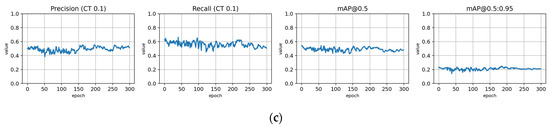
Figure A15.
Fine-tuning the trFull-syrB model with the Lahti-Ruokolahti dataset using symptom rule B (model: trFull-syrB-LRft). (a) Total loss on the training and validation datasets during training. (b) Loss components during training. Bounding box (BB loss), objectness, and classification losses are given for the training (top) and validation (bottom) datasets. (c) Precision, Recall, mAP@0.5, and mAP@0.5:0.95 are presented for the validation dataset. CT: confidence threshold.
References
- Chinellato, F.; Faccoli, M.; Marini, L.; Battisti, A. Distribution of Norway Spruce Bark and Wood-Boring Beetles along Alpine Elevational Gradients: Norway Spruce Bark and Wood Beetles along Altitude. Agr. Forest Entomol. 2014, 16, 111–118. [Google Scholar] [CrossRef]
- Hlásny, T.; König, L.; Krokene, P.; Lindner, M.; Montagné-Huck, C.; Müller, J.; Qin, H.; Raffa, K.F.; Schelhaas, M.-J.; Svoboda, M.; et al. Bark Beetle Outbreaks in Europe: State of Knowledge and Ways Forward for Management. Curr. For. Rep. 2021, 7, 138–165. [Google Scholar] [CrossRef]
- Biedermann, P.H.W.; Müller, J.; Grégoire, J.-C.; Gruppe, A.; Hagge, J.; Hammerbacher, A.; Hofstetter, R.W.; Kandasamy, D.; Kolarik, M.; Kostovcik, M.; et al. Bark Beetle Population Dynamics in the Anthropocene: Challenges and Solutions. Trends Ecol. Evol. 2019, 34, 914–924. [Google Scholar] [CrossRef] [PubMed]
- Bárta, V.; Lukeš, P.; Homolová, L. Early Detection of Bark Beetle Infestation in Norway Spruce Forests of Central Europe Using Sentinel-2. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102335. [Google Scholar] [CrossRef]
- Näsi, R.; Honkavaara, E.; Lyytikäinen-Saarenmaa, P.; Blomqvist, M.; Litkey, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Tanhuanpää, T.; Holopainen, M. Using UAV-Based Photogrammetry and Hyperspectral Imaging for Mapping Bark Beetle Damage at Tree-Level. Remote Sens. 2015, 7, 15467–15493. [Google Scholar] [CrossRef]
- Fernandez-Carrillo, A.; Patočka, Z.; Dobrovolný, L.; Franco-Nieto, A.; Revilla-Romero, B. Monitoring Bark Beetle Forest Damage in Central Europe. A Remote Sensing Approach Validated with Field Data. Remote Sens. 2020, 12, 3634. [Google Scholar] [CrossRef]
- Huo, L.; Persson, H.J.; Lindberg, E. Early Detection of Forest Stress from European Spruce Bark Beetle Attack, and a New Vegetation Index: Normalized Distance Red & SWIR (NDRS). Remote Sens. Environ. 2021, 255, 112240. [Google Scholar] [CrossRef]
- Duarte, A.; Borralho, N.; Cabral, P.; Caetano, M. Recent Advances in Forest Insect Pests and Diseases Monitoring Using UAV-Based Data: A Systematic Review. Forests 2022, 13, 911. [Google Scholar] [CrossRef]
- Näsi, R.; Honkavaara, E.; Blomqvist, M.; Lyytikäinen-Saarenmaa, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Holopainen, M. Remote Sensing of Bark Beetle Damage in Urban Forests at Individual Tree Level Using a Novel Hyperspectral Camera from UAV and Aircraft. Urban For. Urban Green. 2018, 30, 72–83. [Google Scholar] [CrossRef]
- Klouček, T.; Komárek, J.; Surový, P.; Hrach, K.; Janata, P.; Vašíček, B. The Use of UAV Mounted Sensors for Precise Detection of Bark Beetle Infestation. Remote Sens. 2019, 11, 1561. [Google Scholar] [CrossRef]
- Junttila, S.; Näsi, R.; Koivumäki, N.; Imangholiloo, M.; Saarinen, N.; Raisio, J.; Holopainen, M.; Hyyppä, H.; Hyyppä, J.; Lyytikäinen-Saarenmaa, P.; et al. Multispectral Imagery Provides Benefits for Mapping Spruce Tree Decline Due to Bark Beetle Infestation When Acquired Late in the Season. Remote Sens. 2022, 14, 909. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Safonova, A.; Hamad, Y.; Alekhina, A.; Kaplun, D. Detection of Norway Spruce Trees (Picea Abies) Infested by Bark Beetle in UAV Images Using YOLOs Architectures. IEEE Access 2022, 10, 10384–10392. [Google Scholar] [CrossRef]
- Minařík, R.; Langhammer, J.; Lendzioch, T. Detection of Bark Beetle Disturbance at Tree Level Using UAS Multispectral Imagery and Deep Learning. Remote Sens. 2021, 13, 4768. [Google Scholar] [CrossRef]
- Wu, B.; Liang, A.; Zhang, H.; Zhu, T.; Zou, Z.; Yang, D.; Tang, W.; Li, J.; Su, J. Application of Conventional UAV-Based High-Throughput Object Detection to the Early Diagnosis of Pine Wilt Disease by Deep Learning. For. Ecol. Manag. 2021, 486, 118986. [Google Scholar] [CrossRef]
- Lim, W.; Choi, K.; Cho, W.; Chang, B.; Ko, D.W. Efficient Dead Pine Tree Detecting Method in the Forest Damaged by Pine Wood Nematode (Bursaphelenchus Xylophilus) through Utilizing Unmanned Aerial Vehicles and Deep Learning-Based Object Detection Techniques. For. Sci. Technol. 2022, 18, 36–43. [Google Scholar] [CrossRef]
- Li, F.; Liu, Z.; Shen, W.; Wang, Y.; Wang, Y.; Ge, C.; Sun, F.; Lan, P. A Remote Sensing and Airborne Edge-Computing Based Detection System for Pine Wilt Disease. IEEE Access 2021, 9, 66346–66360. [Google Scholar] [CrossRef]
- Sun, Z.; Ibrayim, M.; Hamdulla, A. Detection of Pine Wilt Nematode from Drone Images Using UAV. Sensors 2022, 22, 4704. [Google Scholar] [CrossRef]
- Blomqvist, M.; Kosunen, M.; Starr, M.; Kantola, T.; Holopainen, M.; Lyytikäinen-Saarenmaa, P. Modelling the Predisposition of Norway Spruce to Ips Typographus L. Infestation by Means of Environmental Factors in Southern Finland. Eur. J. Forest Res. 2018, 137, 675–691. [Google Scholar] [CrossRef]
- Viljanen, N.; Honkavaara, E.; Näsi, R.; Hakala, T.; Niemeläinen, O.; Kaivosoja, J. A Novel Machine Learning Method for Estimating Biomass of Grass Swards Using a Photogrammetric Canopy Height Model, Images and Vegetation Indices Captured by a Drone. Agriculture 2018, 8, 70. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. arXiv 2016, arXiv:1612.08242 394. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement 2018. arXiv 2018, arXiv:1804.02767 20. [Google Scholar]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection 2020. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. Scaled-YOLOv4: Scaling Cross Stage Partial Network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Ultralytics/Yolov3: V9.6.0—YOLOv5 v6.0 Release Compatibility Update for YOLOv3 2021. Available online: https://doi.org/10.5281/ZENODO.5701405 (accessed on 10 November 2022).
- Ultralytics/Yolov5: V6.1—TensorRT, TensorFlow Edge TPU and OpenVINO Export and Inference 2022. Available online: https://doi.org/10.5281/ZENODO.6222936 (accessed on 10 November 2022).
- WongKinYiu/ScaledYOLOv4. Available online: https://github.com/WongKinYiu/ScaledYOLOv4 (accessed on 10 November 2022).
- Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression. AAAI 2020, 34, 12993–13000. [Google Scholar] [CrossRef]
- Nesterov, Y.E. A method of solving a convex programming problem with convergence rate O(1/k^2). Dokl. Akad. Nauk SSSR 1983, 269, 543–547. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the 30th International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 17–19 June 2013; Volume 28, pp. 1139–1147. [Google Scholar]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Bourdev, L.; Girshick, R.; Hays, J.; Perona, P.; Ramanan, D.; Zitnick, C.L.; Dollár, P. Microsoft COCO: Common Objects in Context. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. Mixup: Beyond Empirical Risk Minimization. arXiv 2017, arXiv:1710.09412. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; The MIT Press: Cambridge, MA, USA, 1998; ISBN 978-0-262-28001-3. [Google Scholar]
- PyTorch Release 20.06. Available online: https://docs.nvidia.com/deeplearning/frameworks/pytorch-release-notes/rel_20-06.html (accessed on 10 November 2022).
- Padilla, R.; Passos, W.L.; Dias, T.L.B.; Netto, S.L.; da Silva, E.A.B. A Comparative Analysis of Object Detection Metrics with a Companion Open-Source Toolkit. Electronics 2021, 10, 279. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).