Abstract
The development of a network of ground-based telescopes requires detailed astroclimatic studies. This paper presents the spatial distributions of precipitable water vapor (PWV), total cloud cover (TCC) and cloud base height (CBH). With the aim of a representative description of the precipitable water vapor, a method for correcting this characteristic which takes into account the underlying surface is proposed. The method uses the exponential decrease in the water vapor content with the altitude and is based on the calculation of the averaged elevation of the grid nodes around the site. By applying this correction method, the seasonal changes in the median PWV values at the sites of Ali, Muztag-Ata and Suffa, as well as within the Chajnantor area are estimated. We show that the decrease of PWV with the altitude is exponential with a height scale of 1000 m for the sites in South America and Eurasia. The astroclimatic characteristics within the Big Telescope Alt-azimuthal (BTA) region (40N–50N; 35E–55E) are estimated. In this region, the sites suitable for the millimeter and submillimeter (mm/submm) observations are revealed. New sites are Mt. Horai and Mt. Kurapdag. In addition, we show that the Era-5 reanalysis data overestimate the PWV values by 1–2 mm and describe changes in the monthly medians of PWV. Comparison of the calculated medians with the measured PWV show that the correlation coefficient between these characteristics is 0.97.
1. Introduction
Astronomical observations in the millimeter/submillimeter (mm/submm) range of the electromagnetic spectrum are limited by the Earth’s atmosphere. In this spectral range, the Earth’s atmosphere causes a significant attenuation of radiation. One of the main atmospheric gases that is responsible for attenuating radiation in the atmosphere is water vapor. In particular, precipitable water vapor (PWV) is often used for the site characterization. The amount of precipitable water vapor corresponds to the height of the water layer (in mm or cm), which would be formed by complete condensation of the water vapor from a column of atmospheric air with the area of 1 . With a decrease in the content of water vapor, which is distributed along the telescope’s line of sight, transparency of the atmosphere increases.
A number of areas and sites with low water vapor content suitable for mm/submm astronomical observations are known in the world. For example, one of the areas with low water vapor content is the Chajnantor plateau in the Chilean Andes at ∼5000 m elevation above sea level, where the Atacama Large Millimeter/Submillimeter Array (ALMA) is located [1]. Table 1 lists medians of precipitable water vapor at the sites with good astroclimatic conditions [2,3,4,5,6]. In particular, the measurement data show that the medians of PWV at the Chajnantor Plateau are 2.56 mm and 0.72 mm in January and August, respectively. At the Chajnantor summit, the medians of PWV decrease significantly, to 1.08 mm in January and 0.54 mm in August.

Table 1.
Median values of precipitable water vapor at the sites with good astroclimatic conditions [2,3,4,5,6].
A pronounced minimum of PWV is observed in Antarctica. Year-round median values of the PWV at the sites of Dome A, Dome C and the South Pole are listed in Table 1. Due to low air temperatures, the sites of Dome A, Dome C [7,8] and the South Pole are characterized by very low content of water vapor. At these sites, annual medians of PWV do not exceed 0.30 mm.
For comparison, Table 1 lists the medians of PWV for sites, such as Cerro Macon and Mauna Kea [2], which are characterized by very high astroclimatic parameters. The medians at these sites are slightly higher than in Antarctica and equal to 1.02 mm and 1.44 mm at Cerro Macon and Mauna Kea, respectively.
In addition, one of the sites with low and moderate PWV is the Karakaya Hills in Erzurum city. An analysis of the radiosonde data at this site (located at 3170 m above sea level) showed that the median of PWV is 2.7 mm for the period 6 October 2016–15 January 2017. The median increased to 4.00 mm for 1 January 2016–26 September 2017 [6].
In the northern hemisphere, the Tibet Plateau is an area suitable for millimeter and submillimeter observations [9,10]. In particular, Zhao et al. [11] showed that the Lenghu site has very low PWV, ∼1 mm. Amplitudes of intraday PWV fluctuations do not exceed 0.5 mm. In addition, Shantikumar S. Ningombam et al. studied the driest locations in Tibet and compared them with well-known astronomical sites in the world [12,13]. The authors highlighted three sites with high astroclimatic characteristics, including Hanle, Merak and Ali sites within the Himalayan region. The year-round medians of PWV at the Himalayan sites varied from 2.16 mm (Merak) to 2.23 mm (Hanle). Another promising site is Muztag -Ata. Xu et al. found that the annual median of PWV was 2.28 mm and 2.37 mm in 2018 and 2019, respectively [5]. At this site, the driest period with the median less than 2 mm is observed from October to March.
Although some sites with low water vapor content are known, further detailed astroclimatic studies are required for developing a ground-based network of mm/submm telescopes [14,15].
PWV is often estimated using radiosonde data [16,17,18,19,20]. However, the rather sparse network of stations, especially in mountainous regions, as well as the rare frequency of launching radiosondes, do not allow for detailed studies. Other possibilities for estimation of PWV are based on use of GPS data, GNSS data or MODIS observations [21,22].
The most optimal approach for preliminary estimation of PWV within a large region is use of reanalysis data [23,24,25]. The reanalysis data makes it possible to evaluate statistically representative atmospheric parameters including not only PWV, but also other characteristics relevant for astronomical observations (for example, total cloud cover, wind speed, air temperature, atmospheric boundary height, seeing, the Richardson parameter) [26,27,28]. Comparison between PWV changes estimated with the help of satellite and ground-based instruments and reanalysis-derived PWV changes shows a close relationship. For example, Kumar et al. found that at the Varanasi the correlation coefficient between the GPS-derived PWV and the PWV estimated from the Era-Interium reanalysis is close to 0.86 [29]. An analysis of the MODIS-PWV and the Era-5 derived PWV showed that the correlation coefficients are above 0.9 over most of China [22]. The area-averaged correlation coefficient is ∼0.98. The low correlation coefficients are observed near the southwestern border of China (∼0.62).
Long-period changes in PWV show that the Mediterranean coasts, the Alps and northern and inland Europe are characterized by large correlation coefficients (more than 0.97) [30]. The root mean square deviations estimated between changes in the Era-5 PWV and the GPS-PWV range from 1.0 to 1.6 for the Mediterranean coasts and the Alps and from 0.5 to 1.0 for northern and inland Europe. In addition, the studies over Russia showed that MODIS data overestimates the atmospheric optical depth associated with PWV compared to the data of ground-based actinometric observations [31].
This paper is a continuation of our astroclimatic studies in the application of optical, millimeter and submillimeter astronomy [32,33,34]. We discuss the results of a quantitative analysis of atmospheric characteristics, including mean values, medians, mean absolute error, root mean square deviation and correlation coefficient [35,36,37,38]. The study is being carried out to determine the best sites for ground-based mm/submm telescopes as part of the ESMT Submillimeter Teselscopes (ESMT) project [34,39]. Within this project, it is planned to design three mm/submm telescopes in Russia, Uzbekistan and China. We should also note that our studies cover locations with low values of atmospheric diffuse light ranging from 8.3 to 13% (Figure 1). These locations are Baykal Astrophysical Observatory (BAO), Large Solar Telescope (LST-3), Big Telescope Alt-Azimuthal, Crimean Astrophysical Observatory and the Hapcheranga site [34,39].
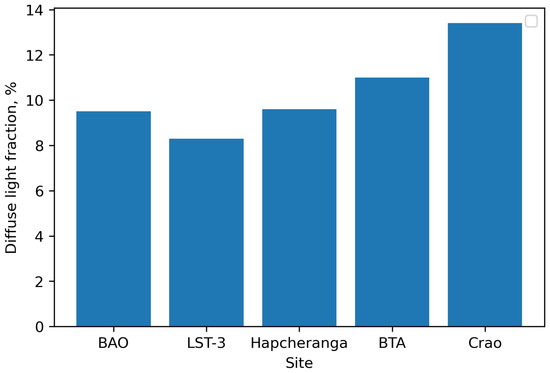
Figure 1.
Diffuse light at astronomical observatories and sites suitable for observations.
2. Data Method to Correct Precipitable Water Vapor Values
In order to estimate spatial distributions of precipitable water vapor, we used the Era-5 reanalysis database [40]. The Era-5 reanalysis data are available with hourly resolution. The horizontal resolution is 0.25. In our study, we used isobaric levels from 1000 hPa to 30 hPa. Each isobaric level corresponds to a certain altitude in the atmosphere.
One of the approaches used for estimating PWV is integration of specific air humidity vertical profiles. In particular, the PWV is calculated using the formula:
where is the water density (1000 ), g is the gravitational acceleration (), is the air specific humidity (g/kg), P is the atmospheric pressure (hPa), is the air pressure near the Earth’s surface (hPa), which defines the lower integration limit, and is the air pressure at the altitude corresponding to the upper integration limit (hPa). The upper integration limit is chosen quite arbitrarily. The arbitrary choice of the upper limit is due to low content of water vapor in the upper layers of the atmosphere. At an altitude of 1.5–2 km, the water vapor pressure is half that at the Earth’s surface, in average. The troposphere (atmospheric layer, from Earth’s surface up to 10–12 km) contains 99% of the atmospheric water vapor. In the calculations, we assumed that the upper limit of integration is 30 hPa.
A significant problem is choice of the lower integration limit, as the lower part of the atmosphere (so-called dynamic atmospheric boundary layer) makes the largest contribution to and, thereby, optical thickness. Radiosonde data and reanalysis make it possible to estimate separately by integrating the vertical profiles in air humidity, as well as to estimate the lower integration limit at the reference radiosounding station. For choosing the lower integration limit, we use either surface air pressure measurements or the approximation of the standard atmosphere.
Another approach applied for estimation of atmospheric water vapor statistics is based on the hourly values of , which are available in the Era-5 reanalysis database. Direct use of the reanalysis data leads to overestimated values of , especially for mountainous areas. The input data in the reanalysis corresponds to a certain volume box limited by grid node. In this case, we can note that values must be corrected. The Era-5 reanalysis data, which include values, profiles of meteorological values and modeled relief, have a limited spatial resolution. values are calculated for grid nodes that may not contain mountain peaks but include lower altitudes. A site suitable for millimeter and submillimeter observations can be remote from the nearest grid node. So, deviations in the PWV values may appear. To take into account the relief, we use a well-known Formula (2) containing an exponential term and a relative altitude difference :
where is the non-dimensional proportionality coefficient, is the water vapor scale height, and = 1000 m. A flowchart of the method for correcting is shown in Figure 2.
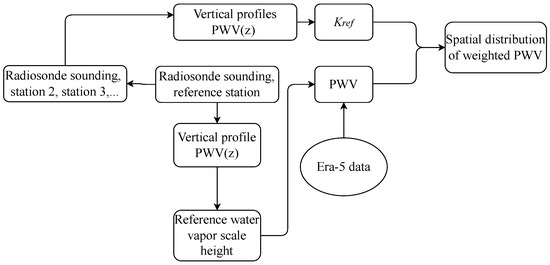
Figure 2.
Flowchart of the method for correcting . The values of PWV are computed using the radiosonde sounding at the nearest reference station. Additional radiosonde stations provide correction of PWV distribution within the region.
The water vapor scale height and the proportionality coefficient are calculated from the best exponential fit to the water vapor content profile obtained from radiosonde soundings launched from the nearest station (Mineralny Vody). At a given site, the coefficient and vary over time. Under different atmospheric conditions, the scale height ranges from 1200 to 2700 m at the BTA. The mean value of is 2280 m. The non-dimensional coefficients are calculated for grid nodes by interpolation of estimated for a set of radiosonde stations within a given region. Adaptation of the method for the sites where the statistics of PWV are known shows that valid calculation of the value should take into account the limited area and depends on the relief model in the Era-5 reanalysis as well as the physical elevation of a given site. For a correct estimate of PWV at a given site, we calculate the relative altitude difference not for a single grid node but within the area around the site. In other words, PWV values are corrected using variable coefficients for different sites, taking into account the relief model and, in particular, the mean difference between the altitude of the mountain summit and the “surrounding terrain”.
3. Precipitable Water Vapor Statistics within the Chajnantor Area
In order to determine how well the Era-5 reanalysis data reproduces real changes in precipitable water vapor, we used the data gathered from radiometer measurements at the Chajnantor Plateau [3]. Using Formula (2), we estimated the mean hourly PWV values within the Chajnantor Plateau. The Era-5-derived precipitable water vapor values are overestimated in comparison with the measurement data. We used the mean absolute error () for estimation of the PWV deviations assessed between the calculated and measured PWV:
where is the mean monthly PWV calculated from the Era-5 reanalysis data, and is the mean monthly measured values of PWV. In average, the mean absolute error is 1.8 mm. The largest falls in winter when water vapor content is the highest. The mean absolute error in winter is 3.1 mm. In summer, decreases to 1.1 mm.
A correct estimation of statistical characteristics of precipitable water vapor, including hourly values, requires the use of a certain method, especially under conditions of low atmospheric moisture. Using Formula (2), we calculated the PWV variations within the Chajnantor area. Figure 3 shows the PWV variations for a period of five days within the Chajnantor area.
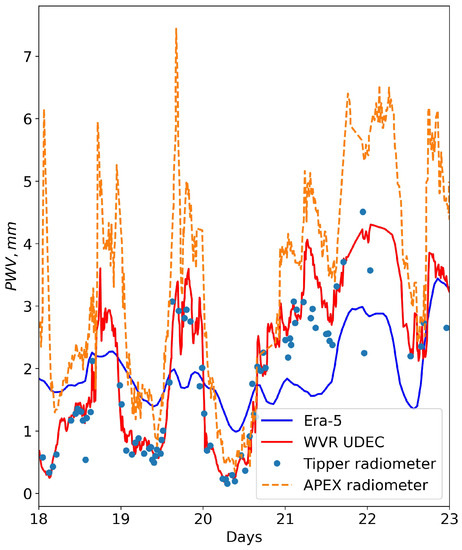
Figure 3.
PWV variations for a period of five days in the Chajnantor area for the period 18 December 2011–23 December 2011. The blue line corresponds to the calculated Era-5 PWV variations. The red line and round markers correspond to the PWV variations at the Cerro Chajnantor summit. The orange line corresponds to the PWV variations at the Chajnantor Plateau.
At the Chajnantor Plateau, measurements were performed with an APEX radiometer operating at 183 GHz [3]. At the Cerro Chajnantor summit, precipitable water vapor was measured by a water vapor radiometer (red line) at 183 GHz and the Tipper radiometer, which integrates radiation over a 103 GHz band, centered at 850 GHz. An analysis of intraday variations in the precipitable water vapor shows that the measured values of PWV significantly deviate from the hourly PWV values estimated from the Era-5 reanalysis data. The mean absolute error is 0.94 mm. We also estimated the root mean square deviation:
and the correlation coefficient:
where and are the Era-5 derived PWV and measured PWV, respectively, and and are the root mean square deviations.
The root mean square deviation of the PWV is 1.06 mm. The correlation coefficient between the PWV variations is 0.57. Thus, the Era-5 reanalysis data passably reflect atmospheric situations with low and high water vapor content in the atmosphere, which are of interest for mm/submm astronomical observations.
For longer averaging periods, consistency of PWV variations estimated from the Era-5 data and the data of the radiometric measurements improves. Figure 4 shows the changes in the mean monthly PWV values estimated from Era-5 data and the changes in the mean monthly measured radiometric PWV values. PWV values are averaged from 2011 to 2014. Statistics of PWV variations estimated from the Era-5 reanalysis data and radiometric data are shown in Table 2. In addition to the mean absolute error estimated for the hourly PWV values, we also estimated the RMS and the correlation coefficient between the PWV time series. Compared to intrahour variations, the mean absolute error of the mean monthly variations in PWV decreases to 0.23 mm, and the RMS decreases to 0.28 mm. The correlation coefficient is 0.97.
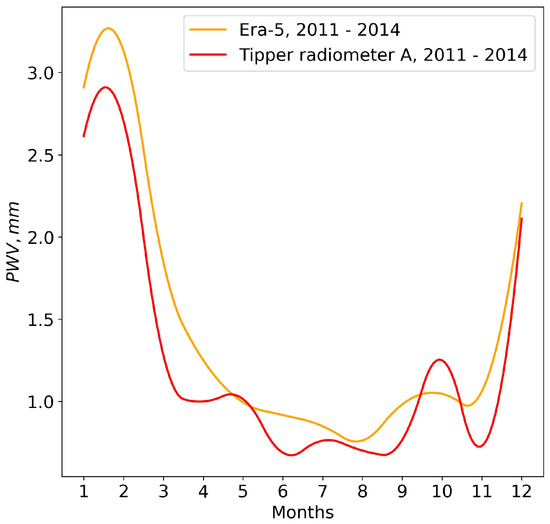
Figure 4.
Changes in mean monthly PWV values estimated from Era-5 reanalysis data and changes in mean monthly measured PWV values within the Chajnantor area.

Table 2.
Statistical characteristics of PWV variations estimated from Era-5 reanalysis data and radiometric measurement data.
4. Atmospheric Parameter Statistics Relevant for the Millimeter/Submillimeter Observations within the BTA Region
Knowledge of statistics in air humidity and precipitable water vapor makes it possible to estimate absorption coefficients along the telescope’s line of sight. In this section, we estimate the spatial changes and seasonal variability in water vapor content in the atmosphere within the BTA region [41]. Using the Era-5 reanalysis data, we obtained the statistically averaged spatial distributions of PWV for different seasons for the period 2010–2020.
4.1. Spatial Distributions of Precipitable Water Vapor within the BTA Region
With the aim of identifying the sites suitable for astronomical observations in the mm/submm wavelength range, we obtained spatial distributions of PWV within the BTA region. We used the Era-5 reanalysis data for mapping. The spatial distributions of PWV averaged for the period 2010–2020 for different seasons are shown in Figure 5. PWV averaging was performed using Formula (7):
where is the hourly mean PWV value, and N is the total number of hours for the period 2010–2020. The analysis of Figure 5 shows that there is a wide area of low PWV values within the BTA region. The average position of the area varies little during the year. However, the PWV values change significantly from season to season. The highest PWV values are observed in summer, while the lowest PWV values correspond to winter.
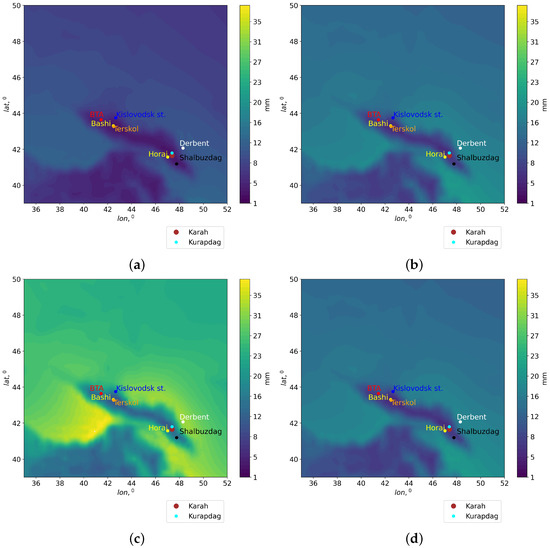
Figure 5.
Spatial distributions of obtained from Era-5 reanalysis data for the period 2010–2020: (a) winter; (b) spring; (c) summer; (d) autumn.
In our studies, in order to correct the PWV values, we compared the variations in precipitable water vapor estimated from the Era-5 data with the PWV obtained using the Global Navigation Satellite System in the BTA region [39]. The data comparison showed that the correlation coefficients varied from 0.71 to 0.94. The best relation between PWV variations was observed at the sites with altitudes from 727 m to 2095 m, with high repeatability of clear sky. In particular, at the Khunzakh with an elevation of 1627 m above sea level, the correlation coefficient was 0.94. At the Kislovodsk mountain astronomical station with an elevation of 2095 m above sea level, the correlation coefficient is also high (∼0.91). The worst correlation coefficient was observed at the Peak Terskol, as the highest site of the analyzed (3121 m above sea level). At this site, the correlation coefficient was 0.71. It is also worth noting that, according to our estimates, the Chajnantor Plateau at an elevation of 5107 m has a correlation coefficient of 0.57.
Using Formula (2) and Era-5 reanalysis data, we estimated the spatial distributions of corrected PWV values for the period 2010–2020. Figure 6 shows the spatial distributions of the corrected PWV values. The correction of PWV values, taking into account the relief, was carried out using the relative altitude difference determined over a large area within the region. In this case, in low landforms, PWV values were not corrected; PWV values for mountain peaks were corrected using Formula (2). In the calculations, we used the Era-5 relief model.
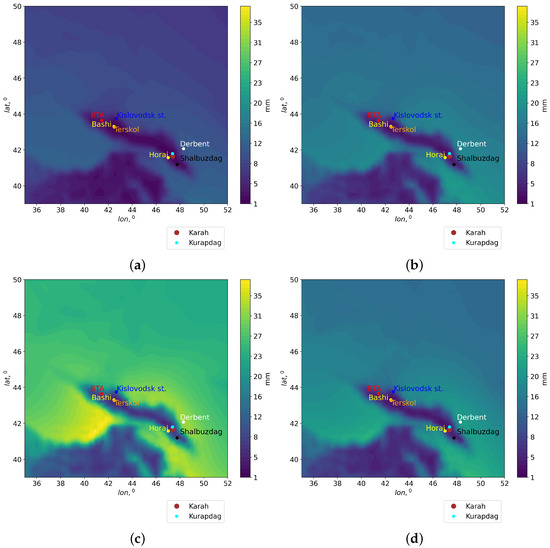
Figure 6.
Era-5 PWV spatial distributions obtained for the period 2010–2020, adapted for mountain peaks: (a) winter; (b) spring; (c) summer; (d) autumn.
The analysis of the corrected spatial distributions shows that PWV values for mountains decreased significantly. As a result of applying the correction method, PWV values at the summit and at the bottom of the mountain began to differ significantly. This is consistent with physical concepts and measurement data of precipitable water vapor.
4.2. Spatial Distributions of Total Cloud Cover within the BTA Region
The duration of sunshine or total cloud cover determines the potential duration of astronomical observations. In order to reveal the sites with minimal total cloudiness, we obtained the spatial distributions of total cloud cover TCC (shown in Figure 7). The TCC values in the Era-5 reanalysis were averaged for the period 2010–2020 for different seasons using Formula (7):
where is the hourly mean value of , and N is the total number of hours from 2010 to 2020.
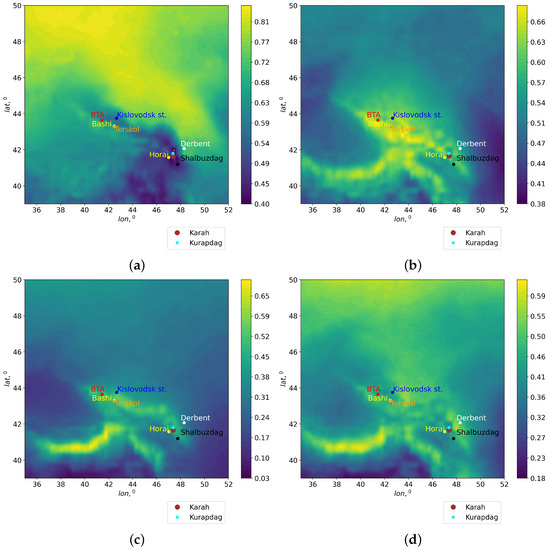
Figure 7.
Spatial distributions of total cloud cover within the BTA region obtained for the period 2010–2020: (a) winter; (b) spring; (c) summer; (d) autumn.
The analysis of Figure 7 shows that the TCC distributions are spatially inhomogeneous. Areas with low TCC are shown in dark blue. The best conditions in both TCC and PWV occur during winter. The sites with the best atmospheric conditions in TCC and PWV include the locations of mountainous Dagestan: Mt. Kurapdag and Mt. Horai. Table 3 shows mean values of TCC at the sites suitable for mm/submm observations. The best conditions in terms of TCC are noted at the location of Mt. Horai and Mt. Kurapdag.

Table 3.
Mean values TCC at the sites suitable for mm/submm observations.
4.3. Spatial Distributions of Cloud Base Height within the BTA Region
For astroclimatic estimation of astronomical observing time within mountainous regions, an important parameter is the cloud base height (CBH). We attribute large values of cloud base height to a higher repeatability of high atmospheric mm/submm transparency. In this case, a high transparency of the atmosphere is due to low water content in the middle and upper troposphere compared to the lower layers of the atmosphere. Based on the Era-5 reanalysis data, we estimated CBH. Spatial distributions of cloud base height for different seasons are shown in Figure 8.
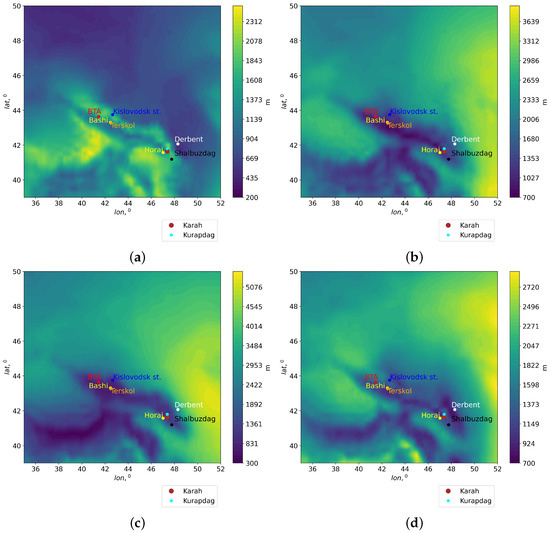
Figure 8.
Spatial distributions of cloud base height for different seasons for the period 2010–2020: (a) winter; (b) spring; (c) summer; (d) autumn.
The analysis of spatial distributions of cloud base height indicates the following features of cloud formation:
- (i)
- In all seasons, an area with low values of cloud base heights is observed over the Caucasus. The “depth” of this area in terms of CBH horizontal gradients varies throughout the year.
- (ii)
- Excluding winter, an extended area with large CBH values is formed in the eastern part of the BTA region. In this region, maximum CBH occurs in summer. Cloud base heights range from ∼3600 to ∼5300 m. In winter, cloud base heights range from ∼900 m to ∼1500 m.
Table 4 shows mean values of CBH at the sites suitable for mm/submm observations. Typical cloud base heights at the BTA site vary from 800 m (summer) to 1500 m (winter). Similar conditions are also observed at the Peak Terskol. The minimum cloud base height values are observed in summer (750 m), and the maximum values correspond to the autumn–winter period (1100–1200 m).

Table 4.
Mean values of CBH at the sites suitable for mm/submm observations.
One of the promising sites, namely Mt. Horai, has intermediate values in cloud base height: 1600 m in summer and 1200 m in autumn and spring. In comparison with Mt.Horai, Mt. Kurapdag has lower cloudiness in summer (1050 m).
In winter, the Kislovodsk Observatory has a high CBH value, ∼1700 m. This value is close to the CBH at the BTA (1500 m).
Thus, Mt. Horai and Mt.Kurapdag are promising for mm/submm observations, not only in terms of PWV, but also in terms of total cloud cover and cloud base heights.
4.4. Nighttime Cloud Fraction Fraction
The estimation of the nighttime cloud fraction is one of the key parameters for evaluating the number of useful nights at an astronomical site [42,43,44]. In order to estimate the number of useful nights at the BTA, we used a similar approach to that described in paper [42]. We used the following methodology for classifying nights:
- (i)
- Clear nights and partly clear nights: we supposed that cloud cover values range from 0 to 20% for the entire night. Clouds may be observed at night, but the total cloud cover ranges from 0 to 20% for 4 or more hours continuously.
- (ii)
- Partly cloudy night: cloud coverage is less than or equal to 40% for 4 or more h.
- (iii)
- Photometric night: a night is termed photometric if it satisfies (i).
- (iv)
- Spectroscopic nights: a night is termed spectroscopic if it satisfies (i) and (ii).
In order to estimate the number of photometric and spectroscopic nights as well as nights with cloud coverage lower than or equal to 50% at the BTA site, we used hourly Era-5 data from 2010 to 2022. The duration of a night at a site is counted from an hour after sunset to an hour before sunrise. Figure 9 and Figure 10 show box and whisker plots for photometric spectroscopic nights for 2010–2021. Table 5 summarizes the number of nights estimated with different thresholds for the cloud coverage at the BTA site. At the BTA site, the averaged number of spectroscopic nights per year estimated from long-term reanalysis data is 67.8 (71.2 for nights with cloud coverage lower than or equal to 50%). The number of photometric nights is less (it is equal to 25.3 per year).
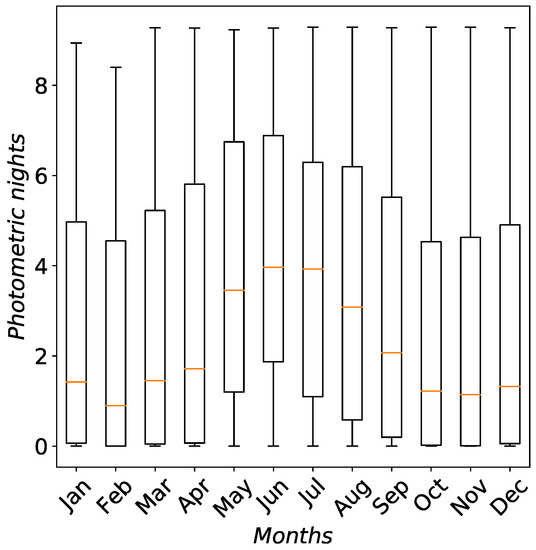
Figure 9.
Box and whisker plots for photometric nights during 2010–2021 at the BTA site. The central horizontal lines inside the boxes are medians; bottoms and tops of the boxes are standard deviations; and ends of the whiskers are the minimum and maximum values.
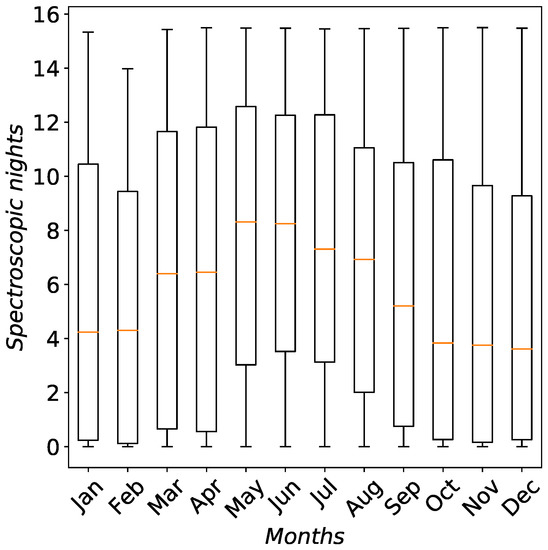
Figure 10.
Box and whisker plots for spectroscopic nights during 2010–2021 at the BTA site. The central horizontal lines inside the boxes are medians; bottoms and tops of the boxes are ± standard deviation; and ends of the whiskers are the minimum and maximum values.

Table 5.
Number of nights for observations at the BTA.
In addition, we compared the annual changes in amount of hours from visual observations at the BTA [45] with the hours estimated from Era-5 reanalysis data. Figure 11 shows annual changes in the amount of hours from visual observations at the BTA with the hours estimated from Era-5 reanalysis data. For spectral nights, the Era-5 data have the best agreement with visual observations at a threshold of 0.5. The total observing time at the BTA is 1453 h per year (Table 6). As Table 6 shows, one of the best sites in Dagestan, namely Mt. Kurapdag, is characterized by a large number of observation hours. The mean number of hours for the period from 2010 to 2021 was 1971 h.
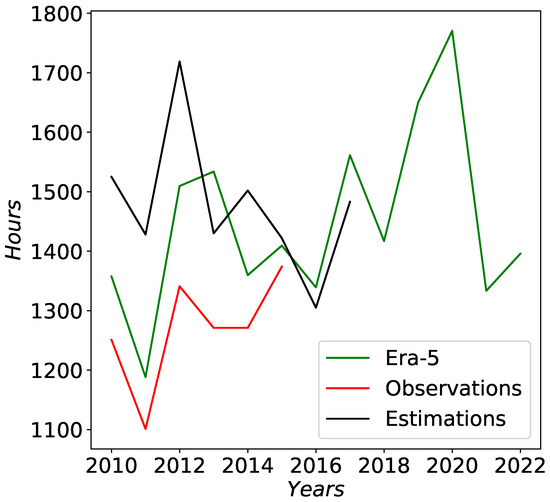
Figure 11.
Annual changes in amount of hours from visual observations at the BTA with the hours estimated from Era-5 reanalysis data. The amount of observation time at the BTA according to the operation service is shown by the black line. The amount of observation time at the telescope according to astronomical observations is shown by the red line. The value in 2022 is the forecast variable (regression analysis).

Table 6.
Estimations of observing time at the BTA. The value in December 2022 is the forecast variable.
5. Seasonal Variations of PWV at the Ali, Muztag-Ata, Suffa, Bta and Peak Terskol
For estimation of water vapor content within the BTA region, we corrected PWV values for a number of sites. Using Formula (2), we estimated the proportionality coefficients at different sites, taking into account ratios between the altitudes of the mountain peak and the “surrounding terrain”.
Our method of PWV correction includes:
- (i)
- The choice of area boundaries within which we should estimate the mean relative altitude difference. In particular, at the BTA, we used a limited area, which includes 4 × 5 grid nodes.
- (ii)
- To calculate the relative altitude difference for an adjacent grid node, we shifted the selected area. Shifts are shown by the red box. The size of this area is fixed for each mesh node.
- (iii)
- Knowing the relative altitude difference at a given site, we calculated the average ratios between precipitable water vapor at the mountain summit and the values corresponding to the “surrounding terrain”.
Figure 12 shows seasonal changes in corrected median PWV values estimated from the Era-5 data at the sites of Ali, Muztag-Ata, Suffa, Bta and Peak Terskol.
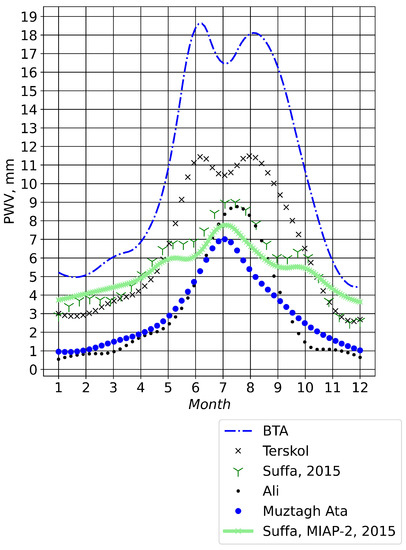
Figure 12.
Seasonal changes in corrected median PWV values estimated from Era-5 reanalysis data at the sites of Ali, Muztag-Ata, Suffa, Bta and Peak Terskol.
Table 7 shows the mean ratios of the precipitable water vapor at the summit to the PWV values corresponding to the “surrounding terrain”. Table 8 shows the mean values of PWV at the sites suitable for mm/submm observations.

Table 7.
Mean ratios of precipitable water vapor at the summit to the PWV values corresponding to the “surrounding terrain” at the sites of Ali, Muztag-Ata, Suffa, Bta and Peak Terskol.

Table 8.
Mean values of PWV at the sites suitable for mm/submm observations.
At the Ali site, the median value of PWV calculated from the Era-5 data is about 2.9 mm. This value exceeds the median value of PWV by a factor of 1.44 estimated in [10] (2.02 mm). The maximum PWV values are observed in summer. The median value is 7.0 mm. In winter, the median value is about 1 mm.
Similar astroclimatic conditions in terms of median PWV values are observed at Muztag-Ata. The median of PWV is 2.9 mm. In comparison with Ali, Muztag-Ata is characterized by a smaller intra-annual amplitude of PWV changes. In summer, the median is 5.7 mm; in winter, the median decreases to 1.0 mm.
At the Suffa International Observatory, medians in PWV are higher compared to Muztag-Ata and Ali. The annual median PWV derived from Era-5 reanalysis is 5.4 mm. The best conditions are observed in December–January when the median values are close to 2.6–2.9 mm. The worst conditions are in July with a median of 8.9 mm. Comparison of the calculated PWV with the PWV measured by MIAP-2 radiometer [46,47,48] shows that MAE is 0.79 mm, and the root mean square deviation is close to 0.87 mm. The correlation coefficient between the measured and calculated monthly PWV values is 0.98.
Following the proposed approach, the medians of PWV were estimated at the Peak Terskol and the site of BTA. At the BTA, the annual median is 10.3 mm. In winter, the median is minimal and equal to 4.9 mm; in summer, the median increases to 17.4 mm. In comparison with the BTA, at the Peak Terskol, the annual median of PWV decreases 1.63 times (the median is 6.3 mm). In summer, at the Peak Terskol, the median varies from 10.5 to 11.5 mm. In winter, the median is 2.9 mm (the minimum of PWV is observed in December).
6. Discussion
The study is aimed at the description of astroclimatic conditions within the BTA region (from 35E to 55E, from 40N to 50N). For the first time, spatial distributions of PWV within the BTA region were obtained. We show that a stable vast area with low water vapor content is formed within the BTA region. We associate this area with high transparency of the atmosphere for mm/submm radiation. In order to estimate water vapor content most closely matched to the measured values, we proposed a method for correcting PWV values, taking into account the relief. The method is based on averaging the elevation of grid notes within a certain area. In calculations, this area contains a certain number of grid nodes (4 × 5 nodes). For each grid node, the relative altitude differences between the mountain top and the surrounding terrain, as well as the corresponding proportionality coefficients, were calculated.
Using the correction method, we estimated the medians of PWV at the Chajnantor Plateau, Ali, Muztag-Ata, Suffa, BTA, Peak Terskol, Mt. Horai and Mt. Kurapdag. We showed that the Era-5 reanalysis reproduces changes in hourly PWV values with a correlation coefficient of 0.57. The consistency of the reanalysis data improves with the measured variations in terms of mean monthly PWV values. The correlation coefficient increases to 0.97.
In the calculations, we used the exponential dependence of PWV on the altitude [49]. Figure 13 shows the correspondence between medians of PWV and site elevation.
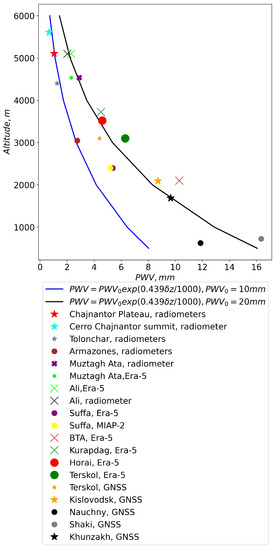
Figure 13.
Dependencies of PWV medians on site elevation above sea level.
With the aim of comparing the PWV dependence, we estimated the medians of PWV at the Chajnantor Plateau, at the sites of Cerro Chajnantor Summit, Tolonchar and Armazones. It should be noted that the authors [4] considered a limited range of altitudes (from 3000 to 5640 m). In this range of altitudes, the authors obtained the dependence:
However, if we consider a wider range of altitudes, we see that the Chajnantor Plateau, Cerro Chajnantor Summit, Tolonchar and Armazones are described well by the dependence:
The analysis of the figure shows that in comparison with the sites of South America, Ali and Muztag-Ata have higher PWV and are described by the dependence:
The PWV estimates obtained at these sites are in good agreement with theoretical dependencies of PWV on altitude. The mean absolute errors decrease with altitude and do not exceed 2.0 mm, on average. We can note that the reanalysis data somewhat overestimate the PWV medians by 1–2 mm compared to the measurement data. A small spread of PWV values indicates that using the reanalysis data and the proposed method, in general, we can estimate the medians of PWV reliably. Considering cases with low values of TCC as well as PWV, we can note that Mt. Kurupdag and Mt. Horai are located in an area suitable for mm/submm astronomical observations.
7. Conclusions
- (i)
- In this article, we make use of the Era-5 reanalysis from 2010 to 2020 over the BTA region to summarize the empirical relation between the total amount of in the atmospheric column and . Our results confirm that in the surface layer of the atmosphere and the water vapor scale height affect the total amount of . The functional relation between the total amount of and are similar among the discussed sites.
- (ii)
- We proposed a method for correcting the PWV values which takes into account the water vapor scale height calculated for the nearest radiosounding station and underlying surface. The method is based on the calculation of the average elevation of the grid nodes around the site of interest. Within the BTA region, we calculated using 20 grid nodes for every site. We believe that taking into account the local orography makes it possible to more accurately parameterize the . Based on the proposed method, the distributions of precipitable water vapor within the BTA region in different seasons were obtained. The analysis of PWV spatial distributions showed that the BTA is located in the belt with low water vapor content, extending southeastward. One of the main conclusions in this paper is that potential sites with low PWV are located east and southeast of BTA in the region (40.5N–42.0N; 46.2E–48.7E). In addition, using the method we estimated seasonal changes in corrected median PWV values at the sites of Ali, Muztag-Ata, Suffa, Bta and Peak Terskol. The statistics obtained are close to the measured PWV at these sites.
- (iii)
- The Era-5 reanalysis passably describes the hourly fluctuations in PWV. The root mean square deviation between measured and calculated values of PVW within the Chajnantor area is 1.06 mm. The correlation coefficient is 0.57. For longer averaging periods, consistency of PWV variations estimated from the Era-5 data and radiometric measurements improves. The correlation coefficient increases to 0.97 for monthly PWV values.
- (iv)
- We found that there are 68–71% spectroscopic nights per year at the BTA. These estimations are in a good agreement with the visual observations. At the BTA, the number of photometric nights derived from the Era-5 data is underestimated by 20% in comparison to that from the visual observations and equal to 25 per year. Using the reanalysis, we estimate that the observing time at the telescope is 1453 hours. At one of the best sites that we found, namely Mt. Kurapdag, the mean number of hours for the period from 2010 to 2021 was 1971 h.
Author Contributions
Investigation, visualization, writing—review and editing: A.Y.S.; methodology: P.G.K. and V.B.K.; formal analysis, investigation, visualization: A.Y.S. and A.V.K.; writing—review and editing: A.Y.S.; software, visualization: A.V.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by RSF grant № 22-72-00049. The study of cloud cover was supported by the Ministry of Science and Higher Education of the Russian Federation.
Data Availability Statement
Data used are available on request from the corresponding author.
Acknowledgments
Measurements of diffuse light were carried out using the Unique Research Facility Large Solar Vacuum Telescope http://ckp-rf.ru/usu/200615/.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wootten, A. The Atacama Large Millimeter Array (ALMA). Proc. SPIE 2002, 4837, 110–118. [Google Scholar] [CrossRef]
- Tremblin, P.; Schneider, N.; Minier, V.; Durand, G.A.; Urban, J. Worldwide site comparison for submillimetre astronomy. Astron. Astrophys. 2012, 548, A65. [Google Scholar] [CrossRef]
- Cortes, F.; Cortes, K.; Reeves, R.; Bustos, R.; Radford, S. Twenty years of PWV measurements in the Chajnantor Area. Astron. Astrophys. 2020, 640, A126. [Google Scholar] [CrossRef]
- Otarola, A.; Breuck, C.D.; Travouillon, T.; Matsushita, S.; Nyman, L.A.; Wootten, A.; Radford, S.J.E.; Sarazin, M.; Kerber, F.; Perez-Beaupuits, J.P. Precipitable Water Vapor, Temperature, and Wind Statistics At Sites Suitable for mm and Submm Wavelength Astronomy in Northern Chile. Publ. Astron. Soc. Pac. 2019, 131, 045001. [Google Scholar] [CrossRef]
- Xu, J.; Li, M.; Esamdin, A.; Wang, N.; Pu, G.; Wang, L.; Feng, G.; Zhang, X.; Ma, S.; Lv, J.; et al. Site-testing at Muztag-Ata site. IV. Precipitable Water Vapor. PASP 2022, 134, 015006. [Google Scholar] [CrossRef]
- Ozdemir, S.; Yesilyaprak, C.; Aktug, B.; Ozturk, D.; Coker, D.; Balbay, R. Precipitable water vapor (PWV) estimations from the site of the Eastern Anatolia Observatory (DAG), a new astronomical observatory in Turkey. Exp. Astron. 2018, 46, 323–336. [Google Scholar] [CrossRef]
- Valenziano, L.; Dall’Oglio, G. Millimetre Astronomy from the High Antarctic Plateau: Site Testing at Dome C. Publ. Astron. Soc. Aust. 1999, 16, 167–174. [Google Scholar] [CrossRef][Green Version]
- Kuo, C.-L. Assessments of Ali, Dome A, and Summit Camp for mm-wave Observations Using MERRA-2 Reanalysis. Astrophys. J. 2017, 848, 64. [Google Scholar] [CrossRef]
- Deng, L.; Yang, F.; Chen, X.; He, F.; Liu, Q.; Zhang, B.; Zhang, C.; Wang, K.; Liu, N.; Ren, A.; et al. Lenghu on the Tibetan Plateau as an astronomical observing site. Nature 2021, 596, 353–356. [Google Scholar] [CrossRef]
- Qian, X.; Yao, Y.; Wang, H.; Zou, L.; Li, Y.; Yin, J. Validation of the WRF Model for Estimating Precipitable Water Vapor at the Ali Observatory on the Tibetan Plateau. Publ. Astron. Soc. Pac. 2020, 132, 125003. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, F.; Chen, X.; Zhang, X.; Ma, J.; Kong, X.; Fu, X.; Li, R.; Wei, Y.; Yao, Z.; et al. Long-term variations in precipitable water vapor and temperature at Lenghu Site. Astron. Astrophys. 2022, 663, A34. [Google Scholar] [CrossRef]
- Ningombam, S.S.; Sethulakshmy, E.S.; Jade, S.; Shrungeshwara, T.S.; Vivek, S.G.; Angchuk, D.; Prabhu, T.P.; Mahay, T.T. Atmospheric opacity using 220 GHz (1.36 mm) radiometer data and water vapor trends over Indian Astronomical Observatory (IAO), Hanle. J. Atmos.-Sol.-Terr. Phys. 2020, 208, 4105404. [Google Scholar] [CrossRef]
- Dumka, U.C.; Kaskaoutis, D.G.; Khatri, P.; Ningombam, S.S.; Sheoran, R.; Jade, S.; Shrungeshwara, T.S.; Rupakheti, M. Water vapour characteristics and radiative effects at high-altitude Himalayan sites. Atmos. Pollut. Res. 2022, 13, 101303. [Google Scholar] [CrossRef]
- Anupama, G.C.; Maheswar, G.; Sriram, S.; Sivarani, T.; Parihar, P.S.; Nagabhushan, S.; Angchuk, D.; Barway, S.; Bhatt, B.C.; Banyal, R.; et al. A 10-m class national large optical-IR telescope. J. Astrophys. Astron. 2022, 43, 32. [Google Scholar] [CrossRef]
- Erasmus, D.A.; Rooyen, R. A satellite survey of cloud cover and water vapor in northwest Africa and southern Spain. Proc. SPIE 2006, 6267, 62671O. [Google Scholar] [CrossRef]
- Li, Z.; Muller, J.-P.; Cross, P. Comparison of precipitable water vapor derived from radiosonde, GPS, and Moderate-Resolution Imaging Spectroradiometer measurements. J. Geophys. Res. Atmos. 2003, 108, 4651. [Google Scholar] [CrossRef]
- Dembelov, M.G.; Bashkuev, Y.B. Estimation of the Tropospheric Moisture Content Derived from GPS Observations, Radio Sounding Data, and Measurements with a Water Vapor Radiometer. Atmos. Ocean. Opt. 2022, 35, 359–365. [Google Scholar] [CrossRef]
- Berezin, I.A.; Timofeyev, Y.M.; Virolainen, Y.A.; Volkova, K.A. Comparison of ground-based microwave measurements of precipitable water vapor with radiosounding data. Atmos. Ocean. Opt. 2016, 29, 274–281. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, Z. Evaluating the Accuracy of Jason-3 Water Vapor Product Using PWV Data from Global Radiosonde and GNSS Stations. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4008–4017. [Google Scholar] [CrossRef]
- Hu, H.; Yang, R.; Lee, W.-C.; Cao, Y.; Mao, J.; Gao, L. Multi-sensor study of precipitable water vapor and atmospheric profiling from microwave radiometer, GNSS/MET, radiosonde, and ECMWF reanalysis in Beijing. J. Appl. Remote Sens. 2020, 14, 044514. [Google Scholar] [CrossRef]
- Gurbuz, G.; Akgul, V.; Gormus, K.S.; Kutoglu, S.H. Assessment of precipitable water vapor over Turkey using GLONASS and GPS. J. Atmos.-Sol.-Terr. Phys. 2021, 222, 105712. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, K.; Yang, L.; Wu, S.; Li, L. Evaluation and calibration of MODIS near-infrared precipitable water vapor over China using GNSS observations and ERA-5 reanalysis dataset. Remote Sens. 2021, 13, 2761. [Google Scholar] [CrossRef]
- Xu, K.; Zhong, L.; Ma, Y.; Zou, M.; Huang, Z. A study on the water vapor transport trend and water vapor source of the Tibetan Plateau. Theor. Appl. Climatol. 2020, 140, 1031–1042. [Google Scholar] [CrossRef]
- Chen, B.; Yu, W.; Wang, W.; Zhang, Z.; Dai, W. A Global Assessment of Precipitable Water Vapor Derived From GNSS Zenith Tropospheric Delays With ERA5, NCEP FNL, and NCEP GFS Products. Earth Space Sci. 2021, 8, e2021EA001796. [Google Scholar] [CrossRef]
- Khutorova, O.G.; Khutorov, V.E.; Teptin, G.M. Interannual Variability of Surface and Integrated Water Vapor and Atmospheric Circulation in Europe. Atmos. Ocean. Opt. 2018, 31, 486–491. [Google Scholar] [CrossRef]
- Slättberg, N.; Lai, H.-W.; Chen, X.; Ma, Y.; Chen, D. Spatial and temporal patterns of planetary boundary layer height during 1979–2018 over the Tibetan Plateau using ERA5. Int. J. Climatol. 2022, 42, 3360–3377. [Google Scholar] [CrossRef]
- Hellemeier, J.A.; Yang, R.; Sarazin, M.; Hickson, P. Weather at selected astronomical sites–an overview of five atmospheric parameters. Mon. Not. R. Astron. Soc. 2019, 482, 4941–4950. [Google Scholar] [CrossRef]
- Han, Y.; Wu, X.; Luo, T.; Qing, C.; Yang, Q.; Jin, X.; Liu, N.; Wu, S.; Su, C. New Cn2 statistical model based on first radiosonde turbulence observation over Lhasa. J. Opt. Soc. Am. 2020, 37, 995–1001. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, S.; Pratap, V.; Singh, A.K. Performance of water vapour retrieval from MODIS and ECMWF and their validation with ground based GPS measurements over Varanasi. J. Earth Syst. Sci. 2021, 130, 41. [Google Scholar] [CrossRef]
- Yuan, P.; Hunegnaw, A.; Alshawaf, F.; Awange, J.; Klos, A.; Teferle, F.N.; Kutterer, H. Feasibility of ERA5 integrated water vapor trends for climate change analysis in continental Europe: An evaluation with GPS (1994–2019) by considering statistical significance. Remote Sens. Environ. 2021, 260, 112416. [Google Scholar] [CrossRef]
- Plahina, I.N.; Pankratova, N.V.; Makhotkina, E.L. Comparison of ground and satellite monitoring of aerosol optical thickness of the atmosphere in Russia. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli Kosmosa 2018, 15, 225–234. [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y.; Bolbasova, L.A.; Kovadlo, P.G.; Kiselev, A.V. Atmospheric parameters at the 6-m Big Telescope Alt-azimuthal site. Mon. Not. R. Astron. Soc. 2020, 493, 723–729. [Google Scholar] [CrossRef]
- Nosov, V.V.; Lukin, V.P.; Nosov, E.V.; Torgaev, A.V.; Afanas’ev, V.L.; Balega, Y.Y.; Vlasyuk, V.V.; Panchuk, V.E.; Yakopov, G.V. Astroclimate Studies in the Special Astrophysical Observatory of the Russian Academy of Sciences. Atmos. Ocean. Opt. 2019, 32, 8–18. [Google Scholar] [CrossRef]
- Khaikin, V.; Lebedev, M.; Shmagin, V.; Zinchenko, I.; Vdovin, V.; Bubnov, G.; Edelman, V.; Yakopov, G.; Shikhovtsev, A.; Marchiori, G.; et al. On the Eurasian SubMillimeter Telescopes Project (ESMT). In Proceedings of the 7th All-Russian Microwave Conference (RMC), Moscow, Russia, 25–27 November 2020; pp. 47–51. [Google Scholar] [CrossRef]
- Burgan, H.I.; Vaheddoost, B.; Aksoy, H. Frequency Analysis of Monthly Runoff in Intermittent Rivers. In Proceedings of the World Environmental and Water Resources Congress 2017: Hydraulics and Waterways and Water Distribution Systems Analysis—Selected Papers from the World Environmental and Water Resources Congress 2017, Sacramento, CA, USA, 21–27 May 2017; pp. 327–334. [Google Scholar] [CrossRef]
- Burgan, H.I.; Aksoy, H. Daily flow duration curve model for ungauged intermittent subbasins of gauged rivers. J. Hydrol. 2022, 604, 127249. [Google Scholar] [CrossRef]
- Eris, E.; Cavus, Y.; Aksoy, H.; Burgan, H.I.; Aksu, H.; Boyacioglu, H. Spatiotemporal analysis of meteorological drought over Kucuk Menderes River Basin in the Aegean Region of Turkey. Theor. Appl. Climatol. 2020, 142, 1515–1530. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y.; Khaikin, V.B.; Mironov, A.P.; Kovadlo, P.G. Statistical Analysis of the Water Vapor Content in North Caucasus and Crimea. Atmos. Ocean. Opt. 2022, 35, 165–175. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kudryavtsev, D.O.; Vlasyuk, V.V. The Largest Russian Optical Telescope BTA: Current Status and Modernization Prospects. In Proceedings of the Ground-Based Astronomy in Russia—21st Century All-Russian Conference, Nizhny Arkhyz, Russia, 21–25 September 2020; pp. 21–31. [Google Scholar] [CrossRef]
- Ningombam, S.S.; Song, H.-J.; Mugil, S.K.; Dumka, U.C.; Larson, E.J.L.; Kumar, B.; Sagar, R. Evaluation of fractional clear sky over potential astronomical sites. Mon. Not. R. Astron. Soc. 2021, 507, 3745–3760. [Google Scholar] [CrossRef]
- Zhang, J.-C.; Ge, L.; Lu, X.-M.; Cao, Z.-H.; Chen, X.; Mao, Y.-N.; Jiang, X.-J. Astronomical Observing Conditions at Xinglong Observatory from 2007 to 2014. PASP 2015, 127, 1292. [Google Scholar] [CrossRef]
- Ningombam, S.S.; Narendra, A.; Bhatt, B.C.; Prabhu, T.P.; Anupama, G.C.; Angchuk, D.; Jorphail, S. Validation of estimated cloud fraction from MERRA-2 and AIRS data using ground based observation over IAO, Hanle. Adv. Space Res. 2020, 66, 826–843. [Google Scholar] [CrossRef]
- Panchuk, A.V. Astronomical climate of the telescope installation site and observation time loss. INASAN Sci. Rep. 2020, 5, 344–350. [Google Scholar]
- Bubnov, G.M.; Abashin, E.B.; Balega, Y.Y.; Bolshakov, O.S.; Dryagin, S.Y.; Dubrovich, V.K.; Marukhno, A.S.; Nosov, V.I.; Vdovin, V.F.; Zinchenko, I.I. Searching for New Sites for THz Observations in Eurasia. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 64–72. [Google Scholar] [CrossRef]
- Bubnov, G.; Vdovin, V.; Khaikin, V.; Tremblin, P.; Baron, P. Analysis of variations in factors of specific absorption of sub-terahertz waves in the Earth’s atmosphere. In Proceedings of the 7th All-Russian Microwave Conference (RMC), Russia, Moscow, 25–27 November 2020; Volume 5, pp. 229–232. [Google Scholar] [CrossRef]
- Balega, Y.; Bataev, D.K.-S.; Bubnov, G.M.; Vdovin, V.F.; Zemlyanukha, P.M.; Lolaev, A.B.; Lesnov, I.V.; Marukhno, A.S.; Marukhno, N.A.; Murtazaev, A.K.; et al. Direct Measurements of Atmospheric Absorption of Subterahertz Waves in the Northern Caucasus. Dokl. Phys. 2022, 61, 1–4. [Google Scholar] [CrossRef]
- Khaikin, V.B.; Shikhovtsev, A.Y.; Mironov, A.P.; Qian, X. A study of the astroclimate in the Dagestan mountains Agul region and at the Ali Observatory in Tibet as possible locations for the Eurasian SubMM Telescopes (ESMT). Proc. Sci. 2002, 425, 72–79. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).