Abstract
For the discrimination of false targets, the discrimination probability can be improved by increasing the number of radar stations. However, that may result in a serious waste of equipment resources when too many radars are involved. An asymptotic subset selection strategy based on target positioning characteristics is proposed to address the above issues. Several effective strategies are considered to select some transmitters and receivers to form a radar subset, such as the rapid shrinkage method, global shrinkage method, and predetermined size method, which can guarantee the preset discrimination performance of limited equipment resources and reduce the waste of resources. All of the selected stations have good spatial distribution or strong discrimination capacity in multistatic radar system. Compared with the exhaustive search, the proposed subset selection strategy affords a significant reduction in terms of time complexity. The simulation results show that the radar subset can maintain approximate discrimination performance with the original multistatic radar systems. At the same time, the proposed method optimizes the number of radar stations and reduces data processing time and required communication links, thus effectively saving operating costs.
1. Introduction
With the rapid advancement of modern electronic technology, electronic warfare represented by electronic jamming has brought severe challenges and threats to the detection performance of radar systems [1,2]. Deception jammers generate false target information on the radar signal receiving system through delay, modulation, and forwarding to cover true targets, which prevents radar station from effectively completing target detection or accurately estimating target parameters [3]. Therefore, a strong jamming countermeasure capability is an important guarantee for the survival of radar system under complex electromagnetic interference conditions.
For deception jamming, monostatic radar can identify false targets utilizing transmission signal optimization [4,5], polarization information [6,7], inverse tracking [8], time-frequency analysis [9], DRFM quantization error [10], and clustering discrimination [11]. However, the target detection process of monostatic radar has only one perspective, and it is impossible to obtain rich environmental information. At the same time, jamming countermeasures highly depend on the radar hardware to a large extent. It is only suitable for some special jamming scenarios. Hence, in the case of high-fidelity deceptive false targets, the anti-jamming effect of monostatic radar is not ideal, and it is difficult to deal with the existing complex electronic jamming.
For the limitations of monostatic radar, multi-radar coordinated operations have become a trend [12,13,14]. In the future battlefield, our various radars will form a multistatic radar system with designated configurations and formations. The system must be equipped with several radars of the same type or different types to construct a large number of radar groups. By connecting radars in different spatial distributions, the multistatic radar system forms a networked detection system that occupies multiple observation angles, multiple frequencies, and multiple working modes to obtain a high-density signal space [15,16,17,18]. Multi-platforms and multi-sensors can effectively improve the target detection performance and parameter estimation accuracy, in contrast to monostatic radar system. [19,20,21,22].
In the fusion center of a multistatic radar system, the information collection and processing require the signal sharing and fusion of each radar, which can effectively distinguish interference and greatly improve the anti-jamming capability of the system. Meanwhile, by managing and scheduling the working mode of each radar, the technical complexity of unified jamming for the whole system is greatly increased.
Most of the existing anti-jamming methods detect targets separately in the multistatic radar system; then, the preprocessed echo information is uniformly sent to the information fusion center. According to the detection results from each radar station, the fusion center obtains the final system detection results for the target based on certain distributed detection criteria [23,24,25]. However, in non-ideal environments, such as a low signal to noise ratio (SNR) or partial radar tracking loss, it is difficult for each radar to detect targets independently. The fusion center cannot jointly process the detection results [26,27,28].
To deal with this problem, multistatic radar system needs to adopt the target joint detection mode to ensure the overall detection probability. At this point, the radar system will work as a whole. Each radar directly transmits the original target echo data to the system information fusion center. In the fusion center, joint detection or parameter estimation is carried out for the target, so as to achieve the optimal effect of jamming countermeasures.
The false target discrimination method based on parameter joint estimation is an effective discrimination algorithm [29,30]. It can be proved that the number of radars is an important parameter of performance, and increasing the number of transmitters or receivers can effectively improve false target discrimination capability. However, as the number of radars increases, communication requirements and computational complexity increase, resulting in unnecessary consumption of equipment resources [31]. Therefore, how to strike a balance between radar resources and identification performance becomes a problem of resource scheduling. For multiple radar detection systems, resource scheduling can be divided into radar layout and parameter selection. For layout optimization, Hana proposed a performance-driven resource allocation scheme [32], and minimized the number of transmitting and receiving radars employed in the estimation process. Hadi clustered the sensor yield to the accuracy threshold and successfully applied a minimum number of utilized sensors [33]. For transmitted parameter selection, Zheng selected an optimal subset of sensors with the predetermined size and implemented the power allocation and bandwidth strategies among them, which achieved better performance within the same resource constraints [34]. Nil extended optimization to multi-target cases, and put forward a joint power and bandwidth allocation strategy [35]. The posterior Cramer Rao Lower Bound was suggested to minimize subarray utilization to a predetermined tracking accuracy and minimized the total utilized power [36]. However, for anti-jamming techniques, resource scheduling has not been further explored.
To solve the above problems, this paper proposes subset selection strategies of gradual shrinkage for false target discrimination. For an existing multistatic radar system, on the premise of satisfied preset false target discrimination performance or limited device resources, multiple iteration screening can choose some transmitters or receivers with better spatial distribution or discrimination ability to form the radar subset, so as to achieve the approximate discrimination capability of the original system. The required equipment is reduced. The amount of data that needs to be processed in the fusion center and the required communication links are reduced. So, this strategy effectively reduces the operating costs and optimizes the radar configuration.
The remainder of the paper is organized as follows. Section 2 introduces the signal model for multistatic radar system with deception jamming. In Section 3, the shrinkage model for different situations is proposed, and the reduced time complexity is deduced. Section 4 presents the simulation results, and conclusions are drawn in Section 5.
2. Signal Model
2.1. Construction of Multistatic Radar System Model
The target joint detection model based on a multistatic radar system is constructed of M transmitters and N receivers. The transmitter located at , , the receiver located at , , and distribution are shown in Figure 1. Each transmitter in the system transmits a set of orthogonal signals with effective bandwidth . Additionally, each narrowband signal is expressed as , where , and is the signal carrier frequency. It is assumed that the total power of the system remains constant and each station transmits signals at the same power.
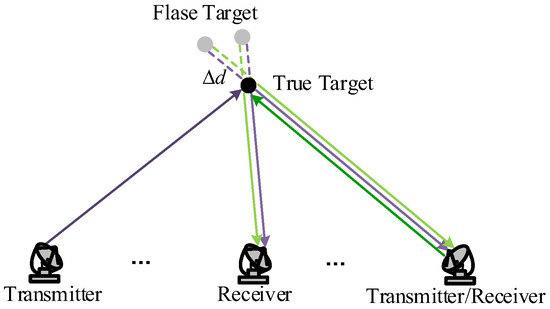
Figure 1.
Multistatic radar system with range deception jamming.
When the jammer captures the signal, it modulates and resends a deception jamming signal that is highly similar to the real target to form a false target. Whether the target is true or false, the echo is an indistinguishable physical signal for the receiving station [26]. Therefore, we construct a compatible target model in this paper. Assuming that echoes are generated on Swerling-I model, the European distance of the transmitting signal from the l-th transmitter to the target and then to the k-th receiver can be expressed as . The echo delay of the true target is , where c is the speed of light.
Suppose the true target carries a self-defensive jammer, and the jammer generates distance deception jamming. The delay of the jamming echo is the sum of the propagation delay and retransmission delay, which can be represented as ; is the retransmission distance. Thus, the echo signal is uniformly structured as:
where is Gaussian noise with zero mean value, the autocorrelation function is , and is unknown complex amplitude.
In order to distinguish between true and false targets, deceptive distance can be utilized as an important criterion. If the receiver receives the echo of a true target, it will be the real physical location in space, and the deceptive distance is zero, while the false target is formed by the jammer modulation retransmission, so is non-vanishing. Therefore, deceptive distance can be used as an estimation parameter to effectively discriminate the deceptive false targets and achieve the purpose of jamming countermeasures.
2.2. False Target Discrimination Method
Cramer Rao Lower Bound (CRLB) determines the lower bound for the variance of any unbiased estimator. With the increase in SNR, the mean square error (MSE) of the estimated parameter’s maximum likelihood estimator (MLE) approaches the CRLB. Ref. [37] proved that MSE and CRLB are asymptotically close in the condition of high SNR. Therefore, CRLB is used to indicate the MSE of the estimated parameter.
For jamming discrimination, the unknown parameter vector of the target is , where , , and are respectively the real and imaginary part of the target unknown complex amplitude, as , and its transmission channel is from transmitter l to receiver k, and stands for matrix transpose. The unbiased estimate of satisfies
where represents the inverse of the matrix, represents the expectation of , and is the Fischer information matrix (FIM) for estimating the parameter vector , which is specifically expressed as
where is the joint probability density function (PDF) of under the condition of , is the conditional expectation of for , and is the observation matrix.
Since the received signal (1) is the function of the time delays and the complex amplitudes , we define a new estimation parameter vector as with . The FIM, which is resorted by the chain rule, can be represented as , where the matrix is the FIM with respect to . The detailed derivation is presented in Appendix A.
At high SNR, the CRLB is infinitely close to the MLE, so it is used to represent the MSE. The Cramer Rao matrix of the estimated parameter is the inverse of the FIM [29,30].
The diagonal element in is the lower bound of the estimated variance of the parameters x, y and , so the estimation precision of is in the third row and the third column of the matrix, as
where represents the element in the third row and third column of the matrix. According to the definition of CRLB, for deceptive distance, the relationship between the minimum limit of estimation accuracy and MSE is ; when SNR is sufficiently high, [37]. Therefore, is used to represent the MSE of parameter . The results for the final CRLB show that the estimation accuracy is inversely proportional to the average effective bandwidth and SNR and is related to the matrix , that is, the estimation accuracy is related to the relative position of the target and the multistatic radar system.
The jamming distance is used as the main feature to identify the jamming. H0: Suppose the identified target is a true target, that is, the jamming distance is zero; H1: Suppose the identified target is a false target, that is, the jamming distance is non-vanishing.
According to the Neyman–Pearson criterion, a discriminator is constructed [31]. Under the condition that the true target discrimination probability is constant, the false target discrimination is carried out, and the threshold is set as , where the discrimination probability for the real target is . For the false target, the discrimination probability is , is the inverse cumulative distribution function of , and is the cumulative distribution function of . The discrimination performance of the discriminator has been verified by simulation, which calculates that the MSE is close to the CRLB, as the SNR is above −15 dB.
3. Shrinkage Model
3.1. Construction of Shrinkage Model
Based on the deceptive false target discrimination method for joint parameter estimation, the number of radars in the system is an important parameter that affects the discrimination probability. The more radars, the stronger the discrimination capability. However, a large number of radars can easily cause equipment redundancy. Due to the low utilization efficiency of certain sites, a waste of resources is unavoidable.
To settle this problem, the selection vectors and can be introduced to construct a partial radar subset in which some transmitters/receivers are selected to replace the whole system, where , and . When the system selects the l-th transmitter or the k-th receiver, and are set as 1, otherwise, they are set as 0, so as to construct the extended design of .
For the final selected radar subset , and respectively contain all transmitting stations or receiving stations that can be selected. So, CRLB of can be defined as . In this paper, only the estimation accuracy of jamming distance is applied, and ’s MSE of radar subset is shown as follows:
When the l-th transmitter and the k-th receiver are selected, the corresponding and in the selection vectors and are set to 1. Based on the partial radars selected in the formula, the deceptive distance estimation accuracy can be calculated, and the discrimination probability of the false target can be further improved.
In a given multistatic radar system, some transmitters and receivers contribute to better jamming discrimination than others because of the different relative positions and parameters for the target and each sensor.
The existing algorithm needs to search all combinations to find the best performing subset. Such an exhaustive search method requires multiple iterations with high complexity. Therefore, this paper proposes some subset selection methods to effectively reduce the number of radar stations in the multistatic radar system. These algorithms reduce station numbers and save communication resources on the premise that the deceptive target discrimination performance meets the system requirements or the best discrimination performance balances the limited equipment resources. In the meantime, compared with the exhaustive search, the computational complexity is effectively reduced.
3.2. Rapid Shrinkage
For multistatic radar system, it is an asymptotic optimization problem to obtain the preset discrimination index with the smallest number of stations. The target function is set to the minimum number of radars, and the constraint condition is that the false target discrimination performance reaches the preset value , as is shown in the formula:
This section proposes a rapid shrinkage strategy for subset selection to obtain the minimum number of devices under a given threshold of discrimination performance. To reduce the time complexity of the screening process, we can select the radar combination with the shortest target distance as the initial subset. Then, the radar station with the best discrimination performance is selected in each round to form the radar subset. After many iterations, the number of selected radars gradually increases. When the discrimination probability reaches the preset threshold or all radars are selected, the iterative process needs to be stopped, and the corresponding selection vectors and are obtained. The operation is shown below, and the specific selection steps are shown in Algorithm 1.
| Algorithm 1: Algorithm of Selection Strategy for Rapid Shrinkage |
  |
Where represents the union of sets, \ represents the matrix deletion.
On the subset selection strategy of the rapid shrinkage method, for a multistatic radar system, the time complexity of finding the initial radar combination is . After that, in each round, one radar station is iteratively selected from the remaining radar stations to join the radar subset, and the time complexity of each round is . Then, the total time complexity of the strategy is , where J is the total number of radars in the final subset. The time complexity of exhaustive search is . A conclusion can be drawn that the time complexity is reduced from the exponential order of exhaustive search to the linear order by the rapid shrinkage method.
3.3. Global Shrinkage
In the process of subset construction, the subsequent selection results can be directly affected by the selection of the initial transmitters and receivers. The selection strategy of rapid shrinkage method is proposed in Section 3.2 for the shrinkage model that can achieve the lowest time complexity. However, the number of stations is only the local minimum, which can not achieve the global optimum. Therefore, there may still be equipment redundancy. This section considers the selection strategy of global shrinkage. Based on Section 3.2, each branch can be scanned from MN channel pairs, and all local minimum values need to be compared to obtain the subset with the best discrimination performance. Although the complexity is increased, the local optimal problem is effectively alleviated. Operations are shown as follows, and specific selection steps are shown in Algorithm 2.
| Algorithm 2: Algorithm of Selection Strategy for Global Shrinkage |
 |
Where represents a belonging relationship between sets.
Through the steps above, the global shrinkage subset selection strategy is obtained. The exploratory shrinkage method reduces the time complexity to , where J is the number of selected radars. According to MN different initial choices, all of the unknown radar combinations in Section 3.2 can be obtained, so as to achieve the effect of global optimal contraction.
3.4. Predetermined Size
In order to use limited resources reasonably, a balance needs to be achieved between discrimination performance and equipment resources. Making full use of existing radars is particularly meaningful for resource optimization, especially when utilization of the system infrastructure is restricted. Motivated by this, an operational policy is proposed in this section. The goal is to select a subset of a predetermined size X that has the greatest distinguishing ability. This knapsack problem can be written as follows:
The selection of the initial transmitter and receiver has a considerable impact on the final result. As mentioned above, there are two ways to find the best pairs as the initial subset. In this section, we choose the initial subset selection method for global shrinkage. For MN preselected initial subset, all pairs are compared to find the best choice as the selected subset.
The selection steps are the same as in Section 3.3 on the shrinkage model, but the main difference lies in the ending conditions. In this section, when the size of the preselected matrix is X, the selection must stop. Then, with the comparison of preselected matrixes, the best subset is singled out. At the same time, the vectors and are updated to suit the choice of the selected transmitters or receivers. The detailed steps can be seen in Algorithm 3.
| Algorithm 3: Algorithm of Selection Strategy for Predetermined Size |
 |
Through the steps above, the predetermined size subset selection strategy is obtained. The time complexity of this algorithm is determined through the initial subset selection, when the initial subset is selected with the shortest target distance. It is similar to the calculation method of Algorithm 1 in Section 3.1. The total time complexity of the strategy is , only replacing the total number of radars J in the final subset by preset amount X. When the initial subset is scanned from MN channel pairs, the predetermined size method reaches the time complexity of . The calculation is similar to Algorithm 2 in Section 3.2.
4. Simulation Results
In the simulation section, the multistatic radar system and jamming discrimination methods are the same as described in Section 2. Three simulations are provided to demonstrate the feasibility and investigate the discrimination performance of the proposed approaches.
4.1. Subset Selection Strategy for Preset Discrimination Performance
Assuming that the system consists of 7 transmitters and 5 receivers, the algorithms introduced in Section 3 are verified by various site layouts. The specific radar distribution and selection results are shown in Figure 2. Setting false target discrimination performance at , all radars of the system have the same transmission power, and , , .
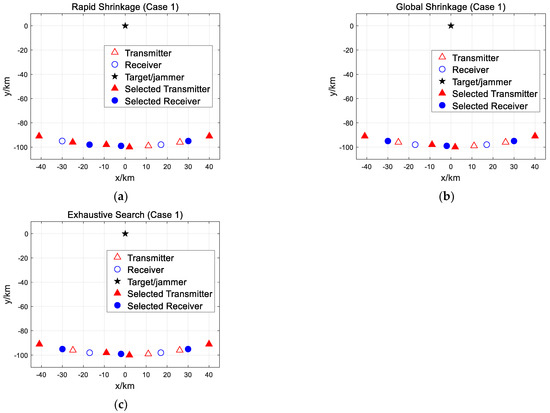
Figure 2.
Simulation for three types of subset selection strategy in case 1: (a) subset selection strategy for rapid shrinkage; (b) subset selection strategy for global shrinkage; (c) subset selection strategy for exhaustive search.
In the layout of case 1, the target carrying a self-defensive jammer is located on the central axis of the maximum aperture in multistatic radar system. The simulation results of rapid shrinkage and global shrinkage are in Figure 2a,b and Table 1; 8 radars and 7 radars are respectively screened out to achieve the preset discrimination performance . It demonstrates that these two algorithms can reduce the number of radars and communication requirements, which saves equipment resources. Notably, the final screening results are also different due to the different methods for selection of the initial radar. Generally speaking, the subset selection strategy for global shrinkage sacrifices time complexity to achieve the optimal discrimination performance, and the economizing of equipment is more obvious. Contrarily, the selection strategy for rapid shrinkage is more suitable for a large number of radars and saves calculation time.

Table 1.
Simulation of different selection strategies.
Figure 2b,c show the same screening results, indicating that the exhaustive search method and global shrinkage method can find the same subset to obtain the optimal solution. However, the global shrinkage subset selection strategy has an edge over the exhaustive search method due to its great capability of reducing time complexity while ensuring the same discrimination performance.
The simulation results of some representative layouts and the selection results are shown in Figure 3 and Table 1. They reveal that the spatial position of radars has a significant influence on the subset selection results. The layout of case 2 has the transmitters and receivers distributed on each side of the target, but has poor discrimination performance and requires more radars to achieve the preset discrimination performance. In case 3, the transmitters and receivers are staggered on one side of the target. The discrimination performance is not as good as in case 1, but it is better than in case 2, indicating that discrimination performs well and the demand for stations is reduced when the transmitters and receivers are scattered.
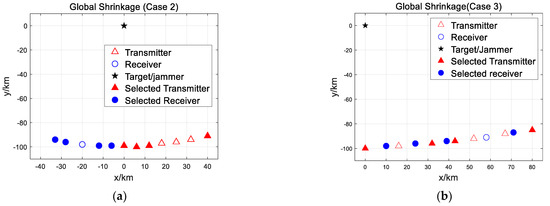
Figure 3.
Simulation results for different scenarios: (a) global shrinkage strategy in Case 2; (b) global shrinkage strategy in Case 3.
All of the experiments were implemented in Matlab 2018b software on a PC with a 3.20 GHz Intel Core I7 CPU and 8 GB memory. The runtime parameters can be observed in Table 1. With the same initial multistatic radar system in case 1, the method of rapid shrinkage requires 0.6763 ms. The method of global shrinkage needs more time, and the simulation result is 2.0671 ms. However, the running time for the exhaustive search method is much longer than that of the proposed methods, requiring 13.1726 ms. All of the simulations show the same results with the efficiency analysis after Algorithms 1 and 2. The subset selection strategies of rapid shrinkage and global shrinkage can effectively improve the speed of selection, which is especially important in complicated combat environment. The proposed method reduces the amount of data processing time and number of required communication links, which effectively saves operating costs.
4.2. Selection Strategy for Subset of Predetermined Size
In this section, a numerical analysis is performed on the subset selection algorithm of predetermined size. The subset size is set to X = 6. There are four typical types of radar layouts, and the selection results are shown in Figure 4 and Table 2.
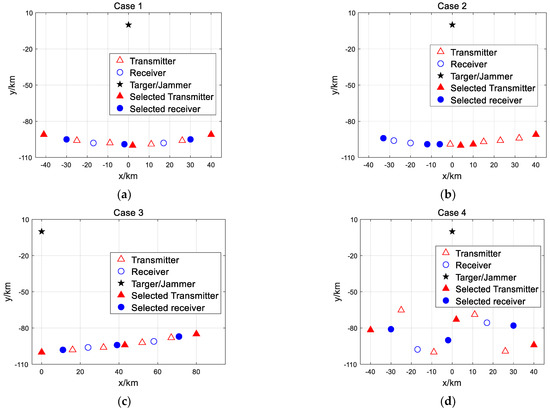
Figure 4.
The different layouts for the subset selection algorithm of predetermined size: (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4.

Table 2.
Simulation for subset selection strategy of predetermined size.
For all cases, transmitters 1 and 7 and receivers 1 and 5 are chosen for the subset, as they provide the best angular spread. Most of the remaining radar stations choose the middle position of aperture, as they may have the best channel conditions. In comparison with case 1 and case 3, this also proves that radar aperture has a great influence on jammer discrimination. When the target is located within the range of the maximum aperture for the multiple radar system, the effectiveness of false target discrimination is much greater than when the target is outside the aperture range. This is because the larger the radar aperture, the higher the angular resolution of the multistatic radar system with respect to the target, and thus the lower the rate of deception. The aggregation distribution mode for the transmitters and the receivers is not as good as in the scattered distribution, as is described in case 2. Compared with case 1, the x-axis coordinates of each radar station in case 4 are consistent with case 1, while the y-axis coordinates increase randomness. Additionally, the simulation results show that the dispersed station method in case 4 has better discrimination performance than that of case 1; case 4 provides further proof of the advantages of scattered distribution in all dimensions, which has better jammer discrimination capabilities than other cases. All of these indexes illustrate the tradeoffs in subset selection.
In comparison with the exhaustive search, the radar subset has the same selection results and discrimination probability under limited sources. The selected subset can yield the best performance among the choices of radar combinations. Thus, it can be proved that it is an effective method to reduce the computational complexity of radar selection under limited instrument conditions.
4.3. Simulation and Analysis of Related Factors
4.3.1. Analysis of SNR and Deceptive Distance
Discrimination probability is affected by many factors in signal processing. This section discusses some factors that affect the results of subset selection. Based on the system configuration in case 1 for the global shrinkage method, only the influence of SNR and deceptive distance on the subset selection strategy is analyzed.
Simulation results are shown in Table 3. The false target discrimination probability is sensitive to SNR and deception distance. As SNR and deceptive distance increase, the number of selected radars in the subset decreases. Sometimes, the discrimination probability will suddenly decrease, because the shrinkage in the number of sites in the selected subset has higher priority when the discrimination probability meets the preset requirements.

Table 3.
Radar subset under different deception distances and SNR.
Where the first row shows the range of deception distance, the first column represents the range of variation in SNR, and the content of the table shows the discrimination performance of the selected subset under the corresponding jamming distance and SNR/the number of selected radars in the subset.
As is shown in Table 3, when SNR or deception distance is very low, the preset discrimination requirements cannot be met even if all radar stations are deployed. In this case, all radar stations need to be utilized to achieve the highest discrimination performance, and the subset selection strategy proposed in this paper is no longer applicable.
4.3.2. Simulation of Single Factors
The influence of variations in global SNR or deceptive distance is mainly analyzed above. However, in actual battlefield environment, each transmission channel between transmitting station and receiving station has its own error characteristics, which are determined by multiple factors such as channel loss, target reflection characteristics, effective bandwidth and transmission power.
The transmission power of different transmitting stations, the sensitivity of different receiving stations and environmental noise in each channel are different, so the SNR of each transmission channel is no longer uniform. In this section, changing SNRs of different channels are taken as an example. The influence of a single variable on subset selection is discussed through simulation. Setting the same parameters as in Section 4.1, for most channels , and the method applied is the global shrinkage algorithm. Assuming that the transmission power of transmitters 3 and 6 is higher than that of the other transmitters, the SNR of the corresponding channels increases to 15 dB. The receiving sensitivity of receiver 5 is low, so the SNR of the corresponding channel decreases to 5 dB. Additionally, the SNR of other channels remains unchanged at 10 dB. After adjusting the SNR of some channels, the selection results for different cases are obtained by simulation.
The simulation results are shown in Figure 5. By comparing Figure 2 and Figure 3 with the global subset selection strategies, it can be seen that the basic rules of selection strategy are the same as in the analysis above, that is, the radar combination of maximum aperture is easier to be selected, and the dispersed distribution mode is better than the clustered distribution mode, etc. However, the simulation in this section shows that the SNR of each channel has a great influence on discrimination performance. Among the three station distribution modes, the transmission channel with a higher SNR is more likely to be selected (transmitters 3 and 6 are selected), and the transmission channel with a lower SNR is more likely to be abandoned (receiver 5 is not selected). Formula (5) proves that the change in bandwidth is the same as that of SNR. If the bandwidth of the transmitting station is larger, that channel is more likely to be selected, which will not be described here.
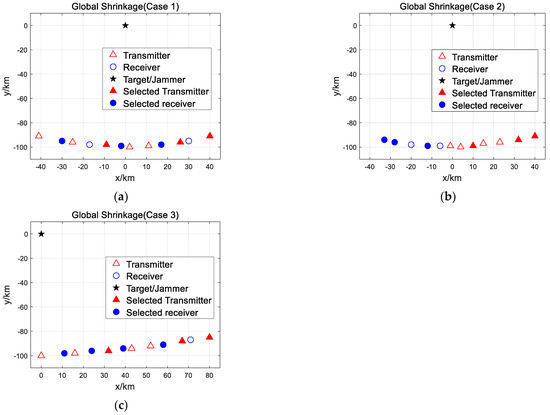
Figure 5.
The influence of SNR variation in each channel: (a) Case 1, (b) Case 2, (c) Case 3.
4.3.3. The Rules for Subset Selection
Therefore, in battlefield environment, the subset selection method is affected by multiple factors, such as SNR, bandwidth, radar station distribution mode, battlefield environment, etc. Every factor will affect the final subset selection method. However, the three subset selection methods proposed in this paper can achieve the required discrimination performance and reduce demand for communication resources.
Based on the above analysis, the rules summarized below can work as meaningful guidelines for subset selection:
- For radar layout, the radar aperture has a great influence on discrimination performance, because it provides a larger angular resolution for target detection. When self-defensive jammer is within the maximum aperture range of multistatic radar system, the simulation result is better than in the situation where the jammer is far away from the aperture center or even outside the maximum aperture range. Therefore, when selecting a subset, the radar combination that constitutes the maximum aperture needs to be selected.
- The choice of the initial radar has a great influence on the results during iterations. Since the selection method for the initial subset is different, the resulting radar selection is also different. The proposed algorithm requires a tradeoff between discrimination performance and time complexity. If missile interception is the targeted scenario, the rapid shrinkage subset selection strategy may be chosen to save more time for the determination of optimal deployment. If the scenarios are radar detection and early warning, the global shrinkage subset selection strategy is recommended to increase the interference countermeasure performance. No matter which method is used, the proposed methods all perform better than the exhaustive search subset method.
- The aggregation distribution mode for transmitters and receivers is not as good as the scattered distribution mode. No matter which dimension is dispersed, more spatial selection possibilities can be obtained, thus improving the discrimination performance of the selected subset. Therefore, it is better to mix the alternative transmitting and receiving radars together, and then scatter the radar stations to an area as large as possible, which is more conductive to selection of the subset.
- If all radars in the multistatic radar system still cannot meet the preset discrimination performance requirements when the SNR is low or the deceptive distance is small, that may result in the inapplicability of the proposed subset selection strategy. Instead, all radar stations will need to be used to identify the false targets.
5. Conclusions
The existing false target discrimination method based on joint parameter estimation increases discrimination probability by adding the number of radars, which may seriously waste system resources. In this paper, some effective strategies were proposed for selecting a subset with gradual shrinkage. On the premise of satisfying preset discrimination performance or balancing limited device resources, the transmitters or receivers with better spatial positions or communication conditions in multistatic radar system are selected gradually to form the radar subset using strategies such as the rapid shrinkage method, global shrinkage method, and predetermined size method, which can minimize the amount of equipment used in the multistatic radar system, reducing the burden of data processing and the communication links required in the fusion center. Compared with the exhaustive search method, the proposed subset selection strategy yields a significant reduction in terms of time complexity. The subset selection strategy was verified by simulation, which showed that a radar subset can maintain approximate discrimination performance comparable to that of the original multistatic radar system. Additionally, the influence of SNR and deceptive distance on the selection strategy was further analyzed. Finally, we provided a summary of some rules that can work as meaningful guidelines for subset selection.
Author Contributions
J.L. (Jieyi Liu) was involved in the computational framework, conceptualization, methodology, data analysis, results interpretation, and paper writing; Z.N. and J.L. (Jingyao Liu) simulated the experiments and processed the measured data; H.L. and S.Z. were involved in methodology; M.G. handled the general supervision of the study and provided solutions to any problems that arose. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant no. 62106185 and 61906146), the Natural Science Foundation of Shaanxi in China (Grant no. 2020JQ-313), and the Fundamental Research Funds for the Central Universities (Grant no. JB210211 and JB210210).
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments, which improved the paper’s quality.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The matrix is the FIM with respect to , which is specifically expressed as
and the conditional joint pdf of observations is
where T is the duration of all transmitted waveforms.
The chain derivation method can be obtained from the literature [29], and the expression of is
where is the all-zero matrix with the dimension of MN×2MN, is the all-zero matrix with the dimension of 2MN × MN, is the identity matrix with the dimension of 2MN × 2MN, and represents the diagonal matrix formed by each vector element on the diagonal.
The matrix P is the Jacobian
The matrix is the partial derivative of the delay with respect to the parameters x, y and
where , , and respectively represent the observation angle of the transmitter/receiver relative to the target, which is specifically expressed as
Through the above derivation, the CRLB matrix can be obtained as
In order to obtain the estimation accuracy of parameters x, y and , it is only necessary to derive the 3 × 3 submatrix in the upper left corner of the CRLB matrix.
The CRLB matrix is determined by matrices and , where is determined by the relative position of the target and radar, and is determined by the target noise ratio and signal bandwidth. represents the average of effective bandwidth, as . The normalized bandwidth is . Additionally, each element in matrix A can be specifically expressed as
References
- Han, X.; He, H.; Zhang, Q.; Yang, L.; He, Y. Suppression of Deception-False-Target Jamming for Active/Passive Netted Radar Based on Position Error. IEEE Sens. J. 2022, 22, 7902–7912. [Google Scholar] [CrossRef]
- Luo, M.; Hao, Z.; Zhu, Y. Intelligent ECCM Technology via Cognition and Agility for the Airborne Radar. J. Eng. 2019, 2019, 6656–6659. [Google Scholar]
- Tan, M.; Wang, C.; Xue, B.; Xu, J. A Novel Deceptive Jamming Approach Against Frequency Diverse Array Radar. IEEE Sens. J. 2021, 21, 8323–8332. [Google Scholar] [CrossRef]
- Ahmed, A.; Zhao, Y.; Bin, T. ECCM Schemes in Netted Radar System Based on Temporal Pulse Diversity. J. Syst. Eng. Electron. 2016, 27, 1001–1009. [Google Scholar]
- Zhang, J.; Zhu, D.; Zhang, G. New Anti-Velocity Deception Jamming Technique Using Pulses with Adaptive Initial Phases. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1290–1300. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Z.-M.; Duan, R. Novel Discrimination Algorithm for Deceptive Jamming in Polarimetric Radar. In Proceedings of the 2012 International Conference on Information Technology and Software Engineering; Springer: Berlin, Germany, 2013; pp. 359–365. [Google Scholar]
- Xiong, W.; Zhang, G.; Wen, F.; Yu, Z.; Yin, J. Trilinear Decomposition-Based Spatial-Polarisational Filter Method for Deception Jamming Suppression of Radar. IET Radar Sonar Navig. 2016, 10, 765–773. [Google Scholar] [CrossRef]
- Krishnamurthy, V.; Pattanayak, K.; Gogineni, S.; Kang, B.; Rangaswamy, M. Adversarial Radar Inference: Inverse Tracking, Identifying Cognition, and Designing Smart Interference. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2067–2081. [Google Scholar] [CrossRef]
- Nouri, M.; Mivehchy, M.; Aghdam, S.A. Adaptive Time-Frequency Kernel Local Fisher Discriminant Analysis to Distinguish Range Deception Jamming. In Proceedings of the 2015 6th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Denton, TX, USA, 13–15 July 2015. [Google Scholar]
- Bandiera, F.; Farina, A.; Orlando, D.; Ricci, G. Detection Algorithms to Discriminate Between Radar Targets and ECM Signals. IEEE Trans. Signal Process. 2010, 58, 5984–5993. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, S. Unsupervised Clustering Method to Discriminate Dense Deception Jamming for Surveillance Radar. IEEE Sens. Lett. 2021, 5, 1–4. [Google Scholar] [CrossRef]
- Griffiths, H. Multistatic, MIMO and Networked Radar: The Future of Radar Sensors? In Proceedings of the 7th European Radar Conference, Paris, France, 30 September–1 October 2010; pp. 81–84. [Google Scholar]
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO Radar: An Idea Whose Time Has Come. In Proceedings of the 2004 IEEE Radar Conference, Philadelphia, PA, USA, 29 April 2004; pp. 71–78. [Google Scholar]
- Haimovich, A.M.; Blum, R.S.; Cimini, L.J. MIMO Radar with Widely Separated Antennas. IEEE Signal Process. Mag. 2008, 25, 116–129. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.S.; Cimini, L.; Chizhik, D.; Valenzuela, R. Spatial Diversity in Radars—Models and Detection Performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Zaimbashi, A. Persymmetric Adaptive Target Detection with Distributed MIMO Radar. IEEE Sens. J. 2020, 20, 7878–7885. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, Y.; Zhang, L.; Zhang, Q.; Du, L. Target Detection for Multistatic Radar in the Presence of Deception Jamming. IEEE Sens. J. 2021, 21, 8130–8141. [Google Scholar] [CrossRef]
- Zaimbashi, A. A Unified Framework for Multistatic Passive Radar Target Detection Under Uncalibrated Receivers. IEEE Trans. Signal Process. 2021, 69, 695–708. [Google Scholar] [CrossRef]
- Orlando, D. A Novel Noise Jamming Detection Algorithm for Radar Applications. IEEE Signal Process. Lett. 2017, 24, 206–210. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, D.; Zhao, Y.; Liu, Z. Moving Target Localization for Multistatic Passive Radar using Delay, Doppler and Doppler Rate Measurements. J. Syst. Eng. Electron. 2020, 31, 939–949. [Google Scholar]
- Zhang, Y.; Ho, K.C. Multistatic Localization in the Absence of Transmitter Position. IEEE Trans. Signal Process. 2019, 67, 4745–4760. [Google Scholar] [CrossRef]
- Gao, Y.; Li, H.; Himed, B. Knowledge-Aided Range-Spread Target Detection for Distributed MIMO Radar in Nonhomogeneous Environments. IEEE Trans. Signal Process. 2017, 65, 617–627. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, L.; Liu, N.; Zhao, S. Correlation Characteristic Analysis in Diversity Multiple-Input Multiple-Output Radar. Electron. Lett. 2017, 53, 349–351. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, L.; Zhao, S.; Liu, N.; Zhang, J. Echo Correlation Analysis in Diversity Multiple-Input Multiple-Output Radars. IET Radar Sonar Navig. 2016, 10, 1112–1117. [Google Scholar] [CrossRef]
- Liu, J.; Gong, M.; Zhang, M.; Li, H.; Zhao, S. An Anti-jamming Method in Multistatic Radar System based on Convolutional Neural Network. IET Signal Process. 2021, 16, 220–231. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Zhou, Y.; Liu, N.; Liu, J. Discrimination of Active False Targets in Multistatic Radar Using Spatial Scattering Properties. IET Radar Sonar Navig. 2016, 10, 817–826. [Google Scholar] [CrossRef]
- Zhao, S.; Liu, N.; Zhang, L.; Zhou, Y.; Li, Q. Discrimination of Deception Targets in Multistatic Radar Based on Clustering Analysis. IEEE Sens. J. 2016, 16, 2500–2508. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Zhou, Y.; Liu, N. Signal Fusion-Based Algorithms to Discriminate Between Radar Targets and Deception Jamming in Distributed Multiple-Radar Architectures. IEEE Sens. J. 2015, 15, 6697–6706. [Google Scholar] [CrossRef]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target Localisation Techniques and Tools for Multiple-Input Multiple-Output Radar. IET Radar Sonar Navig. 2009, 3, 314–327. [Google Scholar] [CrossRef]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target Localization Accuracy Gain in MIMO Radar-Based Systems. IEEE Trans. Inf. Theory 2010, 56, 2783–2803. [Google Scholar] [CrossRef]
- Zhao, S.; Liu, Z. Deception Parameter Estimation and Discrimination in Distributed Multiple-Radar Architectures. IEEE Sens. J. 2017, 17, 6322–6330. [Google Scholar] [CrossRef]
- Godrich, H.; Petropulu, A.; Poor, H.V. A Combinatorial Optimization Framework for Subset Selection in Distributed Multiple-Radar Architectures. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Jamali-Rad, H.; Simonetto, A.; Leus, G. Sparsity-Aware Sensor Selection: Centralized and Distributed Algorithms. IEEE Signal Process. Lett. 2014, 21, 217–220. [Google Scholar] [CrossRef]
- Zheng, N.; Sun, Y.; Song, X.; Chen, S. Joint Resource Allocation Scheme for Target Tracking in Distributed MIMO Radar Systems. J. Syst. Eng. Electron. 2019, 30, 709–719. [Google Scholar]
- Zhang, H.; Liu, W.; Xie, J.; Zhang, Z.; Lu, W. Joint Subarray Selection and Power Allocation for Cognitive Target Tracking in Large-Scale MIMO Radar Networks. J. IEEE Syst. J. 2020, 14, 2569–2580. [Google Scholar] [CrossRef]
- Chen, H.; Ta, S.; Sun, B. Cooperative Game Approach to Power Allocation for Target Tracking in Distributed MIMO Radar Sensor Networks. IEEE Sens. J. 2015, 15, 5423–5432. [Google Scholar] [CrossRef]
- Chiriac, V.M.; He, Q.; Haimovich, A.M.; Blum, R.S. Ziv–Zakai Bound for Joint Parameter Estimation in MIMO Radar Systems. IEEE Trans. Signal Process. 2015, 63, 4956–4968. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).